Mathcad上机实验

Mathcad上机实习指导Mathcad2000上机实习指导Ch1 Mathcad2000简介§1-1 Math cad主菜单框和⼦菜单框点击Windows桌⾯上Mathcad2000图标，即呈现Mathcad⼯作区和Mathcad2000 RESOURCE CENTER(资源中⼼)，关闭中⼼，在上⽅菜单条中，点击“view”→“Toolbars”→“Math”，出现Math主菜单框，⾥⾯有9个⼦菜单框，它们依次为：主菜单计算器图形矩阵求值微积分布尔编程希腊字母符号计算其中，1）Calculator(计算器，内含基本初等函数，四则运算符，开⽅乘⽅，上、下标，绝对值，n!等)；2）Graphs(图形，有平⾯和空间直⾓坐标系，极坐标系)；3）Vector and Matrix (向量与矩阵，⽤于线性代数)；4）Evaluation (赋值，有软等号“=”⽤于数值运算，“→”⽤于符号运算，赋值号“:=”⽤于建⽴函数)；5）Calculus (微积分，含极限，导数，不定积分和定积分)；6）Boolean (布尔运算，含硬等号“=” ，不等号，⼤于等于号和⼩于等于号)；7）Programming (编程，含“if ”，“otherwise ”,“for ”，“while ”等命令)；8）Greek Symbol (希腊字母)；9）Symbolic Keyword (符号关键词,含”solve”,”series”,”factor”,”simplity” )。

红⼗字光标所在区域为Mathcad ⼯作区域，各种运算在此展开。

在上⽅菜单栏最后的“help ”中，可以搜索需要的帮助。

§1-2 建⽴函数函数是我们研究的主要对象，建⽴函数是Mathcad 操作的基本功。

建⽴函数要把等号改为赋值号“:=”，按“：” 键，出现赋值号“:=”，即可建⽴函数, 赋值号“:=”也可从4号⼦菜单框得到。

例如：y(x):=sin(x) ,z(x,y):=ln(x+y). 函数名必须写成y(x),定义函数必须⽤“:=”建⽴分段函数有点复杂，要⽤“if ””（如果）和“otherwise ”（否则）,它们在7号⼦菜单框中。

KMUSTTeaching Records昆明理工大学《上机实验指导书》课程名称：计算机图形学所在系（部）：国资院测绘系学年学期： 2012 — 2013 学年第 2 学期授课专业班级：地信101/土管101/测绘101 班级人数： 27/24/56 讲授教师：李向新教材名称：计算机图形学课程总学时： 64 ；总学分：理论学时: 38 ；实验（或实践）学时: 上机学时: 32 ；辅导（或答疑）学时: 系主任签章：第1部分计算机图形学上机实验大纲1.1 目的与任务计算机图形学上机是计算机图形学课程的组成部分之一，是掌握计算机图形学课程内容的一个重要实践环节。

通过上机实验，一方面可以让学生巩固课堂所学的计算机图形学基础理论，另一方面能让学生掌握基本的OpenGL的编程方法及技能，掌握使用OpenGL绘制基本图形，进行2D及3D维图形变换，生成曲线曲面及构建具有真实感的3D场景。

1.2 基本要求1. 了解OpenGL在计算机图形学中的应用基础知识。

2. 掌握基本的OpenGL的编程方法及技能。

3. 学会使用OpenGL绘制基本图形。

4. 学会使用OpenGL进行2D及3D维图形变换、生成曲线曲面及构建具有真实感的3D场景。

1.3 内容及学时安排上机1：glut工具包的安装及使用 2学时上机2：OpenGL编程练习 2学时上机3：OpenGL中基本几何图形的绘制 2学时上机4：二维图形变换编程练习 2学时上机5：交互式绘图技术编程练习 2学时上机6：三维图形变换编程练习 2学时上机7：OpenGL三维物体表示编程练习 2学时上机8：真实感图形的生成与处理上机 2学时合计 16学时1.4 教学参考书(1) 成思源等编著：计算机图形学，冶金工业出版社，2003.(2) (美)安杰尔（Edward Angel）著；李桂琼，张文祥译: OpenGL程序设计指南（第二版），北京:清华大学出版社，2005.(3) Edward Angel: Interactive Computer Graphics—A Top-Down Approach withOpenGL, Third Edition, Pearson Education, Inc., 2003.(4) F.S. Hill, JR：Computer Graphics Using OpenGL Second Edition, PearsonEducation, Inc., 2003.(5) James D. Foley et al.: Computer Graphics—Principles and Practice, SecondEdition in C, Pearson Education, Inc., 2002.(6) 朱家义：Visual C++程序设计，机械工业出版社，2003。

实验一 Mathcad软件入门及数学计算
一、 实验目的
1. 应用Mathcad软件建立工程；应用软件进行各种数学计算；
2. 掌握Mathcad在计算典型电路中的应用；
二、 实验设备及仪器
安装Mathcad 15 软件的计算机；
三、 实验要求
掌握应用Mathcad软件建立工程的方法，以及应用软件进行代数运算、复数运算、矢量和矩阵运算、解方程和方程组等。

四、 实验内容
1.练习输入如下表达式及方程
x 1 t2
3
t
3
2
−
a x
2
⋅b x⋅
+c
+0
2.
定义如下变量和函数
3.
定义值域变量
4.定义向量并进行向量的运算
5.定义矩阵并进行矩阵的运算
6.试选用支路电流法、回路电流法、网孔电流法的两种求解如下电路的支
路电流i。

图示电路中，R1=R2=10，R3=4，R4=R5=8，R6=2，US3=20，US6=40，求解支路电流i5.。

实验1：线性系统的时域分析及MathCAD 实现一. 实验目的:1. 掌握信号的时域（连续函数和序列）的表示方法, 掌握信号的时域分析与变换，包括信号的叠加，反转，平移，尺度变换。

2. 掌握信号的卷积包括连续函数和离散函数的卷积。

二．实验原理1． 信号的表示方法普通函数：连续函数f(t)=sinx , f(t)=e-at离散函数(序列) f(n)=n 2 f(n)=sin(nwt) 奇异函数：冲击函数 δ(t)、 阶跃函数 u(t)、 斜坡函数 p(t) 抽样函数、 单位冲击序列、单位阶跃序列。

2．信号的时域变换 叠加f(t)=f1(t)+f2(t) 反转f(-t)尺度变换 f(at)3．卷积连续函数的卷积：⎰∞∞--=τττd t f f t f )(2)(1)(离散函数的卷积：∑∞-∞=-=m m n f m f n f )(2)(1)(三．实验过程a ：函数的表示方法b：信号的时域变换5：已知函数求f(1-2t)的波形c：卷积1：连续函数的卷积：2：离散函数的卷积：练习：求下列函数的卷积（1）求f1*f1（2）求f1(n)*f2(n)3．f1(n)=3n u(n) f2(n)=2n u(n)实验2：连续时间信号的频域分析及MathCAD 实现一：实验目的 1：了解周期信号和非周期信号的表示方法 2：了解频域分析的基本原理，掌握傅里叶级数的计算方法 3：掌握傅里叶变换的基本方法 二：实验原理 如果f(t)是周期函数周期为T它的三角傅里叶级数的表达式为∑∞=++=1110)sin cos (2)(k k k t b t k a a t f ωω其中 ⎰⎰⎰+++===Tt t n Tt t n Tt t dtt n t f Tb dt t n t f Ta dtt f T a 000000)sin()(2)cos()(2)(2110ωω它的指数傅里叶级数 ∑∞-∞==k t jn ne c tf 1)(ω 其中 ⎰+-=Tt t t jn n dt e t f T c 001)(2ω周期函数的频谱图 22n n n b a A +=A n ～ω Cn ～ω的关系图非周期函数的傅里叶变换：⎰∞∞--=dt et f F tj 1)()(ωω 反变换为⎰∞∞-=dt e F t f t j 1)(21)(ωωπ三．实验过程1． 周期函数的表示方法矩形周期函数的表示方法2．求周期函数的傅里叶级数求每个频率的的波形图当n=1 ：为基波当n=2，3 ……：为二次谐波,三次谐波…. 直到n次谐波3．周期函数的频谱图绘出A n～ω关系图绘出Cn～ω的关系图4． 非周期函数的傅里叶变换绘制｜F(ω)｜～ω图5． 傅里叶变换的符号计算方法t 上点击菜单symbolics →transform → fourier计算结果同理将光标停在ω处 symbolics →transform →Inverse fourier 可求傅里叶反变换。

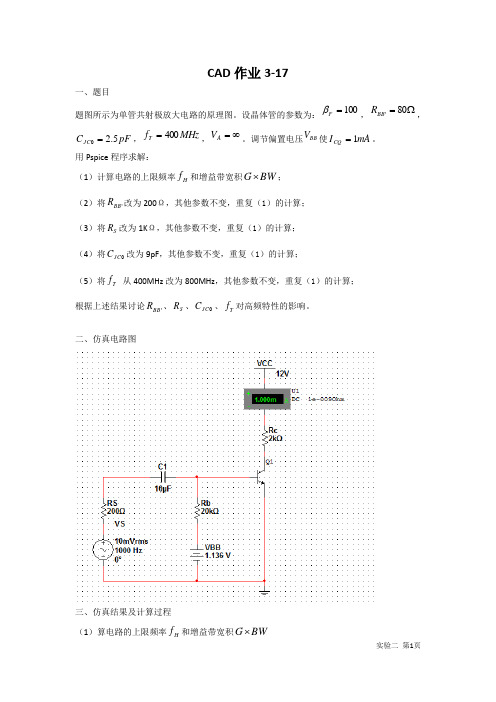
CAD 作业3-17一、题目题图所示为单管共射极放大电路的原理图。

设晶体管的参数为：100=F β，Ω=80'BB R ，pF C JC 5.20=，MHz f T 400=，∞=A V 。

调节偏置电压BB V 使mA I CQ 1=。

用Pspice 程序求解：（1）计算电路的上限频率H f 和增益带宽积BW G ⨯； （2）将'BB R 改为200Ω，其他参数不变，重复（1）的计算； （3）将S R 改为1K Ω，其他参数不变，重复（1）的计算； （4）将0JC C 改为9pF ，其他参数不变，重复（1）的计算；（5）将T f 从400MHz 改为800MHz ，其他参数不变，重复（1）的计算； 根据上述结果讨论'BB R 、S R 、0JC C 、T f 对高频特性的影响。

二、仿真电路图三、仿真结果及计算过程（1）算电路的上限频率f 和增益带宽积BW G ⨯)(21bc be e T C C r f +=π Ω=+=∴1.159)(21bc be T e C C f r π最高增益为20.568dB=10.676, H f =21.132MHz, L f =1.632HzR改为200Ω（2）将BB'最高增益为20.514dB=10.6096,f=14.46MHz,f=1.632HzR改为1KΩ（3）S最高增益为20.472dB=10.5584,f=14.46MHz,f=1.852HzC改为9pF（4）JC最高增益为20.39dB=10.459,f=3.346MHZ f=1.612Hz（5）T f 改为800MHz)(21bc be e T C C r f +=π Ω=+=∴6.79)(21bc be T e C C f r π最高增益为25.184dB=18.163, H f =22.053MHz L f =2.216Hz 得增益带宽积BW G ⨯＝400.56MHz四、原因分析根据上述结果讨论'BB R 、S R 、0JC C 、T f 对高频特性的影响。

mathematica实验报告Mathematica 实验报告一、实验目的本实验旨在深入了解和掌握 Mathematica 软件的基本功能和操作方法，通过实际的案例和问题解决，提升运用 Mathematica 进行数学计算、数据分析、图形绘制以及编程的能力。

二、实验环境操作系统：Windows 10Mathematica 版本：121三、实验内容与步骤（一）数学计算1、基本运算在 Mathematica 中，直接输入数学表达式进行计算，例如：计算 2＋ 3 4 的结果，输入｀2 ＋ 3 4` ，得到结果 14。

2、函数计算使用内置函数进行复杂的数学运算，如计算正弦函数｀SinPi ／ 6`的值，结果为 05。

（二）数据分析1、数据导入通过｀Import` 函数导入外部数据文件，如 CSV 格式的数据文件。

假设我们有一个名为｀datacsv` 的文件，包含两列数据｀x` 和｀y` ，使用｀data ＝ Import"datacsv"｀即可将数据导入。

2、数据处理对导入的数据进行处理，如计算平均值、方差等统计量。

可以使用｀Meandata` 计算平均值，｀Variancedata` 计算方差。

（三）图形绘制1、二维图形绘制简单的函数图形，如｀PlotSinx, ｛x, 0, 2 Pi}｀绘制正弦函数在｀0` 到｀2 Pi` 区间的图形。

2、三维图形绘制三维图形，如｀Plot3Dx^2 ＋ y^2, ｛x, －2, 2}，｛y, －2, 2}｀绘制一个抛物面。

（四）编程实践1、定义函数使用｀Function` 关键字定义自己的函数，例如定义一个计算阶乘的函数｀factorialn_ ：＝ Ifn ＝＝ 0, 1, n factorialn 1` 。

2、循环结构使用｀For` 循环和｀While` 循环实现重复操作，例如使用｀For`循环计算 1 到 10 的和，｀sum ＝ 0; Fori ＝ 1, i ＜＝ 10, i+＋， sum ＋＝ i; sum` 。

《Mathematica软件应用与开发》实验指导书实验1、Mathematica绘图(一)、实验类型：验证型(二)、实验类别：基础实验(三)、每组人数：1(四)、实验要求：选修(五)、实验学时：3个学时(六)、实验目的：（1）了解Mathematica基本操作；（2）掌握Mathematica基本运算：因式分解、多项式展开、部分分式展开以及解方程（组）或不等式（组）；（3）熟悉Mathematica中的列表处理方法；（4）掌握一般的二维显函数图形绘制、极坐标图形绘制方法；（5）掌握动态图形绘制方法。

(七)、预备知识：(八)、实验内容：1.1 计算:（1）344214625.4+++-πe ； （2）sin50°-tan2+cos15°/cot5+sec0.6.1.2 完成以下多项式与有理式操作练习：(1)展开多项式3)(z y x ++，42)3()(c b a b a +-++；Expand[](2)分解因式z y z x y xy y x x 22322322-++--；Factor[](3)将)1)(1(2123x x x x ++++,43232237741xx x x x x x ++--++--展开成部分分式之和. Apart[]1.3 定义矩阵⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=115141312111981654321M ，借助于Mathematica 帮助完成如下操作：（1）M T 、M 的行列式、M 的逆矩阵；（2）计算矩阵M 各行的和与各列的和，并将它们存入两个不同的数组；（3）将矩阵M 的第三行第二列元素替换成0；（4）提取矩阵M 的2、4列第2、3行元素构成新的矩阵.（提示：（2）、（3）、（4）使用F1，浏览用户手册或查资料）1.4 试在不同范围内绘制x y sinh 1=，|sin |2x y =，|1|323--=x y 的图形，然后将不同函数组合到一个坐标系内.1.5 对于参数方程和极坐标方程描绘的曲线，通过设置参数动画观察参数与曲线图形的关系.(1)参数方程：cos x a t =，)20(sin π≤≤=t t b y ，a ，b 取不同值；(2)极坐标方程θρcos 1+=和)cos(θρa =.(九)、实验操作习题1.1程序代码：E^(4.5)-1/Pi+Sqrt[2^2+4^6]/4+3^(1/4)Sin[50Degree]-Tan[2]+Cos[15Degree]/Cot[5]+Sec[0.6]习题1.2程序代码：Expand[(x+y+z)^3]Expand[(a+b)^2+(a-b+3c)^4]Factor[x^3-x^2*y-x*y^2+y^3+2x^2*z-2y^2*z]Apart[(1+2*x+x^3)/((1+x)(1+x^2))]Apart[(-1-4*x+7*x^2+7*x^3)/(-x-x^2+3*x^3+2*x^4)]习题1.3程序代码:M={{1,2,3,4},{5,6,1,8},{9,1,11,12},{13,14,15,1}}M1=Transpose[M]//MatrixFormM2=Det[M]//MatrixFormM3=Inverse[M]//MatrixFormM4=(M[[All,1]]+M[[All,2]]+M[[All,3]]+M[[All,4]])//MatrixF ormM5=(M[[1,All]]+M[[2,All]]+M[[3,All]]+M[[4,All]])//MatrixF ormReplacePart[M,{3,2}->0]{{Take[M[[2,2]]],Take[M[[2,4]]]},{Take[M[[3,2]]],Take[M[[ 3,4]]]}}习题1.4程序代码:p1=Plot[Sinh[x],{x,-3,3}];p2=Plot[Abs[Sin[x]],{x,-2*Pi,2*Pi}];p3=Plot[3-Abs[x^2-1],{x,-2,2}];Show[p1,p2,p3]习题1.5程序代码:Animate[ParametricPlot[{a Cos[t],b Sin[t]},{t,-2Pi,2Pi}],{a,-4,4,1},{b,-5,5}]Animate[PolarPlot[{1+Cos[θ],Cos[a*θ]},{θ,-2Pi,2Pi}],{a,-4,4,1}]实验二、导数、微分、Taylor公式(一)、实验类型：综合型(二)、实验类别：基础实验(三)、每组人数：1(四)、实验要求：选修(五)、实验学时：3个学时(六)、实验目的：熟悉并掌握Mathematica中导数、微分、函数的n阶泰勒公式、函数的n次近似多项式的程序命令。

例题:用一批长度为4ｍ的圆钢,下长度为698ｍｍ的零件4000个和长度为518ｍｍ的零件3600个。

如何下料才能使消耗的圆钢数量最少？解：(一) 建立机械优化设计数学模型(设计变量、目标函数、约束条件)设698ｍｍ的零件记为①，518ｍｍ的零件记为②。

对本例题,若只用4ｍ长的圆钢,则总共有6种下料方案:下5个零件①，0个零件②，利用率87% （) 方案一下0个零件①，7个零件②,利用率91％（）方案二下4个零件①，2个零件②,利用率96% （）方案三下3个零件①，3个零件②,利用率91％（) 方案四(1)下2个零件①，5个零件②,利用率99％（）方案五下1个零件①,6个零件②，利用率95% （）方案六从式（1)可知,用4ｍ长的圆钢总共有6种下料方法.现用、、、、、分别表示按这种方式下料所需的圆钢数量，则下料方案可用表1表示。

表1 下料方案Tab。

1 Cutting material plan原钢种类(m）数量零件①零件②方案4 5 0 方案一4 0 7 方案二4 4 2 方案三4 3 3 方案四4 25 方案五4 1 6 方案六表示为数学模型就是(2)5+4+3+2+≥4000 (3)7+2++5+6≥3600 （4）Ｘ1≥0,Ｘ2≥0，Ｘ3≥0,Ｘ4≥0,Ｘ5≥0,Ｘ6≥0 (5)式（2)称为目标函数，式(3)、式(4）和式(5）都称为约束条件。

例题用数学语言描述为:在约束条件（3)、(4）和(5)的限制下,求目标函数（2)达到最小值时的数值。

（二）选择合适的优化方法。

由于本题数学模型中的目标函数和所有约束函数都是设计变量的线性函数,因此该问题为典型的线性规划问题,优化方法选用单纯性法。

（三)上机计算，求得最优解。

计算程序使用DCXF。

EXE。

具体程序使用方法请大家参看《机械优化设计上机实验指导书》。

上机求得结果为：（四）結果分析分析与评判率由88 。

5％提高到97%，提高了法二利用Mathcad 2001软件求解（具体求解过程参看：Mathcad 讲义提纲和“Mathcad在工程技术中的应用讲座"）思考题：平板下料问题，如果已知平板材料长和宽分别为a和b,如果需要尺寸如图示矩形、椭圆、圆和平行四边形分别为N1、N2、N3和N4个，问如何进行下料使所需要的平板数量最少？。