《平方根》学案

课题：13.1平方根（第1课时）学案一、教学目标1.经历算术平方根概念的形成过程，了解算术平方根的概念.2.会求某些正数（完全平方数）的算术平方根并会用符号表示.二、教学重点和难点1.重点：算术平方根的概念.2.难点：算术平方根的概念.（本节课需要的各种图表要提前画好）三、教学过程请看下面的例子.学校要举行美术作品比赛，扎西很高兴.他想裁出一块面积为25平方分米的正方形画布，画上自己的得意之作参加比赛，这块正方形画布的边长应取多少分米？（师演示一张面积为25平方分米的纸）（一）谁来说这块正方形画布的边长应取多少分米？你是怎么算出来的？答：因为52＝25（板书：因为52＝25），所以这个正方形画布的边长应取5分米（板书：所以边长＝5分米）.（二）（完成下表）这个实例中的问题、填表中的问题实际上是一个问题，什么问题？它们都是已知正方形面积求边长的问题.通过解决这个问题，我们就有了算术平方根的概念.正数3的平方等于9，我们把正数3叫做9的算术平方根. 正数4的平方等于16，我们把正数4叫做16的算术平方根. 说说6和36这两个数？……（多让几位同学说，学生说得不正确的地方教师随即纠正） 说说1和1这两个数？同桌之间互相说一说5和25这两个数.（同桌互相说） 说了这么多，同学们大概已经知道了算术平方根的意思.那么什么是算术平方根呢？还是先在小组里讨论讨论，说说自己的看法. （三）什么是算术平方根呢？如果一个正数的平方等于a ，那么这个正数叫做a 的算术平方根请大家把算术平方根概念默读两遍.（生默读）（师让学生拿出提前准备好这样的10张卡片，一面写1－10，另一面写1－10的平方.生任意抽一张卡片，让其他学生回答平方或算术平方根。

（按以上过程抽完所有卡片）如果一个正数的平方等于a ，那么这个正数叫做a 的算术平方根.为了书写方便，我们把aa 的算.师：（指准上图）看到没有？这根钓鱼杆似的符号叫做根号，a 叫a 的算术平方根.根号被开方数a例 求下列各数的算术平方根： (1)4964； (2)0.0001. （要注意解题格式，解题格式要与课本第68页上的相同） （四）自我检测 1.填空：(1)因为_____2=64，所以64的算术平方根是______，＝______；(2)因为_____2=0.25，所以0.25的算术平方根是______，即______；(3)因为_____2=1649，所以1649的算术平方根是______，______.2.求下列各式的值：______；＝______；______；______；______；＝______.3.根据112＝121，122＝144，132＝169，142＝196，152＝225，162＝256，172＝289，182＝324，192＝361，填空并记住下列各式：_______，＝_______，＝_______，＝_______，_______，_______，_______，_______，_______. （学生记住没有，教师可以利用卡片进行检查，并要求学生课后记熟）4.辨析题：卓玛认为，因为(－4)2＝16，所以16的算术平方根是－4.你认为卓玛的看法对吗？为什么？（五）归纳小结，布置作业a a叫做被开方数.（作业：P习题1.要求学生按课本例题的格式做）75课题：13.1平方根（第2课时）学案一、教学目标1.通过由正方形面积求边长，加深对算术平方根概念的理解，感受无理数，初步了解无限不循环小数的特点.2.会用计算器求算术平方根.二、教学重点和难点1.重点：感受无理数.2.难点：感受无理数.（本节课使用计算器，最好每个同学都要有计算器）三、教学过程（一）基本训练，巩固旧知1.填空：如果一个正数的平方等于a，那么这个正数叫做a的_______________，记作_______.2.填空：(1)因为_____2＝36，所以36的算术平方根是_______＝_____；(2)因为(____)2＝964，所以964的算术平方根是_______，即_____；(3)因为_____2＝0.81，所以0.81的算术平方根是_______，即_____；(4)因为_____2＝0.572，所以0.572的算术平方根是_______，_____.3.师抽卡片生口答.数、小数、a2等形式）（二）（看下图）这个正方形的面积等于4，它的边长等于多少？谁会用算术平方根来说这个正方形边长和面积的关系？这个正方形的面积等于1，它的边长等于多少？ 用算术平方根来说这个正方形边长和面积的关系？ 师：（指准图）这个正方形的边长等于面积1的算术平方根，也就边长） 生：等于1.（师板书：＝1） （看下图）这个正方形的面积等于2，它的边长等于什么？（稍停）因为边边长＝.（上面三个图的位置如下所示）面积＝4面积＝1面积＝2边长＝4＝2边长＝2边长＝1＝1面积＝2面积＝1面积＝421在1和2之间的数有很多，它的平方等于多少？第一条线索是那个数在1和2之间，第二条线索是那个数的平方恰好等于2..我们在1和2之间找一个数，譬如找1.3，（板书：1.32＝）1.3的平方等于多少？（师生共同用计算器计算）1.69不到2，说明1.3比我们要找的那个数小.1.3小了，那我们找1.5，1.5的平方等于多少？（师生共同用计算器计算）2.25超过2，说明1.5比我们要找的那个数大.找1.3小了，找1.5又大了，下面怎么找呢？大家用计算器，算一算，找一找，哪个数的平方恰好等于2？1.41421356点点点，可见是一个小数，这个小数与我们以前学过的小数相比有点不同，有什么不同呢？第一，这个小数是无限小数（板书：无限）.还有别的无限不循环小数吗？无限不循环小数还有很多）.可以利用计算器来求.下面我们就用计算器来求一个数的算术平方根.（师出示例题）例用计算器求下列各式的值：精确到0.001）；（按键时，教师要领着学生做；解题格式要与课本上的相同）（四）自我检测4.填空：(1)面积为9＝；(2)面积为7≈（利用计算器求值，精确到0.001）.5.用计算器求值：＝；＝；≈（精确到0.01）.6.选做题：(1)用计算器计算，并将计算结果填入下表：器，直接写出下列各式的值：＝，＝，＝，＝ .练习1.）（作业：P72课题：13.1平方根（第3课时）一、教学目标1.经历平方根概念的形成过程，了解平方根的概念，会求某些正数（完全平方数）的平方根.2.经历有关平方根结论的归纳过程，知道正数有两个平方根，它们互为相反数，0的平方根是0，负数没有平方根.二、教学重点和难点1.重点：平方根的概念.2.难点：归纳有关平方根的结论.三、教学过程（一）基本训练，巩固旧知1.填空：如果一个的平方等于a，那么这个叫做a的算术平方根，a的算术平方根记作 .2.填空：(1)面积为16＝；(2)面积为15≈（利用计算器求值，精确到0.01）.3.填空：(1)因为1.72＝2.89，所以2.89的算术平方根等于，即＝；(2)因为1.732＝2.9929，所以3的算术平方根约等于，≈ .（三）如果一个正数的平方等于9，这个正数是多少？如果一个数的平方等于9，这个数是多少？和算术平方根的概念类似，（指准32＝9）我们把3叫做9的平方根，（指准(-3)2＝9）把－3也叫做9的平方根，也就是3和－3是9的平方根（板书：3和－3是9的平方根）.我们再来看几个例子.（师出示下表）平方根：如果一个数的平方等于a，那么这个数叫做a的平方根. 平方根概念与算术平方根概念只有一点点区别，哪一点点区别？（出示例题）例求下面各数的平方根：(1)100； (2)0.25； (3)0； (4)－4；(1)因为（±10）2＝100），所以100的平方根是＋10和－100的平方是0，正数的平方是正数，负数的平方还是正数，所以任何数的平方都不会等于－4.这说明什么？（例题）从这个例题你能得出什么结论？（稍停片刻）正数有几个平方根？0有几个平方根？负数有几个平方根？请学生小组讨论正数有_________________平方根（板书：正数有两个平方根）.平方根有什么关系？0的平方根_________________个，平方根是_________________.负数_________________平方根大家把平方根的这三条结论读两遍.（四）自我检测1.填空：(1)因为（）2＝49，所以49的平方根是；(2)因为（）2＝0，所以0的平方根是；(3)因为（）2＝1.96，所以1.96的平方根是；2.填表后填空：(1)121的平方根是，121的算术平方根是；(2)0.36的平方根是，0.36的算术平方根是；(3) 的平方根是8和－8，的算术平方根是8；(4) 的平方根是35和35，的算术平方根是35.6.判断题：对的画“√”，错的画“×”.(1)0的平方根是0 （）(2)－25的平方根是－5；（）(3)－5的平方是25；（）(4)5是25的一个平方根；（）(5)25的平方根是5；（）(6)25的算术平方根是5；（）(7)52的平方根是±5；（）(8)(-5)2的算术平方根是－5. （）。

七年级数学下《平方根》教案一、教学目标1.知识与技能：学生能够理解平方根的概念，掌握平方根的基本性质，能够进行简单的平方根运算。

2.过程与方法：通过观察、思考和探究，培养学生的数学思维能力和解决问题的能力。

3.情感态度与价值观：激发学生对数学的好奇心和探究欲，培养他们认真思考、勇于探索的精神。

二、教学内容与过程1.导入：通过回顾正方形的面积，引出平方根的概念。

教师可提出一些问题，如：“如果一个正方形的面积为8平方米，那么它的边长是多少？”引导学生思考并引出平方根的概念。

2.知识讲解：详细讲解平方根的定义、性质和运算方法。

通过实例进行解释，帮助学生深入理解平方根的概念。

同时，强调平方根与算术平方根的区别与联系。

3.探究活动：设计探究活动，让学生自己动手操作，探索平方根的基本性质和运算方法。

探究活动可以包括求一些数的平方根、比较不同数的平方根的大小等。

4.应用实践：设计实际问题，让学生运用所学知识解决，如求一些实际问题中的平方根等。

同时，可以引导学生探索平方根在实际生活中的应用。

5.总结与提升：总结平方根的主要知识点，强调重点和难点。

通过综合性题目，提升学生运用知识解决实际问题的能力。

同时，可以引导学生思考平方根与其他数学知识的联系，为后续学习打下基础。

三、教学方法与手段1.教学方法：采用启发式、探究式和合作学习的方法，引导学生主动探索和思考。

同时，注重实例教学，通过实例帮助学生理解抽象的数学概念。

2.教学手段：利用实物模型、PPT演示、数学软件等辅助教学工具，帮助学生更好地理解平方根的概念和性质。

同时，鼓励学生动手操作，培养他们的实践能力。

四、教学评价与反馈1.课堂互动：通过课堂提问、小组讨论等方式，及时了解学生的学习情况，调整教学策略。

同时，鼓励学生积极参与课堂活动，发表自己的观点和见解。

2.作业评价：布置相关练习题，要求学生按时完成，并进行批改和反馈。

同时，关注学生的作业完成情况，对有困难的学生进行个别辅导。

2024--2025学年度七年级数学上册学案4.2平方根(2)【学习目标】1.了解平方根、开平方的概念，理解平方根的性质；2.了解平方根与算术平方根的区别与联系，会求一个数的平方根，进一步明确平方与开平方是互逆的运算关系.【自主学习】1.平方根的定义： 如果一个数x 的平方等于a ，即____________，那么这个数____就叫做 的平方根，记为“__________”，读作“________________”.2.平方根的性质: 一个正数有_____个平方根.0只有_______平方根，它是_______；负数_______平方根. 注意：平方根等于本身的数是（1）a a =2==⎩⎨⎧-a a 00<≥a a （2）()a a =2（0≥a ） 3.开平方的定义：求一个数a 的________的运算，叫做开平方，其中a 叫做________.4.平方根与算术平方根的联系与区别联系：(1)具有包含关系： 包含 .(2)存在条件相同：平方根和算术平方根都是只有非负数才有.(3)0的平方根是 ，算术平方根是 .区别：(1)个数不同：一个正数有 平方根，而一个正数的算术平方根 个.(2)表示法不同：正数a 的平方根表示为 ，算术平方根表示为 .(3)取值范围不同：正数平方根一正一负，互为相反数；正数算术平方根只有一个.【典型例题】知识点一 求一个数的平方根1．实数9的平方根为（ ）A ．3 B ．3- C ．3± D ．3±2.下列各式中，正确的是（ ）A.√25=±5B. (−√4)2=16C. √(−2)2=−2D.±√25=±5知识点二 平方根的性质3．下列结论正确的是（ ）A ．()22-的平方根是2-B ．()2π4-的算术平方根是4π-C ．一个数的算术平方根一定是正数D ．算术平方根等于本身的数是1 4.如果某数的平方根是和，那么这个数是( )A.5B.-5C.169D.-169【巩固训练】1．下列式子错误的是（ ）A ．0.090.3±±B 0.250.5=±C ．12111-=-D 911645 2.下列等式成立的是（ ）A ．b a b a +=+2)(B ．b a b a -=-2)( C ．a a =2 D ．24a a = 3.若，则的值是( ) A. 2 B. C. 5 D. 4.5．已知192-的整数部分是m ，小数部分是n ，则m = ，n = ．6.求下列各数的平方根(1)1.21；(2)0.01；(3)279；(4)(－13)2；(5)－(－4)37.求满足下列未知数的 (1)(2) (3)8.已知的平方根是±3，的算术平方根为2，求与的值；9．已知a ，b 满足等式()21303a b ++-=，20212020a b=4.2平方根（2）【自主学习】1. 2x =a x a ±a正负根号a2. 两 1 0 没有 03. 平方根 被开方数4. 平方根 算术平方根 0 0如果一个数x 的平方等于a ，那么这个数；如果一个正数x 的平方等于a ，那么这个数两 1 ±a a【典型例题】1. B2.D3.C【巩固训练】1. （1）√ （2）√（3）× （4）√2. 6±3. 3； 414. C5.（1）95x ±= （2）2-4x 或=（3）2325-或 6.813、35、0.1、1.1±±±±±、7.a=-1，x=9 8.32±；6±9.x=2，y=±5，原式=33。

平 方 根 （一）学习目标：1.了解算术平方根的概念，会用根号表示正数的算术平方根，并了解算术平方根的非负性。

2.了解开方与乘方互为逆运算，会用平方运算求某些非负数的算术平方根。

教学重点：算术平方根的概念。

教学难点：根据算术平方根的概念正确求出非负数的算术平方根。

学习过程一、自主探究（享受探究的快乐）1、填空：①因为32=9，所以（ ）是（ ）的算术平方根；因为52 =25；所以（ ）是（ ）的算术平方根。

②9的算术平方根是（ ）；25的算术平方根是（ ）。

③因为2x =a （x 为正数）， 所以（ ）是（ ）的算术平方根； 正数a 的算术平方根记为（ ），读作（ ），a 叫做（ ）。

④0的算术平方根是（ ），记为（ ）。

2．（口答）说出一个正数让你的同伴回答它的算术平方根吧。

3.请试着用新的运算符号表达一个正数的算术平方根。

4、我思考，我收获：-4的算术平方根是多少? a 中的a 的取值有什么要求?二、自我尝试（相信自己，你一定能行）1、求下列各数的算术平方根。

①100 ②6449 ③0.01 ④322、求下列各式的值 ①25 ②81.0 ③1 ④0 ⑤2516 ⑥2)3(-⑦416三、补偿提高(更上层楼)1．49的算术平方根是( ),7的算术平方根是（ ）2．16的算术平方根是（ ），16的算术平方根是（ ） 16的值是（ ）3．若x =6成立，则x =（ ）4．3x -4为25的算术平方根，求x 的值。

四、拓展提高（开放思路）1．当x 取何值时，1-x 有意义？2．若a +1-b =0成立，试求a 与b 的值。

五、小结，归纳梳理，整合内化本节课你学习了哪些知识？在探索知识的过程中，你有哪些收获？你还有哪些困惑？和你的同伴交流一下吧.六、学习收获：七、作业布置：同步训练第53页自我尝试部分的第5题和第6题。

第 1 讲平方根知识要点1、平方根（ 1）平方根的意义：如果一个数的平方等于 a ，这个数就叫做 a 的平方根。

a 的平方根记作:2a或a 。

（2）平方根的性质①一个正数有两个平方根，它们互为相反数。

比如： 4 的平方根记作“±4”，读作“正负根号4”。

81 的平方根记作“±81”，读作“正负根号81”②0 有一个平方根，它是 0 本身③负数没有平方根。

由此，我们可以知道，被开方数一定要为非负数。

（即 a0 ）（3）开平方运算求一个数的平方根的运算，叫作开平方。

注意：①一个正数开平方，它的结果有两个（即 a ）② 0 开平方就是 0③负数不能开平方（4）平方和开平方互为逆运算；（5）重要性质：a2a a 2a(a 0)2、算术平方根（ 1）算术平方根的意义：非负数 a 的正的平方根。

一个非负数 a 的平方根用符号表示为：“ a ”，读作：“根号a”，其中 a 叫做被开方数（ 2）算术平方根的性质①正数 a 的算术平方根是一个正数；②0 的算术平方根是 0；③负数没有算术平方根例 1求下列各数的平方根：（格式）（ 1） 25；（2）0.81（3）15；（4）（-2）2（5）16（6）0(7) 21(8)9 814(9 )1022(10)（2 4）例 2填空（1）一个数的平方等于它本身，这个数是。

一个数的平方根等于它本身，这个数是。

（ 2）若 3a+1 没有平方根，那么 a 一定。

（ 3）若 4a+1 的平方根是± 5，则 a=。

（ 4）一个数 x 的平方根等于 m+1和 m-3，则 m=。

x=。

例 3x为何值时，下列代数式有意义。

（ 1） 3 2x（ 2）x22 x（3）13x1（ 4） x23（ 5）x1（6）( x 1)2x1练习1、若 |a-9|+（b-4 ）2=0，则a的平方根是。

b2、求下列各式中的 x:(1) x2=16(2) x2=25 49(3)x2=15(4)4x2 =813、已知 2a-1 的算术平方根是3， 3a+b-1 的平方根是± 4，求 a+2b 的平方根。

11.1 平方根与立方根——平方根学案一、情境引入如果要剪出一块面积为25cm 2的正方形纸片, 其边长为多少呢？这个问题实质上就是要找一个数,这个数的平方等于252=25边长，所以，其边长为5cm 。

又：面积为16 cm 2则其边长为 ；面积为9cm 2则其边长为 ； 那面积为a cm 2则其边长为 ；这时，可设其边长为 x ， 得到 x 2 = a .二、算一算探究交流：一对互为相反数的的数的平方有什么关系？探究交流：平方得25的数有几个？分别是什么？这两个数有什么关系?它们的和等于多少呢?三、新课（预习课本P2-4）1、平方根的概念：如果一个数的平方等于 a , 那么这个数 叫做 a 的平方根. 就是说, 当 x 2 =a (a≥0) 时, 称 x 是 a 的平方根.2、在上面的问题中,我们知道因为=25,所以5是25的一个平方根.探究交流:25的平方根只有一个吗?还有没有别的数的平方也等于25?探究交流:如何求一个数的平方根?求一个数的平方根的关键是什么呢?例1、 求100的平方根解：因为102=100, 且(-10)2=100所以10和-10都是100的平方根.所以100的平方根为 ±10.3、探究平方根的性质：（1）16的平方根是什么？ （2）0的平方根是什么？（3） 的平方根是什么？（4）-4有没有平方根？为什么？性质：（1） 一个正数有( )个平方根,它们互为( ) 数,它们的和等于( )（2） 0的平方根是( ),是它( )（3） ( )数没有平方根.=25.0=22=-2)2(=⎪⎭⎫⎝⎛231=⎪⎭⎫ ⎝⎛-231=-2)5.0(25914、算术平方根：温馨提示:0的算术平方根还是0求一个非负数的平方根的运算，叫做开平方。

将一个正数开平方，关键是找出它的算术平方根。

开平方就是找正数的平方根。

四、课堂练习：1. 判断题下列叙述正确的打“√”，错误的打“×”：（1）25的平方根是 ±5; ⑵ ±3是9的平方根 ; ⑶ 4的平方根是2;⑷ 9是81的一个平方根; (5) -9的平方根是 -3; (6) 0的平方根是 0;3、直接说出下列各数的平方根（1）25； （2） （3）0；（4）4、填空（1）.如果一个正数有一个平方根是 5 ，那么另一个平方根是( )则这个数的值是 ( )（2）.一个数的平方根等于它本身，这个数是( )（3）.若3a 没有平方根，那么a 一定是 数.（正、负）五、能力提升1、81的算术平方根是( )；的算术平方根是( )2、 一个正数的两个平方根为m+1和m －3，则m= 。

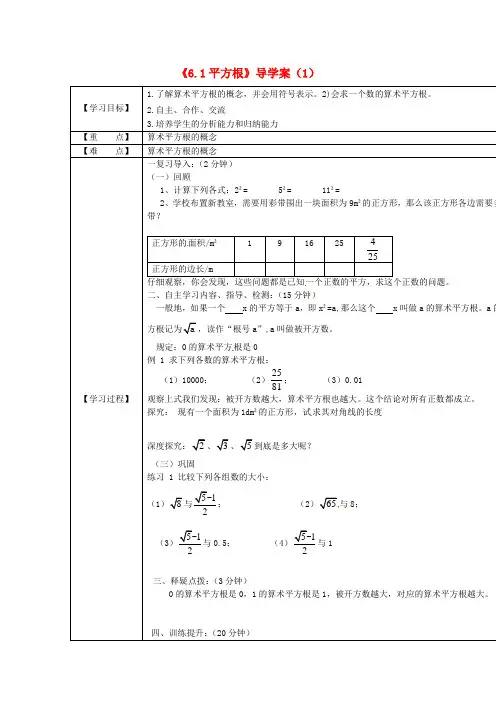
《6.1平方根》导学案（1）【学习目标】1.了解算术平方根的概念，并会用符号表示。

2)会求一个数的算术平方根。

2.自主、合作、交流3.培养学生的分析能力和归纳能力【重点】算术平方根的概念【难点】算术平方根的概念一复习导入：（2分钟）正方形的面积/m² 1 9 16 25 425正方形的边长/m仔细观察，你会发现，这些问题都是已知一个正数的平方，求这个正数的问题。

一般地，如果一个 x那么这个 x方根记为a，读作“根号规定：0的算术平方根是0）25 81；探究：现有一个面积为1dm²的正方形，试求其对角线的长度深度探究：2、3、5到底是多大呢？（1）8与512-；（2）65与8；）51-与）51-与0的算术平方根是0，1的算术平方根是1，被开方数越大，对应的算术平方根越大。

A ．9B ．9C ．-9D ．3已知正方形的边长为a ；②S ；③平方根；④a 是 A ．①③ B ．②③ C ．①④ D ．②④如果y 4. 计算22的结果是（ ）-2 B ．2 C ．25．2623二、填空题（细心填一填）一个数的算术平方根是，这个数是________2. 算术平方根等于它本身的数有______________。

3. 81的算术平方根是4. 144=_______；4925=________；0.01________；0025.0=_______。

196；28_________；169256=___________1. 求下列各数的算术平方根：。

13.1 平方根（第一课时）【学习目标】1.了解算术平方根的概念，会用根号表示正数的算术平方根，并了解算术平方根的非负性，会用平方运算求某些非负数的算术平方根。

2、会用计算器求一个数的算术平方根.3、能用夹值法求一个数的算术平方根的近似值.【预习导学】1.算数平方根的概念（1）()()2416=∴的算数平方根是， ()=即. 答案：16 4 16 4 （2）()()()20=∴的算数平方根是，()=即答案：0 0 0 0 0（3）①一般地，如果一个正数x 的平方等于a ，即2x =a ，那么这个 叫做a 的 ．a 的算术平方根，记为 ，读作“ ”，a 叫做被开方数．②规定：0的算术平方根是 .答案：①正数x 算术平方根 a 根号a ②02. 2及其大小（1）用两个面积为1（图1）的小正方形拼成一个面积为2（图2）的大正方形，则大正方形的边长= .答案：2（2）2的小数部分无限，且小数部分不循环，是 小数.答案：无限不循环3、用计算器求算术平方根根据显示屏显示的结果取近似值. 答案：【合作研讨】探究点一、 求某些非负数的算术平方根例1.求下列各数的算术平方根(1) (－3.9)2；(2) 0. 81；(3) 241. 思路点拨：a 的算术平方根用a 表示，它表示一种运算，如4表示求4的算术平方根.解析：(1)∵(－3.9)2＝3.92=15.21.∴15.21 的算术平方根是3.9， 即2(-3.9)＝3.9； (2) ∵0. 92＝0. 81，∴0. 81的算术平方根是0. 9， 即＝ 0. 9（3） ∵241=94，23924⎛⎫= ⎪⎝⎭ ∴94的算术平方根为32即13242= 跟踪训练1、（湖州中考）4的算术平方根是（ ）A ．2B ．2-C ．2±D ．16【答案】A2、答案：D3、探究点二、夹值法求算术平方根的近似值例2、用夹值法求10的近似值（精确到0.1）思路点拨：先估计其整数的范围，再估计十分位的范围，最后估计百分位的范围，按照四舍五入的方法确定结果.解析：先估计10在3～4之间，再利用平方关系估计其3.1～3.2之间，再估计其大于3.15，进而取近似值.跟踪训练4、估计30的值（）（A）在3到4之间（B）在4到5之间（C）在5到6之间（D）在6到7之间答案：C5、估算19+2的值是在( )（A）5和6之间（B）6和7之间（C）7和8之间（D）8和9之间答案：B【当堂检测】一、选择题1、9的算术平方根是（）.A.3B.C.D.81答案：A2．下列各式正确的是A．=B．=2 C．=0.05 D．=－7答案：A3、（邵阳中考）3最接近的整数是（） A．0 B．2 C．4 D．5 【答案】B二、填空题4、2的算术平方根是 .答案：2三、解答题5、求下列各式的值（1）－（(2)(3)答案：（1）－0.1 (2)5 （3）10－3四、选做题6、小刚同学的房间地板面积为16米2，恰好由64块正方形的地板砖铺成，求每块地板砖的边长是多少？ 解析：设每块地板砖的边长为x 米， 由题意得64•x 2 = 16，即x 2 ==，所以x =答：边长为0.5米．【课后作业】1、3－2的算术平方根是 A ． B ． C ．3 D ．6答案：B 点拨：2113==93- 2、（2009黔东南中考）下列运算正确的是（ ）A 、39±=B 、33-=-C 、93=D 、932=-【答案】C3、若的算术平方根是3，则a =________解析：因为的算术平方根是3，所以= 9，则a = 81．答案：815、求下列各式的值（1）（2）124－（－0.5）－2(3)解析：（1）原式=110.30.535⨯+⨯=0.2（2）原式=944-=2.5（3）原式=131 6=5 3515 -+-6、若 =2,求2x+5的算术平方根. 解析：∵ =2∴x=2,∴2x+5的算数平方根37、。

《6.1平方根》6.1平方根（1）【学习目标】1. 了解数的算术平方根的定义，会用根号表示一个数的算术平方根， 并理解算术平方根的双重非负性2. 能利用算术平方根的定义求一个非负数的算术平方根【学习重点】了解算术平方根的概念、性质、会用根号表示一个正数的算术平方根 【学习难点】理解算术平方根的双重非负性 ［探究研讨］【活动1】学校要举行金秋美术作品比赛，小欧很高兴，他想裁出一块面积为 25 dm 2的正自学教材，回答问题：1. 一般地，如果一个—数x 的平方等于a ，即x 2=a,那么这个 _________________ 叫做a 的 ___________ .a的算术平方根记为 梟，读作“根号a ”，a 叫做被开方数.规定： __________________ 的算术平方根是0.记作■, 0 = ______2. 由以上定义可知如果 x 2=a ,那么x 就叫a 的算术平方根吗？判断下列语句是否正确？①5是25的算术平方根（ ）②-6是36的算术平方根（ ） ③0.01是0.1的算术平方根（）④-5是-25的算术平方根（）3.3的算术平方根可表示为 ___________ ,4的算术平方根可表示为 __________ ,你还能表示出那些数的算术平方根？写在下面，和同座交流一下 ________________________________________________4.试一试：你能根据等式：122=144说出144的算术平方根是多少吗？并用等式表示出来.【活动2】例：求下列各数的算术平方根:［跟踪训练］1、1.非负数a 的算术平方根表示为 —,225的算术平方根是 _______________ ,0.64的算术平方根 ____ , 0的算术平方根是 ______12.丄的算术平方根是（ ）4(1) 100 ； (2);(3) 0.0001 64;住）0 ；1 1A. B . C16 83.若x是49的算术平方根，则x=()A. 7B. —7C. 49D. 12—494.小明房间的面积为10.8米2,房间地面恰好由120块相同的正方形地砖铺成, 每块地砖的边长是［变式训练］想一想：下列式子表示什么意思？你能求出它们的值吗?⑶、...（一3）2⑷025［跟踪训练］1. 81一2；2. _______________________ 朋的算术平方根是3. 若.X 4 7，则x的算术平方根是（）A. 49B. 53C.7 D【活动3】思考：—4有算术算术平方根吗？为什么?总结：1.正数有_____________________ 的算术平方根0 的算术平方根是____________________负数________________________2. 对于a : a 0 ■_ > 具有双重非负性.a_o［跟踪训练］1•下列哪些数有算术平方根?0.03 ,丄16, n, 0 , (-3 ) 2, (-1 )2. 下列各式中无意义的是（）A. ■. 7 B . .. 7 C. . 7 D3. 下列运算正确的是( )A. 33B . 3 3C. 79 ^3 D. 79 34.若下列各式有意义，在后面的横线上写出x的取值范围：⑴X⑵5.若a 2 vb3 0，贝U a= ,b= , ____ a 2b ________［提升能力］1. 一个自然数的算术平方根为a，那么与这个自然数相邻的下一个自然数的算术平方根是2. 一个正方形的面积扩大为原来的4倍，它的边长变为原来的________ 倍，面积扩大为原来的9倍，它的边长变为原来的________ 倍，面积扩大为原来的n倍，它的边长变为原来的 _______ 倍.3. 如图：-------- 1 I ------------- 1------------0 a b那么，、a b有意义吗？4. 要使代数式止2有意义，则X的取值范围是（）3A. x 2B. x 2C. x 2D. x 25. 若x 1 y 32J x y z 0，求x,y,z的值。

13.1 平方根（1）【学习目标】1.了解算术平方根的概念，会用根号表示正数的算术平方根，并了解算术平方根的非负性。

2.了解开方与乘方互为逆运算，会用平方运算求某些非负数的算术平方根。

【学习过程】预习课本68—72，解决下列问题： 一、掌握算术平方根概念问题：学校要举行金秋美术作品比赛，小欧很高兴，他想裁出一块面积为252dm 的正方形画布，画上自己的得意之作参加比赛，这块正方形画布的边长应取多少d m ？ 如果这块画布的面积是212dm ？（这个问题实际上是已知一个正数的平方，求这个正数的问题）1.填表2.什么是一个正数a3.填表4．一个非负数a 的算术平方根记为： ，读作： a 叫 5．求下列各式的值（1）64 (2) 81 (3) 0 (4) 254 (5) 25.0 （6）1 （7）25解：6．在式子a 中，， a 0二、感受2的大小探究： 怎样用两个面积为1的小正方形拼成一个面积为2的大正方形？方法1：课本中的方法 方法2：问题：（1）这个大正方形的边长应该是多少呢？（2）2到底是个多大的数？你能求出它的值吗？（3）如何估计2大小呢？※：2是一个 的小数 三、巩固练习1.非负数a 的算术平方根表示为___ ，225的算术平方根是____ ，0的算术平方根是____， 1的算术平方根是____。

2.____,_____=== 。

3.____, 0.64-的算平方根__ __，（-3）2的算术平方根是 。

4.若x 是49的算术平方根，则x = ，若5=x ，则x= 。

5.若7=，则x 的算术平方根是（ ）A. 49 B. .6.若()2130x y -+++=，求,,x y z 的值。

13.1平方根（2）【学习目标】1．掌握平方根的概念，明确平方根和算术平方根之间的联系和区别.2．能用符号正确地表示一个数的平方根，理解开平方运算和乘方运算之间的互逆关系. 【学习过程】 一、概念的理解 1．情境问题⑴ 如果一个数的平方等于9，这个数= ； ⑵ 若2542=x ，则x = ；⑶ 若x 2=0, 则x = ； ⑷ 有没有一个数的平方等于-9呢？。

《2.3平方根（1）》学案学习目标：了解数的平方根的概念．会用根号表示一个数的平方根。

了解开平方与乘方是互逆的运算，会求非负数的平方根。

重点难点：一个数的平方根的概念理解及表示方法学习过程：一.导入 :根据课本提供的情境提出问题。

由勾股定理可知AB²=12²+5²=169， AB=13A′B′=1²+2²=5，那么A′B′=？如果一个数的平方等于9，这个数是几？一个数的平方等于2呢？想知道这个数的结果吗?我们来学习——平方根二..新授：例如：2²=4，（-2）²=4，±2叫做4的平方根。

10²=100，（-10）²=100，±10叫做100的平方根13²=169，（--13）²=169，±13叫做169的平方根。

一般地，如果一个数的平方等于a，那么这个数叫做a的平方根，也称为二次方根。

也就是说，如果x²=a，那么x叫做a的平方根。

交流：1．9的平方根是什么？25的平方根是什么？2、0的平方根是什么？0的平方根有几个？3、-4、-8、-36有平方根吗？为什么？结论：一个正数有两个平方根，它们互为相反数；0只有一个平方根，它是0本身；负数没有平方根。

求一个数a的平方根的运算,叫做开平方.表示方法：一个正数的平方根有2个，它们互为相反数。

一个正数a的正的平方根，记作“ ” 一个正数a的负的平方根记作“- ”，这两个平方根合起来记作“± ”，读作“正负根号a”。

例如，2的平方根记作“± ”，读作“正负根号2”。

81的平方根记作“± ”，读作“正负根号81”例1 求下列各数的平方根：（1）25；（2）0.81;（3）15；（4）（-2）²(5) 625 （6）0:(7) 2 (8) 10²²(9) 0.0081 (10) 6三、归纳总结：由学生交流四、巩固练习：1、一个数的平方等于它本身，这个数是。

2.2平方根学习目标：(一)教学知识点1.了解平方根的概念、开平方的概念.2.明确算术平方根与平方根的区别与联系.3.进一步明确平方与开方是互为逆运算.(二)能力训练要求1.加强概念形成过程的教学，让学生不仅掌握概念，而且知晓它的理论数据.2.提倡学生进行自学，并能与同学互相交流与合作，变学会知识为会学知识.3.培养学生的求同和求异思维，能从相似的事物中观察到P X 们的共同点和不同点.(三)情感与价值观要求通过学生在学习中互相帮助、相互合作，并能对不同概念进行区分，培养大家的团队精神，以及认真仔细的学习态度，为学生将来走上社会而做准备，使他们能在工作中保持严谨的态度，正确处理好人际关系，成为各方面的佼佼者.学习重点：1.了解平方根、开平方的概念.2.了解开方与乘方是互逆的运算，会利用这个互逆运算关系求某些非负数的算术平方根和平方根3.了解平方根与算术平方根的区别与联系.学习难点：1.平方根与算术平方根的区别与联系.2.负数没有平方根，即负数不能进行开平方运算的原因.预习.导学1、上节课我们学习了算术平方根的概念，性质.知道若一个正数x的平方等于a，即x2=a.则x叫a的算术平方根，记作x=a，而且a也是非负数，比如正数22=4，则2叫4的算术平方根，4叫2的平方，但是(－2)2=4，则－2叫4的什么根呢？下面我们就来讨论这个问题.2、平方根、开平方的概念3、请大家先思考两个问题.(1)9的算术平方根是3，也就是说，3的平方是9，还有其他的数，它的平方也是9吗？(2)平方等于254的数有几个？平方等于0.64的数呢？ 4、根据上一节课的内容，我们知道了是9的算术平方根，52是254的算术平方根，那么－3，－52叫9、254的什么根呢？请大家认真看书后回答. 5、由平方根和算术平方根的定义。

6、平方根的性质，请大家思考以下问题.(1)一个正数有几个平方根.(2)0有几个平方根?(3)负数呢？7、什么叫开平方呢？8、平方根与算术平方根的联系与区别学习过程：［例］求下列各数的平方根.(1)64； (2)12149； (3)0.0004； (4)(－25)2；(5)11. 想一想 (1)(64)2等于多少？(12149)2等于多少？ (2)(2.7)2等于多少？(3)对于正数a ，(a )2等于多少？课堂练习(一)随堂练习1.求下列各数的平方根1.44，0，8，49100，441，196，10－42.填空(1)25的平方根是_________； (2)2)5( =_________； (3)(5)2=_________.(4)如果x2=a,(x为正数)那么x叫做__________________.(5)| 2|的算术平方根是_________,0算术平方根是__________.(6)9的平方是_________,9的平方根是__________,—9是______的一个平方根，（—4）2的平方根是___________.(7)平方根等于它本身的数是____________,算术平方根等于它本身的数有_________________,作业：活动与探究1.对于任意数a，2a一定等于a吗？2.a中的被开方数a在什么情况下有意义，(a)2等于什么？。

平⽅根与⽴⽅根学案12.1.1 平⽅根（第⼀课时）【平⽅根】如果⼀个数x 的平⽅等于a ，那么，这个数x 就叫做a 的平⽅根；也即，当)0(2≥=a a x 时，我们称x 是a 的平⽅根，记做：)0(≥±=a a x 。

因此：1.当a=0时，它的平⽅根只有⼀个，也就是0本⾝；2.当a ＞0时，也就是a 为正数时，它有两个平⽅根，且它们是互为相反数，通常记做：a x ±=。

3.当a ＜0时，也即a 为负数时，它不存在平⽅根。

例1.（1）的平⽅是64，所以64的平⽅根是；（2）的平⽅根是它本⾝。

（3）若x 的平⽅根是±2，则x=；的平⽅根是（4）当x 时，x 23－有意义。

（5）⼀个正数的平⽅根分别是m 和m-4，则m 的值是多少？这个正数是？ 1、若x 2= a ，则叫的平⽅根，如16的平⽅根是，972的平⽅根是2、3±表⽰的平⽅根，12-表⽰12的3、196的平⽅根有个，它们的和为4、下列说法是否正确？说明理由（1）0没有平⽅根；（2）—1的平⽅根是1±；（3）64的平⽅根是8；（4）5是25的平⽅根；（5）636±=5、求下列各数的平⽅根（1）100 （2）)8()2(-?- （3）1.21 （4）49151◆典例分析例若42-m 与13-m 是同⼀个数的平⽅根，试确定m 的值●拓展提⾼⼀、选择1、如果⼀个数的平⽅根是a+3和2a-15，那么这个数是（）A 、49B 、441C 、7或21D 、49或441 2、2)2(-的平⽅根是（）A 、4 B 、2 C 、-2 D 、2± ⼆、填空3、若5x+4的平⽅根为1±，则x=4、若m —4没有平⽅根，则|m —5|=5、已知1-a 的平⽅根是4±，3a+b-1的平⽅根是4±，则a+2b 的平⽅根是三、解答题6、a 的两个平⽅根是⽅程3x+2y=2的⼀组解（1）求a 的值（2）2a 的平⽅根7、已知1-x +∣x+y-2∣=0 求x-y 的值12.1.1平⽅根（第⼆课时）【算术平⽅根】：（1）如果⼀个正数x 的平⽅等于a ，即a x =2，那么，这个正数x 就叫做a 的算术平⽅根，记为：“a ”，读作，“根号a”，其中，a 称为被开⽅数。

平方根导学案一、引言在数学中，平方根是一个常见的概念。

它表示一个数值的平方根，即找到一个数，将其平方后得到给定的数值。

平方根在实际生活中有着广泛的应用，如建筑、工程、科学研究等领域。

本篇导学案将带领大家了解平方根的概念、性质和计算方法。

二、平方根的定义平方根是指给定数值的平方为该数值的非负实数解。

一般来说，平方根可以表示为以下形式：如果a² = b且a≥0，则a被称为b的平方根，记作a = √b。

例如，2的平方根为√2，因为√2² = 2。

三、平方根的性质1. 非负数的平方根都是非负数。

2. 负数没有实数平方根，可以用虚数单位i表示。

3. 非负实数的平方根有两个，正数的平方根和负数的平方根。

四、求平方根的方法1. 试算法：通过试探一个数，使其平方的结果接近给定值，逐步逼近目标值的平方根。

2. 袖珍计算器：现代计算器通常内置了求平方根的功能，可以直接输入数字并求得平方根。

3. 牛顿迭代法：通过不断逼近函数的零点，求得方程的解。

以求解平方根为例，设f(x) = x² - a，利用牛顿迭代公式x[n+1] = (x[n] +a/x[n])/2，通过不断迭代逼近平方根的值。

五、常见的平方根运算规则1. 两个平方根之和的平方根等于各自平方根的和。

即，√a + √b = √(a+b)。

2. 两个平方根之差的平方根等于各自平方根的差。

即，√a - √b = √(a-b)。

3. 一个数的平方根的平方等于该数的绝对值。

即，(√a)² = |a|。

4. 两个平方根的乘积等于它们的积的平方根。

即，√a × √b = √(a×b)。

5. 两个平方根的商等于它们的商的平方根。

即，√a ÷ √b = √(a÷b)。

六、例题演练1. 求√9的值解：√9 = 3，因为3² = 9。

2. 求√(16×25)的值解：√(16×25) = √400 = 20，因为20² = 400。

平方根教学案例（优秀范文5篇）第一篇：平方根教学案例平方根教学案例教学目标1掌握平方根的概念，明确平方根和算术平方根之间的联系和区别；2能用符号正确地表示一个数的平方根，理解开平方运算和乘方运算之间的互逆关系；3培养学生的探究能力和归纳问题的能力。

教学重点平方根的概念和求数的平方根。

教学难点平方根和算术平方根的联系与区别。

教学过程引入概念如果一个数的平方等于9，这个数是多少？设计意图学生思考并讨论，使学生明白这样的数有两个，它们是3和－3。

受前面知识的影响学生可能不易想到－3这个数，这时可提醒学生，这里的这个数可以是负数。

注意（－3）2＝9中括号的作用。

又如：x2＝ 9，则x等于多少呢？又如：x2＝ 9，则x等于多少呢？使学生完成课本45页的填表。

设计意图通过填表中的x的值，进一步加深对“两个互为相反数的平方等于同一个数”的印象，为平方根的引入做准备。

给出平方根的概念：如果一个数的平方等于ａ，那么这个数就叫做ａ的平方根．即：如果x2＝a，那么x叫做ａ的平方根。

求一个数的平方根的运算，叫做开平方。

例如：±3的平方等于9，9的平方根是±3，所以平方与开平方互为逆运算。

观察：课本45页中的图6.1-2。

中的两个图描述了平方与开平方互为逆运算的运算过程，揭示了开平方运算的本质。

设计意图通过此例使学生明白平方根可以从平方运算中求得，并能规范地表述一个数的平方根．这个例题也为后面探讨平方根的特征做好准备。

例1（课本45页的例4）求下列各数的平方根：（1）100；（2）；（3）0．25。

教师要规范书写格式。

深化概按照平方根的概念，请同学们思考并讨论下列问题：正数的平方根有什么特点？0的平方根是多少？负数有平方根吗？建议：可引导学生通过观察x2＝a中的a和x的取值范围和取值个数得出。

根据上面讨论得出的结果得课本46归纳设计意图加深对符号意义的理解和对平方根概念的灵活应用。

测试学生对平方根概念的掌握情况。

平方根数学备课教案平方根数学备课教案【5篇】理解开平方与平方是一对互逆的运算，会用平方根的概念求某些数的平方根，并能用根号加以表示，能用科学计算器求平方根及其近似值。

下面给大家分享平方根数学备课教案，欢迎阅读！平方根数学备课教案精选篇1人教版七年级数学下册《平方根》教学设计PPT课件导学案教案课题：平方根（1）教学目标 1.了解算术平方根的概念，会用根号表示正数的算术平方根，并了解算术平方根的非负性；2.了解开方与乘方互为逆运算，会用平方运算求某些非负数的算术平方根；3.通过对实际生活中问题的解决，让学生体验数学与生活实际是紧密联系着的，通过探究活动培养动手能力和激发学生学习数学的兴趣。

教学难点根据算术平方根的概念正确求出非负数的算术平方根。

知识重点算术平方根的概念。

教学过程（师生活动）设计理念情境导入同学们，20__年10月15日，这是我们每个中国人值得骄傲的日子．因为这一天，“神舟”五号飞船载人航天飞行取得圆满成功，实现了中华民族千年的飞天梦想（多媒体同时出示“神舟”五号飞船升空时的画面）．那么，你们知道宇宙飞船离开地球进人轨道正常运行的速度是在什么范围吗？这时它的速度要大于第一宇宙速度（米／秒）而小于第二宇宙速度：（米／秒）．、的大小满足 .怎样求、呢？这就要用到平方根的概念，也就是本章的主要学习内容．这节课我们先学习有关算术平方根的概念．请看下面的问题．“神舟”五号成功发射和安全着陆，标志着我国在攀登世界科技高峰的征程上又迈出具有重大历史意义的一步，是我们伟大祖国的荣耀．此内容有感染力，使学生对本章知识的应用价值有一个感性认识，同时激发学生的好奇心和学习的兴趣．这里的计算实际上是已知幂和乘方的指数求底数的问题，是乘方的逆运算，学生以前没有见过，由此引出了本章所要研究的主要内容，以及研究这些内容的大体思路．提出问题感知新知多媒体展示教科书第160页的问题（问题略），然后提出问题：你是怎样算出画框的边长等于5dm的呢？（学生思考并交流解法）这个问题相当于在等式扩=25中求出正数x的值．练习：教科书第160页的填表．练习：教科书第160页的填表．这个问题抽象成数学问题就是已知正方形的面积求正方形的边长，这与学生以前学过的已知正方形的边长求它的面积的过程互逆，教学时可以让学生初步体会这种互逆的过程，为后面的学习做准备。

初中数学《平方根》教案平方根，又叫二次方根，表示为〔 plusmn; radic;￣〕，其中属于非负数的平方根称之为算术平方根。

一个正数有两个实平方根，它们互为相反数，负数没有平方根。

下面就是小编给大家带来的初中数学《平方根》教案，希望能帮助到大家! 数学《平方根》教案一一、教学目标1.理解一个数平方根和算术平方根的意义;2.理解根号的意义，会用根号表示一个数的平方根和算术平方根;3.通过本节的训练，提高学生的逻辑思维能力;4.通过学习乘方和开方运算是互为逆运算，体验各事物间的对立统一的辩证关系，激发学生探索数学奥秘的兴趣.二、教学重点和难点教学重点：平方根和算术平方根的概念及求法.教学难点：平方根与算术平方根联系与区别.三、教学方法讲练结合.四、教学手段幻灯片.五、教学过程(一)提问1.已知一正方形面积为50平方米，那么它的边长应为多少?2.已知一个数的平方等于1000，那么这个数是多少?3.一只容积为0.125立方米的正方体容器，它的棱长应为多少?这些问题的共同特点是：已知乘方的结果，求底数的值，如何解决这些问题呢?这就是本节内容所要学习的.下面作一个小练习：填空1.( )2=9;2.( )2 =0.25;3.5.( )2=0.0081.学生在完成此练习时，最容易出现的错误是丢掉负数解，在教学时应注意纠正.由练习引出平方根的概念.(二)平方根概念如果一个数的平方等于a，那么这个数就叫做a的平方根(二次方根).用数学语言表达即为：若x2=a，则x叫做a的平方根.由练习知： plusmn;3是9的平方根;plusmn;0.5是0.25的平方根;0的平方根是0;plusmn;0.09是0.0081的平方根.由此我们看到+3与-3均为9的平方根，0的平方根是0，下面看这样一道题，填空：( )2=-4学生思考后，得到结论此题无答案.反问学生为什么?因为正数、0、负数的平方为非负数.由此我们可以得到结论，负数是没有平方根的.下面总结一下平方根的性质(可由学生总结，教师整理).(三)平方根性质1.一个正数有两个平方根，它们互为相反数.2.0有一个平方根，它是0本身.3.负数没有平方根.(四)开平方求一个数a的平方根的运算，叫做开平方的运算.由练习我们看到+3与-3的平方是9，9的平方根是+3和-3，可见平方运算与开平方运算互为逆运算.根据这种关系，我们可以通过平方运算来求一个数的平方根.与其他运算法则不同之处在于只能对非负数进行运算，而且正数的运算结果是两个。

《平方根》学案一、学习目标1.掌握平方根的概念和性质，会求一个非负数的平方根2.会用符号表示一个非负数的平方根3.知道平方根和算术平方根之间的联系和区别二、自学指导自学教材72页“思考”—74页的内容，将重点地方作上记号，并完成以下练习。

1.___________________________________那么这个数叫做a 的平方根或二次方根，如果x 2 =a ，那么_____叫做_____的平方根。

2._________________________________________叫做开平方。

3.正数有____个平方根，它们__________；0的平方根是___；负数________。

4.正数a 的算术平方根可以用______表示，正数a 的负的平方根，可以用符号______表示，正数a 的平方根可以用符号_______表示，读作____________。

5.（1）49的平方根是______，算术平方根是______；（2）0的平方根是______，算术平方根是______。

6.下列说法中，正确的是（ ）A. －4是（－4）2的算术平方根B.36的平方根是±6C.9的平方根是3D.0.01的平方根是±0.00017.求下列各数的平方根。

（1）225； （2）100001； （3）0.818.求下列各式的值。

（1）121； (2) －0036.0； （3）±4936三、师生点评1.请学生口答自学指导中的1—6题。

2.师生集体点评学生板演的第7、8题。

四、随堂练习1.已知一个正数的平方根是a+3和2a －6，则这个正数是__________。

2.判断题（1）9=±3。

（ ）（2）32是94的一个平方根。

（ ）（3）（－8）2的平方根是－8。

（ ）（4）16的平方根是±16。

（ ）3.求下列各式中的x 。

(1) （x －2）2=4 （2）x 2－4936=0五、拓展训练如果︱a －2b ︱+（b+c ）2+1 c =0，求a+b －c 的平方根。