第十三章早期量子论和量子力学基础

量子力学基础量子力学是20世纪物理学的一大突破，它不仅揭示了微观世界的奇妙现象，还对我们对世界的认知方式产生了颠覆性的影响。

在这篇文章中，我们将探讨量子力学的基本概念、原理和应用，并探讨一些关于量子力学的哲学和思考。

量子力学最早的基础可以追溯到1900年，当时德国物理学家马克斯·普朗克提出了能量的量子化概念。

他发现，能量不是连续的，而是以分立的单位存在，即能量量子。

这个想法颠覆了经典物理学中连续和无限的观念，揭示了微观世界的离散性质。

1905年，阿尔伯特·爱因斯坦进一步推动了量子力学的发展，他提出了光的粒子性。

根据他的理论，光被看作是由一系列离散的粒子组成的，这些粒子被称为光子。

这个概念对光的行为做出了解释，也为后来量子力学的发展奠定了基础。

量子力学的核心是波粒二象性。

根据量子力学，微观粒子既可以表现出粒子性，也可以表现出波动性。

这就是说，微观粒子既可以像粒子一样独立存在，也可以像波一样传播和干涉。

这种双重性质在经典物理学中是难以理解的，但在量子力学中却是普遍存在的。

著名的双缝干涉实验就是一个很好的例子。

在这个实验中，一束光通过两个狭缝后形成干涉图案。

如果光被看作是粒子，那么预期结果应该是两个狭缝后出现两个亮斑。

然而，实验结果却展示出了干涉条纹。

只有将光看作是波动性的才能解释这个结果。

这种波粒二象性的存在挑战了我们对物质的传统认知，并使量子力学成为一门充满挑战的科学。

量子力学还有一个重要的概念是不确定性原理，由奥地利物理学家维尔纳·海森堡提出。

不确定性原理认为，我们无法同时准确测量一个粒子的位置和动量。

如果我们尝试使用更准确的测量工具来测量粒子的位置，那么对粒子动量的测量就会变得不确定，反之亦然。

这种无法完全确定一个粒子状态的现象被称为测不准原理。

量子力学的发展产生了许多令人惊叹的应用。

其中最著名的是量子计算和量子通信。

量子计算利用了量子叠加和纠缠的特性，在某些问题上可以迅速解决，远远超过了传统计算机的能力。

第十三章 早期量子论和量子力学基础练 习 一一. 选择题1. 内壁为黑色的空腔开一小孔，这小孔可视为绝对黑体，是因为它（ B ） (A) 吸收了辐射在它上面的全部可见光； (B) 吸收了辐射在它上面的全部能量； (C) 不辐射能量； (D) 只吸收不辐射能量。

2. 一绝对黑体在温度T 1 = 1450K 时，辐射峰值所对应的波长为λ1，当温度降为725K 时，辐射峰值所对应的波长为λ2，则λ1/λ2为（ D ） (A)2； (B) 2/1； (C) 2 ； (D) 1/2 。

3. 一般认为光子有以下性质（ A ）(1) 不论在真空中或介质中的光速都是c ；(2) 它的静止质量为零；(3) 它的动量为h ν/c 2； (4) 它的动能就是它的总能量；(5) 它有动量和能量，但没有质量。

以上结论正确的是 （ A ）(A) （2）（4）； (B) （3）（4）（5）； (C) （2）（4）（5）； (D) （1）（2）（3）。

4. 已知某单色光照射到一金属表面产生了光电效应，若此金属的逸出电势是U 0（使电子从金属逸出需做功eU 0），则此单色光的波长λ必须满足：（A ） (A) 0hc eU λ≤； (B) 0hc eU λ≥； (C) 0eU hc λ≤； (D) 0eU hcλ≥。

二. 填空题1. 用辐射高温计测得炉壁小孔的辐射出射度为22.8W/cm 2，则炉内的温度为 1.416×103K 。

2. 设太阳表面的温度为5800K ，直径为13.9×108m ，如果认为太阳的辐射是常数，表面积保持不变，则太阳在一年内辐射的能量为 1.228×1034 J ，太阳在一年内由于辐射而损失的质量为1.3647×1017 kg 。

3. 汞的红限频率为1.09×1015Hz ，现用λ=2000Å的单色光照射，汞放出光电子的最大初速度0v =57.7310 m/s ⨯ ，截止电压U a = 1.7V 。

第13章　早期量子论和量子力学基础13-1 估测星球表面温度的方法之一是：将星球看成黑体，测量它的辐射峰值波长λm ，利用维恩位移定律便可估计其表面温度。

如果测得北极星和天狼星的λm 分别为0.35 μm 和0.29 μm，试计算它们的表面温度。

解：根据维恩位移定律，可知与黑体辐射本领极大值相对应的波长与绝对温度T 的乘积为一常数。

则北极星表面温度：天狼星表面温度：。

13-2 在加热黑体过程中，其单色辐出度的峰值波长是由0.69 μm 变化到0.50μm，求总辐出度改变为原来的多少倍?解：设加热前后黑体的温度分别为T 1、T 2，其单色辐出度的峰值波长分别为、，则根据维恩位移定律，可得黑体温度之比为：根据斯特藩-玻尔兹曼定律，可得总辐出度之比为：因此，总辐出度变为原来的3.63倍。

13-3 假设太阳表面温度为5 800 K ，太阳半径为6.96×108 m 。

如果认为太阳的辐射是稳定的，求太阳在1年内由于辐射，它的质量减小了多少?解：由斯特藩一玻尔兹曼定律，太阳通过其表面辐射出的总功率为：太阳在一年内辐射出的总能量为。

由狭义相对论质能关系，可得太阳在一年内的质量亏损：*13-4 黑体的温度T 1＝6000 K ，问λ1＝0.35 μm 和λ2＝0.70 μm 的单色辐出度之比等于多少?当温度上升到T 2＝7000 K 时，λ1的单色辐出度增加到原来的多少倍?解：（1）利用普朗克单色辐出度公式：可得时，和的单色辐出度之比：而因此，单色辐出度之比：。

（2）当黑体温度上升到时，的单色辐出度：与温度为T 1时，黑体的单色辐出度的比值：解得：代入上式可得：。

*13-5 假定太阳和地球都可以看成黑体，如太阳表面温度T S ＝6 000 K ，地球表面各处温度相同，试求地球的表面温度（已知太阳的半径R S ＝6.96×105 km ，太阳到地球的距离r ＝1.496×108 km ）。

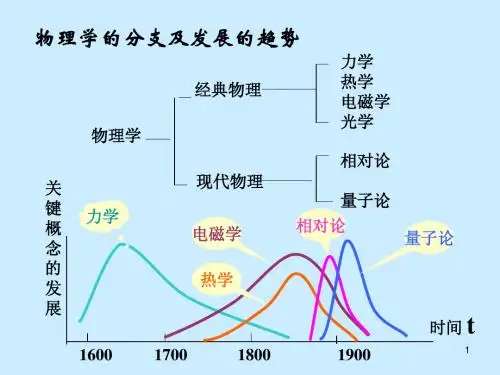
量子力学的建立与发展历程具有重要历史意义，可以归纳为以下四个阶段：
早期量子论阶段：在这一阶段，科学家们开始发现原子并非固体不可压缩的小球体，而是具有空间结构。

19世纪末，一系列实验和观察表明原子具有离散能级，并且能发生辐射和吸收。

这些发现为后来的量子力学奠定了基础。

旧量子论阶段：在这一阶段，科学家们开始用量子化概念来解释原子结构和原子光谱的规律性。

这些努力为后来的量子力学框架的形成提供了启示和参考。

量子力学的建立阶段：这一阶段开始于20世纪初，科学家们提出了许多重要的量子力学原理，如波粒二象性、不确定性原理、哈密顿表述和薛定谔方程等。

这些原理为量子力学的发展奠定了坚实的基础。

量子力学的发展与完善阶段：在这一阶段，科学家们不断探索和研究量子力学的各种应用，包括半导体物理、超导现象、核物理、粒子物理等。

这些应用不断推动着量子力学的发展和完善。

总之，量子力学的发展历程是一个充满挑战与突破的历史过程。

科学家们通过不懈的努力和深入的研究，逐步建立起一套完整的量子力学理论体系，为现代物理学的发展奠定了坚实的基础。

量子力学基础知识一、引言量子力学是研究微观领域的物质与能量相互作用的理论框架。

自从其诞生以来，量子力学一直在推动科学的发展，并给人们对宇宙的认识带来了巨大的变革。

本文将介绍量子力学的基础知识，包括量子力学的起源、基本原理、波粒二象性以及量子力学的测量等内容。

二、量子力学的起源量子力学起源于20世纪20年代，由一系列学者的贡献构建而成。

其中，德国物理学家普朗克的能量量子化假设和波尔的量子化条件为量子力学的产生奠定了基础。

普朗克假设能量的辐射是离散的，而非连续的，基于这一假设，波尔提出了电子只能存在于特定的能级上，并且在能级间跃迁时会放出或吸收能量。

这些基本思想为量子力学的建立提供了理论依据。

三、量子力学的基本原理1. 状态和波函数在量子力学中，一个粒子的状态可以由波函数来描述。

波函数是一个数学函数，描述了粒子在空间中的概率分布情况。

根据波函数的不同形式，可以分为定态波函数和非定态波函数。

定态波函数描述的是粒子在确定能级的状态，而非定态波函数描述的是粒子在多个能级之间的叠加态。

2. 波粒二象性量子力学中最重要的原理之一是波粒二象性。

根据波粒二象性，物质既可以表现出波动性，又可以表现出粒子性。

对于微观粒子，如电子、光子等，它们的波动特性可以通过波函数来描述，而粒子性则体现在其具有一定的质量和动量。

3. 不确定性原理不确定性原理是量子力学的又一基本原理。

它指出，在同一时刻，无法准确测量一个粒子的多个性质，如位置和动量，或者能量和时间。

这是因为在测量的过程中，会对被测量粒子产生扰动，从而导致测量结果的不准确性。

四、量子力学的测量在量子力学中，粒子的测量是通过测量算符来实现的。

测量算符对应于一个可观测量，如位置、动量、能量等。

在测量的过程中，波函数会坍缩到一个特定的本征态上，这个本征态对应于特定的测量结果。

五、应用与展望量子力学在科学技术领域有着广泛的应用。

其中，量子计算、量子通信和量子物质等领域备受关注。