工程力学--材料力学(北京科大、东北大学版)第4版第九章习题答案

弟二早习题3-1试求图视各轴在指泄横截而1-1、2-2和3-3上的扭矩，并在各截而上表示出钮矩的方向。

(b)题3 I图3-2 试绘出下列各轴的钮矩图，并求卩」。

2mD cfr@=©=33-3 ma=2OON.m 9mb=4OON.m 9mc=6OON 9m. (b)3-4 一传动轴如图所示，已知 ma=130N ・・cm, mb=300N.cm, mc=i, md=70N.cm;^段轴的直径分别为：Dab=5cm, Dbc=7.5cm, Dcd=5cm（1） 画出扭矩图；（2） 求1 •仁2・2、3・3截而的最大切应力。

3-5图示的空心圆轴，外径D=8cm,内径d=6.25cm,承受扭矩m=1000N.m. （1） 求（2） 绘出横截面上的切应力分布图： （3）求单位长度扭转角，已知G=80000Mpa.3-6已知变截而钢轴上的外力偶矩^=1800N.m, Wf=1200N.m,试求最大切应力和最大相对扭矩。

已知G=80dbpa ・3M试绘下列各轴的扭矩(a)题3-6图3-7 一钢轴的转矩n=240/min.传递功率^=44.1kN.m.已知[^=40Mpa,=1W,6=80*MPa,试按强度和冈帔条件汁算轴的直径解：轴的直径由强度条件确左，rf>60-7wn o3-8图示实心轴通过牙嵌离合器把功率传给空心轴。

传递的功率ft=7.5kw,轴的转速n=100r/min,试选择实心轴直径占和空心轴外径“。

已知%心入5,题L8图3-9图示AB轴的转速n=120r/min,从B轮上输入功率丹=40kw,此功率的一半通过锥齿轮传给垂直轴V,另一半功率由水平轴H传疋。

已知锥齿轮的节圆直径=600mm：各轴直径为^-=100111111, “=80mm, “=60fnfn, KLzOlWPa,试对各轴进行强度校核。

3-10船用推进器的轴，一段是实心的，直径为280mm,另一段是空心的，其内径为外径的一半。

静力学部分第一章基本概念受力图2-1 解：由解析法，23cos 80RX F X P P N θ==+=∑12sin 140RY F Y P P N θ==+=∑故：161.2R F N ==1(,)arccos 2944RY R R F F P F '∠==2-2解：即求此力系的合力，沿OB 建立x 坐标，由解析法，有123cos45cos453RX F X P P P KN==++=∑ 13sin 45sin 450RY F Y P P ==-=∑ 故：3R F KN == 方向沿OB 。

2-3 解：所有杆件均为二力杆件，受力沿直杆轴线。

（a ） 由平衡方程有：0X =∑ sin 300AC AB F F -=0Y =∑ cos300AC F W -=0.577AB F W =（拉力） 1.155AC F W =（压力）（b ） 由平衡方程有：0X =∑ cos 700AC AB F F -=0Y =∑ sin 700AB F W -=1.064AB F W =（拉力）0.364AC F W =（压力）（c ） 由平衡方程有：0X =∑ cos 60cos300AC AB F F -=0Y =∑ sin 30sin 600AB AC F F W +-=0.5AB F W = (拉力)0.866AC F W =（压力）（d ） 由平衡方程有：0X =∑ sin 30sin 300AB AC F F -=0Y =∑ cos30cos300AB AC F F W +-=0.577AB F W = (拉力)0.577AC F W = (拉力)2-4 解：（a ）受力分析如图所示：由0x =∑cos 450RA F P -=15.8RA F KN ∴=由0Y =∑sin 450RA RB F F P +-=7.1RB F KN ∴=(b)解：受力分析如图所示：由x =∑cos 45cos 450RA RB F F P --=0Y =∑sin 45sin 450RA RB F F P -=联立上二式，得： 22.410RA RB F KNF KN ==2-5解：几何法：系统受力如图所示三力汇交于点D ，其封闭的力三角形如图示所以： 5RA F KN = （压力） 5RB F KN =（与X 轴正向夹150度） 2-6解：受力如图所示：已知，1R F G = ，2AC F G =由0x =∑ cos 0AC r F F α-=12cos G G α∴=由0Y =∑ sin 0AC N F F W α+-=2sin N F W G W α∴=-⋅=2-7解：受力分析如图所示，取左半部分为研究对象由0x =∑ cos 45cos 450RA CB P F F --=0Y =∑sin 45sin 450CB RA F F '-= 联立后，解得： 0.707RA F P = 0.707RB F P =由二力平衡定理 0.707RB CB CB F F F P '===2-8解：杆AB ，AC 均为二力杆，取A 点平衡由x =∑cos 60cos300AC AB F F W ⋅--=0Y =∑sin 30sin 600AB AC F F W +-=联立上二式，解得：7.32AB F KN=-（受压）27.3AC F KN=（受压）2-9解：各处全为柔索约束，故反力全为拉力，以D ，B 点分别列平衡方程（1）取D 点，列平衡方程由x =∑sin cos 0DB T W αα-=DB T Wctg α∴==（2）取B 点列平衡方程：由0Y =∑sin cos 0BDT T αα'-=230BD T T ctg Wctg KN αα'∴===2-10解：取B 为研究对象：由0Y =∑sin 0BC F P α-=sin BC P F α∴=取C 为研究对象：由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式，且有BCBC F F '= 解得：2cos 12sin cos CE P F ααα⎛⎫=+⎪⎝⎭取E 为研究对象：由0Y =∑ cos 0NH CEF F α'-=CECE F F '= 故有：22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2-11解：取A 点平衡：x =∑sin 75sin 750AB AD F F -=0Y =∑cos 75cos 750AB AD F F P +-=联立后可得： 2cos 75AD AB PF F ==取D 点平衡，取如图坐标系：x =∑cos5cos800ADND F F '-=cos5cos80ND ADF F '=⋅由对称性及ADAD F F '=cos5cos5222166.2cos80cos802cos 75N ND AD P F F F KN'∴===⋅=2-12解：整体受力交于O 点，列O 点平衡由x =∑cos cos300RA DC F F P α+-=0Y =∑sin sin 300RA F P α-=联立上二式得：2.92RA F KN=1.33DC F KN=（压力） 列C 点平衡x =∑405DC AC F F -⋅=0Y =∑ 305BC AC F F +⋅=联立上二式得： 1.67AC F KN=（拉力）1.0BC F KN=-（压力）2-13解：（1）取DEH 部分，对H 点列平衡x =∑0RD REF F '= 0Y =∑0RD F Q -=联立方程后解得：RD F =2REF Q '=（2）取ABCE 部分，对C 点列平衡x =∑cos 450RE RA F F -=0Y =∑sin 450RB RA F F P --=且RE REF F '=联立上面各式得：RA F =2RB F Q P=+（3）取BCE 部分。

工程力学第9章答案第9章弹性杆件横截面上的切应力分析9－1 扭转切应力公式p /)(I M x ρρτ=的应用范围有以下几种，试判断哪一种是正确的。

（A ）等截面圆轴，弹性范围内加载；（B ）等截面圆轴；（C ）等截面圆轴与椭圆轴；（D ）等截面圆轴与椭圆轴，弹性范围内加载。

正确答案是 A 。

解：p )(I M x ρρτ=在推导时利用了等截面圆轴受扭后，其横截面保持平面的假设，同时推导过程中还应用了剪切胡克定律，要求在线弹性范围加载。

9－2 两根长度相等、直径不等的圆轴承受相同的扭矩受扭后，轴表面上母线转过相同的角度。

设直径大的轴和直径小的轴的横截面上的最大切应力分别为max 1τ和max 2τ，切变模量分别为G 1和G 2。

试判断下列结论的正确性。

（A ）max 1τ＞max 2τ；（B ）max 1τ＜max 2τ；（C ）若G 1＞G 2，则有max 1τ＞max 2τ；（D ）若G 1＞G 2，则有max 1τ＜max 2τ。

正确答案是 C 。

解：因两圆轴等长，轴表面上母线转过相同角度，指切应变相同，即γγγ==21由剪切胡克定律γτG =知21G G >时，max 2max 1ττ>。

9－3 承受相同扭矩且长度相等的直径为d 1的实心圆轴与内、外径分别为d 2、)/(222D d D =α的空心圆轴，二者横截面上的最大切应力相等。

关于二者重之比（W 1/W 2）有如下结论，试判断哪一种是正确的。

（A ）234)1(α-；（B ）)1()1(234αα--；（C ）)1)(1(24αα--；（D ）)1/()1(2324αα--。

正确答案是 D 。

解：由max 2max1ττ=得)1(π16π1643231α-=D M d M xx即31421)1(α-=D d（1）)1(222212121α-==D d A A W W （2）（1）代入（2），得2324211)1(αα--=W W9－4 由两种不同材料组成的圆轴，里层和外层材料的切变模量分别为G 1和G 2，且G 1 = 2G 2。

第一章参考答案1-1：解：(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3= -P(d):N1=-2P,N2=P(e):N1= -50N,N2= -90N(f):N1=0.896P,N2=-0.732P注（轴向拉伸为正，压缩为负）1-2：解：σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa ∴σmax=35.3Mpa1-3：解：下端螺孔截面：σ1=19020.065*0.045P S=15.4Mpa上端单螺孔截面：σ2=2PS =8.72MPa上端双螺孔截面：σ3= 3PS =9.15Mpa∴σmax =15.4Mpa1-4：解：受力分析得：F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5 MPa1-5：解:F=6PS1=h*t=40*4.5=180mm2S2=(H-d)*t=(65-30)*4.5=157.5mm 2∴σmax=2FS =38.1MPa1-6:解: (1)σAC =-20MPa,σCD =0,σDB =-20MPa;△ l AC =NL EA =AC LEA σ=-0.01mm△ l CD =CD LEA σ=0△ L DB =DB LEA σ=-0.01mm(2) ∴AB l ∆=-0.02mm1-7:解:31.8127AC AC CB CB P MPa S P MPa S σσ==== AC AC AC L NL EA EA σε===1.59*104,CB CB CB L NL EA EA σε===6.36*104 1-8:解:Nll EAl l ε∆=∆= ∴NEA ε=62.54*10N EA N ε∴==1-9：解：208,0.317E GPa ν==1-10：解：[][]max 59.5MPa σσ=<1-11：解：（1）当45oα=，[]11.2σσ=>强度不够 （2）当60oα=，[]9.17σσ=< 强度够 1-12：解：[]360,200200200*1013.3100*150*10Y p kNS P kNS MPa A σσ-==∴=====<∑1-13：解：[]max 200213MPa MPa σ=<1-14：解：1.78, 1.26d cm d cm ==拉杆链环1-15 解：BC F ==70.7 kN70.70.505140F S FS σσ=∴=== 查表得： 45*45*31-16解：(1)[]2401601.5s s n σσ===MPa[][]24P SP dσσπ≤∴≤24.4D mm∴=(2)2119.51602P P MPa MPa S d σπ===≤⎛⎫⎪⎝⎭1-17 解：（1）2*250*6154402D F P A N π⎛⎫=== ⎪⎝⎭ 78.4AC F MPa S σ== 300 3.8378.4s n σσ∴===[][]''''60*3.14*15*1542390F S F S Nσσ===='61544014.521542390F n F ===≈1-18 解：P=119kN1-19 解：::3:4:535()44AB BC AB BC S P S S P S P =∴==拉，[][][]112841123484AB AB S A kN S P kN P kN σ=====同理所以最大载荷 84kN1-20 解： P=33.3 kN1-21 解：71,,12123A B C P F F P F P ===1-22 解：10MAX MPa σ=-1-23 解：A B X R R R =∴==∑t r l l ∆=∆ t AB l l t α∆=21211111223533131.3cd R AC DB CD AC CD CD AF CD MAX Rl Rl l l l l EA EA Rl Rl Rl l EA EA EA EA t EA t R l S MPa A ααασ∆=∆+∆+∆=+=+=∴====第二章习题2-1 一螺栓连接如图所示，已知P=200 kN ， =2 cm ，螺栓材料的许用切应力[τ]=80Mpa ，试求螺栓的直径。

工程力学材料力学（北京科技大学与东北大学）第一章轴向拉伸和压缩1-1：用截面法求下列各杆指定截面的内力解：(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3= -P(d):N1=-2P,N2=P(e):N1= -50N,N2= -90N(f):N1=0.896P,N2=-0.732P注（轴向拉伸为正，压缩为负）1-2：高炉装料器中的大钟拉杆如图a所示，拉杆下端以连接楔与大钟连接，连接处拉杆的横截面如图b所示；拉杆上端螺纹的内径d=175mm。

以知作用于拉杆上的静拉力P=850kN，试计算大钟拉杆的最大静应力。

解：σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa∴σmax=35.3Mpa1-3：试计算图a所示钢水包吊杆的最大应力。

以知钢水包及其所盛钢水共重90kN，吊杆的尺寸如图b所示。

解：下端螺孔截面：σ1=19020.065*0.045P S=15.4Mpa上端单螺孔截面：σ2=2P S =8.72MPa 上端双螺孔截面：σ3= 3P S =9.15Mpa∴σmax =15.4Mpa1-4：一桅杆起重机如图所示，起重杆AB为一钢管，其外径D=20mm,内径d=18mm;钢绳CB 的横截面面积为0.1cm2。

已知起重量P=2000N，试计算起重机杆和钢丝绳的应力。

解：受力分析得：F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5 MPa1-5：图a所示为一斗式提升机.斗与斗之间用链条连接,链条的计算简图如图b 所示,每个料斗连同物料的总重量P=2000N.钢链又两层钢板构成,如c所示.每个链板厚t=4.5mm,宽h=40mm,H=65mm,钉孔直径d=30mm.试求链板的最大应力.解:F=6PS 1=h*t=40*4.5=180mm 2S2=(H-d)*t=(65-30)*4.5=157.5mm 2∴σmax=2F S =38.1MPa1-6:一长为30cm 的钢杆,其受力情况如图所示.已知杆截面面积A=10cm2,材料的弹性模量E=200Gpa,试求;(1) AC. CD DB 各段的应力和变形.(2) AB 杆的总变形.解: (1)σAC =-20MPa,σCD =0,σDB =-20MPa;△ l AC =NL EA =AC LEA σ=-0.01mm△ l CD =CD LEA σ=0△ L DB =DB LEA σ=-0.01mm(2) ∴ABl∆=-0.02mm1-7:一圆截面阶梯杆受力如图所示,已知材料的弹性模量E=200Gpa,试求各段的应力和应变.解:31.8127ACACCBCBPMPaSPMPaSσσ====ACACACLNLEA EAσε===1.59*104,CBCBCBLNLEA EAσε===6.36*1041-8:为测定轧钢机的轧制力,在压下螺旋与上轧辊轴承之间装置一测压用的压头.压头是一个钢制的圆筒,其外径D=50mm,内径d=40mm,在压头的外表面上沿纵向贴有测变形的电阻丝片.若测得轧辊两端两个压头的纵向应变均为ε=0.9*10-2,试求轧机的总轧制压力.压头材料的弹性模量E=200Gpa.解:QNllEAllε∆=∆=∴NEAε=62.54*10N EA Nε∴==1-9：用一板状试样进行拉伸试验，在试样表面贴上纵向和横向的电阻丝来测定试样的改变。

工程力学第4版材料力学答案第二章习题参考答案2-1解：2-2 解：2-3 解：2-4 解：2-5 解：2-6解：所以都满足 2-7 解：2-8 解：：2-9 解：第三章习题参考答案3.1据截面沿指定截面i-i (i=123)将杆截为两段，考虑任一段的平衡即可得该指定截面上的扭矩，例如题b:（1）1-1截面由=0，1+2-=0 得=1+2=3kN.m（方向如图所示，为负扭矩）（2）2-2截面由=0，1+2-6+=0 得=6-2-1=3kN.m (方向如图所示，为正扭矩) （3）3-3截面由=0，=0由以上各扭矩的计算式可知，轴内任一横截面的扭矩，在数值上就等于该截面一侧各外力偶矩值的代数和；而扭矩的方向则与截面任一侧合外力偶的方向规则可迅速求得任一截面的扭矩，而无须将轴截开。

剧此规则可得a各截面的扭矩：=3kN.m，==-2kN.m3-2解：（a）=2，（b）=43-3解：（a）=600N.m ，（b）=400N.m3-4 解：=-130N.m，=170 N.m，=70N.m=5.3 MPa , =2.05 MPa , =2.85MPa3-5 解：3-6 解：（1）各段轴横截面的扭矩：AB段（负扭矩）BC段（为负扭矩）(2) 最大剪应力计算：因两段轴扭矩不同，所以应分别计算每段轴内横截面的最大剪应力值，然后加以比较找到最大减应力值。

AB段BC段比较得最大剪应力发生在BC段，其数值为(3)最大相对扭转角因轴内各截面扭矩方向都一致，所以最大相对扭转角即为整个轴长的总扭转角。

在使用扭转角公式时，注意到该式的使用条件必须是对应于所算转角的长度段内，、、T为常数。

故分别计算两段轴的扭转角，然后相加即得最大相对扭转角。

+0.0213弧度=1.22度3-7解：轴的直径由强度条件确定，。

3-8解：（1）外力偶矩的计算（2）两轴各截面传递的扭矩（3）实心轴所需直径由得选d=45mm.(4) 空心轴的外、内选择由得选所以。

材料力学刘鸿文第四版答案【篇一：工程力学--材料力学(北京科大、东北大学版)第4版习题答案第二到九章】，被冲剪钢板的剪切强度极限=360 mpa。

求在最大冲力作用下所能冲剪圆孔的最小直径d和钢板的最大厚度。

2-42-8 图示夹剪，销子c的之间直径为0.6 cm，剪直径与销子直径相同的铜丝时，若力p=200 n，a=3 cm，b=15 cm，求铜丝与销子横截面上的平均切应力。

2-9 一冶炼厂使用的高压泵安全阀如图所示，要求当活塞下高压液体的压强达到p=3.4 mpa时，使安全销沿1-1和2-2两截面剪断，从而使高压液体流出，以保证泵的安全。

已知活塞直径d=5.2cm，安全销采用15号钢，其剪切强度极限=320 mpa，试确定安全销的直径d。

参考答案2-1解：2-2 解：【篇二：材料力学试题b及答案】型： b 卷一、简答题（共33 分，每小题各3 分）1、如图所示。

直杆bd，横截面积为a，容重为?，杆件中央c处插入一圆轴，轴的两端支承在支架上，杆bd的轴力图为。

（第1题图）2、一铸铁悬臂梁受力如图，截面为字形，放置的方式有如下两种选择，合理的放置形式是()种形式。

（a）( b ) （第2题图）3、试根据受载情况判断可能的断口方位是（）。

（a） ( b )4、如图所示，螺栓在拉力f作用下，已知材料的剪切许用应力???和拉伸许用应力???之间的关系约为???=0.6???。

螺栓直径d与螺栓头部高度h的合理比值d/h为a. 1b. 2.4c. 0.67d. 6.7e. 0.15（第4题图）（第5题图） 5．如图机车车轴所受交变应力的循环特征r= .试卷类型：（b）卷考核方式：（闭）卷共 5 页第 1 页试题要求: 1.试题后标注本题得分;2.试卷应附有评卷用标准答案,并有每题每步得分标准;3.试卷必须提前一周送考试中心;4.考试前到指定地点领取试卷；5.考生不得拆散试卷，否则试卷无效。

学号；姓名：班级：。

工程力学材料力学（北京科技大学与东北大学）第一章轴向拉伸与压缩1-1：用截面法求下列各杆指定截面得内力解：(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3= -P(d):N1=-2P,N2=P(e):N1= -50N,N2= -90N(f):N1=0、896P,N2=-0、732P注（轴向拉伸为正，压缩为负）1-2：高炉装料器中得大钟拉杆如图a所示，拉杆下端以连接楔与大钟连接，连接处拉杆得横截面如图b所示；拉杆上端螺纹得内径d=175mm。

以知作用于拉杆上得静拉力P=850kN，试计算大钟拉杆得最大静应力。

解：σ1=2118504P kNS dπ==35、3Mpaσ2=2228504P kNS dπ==30、4MPa∴σmax=35、3Mpa1-3：试计算图a所示钢水包吊杆得最大应力。

以知钢水包及其所盛钢水共重90kN，吊杆得尺寸如图b所示。

解：下端螺孔截面：σ1=19020.065*0.045P S=15、4Mpa上端单螺孔截面：σ2=2P S =8、72MPa上端双螺孔截面：σ3= 3P S =9、15Mpa∴σmax =15、4Mpa1-4：一桅杆起重机如图所示，起重杆AB为一钢管，其外径D=20mm,内径d=18mm;钢绳CB 得横截面面积为0、1cm2。

已知起重量P=2000N，试计算起重机杆与钢丝绳得应力。

解：受力分析得：F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47、7MPaσBC=22FS=103、5 MPa1-5：图a所示为一斗式提升机、斗与斗之间用链条连接,链条得计算简图如图b 所示,每个料斗连同物料得总重量P=2000N、钢链又两层钢板构成,如c所示、每个链板厚t=4、5mm,宽h=40mm,H=65mm,钉孔直径d=30mm、试求链板得最大应力、解:F=6PS 1=h*t=40*4、5=180mm 2S2=(H-d)*t=(65-30)*4、5=157、5mm2∴σmax=2F S =38、1MPa1-6:一长为30cm 得钢杆,其受力情况如图所示、已知杆截面面积A=10cm2,材料得弹性模量E=200Gpa,试求;(1) AC 、 CD DB 各段得应力与变形、 (2) AB 杆得总变形、解: (1)σAC =-20MPa,σCD =0,σDB =-20MPa;△ l AC =NL EA =AC LEA σ=-0、01mm△ l CD =CD LEA σ=0△ L DB =DB LEA σ=-0、01mm (2) ∴ABl ∆=-0、02mm1-7:一圆截面阶梯杆受力如图所示,已知 材料得弹性模量E=200Gpa,试求各段得应力与应变、 解:31.8127AC ACCB CBPMPa S PMPa S σσ====AC AC AC LNL EA EA σε===1、59*104,CB CB CB LNL EA EA σε===6、36*1041-8:为测定轧钢机得轧制力,在压下螺旋与上轧辊轴承之间装置一测压用得压头、压头就是一个钢制得圆筒,其外径D=50mm,内径d=40mm,在压头得外表面上沿纵向贴有测变形得电阻丝片、若测得轧辊两端两个压头得纵向应变均为ε=0、9*10-2,试求轧机得总轧 制压力、压头材料得弹性模量E=200Gpa 、 解:QNl l EA l l ε∆=∆=∴N EA ε=62.54*10N EA N ε∴==1-9：用一板状试样进行拉伸试验，在试样表面贴上纵向与横向得电阻丝来测定试样得改变。

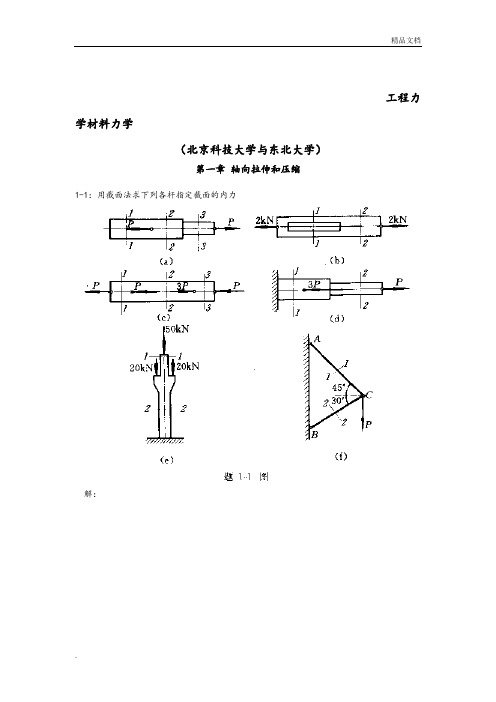
工程力学材料力学（北京科技大学与东北大学）第一章轴向拉伸和压缩1-1：用截面法求下列各杆指定截面的内力解：(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3= -P(d):N1=-2P,N2=P(e):N1= -50N,N2= -90N(f):N1=0.896P,N2=-0.732P注（轴向拉伸为正，压缩为负）1-2：高炉装料器中的大钟拉杆如图a所示，拉杆下端以连接楔与大钟连接，连接处拉杆的横截面如图b所示；拉杆上端螺纹的内径d=175mm。

以知作用于拉杆上的静拉力P=850kN，试计算大钟拉杆的最大静应力。

解：σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa∴σmax=35.3Mpa1-3：试计算图a所示钢水包吊杆的最大应力。

以知钢水包及其所盛钢水共重90kN，吊杆的尺寸如图b所示。

解：下端螺孔截面：σ1=19020.065*0.045P S=15.4Mpa上端单螺孔截面：σ2=2P S =8.72MPa 上端双螺孔截面：σ3= 3P S =9.15Mpa∴σmax =15.4Mpa1-4：一桅杆起重机如图所示，起重杆AB为一钢管，其外径D=20mm,内径d=18mm;钢绳CB 的横截面面积为0.1cm2。

已知起重量P=2000N，试计算起重机杆和钢丝绳的应力。

解：受力分析得：F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5 MPa1-5：图a所示为一斗式提升机.斗与斗之间用链条连接,链条的计算简图如图b 所示,每个料斗连同物料的总重量P=2000N.钢链又两层钢板构成,如c所示.每个链板厚t=4.5mm,宽h=40mm,H=65mm,钉孔直径d=30mm.试求链板的最大应力.解:F=6PS 1=h*t=40*4.5=180mm 2S2=(H-d)*t=(65-30)*4.5=157.5mm 2∴σmax=2F S =38.1MPa1-6:一长为30cm 的钢杆,其受力情况如图所示.已知杆截面面积A=10cm2,材料的弹性模量E=200Gpa,试求;(1) AC. CD DB 各段的应力和变形.(2) AB 杆的总变形.解: (1)σAC =-20MPa,σCD =0,σDB =-20MPa;△ l AC =NL EA =AC LEA σ=-0.01mm△l CD =CD LEA σ=0△L DB =DB LEA σ=-0.01mm(2) ∴ABl∆=-0.02mm1-7:一圆截面阶梯杆受力如图所示,已知材料的弹性模量E=200Gpa,试求各段的应力和应变.解:31.8127ACACCBCBPMPaSPMPaSσσ====ACACACLNLEA EAσε===1.59*104,CBCBCBLNLEA EAσε===6.36*1041-8:为测定轧钢机的轧制力,在压下螺旋与上轧辊轴承之间装置一测压用的压头.压头是一个钢制的圆筒,其外径D=50mm,内径d=40mm,在压头的外表面上沿纵向贴有测变形的电阻丝片.若测得轧辊两端两个压头的纵向应变均为ε=0.9*10-2,试求轧机的总轧制压力.压头材料的弹性模量E=200Gpa.解:QNllEAllε∆=∆=∴NEAε=62.54*10N EA Nε∴==1-9：用一板状试样进行拉伸试验，在试样表面贴上纵向和横向的电阻丝来测定试样的改变。

第二章习题2-1 一螺栓连接如图所示，已知P=200 kN， =2 cm，螺栓材料的许用切应力[τ]=80Mpa，试求螺栓的直径。

2-2 销钉式安全离合器如图所示，允许传递的外力偶距 m=10kN·cm，销钉材料的剪切强度极限=360 Mpa，轴的直径D=30mm，为保证m＞30000 N·cm 时销钉被剪切断，求销钉的直径 d。

2-3 冲床的最大冲力为400 kN，冲头材料的许用应力[σ]=440Mpa，被冲剪钢板的剪切强度极限=360 Mpa。

求在最大冲力作用下所能冲剪圆孔的最小直径D和钢板的最大厚度。

2-4 已知图示铆接钢板的厚度=10 mm，铆钉的直径为[τ]=140 Mpa，许用挤压应力[]=320 Mpa，P=24 kN，试做强度校核。

2-5 图示为测定剪切强度极限的试验装置。

若已经低碳钢试件的直径D=1 cm，剪断试件的外力P=50.2Kn，问材料的剪切强度极限为多少？2-6一减速机上齿轮与轴通过平键连接。

已知键受外力P=12 kN，所用平键的尺寸为b=28 mm，h=16 mm，l=60 mm，键的许用应力[τ]=87 Mpa，[]=100 Mpa。

试校核键的强度。

2-7图示连轴器，用四个螺栓连接，螺栓对称的安排在直径D=480 mm的圆周上。

这个连轴结传递的力偶矩m=24 kN·m，求螺栓的直径d需要多大？材料的许用切应力[τ]=80 Mpa。

（提示：由于对称，可假设个螺栓所受的剪力相等）2-8 图示夹剪，销子C的之间直径为0.6 cm，剪直径与销子直径相同的铜丝时，若力P=200 N，a=3 cm，b=15 cm，求铜丝与销子横截面上的平均切应力。

2-9 一冶炼厂使用的高压泵安全阀如图所示，要求当活塞下高压液体的压强达到p=3.4 Mpa时，使安全销沿1-1和2-2两截面剪断，从而使高压液体流出，以保证泵的安全。

已知活塞直径D=5.2cm，安全销采用15号钢，其剪切强度极限=320 Mpa，试确定安全销的直径d。

第9章平面体系的几何组成分析习题.【解】若上部结构与地基之间的连接比较多（N4）,能够考虑先将上部结构中的某•刚片与地基连成一个大刚片。

然后，在考虑这个大刚片与上部其它杆件的连接。

本例中，上部结构与地基之间用4个约束连接。

杆件ABE与地基之间用钗A和一根不同过该絞的链杆B相连，组成几何不变体系，且没有多余约束。

所以，能够将杆件ABE与地基看成一个没有多余约束的大刚片。

杆件FCD用三根既不相互平行又不相交于一点的链杆（链杆EF、链杆C、链杆D）与这个大刚片相连，组成一个更大的几何不变体系，且没有多余约束。

杆件ABE与地基之间用平行链杆A和一根不同过该絞的链杆B相连，组成几何不变体系，且没有多余约束。

将杆件ABE与地基看成一个没有多余约束的大刚片。

杆件FCD用三根既不相互平行又不相交于一点的链杆（链杆EF、链杆C、链杆D）与这个大刚片相连，组成一个更大的几何不变体系，且没有多余约束。

-I*羡诊为习题（C）图若上部结构中有皎接三角形，能够考虑将这些三角形看成刚片，然后在进行分析。

刚片I与地基组成•个没有多余约束的大刚片。

这个大刚片与刚片II用三根既不相互平行又不相交于一点的链杆相连，组成一个更大的几何不变体系，且没有多余约束。

习题（d）图将扩大的三角形看成刚片。

先分析一部分：左边的刚片与地基组成一个大刚片ABCD。

增加二元体：在大刚片ABCD上增加二元体DE杆和链杆E,组成一个更大的刚片。

此刚片与刚片GH1F由三根延长线交于H点的链杆（杆件CG、杆件FE、链杆1）相连。

故，体系为瞬变体系。

若上部结构与地基之间用三个约束连接，且符合几何不变体系的组成规律，能够只分析上部结构。

上部结构的分析结论就是整个体系的分析结论。

若折杆只用两个较与其它物体相连，能够将折杆看成是连接两个钗的直杆。

去掉二元体。

剩下部分为两个刚片用两个钗连接，为几何不变体系,且有一个多余约束。

故，整体体系也为几何不变体系，且有一个多余约束。

第九章习题9-1 图示的细长压杆均为圆杆，其直径d均相同．材料是Q 235钢．E＝。

其中：图a为两端铰支；图b为—端固定，一端210 GPa铰支；图c为两端固定，试判别哪一种情形的t临界力最大，哪种其次，。

哪种最小?若四杆直径d＝16cm，试求最大的临界力Pcr9-2 图示压杆的材料为Q 235钢，E＝210GPa在正视图a的平面内，两端为铰支，在俯视图b的平面内，两端认为固定。

试求此杆的临界力。

SHAPE \* MERGEFORMAT9-3 图示立柱由两根10号槽钢组成，立柱上端为球铰，下端固定，柱长L＝6m，试求两槽钢距离a值取多少立柱的临界力最大?其佰是多少?已知材料的弹性模量E＝200 GPa．比例极限σp＝200MPa。

9-4 图示结构AB为圆截面直杆，直径d＝80mm，A端固定，B端与BC 直秆球铰连接。

BC杆为正方形截面，边长a＝70 mm，C端也是球铰。

两杆材料相同，弹性模量E＝200GPa，比例极限σp＝200 MPa，长度l＝3m，求该结构的临界力。

9-5 图示托架中杆AB的直径d＝4 cm，长度l＝80 cm．两端可视为铰支，材料是Q235钢。

(1)试按杆AB的稳定条件求托架的临界力Qcr;(2)若巳知实际载荷Q=70 kN，稳定安全]＝2，问此托架是否安全?系数[nst9-6 悬臀回转吊车如图所示，斜杆AB由钢管制成，在B点铰支；铜管的外径D＝100mm，内径d＝86mm，杆长l＝3m,材料为Q235钢,E＝200 GPa、起重量Q＝20 kN，稳定安全系数[n]＝2．5。

试校核斜杆的稳定性。

st9—7 矿井采空区在充填前为防止顶板陷落，常用木柱支撑，若木柱为]＝4,求木红松，弹性模量E＝10GPa．直径d＝l 4cm规定稳定安全系数[nst柱所允许承受的顶板最大压力。

9—8 螺旋千斤顶（图9-16）的最大起重量P＝150 kN，丝杠长l＝0.5m,]材料为45号钢，E＝210 GPa．规定稳定安全系数[nst＝4.2，求丝杠所允许的最小内直径d。