【管理资料】生产运营管理计算题..汇编

考试必备【生产运作管理】经典计算题（带解释和答案）考试必备【生产运作管理】经典计算题(带解释和答案)重心法求工厂设置地1、某企业决定在武汉设立一生产基地，数据如下表。

利用重心法确定该基地的最佳位置。

假设运输量与运输成本存在线性关系（无保险费）。

工厂坐标年需求量/件 D1 （2，2） 800 D2 （3，5） 900 D3 （5，4） 200 D4 (8，5) 100解：X=(800*2+900*3+200*5+100*8)/(800+900+200+100)=3.05Y=(800*2+900*5+200*4+100*5)/(800+900+200+100)=3.7. 所以最佳位置为（3.05，3.7）。

1. 某跨国连锁超市企业在上海市有3家超市，坐标分别为（37，61）、（12，49）、（29，20）。

现在该企业打算在上海建立分部，管理上海市的业务。

假设3家超市的销售额是相同的。

(6.3.24)（1）用重心法决定上海分部的最佳位置。

解：因为3家超市的销售额相同，可以将他们的销售额假设为1. 上海分部的最佳位置，也就是3家超市的重心坐标，可以这样计算：x=(37+12+29)/3=27 y=(61+49+20)/3=43.3（2）如果该企业计划在上海建立第四家超市，其坐标为（16，18），那么如果计划通过，上海分部的最佳位置应该作何改变？解：增加一家超市后，重心坐标将变为：x=(37+12+29+16)/4=24.3 y=(61+49+20+18)/.4=37成本结构1、某商店销售服装，每月平均销售400件，单价180元/件，每次订购费用100元，单件年库存保管费用是单价的20%，为了减少订货次数，现在每次订货量是800件。

试分析：（1）该服装现在的年库存总成本是多少？(15000元)（2）经济订货批量（EOQ ）是多少？(163件) （1）总成本=（800/2）*180*20%+（400*12/800）*100=15000元（2）EOQ =H DS 2=800/)12*400(100*12*400*2=163件（3）EOQ 总成本=（163/2）*180*20%+（400*12/163）*100=5879元（4）年节约额=15000-5879=9121元节约幅度=（9124/15000）*100%=60.81%2、某食品厂每年需要采购3000吨面粉用于生产，每次采购订货手续费为300元，每吨产品的年库存成本为20元，请计算该食品厂采购面粉的经济订货批量EOQ 。

【生产运作管理】重心法求工厂设置地1、某企业决定在武汉设立一生产基地，数据如下表。

利用重心法确定该基地的Y=(800*2+900*5+200*4+100*5)/(800+900+200+100)=3.7. 所以最佳位置为（3.05，3.7）。

1. 某跨国连锁超市企业在上海市有3家超市，坐标分别为（37，61）、（12，49）、（29，20）。

现在该企业打算在上海建立分部，管理上海市的业务。

假设3家超市的销售额是相同的。

(6.3.24)（1） 用重心法决定上海分部的最佳位置。

解：因为3家超市的销售额相同，可以将他们的销售额假设为1. 上海分部的最佳位置，也就是3家超市的重心坐标，可以这样计算： x=(37+12+29)/3=27 y=(61+49+20)/3=43.3（2） 如果该企业计划在上海建立第四家超市，其坐标为（16，18），那么如果计划通过，上海分部的最佳位置应该作何改变？解：增加一家超市后，重心坐标将变为： x=(37+12+29+16)/4=24.3 y=(61+49+20+18)/.4=37成本结构1、某商店销售服装，每月平均销售400件，单价180元/件，每次订购费用100元，单件年库存保管费用是单价的20%，为了减少订货次数，现在每次订货量是800件。

试分析：（1）该服装现在的年库存总成本是多少？(15000元)（2）经济订货批量（EOQ ）是多少？(163件) （1）总成本=（800/2）*180*20%+（400*12/800）*100=15000元 （2）EOQ=HDS 2=800/)12*400(100*12*400*2=163件（3）EOQ 总成本=（163/2）*180*20%+（400*12/163）*100=5879元（4）年节约额=15000-5879=9121元节约幅度=（9124/15000）*100%=60.81%2、某食品厂每年需要采购3000吨面粉用于生产，每次采购订货手续费为300元，每吨产品的年库存成本为20元，请计算该食品厂采购面粉的经济订货批量EOQ 。

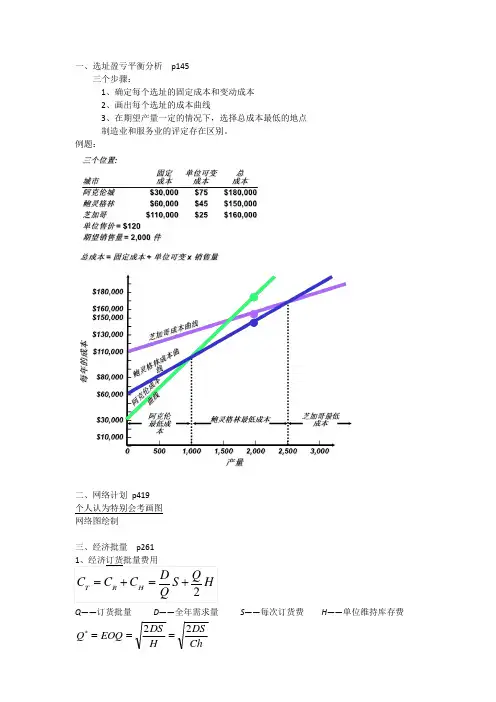
一、选址盈亏平衡分析 p145三个步骤：1、确定每个选址的固定成本和变动成本2、画出每个选址的成本曲线3、在期望产量一定的情况下，选择总成本最低的地点制造业和服务业的评定存在区别。

例题：二、网络计划 p419个人认为特别会考画图网络图绘制三、经济批量 p261Q——订货批量 D ——全年需求量 S——每次订货费 H ——单位维持库存费 ChDS H DS EOQ Q 22===*Q*—为经济订货批量C — 购买的单位货物的成本；S — 每次订货发生的费用（与供应商的联系费、采购人员旅差费等）；H — 单位货物每年的存储成本（H=C ⨯h ；h 为一常数，库存保管费用率）；平均库存量 = Q/2在经济订货批量为EOQ 时•d 为需求率，即单位时间内的需求量； • LT 为订货提前期。

某公司以单价10元每年购入8000单位某种产品，每次订货费用为30元，资金年利息率为12%，仓储费用按所存储货物价值的18%计算。

若每次订货的提前期为2周，试求经济订货批量、最低年总成本、年订货次数和订货点（一年按52周计算）。

• 已知： P=10元/件；D=8000件；S=30元；LT=2周H=10*12%+10*18%=3元/件.年。

则，经济批量：最低年总费用为：CT=p ·D+（D/Q ）·S+(Q/2) ·H8000*10+（8000/400）*30+（400/2）*3=81200元年订货次数：n=D/EOQ=8000/400=20次订货点：RL=（D/52一年52周）*LT=8000/52*2=307.7=308件2、经济生产批量EPL 则：经济生产批量为：最大库存：Q1= tp ⨯（p-d ）=Q*（p-d ）/ p平均库存= Q1 / 2=Q*（p-d ）/ （2p ）年总成本：T c =C ⨯D+（D /Q*）⨯S+[ Q*（p-d ）/ （2p ）]⨯H年生产次数：n=D / EPL订货点：RL=d ⨯LT例题（典型的EPL 问题）；根据预测，市场每年对X 公司生产的产品的需求量为 20000台，一年按250个工作日计算。

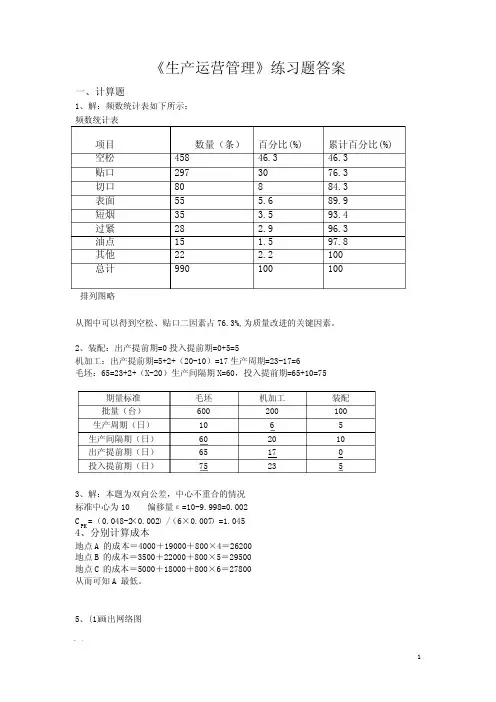
《生产运营管理》练习题答案一、计算题1、解：频数统计表如下所示：频数统计表项目 数量（条） 百分比(%) 累计百分比(%) 空松 458 46.3 46.3贴口 297 30 76.3切口 80 8 84.3表面 55 5.6 89.9短烟 35 3.5 93.4过紧 28 2.9 96.3油点 15 1.5 97.8其他 22 2.2 100总计 990 100 100排列图略从图中可以得到空松、贴口二因素占76.3%,为质量改进的关键因素。

2、装配：出产提前期=0投入提前期=0+5=5机加工：出产提前期=5+2+（20-10）=17生产周期=23-17=6毛坯：65=23+2+（X-20）生产间隔期X=60，投入提前期=65+10=75期量标准 毛坯 机加工 装配批量（台） 600 200 100生产周期（日） 10 6 5生产间隔期（日） 60 20 10出产提前期（日） 65 17 0投入提前期（日） 75 23 53、解：本题为双向公差，中心不重合的情况标准中心为10 偏移量ε=10-9.998=0.002CPK =（0.048-2×0.002）/（6×0.007）=1.0454、分别计算成本地点A的成本＝4000＋19000＋800×4＝26200 地点B的成本＝3500＋22000＋800×5＝29500 地点C的成本＝5000＋18000＋800×6＝27800 从而可知A最低。

5、(1)画出网络图① A ② B ③ D④ EF⑤ G ⑥(2)关键线路A-B-D-F-G ，37天(3)A-B-D-E 38天6、（1）设固定成本为F，单位产品的变动成本为c,年销售量为Q ，单位产品的销售价格为p. 2013年Q=240/100=2.4(万件)2014年Q=320/100=3.2(万件)200=F+c*2.4256=F+c*3.2F=32(万元) c=70元/件Q 0=F/(p-c)=1.067(万件)（2）当销售量为20000件时利润P=20000*100-320000-20000*70=280000元7、解经济订货批量为：HDS EOQ 2 1206.03636002=600（件）年订购次数=3600÷600=6（次）年订购总成本=6×36=216（元）年保管总成本=（600÷2）×0.72=216（元）年库存总成本TC =4328、已知：2, 2DS D Q Q TC DC S iC iC Q 当C＝5.00元时，EOQ＝632，不可行；当C＝4.50元时，EOQ＝667，可行。

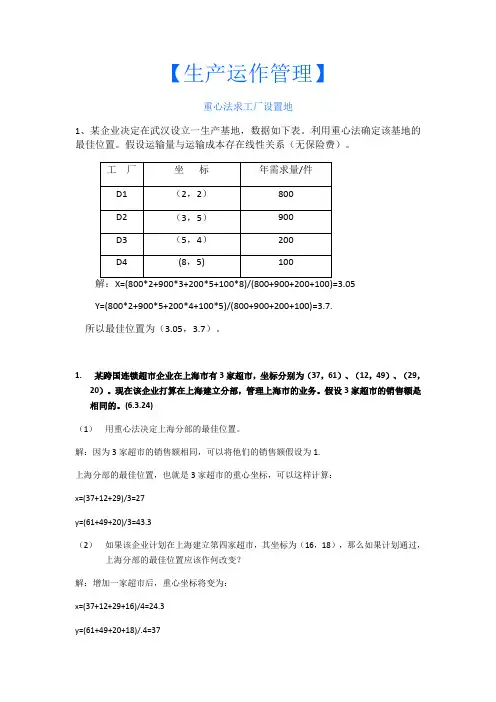
【生产运作管理】重心法求工厂设置地1、某企业决定在武汉设立一生产基地，数据如下表。

利用重心法确定该基地的最佳位置。

假设运输量与运输成本存在线性关系（无保险费）。

工厂坐标年需求量/件D1（2，2）800D2（3，5）900D3（5，4）200D4(8，5)100解：X=(800*2+900*3+200*5+100*8)/(800+900+200+100)=3.05Y=(800*2+900*5+200*4+100*5)/(800+900+200+100)=3.7.所以最佳位置为（3.05，3.7）。

1.某跨国连锁超市企业在上海市有3家超市，坐标分别为（37，61）、（12，49）、（29，20）。

现在该企业打算在上海建立分部，管理上海市的业务。

假设3家超市的销售额是相同的。

(6.3.24)（1）用重心法决定上海分部的最佳位置。

解：因为3家超市的销售额相同，可以将他们的销售额假设为1.上海分部的最佳位置，也就是3家超市的重心坐标，可以这样计算：x=(37+12+29)/3=27y=(61+49+20)/3=43.3（2）如果该企业计划在上海建立第四家超市，其坐标为（16，18），那么如果计划通过，上海分部的最佳位置应该作何改变？解：增加一家超市后，重心坐标将变为：x=(37+12+29+16)/4=24.3y=(61+49+20+18)/.4=37成本结构1、某商店销售服装，每月平均销售400件，单价180元/件，每次订购费用100元，单件年库存保管费用是单价的20%，为了减少订货次数，现在每次订货量是800件。

试分析：（1）该服装现在的年库存总成本是多少？(15000元)（2）经济订货批量（EOQ ）是多少？(163件) （1）总成本=（800/2）*180*20%+（400*12/800）*100=15000元 （2）EOQ =HDS 2=800/)12*400(100*12*400*2=163件（3）EOQ 总成本=（163/2）*180*20%+（400*12/163）*100=5879元 （4）年节约额=15000-5879=9121元 节约幅度=（9124/15000）*100%=60.81%2、某食品厂每年需要采购3000吨面粉用于生产，每次采购订货手续费为300元，每吨产品的年库存成本为20元，请计算该食品厂采购面粉的经济订货批量EOQ 。

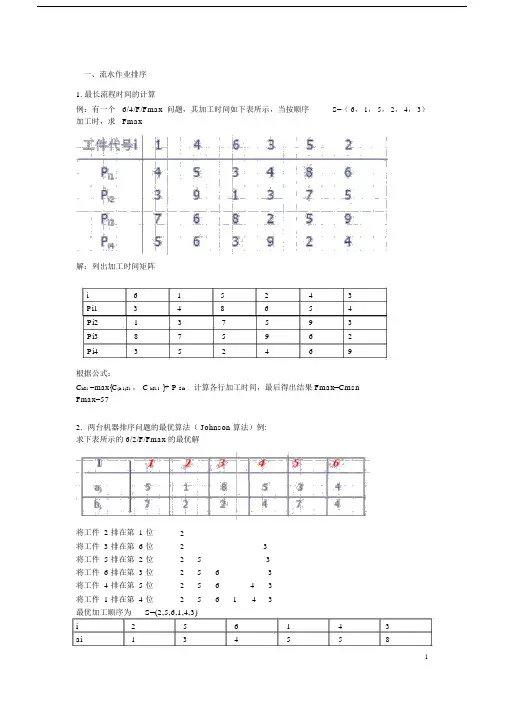
一、流水作业排序1.最长流程时间的计算例：有一个6/4/F/Fmax 问题，其加工时间如下表所示，当按顺序S=（ 6， 1， 5， 2， 4， 3）加工时，求Fmax解：列出加工时间矩阵i615243Pi1348654Pi2137593Pi3875962Pi4352469根据公式：C kSi =max{C(k-1)Si， C kSi-1 }+ P Sik，计算各行加工时间，最后得出结果 Fmax=CmsnFmax=572.两台机器排序问题的最优算法（ Johnson 算法）例:求下表所示的 6/2/F/Fmax 的最优解将工件 2 排在第 1 位2将工件 3 排在第 6 位23将工件 5 排在第 2 位253将工件 6 排在第 3 位2563将工件 4 排在第 5 位25643将工件 1 排在第 4 位256143最优加工顺序为S=(2,5,6,1,4,3)i256143ai134558bi274742由上表可算出，Fmax =283. 一般 n/m/F/Fmax 的最算法( 一 )Palmar 算法（λ i=∑ [k-(m+1)/2]P ik k=1,2,⋯,m按λ i不增的序排列工件）例:有一个 4/3/F/Fmax, 其加工如下表所示 , 用 Palmar 求解 .解：λ i=∑ [k-(3+1)/2]P ik，k=1,2，3λi=-Pi1+Pi3于是，λ 1=-P11+P13 =-1+4=3λ2=-P21+P23 ==2+5=3λ3=-P31+P33 =-6+8=2λ4=-P41+P43 =-3+2=-1按λ i不增的序排列工件，得到加工序（1， 2， 3， 4）和（ 2,1,3,4），算，二者都是最序，Fmax=28( 二 ) 关工件法例 : 有一个 4/3/F/Fmax, 其加工如下表所示, 用关工件法求解.解：由上表可知，加工最的是 3 号工件， Pi1<=Pi3 的工件 1 和 2，按 Pi1 不减的序排成 Sa=(1,2),Pi1>Pi3 的工件 4 号工件，Sb=(4), 得到加工序（ 1,2,3,4 ）。

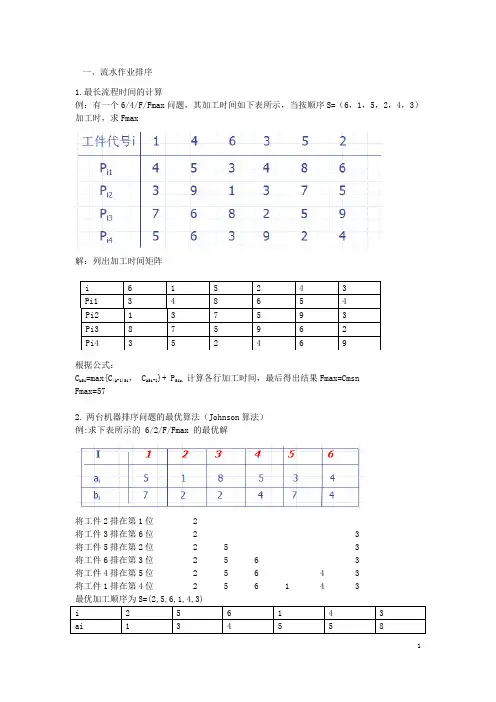
一、流水作业排序1.最长流程时间的计算例：有一个6/4/F/Fmax问题，其加工时间如下表所示，当按顺序S=（6，1，5，2，4，3）加工时，求Fmax解：列出加工时间矩阵i 6 1 5 2 4 3Pi1 3 4 8 6 5 4Pi2 1 3 7 5 9 3Pi3 8 7 5 9 6 2Pi4 3 5 2 4 6 9根据公式：C kSi=max{C(k-1)Si， C kSi-1}+ P Sik，计算各行加工时间，最后得出结果Fmax=CmsnFmax=572.两台机器排序问题的最优算法（Johnson算法）例:求下表所示的 6/2/F/Fmax 的最优解将工件2排在第1位 2将工件3排在第6位 2 3将工件5排在第2位 2 5 3将工件6排在第3位 2 5 6 3将工件4排在第5位 2 5 6 4 3将工件1排在第4位 2 5 6 1 4 3i 2 5 6 1 4 3ai 1 3 4 5 5 8bi 2 7 4 7 4 2由上表可计算出， Fmax =283. 一般n/m/F/Fmax 问题的最优算法(一)Palmar 算法（λi= ∑ [k-(m+1)/2]P ik k=1,2,…,m 按λi 不增的顺序排列工件 ） 例:有一个4/3/F/Fmax 问题,其加工时间如下表所示,用Palmar 求解.解：λi= ∑ [k-(3+1)/2]P ik ，k=1,2，3λi=-Pi1+Pi3于是，λ1=-P11+P13 =-1+4=3 λ2=-P21+P23 ==2+5=3 λ3=-P31+P33 =-6+8=2 λ4=-P41+P43 =-3+2=-1按λi 不增的顺序排列工件 ，得到加工顺序（1，2，3，4）和（2,1,3,4），经计算，二者都是最优顺序，Fmax=28 (二)关键工件法例:有一个4/3/F/Fmax 问题,其加工时间如下表所示,用关键工件法求解.解：由上表可知，加工时间最长的是3号工件，Pi1<=Pi3的工件为1和2，按Pi1不减的顺序排成Sa=(1,2),Pi1>Pi3的工件为4号工件，Sb=(4),这样得到加工顺序为（1,2,3,4）。

一、流水作业排序1.最长流程时间的计算例：有一个6/4/F/Fmax问题，其加工时间如下表所示，当按顺序S=（6，1，5，2，4，3）加工时，求Fmax解：列出加工时间矩阵根据公式：C kSi=max{C(k-1)Si， C kSi-1}+ P Sik，计算各行加工时间，最后得出结果Fmax=CmsnFmax=572.两台机器排序问题的最优算法（Johnson算法）例:求下表所示的 6/2/F/Fmax 的最优解将工件2排在第1位 2将工件3排在第6位 2 3将工件5排在第2位 2 5 3将工件6排在第3位 2 5 6 3将工件4排在第5位 2 5 6 4 3将工件1排在第4位 2 5 6 1 4 3最优加工顺序为S=(2,5,6,1,4,3)由上表可计算出， Fmax =283.一般n/m/F/Fmax问题的最优算法(一)Palmar算法（λi= ∑ [k-(m+1)/2]P ik k=1,2,…,m 按λi不增的顺序排列工件）例:有一个4/3/F/Fmax问题,其加工时间如下表所示,用Palmar求解.解：λi= ∑ [k-(3+1)/2]P ik，k=1,2，3λi=-Pi1+Pi3于是，λ1=-P11+P13 =-1+4=3λ2=-P21+P23 ==2+5=3λ3=-P31+P33 =-6+8=2λ4=-P41+P43 =-3+2=-1按λi不增的顺序排列工件，得到加工顺序（1，2，3，4）和（2,1,3,4），经计算，二者都是最优顺序，Fmax=28(二)关键工件法例:有一个4/3/F/Fmax问题,其加工时间如下表所示,用关键工件法求解.解：由上表可知，加工时间最长的是3号工件，Pi1<=Pi3的工件为1和2，按Pi1不减的顺序排成Sa=(1,2),Pi1>Pi3的工件为4号工件，Sb=(4),这样得到加工顺序为（1,2,3,4）。

经计算，Fmax=28二、生产能力的计算（一）、对于加工装配式生产，生产能力是一个模糊的概念。

一、流水作业排序1.最长流程时间的计算例：有一个6/4/F/Fmax问题，其加工时间如下表所示，当按顺序S=（6，1，5，2，4，3）加工时，求Fmax解：列出加工时间矩阵i 6 1 5 2 4 3Pi1 3 4 8 6 5 4Pi2 1 3 7 5 9 3Pi3 8 7 5 9 6 2Pi4 3 5 2 4 6 9根据公式：C kSi=max{C(k-1)Si， C kSi-1}+ P Sik，计算各行加工时间，最后得出结果Fmax=CmsnFmax=572.两台机器排序问题的最优算法（Johnson算法）例:求下表所示的 6/2/F/Fmax 的最优解将工件2排在第1位 2将工件3排在第6位 2 3将工件5排在第2位 2 5 3将工件6排在第3位 2 5 6 3将工件4排在第5位 2 5 6 4 3将工件1排在第4位 2 5 6 1 4 3i 2 5 6 1 4 3ai 1 3 4 5 5 8bi 2 7 4 7 4 2由上表可计算出， Fmax =283. 一般n/m/F/Fmax 问题的最优算法(一)Palmar 算法（λi= ∑ [k-(m+1)/2]P ik k=1,2,…,m 按λi 不增的顺序排列工件 ） 例:有一个4/3/F/Fmax 问题,其加工时间如下表所示,用Palmar 求解.解：λi= ∑ [k-(3+1)/2]P ik ，k=1,2，3λi=-Pi1+Pi3于是，λ1=-P11+P13 =-1+4=3 λ2=-P21+P23 ==2+5=3 λ3=-P31+P33 =-6+8=2 λ4=-P41+P43 =-3+2=-1按λi 不增的顺序排列工件 ，得到加工顺序（1，2，3，4）和（2,1,3,4），经计算，二者都是最优顺序，Fmax=28 (二)关键工件法例:有一个4/3/F/Fmax 问题,其加工时间如下表所示,用关键工件法求解.解：由上表可知，加工时间最长的是3号工件，Pi1<=Pi3的工件为1和2，按Pi1不减的顺序排成Sa=(1,2),Pi1>Pi3的工件为4号工件，Sb=(4),这样得到加工顺序为（1,2,3,4）。

一、流水作业排序1.最长流程时间的计算例：有一个6/4/F/Fmax问题，其加工时间如下表所示，当按顺序S=（6，1，5，2，4，3）加工时，求Fmax解：列出加工时间矩阵式：C kSi=max{C(k-1)Si，C kSi-1}+P Sik，计算各行加工时间，最后得出结果Fmax=CmsnFmax=572.两台机器排序问题的最优算法（Johnson算法）例:求下表所示的 6/2/F/Fmax 的最优解将工件2排在第1位 2将工件3排在第6位 2 3将工件5排在第2位 2 5 3将工件6排在第3位 2 5 6 3将工件4排在第5位 2 5 6 4 3将工件1排在第4位 2 5 6 1 4 3由上表可计算出， Fmax =283.一般n/m/F/Fmax问题的最优算法(一)Palmar算法（λi= ∑ [k-(m+1)/2]P ik k=1,2,…,m 按λi不增的顺序排列工件）例:有一个4/3/F/Fmax问题,其加工时间如下表所示,用Palmar求解.解：λi= ∑ [k-(3+1)/2]P ik，k=1,2，3λi=-Pi1+Pi3于是，λ1=-P11+P13 =-1+4=3λ2=-P21+P23 ==2+5=3λ3=-P31+P33 =-6+8=2λ4=-P41+P43 =-3+2=-1按λi不增的顺序排列工件，得到加工顺序（1，2，3，4）和（2,1,3,4），经计算，二者都是最优顺序，Fmax=28(二)关键工件法例:有一个4/3/F/Fmax问题,其加工时间如下表所示,用关键工件法求解.解：由上表可知，加工时间最长的是3号工件，Pi1<=Pi3的工件为1和2，按Pi1不减的顺序排成Sa=(1,2),Pi1>Pi3的工件为4号工件，Sb=(4),这样得到加工顺序为（1,2,3,4）。

经计算，Fmax=28二、生产能力的计算（一）、对于加工装配式生产，生产能力是一个模糊的概念。

一、流水作业排序1。

最长流程时间的计算例：有一个6/4/F/Fmax 问题,其加工时间如下表所示，当按顺序S=（6，1,5，2，4,3）加工时，求Fmax根据公式： C kSi =max ｛C （k-1）Si , C kSi —1}+ P Sik ，计算各行加工时间,最后得出结果Fmax=Cmsn Fmax=572. 两台机器排序问题的最优算法（Johnson 算法) 例:求下表所示的 6/2/F/Fmax 的最优解 将工件2排在第1位 2将工件3排在第6位 2 3 将工件5排在第2位 2 5 3 将工件6排在第3位 2 5 6 3 将工件4排在第5位 2 5 6 4 3 将工件1排在第4位 2 5 6 1 4 3 由上表可计算出， Fmax =283. 一般n/m/F/Fmax 问题的最优算法 （一)Palmar 算法（λi= ∑ [k-（m+1）/2］P ik k=1,2，…,m 按λi 不增的顺序排列工件 ) 例：有一个4/3/F/Fmax 问题,其加工时间如下表所示,用Palmar 求解。

解：λi= ∑ ［k —（3+1)/2]P ik ，k=1，2，3λi=—Pi1+Pi3于是，λ1=-P11+P13 =—1+4=3 λ2=-P21+P23 ==2+5=3 λ3=—P31+P33 =—6+8=2 λ4=—P41+P43 =—3+2=—1按λi 不增的顺序排列工件 ,得到加工顺序(1，2,3,4）和（2，1，3，4），经计算，二者都是最优顺序，Fmax=28 (二）关键工件法例：有一个4/3/F/Fmax 问题，其加工时间如下表所示，用关键工件法求解。

解:由上表可知,加工时间最长的是3号工件，Pi1〈=Pi3的工件为1和2，按Pi1不减的顺序排成Sa=（1,2），Pi1〉Pi3的工件为4号工件,Sb=(4），这样得到加工顺序为(1，2，3,4）。

经计算，Fmax=28 二、生产能力的计算（一)、对于加工装配式生产，生产能力是一个模糊的概念.大量生产，品种单一，可用具体产品数表示；大批生产,品种数少,可用代表产品数表示;多品种、中小批量生产,则只能以假定产品（Pseudo-product)的产量来表示。