高二数学上学期期末复习训练三新编不等式单元

高二数学期末复习一（不等式3）一、选择题1.设全集I =R ，集合P ={x |2x 2－x ＜0}，集合Q ={x |x 1≤2}，则( )A.P ∩ R Q=φB.P =R QC.P ∪Q =RD.P ∪Q ={x |x ＞0} 2.|x |≤2是|x +1|≤1成立的( )A 充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分又不必要条件3.不等式xx 1-≥2的解集为( ) A.［－1,0］ B.［－1,+∞］ C.(－∞,－1］ D.(－∞,－1］∪(0,+∞)4.若关于x 的不等式(a 2－1)x 2－(a －1)x －1＜0对于x ∈R 成立，则实数a 的取值范围是( )A.(－53，1]B.［－53，1］C.(－53，1)D.(－∞,－53)∪［1,+∞) 5.设A ={x |x 2－2x －3＞0},B ={x |x 2+ax +b ≤0}，若A ∪B =R ，A ∩B =(3，4)，则a +b 等于( )A.7B.－1C.1D.－76.设A ={x ||x －1|<2},B ={x |x x 2->0},则A ∩B 等于( ) A.{x |－1<x <3} B.{x |x <0或x >2} C.{x |－1<x <0}D.{x |－1<x <0或2<x <3} 7.若关于x 的不等式|x +2|+|x －1|＜a 的解集是∅,则a 的取值范围是( )A.(3，+∞)B.［3，+∞］C.(－∞，3］D.(－∞，3)8.不等式2)1()3(2--+x x x ≤0的解集是( ) A.{x |1≤x ＜2} B.{x |1＜x ＜2或x =－3} C.{x |1≤x ＜2或x =－3} D.{x |1≤x ≤2或x =－3}9.实数x 满足log 3x =1+sin θ,则|x －1|+|x －9|的值为( )A.8B.－8C.8或－8D.与θ有关10.函数f (x )、g (x )的定义域为R ,且f (x )≥0的解集为{x |1≤x ＜2},g (x )≥0的解集为∅,则不等式f (x )·g (x )>0的解集为( )A.{x |1≤x ＜2 }B.RC.∅D.{x |x <1或x ≥2}二、填空题11.方程|21-+x x |=xx -+21的解集是__________. 12.建造一个容积为18 m 3，深为2 m 的长方体无盖水池，如果池底和池壁每平方米的造价分别为200元和150元，那么池的最低造价为__________.13.设a ,a +1,a +2为钝角三角形的三边，则a 的取值范围是__________.14.已知关于x 的不等式|ax +2|<8的解集为(－3,5),则a =__________.三、解答题15解不等式(x 2+x +1)(x +1)3(x －2)2(3－x )＞0.16已知函数f (x )=264xx -+,g (x )=x 2－3ax +2a 2(a ＜0)，若不存在实数x 使得f (x )＞1和 g (x )＜0同时成立，试求a 的范围.17已知实数p 满足不等式212++x x <0,试判断方程u 2－2u +5－p 2=0有无实根,并给出证明. 18行驶中的汽车，在刹车时由于惯性作用，要继续往前滑行一段距离才能停下，这段距离叫做刹车距离.在某种路面上，某种型号汽车的刹车距离y (m)与汽车的车速x (km/h)满足下列关系:y =100nx +4002x (n 为常数，且n ∈N ). 我们做过两次刹车试验，有关数据如下图所示，其中⎩⎨⎧<<<<.1513,7521y y(1)求出n 的值；(2)要使刹车距离不超过18.4 m ，则行驶的最大速度应为多少？19已知不等式(m 2+4m －5)x 2－4(m －1)x +3>0对一切实数x 恒成立,求实数m 的取值范围.20 若不等式组⎪⎩⎪⎨⎧<+++>--05)25(2,0222k x k x x x 的整数解只有－2,k 应取何值?不等式(二)(A 卷)一、选择题1:A 2:B 3 A 4. A 5 D 6 D 7. C 8. C 9 A 10. D二、填空题11. {x |－1≤x ＜2＝ 12 5400元 13 1＜a ＜3 14 －2三、解答题15解:∵x 2+x +1＞0恒成立，∴不等式等价于⎩⎨⎧≠<-+20)3)(1(x x x －1＜x ＜2或2＜x ＜3.∴不等式的解集为{x |－1＜x ＜2或2＜x ＜3}.16解:由f (x )＞1，得264x x -+＞1, 化简整理得)2)(3()1)(2(+-+-x x x x ＜0. 解得－2＜x ＜－1或2＜x ＜3.即f (x )＞1的解集为A ={x |－2＜x ＜－1或2＜x ＜3}.由g (x )＜0得x 2－3ax +2a 2＜0,即(x －a )(x －2a )＜0(a ＜0).则g (x )＜0的解集为B ={x |2a ＜x ＜a ,a ＜0}.根据题意，有A ∩B =∅.因此，a ≤－2或－1≤2a ＜0.故a 的范围是{a |a ≤－2或－21≤a ＜0}. 17解:由212++x x <0,解得－2<x <－21. ∴－2<p <－21. 方程u 2－2u +5－p 2=0的判别式Δ=4(p 2－4).∵－2<p <－21,∴41<p 2<4.∴Δ<0. 由此得出方程u 2－2u +5－p 2=0无实根.18解:(1)由图象知，y 1=10040n +4001600=4+52n , y 2=1007n +4004900=107n +449. 由于5＜y 1＜7,13＜y 2＜15,∴⎪⎪⎩⎪⎪⎨⎧<+<<+<,1544910713,75245n n 即⎪⎪⎩⎪⎪⎨⎧<<<<.14551415,2155n n n ∴25＜n ＜1455. 又∵n ∈N ,∴n =3.(2)根据题意，得y =1003x +4002x ≤18.4. ∴x 2+12x －7360≤0,即(x +92)(x －80)≤0.由于x ＞0,∴0＜x ≤80,即行驶的最大速度为80 km/h.19解:(1)当m 2+4m －5=0,即m =1或m =－5时,显然m =1符合题意,m =－5不合题意.(2)当m 2+4m －5≠0时,要使二次不等式对一切x ∈R 恒成立,必须⎩⎨⎧<>-+,0Δ,0542m m 即⎪⎩⎪⎨⎧<-+--=>-+.0)54(12)1(16Δ,054222m m m m m 解得1<m <19.综合(1)(2)得m 的取值范围为［1,19).20 解:由x 2－x －2>0,解得x <－1或x >2.由2x 2+(5+2k )x +5k <0化为(2x +5)(x +k )<0.∵－2是其解,∴k <2. ∴－25<x <－k . ∴原不等式组可以化为①⎪⎩⎪⎨⎧-<<--<k x x 25,1或②⎪⎩⎪⎨⎧-<<->.25,2k x x ∵k <2,∴－k >－2.∴①的整数解为－2,而要使②无整数解,只有－k ≤3,即k ≥－3.∴－3≤k <2.沁园春·雪 <毛泽东>北国风光，千里冰封，万里雪飘。

高二数学上册第三章不等式练习题精编不等式，用不等号能够将两个分析式连结起来所成的式子。

以下是查词典数学网为大家整理的高二数学上册第三章不等式练习题，希望能够解决您所碰到的有关问题，加油，查词典数学网向来陪同您。

一、选择题1.以下式子① 3x=5; ② a③ 3m-1④ 5x+6y; ⑤ a+2⑥-12 中，不等式有()个A、2B、3C、4D、52.以下不等关系中，正确的选项是( )A 、 a 不是负数表示为 a B、 x 不大于 5 可表示为x5C、x 与 1 的和是非负数可表示为x+1D 、 m 与 4 的差是负数可表示为m-403.若 mA 、m-2n-2B 、 2m2n C、 -2m-2n D 、4.以下说法错误的选项是( )A 、1 不是 x2 的解B、 0 是 x1 的一个解C、不等式 x+33 的解是 x0 D 、 x=6 是 x-70 的解集5.以下数值： -2， -1.5，-1， 0，1.5， 2 能使不等式 x+32 建立的数有 ( )个. A、2 B、3 C、4 D、56.不等式 x-23 的解集是 ( )A 、 x2 B 、 x3 C、 x5 D 、 x57.假如对于 x 的不等式 (a+1)xa+1 的解集为x1，那么 a 的取值范围是()A 、a0 B、a0 C、a-1 D、 a-18.已知对于 x 的不等式x-a1 的解集为x2，则 a 的取值是 ( )A、0B、1C、2D、39.知足不等式x-13 的自然数是 ( )A、1，2，3， 4B、0， 1， 2， 3， 4C、 0，1，2，3D、无量多个10.以下说法中：①若ab，则 a-b②若 ab，则 ac2③若 acbc，则 a④若 ac2bc2，则 ab.正确的有 ( )A、1 个B、2 个C、3 个D、4 个11.以下表达中正确的选项是( )A 、若 x2x ，则 x0B 、若 x20，则 x0C、若 x1 则 x2x12.假如不等式axA 、a0 B、a0 C、a0 D、a0二、填空题1.不等式 2x5 的解有 ________个.2.a 的 3 倍与 b 的差小于 0 用不等式可表示为_______________.3.假如一个三角形的三条边长分别为5， 7，x，则 x 的取值范围是 ______________.4.在-25.以下各数 0， -3， 3，-0.5， -0.4，4，-20 中， ______是方程x+3=0 的解 ;_______是不等式x+3___________________ 是不等式 x+30.6.不等式 6-x0 的解集是 __________.7.用或填空：(1)若 xy ，则 - ; (2) 若 x+2y+2 ，则 -x______-y;(3)若 ab，则 1-a ________ 1-b;(4) 已知 x-5 y-5 ，则 x ___ y.8.若∣ m-3∣ =3-m，则 m 的取值范围是 __________.9.不等式 2x-15 的解集为 ________________.10.若 6-5a6-6b，则 a 与 b 的大小关系是 ____________.11.若不等式 -3x+n0 的解集是 x2，则不等式 -3x+n0 的解集是________.12.三个连续正整数的和不大于12，切合条件的正整数共有________组 .13.假如 a-2，那么 a 与的大小关系是 ___________.14.由 xy，得 axay，则 a ______0三、解答题1.依据以下的数目关系，列出不等式(1)x 与 1 的和是正数(2)y 的 2 倍与 1 的和大于 3(3)x 的与 x 的 2 倍的和是非正数(4)c 与 4 的和的 30%不大于 -2(5)x 除以 2 的商加上 2，至多为5(6)a 与 b 的和的平方不小于22.利用不等式的性质解以下不等式，并把解集在数轴上表示出来 .(1)4x+33x (2)4-x4(3) 2x-40 (4)- x+253.已知有理数m、 n 的地点在数轴上如下图，用不等号填空.(1)n-m ____0; (2)m+n _____0; (3)m-n ____0;(4)n+1 ____0; (5)mn ____0; (6)m-1____0.4.已知不等式5x-26x+1 的最小正整数解是方程3x- ax=6 的解，求 a 的值 .5.试写出四个不等式，使它们的解集分别知足以下条件：(1)x=2 是不等式的一个解 ;(2)-2， -1， 0 都是不等式的解 ;(3)不等式的正整数解只有 1， 2， 3;(4)不等式的整数解只有 -2， -1，0， 1.6.已知两个正整数的和与积相等，求这两个正整数.解：不如设这两个正整数为a、 b，且 a b，由题意得：ab=a+b ①则 ab=a+bb+b=2b ， a2∵ a 为正整数， a=1 或 2.(1)当 a=1 时，代入①式得 1b=1+b 不存在(2)当 a=2 时，代入①式得 2b=2+b ，b=2.所以，这两个正整数为2和 2.认真阅读以上资料，依据阅读资料的启迪，思虑：能否存在三个正整数，它们的和与积相等?试说明你的原由.7.依据等式和不等式的基天性质，我们能够获得比较两个数大小的方法：若A-B0 ，则 A 若 A-B=0 ，则 A=B; 若 A-B0 ，则 A⒈若一个角的余角不大于它的补角的1/3，则这个角的范围是()⒉某商品进价为800 元，售价为1200 元，因为受市场供求关系的影响，现准备打折销售，但要求收益率 (收益率 =售价 - 进价 /进价 *100%) 不底于 5%，则起码可打 ()A.6 折B.7 折C.8 折D.9 折⒊在以下不等式中，与3-2x/3-1 的解集同样的是()A.2x+60B.2x-60C.2x-60D.2x+60⒋不等式 3/7x5/4x 建立的条件是 ()⒌学生体质评论指标规定：握力体重指数m=( 握力 /体重)*100 ，七年级男生的合格标准是 m30。

高二数学单元测试（ 不 等 式 ）班级 学号 姓名 成绩一、选择题：（每小题5分，共50分）1、不等式b ax >的解集不可能是 （ ）A ．φB ．RC ．),(+∞a bD ．),(ab --∞2、以下四个命题中，正确命题有 （ ） ①b a b a >⇒>；②b a b a >⇒>；③b a b a >⇒>；④b a b a >⇒>． A ．1个 B ．2个 C ．3个 D ．4个3、不等式xx 1<的解集是 （ ） A ．{}1-≤x x B ．{}1 1>-<x x x 或 C ．{}11<<-x x D ．{}10 1<<-<x x x 或4、设{}42≥-=x xA ，{}42<-=x x B ，则集合B A ,满足 （ ）A ．B AC R = B ．R B A =⋃ C ．φ=⋂B AD ．A B C R =5、下列不等式中，解集为R 的是： （ ）A ．|x －3|>x －3B ．12222+-+-x x x x > 1C ．21≥+x xD ． 021log 221≥+x6、使不等式a x x <-+-43能成立的条件是 ( )A 、0<a<101 B 、0<a ≤1 C 、101<a<1 D 、a>1 7、设1>>b a ，111++=a b y ，a b y =2，113--=a b y ，则1y ，2y ，3y 的大小关系是 （ ）A ．1y <2y <3yB ．2y <1y <3yC ．3y <2y < 1yD ．2y <3y <1y 8、若+∈R y x ,，且y x a y x +≤+恒成立，则a 的最小值是 （ ）A ．22B ．2C ．2D ．19、已知函数)(x f 、)(x g )(R x ∈，且不等式)0()()(><+a a x g x f 的解集是M ， 不等式)0()()(><+a a x g x f 的解集是N ，则解集M 与N 的关系是A ．M N ⊂B ．N M =C ．N M ⊆D ．N M ⊂ （ ） 10、4个茶杯和5包茶叶的价格之和小于22元，而6个茶杯和3包茶叶的价格之和大于 24元，2个茶杯和3包茶叶的价格比较 （ ）A ．2个茶杯贵B ． 3包茶叶贵C ． 二者相同D ． 无法确定二、填空题：（每小题6分，共30分）11、函数122)(--=x x f 的定义域是 。

卜人入州八九几市潮王学校高二数学不等式期末复习一、选择题(每一小题4分，一共40分)1.(05〕不等式1312+-x x >0的解集为〔〕 A.{x |x <31-，或者x >21} B.{x |31-<x <21}C.{x |x >21}D.{x |x >31-}2.假设a<0,1<b <0,那么以下不等式中正确的选项是〔〕 A.a <ab 2<abB.ab 2<a <abC.a <ab <ab 2D.ab 2<ab <a3.f(x)=⎩⎨⎧<--≥+-)0()0(22x x x x x x ,那么不等式f(x)+2>0的解集为〔〕 A.(2,2)B.(),2()2,+∞⋃-∞ C.(-1,1)D.(),1()1,+∞⋃∞4.假设不等式〔a 2〕x 2+2(a 2)x 4＜0任意实数x 恒成立，那么实数a 的取值范围是 A.〔∞，2〕∪〔2，∞〕B.〔∞，2〕C.〔2，2〕D.〔2，2]5.0)2(<-a a 是12>a成立的() 6.(05)设a 、b ∈R ,a 2+2b 2=6,那么a +b 的最小值为〔〕A.3B.235-C.3D.27-ax 2+bx +c >0的解集为{x |31-<x <2}，那么不等式cx 2+bx +a <0的解是〔〕 A.{x |－3<x <21}B.{x |x <－3或者x >21}C.{x |－2<x <31}D.{x |x <－2或者x >31} 8.函数f(x)在R 上是增函数，A(0,2)、B(4,2)是其图象上的两个点，那么不等式|f(x +2)|<2的解集为() A.(2,2)B.(),2()2,+∞⋃-∞- C.(0,4)D.(),4()0,+∞⋃∞-x 的不等式|x +2|+|x 1|<a 的解集为∅，那么a 的取值范围为〔〕A ．(3，+∞)B ．[3，)∞+C ．-∞(，3]D ．-∞(，3)10.(05)在R 上定义运算⊗，其法那么为：x ⊗y =x (1y ).假设不等式(x -a )⊗(x +a )<1对任意实数x 均成立，那么()A.1<a <1B.0<a <2 C.2321<<-a D.2123<<-a 二、填空题〔每一小题4分，一共16分〕3252---x x x＜1的解集为0>x ，那么xx 432--的最大值是 2)(b a baab b a R b a ++∈和，则、的大小关系是________________________14.不等式组⎩⎨⎧<+-<+-08603422x x x x 的解集是不等式0922<+-a x x 的解集的子集，那么实数a 的取值范围是三、解答题(一共44分)15.〔10分〕(05)函数f (x )和g(x )的图象关于原点对称，且f (x )=x 2+x .(1)求函数g(x )解析式；(2)解不等式g(x )≥f(x )|x 1|16.〔10分〕某山区有一座水库，设计最大容积为256000m 3,据预测，山区在雨季时水库的入水量S(m 3)功与天数n (N n ∈)的关系是S=9000)24(+n n (n ≤30).水库原有水量为160000m 3，水闸泄水量每天为8000m 3,假设在雨季到来的第一天就开闸泄洪，问一周(7天)内会发生危险吗？并说明理由(水库水量超过其最大库容量，那么会发生危险).17.(1分〕设f(x)lgx a 、b 是满足f a f b f2ba +的实数，其中ab 求证：〔1〕a<1<b;(2)2<4b b2<3.18..(12分)假设非零函数f (x )满足以下条件：(1)对任意实数均有f (a b )=)()(b f a f ；(2)当x <0时，f (x )>1；(3)f (4)=161.解不等式f (x 3)f(5x 2)≤41.参考答案一、1A2A3A4D5A6C7A8A9C10C二、11、{x|-1<x<1或者2<x<3}11、342-13、2)(b a ba ab b a +>14、a<9三、15、〔1〕g(x)=-x 2+2x 〔2〕[-1，21] 16、解：设设雨季第n 天发生危险，那么160000+S-8000n>256000,即9000)24(+n n -8000n>96000,化简得n 2+24n-8⨯144>0,解得n>24.17、〔1〕证明：由f(a)=f(b)，得|lga|=|lgb|,因0<a<b,那么lga ≠lgb,1,0lg ,lg lg =∴=-=∴ab ab b a 即以0<a<b,b a <<<∴10 (2)由f(b)=2f(2b a +)，得|lgb|=2|lg 2b a +|,b a <<<10 ,12=>+∴ab ba , 即4b-b 2=a 2+2,又0<a<1,2<a 2+2<3，即有2<4b-b 2<318、解：令a=b ，知f(0)=1,那么)(1)()0()0()(b f b f f b f b f ==-=-， )()()()()]([)(b f a f b f a f b a f b a f =-=--=+∴，0)2()2()22()(≥=+=∴x f x f x x f x f ，41)2(,161)2()4(2±=∴==∴f f f .41)2(,1)2(0,1)2(,1)2()2()22(=<<∴>-=-=-f f f f f f 则且又.帮原不等式转化为 f[(x-3)+(5-x 2)]≤f(2)设1)()(,1)(,212121>>-<x f x f x x f x x 即则，x x 2532≥-+-∴解得10≤≤x故所求不等式解集为{x|10≤≤x }.。

高二数学期末复习题（三）一、选择题1、在等差数列{a n}中，已知a4，a7是函数f（x）=x2﹣4x+3的两个零点，则{a n}的前10项和等于（）A．﹣18 B．9 C．18 D．202、已知数列1，3，5，7，…则其前n项和S n为（）A．n2+1﹣B．n2+2﹣C．n2+1﹣ D．n2+2﹣3、已知等比数列{a n}的前n项和为S n，S4=1，S8=3，则a9+a10+a11+a12=（）A．8 B．6 C．4 D．24、设S n为等差数列{a n}的前n项和，a4=4，S5=15，若数列{}的前m项和为，则m=（）A．8 B．9 C．10 D．115、对于常数m，n，“mn＞0”是“方程mx2+ny2=1点曲线是椭圆”的（）条件．A．充分不必要B．必要不充分C．充分必要D．既不充分也不必要6、已知椭圆x2+my2=1的长轴长是短轴长的2倍，则实数m的值是（）A．2B．或4C．D．或27、设点P是椭圆=1（a＞b＞0）上一动点，F1，F2是椭圆的两个焦点，若•=0，tan∠PF2F1=2，则椭圆的离心率为（）A．+2B．﹣2C．D．8、已知直线（k+1）x+（2k﹣1）y+6k=0恒过定点A，若点A在直线mx+ny+4=0（m＞0，n＞0）上，则+的最小值是（）A．9B．C．3D．29、在△ABC中，若，则的最小值为（）A ．B ．C ．D ．10、对一切不等式x 4+（a ﹣1）x 2+1≥0恒成立，则a 的取值范围是（ ）A ．a ≥﹣1B ．a ≥0C ．a ≤3D ．a ≤111、椭圆上有n 个不同的点P 1，P 2，P 3，…，P n ，椭圆右焦点F ，数列{|P n F |}是公差大于的等差数列，则n 的最大值为（ ）A ．2017B ．2018C ．4036D ．403712、设A ，B 是椭圆C ：=1（m ＞0）长轴的两个端点，若C 上存在点M 满足∠AMB=120°，则m 的取值范围是（ ） A ．[，2）∪（2，2）B ．[，2]∪[2，6]C ．（0，）∪（2，+∞） D ．（0，]∪（6，+∞）二、 填空题13、双曲线与椭圆x 216＋y 264＝1有相同的焦点，它的一条渐近线为y ＝x ，则双曲线方程为______________________。

高二文科数学第一学期期末复习《不等式关系及不等式》一、 知识点回顾： 考点一：不等式的解法例1：不等式2320x x -+>的解集是 A ．{}21x x x <->-或 B ．{}12x x x <>或C ．{}12x x <<D ．{}21x x -<<-练习1： 不等式102x x +≥-的解集为 A ．{|12}x x -≤≤B ．{|12}x x -≤<C ．{|1x x ≤-或2}x ≥D ．{|1x x ≤-或2}x >练习2：函数y 的定义域为 ．练习3：若不等式ax 2＋bx －2>0的解集为⎩⎨⎧⎭⎬⎫x |－2<x <－14，则a ＋b 等于( )A ．－18B ．8C ．－13D ．1练习4：已知不等式2230x x --<的解集为A ，不等式2450x x +-<的解集为B . （1）求A B ；（2）若不等式20x ax b ++<的解集是AB ，求20ax x b ++<的解集.练习5:设已知条件2:8200p x x -->；:q 1x a >+或1x a <-；若q ⌝是p ⌝的充分而不必要条件，求正实数a 的取值范围．考点二：二元一次不等式组和线性规划问题例2：若 226x y x y ≥⎧⎪≥⎨⎪+≤⎩，则目标函数3z x y =+的取值范围是 ．练习6：如果实数,x y 满足:102010x y x y x -+≤⎧⎪+-≤⎨⎪+≥⎩，则目标函数4z x y =+的最大值为A ．2B ．3C ．27D ．4练习7:221x y x y +--+()()0≥表示的平面区域是练习8:某公司生产甲、乙两种桶装产品．已知生产甲产品1桶需耗A 原料1千克、B 原料2千克；生产乙产品1桶需耗A 原料2千克，B 原料1千克．每桶甲产品的利润是300元，每桶乙产品的利润是400元．公司在生产这两种产品的计划中，要求每天消耗A 、B 原料都不超过12千克．那么通过合理安排生产计划，每天生产的甲、乙两种产品分别多少桶时，公司共可获得的最大利润？并求出该最大利润.★例3：已知点P （x ，y ）的坐标满足条件41x y y x x +≤⎧⎪≥⎨≥⎪⎩，点O 为坐标原点，那么|PO |的最小值等于 ，最大值等于 ．★练习9：若实数x ，y 满足⎩⎪⎨⎪⎧x －y ＋1≤0，x >0，则yx －1的取值范围是( )A ．(－1,1)B ．(－∞，－1)∪(1，＋∞)C ．(－∞，－1)D ．[1，＋∞) 考点三：基本不等式及应用重要不等式：对于任意实数,a b ，有22____2a b ab +，当且仅当________时，等号成立.基本不等式：设,(0,)a b ∈+∞，则2a b+________时，不等式取等号. 例4：已知t >0，则函数y ＝t 2－4t ＋1t的最小值为练习10：在下列各函数中，最小值等于2的函数是( )A ．y ＝x ＋1xB ．y ＝cos x ＋1cos x (0<x <π2)C ．y ＝x 2＋3x 2＋2D ．y ＝e x ＋4e x －2练习11：已知正项等比数列{}n a 满足：7652a a a =+，如果存在两项m n a a 和14a ，则14m n+的最小值为 A ．32 B ．53 C ．256D ．不存在练习12:国际上钻石的重量计量单位为克拉．已知某种钻石的价值（美元）与其重量（克拉）的平方成正比，且一颗重为3克拉的该钻石的价值为54000美元． （Ⅰ）写出钻石的价值y 关于钻石重量x 的函数关系式；（Ⅱ）把一颗钻石切割成两颗钻石，若两颗钻石的重量分别为m 克拉和n 克拉，试证明：当n m =时，价值损失的百分率最大．（注:价值损失的百分率=100%-⨯原有价值现有价值原有价值；在切割过程中的重量损耗忽略不计）★练习13：证明不等式：a ，b ，c ∈R ，a 4＋b 4＋c 4≥abc (a ＋b ＋c )．二、 基础自测： 1．如果1a b <<-，则有A ．2211b a b a <<< B ．2211a b b a <<< C ．2211b a a b <<<D ．2211a b a b <<<2．不等式组300x x y x y ≤⎧⎪+≥⎨⎪-≥⎩表示的平面区域的面积等于A ．29 B ．9 C ．227 D ．183．下列二元一次不等式组可用来表示图中阴影部分表示的平面区域的是A ．10220x y x y +-≥⎧⎨-+≥⎩B ．10220x y x y +-≤⎧⎨-+≤⎩C ．10220x y x y +-≥⎧⎨-+≤⎩D ．10220x y x y +-≤⎧⎨-+≥⎩4. 若A ＝(x ＋3)(x ＋7)，B ＝(x ＋4)(x ＋6)，则A 、B 的大小关系为________．5．已知命题p ：44x a -<-<，命题q ：230x x --<()()，且q 是p 的充分而不必要条件，求a 的取值范围.高二文科数学第一学期期末复习《不等式关系及不等式》答案例1、B 练1、D 2、[-1,6] 3、C练4、解：（1）解不等式2230x x --<，得{}|13A x x =-<<……2分解不等式2450x x +-<，得{}|51B x x =-<< ……4分{}|53A B x x ∴=-<< ……6分（2）由20x ax b ++<的解集是（－5,3） ∴2550930a b a b -+=⎧⎨++=⎩，解得215a b =⎧⎨=-⎩……8分22150x x ∴+-< ，-3＜x ＜25， ……10分故不等式解集为5|32x x ⎧⎫-<<⎨⎬⎩⎭……12分 练5、解: 由020x 8x 2>-- 解得:10x >或2x -< ……3分又因:q a 1x +>或a 1x -<∴ p ⌝:10x 2≤≤-, q ⌝:a 1x a 1+≤≤- ……6分 q ⌝是p ⌝的充分不必要条件，∴⎪⎩⎪⎨⎧-≥-≤+>2a 110a 10a ……10分解得: 3a 0≤<所以所求a 的取值范围是(]3,0. ……12分例2、[]14,8 练6、C 练7、A练8、解：设每天分别生产甲产品x 桶，乙产品y 桶，相应的利润为z 元， 则⎩⎪⎨⎪⎧x ＋2y ≤12，2x ＋y ≤12，x ≥0，y ≥0，z ＝300x ＋400y ， ………… 6分在坐标平面内画出该不等式组表示的平面区域及直线300x ＋400y ＝0， …………10分 平移该直线，当平移到经过该平面区域内的点A (4,4)时，相应直线在y 轴上的截距达到最大， …………12分此时z ＝300x ＋400y 取得最大值，最大值是z ＝300×4＋400×4＝2 800，即该公司生产甲产品4桶乙产品4桶时可获得的最大利润是2 800元． …………14分 例3、10;2 练9、B例4、-2 练10、D 练11、A练12、解：（Ⅰ）由题意可设价值与重量的关系式为：2kx y = ………… 2分 ∵ 3克拉的价值是54000美元∴ 23k 54000⋅=解得：6000k = ………… 4分 ∴ 2x 6000y ⋅=答：此钻石的价值与重量的函数关系式为2x 6000y ⋅=. …… 6分（Ⅱ）若两颗钻石的重量为m 、n 克拉 则原有价值是()2n m 6000+，现有价值是22n 6000m 6000+ ………… 8分 价值损失的百分率=()()%100n m 6000n 6000m 6000n m 60002222⨯+--+ ()()21n m 2n m 2%100n m mn 2222=+⎪⎭⎫ ⎝⎛+⨯≤⨯+= ………… 11分 当且仅当n m =时取等号答：当n m =时,价值损失的百分率最大. ………… 14分练习13：证明 ∵a 4＋b 4≥2a 2b 2，b 4＋c 4≥2b 2c 2，c 4＋a 4≥2c 2a 2，∴2(a 4＋b 4＋c 4)≥2(a 2b 2＋b 2c 2＋c 2a 2) 即a 4＋b 4＋c 4≥a 2b 2＋b 2c 2＋c 2a 2.又a 2b 2＋b 2c 2≥2ab 2c ，b 2c 2＋c 2a 2≥2abc 2， c 2a 2＋a 2b 2≥2a 2bc .∴2(a 2b 2＋b 2c 2＋c 2a 2)≥2(ab 2c ＋abc 2＋a 2bc )， 即a 2b 2＋b 2c 2＋c 2a 2≥abc (a ＋b ＋c )． ∴a 4＋b 4＋c 4≥abc (a ＋b ＋c )．二、基础自测：1、A2、B3、A4、A<B5. 解： 设q ，p 表示的范围为集合A ，B ，则A ＝(2,3)，B ＝(a －4，a ＋4)． ………… 4分 由于q 是p 的充分而不必要条件，则有A 是B 的真子集， ………… 6分即⎩⎪⎨⎪⎧a －4≤2，a ＋4>3或 ⎩⎪⎨⎪⎧a －4<2，a ＋4≥3，………… 10分解得－1≤a ≤6. ………… 12分。

高二不等式练习题不等式是数学中常见的概念，它们广泛应用于各种领域的问题求解。

高二学生在学习数学过程中，需要掌握和熟练运用不等式的性质和解题技巧。

本文将针对高二不等式练习题，以解析的方式进行讲解和分析。

通过练习题的讲解，旨在帮助学生深入理解不等式，并提高解题水平。

1. 题目一求解不等式：2x - 3 > 7解析：首先，我们将不等式中的常数项移到左边，得到2x - 3 - 7 > 0，简化为2x - 10 > 0。

然后，将不等式两边都除以2，得到x - 5 > 0。

最后，将不等式表示为(x - 5) × 1 > 0。

根据乘积为正的性质可知，当(x - 5) > 0时，不等式成立。

解得x > 5。

2. 题目二求解不等式：3(x + 2) < 4x - 1 ≤ 5(x - 3)解析：首先，我们对不等式进行展开和整理，得到3x + 6 < 4x - 1 ≤5x - 15。

化简后可得-x - 6 < 0 ≤ 2x - 14。

进一步整理为-6 < x ≤ 8。

因此，不等式的解集为-6 < x ≤ 8。

3. 题目三求解不等式：(x - 3)(x + 2) ≤ 0解析：首先，我们需要找到不等式的零点。

解方程(x - 3)(x + 2) = 0，可以得到x = 3和x = -2。

根据零点的位置，我们将数轴分成三段：x < -2，-2 ≤ x ≤ 3，x > 3。

然后，我们选取每一段的测试点进行判断。

当x < -2时，我们取x = -3，代入不等式可以得到(-3 - 3)(-3 + 2) ≤ 0，即-6 ≤ 0，成立。

当-2 ≤ x ≤ 3时，我们取x = 0，代入不等式得到(0 - 3)(0 + 2)≤ 0，即-6 ≤ 0，成立。

当x > 3时，我们选取x = 4，代入不等式可以得到(4 - 3)(4 + 2) ≤ 0，即6 ≤ 0，不成立。

期末复习卷2（不等式）一、单选题1.(2021河南高二期末)设a=x2-2x+2,b=1-x,则实数a与b的大小关系为()A.a>bB.a=bC.a<bD.与x有关2.不等式2+x-x2<0的解集为()A.(-∞,-1)∪(2,+∞)B.(-2,1)C.(-1,2)D.(-∞,-2)∪(1,+∞)3.(2021福建泉州高一期末)若不等式ax2+bx-1≥0的解集是x-12≤x≤-13,则a=()A.-6B.-5C.65D.64.(2021安徽黄山高一期末)下列不等式正确的是()A.若a<b,则a2<b2B.若a>b,则ac>bcC.若a>b>0,c>d>0,e>f>0,则ace>bdfD.若a>b>c>0,d>e>f>0,则>>5.已知>0，则=2−4r1的最小值为()A.−2B.12C.1D.26.(2021云南高三期末)如果两个正方形的边长分别为x,y,且x+y=1,那么它们的面积之和的最小值是()A.14B.12C.1D.27.(2021湖北高三一模)已知正数a,b是关于x的函数y=x2-(m2+4)x+m的两个零点,则1+1的最小值为()A.2B.22C.4D.428.设>0，>0，+=1，则下列说法错误的是．()A.B的最大值为14B.2+2的最小值为12C.4+1的最小值为9D.+的最小值为2二、多选题9.若1<1<0,则下列说法正确的是()A.a<bB.a>bC.a2<b2D.ab<b210.(2021湖北高三月考)若非零实数a,b满足a>b,则下列结论正确的是()A.a+b≥2BB.a2+b2>2abC.|a+b|<2(2+2)D.(a+b)1+1>411.(2020广东高一期中)已知y=ax2+bx+c,不等式ax2+bx+c>0的解集是{x|1<x<3},下列说法正确的是()A.a>0B.a+b+c=0C.关于x的不等式cx2+bx+a>0的解集是x13<x<1D.如果am2+bm+c>0,则a(m+2)2+b(m+2)+c<012.已知正数，，则下列不等式中恒成立的是()A.+≥22B.(+p(1+1)≥4 C.≥2B D.2B r>B三、填空题13.(2021山东日照高一期末)不等式-1>0的解集为.14.(2020天津,14)已知a>0,b>0,且ab=1,则12+12+8r的最小值为.15.(2021上海黄浦格致中学高一期末)定义区间[a,b](a<b)的长度为b-a,若关于x的不等式x2-4x+m≤0的解集的区间长度为2,则实数m的值为.16.某校要建一个面积为200 2的长方形花园，并且在四周要修建出宽为2 和4 的小路(如图所示).要使得花园和小路占地总面积最小，则花园的长应为；最小面积为2．四、解答题17.(10分)解下列不等式：(1)2+3−22>0．(2)o3−p≤o+2)−1．(3)2−2+3>0．18.(12分)(2021吉林高一期末)已知x>0,y>0,且x+4y=40.(1)求xy的最大值;(2)求1+1的最小值.19.(12分)(2021云南昆明高二期末)已知函数y=x+1-1(x≠1).(1)解不等式(x-1)x+1-1>3;(2)当x>1时,求x+1-1的最小值.20.(12分)如图，某人计划用篱笆围成一个一边靠墙(墙的长度没有限制)的矩形生态种植园.设生态种植园的长为B，宽为B．(1)若生态种植园面积为722，则，为何值时，可使所用篱笆总长最小?(2)若使用的篱笆总长度为30，求1+2的最小值．21.(12分)(2021山东济宁高一期末)设函数y=ax2+(b-2)x+3.(1)若不等式ax2+(b-2)x+3>0的解集为(-1,1),求实数a,b的值;(2)若b=-a-1,且存在x∈R,使ax2+(b-2)x+3>4成立,求实数a的取值范围.22.(12分)(2021云南曲靖第二中学高一期末)设y=x2-(a-1)x+a-2(a∈R).(1)若不等式x2-(a-1)x+a-2≥-2对一切实数x恒成立,求实数a的取值范围;(2)解关于x的不等式x2-(a-1)x+a-2<0.期末复习卷2（不等式）参考答案1a-b=x2-x+1=x-122+34>0恒成立,所以a>b.故选A.2x2-x-2>0,即(x-2)(x+1)>0,解得x<-1或x>2,所以不等式2+x-x2<0的解集为(-∞,-1)∪(2,+∞).故选A.3不等式ax2+bx-1≥0的解集为x-12≤x≤-13,∴-12,-13为方程ax2+bx-1=0的两个根,∴根据根与系数的关系可得-12×-13=-1,解得a=-6.故选A.4A,若a=-3,b=2,则a2>b2,错误;对于B,若c=0,则ac=bc,错误;对于C,若a>b>0,c>d>0,e>f>0,由不等式的基本性质可得ace>bdf,正确;对于D,若a=3,b=2,c=1,d=3,e=2,f=1,则===1,错误.故选C.5.【答案】A解：>0，则=2−4r1=+1−4≥4=−2，当且仅当=1，即=1时，等号成立，则=2−4r1的最小值为−2．故选A．6x2+y2≥2xy,所以2(x2+y2)≥x2+y2+2xy=(x+y)2=1,所以x2+y2≥12,当且仅当x=y=1时,等号成立.因此,两个正方形的面积之和x2+y2的最小值为12.故选B.7,正数a,b是关于x的方程x2-(m2+4)x+m=0的两根,可得a+b=m2+4,ab=m>0,则1+1=r B=m+4≥4,当且仅当m=4,即m=2时等号成立.经检验知当m=2时,方程x2-(m2+4)x+m=0有两个正实数解.所以1+1的最小值为4.故选C.8.【答案】D【解析】解：由题意，对各选项依次进行分析：对，因为正实数，满足+=1，所以1=+≥2B，当且仅当==12时等号成立，所以B≤14，当且仅当==12时等号成立，故B有最大值14，故A 正确;对，因为(+p2=2+2+2B=1，所以2+2=1−2B≥1−2×112，当且仅当==12时等号成立，所以2+2有最小值12，故B正确．对，利用基本不等式，有4+1=+=4++5=9=1=，即=23=13时等号成立，故4+1有最小值9，故C正确；对，由题意，得(+p2=++2B=1+2B≤1+=2，故+≤2，当且仅当==12时等号成立，即+有最大值2，故D错误．故选D．9.答案BCD解析因为1<1<0,故a<0,b<0,b<a,即b<a<0,故B正确,A错误.对于C,a2-b2=(a-b)(a+b),而a+b<0,a-b>0,故a2-b2<0,即a2<b2,故C正确.对于D,ab-b2=b(a-b)<0,故ab<b2,故D正确.故选BCD.10.答案BC解析对于A,若a,b均为负数,则不等式显然不成立,故A错误;对于B,显然成立,故B正确;对于C,在a2+b2>2ab两边同时加上a2+b2,得2(a2+b2)>(a+b)2,则|a+b|<2(2+2)成立,故C正确;对于D,取a=2,b=-1,则(a+b)1+1=(2-1)×12+1-1=-12<4,则(a+b)1+1>4不成立,故D错误.故选BC.11.答案BCD解析对于A,ax2+bx+c>0的解集是{x|1<x<3},则a<0,故A不正确;对于B,由题意知x=1是方程ax2+bx+c=0的一个实数根,故a+b+c=0,故B正确;对于C,由题意知x=1和x=3是方程ax2+bx+c=0的两个实数根,则由根与系数的关系得=-4,=3,则不等式cx2+bx+a>0变为x2+x+1<0,即3x2-4x+1<0,解不等式得x的取值范围为x13<x<1,故C正确;对于D,如果am2+bm+c>0,则1<m<3,故3<m+2<5,则a(m+2)2+b(m+2)+c<0,故D正确.故选BCD.12.【答案】ABC【解析】解：因为，均为正数，所以++1B≥2B+1B≥22，当且仅当==22时，等号成立，A正确;因为，均为正数，所以(+p(1+1)=++2≥2·+2=4，当且仅当=时，等号成立，B正确;因为，均为正数，所以2+2≥2B>0，∴2+2B≥2B，当且仅当=时，等号成立，C正确;因为，均为正数，所以+≥2B，∴2B r≤1，所以2B r≤B，当且仅当=时，等号成立，不正确．故选ABC．13.(2021山东日照高一期末)不等式-1>0的解集为.答案(-∞,0)∪(1,+∞)解析由-1>0,解得x<0或x>1,即原不等式的解集为(-∞,0)∪(1,+∞).14.(2020天津,14)已知a>0,b>0,且ab=1,则12+12+8r的最小值为.答案4解析∵ab=1,∴b=1.∴12+12+8r=12+2+8r1=121++8r1.令1+a=t>0,则原式=2+8≥22·8=24=4.当且仅当t2=16,即t=4时,等号成立,此时1+a=4.15.(2021上海黄浦格致中学高一期末)定义区间[a,b](a<b)的长度为b-a,若关于x的不等式x2-4x+m≤0的解集的区间长度为2,则实数m的值为.答案3解析设x1,x2是方程x2-4x+m=0的两个根,则x1+x2=4,x1x2=m,∴|x1-x2|=(1+2)2-412=16-4=2,解得m=3.16.某校要建一个面积为200 2的长方形花园，并且在四周要修建出宽为2 和4 的小路(如图所示).要使得花园和小路占地总面积最小，则花园的长应为；最小面积为2．【答案】20,392解：设花园的长为B，则花园的宽为200，又设花园占地面积为B2，依题意，得=(+ 8)(200+4)=232+4(+400)⩾232+4×2b400=392，当且仅当=400，即=20时取“=”．所以花园的长为20，宽为10时，占地总面积最小为392 2．故答案为20；392．17.(10分)解下列不等式：(1)2+3−22>0．(2)o3−p≤o+2)−1．(3)2−2+3>0．【答案】解：(1)原不等式可化为22−3−2<0，所以(2+1)(−2)<0，故原不等式的解集是{U−12< <2}．(2)原不等式可化为22−−1≥0．所以(2+1)(−1)≥0，故原不等式的解集为{U≤−12或≥1}．(3)由2−2+3=(−1)2+2>0对任意的∈恒成立，故原不等式的解集是．18.(12分)(2021吉林高一期末)已知x>0,y>0,且x+4y=40.(1)求xy的最大值;(2)求1+1的最小值.解(1)因为x>0,y>0,所以40=x+4y≥24B=4B(当且仅当x=4y,即x=20,y=5时,等号成立).所以xy≤100,因此xy的最大值为100.(2)因为x+4y=40,即140(x+4y)=1,所以1+1=140(x+4y)1+1=1405+4+≥1405+24·=940当且仅当x=2y,即x=403,y=203时,等号成立.所以1+1的最小值为940.19.(12分)(2021云南昆明高二期末)已知函数y=x+1-1(x≠1).(1)解不等式(x-1)x+1-1>3;(2)当x>1时,求x+1-1的最小值.解(1)由(x-1)x+1-1>3,得x2-x-2>0.又x≠1,所以解得x>2或x<-1,即原不等式的解集为(-∞,-1)∪(2,+∞). (2)当x>1时,x-1>0,y=x+1-1=x-1+1-1+1≥2+1=3,当且仅当x-1=1-1,即x=2或x=0(舍)时,等号成立.所以x+1-1的最小值是3.20.(12分)如图，某人计划用篱笆围成一个一边靠墙(墙的长度没有限制)的矩形生态种植园.设生态种植园的长为B，宽为B．(1)若生态种植园面积为722，则，为何值时，可使所用篱笆总长最小?(2)若使用的篱笆总长度为30，求1+2的最小值．【答案】解：(1)由已知可得B=72，其中>0，>0，篱笆总长为(+2p．又因为+2≥22B=24，当且仅当=2，即=12，=6时等号成立．所以当=12，=6时，可使所用篱笆总长最小．(2)由已知得+2=30，>0，>0，又因为(1+2)(+2p=5+2+2≥5+=9，所以1+2≥310，当且仅当2=2，即=，即=10，=10时等号成立．所以1+2的最小值是310．21.(12分)(2021山东济宁高一期末)设函数y=ax2+(b-2)x+3.(1)若不等式ax2+(b-2)x+3>0的解集为(-1,1),求实数a,b的值;(2)若b=-a-1,且存在x∈R,使ax2+(b-2)x+3>4成立,求实数a的取值范围.由题意可知,方程ax2+(b-2)x+3=0的两根是-1,1,=0,1,解得=-3,=2.(2)存在x∈R,使ax2+(b-2)x-1>0成立,将b=-a-1代入上式可得ax2-(a+3)x-1>0成立.当a≥0时,显然存在x∈R使得上式成立;当a<0时,需使方程ax2-(a+3)x-1=0有两个不相等的实根,所以Δ=(a+3)2+4a>0,即a2+10a+9>0,解得a<-9或-1<a<0.综上可知,a的取值范围是(-∞,-9)∪(-1,+∞).22.(12分)(2021云南曲靖第二中学高一期末)设y=x2-(a-1)x+a-2(a∈R).(1)若不等式x2-(a-1)x+a-2≥-2对一切实数x恒成立,求实数a的取值范围;x的不等式x2-(a-1)x+a-2<0.由题意,不等式x2-(a-1)x+a-2≥-2对于一切实数x恒成立,等价于x2-(a-1)x+a≥0对于一切实数x恒成立.所以Δ=(a-1)2-4a≤0,解得3-22≤a≤3+22.故实数a的取值范围为[3-22,3+22].(2)不等式x2-(a-1)x+a-2<0,即[x-(a-2)](x-1)<0.当a-2>1,即a>3时,不等式的解集为{x|1<x<a-2};当a-2=1,即a=3时,不等式的解集为⌀;当a-2<1,即a<3时,不等式的解集为{x|a-2<x<1}.综上所述,当a<3时,不等式的解集为{x|a-2<x<1};当a=3时,不等式的解集为⌀;当a>3时,不等式的解集为{x|1<x<a-2}.。

“不等式”复习测试题1．设a b <，c d <，则下列不等式中一定成立的是（ ）A ．d b c a ->-B ．bd ac >C ．d b c a +>+D ．c b d a +>+2．不等式xx 1>的解集是（ ） A ．}1{<x x B ．1{-<x x 或}1>xC ．01{<<-x x 或}1>xD ．}11{<<-x x3．若011<<ba ，则下列结论不正确的是（ ） A ．22b a < B ．2b ab < C ．2>+ba ab D ．||||||b a b a +>+ 4．“0>>b a ”是“222b a ab +<”的（ ） A ．充分而不必要条件 B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件5．下列各式中最小值是2的是（ ）A ．y x ＋x yB ．4522++x x C ．tan x ＋cot x D ． x x -+22 6．已知()f x 是奇函数，且在（－∞，０）上是增函数，(2)0f =，则不等式()0xf x <的解集是（ ）A ．{|20,2}x x x -<<>或B ． {|20,}x x -<<或0<x<2C ．}22|{>-<x x x 或D ．{|2,02}x x x <-<<或7．不等式 022>++bx ax 的解集是)31,21(-，则b a -的值等于 。

8．比较13)(2+-=x x x f 与12)(2-+=x x x g 的大小关系 。

9．设0>x ，则函数xx y 164--=的最大值为 。

10．如果a x x ≥+++|9||1|对任意实数x 总成立,则a 的取值范围是 。

高二上不等式练习题不等式在高中数学学科中占有重要地位，它是代数与几何交叉的一个重要分支。

在高二上这个学期里，我们将会学习不等式的性质、解法和应用。

为了帮助大家更好地掌握不等式的知识，接下来我将为大家提供一些高二上不等式练习题。

1. 求解不等式：3x - 2 < 4x + 12. 将下列不等式改写成集合表示：-2 < x ≤ 53. 根据给定条件，求解不等式：4 - 3x > 10，-2 ≤ x < 54. 求解不等式组：{x + y ≥ 3, 2x - y < 4}5. 求解绝对值不等式：|2x - 1| < 56. 根据条件，求解复合不等式：3 ≤ x - 2 < 5，1 < y ≤ 4解答：1. 首先将不等式中的x移到一边，得到3x - 4x < 1 + 2化简得到-x < 3将不等式两边乘以-1，注意此时需要反转不等号的方向，得到x > -32. 集合表示为 (-2, 5]3. 在这个题目中，不等式给出了两个条件：4 - 3x > 10，-2 ≤ x < 5先解第一个不等式：4 - 3x > 10将x移到一边得到-3x > 6乘以-1并反转不等号得到3x < -6再除以3得到x < -2接下来解第二个不等式：-2 ≤ x < 5根据这个条件，我们可以确定-2 ≤ x，所以x的取值范围是大于等于-2的数所以综合以上两个条件，x的取值范围是-2 ≤ x < -24. 首先解第一个不等式：x + y ≥ 3将y移到一边得到x ≥ 3 - y然后解第二个不等式：2x - y < 4将y移到一边得到2x < 4 + y再除以2得到x < 2 + y/2综合以上两个不等式的解，得到{x | x ≥ 3 - y 且 x < 2 + y/2}5. 首先将绝对值不等式拆分成两个条件：2x - 1 < 5 和 -(2x - 1) < 5解第一个不等式：2x - 1 < 5将1移到一边得到2x < 5 + 1化简得到2x < 6再除以2得到x < 3解第二个不等式：-(2x - 1) < 5将负号移到一边得到2x - 1 > -5将1移到一边得到2x > -5 + 1化简得到2x > -4再除以2得到x > -2综合以上两个不等式的解，得到{x | -2 < x < 3}6. 首先解第一个不等式：3 ≤ x - 2 < 5将2移到一边得到3 + 2 ≤ x < 5 + 2化简得到5 ≤ x < 7然后解第二个不等式：1 < y ≤ 4根据给定条件，y的取值范围是大于1小于等于4的数，即1 < y ≤ 4综合以上两个不等式的解，得到{x, y | 5 ≤ x < 7 且1 < y ≤ 4}通过以上六个不等式的练习题，我们可以更好地理解和掌握高二上的不等式知识。

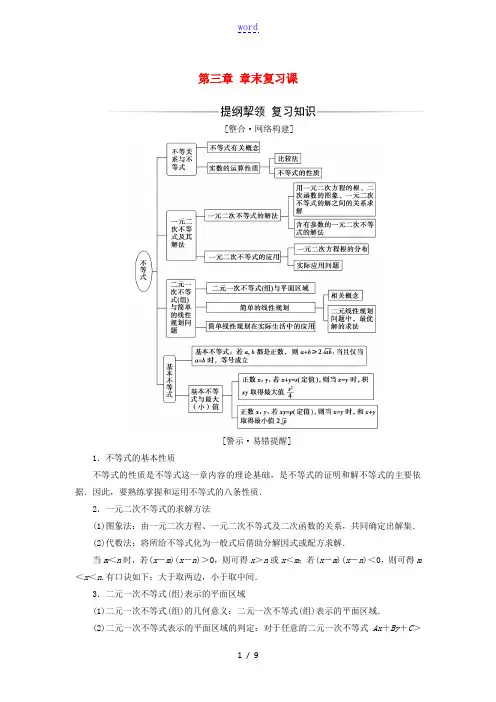
第三章章末复习课[整合·网络构建][警示·易错提醒]1．不等式的基本性质不等式的性质是不等式这一章内容的理论基础，是不等式的证明和解不等式的主要依据．因此，要熟练掌握和运用不等式的八条性质．2．一元二次不等式的求解方法(1)图象法：由一元二次方程、一元二次不等式及二次函数的关系，共同确定出解集．(2)代数法：将所给不等式化为一般式后借助分解因式或配方求解．当m＜n时，若(x－m)(x－n)＞0，则可得x＞n或x＜m；若(x－m)(x－n)＜0，则可得m ＜x＜n.有口诀如下：大于取两边，小于取中间．3．二元一次不等式(组)表示的平面区域(1)二元一次不等式(组)的几何意义：二元一次不等式(组)表示的平面区域．(2)二元一次不等式表示的平面区域的判定：对于任意的二元一次不等式Ax＋By＋C＞0(或＜0)，无论B 为正值还是负值，我们都可以把y 项的系数变形为正数，当B ＞0时，①Ax ＋By ＋C ＞0表示直线Ax ＋By ＋C ＝0上方的区域；②Ax ＋By ＋C ＜0表示直线Ax ＋By ＋C ＝0下方的区域．4．求目标函数最优解的两种方法(1)平移直线法．平移法是一种最基本的方法，其基本原理是两平行直线中的一条上任意一点到另一条直线的距离相等；(2)代入检验法．通过平移法可以发现，取得最优解对应的点往往是可行域的顶点，其实这具有必然性．于是在选择题中关于线性规划的最值问题，可采用求解方程组代入检验的方法求解．5．运用基本不等式求最值，把握三个条件(易错点) (1)“一正”——各项为正数；(2)“二定”——“和”或“积”为定值； (3)“三相等”——等号一定能取到．专题一 不等关系与不等式的基本性质1．同向不等式可以相加，异向不等式可以相减；但异向不等式不可以相加，同向不等式不可以相减．(1)若a ＞b ，c ＞d ，则a ＋c ＞b ＋d ； (2)若a ＞b ，c ＜d ，则a －c ＞b －a .2．左右同正不等式：同向的不等式可以相乘，但不能相除；异向不等式可以相除，但不能相乘．(1)若a ＞b ＞0，c ＞d ＞0，则ac ＞bd ； (2)若a ＞b ＞0，0＜c ＜d ，则a c ＞bd.3．左右同正不等式，两边可以同时乘方或开方：若a ＞b ＞0，则a n ＞b n或n a ＞nb . 4．若ab ＞0，a ＞b ，则1a ＜1b ；若ab ＜0，a ＞b ，则1a ＞1b.[例1] 已知a ＞0，b ＞0，且a ≠b ，比较a 2b ＋b 2a 与a ＋b 的大小．解：因为⎝ ⎛⎭⎪⎫a 2b ＋b 2a －(a ＋b )＝a 2b －b ＋b 2a －a ＝ a 2－b 2b ＋b 2－a 2a ＝(a 2－b 2)⎝ ⎛⎭⎪⎫1b －1a ＝(a 2－b 2)a －b ab ＝（a －b ）2（a ＋b ）ab，因为a ＞0，b ＞0，且a ≠b ， 所以(a －b )2＞0，a ＋b ＞0，ab ＞0，所以⎝ ⎛⎭⎪⎫a 2b ＋b 2a －(a ＋b )＞0，即a 2b ＋b 2a ＞a ＋b .归纳升华不等式比较大小的常用方法(1)作差比较法：作差后通过分解因式、配方等手段判断差的符号得出结果． (2)作商比较法：常用于分数指数幂的代数式． (3)乘方转化的方法：常用于根式比较大小． (4)分子分母有理化． (5)利用中间量．[变式训练] (1)已知0＜x ＜2，求函数y ＝x (8－3x )的最大值； (2)设函数f (x )＝x ＋2x ＋1，x ∈[0，＋∞)，求函数f (x )的最小值． 解：(1)因为0＜x ＜2，所以0＜3x ＜6，8－3x ＞0， 所以y ＝x (8－3x )＝13×3x ·(8－3x )≤13⎝ ⎛⎭⎪⎫3x ＋8－3x 22＝163，当且仅当3x ＝8－3x ，即x ＝43时，取等号，所以当x ＝43时，y ＝x (8－3x )有最大值为163.(2)f (x )＝x ＋2x ＋1＝(x ＋1)＋2x ＋1－1，因为x ∈[0，＋∞)，所以x ＋1＞0，2x ＋1＞0， 所以x ＋1＋2x ＋1≥2 2. 当且仅当x ＋1＝2x ＋1， 即x ＝2－1时，f (x )取最小值． 此时f (x )min ＝22－1.专题二 一元二次不等式的解法 一元二次不等式的求解流程如下： 一化——化二次项系数为正数．二判——判断对应方程的根． 三求——求对应方程的根． 四画——画出对应函数的图象． 五解集——根据图象写出不等式的解集． [例2] (1)解不等式：－1＜x 2＋2x －1≤2； (2)解不等式a （x －1）x －2＞1(a ≠1)．解：(1)原不等式等价于⎩⎪⎨⎪⎧x 2＋2x －1＞－1，x 2＋2x －1≤2，即⎩⎪⎨⎪⎧x 2＋2x ＞0， ①x 2＋2x －3≤0. ② 由①得x (x ＋2)＞0，所以x ＜－2或x ＞0； 由②得(x ＋3)(x －1)≤0， 所以－3≤x ≤1.将①②的解集在数轴上表示出来，如图所示．求其交集得原不等式的解集为{x |－3≤x ＜－2或0＜x ≤1}．(2)原不等式可化为a （x －1）x －2－1＞0，即(a －1)⎝⎛⎭⎪⎫x －a －2a －1(x －2)＞0(*)， ①当a ＞1时，(*)式即为⎝⎛⎭⎪⎫x －a －2a －1(x －2)＞0，而a －2a －1－2＝－a a －1＜0，所以a －2a －1＜2，此时x ＞2或x ＜a －2a －1. ②当a ＜1时，(*)式即为⎝⎛⎭⎪⎫x －a －2a －1(x －2)＜0， 而2－a －2a －1＝aa －1， 若0＜a ＜1，则a －2a －1＞2，此时2＜x ＜a －2a －1； 若a ＝0，则(x －2)2＜0，此时无解； 若a ＜0，则a －2a －1＜2，此时a －2a －1＜x ＜2. 综上所述，当a ＞1时，不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x ＜a －2a －1或x ＞2； 当0＜a ＜1时，不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪2＜x ＜a －2a －1； 当a ＝0时，不等式的解集为∅； 当a ＜0时，不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪a －2a －1＜x ＜2.归纳升华含参数的一元二次不等式的分类讨论(1)对二次项系数含有参数的一元二次不等式，要注意对二次项系数是否为零进行讨论，特别当二次项系数为零时需转化为一元一次不等式问题来求解．(2)对含参数的一元二次不等式，在其解的情况不明确的情况下，需要对其判别式分Δ＞0，Δ＝0，Δ＜0三种情况并加以讨论．(3)若含参数的一元二次不等式可以转化成用其根x 1，x 2表示的形如a (x －x 1)(x －x 2)的形式时，往往需要对其根分x 1＞x 2、x 1＝x 2，x 1＜x 2三种情况进行讨论，或用根与系数的关系帮助求解．[变式训练] 定义在(－1，1)上的奇函数f (x )在整个定义域上是减函数，且f (1－a )＋f (1－a 2)＜0，某某数a 的取值X 围．解：因为f (x )的定义域为(－1，1)，所以⎩⎪⎨⎪⎧－1＜1－a ＜1，－1＜1－a 2＜1， 所以⎩⎨⎧0＜a ＜2，－2＜a ＜2且a ≠0，所以0＜a ＜2，①原不等式变形为f (1－a )＜－f (1－a 2)． 由于f (x )为奇函数，有－f (1－a 2)＝f (a 2－1)， 所以f (1－a )＜f (a 2－1)． 又f (x )在(－1，1)上是减函数， 所以1－a ＞a 2－1，解得－2＜a ＜1.② 由①②可得0＜a ＜1， 所以a 的取值X 围是(0，1)． 专题三 简单的线性规划问题 线性规划问题在实际中的类型主要有：(1)给定一定数量的人力、物力资源，求如何运用这些资源，使完成任务量最大，收到的效益最高；(2)给定一项任务，问怎样统筹安排，使得完成这项任务耗费的人力、物力资源最少. [例3] 某厂用甲、乙两种原料生产A ，B 两种产品，制造1 t A ，1 t B 产品需要的各种原料数、可得到利润以及工厂现有各种原料数如下表：原料 每种产品所需原料/t现有原料数/tAB甲 2 1 14 乙 1 3 18 利润/(万元/t)53____(1)在现有原料条件下，生产A ，B 两种产品各多少时，才能使利润最大？(2)每吨B 产品的利润在什么X 围变化时，原最优解不变？当超出这个X 围时，最优解有何变化？解：(1)生产A ，B 两种产品分别为x t ，y t ，则利润z ＝5x ＋3y ，x ，y 满足⎩⎪⎨⎪⎧2x ＋y ≤14.x ＋3y ≤18，x ≥0，y ≥0，作出可行域如图所示：当直线5x ＋3y ＝z 过点B ⎝ ⎛⎭⎪⎫245，225时，z 取最大值3715，即生产A 产品 245 t ，B 产品 225t 时，可得最大利润．(2)设每吨B 产品利润为m 万元，则目标函数是z ＝5x ＋my ，直线斜率k ＝－5m，又k AB ＝－2，k CB ＝－13，要使最优解仍为B 点，则－2≤－5m ≤－13，解得52≤m ≤15.归纳升华解答线性规划应用题的步骤(1)列：设出未知数，列出约束条件，确定目标函数． (2)画：画出线性约束条件所表示的可行域．(3)移：在线性目标函数所表示的一组平行线中，利用平移的方法找出与可行域有公共点且纵截距最大或最小的直线．(4)求：通过解方程组求出最优解． (5)答：作出答案．[变式训练] 已知x >0，y >0，x ＋2y ＋2xy ＝8，则x ＋2y 的最小值是( ) A ．3B ．4C.92D.112解析：法一：依题意得，x ＋1>1，2y ＋1>1，易知(x ＋1)·(2y ＋1)＝9，则(x ＋1)＋(2y ＋1)≥2（x ＋1）（2y ＋1）＝29＝6，当且仅当x ＋1＝2y ＋1＝3，即x ＝2，y ＝1时，等号成立，因此有x ＋2y ≥4，所以x ＋2y 的最小值为4.法二：由题意得，x ＝8－2y 2y ＋1＝－（2y ＋1）＋92y ＋1＝－1＋92y ＋1， 所以x ＋2y ＝－1＋92y ＋1＋2y ＝－1＋92y ＋1＋2y ＋1－1，≥292y ＋1·（2y ＋1）－2＝4，当且仅当2y ＋1＝3，即y ＝1时，等号成立． 答案：B专题四 成立问题(恒成立、恰成立等)[例4] 已知函数f (x )＝mx 2－mx －6＋m ，若对于m ∈[1，3]，f (x )<0恒成立，某某数x 的取值X 围．解：因为mx 2－mx －6＋m <0， 所以m (x 2－x ＋1)－6<0， 对于m ∈[1，3]，f (x )<0恒成立⇔⎩⎪⎨⎪⎧1×（x 2－x ＋1）－6<0，3×（x 2－x ＋1）－6<0， 即为⎩⎪⎨⎪⎧1－212<x <1＋212，1－52<x <1＋52，计算得出：1－52<x <1＋52.所以实数x 的取值X 围：1－52<x <1＋52.归纳升华不等式恒成立求参数X 围问题常见解法(1)变更主元法：根据实际情况的需要确定合适的主元，一般将知道取值X 围的变量看作主元． (2)分离参数法：若f (a )<g (x )恒成立，则f (a )<g (x )min ； 若f (a )>g (x )恒成立，则f (a )>g (x )max . (3)数形结合法：利用不等式与函数的关系将恒成立问题通过函数图象直观化．[变式训练] 已知函数y ＝2x 2－ax ＋10x 2＋4x ＋6的最小值为1，某某数a 的取值集合．解：由y ≥1即2x 2－ax ＋10x 2＋4x ＋6≥1⇒x 2－(a ＋4)x ＋4≥0恒成立，所以Δ＝(a ＋4)2－16≤0，解得－8≤a ≤0(必要条件)． 再由y ＝1有解，即2x 2－ax ＋10x 2＋4x ＋6＝1有解，即x 2－(a ＋4)x ＋4＝0有解，所以Δ＝(a ＋4)2－16≥0，解得a ≤－8或a ≥0. 综上即知a ＝－8或a ＝0时，y min ＝1， 故所某某数a 的取值集合是{－8，0}． 专题五 利用分类讨论思想解不等式 [例5] 解关于x 的不等式x －ax －a 2<0(a ∈R)． 分析：首先将不等式转化为整式不等式(x －a )(x －a 2)<0，而方程(x －a )(x －a 2)＝0的两根为x 1＝a ，x 2＝a 2，故应就两根a 和a 2的大小进行分类讨论．解：原不等式等价于(x －a )(x －a 2)<0.(1)若a ＝0，则a ＝a 2＝0，不等式为x 2<0，解集为∅； (2)若a ＝1，则a 2＝1，不等式为(x －1)2<0，解集为∅； (3)若0<a <1，则a 2<a ，故解集为{x |a 2<x <a }； (4)若a <0或a >1，则a 2>a ，故解集为{x |a <x <a 2}． 归纳升华分类讨论思想解含有字母的不等式时，往往要对其中所含的字母进行适当的分类讨论．分类讨论大致有以下三种：(1)对不等式作等价变换时，正确运用不等式的性质而引起的讨论． (2)对不等式(组)作等价变换时，由相应方程的根的大小比较而引起的讨论． (3)对不等式作等价变换时，由相应函数单调性的可能变化而引起的讨论．[变式训练] 已知奇函数f (x )在区间(－∞，＋∞)上单调递减，α，β，γ∈R 且α＋β>0，β＋γ>0，γ＋α>0.试判断f (α)＋f (β)＋f (γ)的值与0的关系．解：因为f(x)为R上的减函数，且α>－β，β>－γ，γ>－α，所以f(α)<(－β)，f(β)<f(－γ)，f(γ)<f(－α)，又f(x)为奇函数，所以f(－β)＝－f(β)，f(－α)＝－f(α)，f(－γ)＝－f(γ)，所以f(α)＋f(β)＋f(γ)<f(－β)＋f(－γ)＋f(－α)＝－[f(β)＋f(γ)＋f(α)]，所以f(α)＋f(β)＋f(γ)<0.。

第六章 不等式第1课时不等式的概念和性质一. 选择题1．如果-1<a<b<0，则有( )A ）a b 11<<b 2<a 2B ）a b 11<<a 2<b 2 C ）b a 11<<b 2<a 2D ）ba 11<<a 2<b22．若0<a<1，则下列不等式中正确的是（ ） A ）(1-a)1/3>(1-a)1/2B ）log )1(a -(1+a)>0C ）(1-a)3>(1+a)2D ）(1-a )1+a >13．若a 、b 、c 、d 四个数满足条件：（1）d>c (2) a+b=c+d (3) a+d<b+c 则有（ ）A ）b>c>a>dB ）a>d>c>bC ）d>b>a>cD ）b>d>c>a4．当x>y>0时，比较p=x 3+13xy 2与q=5x 2y+9y 3的大小关系是（ ）A ）p>qB ）p<qC ）p=qD ）不能确定5．如果b a >>0且0>+b a ，那么以下不等式正确的个数是（ ） ①b a 11<②ba 11>③33ab b a <④23ab a <⑤32b b a < A ）2 B ）3 C ）4 D ）5 二．填空题6．设0>a ，0>b ，则下面两式的大小关系为)]1lg()1[lg(21__________)1lg(b a ab ++++7 .b 克糖水中有a(b>a>0)克糖,若再加入m(m>0)克糖,则糖水变甜了,试根据这个事实提练一个不等式__________8, 已知A n (n,a n )为函数y=12+x 上的点,B n (n,b n )为函数y=x 上的点,其中n ∈N *,设c n =a n -b n ,则c n 与c 1+n 的大小关系为___________ 三．解答题9．设a 、b 、m 、n ∈+R 且m+n=1,试比较nb ma +与b n a m +的大小。

不等式复习题一、选择题（每小题5分，共6小题30分）1. 设,则下列不等式成立的是( )【答案】BA. B. C. D.【解析】∵,∴,,∴.2. 函数的定义域是( )【答案】CA. B. C. D.【解析】要使函数有意义,则且,即,故定义域为.3. 若对于任意的,不等式恒成立,则实数的取值范围为( )【答案】AA. B. C. D.【解析】由,, 令,则, 当且仅当时,取得最小值.此时取得最大值, 所以对于任意的,不等式恒成立,则.4. 已知，则下列各式不成立的是()【答案】DA. B. D.【解析】A：∵，∴，当且仅当，，即时取等号，因此正确；B：∵，∴，当且仅当时取等号，因此正确；C：∵，∴，所以，正确；D：因为，所以，故不正确.故答案选D.5. 若,,,则的最小值为( )【答案】CA. B. C. D.【解析】若,,,即,则,当且仅当取得最小值. 6. 已知函数是定义在上的偶函数, 且在区间单调递增. 若实数满足, 则的最小值是（）【答案】CA. B. C. D.【解析】，,,，即. 由偶函数性质：，注意到时，为增函数，故，的最小值是.二、填空题（每小题5分，共4小题20分）7. 已知，则的最小值等于__________ .【答案】【解析】，当且仅当时取等号，故最小值为.8. 不等式的解集为__________.【答案】【解析】由已知可得,故解集为.9. 已知实数满足，则的最大值是__________．【答案】【解析】可行域如图中阴影部分所示，由，解得交点为，所以令，则．10. 已知关于的不等式在上恒成立，则实数的取值范围是____．【答案】【解析】因为不等式在R上恒成立．∴，解得，故答案为.三、解答题（每小题12分，共4小题48分）11. 设集合(1)求集合(2)若不等式的解集是求的值．【答案】(1)(2)【解析】，(1)．(2)∵的解集为∴和为方程的两根，故∴12. 设的内角,,所对的边分别是,,.且. (1)求角的大小;(2)若,求的取值范围.【答案】(1); (2).【解析】(1)∵. 结合余弦定理. 又,,.∴. ∴,则. (2)由余弦定理.. 可得, ∴,又.∴.13. 已知的定义域，的定义域为，当时，求的取值范围．【答案】∞．【解析】由，得．∴或，即，由，得．∵，∴∴．∵，∴或，即或，且．故当时，实数的取值范围为．14. 已知函数满足. (1) 不等式的解集为，求的值. (2)设,解关于的不等式.【答案】见解析.【解析】（1）即，. 由不等式的解集为，知，是方程的两根，∴，. （2）. ①若，则，∴解集为；②若，则. 当时，则，∴解集为；当时，则，∴解集为；当时，则，∴解集为；。

高二数学期末复习一〔不等式3〕一、选择题1.设全集I =R ,集合P ={x |2x 2－x ＜0},集合Q ={x |x 1≤2},那么( ) A.P ∩ R Q=φ B.P =R Q C.P ∪Q =RD.P ∪Q ={x |x ＞0} 2.|x |≤2是|x +1|≤1成立的( )A 充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分又不必要条件3.不等式xx 1-≥2的解集为( ) A.［－1,0］ B.［－1,+∞］ C.(－∞,－1］ D.(－∞,－1］∪(0,+∞)4.假设关于x 的不等式(a 2－1)x 2－(a －1)x －1＜0对于x ∈R 成立,那么实数a 的取值范围是( )A.(－53,1]B.［－53,1］C.(－53,1)D.(－∞,－53)∪［1,+∞) 5.设A ={x |x 2－2x －3＞0},B ={x |x 2+ax +b ≤0},假设A ∪B =R ,A ∩B =(3,4),那么a +b 等于( )A.7B.－1C.1D.－76.设A ={x ||x －1|<2},B ={x |x x 2->0},那么A ∩B 等于( ) A.{x |－1<x <3} B.{x |x <0或x >2} C.{x |－1<x <0}D.{x |－1<x <0或2<x <3} 7.假设关于x 的不等式|x +2|+|x －1|＜a 的解集是∅,那么a 的取值范围是( )A.(3,+∞)B.［3,+∞］C.(－∞,3］D.(－∞,3)8.不等式2)1()3(2--+x x x ≤0的解集是( ) A.{x |1≤x ＜2} B.{x |1＜x ＜2或x =－3} C.{x |1≤x ＜2或x =－3} D.{x |1≤x ≤2或x =－3}9.实数x 满足log 3x =1+sin θ,那么|x －1|+|x －9|的值为( )A.8B.－8C.8或－8D.与θ有关10.函数f (x )、g (x )的定义域为R ,且f (x )≥0的解集为{x |1≤x ＜2},g (x )≥0的解集为∅,那么不等式f (x )·g (x )>0的解集为( )A.{x |1≤x ＜2 }B.RC.∅D.{x |x <1或x ≥2}二、填空题11.方程|21-+x x |=xx -+21的解集是__________. 12.建造一个容积为18 m 3,深为2 m 的长方体无盖水池,如果池底和池壁每平方米的造价分别为200元和150元,那么池的最低造价为__________.13.设a ,a +1,a +2为钝角三角形的三边,那么a 的取值范围是__________.14.关于x 的不等式|ax +2|<8的解集为(－3,5),那么a =__________.三、解做题15解不等式(x 2+x +1)(x +1)3(x －2)2(3－x )＞0.16函数f (x )=264xx -+,g (x )=x 2－3ax +2a 2(a ＜0),假设不存在．．．实数x 使得f (x )＞1和 g (x )＜0同时成立,试求a 的范围.17实数p 满足不等式212++x x <0,试判断方程u 2－2u +5－p 2=0有无实根,并给出证实. 18行驶中的汽车,在刹车时由于惯性作用,要继续往前滑行一段距离才能停下,这段距离叫做刹车距离.在某种路面上,某种型号汽车的刹车距离y (m)与汽车的车速x (km/h)满足以下关系:y =100nx +4002x (n 为常数,且n ∈N ). 我们做过两次刹车试验,有关数据如以下图所示,其中⎩⎨⎧<<<<.1513,7521y y(1)求出n 的值；(2)要使刹车距离不超过18.4 m,那么行驶的最大速度应为多少？19不等式(m 2+4m －5)x 2－4(m －1)x +3>0对一切实数x 恒成立,求实数m 的取值范围.20 假设不等式组⎪⎩⎪⎨⎧<+++>--05)25(2,0222k x k x x x 的整数解只有－2,k 应取何值?不等式(二)(A 卷)一、选择题1:A 2:B 3 A 4. A 5 D 6 D 7. C 8. C 9 A 10. D二、填空题11. {x |－1≤x ＜2＝ 12 5400元 13 1＜a ＜3 14 －2三、解做题15解:∵x 2+x +1＞0恒成立,∴不等式等价于⎩⎨⎧≠<-+20)3)(1(x x x ⇔－1＜x ＜2或2＜x ＜3.∴不等式的解集为{x |－1＜x ＜2或2＜x ＜3}.16解:由f (x )＞1,得264x x -+＞1, 化简整理得)2)(3()1)(2(+-+-x x x x ＜0. 解得－2＜x ＜－1或2＜x ＜3.即f (x )＞1的解集为A ={x |－2＜x ＜－1或2＜x ＜3}.由g (x )＜0得x 2－3ax +2a 2＜0,即(x －a )(x －2a )＜0(a ＜0).那么g (x )＜0的解集为B ={x |2a ＜x ＜a ,a ＜0}.根据题意,有A ∩B =∅.因此,a ≤－2或－1≤2a ＜0.故a 的范围是{a |a ≤－2或－21≤a ＜0}. 17解:由212++x x <0,解得－2<x <－21. ∴－2<p <－21. 方程u 2－2u +5－p 2=0的判别式Δ=4(p 2－4).∵－2<p <－21,∴41<p 2<4.∴Δ<0. 由此得出方程u 2－2u +5－p 2=0无实根.18解:(1)由图象知,y 1=10040n +4001600=4+52n , y 2=1007n +4004900=107n +449. 由于5＜y 1＜7,13＜y 2＜15,∴⎪⎪⎩⎪⎪⎨⎧<+<<+<,1544910713,75245n n 即⎪⎪⎩⎪⎪⎨⎧<<<<.14551415,2155n n n ∴25＜n ＜1455. 又∵n ∈N ,∴n =3.(2)根据题意,得y =1003x +4002x ≤18.4. ∴x 2+12x －7360≤0,即(x +92)(x －80)≤0.由于x ＞0,∴0＜x ≤80,即行驶的最大速度为80 km/h.19解:(1)当m 2+4m －5=0,即m =1或m =－5时,显然m =1符合题意,m =－5不合题意.(2)当m 2+4m －5≠0时,要使二次不等式对一切x ∈R 恒成立,必须⎩⎨⎧<>-+,0Δ,0542m m 即⎪⎩⎪⎨⎧<-+--=>-+.0)54(12)1(16Δ,054222m m m m m 解得1<m <19.综合(1)(2)得m 的取值范围为［1,19).20 解:由x 2－x －2>0,解得x <－1或x >2.由2x 2+(5+2k )x +5k <0化为(2x +5)(x +k )<0.∵－2是其解,∴k <2. ∴－25<x <－k . ∴原不等式组可以化为①⎪⎩⎪⎨⎧-<<--<k x x 25,1或②⎪⎩⎪⎨⎧-<<->.25,2k x x ∵k <2,∴－k >－2.∴①的整数解为－2,而要使②无整数解,只有－k ≤3,即k ≥－3.∴－3≤k <2.。

卜人入州八九几市潮王学校不等式高二数学复习一．选择题1．设a b <，c d <，那么以下不等式中一定成立的是〔〕A ．d b c a ->-B ．bd ac >C ．d b c a +>+D ．c b d a +>+2．不等式xx 1>的解集是〔〕 A ．}1{<x x B ．1{-<x x 或者}1>xC ．01{<<-x x 或者}1>x D ．}11{<<-x x 3．假设011<<ba ，那么以下结论不正确的选项是〔〕 A ．22b a <B ．2b ab <C ．2>+ba ab D ．||||||b a b a +>+ 4．“0>>b a 〞是“222b a ab +<〞的〔〕 A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件5．以下各式中最小值是2的是〔〕A ．y x ＋x yB ．4522++x x C ．tan x ＋cot x D ．x x -+226．()f x 是奇函数，且在〔－∞，０〕上是增函数，(2)0f =，那么不等式()0xf x <的解集是〔〕A ．{|20,2}x x x -<<>或B ．{|20,}x x -<<或0<x<2 C ．}22|{>-<x x x 或D ．{|2,02}x x x <-<<或二、填空题7．不等式022>++bx ax 的解集是)31,21(-，那么b a -的值等于. 8．比较13)(2+-=x x x f 与12)(2-+=x x x g 的大小关系. 9．设0>x ，那么函数xx y 164--=的最大值为。

10．假设a x x ≥+++|9||1|对任意实数x 总成立,那么a 的取值范围是.11．设(b a ,)是直线x+y=3上的点，那么b a 22+的最小值是.12.某公司一年购置某种货物400吨，每次都购置x 吨，运费为4万元/次，一年的总存储费用为4x 万元，要使一年总运费与总存储费用之和最小，那么x=吨. 三、解答题13．解不等式：(1)022>---x x x a (2)10832<--x x 14．a 、b +∈R ，且1=+b a ，求证：91111≥⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+b a 。