运筹学最短路问题excel求解

图 13-1第十三章 运筹学问题的Excel 建模及求解 学习运筹学的目的在于学会用运筹学的方法解决实践中的管理问题.注重学以致用.很多实际问题利用人工计算要经过长时间的艰苦工作才能完成甚至根本无法求解.但若使用运筹学软件则瞬间就能解决.因此在学习过程中不仅要掌握运筹学的基本理论和计算方法.还要充分利用现代化的手段和技术.微软的电子表格软件（Microsoft Excel ）为展示和分析许多运筹学问题提供了一个功能强大而直观的工具.它现在已经被应用于管理实践中.本章将重点介绍如何建立和求解规划问题的电子表格模型.对于解决大量的中、小规模的实际规划问题.电子表格软件是远远优于传统的代数算法的.第一节 Excel 中的规划求解工具本节中.我们将举例说明如何使用微软Excel 以电子表格的形式建立线性规划模型.并利用Excel 中的规划求解工具对模型求解.一、在Excel 中加载规划求解工具要使用Excel 应首先安装MicrosoftOffice.然后从屏幕左下角的[开始]—[程序]中找到Microsoft Excel 并启动.在Excel 的主菜单中点击[工具]—[加载宏].选择“规划求解”.如图13-1所示.点击[确定]后.在工具菜单中将增加[规划求解]选项. 二、在Excel 中建立线性规划模型我们以例2-1为例说明如何在电子表格中建立该问题的线性规划模型.建立电子表格模型时既可以直接利用问题中所给的数据和信息.也可以利用已建立的代数模型.本例的代数模型为：图 13-2 图 13-3目标函数 21300200x x Z +=max⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≤≤≤+≤+0,124164821222..21212121x x x x x x x x t s图13-2显示了将该例的数据转送到电子表格中后所建立的电子表格数学模型（本例是一个线性规划模型）.其中显示数据的单元格称为数据单元格.包括生产每单位药品Ⅰ和Ⅱ所需要的4种设备的台时数（单元格C5：D8）.药品Ⅰ和Ⅱ的单位利润（单元格C9：D9）.4种设备可用的台时数（单元格G5：G8）.我们要做的决策是两种药品各生产多少；对这一决策的约束条件是生产两种药品所需的4种设备台时的限制；判断这些决策的优劣程度的指标是生产这两种药品所获得的总利润（决策目标）.如图13-3所示.将决策变量（药品Ⅰ、Ⅱ的产量）分别放入单元格C10和D10.正好在两种药品所在列的数据单元格的下面.由于不知道这些产量会是多少.故在图13-3中均设为零（空白的单元格默认取值为零.实际上.除负值外的任何一个试验解都可以）.以后在寻找产量最佳组合时这些数值会被改变.因此.含有需要做出决策的单元格称为可变单元格.两种药品所需的4种设备台时总数分别放入单元格E5至E8.正好在对应数据单元格的右边.由于所需的各种设备台时总数取决两种药品的实际产量.如：E5=C5×C10+D5×D10（可直接将公式写入E5.也可利用SUMPRODUCT 函数.E5=SUMPRODUCT （C5：D5.C10：D10）.此函数可以计算若干维数相同的数组的彼此对应元素乘积之和）.因此当产量为零时所需各种设备台时的总数也为零.由于E5至E8单元格每个都给出了依赖于可变单元格（C10和D10）的输出结果.它们因此被称为输出单元格.作为输出单元格的结果.4种设备台时数的总需求图 13-4图 13-5 量不应超过其可用台时数的限制.所以用F 列中的 来表示.两种药品的总利润作为决策目标进入单元格E9.正好位于用来帮助计算总利润的数据单元格的右边.类似于E 列的其他输出单元格.E9 = C9×C10+D9×D10或E9 = SUMPRODUCT （C9：D9.C10：D10）.由于它是在对产量做出决策时目标值定为尽可能大的特殊单元格.所以被称为目标单元格.根据对上述建模过程的总结.在电子表格中建立线性规划模型的步骤可归纳如下：1．收集问题的数据.并将数据输入电子表格的数据单元格；2．确定需要做出的决策.并且指定可变单元格显示这些决策；3．确定对这些决策的限制（约束条件）.并将以数据和决策表示的被限制的结果放入输出单元格；4．选择要输入目标单元格的以数据和决策表示的决策目标.三、应用电子表格求解线性规划模型上例的求解过程可通过在Excel 的工具菜单中选择“规划求解”开始.“规划求解”对话框如图13-4所示.“规划求解”开始前.可通过键入单元格地址或选中单元格的方式确定模型的每个组成部分设置在电子表格的何处（单击暂时隐藏对话框.再从工作表中选定单元格.然后再次单击）.如目标单元格地址为E9.可变单元格地址范围为C10：D10.并选中最大值（M ）表示要最大化目标单元格.约束条件的设定可通过点击对话框中的“添加”按钮.弹出图13-5所示的添加约束对话框.由于各种设备台时的总需求量均不应超过可用台时数的限制.故单元格E5到E8必须小于或等于对应的单元格G5到G8.即在添加约束对话框的左端输入范围E5：E8（可用选中单元格的方图 13-6图 13-7图 13-8式）.中间选择<=（点开下拉列表进行选择）.右端输入范围G5：G8.如果模型中还包含其他类型的函数约束.则可点击“添加”按钮以弹出一个新的添加约束对话框.根据输出单元格与约束值之间的关系在对话框中间的下拉列表中选择适当的约束类型.以增加新的约束.但本例中已无其他约束了.所以只要点击“确定”按钮返回“规划求解”对话框.如果需要修改或删除已添加的约束.可选中该约束后点击“更改”或“删除” 按钮.到现在为止“规划求解”对话框已根据图13-3的电子表格描述了整个模型（见图13-4）.但在求解模型前还需要进行最后一个程序.点击“选项”按钮弹出图13-6所示的选项对话框.这个对话框中是一些关于如何求解问题的细节的选项.对于决策变量取值非负的线性规划模型.最主要的选项是“采用线性模型”和“假定非负”选项.（见图13-6）.关于其他选项.对小型问题来说接受图中所示的默认值通常比较合适.点击“确定”按钮返回“规划求解”对话框.现在可以点击“规划求解”对话框中的“求解”按钮了.它会在后台开始对问题进行求解.对于一个小型问题.几秒钟之后“规划求解”就会显示运行结果.如图13-7所示.它会显示已经找到了一个最优解.如果模型没有可行解或没有最优解.对话框会显示“规划求解找不到可行解”或“设定的单元格值不能集中”.对话框还显示了产生各种报告的选项.后面将会介绍.选择“保存规划求解结果” 并点击“确定” 按钮.返回电子表格模型.求解模型之后.如图13-8所示.“规划求解”用最优解和最图 13-9优值代替了可变单元格和目标单元格中的初始值.因此.最优解是生产4公斤药品Ⅰ和2公斤药品Ⅱ.最优值为1400元.与图解法的结果一致.图13-9显示的是例2-2的电子表格模型及求解过程.这个问题的电子表格模型建立与求解过程与例2-1描述的基本相同.数据单元格（C5：E8）、（C9：E9）和（H5：H8）分别存放三种原料B 1、B 2、B 3每斤所含四种营养成分的数量、每斤原料的单价以及食品所要求的最低营养成分的含量限制.可变单元格（C10：E10）存放三种原料配比情况（图13-9的左上部分）.输出单元格（F5：F8）给出了食品中实际的营养成分含量.目标单元格（F9）显示了该种食品的总成本（图13-9的左下部分）.图13-9的右下角显示了“规划求解”对话框的主要部分.包括为目标单元格和可变单元格设定的地址.约束条件F5≥H5.F6≥H6.F7≥H7和F8≥H8通过“添加约束”对话框显示在“规划求解” 对话框中.由于目标是最小化总成本.所以选择了“最小值（N ）”.图13-9的右上角显示了点击“规划求解” 对话框的“选项”按钮后所选择的选项.“采用线性模型”先期定义了这个模型是线性规划模型.“假定非负”选项定义了可变单元格必须是非负约束.因为食品的配比不可能出现负值.点击“规划求解” 对话框的求解按钮后.得到了图13-9中电子表格的可变单元格中显示的最优解.即该食品配比为原料B 1 是1.94斤.原料B 3是2.36斤.成本为109.72元.与单纯形法人工求解不同.如果输出单元格、可变单元格或目标单元格结果不是整数.电子表格是以小数而非分数形式显示的.本例结果以四图 13-10舍五入的方式保留了两位小数.第二节 线性规划的应用问题一、合理用料问题这是第二章第五节的第一个问题.由于原料胶管的长度为15分米.而输液管、止血带和听诊器胶管分别长5.7、4.2和3.1分米.所以每根原料胶管最多可截三种材料依次为2根、3根和4根.即总的截法不超过3×4×5 = 60（种）.又由于每种截法的料头不能超过2分米.所以可先通过电子表格进行试算以选择其中可行的几种截法.再利用线性规划的方法找出用料根数最少的方案.如图13-10的左上部分所示.单元格C4至E4显示三种胶管的长度；C5至E5输入不同的方法截出每种胶管的根数；F4为对应C5至E5的不同截法所剩料头的长度. F5通过判断剩余料头的长度是否在0到2之间显示出该种解法是否可行.单元格F4和F5的公式见图13-10的左下部分.不断变换C5至E5的可能取值并选择其中可行的截法（共6种）.在电子表格中建立该问题的线性规划模型.数据单元格为C9：H11、C12：H12和K9：K12.分别显示每种截法截一根原料胶管时得到三种不同材料的数量、每种截法截取一次所用胶管的数量和三种材料的需要量；可变单元格C13：H13显示采用每种截法所截的胶管原料数；输出单元格I9：I12列出了某一截取方案实际获得的三种材料数量.每种材料的数量等于各种截法截得该材料数与对应截法所截原料数的乘积之和.如输液管的数量I9 = SUMPRODUCT(C9:H9,C13:H13)；目标单元格I12图 13-11为总用料数.应等于各种截法所截原料数之和,即I12 = SUM(C13:H13).图13-10的右半部分显示了“规划求解”对话框及“选项”对话框的内容.该问题的目标是所用的胶管原料的总根数最少.因此设置目标单元格为I12等于最小值.由于实际获得的材料数量必须满足需求量的要求.考虑到最优方案（各种截法的某一组合）不一定能使截出的三种材料数量恰好等于需要的数量.而某种材料超过需求量是允许的.故在添加约束时可设置实际截得的数量大于等于需求量.即I9：I12>=K9：K12（本题中.该约束取“>=”和“=”的结果是相同的）；又由于截出的各种材料数量均为整数.因此约束中应包括决策变量取整数的限制.即C13:H13=整数.图13-10的左上部分显示了该问题的最优方案为：分别用第二种、第四种和第五种截法截取原料40、60和10根.共用原料110根.与第二章中用大M 法求解的结果一致.二、放射科的业务安排图13-11显示了第二章问题二的电子表格模型及求解过程.该问题的数据包括：进行三种检查的单位时间（C5：E5）.三种检查设备每月的可用时间（C9：E9）.三项业务每月最多提供量（H6）以及每项业务的单位利润（C10：E10）.可变单元格为C6至E6.给出三项业务每月的实际发生数量.输出单元格为C7至E7和F6.分别表示根据各项业务的实际发生数量产生的设备使用时间及实际的总业务量.目标单元格F10显示由每项业务的单位利润及每月实际发生数量计算的总利润.图13-11的左下部分给出了输出单元格及目标单元格的公式.图13-11右下部分的“规划求解”对话框显示了求解时应注意的问题：求目标单元格的最大值（利润最大）；约束为设备的实际使用时间小于等于设备的可用时间及实际总业务量小于等于总业务提供量的限制.打开“选项”对话框.仍选择“采用线性模型”和“假定非负”.回到“规划求解”并按“求解”按钮.得到问题的最优方案为：每月X 线及CT 检查的业务量分别为1320人次和480人次.磁共振业务量为0.即不必购买该设备；按最优方案安排业务每月可获利55200元.在电子表格上建立线性规划或其它问题模型的方式是非常灵活的.不必拘泥于一种固定的模式.本书仅提供了一种建立模型的思路.读者可根据不同问题的特点以及个人的习惯或喜好建立不同风格的电子表格模型.第三节 线性规划的灵敏度分析前面指出线性规划模型的许多参数.都只是对实际数据的大致估计.而不可能在研究的时候就获得精确的数值.通过灵敏度分析可以得出每一个估计的数据需要精确到何种程度.才能保持解的最优性.回忆例2-1某制药厂的生产计划问题.其求解结果如图13-8所示.即生产4公斤药品Ⅰ和2公斤药品Ⅱ.总利润为1400元.但该最优解是在假设所有的模型参数都准确的前提下做出的.在此基础上.管理层如果进一步考虑下列问题：1．如果在该厂生产的药品中.有一个单位利润的估计值是不准确的.将会发生怎样的情况？2．如果该工厂两种药品的单位利润的估计都是不准确的.又将会怎样？3．如果改变该厂某种设备可用于生产的时间.会对结果产生什么影响？4．如果四种设备可用于生产的时间同时改变.又会对结果产生何种影响？ 在本节中.我们将重点介绍如何利用“规划求解”中的“敏感性报告”对目标函数系数j c 以及约束条件右端值i b 的变动进行灵敏度分析.分析的内容主要是系数在什么范围内变化时.已得到的最优解保持不变.即发现哪些系数不太敏感（由于在较大范围内变化时.最优解保持不变.故可以进行粗略估计）.哪些系数比较敏感（即使微小的改变都会对最优解产生影响.故必须对其精确定义）.图 13-12图 13-13一、目标函数系数变动的灵敏度分析首先介绍目标函数系数的灵敏度分析.回顾一下就可以知道.这些系数表示各种决策对总目标的单位贡献.下面以例2-1某药厂的生产计划问题的目标函数系数变动情况进行讨论.问题1：如果该药厂一种药品的单位利润的估计是不精确的.结果怎样？ 首先看一下.如果药品Ⅱ的单位利润300元的估计是不精确的情况.假设：药品Ⅱ的单位利润 = 电子表格中D9单元格中的数据现在.2c =300元.下面我们来分析一下在保持最优解)2,4(),(21 x x 不变的条件下.2c 可能的最大值与最小值.这样.也就可以看出2c 为300元的这一估计能够在多大程度上偏离实际值而不会改变解的最优性.（一）使用电子表格进行灵敏度分析电子表格的一个强大的优点就是可以方便互动地展开各种形式的灵敏度分析.通过运用规划求解工具来求解最优解.模型参数值的改变所造成的影响一下子就可以显示出来.为了说明这一点.图13-12显示了药品Ⅱ的单位利润从开始的2c =300元降到2c =250元的情况.与图13-8相比.最优解没有丝毫的变化.事实上.该问题唯一的变动是电子表格中C9单元格中的数据从300元降到250元.以及E9单元格总利润减少了100元（因为每单位药品Ⅱ所提供的利润减少了50元）.因为最优解没有变动.我们可以知道在不影响最优解的前提下.药品Ⅱ的单位利润2c =300元的最初估计是较高的.图 13-14那么.如果这一估计值较低又会怎样呢？图13-13表示了将2c =300元增加到2c =350元的情况.同样.最优解没有发生变化.因为.增加或减少最初的2c =300元均不会对最优解产生任何影响.2c 就不是很敏感的系数.也就不需要为了保证最优解不会改变.而花很大力气去得到2c 的更精确的值.但是对2c 的研究至此并没有结束.因为实际值很可能会超出250到350元这一范围.那么在保持最优解不变的条件下.2c 到底可以在什么样的范围内取值呢？当然可以在电子表格中采取试验的方法.不断增加或减少的2c 值.直到最优解发生改变.以找到最优解发生变化时对应的2c 值.但是.这样计算太麻烦了.是否有简便一些的方法呢？答案是肯定的.（二）利用敏感性报告进行目标系数的灵敏度分析如图13-7所示.在求得最优解之后.规划求解工具会给出相应的信息.同时.在其右边列出了它可以提供的三个报告.选择第二项敏感性报告的选项.就可以得到灵敏度的分析报告.它显示在模型的工作表之前.图13-14显示了本例敏感性报告中的一部分.终值一栏表明了问题的最优解.第二栏给出了递减成本.递减成本提供了为使决策变量取正值.相应的目标系数需要减少的数量.对于本例.由于两决策变量的取值均为正数.故递减成本均为零.第三栏表示了目标函数的现值.最后两栏表示为使最优解保持不变.目标系数允许增加与减少的最大值.例如.考虑决策变量X 1的目标系数1c .从图13-14中表示产品Ⅰ的一行中可知.1c 可以减少50.可以增加1E+30.在电子表格中1E+30是1030的缩写.Excel 使用这一极大的数值来表示无穷大.因此.从灵敏度的分析报告中可知：1c 的现值： 2001c 的允许增加值： 无穷大 此时1c 无上限1c 的允许减少值： 50 此时150502001=-≥c1c 的变化范围： 1501≥c因此.只要在上面的变化范围内变动.并且不改变模型的其他任何内容.最优解将始终保持在)2,4(),(21=x x 不变.该药厂的另一药品的单位利润的变化范围也可以用同样的方法得出.2c 是药品Ⅱ的单位利润.表中表示药品Ⅱ的第二行给出了下面关于2c 的信息：2c 的现值： 3002c 的允许增加值： 100 此时4001003002=+≤c 2c 的允许减少值： 300 此时03003002=-≥c 2c 的变化范围： 40002≤≤c 目标函数的两个系数的允许变化范围都很大.因此.尽管药品Ⅰ和药品Ⅱ的单位利润可能仅仅是实际值的一个粗略估计.我们也可以相信.这个估计值对最优解的正确性不会有影响.但在一些线性规划模型中.目标系数微小的变动都可能会影响最优解.这样的系数称为敏感参数.灵敏度的分析报告中会直接显示目标中哪些系数是敏感的.这些系数允许的变化区域很小.因此.必须格外小心.尽量取得这些数据的精确值.在求得模型的最优解之后.目标系数的允许变化范围还有一个很重要的用途.在问题的线性规划分析结束之后.如果外界的环境发生了一定的变化.灵敏度分析可以在无需重新求解的情况下.表明模型参数的变化是否造成了最优解的改变.例如经过一段时间以后.如果药品的单位利润发生了较大的变化.通过其允许变化范围.可以一眼看出原来的最优组合是否依然适用.有了目标系数的允许变化范围.在判断问题时.就不需要重新建模与求解.这一点对线性规划问题的解决是有很大帮助的.特别是在处理一个大型模型时.（三）目标系数的同时变动因为存在许多不确定性因素.目标函数系数的值.如单位利润.通常都只是对图 13-15实际值的估计.上面所讨论的是只有一个系数变动时的情况.这类问题在求解一个系数的允许变化范围时.假设其他所有系数都是正确的.研究的系数是唯一可能与实际值不符的变动的系数.但事实上.所有的系数（至少一个以上）可能同时都是不准确的.如果这样的话.是否可能会导致求得的最优解不正确呢？这是最关键的问题.如果可能对最后的结果产生影响.就必须对这些系数作进一步的分析.另一方面.如果灵敏度分析表明目前的参数估计不会影响最优解的正确性.那么.管理者可以增加对该模型及其所提供的解决方法的信心.以下将介绍如何在不重新求解模型的条件下.确定如果目标函数的几个系数同时变化.可能造成的对最优解的影响．我们仍利用例2-1提出如下问题：问题2：如果该药厂两种药品的单位利润的估计都是不准确的.将会对结果产生怎样的影响？例如.原来药品Ⅰ和药品Ⅱ的单位利润分别为200元和300元.现在由于原料成本的变化.每公斤药品Ⅰ和药品Ⅱ的单位利润分别变为180元和355元.最优解是否发生变化？在分析多个系数同时变动的情况时.仍然要使用敏感性报告中提供的每个系数的允许增加值和减少值数据.下面介绍多个系数同时变动的百分之百法则.首先定义j c 的允许增加（减少）百分比为j c 的增加量（减少量）除以j c 的允许增加量（允许减少量）的值.这样我们可以计算出1c 的允许减少百分比为%4050/)180200(=-.2c 的允许增加百分比为%55100/)300355(=-.2c 的允许减少百分比与2c 的允许增加百分比之和为%95%55%40=+.目标函数系数同时变动的百分之百法则：如果目标函数的系数同时变动.当其所有允许增加百分比和允许减少百分比之和不超过百分之百时.最优解不会改变.如果超过百分之百.则不能确定最优解是否改变.因为本例中1c 的允许减少百分比与2c 的允许增加百分比之和为95%不超过100%.所以当每公斤药品Ⅰ的利润减少为180元.每公斤药品Ⅱ的利润增加为355元时.此线性规划最优解仍然为药品Ⅰ生产4公斤和药品Ⅱ生产2公斤（即2,421==x x ）.此时有最大利润为143071072023554180=+=⨯+⨯（元）.如图13-15所示.这一法则并没有表示出.在变动百分比之和超过百分之百的情况下.可能的结果.这一结果还有赖于系数变动的方向.但是.只要变动百分比之和不超过百分之百.最优解是肯定不会改变的.记住.我们可以让单一的目标函数系数在整个允许范围内变动.但这只有在其他目标函数系数都不变的情况下才有效.如果多个系数同时变动.我们必须研究各个系数的变动百分比.二、约束右端值的灵敏度分析之所以要分析函数约束右端值变动的原因与前面一样.因为在建模时.还不能得到模型的这些参数的精确值.只能对其作粗略的估计.因此.我们希望知道在这些估计不准确的情况下会产生怎样的后果.除此之外一个更主要的理由是因为.这些常数（通常代表资源的可用量）往往不是由外界决定的而是管理层的政策决策.因此管理者希望知道如果改变这些决策是否会提高最终的收益.影子价格分析就是为管理者提供这方面的信息.下面是关于例2-1的第三个问题：问题3：如果改变该厂某设备可用于生产的时间.结果将如何？（一）约束右端值的影子价格分析回忆第二章中关于影子价格的经济含义.我们知道影子价格代表单位资源在最优利用的条件下所产生的经济效果.即在模型获得最优解的情况下.约束条件右端值在一定范围内每增加（减少）一个单位.使目标函数值增加（减少）的量.其中.一定范围是指保持影子价格不变的右端值变化范围.在影子价格分析中.每次分析一个函数约束.可以将该函数约束右端值的常数增加一个单位后重新求解.观察目标函数值增加的量来确定影子价格.也可以利用灵敏度报告中提供的关于每一个函数约束的影子价格数据.从一个约束的影子价格中就可以直接看出.决策改变而引起的约束常数的改变所造成的影响.只要约束常数的变动不大.那么目标函数值的变动就等于约束常数的变动（正或负）乘以影子价格.为了说明影子价格的含义.我们以第二章。

运筹学问题的Excel建模及求解图 13-1第十三章 运筹学问题的Excel 建模及求解学习运筹学的目的在于学会用运筹学的方法解决实践中的管理问题，注重学以致用.很多实际问题利用人工计算要经过长时间的艰苦工作才能完成甚至根本无法求解，但若使用运筹学软件则瞬间就能解决.因此在学习过程中不仅要掌握运筹学的基本理论和计算方法，还要充分利用现代化的手段和技术.微软的电子表格软件（Microsoft Excel ）为展示和分析许多运筹学问题提供了一个功能强大而直观的工具，它现在已经被应用于管理实践中.本章将重点介绍如何建立和求解规划问题的电子表格模型，对于解决大量的中、小规模的实际规划问题，电子表格软件是远远优于传统的代数算法的.第一节 Excel 中的规划求解工具本节中，我们将举例说明如何使用微软Excel 以电子表格的形式建立线性规划模型，并利用Excel 中的规划求解工具对模型求解.一、在Excel 中加载规划求解工具要使用Excel 应首先安装MicrosoftOffice ，然后从屏幕左下角的[开始]—[程序]中找到Microsoft Excel 并启动.在Excel 的主菜单中点击[工具]—[加载宏]，选择“规划求解”，如图13-1所示.点击[确定]后，在工具菜单中将增加[规划求解]选项.二、在Excel 中建立线性规划模型 我们以例2-1为例说明如何在电子表格中建立该问题的线性规划模型.建立电子表格模型时既可以直接利用问题中所给的数据和信息，也可以利用已建立的代数模型.本例的代数模型为：图 13-2 图 13-3目标函数 21300200x x Z +=max⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≤≤≤+≤+0,124164821222..21212121x x x x x x x x t s图13-2显示了将该例的数据转送到电子表格中后所建立的电子表格数学模型（本例是一个线性规划模型）.其中显示数据的单元格称为数据单元格，包括生产每单位药品Ⅰ和Ⅱ所需要的4种设备的台时数（单元格C5：D8），药品Ⅰ和Ⅱ的单位利润（单元格C9：D9），4种设备可用的台时数（单元格G5：G8）.我们要做的决策是两种药品各生产多少；对这一决策的约束条件是生产两种药品所需的4种设备台时的限制；判断这些决策的优劣程度的指标是生产这两种药品所获得的总利润（决策目标）.如图13-3所示，将决策变量（药品Ⅰ、Ⅱ的产量）分别放入单元格C10和D10，正好在两种药品所在列的数据单元格的下面.由于不知道这些产量会是多少，故在图13-3中均设为零（空白的单元格默认取值为零.实际上，除负值外的任何一个试验解都可以）.以后在寻找产量最佳组合时这些数值会被改变.因此，含有需要做出决策的单元格称为可变单元格.两种药品所需的4种设备台时总数分别放入单元格E5至E8，正好在对应数据单元格的右边.由于所需的各种设备台时总数取决两种药品的实际产量，如：E5=C5×C10+D5×D10（可直接将公式写入E5，也可利用SUMPRODUCT 函数，E5=SUMPRODUCT （C5：D5，C10：D10），此函数可以计算若干维数相同的数组的彼此对应元素乘积之和），因此当产量为零时所需各种设备台时的总数也为零.由于E5至E8单元格每个都给出了依赖于可变单元格（C10和D10）的输出结果，它们因此被称为输出单元格.作为输出单元格的结果，4种设备台时数的图 13-4图 13-5总需求量不应超过其可用台时数的限制，所以用F 列中的 来表示.两种药品的总利润作为决策目标进入单元格E9，正好位于用来帮助计算总利润的数据单元格的右边.类似于E 列的其他输出单元格，E9 = C9×C10+D9×D10或E9 = SUMPRODUCT （C9：D9，C10：D10）.由于它是在对产量做出决策时目标值定为尽可能大的特殊单元格，所以被称为目标单元格.根据对上述建模过程的总结，在电子表格中建立线性规划模型的步骤可归纳如下：1．收集问题的数据，并将数据输入电子表格的数据单元格；2．确定需要做出的决策，并且指定可变单元格显示这些决策；3．确定对这些决策的限制（约束条件），并将以数据和决策表示的被限制的结果放入输出单元格；4．选择要输入目标单元格的以数据和决策表示的决策目标.三、应用电子表格求解线性规划模型上例的求解过程可通过在Excel 的工具菜单中选择“规划求解”开始.“规划求解”对话框如图13-4所示.“规划求解”开始前，可通过键入单元格地址或选中单元格的方式确定模型的每个组成部分设置在电子表格的何处（单击暂时隐藏对话框，再从工作表中选定单元格，然后再次单击）.如目标单元格地址为E9，可变单元格地址范围为C10：D10，并选中最大值（M ）表示要最大化目标单元格.约束条件的设定可通过点击对话框中的“添加”按钮，弹出图13-5所示的添加约束对话框.由于各种设备台时的总需求量均不应超过可用台时数的限制，故单元格E5到E8必须小于或等于对应的单元格G5到G8.即在添加约束对话框的左端输入范围E5：E8（可用选中单元格图 13-6图 13-7的方式），中间选择<=（点开下拉列表进行选择），右端输入范围G5：G8.如果模型中还包含其他类型的函数约束，则可点击“添加”按钮以弹出一个新的添加约束对话框，根据输出单元格与约束值之间的关系在对话框中间的下拉列表中选择适当的约束类型，以增加新的约束.但本例中已无其他约束了，所以只要点击“确定”按钮返回“规划求解”对话框.如果需要修改或删除已添加的约束，可选中该约束后点击“更改”或“删除” 按钮.到现在为止“规划求解”对话框已根据图13-3的电子表格描述了整个模型（见图13-4）.但在求解模型前还需要进行最后一个程序，点击“选项”按钮弹出图13-6所示的选项对话框，这个对话框中是一些关于如何求解问题的细节的选项.对于决策变量取值非负的线性规划模型，最主要的选项是“采用线性模型”和“假定非负”选项，（见图13-6）.关于其他选项，对小型问题来说接受图中所示的默认值通常比较合适，点击“确定”按钮返回“规划求解”对话框.现在可以点击“规划求解”对话框中的“求解”按钮了，它会在后台开始对问题进行求解.对于一个小型问题，几秒钟之后“规划求解”就会显示运行结果.如图13-7所示，它会显示已经找到了一个最优解.如果模型没有可行解或没有最优解，对话框会显示“规划求解找不到可行解”或“设定的单元格值不能集中”.对话框还显示了产生各种报告的选项，后面将会介绍.选择“保存规划求解结果” 并点击“确定” 按钮，返回电子表格模型.求解模型之后，如图13-8图 13-9所示，“规划求解”用最优解和最优值代替了可变单元格和目标单元格中的初始值.因此，最优解是生产4公斤药品Ⅰ和2公斤药品Ⅱ，最优值为1400元，与图解法的结果一致.图13-9显示的是例2-2的电子表格模型及求解过程.这个问题的电子表格模型建立与求解过程与例2-1描述的基本相同，数据单元格（C5：E8）、（C9：E9）和（H5：H8）分别存放三种原料B 1、B 2、B 3每斤所含四种营养成分的数量、每斤原料的单价以及食品所要求的最低营养成分的含量限制，可变单元格（C10：E10）存放三种原料配比情况（图13-9的左上部分）.输出单元格（F5：F8）给出了食品中实际的营养成分含量，目标单元格（F9）显示了该种食品的总成本（图13-9的左下部分）.图13-9的右下角显示了“规划求解”对话框的主要部分，包括为目标单元格和可变单元格设定的地址，约束条件F5≥H5，F6≥H6，F7≥H7和F8≥H8通过“添加约束”对话框显示在“规划求解” 对话框中.由于目标是最小化总成本，所以选择了“最小值（N ）”.图13-9的右上角显示了点击“规划求解” 对话框的“选项”按钮后所选择的选项，“采用线性模型”先期定义了这个模型是线性规划模型，“假定非负”选项定义了可变单元格必须是非负约束，因为食品的配比不可能出现负值.点击“规划求解” 对话框的求解按钮后，得到了图13-9中电子表格的可变单元格中显示的最优解，即该食品配比为原料B 1 是1.94斤，原料B 3是2.36斤，成本为109.72元.与单纯形法人工求解不同，如果输出单元格、可变单元图 13-10格或目标单元格结果不是整数，电子表格是以小数而非分数形式显示的，本例结果以四舍五入的方式保留了两位小数.第二节 线性规划的应用问题一、合理用料问题这是第二章第五节的第一个问题，由于原料胶管的长度为15分米，而输液管、止血带和听诊器胶管分别长5.7、4.2和3.1分米，所以每根原料胶管最多可截三种材料依次为2根、3根和4根，即总的截法不超过3×4×5 = 60（种）.又由于每种截法的料头不能超过2分米，所以可先通过电子表格进行试算以选择其中可行的几种截法，再利用线性规划的方法找出用料根数最少的方案.如图13-10的左上部分所示，单元格C4至E4显示三种胶管的长度；C5至E5输入不同的方法截出每种胶管的根数；F4为对应C5至E5的不同截法所剩料头的长度， F5通过判断剩余料头的长度是否在0到2之间显示出该种解法是否可行，单元格F4和F5的公式见图13-10的左下部分.不断变换C5至E5的可能取值并选择其中可行的截法（共6种），在电子表格中建立该问题的线性规划模型.数据单元格为C9：H11、C12：H12和K9：K12，分别显示每种截法截一根原料胶管时得到三种不同材料的数量、每种截法截取一次所用胶管的数量和三种材料的需要量；可变单元格C13：H13显示采用每种截法所截的胶管原料数；输出单元格I9：I12列出了某一截取方案实际获得的三种材料数量，每种材料的数量等于各种截法截得该材料数与对应截法所截原料数的乘积之和，如输液管的数量I9 = SUMPRODUCT(C9:H9,C13:H13)；目标单元格I12为总用料数，应等于各种截法所截原料数之和,即I12 = SUM(C13:H13).图13-10的右半部分显示了“规划求解”对话框及“选项”对话框的内容.该问题的目标是所用的胶管原料的总根数最少，因此设置目标单元格为I12等于最小值.由于实际获得的材料数量必须满足需求量的要求，考虑到最优方案（各种截法的某一组合）不一定能使截出的三种材料数量恰好等于需要的数量，而某种材料超过需求量是允许的，故在添加约束时可设置实际截得的数量大于等于需求量，即I9：I12>=K9：K12（本题中，该约束取“>=”和“=”的结果是相同的）；又由于截出的各种材料数量均为整数，因此约束中应包括决策变量取整数的限制，即C13:H13=整数.图13-10的左上部分显示了该问题的最优方案为：分别用第二种、第四种和第五种截法截取原料40、60和10根，共用原料110根，与第二章中用大M法求解的结果一致.二、放射科的业务安排图13-11显示了第二章问题二的电子表格模型及求解过程.该问题的数据包括：进行三种检查的单位时间（C5：E5），三种检查设备每月的可用时间（C9：E9），三项业务每月最多提供量（H6）以及每项业务的单位利润（C10：E10）.可变单元格为C6至E6，图 13-11给出三项业务每月的实际发生数量.输出单元格为C7至E7和F6，分别表示根据各项业务的实际发生数量产生的设备使用时间及实际的总业务量.目标单元格F10显示由每项业务的单位利润及每月实际发生数量计算的总利润.图13-11的左下部分给出了输出单元格及目标单元格的公式.图13-11右下部分的“规划求解”对话框显示了求解时应注意的问题：求目标单元格的最大值（利润最大）；约束为设备的实际使用时间小于等于设备的可用时间及实际总业务量小于等于总业务提供量的限制.打开“选项”对话框，仍选择“采用线性模型”和“假定非负”，回到“规划求解”并按“求解”按钮，得到问题的最优方案为：每月X 线及CT 检查的业务量分别为1320人次和480人次，磁共振业务量为0，即不必购买该设备；按最优方案安排业务每月可获利55200元.在电子表格上建立线性规划或其它问题模型的方式是非常灵活的，不必拘泥于一种固定的模式.本书仅提供了一种建立模型的思路，读者可根据不同问题的特点以及个人的习惯或喜好建立不同风格的电子表格模型.第三节 线性规划的灵敏度分析前面指出线性规划模型的许多参数，都只是对实际数据的大致估计，而不可能在研究的时候就获得精确的数值.通过灵敏度分析可以得出每一个估计的数据需要精确到何种程度，才能保持解的最优性.回忆例2-1某制药厂的生产计划问题，其求解结果如图13-8所示，即生产4公斤药品Ⅰ和2公斤药品Ⅱ，总利润为1400元.但该最优解是在假设所有的模型参数都准确的前提下做出的，在此基础上，管理层如果进一步考虑下列问题：1．如果在该厂生产的药品中，有一个单位利润的估计值是不准确的，将会发生怎样的情况？2．如果该工厂两种药品的单位利润的估计都是不准确的，又将会怎样？3．如果改变该厂某种设备可用于生产的时间，会对结果产生什么影响？4．如果四种设备可用于生产的时间同时改变，又会对结果产生何种影响？ 在本节中，我们将重点介绍如何利用“规划求解”中的“敏感性报告”对目标函数系数j c 以及约束条件右端值i b 的变动进行灵敏度分析.分析的内容主要是系数在什么范围内变化时，已得到的最优解保持不变，即发现哪些系数不图 13-12太敏感（由于在较大范围内变化时，最优解保持不变，故可以进行粗略估计），哪些系数比较敏感（即使微小的改变都会对最优解产生影响，故必须对其精确定义）.一、目标函数系数变动的灵敏度分析首先介绍目标函数系数的灵敏度分析，回顾一下就可以知道，这些系数表示各种决策对总目标的单位贡献.下面以例2-1某药厂的生产计划问题的目标函数系数变动情况进行讨论.问题1：如果该药厂一种药品的单位利润的估计是不精确的，结果怎样？ 首先看一下，如果药品Ⅱ的单位利润300元的估计是不精确的情况，假设：药品Ⅱ的单位利润 = 电子表格中D9单元格中的数据现在，2c =300元，下面我们来分析一下在保持最优解)2,4(),(21 x x 不变的条件下，2c 可能的最大值与最小值.这样，也就可以看出2c 为300元的这一估计能够在多大程度上偏离实际值而不会改变解的最优性.（一）使用电子表格进行灵敏度分析电子表格的一个强大的优点就是可以方便互动地展开各种形式的灵敏度分析.通过运用规划求解工具来求解最优解，模型参数值的改变所造成的影响一下子就可以显示出来.为了说明这一点，图13-12显示了药品Ⅱ的单位利润从开始的2c =300元降到2c =250元的情况，与图13-8相比，最优解没有丝毫的变化.事实上，该问题唯一的变动是电子表格中C9单元格中的数据从300元降到250元，以及E 9单元格总利润减少了100元（因为每单位药品Ⅱ所提供的利润减少了50元）.因为最优解没有变动，我们可以知道在不图 13-14 影响最优解的前提下，药品Ⅱ的单位利润2c =300元的最初估计是较高的.那么，如果这一估计值较低又会怎样呢？图13-13表示了将2c =300元增加到2c =350元的情况.同样，最优解没有发生变化.因为，增加或减少最初的2c =300元均不会对最优解产生任何影响，2c 就不是很敏感的系数，也就不需要为了保证最优解不会改变，而花很大力气去得到2c 的更精确的值.但是对2c 的研究至此并没有结束，因为实际值很可能会超出250到350元这一范围，那么在保持最优解不变的条件下，2c 到底可以在什么样的范围内取值呢？当然可以在电子表格中采取试验的方法，不断增加或减少的2c 值，直到最优解发生改变，以找到最优解发生变化时对应的2c 值.但是，这样计算太麻烦了，是否有简便一些的方法呢？答案是肯定的.（二）利用敏感性报告进行目标系数的灵敏度分析如图13-7所示，在求得最优解之后，规划求解工具会给出相应的信息，同时，在其右边列出了它可以提供的三个报告.选择第二项敏感性报告的选项，就可以得到灵敏度的分析报告，它显示在模型的工作表之前.图13-14显示了本例敏感性报告中的一部分.终值一栏表明了问题的最优解，第二栏给出了递减成本，递减成本提供了为使决策变量取正值，相应的目标系数需要减少的数量.对于本例，由于两决策变量的取值均为正数，故递减成本均为零.第三栏表示了目标函数的现值，最后两栏表示为使最优解保持不变，目标系数允许增加与减少的最大值.例如，考虑决策变量X 1的目标系数1c ，从图13-14中表示产品Ⅰ的一行中可知，1c 可以减少50，可以增加1E+30.在电子表格中1E+30是1030的缩写，Excel 使用这一极大的数值来表示无穷大.因此，从灵敏度的分析报告中可知：1c 的现值： 2001c 的允许增加值： 无穷大 此时1c 无上限1c 的允许减少值： 50 此时150502001=-≥c1c 的变化范围： 1501≥c因此，只要在上面的变化范围内变动，并且不改变模型的其他任何内容，最优解将始终保持在)2,4(),(21=x x 不变.该药厂的另一药品的单位利润的变化范围也可以用同样的方法得出，2c 是药品Ⅱ的单位利润，表中表示药品Ⅱ的第二行给出了下面关于2c 的信息：2c 的现值： 3002c 的允许增加值： 100 此时4001003002=+≤c 2c 的允许减少值： 300 此时03003002=-≥c 2c 的变化范围： 40002≤≤c 目标函数的两个系数的允许变化范围都很大，因此，尽管药品Ⅰ和药品Ⅱ的单位利润可能仅仅是实际值的一个粗略估计，我们也可以相信，这个估计值对最优解的正确性不会有影响.但在一些线性规划模型中，目标系数微小的变动都可能会影响最优解.这样的系数称为敏感参数.灵敏度的分析报告中会直接显示目标中哪些系数是敏感的，这些系数允许的变化区域很小，因此，必须格外小心，尽量取得这些数据的精确值.在求得模型的最优解之后，目标系数的允许变化范围还有一个很重要的用途.在问题的线性规划分析结束之后，如果外界的环境发生了一定的变化，灵敏度分析可以在无需重新求解的情况下，表明模型参数的变化是否造成了最优解的改变.例如经过一段时间以后，如果药品的单位利润发生了较大的变化，通过其允许变化范围，可以一眼看出原来的最优组合是否依然适用.有了目标系数的允许变化范围，在判断问题时，就不需要重新建模与求解，这一点对线性规划问题的解决是有很大帮助的，特别是在处理一个大型模型时.（三）目标系数的同时变动因为存在许多不确定性因素，目标函数系数的值，如单位利润，通常都只是对实际值的估计.上面所讨论的是只有一个系数变动时的情况，这类问题在求解一个系数的允许变化范围时，假设其他所有系数都是正确的，研究的系数是唯一可能与实际值不符的变动的系数.但事实上，所有的系数（至少一个以上）可能同时都是不准确的，如果这样的话，是否可能会导致求得的最优解不正确呢？这是最关键的问题.如果可能对最后的结果产生影响，就必须对这些系数作进一步的分析.另一方面，如果灵敏度分析表明目前的参数估计不会影响最优解的正确性，那么，管理者可以增加对该模型及其所提供的解决方法的信心.以下将介绍如何在不重新求解模型的条件下，确定如果目标函数的几个系数同时变化，可能造成的对最优解的影响．我们仍利用例2-1提出如下问题：问题2：如果该药厂两种药品的单位利润的估计都是不准确的，将会对结果产生怎样的影响？例如，原来药品Ⅰ和药品Ⅱ的单位利润分别为200元和300元，现在由于原料成本的变化，每公斤药品Ⅰ和药品Ⅱ的单位利润分别变为180元和355元，最优解是否发生变化？在分析多个系数同时变动的情况时，仍然要使用敏感性报告中提供的每个系数的允许增加值和减少值数据，下面介绍多个系数同时变动的百分之百法则.首先定义j c 的允许增加（减少）百分比为j c 的增加量（减少量）除以j c 的允许增加量（允许减少量）的值.这样我们可以计算出1c 的允许减少百分比为%4050/)180200(=-，2c 的允许增加百分比为%55100/)300355(=-，2c 的允许减少百分比与2c 的允许增加百分比之和为%95%55%40=+.目标函数系数同时变动的百分之百法则：如果目标函数的系数同时变动，当其所有允许增加百分比和允许减少百分比之和不超过百分之百时，最优解不会改变，如果超过百分之百，则不能确定最优解是否改变.因为本例中1c 的允许减少百分比与2c 的允许增加百分比之和为95%不超过100%，所以当每公斤药品Ⅰ的利润减少为180元，每公斤药品Ⅱ的利润增加为355元时，此线性规划最优解仍然为药品Ⅰ生产4公斤和药品Ⅱ生产2公斤（即2,421==x x ），此时有最大利润为143071072023554180=+=⨯+⨯（元），如图13-15所示.这一法则并没有表示出，在变动百分比之和超过百分之百的情况下，可能的结果.这一结果还有赖于系数变动的方向.但是，只要变动百分比之和不超过百分之百，最优解是肯定不会改变的.记住，我们可以让单一的目标函数系数在整个允许范围内变动，但这只有在其他目标函数系数都不变的情况下才有效.如果多个系数同时变动，我们必须研究各个系数的变动百分比.二、约束右端值的灵敏度分析之所以要分析函数约束右端值变动的原因与前面一样，因为在建模时，还不能得到模型的这些参数的精确值，只能对其作粗略的估计.因此，我们希望知道在这些估计不准确的情况下会产生怎样的后果.除此之外一个更主要的理由是因为，这些常数（通常代表资源的可用量）往往不是由外界决定的而是管理层的政策决策.因此管理者希望知道如果改变这些决策是否会提高最终的收益.影子价格分析就是为管理者提供这方面的信息.下面是关于例2-1的第三个问题：问题3：如果改变该厂某设备可用于生产的时间，结果将如何？（一）约束右端值的影子价格分析回忆第二章中关于影子价格的经济含义，我们知道影子价格代表单位资源在最优利用的条件下所产生的经济效果.即在模型获得最优解的情况下，约束条件右端值在一定范围内每增加（减少）一个单位，使目标函数值增加（减少）的量.其中，一定范围是指保持影子价格不变的右端值变化范围.在影子价格分析中，每次分析一个函数约束，可以将该函数约束右端值的常数增加一个单位后重新求解，观察目标函数值增加的量来确定影子价格，也可以利用灵敏度报告中提供的关于每一个函数约束的影子价格数据.从一个约束的影子价格中就可以直接看出，决策改变而引起的约束常数的改变所造成的影响.只要约束常数的变动不大，那么目标函数值的变动就等于约束常数的变动（正或负）乘以影子价格.为了说明影子价格的含义，我们以第二。

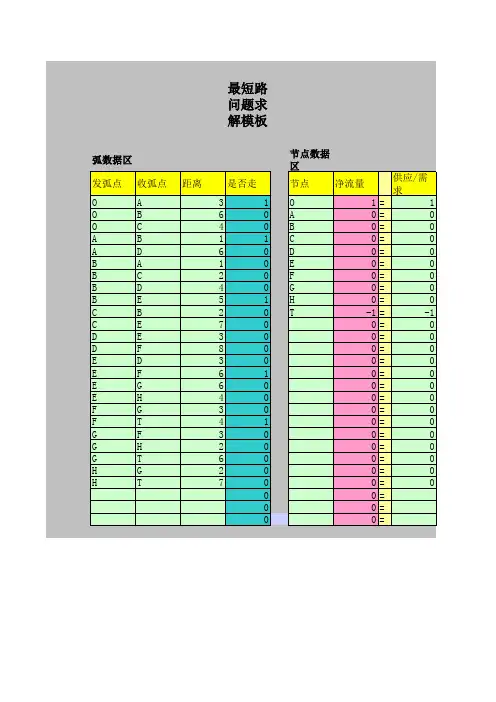
图 13-1第十三章 运筹学问题的Excel 建模及求解 学习运筹学的目的在于学会用运筹学的方法解决实践中的管理问题，注重学以致用.很多实际问题利用人工计算要经过长时间的艰苦工作才能完成甚至根本无法求解，但若使用运筹学软件则瞬间就能解决.因此在学习过程中不仅要掌握运筹学的基本理论和计算方法，还要充分利用现代化的手段和技术.微软的电子表格软件（Microsoft Excel ）为展示和分析许多运筹学问题提供了一个功能强大而直观的工具，它现在已经被应用于管理实践中.本章将重点介绍如何建立和求解规划问题的电子表格模型，对于解决大量的中、小规模的实际规划问题，电子表格软件是远远优于传统的代数算法的.第一节 Excel 中的规划求解工具本节中，我们将举例说明如何使用微软Excel 以电子表格的形式建立线性规划模型，并利用Excel 中的规划求解工具对模型求解.一、在Excel 中加载规划求解工具要使用Excel 应首先安装MicrosoftOffice ，然后从屏幕左下角的[开始]—[程序]中找到Microsoft Excel 并启动.在Excel 的主菜单中点击[工具]—[加载宏]，选择“规划求解”，如图13-1所示.点击[确定]后，在工具菜单中将增加[规划求解]选项. 二、在Excel 中建立线性规划模型我们以例2-1为例说明如何在电子表格中建立该问题的线性规划模型.建立电子表格模型时既可以直接利用问题中所给的数据和信息，也可以利用已建立的代数模型.本例的代数模型为：图 13-2 图 13-3目标函数 21300200x x Z +=max⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≤≤≤+≤+0,124164821222..21212121x x x x x x x x t s图13-2显示了将该例的数据转送到电子表格中后所建立的电子表格数学模型（本例是一个线性规划模型）.其中显示数据的单元格称为数据单元格，包括生产每单位药品Ⅰ和Ⅱ所需要的4种设备的台时数（单元格C5：D8），药品Ⅰ和Ⅱ的单位利润（单元格C9：D9），4种设备可用的台时数（单元格G5：G8）.我们要做的决策是两种药品各生产多少；对这一决策的约束条件是生产两种药品所需的4种设备台时的限制；判断这些决策的优劣程度的指标是生产这两种药品所获得的总利润（决策目标）.如图13-3所示，将决策变量（药品Ⅰ、Ⅱ的产量）分别放入单元格C10和D10，正好在两种药品所在列的数据单元格的下面.由于不知道这些产量会是多少，故在图13-3中均设为零（空白的单元格默认取值为零.实际上，除负值外的任何一个试验解都可以）.以后在寻找产量最佳组合时这些数值会被改变.因此，含有需要做出决策的单元格称为可变单元格.两种药品所需的4种设备台时总数分别放入单元格E5至E8，正好在对应数据单元格的右边.由于所需的各种设备台时总数取决两种药品的实际产量，如：E5=C5×C10+D5×D10（可直接将公式写入E5，也可利用SUMPRODUCT 函数，E5=SUMPRODUCT （C5：D5，C10：D10），此函数可以计算若干维数相同的数组的彼此对应元素乘积之和），因此当产量为零时所需各种设备台时的总数也为零.由于E5至E8单元格每个都给出了依赖于可变单元格（C10和D10）的输出结果，它们因此被称为输出单元格.作为输出单元格的结果，4种设备台时数的总需求。

用Excel求解网络规划问题
文摘：用Excel提供的“规划求解”功能解决了网络规划问题中的主要问题：最大流问题、最小代价流问题、最短路问题和网络计划关键路径问题。

主题词：最大流问题，最小代价流问题，最短路问题，关键路径问题
在生产实践和社会生活中，有许多现实的网络，如电力网、通讯网、铁路网等。

研究这些网络的管理决策问题就是网络规划，它是运筹学中一个重要的分支。

网络规划中主要问题有：最大流问题、最小代价流问题、最短路问题和网络计划关键路径问题。

用
Excel提供的“规划求解”功能可以解决许多问题，可以解方程(组)，可以解线*规划和非线*规划问题。

本文举例说明如何使用这一功能求解运筹学中的网络规划问题。

例题：基于office2010求解最短路问题用Excel 求解最短路问题的原理设决策变量为xij ，当xij=1，表示最短路P*通过边<vi,vj>；当xij=0，表示最短路P*不通过边<vi,vj>；最短路P*中，除起点和终点之外，每个点的进出度数和为0，起点为1，终点为- 1。

目标函数为各边权数与对应决策变量xij 的乘积之和的最小值。

步骤：第一步：制作表格，第一行依次输入：从、到、是否走、距离、节点、净流量、空、供应/需求；在相应列输入已知数据（是否走列填0；供应/需求列依次填1,0,0,…，0,0，-1）。

并在到列数据下空一格，输入总距离。

第二步：在净流量列全都输入=SUMIF （从，节点，是否走）-SUMIF （到，节点，是否走），回车，得到净流量列全为0.第三步:在总距离同一行右边单元格Z 内输入=SUMPRODUCT （是否走，距离），回车，得到0.第四步：选中Z ，单击菜单栏中<数据>，选择<规划求解>。

设置规划求解参数。

目标函数为最小值；可变单元格为是否走列；遵守约束为净流量=供应/需求；√使无约束变量为非负数；选择求解方法为单纯线性规划。

第五步：点击求解，并确定。

解：i ）制作表格，第一行依次输入：从、到、是否走、距离、节点、净流量、空、供应/需求；在从列输入V1，V1,V2,V2,V2,V3,V3,V4,V4,V5,V5,V6;到列输入V2，V3，V3，V4，V5，V4，V6，V5，V6，V6，V7，V7；是否走列输入V1V2V3V4V5V6V752 52442 441 630,0,0,0,0,0,0,0,0,0,0,0；距离列输入5,2,2,4,5,2,4,4,4,1,3,6；节点列输入V1，V2，V3，V4，V5，V6，V7；空列输入=，=，=，=，=，=，=；供应/需求列输入1,0，0,0,0,0，-1.如下图：ii）在净流量列单元格内全都输入=SUMIF(A2:A13,E2:E8,C2:C13)-SUMIF(B2:B13,E2:E8,C2:C13)，回车（注意：选择复制粘贴时，切勿使用键盘下键，不然改变单元格内公式，直接按enter键即可），得到净流量列全为0.如下图：iii）在总距离同一行右边单元格Z内输入=SUMPRODUCT(C2:C13,D2:D13)，回车，得到0.如下图：iv）选中Z，单击菜单栏中<数据>，选择<规划求解>，设置规划求解参数。

第2章 线性规划的计算机求解及应用举例§1线性规划模型在电子表格中的布局线性规划模型在电子表格中布局的好坏关系到问题可读性和求解方便性的高低。

本节以第一章中的例1（资源分配问题）为例来说明一下如何在电子表格中描述线性规划模型，让我们回顾一下第一章中例1的数学模型：Max 1243Z x x =+. 1212126282318,0x x x x x x ≤⎧⎪≤⎪⎨+≤⎪⎪≥⎩ （）一般来说，在与问题相关的表格的基础上稍加调整就可以在电子表格中形成一个十分清晰的模型描述。

我们以表1-1为基础在Excel 电子表格中将上述问题描述如图2-1。

§2用Excel 规划求解工具求解线性规划模型Excel 中有一个工具叫规划求解，可以方便地求解线性规划模型。

“规划求解”加载宏是Excel 的一个可选加载模块，在安装Excel 时，只有在选择“定制安装”或完全安装时才可以选择装入这个模块。

如果你现在的Excel 窗口菜单栏的“工具”菜单中没“规划求解”选项，可以通过“工具”菜单的“加载宏”选项打开“加载宏”对话框来添加“规划求解”（见图2-2）。

在应用规划求解工具以前，要首先确认在Excel 电子表格中包括决策变量、目标函数、约束函数三种信息的单元格或单元格区域。

图2-1中的电子表格中就已经有了这部分内容：决策变图2-1 资源分配问题的模型在Excel 电子表格的布局及公式图2-2 加载宏对话框量在C9和D9单元格中；目标函数的系数在第8行；约束函数在第5、6和7行。

因为我们不知道决策变量的值是多少，所以就在决策变量所在的单元格中填上初始值“0”，当然也可以什么都不填，系统会默认它为0，在求解以后Excel会自动将它们替换成决策变量的最优解。

下面我们接着上节的内容用Excel规划求解将第一章例1的资源分配问题解一遍。

首先将要求解模型的所有相关信息和公式像图2-1那样填入电子表格中后，再选取[工具] | [规划求解]命令后，弹出图2-3所示的“规划求解参数”对话框。

第2章 线性规划的计算机求解及应用举例§1线性规划模型在电子表格中的布局线性规划模型在电子表格中布局的好坏关系到问题可读性和求解方便性的高低。

本节以第一章中的例1（资源分配问题）为例来说明一下如何在电子表格中描述线性规划模型，让我们回顾一下第一章中例1的数学模型：Max 1243Z x x =+s.t. 1212126282318,0x x x x x x ≤⎧⎪≤⎪⎨+≤⎪⎪≥⎩ （2.1）一般来说，在与问题相关的表格的基础上稍加调整就可以在电子表格中形成一个十分清晰的模型描述。

我们以表1-1为基础在Excel 电子表格中将上述问题描述如图2-1。

§2用Excel 规划求解工具求解线性规划模型Excel 中有一个工具叫规划求解，可以方便地求解线性规划模型。

“规划求解”加载宏是Excel 的一个可选加载模块，在安装Excel 时，只有在选择“定制安装”或完全安装时才可以选择装入这个模块。

如果你现在的Excel 窗口菜单栏的“工具”菜单中没“规划求解”选项，可以通过“工具”菜单的“加载宏”选项打开“加载图2-1 资源分配问题的模型在Excel 电子表格的布局及公式图2-2 加载宏对话框宏”对话框来添加“规划求解”（见图2-2）。

在应用规划求解工具以前，要首先确认在Excel电子表格中包括决策变量、目标函数、约束函数三种信息的单元格或单元格区域。

图2-1中的电子表格中就已经有了这部分内容：决策变量在C9和D9单元格中；目标函数的系数在第8行；约束函数在第5、6和7行。

因为我们不知道决策变量的值是多少，所以就在决策变量所在的单元格中填上初始值“0”，当然也可以什么都不填，系统会默认它为0，在求解以后Excel会自动将它们替换成决策变量的最优解。

下面我们接着上节的内容用Excel规划求解将第一章例1的资源分配问题解一遍。

首先将要求解模型的所有相关信息和公式像图2-1那样填入电子表格中后，再选取[工具] | [规划求解]命令后，弹出图2-3所示的“规划求解参数”对话框。

附件2《运筹学》最短路、最小费用最大流经典作品关于钢管订购和运输的优化模型队员：陈显健陈瑜斌陈振松2007年6月5日摘 要： 本文首先运用图论知识中的最短路算法求出i S 到j A 的最优路径。

然后将模型转化为最小费用最大流的网络优化问题，从而求出近似最优解。

在分析出求解该网络优化模型的解法后，运用Lingo 软件包求出了该问题的近似最优解。

对问题一而言，求出了较优的订购和运输计划（见表三），其最小费用为1291630万元。

对于第二个问题而言，可得出钢厂6S 的钢管销价的变化对购运计划和总费用的影响最大；钢管厂1S 的钢管产量的上限的变化对总费用的影响最大，钢管厂3S 的产量上限的变化对购运计划的影响最大。

对问题三，给出了一般解，求出了较优的订购和运输计划（见表四），其最小费用为1396099万元，最后对模型进行了综合评价并提出了改进方向。

关键词：网络流 最小费用最大流一、 问题重述要铺设一条1521A A A →→→ 的输送天然气的主管道，如图一所示,经筛选后可以生产这种主管道的钢厂有721,,,S S S 。

图中粗线表示铁路，单细线表示公路，双细线表示要铺设的管道（假设沿管道或者原来有公路，或者建有施工公路），圆圈表示火车站，每段铁路、公路和管道旁的阿拉伯数字表示里程（单位km ）。

为了方便，1km 主管道称为1单位钢管。

一个钢厂如果承担制造这种钢管，至少需要生产500个单位。

钢厂i S 在指定期限内能生产该钢管的最大生产数量为i s 个单位，钢厂出厂销价为i p 万元，如下表：表一1单位钢管的铁路运价如下表：（表二）1000km 以上每增加1至100km 运价增加5万元。

公路运输费用为1单位管道每公里0.1万元（不足整公里的按整公里计算）。

管道可由铁路、公路运往铺设地点（不只是运到点1521A A A →→→ ，而是管道全线）。

要求：（1） 请制定一个主管道钢管的订购和运输计划，使总费用最小，并给出总费用。