初中数学竞赛中的反比例函数问题

初中数学竞赛：双曲线形如xky =(0≠k )的函数叫做反比例函数，它的图象是由两条曲线组成的双曲线，与双曲线相关的知识有：1． 双曲线解析式xky =中的系数k 决定图象的大致位置及y 随x 变化的状况．2．双曲线图象上的点是关于原点O 成中心对称，在k >0时函数的图象关于直线x y =轴对称；在k <0时函数的图象关于直线x y -=轴对称．3．自变量的取值是不等于零的全体实数，双曲线向坐标轴无限延伸但不能接近坐标轴． 【例题求解】【例1】 已知反比例函数xky =的图象与直线x y 2=和1+=x y 过同一点，则当0>x 时，这个反比例函数的函数值y 随x 的增大而 (填增大或减小)． 思路点拨 确定k 的值，只需求出双曲线上一点的坐标即可．注：(1)解与反比函数相关问题时，充分考虑它的对称性(关于原点O 中心称，关于x y ±=轴对称)，这样既能从整上思考问题，又能提高思维的周密性．(2)一个常用命题：如图，设点A 是反比例函数xky =(0≠k )的图象上一点，过A 作AB ⊥x 轴于B ，过A 作AC ⊥y 轴于C ，则 ①S △AOB =k 21； ②S 矩形OBAC =k ．【例2】 如图，正比例函数kx y = (0>k )与反比例函数xy 1=的图象相交于A 、C 两点，过A 作AB ⊥x 轴于B ，连结BC ，若S △ABC 的面积为S ，则( ) A ．S=1 B ．S =2 C ．S=k D ．S=2k思路点拨 运用双曲线的对称性，导出S △AOB 与S △OBC 的关系．【例3】 如图，已知一次函数8+-=x y 和反比例函数xky =(0≠k )的图象在第一象限内有两个不同的公共点A 、B ． (1)求实数k 的取值范围；(2)若△AOB 面积S ＝24，求k 的值．思路点拨 (1)两图象有两个不同的公共点，即联立方程组有两组不同实数解； (2)S △AOB= S △COB S- S △COA ，建立k 的方程．【例4】 如图，直线221+=x y 分别交x 、y 轴于点A 、C ，P 是该直线上在第一象限内的一点，PB ⊥x 轴于B ，S △ABP =9． (1)求点P 的坐标；(2)设点R 与点P 在同一个反比例函数的图象上，且点R 在直线PB 的右侧，作PT ⊥x 轴于F ，当△BRT 与△AOC 相似时，求点R 的坐标．思路点拨 (1)从已知的面积等式出发，列方程求P 点坐标；(2)以三角形相似为条件，结合线段长与坐标的关系求R 坐标，但要注意分类讨论．【例5】 如图，正方形OABC 的面积为9，点O 为坐标原点，点A 在x 轴上，点C 在y 轴上， 点B 在函数x k y =(0>k ，0>x )的图象上，点P(m ，n )是函数xky = (0>k ，0>x )的图象上的任意一点，过点P 分别作x 轴、y 轴的垂线，垂足分别为E 、F ，并设矩形OEPF 和正方形OABC 不重合部分的面积为S ． (1)求B 点坐标和k 的值； (2)当29=S 时，求点P 的坐标； (3)写出S 关于m 的函数关系式．思路点拨 把矩形面积用坐标表示，A 、B 坐标可求，S 矩形OAGF 可用含n 的代数式表示，解题的关键是双曲线关于x y =对称，符合题设条件的P 点不惟一，故思考须周密．注：求两个函数图象的交点坐标，一般通过解这两个函数解析式组成的方程组得到，求符合某种条件的点的坐标，需根据问题中的数量关系和几何元素间的关系建立关于纵横坐标的方程(组)，解方程(组)便可求得有关点的坐标，对于几何问题，还应注意图形的分类讨论．专题训练1． 若一次函数b kx y +=的图象如图所示，则抛物线b kx x y ++=2的对称轴位于y 轴的 侧；反比例函数xkby =的图象在第 象限，在每一个象限内，y 随x 的增大而 ．2．反比例函数xky =的图象经过点A(m ，n)，其中m ，n 是一元二次方程042=++kx x 的两个根，则A 点坐标为 ．3．如图：函数kx y -=（k ≠0）与xy 4-=的图象交于A 、B 两点，过点A 作AC ⊥y 轴，垂足为点C ，则△BOC 的面积为 ．4．已知，点P(n ，2n)是第一象限的点，下面四个命题：(1)点P 关于y 轴对称的点P 1的坐标是(n ，-2n)； (2)点P 到原点O 的距离是5n ；(3)直线 y=-nx+2n 不经过第三象限；(4)对于函数y=nx，当x ＜0时,y 随x 的增大而减小；其中真命题是 .(填上所有真命题的序号)5．已知反比例函数y=1mx-的图像上两点A(x 1，y 1)、B （x 2，y 2），当x 1＜0＜x 2时，有y 1＜y 2 ,则m 的取值范围是( ) A ．m ＜O B ．m ＞0 C. m ＜12 D.m ＞126．已知反比例函数xky =的图象如图所示，则二次函数222k x kx y +-=的图象大致为( )7．已知反比例函数),0(≠=k xky 当0<x 时，y 随x 的增大面增大，那么一次函数k kx y -=的图象经过( )A ．第一、二、三象限B ．第一、二、四象限C ．第一、三、四象限D ．第二、三、四象限 8．如图，A 、B 是函数xy 1=的图象上的点，且A 、B 关于原点O 对称，AC ⊥x 轴于C ，BD ⊥x 轴于D ，如果四边形ACBD 的面积为S ，那么( ) A ． S ＝1 B ．1<S<2 C ．S>2 D ．S ＝29．如图，已知一次函数y=kx+b(k ≠O)的图像与x 轴、y 轴分别交于A 、B 两点，且与反比例函数y=xm(m ≠0)的图像在第一象限交于C 点，CD 垂直于x 轴，垂足为D ．若OA=OB=OD=l ． （1）求点A 、B 、D 的坐标；（2）求一次函数和反比例函数的解析式．10．已知A(x 1、y 1)，B(x 2，y 2)是直线2+-=x y 与双曲线xky =(0≠k )的两个不同交点．(1)求k 的取值范围；(2)是否存在这样k 的值，使得211221)2)(2(x x x x x x +=--?若存在，求出这样的k 值；若不存在，请说明理由．11．已知反比例函数2ky x=和一次函数y ＝2x-1，其中一次函数图像经过(a ，b)，(a+1，b+k)两点．(1)求反比例函数的解析式；(2)如图，已知点A 在第一象限，且同时在上述两个函数的图像上，求A 点坐标； (3)利用(2)的结果，请问：在x 轴上是否存在点P ，使ΔAOP 为等腰三角形？若存在，把符合条件的P 点坐标都求出来；若不存在，请说明理由.12．反比例函数xky =的图象上有一点P(m ，n)，其中m 、n 是关于t 的一元二次方程032=+-k t t 的两根，且P 到原点O 的距离为13，则该反比例函数的解析式为 ．13．如图，正比例函数x y 3=的图象与反比例函数xky =(0>k )的图象交于点A ，若k 取1，2，3…20，对应的Rt △AOB 的面积分别为S 1，S 2，…，S 20，则S 1+S 2+…+S 20= ．14．老师给出一个函数y=f(x)，甲、乙、丙、丁四位同学各指出这个函数的一个性质： 甲：函数图像不经过第三象限； 乙：函数图像经过第一象限；丙：当x ＜2时，y 随x 的增大而减小； 丁：当x ＜2时，y ＞0已知这四位同学叙述都正确，请构造出满足上述所有性质的一个．．函数： ．15．已知反比例函数xy 12=的图象和一次函数7-=kx y 的图象都经过点P(m ，2)． (1)求这个一次函数的解析式；(2)如果等腰梯形ABCD 的顶点A 、B 在这个一次函数的图象上，顶点C 、D 在这个反比例函数的图象上，两底AD 、BC 与y 轴平行，且A 、B 的横坐标分别为a 和2+a ，求a 的值． 16．如图，直线经过A(1，0)，B(0，1)两点，点P 是双曲线xy 21=(0>x )上任意一点，PM ⊥x 轴，PN ⊥y 轴，垂足分别为M ，N ．PM 与直线AB 交于点E ，PN 的延长线与直线AB 交于点F ．(1) 求证：AF ×BE ＝1；(2)若平行于AB 的直线与双曲线只有一个公共点，求公共点的坐标． (2003年江汉油田中考题)17．已知矩形ABCD 的面积为36，以此矩形的对称轴为坐标轴建立平面直角坐标系．．．．．．．．．．．．．．．．．．．．．，设点A 的坐标为(x ，y)，其中x>0，y>0．(1)求出y 与x 之间的函数关系式，求出自变量x 的取值范围；(2)用x 、y 表示矩形ABCD 的外接圆的面积S ，并用下列方法，解答后面的问题：方法：∵2222()2k k a a k a a +=-+ (k 为常数且k>0，a ≠0)，且 2()0k a a-≥∴．2222k a k a+≥．∴当k a a-=0，即a k =±时，222k a a +取得最小值2k ．问题：当点A 在何位置时，矩形ABCD 的外接圆面积S 最小?并求出S 的最小值；(3)如果直线y=mx+2(m<0)与x 轴交于点P ，与y 轴交于点Q ，那么是否存在这样的实数m ，使得点P 、Q 与(2)中求出的点A 构成△PAQ 的面积是矩形ABCD 面积的16?若存在，请求出m的值；若不存在，请说明理由．参考答案。

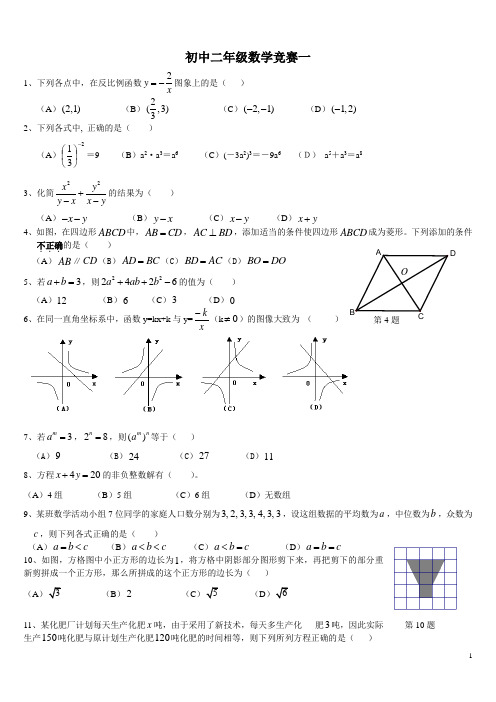
初中二年级数学竞赛一1、下列各点中，在反比例函数2y x=-图象上的是（ ） （A ）(2,1) （B ）2(,3)3（C ）(2,1)-- （D ）(1,2)- 2、下列各式中, 正确的是（ ）（A ）231-⎪⎭⎫⎝⎛＝9 （B ）a 2·a 3＝a 6 （C ）(－3a 2)3＝－9a 6 （Ｄ） a 5＋a 3＝a 83、化简22x y y x x y+--的结果为（ ） （A ）x y -- （B ）y x - （C ）x y - （D ）x y +4、如图，在四边形ABCD 中，AB CD =，AC BD ⊥，添加适当的条件使四边形ABCD 成为菱形。

下列添加的条件不正确．．．的是（ ） （A ）AB ∥CD （B ）AD BC =（C ）BD AC =（D ）BO DO =5、若3a b +=，则222426a ab b ++-的值为（ ） （A ）12 （B ）6 （C ）3 （D ）0 6、在同一直角坐标系中，函数y=kx+k 与y=xk-（k 0≠）的图像大致为 （ ）7、若3m a =，28n=，则()m n a 等于（ ）（A ）9 （B ）24 （C ）27 （D ）11 8、方程420x y +=的非负整数解有（ ）。

（A ）4组 （B ）5组 （C ）6组 （D ）无数组9、某班数学活动小组7位同学的家庭人口数分别为3,2,3,3,4,3,3，设这组数据的平均数为a ，中位数为b ，众数为c ，则下列各式正确的是（ ）（A ）a b c =< （B ）a b c << （C ）a b c <= （D ）a b c ==10、如图，方格图中小正方形的边长为1，将方格中阴影部分图形剪下来，再把剪下的部分重新剪拼成一个正方形，那么所拼成的这个正方形的边长为（ ） （A（B ）2 （C（D11、某化肥厂计划每天生产化肥x 吨，由于采用了新技术，每天多生产化 肥3吨，因此实际生产150吨化肥与原计划生产化肥120吨化肥的时间相等，则下列所列方程正确的是（ ）D第4题 第10题（A ）1201503x x =+ （B ）1201503x x =- （C ）1201503x x =+ （D ）1201503x x =-12、下图是四个边长相等的正方形，其中阴影部分面积较大的是（）13、如果,,a b c 是非零有理数，且0a b c ++=，那么a b c abca b c abc+++的所有可能的值是（ ） （A ）0 （B ）1或1- （C ）2或2- （D ）0或2-14、如图，OB 平分CBA ∠，CO 平分ACB ∠，且MN BC ，设12,24,18AB BC AC ===，则AMN ∆的周长为（ ）（A ）30 （B ）33 （C ）36 （D ）3915、在平面直角坐标系中，O 为坐标原点，直线122y x =+与y 轴交于点A ，点P 在直线上，且满足AOP ∆为等腰三角形，则满足条件的点P 有（ ）（A ）1个 （B ）2个 （C ）3个 （D ）4个 16、如图，正方形ABCD 中，点E 是CD 边上一点，连接AE ， 交对角线BD 于点F ，连接CF ，则图中全等三角形共有（ ） （A ）1对 （B ）2对 （C ）3对 （D ）4对17、直线y=x 与双曲线y=x 1相交于A 、C 两点,AB ⊥x 轴于B,CD ⊥x 轴于D, 四边形ABCD 的面积为（ ） （Ａ）1 ()B 23 ()C 2 ()D 2518、已知一个凸n 边形的n 个内角与某一个外角之和为1350°，则n 为（ ）。

用反比例函数解决问题要点一、利用反比例函数解决实际问题1.基本思路：建立函数模型，即在实际问题中求得函数解析式，然后应用函数的图象和性质等知识解决问题.2.一般步骤如下：（1）审清题意，根据常量、变量之间的关系，设出函数解析式，待定的系数用字母表示.（2）由题目中的已知条件，列出方程，求出待定系数.（3）写出函数解析式，并注意解析式中变量的取值范围.（4）利用函数解析式、函数的图象和性质等去解决问题.要点二、反比例函数在其他学科中的应用1.当圆柱体的体积一定时，圆柱的底面积是高的反比例函数；2.当工程总量一定时，做工时间是做工速度的反比例函数；3.在使用杠杆时，如果阻力和阻力臂不变，则动力是动力臂的反比例函数；电压一定，输出功率是电路中电阻的反比例函数.要点三、反比例函数中的最值问题理论：若0a >，0b >，则a b +³a b =时等号成立）例题：对于函数()10y x x x=+>，当x 取何值时，函数y 的值最小？最小值是多少？0x Q >，12y x x \=+³=，当且仅当1x x =时，等号成立，由1x x=得：1x =或10x =-<（舍去），经检验，1x =是方程1x x =的解，故当x=1时，函数y 的值最小，最小值是2题型一:反比例函数实际问题与图象1．已知矩形的面积为 10，它的长y 与宽x 之间的关系用图象大致可表示为（ ）A ．B ．C ．D ．2．当温度不变时，某气球内的气压(kPa)p 与气体体积2(m )V 成反比例函数关系（其图象如图所示），已知当气球内的气压120kPa p >时，气球将爆炸，为了安全起见，气球内气体体积V 应满足的条件是（ ）A ．不大于24m 5B ．大于25m 4C ．不小于24m 5D ．小于25m 43．伟大的古希腊哲学家、数学家、物理学家阿基米德有句名言：“给我一个支点，我可以撬动地球！”这句名言道出了“标杆原理”的意义和价值．“标杆原理”在实际生产和生活中，有着广泛的运用．比如：小明用撬棍撬动一块大石头，运用的就是“标杆原理”．已知阻力1(N)F 和阻力臂1(m)L 的函数图像如图，若小明想使动力2F 不超过150N ，则动力臂2L 至少需要（ ）m ．A ．2B ．1C ．6D ．44．体育课上，甲、乙、丙、丁四位同学进行跑步训练，如图用四个点分别描述四位同学的跑步时间y（分钟）与平均跑步速度x（米/分钟）的关系，其中描述甲、丙两位同学的y与x之间关系的点恰好在同一个反比例函数的图像上，则在这次训练中跑的路程最多的是（）A．甲B．乙C．丙D．丁5．某商家设计了一个水箱水位自动报警仪，其电路图如图1所示，其中定值电阻110ΩR=，2R是一个压敏电阻，用绝缘薄膜包好后放在一个硬质凹形绝缘盒中，放入水箱底部，受力面水平，承受水压的面积S为0.012m，压敏电阻2R的阻值随所受液体压力F的变化关系如图2所示（水深h越深，压力F越大），电源电压保持6V不变，当电路中的电流为0.3A时，报警器（电阻不计）开始报警，水的压强随深度变化的关系图象如图3所示（参考公式：UIR =，F pS=，1000Pa1kPa=）．则下列说法中不正确的是（）A．当水箱未装水（0mh=）时，压强p为0kPaB．当报警器刚好开始报警时，水箱受到的压力F为40NC．当报警器刚好开始报警时，水箱中水的深度h是0.8mD．若想使水深1m时报警，应使定值电阻1R的阻值为12W题型二:利用反比例函数解决实际问题1．如图是某种电子理疗设备工作原理的示意图,其开始工作时的温度是20℃，然后按照一次函数关系一直增加到70℃，这样有利于打通病灶部位的血液循环，在此温度下再沿反比例函数关系缓慢下降至35℃，然后在此基础上又沿着一次函数关系一直将温度升至70℃，再在此温度下沿着反比例函数关系缓慢下降至，35℃如此循环下去．（1）t的值为；:分钟内温度大于或等于50℃时，治疗效果最好，则维持这个温度范围的持（2）如果在0t续时间为分钟．2．心理学家研究发现，一般情况下，一节课40分钟中，学生的注意力随教师讲课的变化而变化.开始上课时，学生的注意力逐步增强，中间有一段时间学生的注意力保持较为理想的稳定状态，随后学生的注意力开始分散.经过实验分析可知，学生的注意力指标数y随时间x （分钟）的变化规律如图所示（其中AB、BC分别为线段，CD为双曲线的一部分）：(1)开始上课后第五分钟时与第三十分钟时相比较，何时学生的注意力更集中？(2)一道数学竞赛题，需要讲19分钟，为了效果较好，要求学生的注意力指标数最低达到36，那么经过适当安排，老师能否在学生注意力达到所需的状态下讲解完这道题目？请说明理由.3．某水果生产基地在气温较低时，用装有恒温系统的大棚栽培一种新品种水果，如图是试验阶段的某天恒温系统从开启到关闭后，大棚内的温度()y ℃与时间()h x 之间的函数关系，其中线段，表示恒温系统开启后阶段，双曲线的一部分CD 表示恒温系统关闭阶段．请根据图中信息解答下列问题：(1)这个恒温系统设定的恒定温度为多少℃；(2)求全天的温度y 与时间x 之间的函数关系式；(3)若大棚内的温度低于()10℃不利于新品种水果的生长，问这天内，相对有利于水果生长的时间共多少小时？4．心理学研究发现，一般情况下，在一节45分钟的课中，学生的注意力随学习时间的变化而变化．开始学习时，学生的注意力逐步增强，中间有一段时间学生的注意力保持较为理想的稳定状态，随后学生的注意力开始分散．经过实验分析可知，学生的注意力指标数y、分别为线段，CD为双曲线的一部随时间x (分钟)的变化规律如下图所示(其中AB BC分)．(1)求注意力指标数y与时间x (分钟)之间的函数表达式；(2)开始学习后第4分钟时与第35分钟时相比较，何时学生的注意力更集中？(3)某些数学内容的课堂学习大致可分为三个环节：即“教师引导，回顾旧知；自主探索，合作交流；总结归纳，巩固提高”，其中“教师引导，回顾旧知”环节10分钟；重点环节“自主探索，合作交流”这一过程一般需要30分钟才能完成，为了确保效果，要求学习时的注意力指标数不低于40，请问：这样的课堂学习安排是否合理？并说明理由．5．如图所示，小明家饮水机中原有水的温度是20，开机通电后，饮水机自动开始加热，此过程中水温y （°C ）与开机时间x （分）满足一次函数关系．当加热到100°C 时自动停止加热，随后水温开始下降，此过程中水温y （°C ）与开机时间x （分）成反比例关系．当水温降至20°C 时，饮水机又自动开始加热……，不断重复上述程序．根据图中提供的信息，解答下列问题：(1)当05x ££时，求水温y （°C ）与开机时间x （分）的函数关系式；(2)求图中t 的值；(3)有一天，小明在上午7:20（水温20°C ），开机通电后去上学，11:33放学回到家时，饮水机内水的温度为多少°C ？并求：在7:2011:33——这段时间里，水温共有几次达到100°C ？6．据医学研究，使用某种抗生素可治疗心肌炎，某一患者按规定剂量服用这种抗生素，已知刚服用该抗生素后，血液中的含药量y（微克）与服用的时间x成正比例药物浓度达到最高后，血液中的含药量y（微克）与服用的时间x成反比例，根据图中所提供的信息，回答下列问题：(1)抗生素服用_______小时时，血液中药物浓度最大，每毫升血液的含药量有____微克；(2)根据图象求出药物浓度达到最高值之后，y与x之间的函数解析式及定义域；(3)求出该患者服用该药物10小时时每毫升血液的含药量y．题型三：最值问题1．阅读与思考任务：(1)填空：已知0x >，只有当x =______时，4x x+有最小值，最小值为______．(2)如图，P 为双曲线()60y x x =>上的一点，过点P 作PC x ⊥轴于点C ，PD y ⊥轴于点D ，求PC PD +的最小值．2．【操作发现】由()20a b -³得，222a b ab +³；如果两个正数a ，b ，即0a >，0b >，则有下面的不等式：a b +³，当且仅当a b =时取到等号．例如：已知0x >，求式子4x x +的最小值．解：令a x =，4b x =，则由a b +³44x x +³=，当且仅当4x x =时，即2x =时式子有最小值，最小值为4．(1)【问题解决】请根据上面材料回答下列问题：已知0x >，当x 为多少时，代数式9x x +的最小值为；(2)【灵活运用】当2x >时，求12x x +-的最小值；(3)【学以致用】如图，民民同学想做一个菱形风筝，现在有一根长120cm 的竹竿，他准备把它截成两段做成风筝的龙骨即菱形的对角线AC ，BD ，请你帮他设计一下，当AC 为多少cm 时菱形的面积最大，最大值为2cm （直接写出结果）．3．由2()0a b -³得，222a b ab +³；如果两个正数a ，b ，即0,0a b >>，则有下面的不等式：a b +³，当且仅当a b =时取到等号．例如：已知0x >，求式子4x x+的最小值．解：令4,a x b x ==，则由a b +³44x x +³=，当且仅当4x x =时，即2x =时，式子有最小值，最小值为4．请根据上面材料回答下列问题：(1)当0x >，式子x +16x的最小值为 ；(2)当0x <，代数式364+x x最大值为多少？并求出此时x 的值；(3)用篱笆围一个面积为32平方米的长方形花园，使这个长方形花园的一边靠墙（墙长20米），问这个长方形的长、宽各为多少时，所用的篱笆最短，最短的篱笆是多少？4．阅读材料：①对于任意实数a 和b ，都有2()0a b -³，∴2220a ab b -+³，得到222a b ab +³，当且仅当a b =时，等号成立．②任意一个非负实数都可写成一个数的平方的形式.即：如果a ≥0，则2a =．如：22=等．例：①用配方法求代数式2283x x -+的最小值．②已知0a >，求证：12a a+>①解：由题意得：222832(2)5x x x -+=--，∵22(2)0x -³，且当2x =时，22(2)0x -=，∴22(2)55x --³-，∴当2x =时，代数式2283x x -+的最小值为：5-；②证明：∵0a >，∴2122a a +=+>=∴12a a +>12a a =，即请解答下列问题：某园艺公司准备围建一个矩形花圃，其中一边靠墙（墙足够长），另外三边用篱笆围成（如图所示）.设垂直于墙的一边长为x 米.(1)若所用的篱笆长为36米，那么：①当花圃的面积为144平方米时，垂直于墙的一边的长为多少米？②设花圃的面积为S 米2，求当垂直于墙的一边的长为多少米时，这个花圃的面积最大？并求出这个最大面积；(2)若要围成面积为200平方米的花圃，需要用的篱笆最少是多少米？题型四：反比例函数综合运用1．如图是4个台阶的示意图，每个台阶的高和宽分别是1和2，每个台阶凸出的角的顶点记作m T （m 为1～4的整数），函数()0k y x x =>的图象为曲线L ，若曲线L 使得14T T :，这些点分布在它的两侧，每侧各2个点，则k 的取值范围是（ ）A ．812k ££B ．812k £<C ．812k <£D ．812k <<2．如图，矩形ABCD 对角线的交点为O ，点P 在x 轴的正半轴上，DC 平分BDP Ð，PAD V 的面积为6．若双曲线()0k y x x=>经过点D ，交PD 于点Q ，且PQ DQ =，则k 的值为 ．3．如图，已知点()1,A a 和点()3,B b 是直线y mx n =+与双曲线(0)k y k x =>的交点，AOB V 的面积为43．(1)求k 的值；(2)设()111,P x y ，()222,P x y 是反比例函数在同一象限上任意不重合的两点，1212y y M x x =+，2112y y N x x =+，判断M ，N的大小，并说明理由．4．已知反比例函数k y x =的图象经过点()A ．(1)试确定此反比例函数的解析式；(2)点O 是坐标原点，将线段OA 绕O 点顺时针旋转30°得到线段OB ．判断点B 是否在此反比例函数的图象上，并说明理由；(3)已知点()6P m +也在此反比例函数的图象上（其中0m <），过P 点作x 轴的垂线，交x 轴于点M ．若线段PM 上存在一点Q ，使得OQM V 的面积是12，设Q 点的纵坐标为n ，求29n -+的值．5．如图，矩形ABCD的两边AD，AB的长分别为3，8，边BC落在x轴上，E是DC的中点，连接AE，反比例函数myx=的图象经过点E，与AB交于点F．(1)求AE的长；(2)若2AF AE-=，求反比例函数的表达式；(3)在（2）的条件下，连接矩形ABCD两对边AD与BC的中点M，N，设线段MN与反比例函数图象交于点P，将线段MN沿x轴向右平移n个单位，若MP NP<，直接写出n的取值范围．课后练习1．已知蓄电池的电压为定值，使用某蓄电池时，电流I(单位：A)与电阻R(单位：W )是反比例函数关系，它的图象如图所示，则当电阻为6W 时，电流为( )A ．3AB ．4AC ．6AD ．8A2．如图1是一个亮度可调节的台灯，其灯光亮度的改变，可以通过调节总电阻控制电流的变化来实现．如图2是该台灯的电流()A I ．与电阻()R W 成反比例函数的图象，该图象经过点()880,0.25P ．根据图象可知，下列说法正确的是（ ）A ．当0.25R <时，880I <B ．I 与R 的函数关系式是()2000I R R=>C ．当1000R >时，0.22I >D ．当8801000R <<时，I 的取值范围是0.220.25I <<3．某蔬菜生产基地在气温较低时，用装有恒温系统的大棚栽培一种新品种蔬菜．图是试验阶段的某天恒温系统从开启到关闭后，大棚内的温度()C y °与时间()h x 之间的函数关系，其中线段AB 、BC 表示恒温系统开启阶段，双曲线的一部分CD 表示恒温系统关闭阶段．请根据图中信息解答下列问题：(1)求这天的温度y 与时间()024x x ££的函数关系式；(2)若大棚内的温度低于10C °时，蔬菜会受到伤害．问这天内，恒温系统最多可以关闭多少小时，才能使蔬菜避免受到伤害？4．心理学家研究发现，一般情况下，一节课40分钟中，学生的注意力随教师讲课的变化而变化：开始上课时，学生的注意力逐步增强，中间有一段时间学生的注意力保持较为理想的稳定状态，随后学生的注意力开始分散．经过实验分析可知，学生的注意力指标数y 随时间x （分钟）的变化规律如图所示（其中AB BC ，分别为线段，BC x ∥轴，CD 为双曲线的一部分），其中AB 段的关系式为220y x =+．(1)点B 坐标为_______；(2)根据图中数据，求出CD 段双曲线的表达式；(3)一道数学竞赛题，需要讲20分钟，为了效果较好，要求学生的注意力指标数最低达到32，那么经过适当安排，老师能否在学生注意力达到所需的状态下讲解完这道题目?5．为确保身体健康，自来水最好烧开（加热到100℃）后再饮用．某款家用饮水机，具有加热、保温等功能．现将20℃的自来水加入到饮水机中，先加热到100℃．此后停止加热，水温开始下降，达到设置的饮用温度后开始保温．比如事先设置饮用温度为50℃，则水温下降到50℃后不再改变，此时可以正常饮用．整个过程中，水温()y ℃与通电时间()min x 之间的函数关系如图所示．(1)水温从20℃加热到100℃，需要______min ；请直接写出加热过程中水温y 与通电时间x 之间的函数关系式：______；(2)观察判断：在水温下降过程中，y 与x 的函数关系是______函数，并尝试求该函数的解析式；(3)已知冲泡奶粉的最佳温度在40℃左右，某家庭为了给婴儿冲泡奶粉，将饮用温度设置为40℃．现将20℃的自来水加入到饮水机中，此后开始正常加热．则从加入自来水开始，需要等待多长时间才可以接水冲泡奶粉？6．如图是8个台阶的示意图，每个台阶的高和宽分别是1和2，每个台阶凸出的角的顶点记作m T （m 为18: 的整数）函数()0k y x x=<的图像为曲线L ，若曲线L 使得18~T T 这些点分布在它的两侧，每侧各4个点，则k 的取值范围是（ ）A ．3628k -<<-B ．2214k -<<-C ．2012k -<<-D ．3426k -<<-7．阅读理解：若三个非零实数x ，y ，z 满足：只要其中一个数的倒数等于另外两个数的倒数的和，则称这三个实数x ，y ，z 构成“和谐三数组”．(1)若A(m ，y 1)，B(m ＋1，y 2)，C(m ＋3，y 3)三点均在反比例函数4y x=的图象上，且三点的纵坐标恰好构成“和谐三数组”，求实数m 的值；(2)若实数a ，b ，c 是“和谐三数组”，且满足a ＞b ＞c ＞0，求点(,)c c P a b与原点O 的距离OP 的取值范围．8．如图直角坐标系中，矩形ABCD 的边BC 在x 轴上，点B 、D 的坐标分别为B （1，0），D （3，3）．（1）点C 的坐标 ；（2）若反比例函数()0k y k x=¹的图象经过直线AC 上的点E ，且点E 的坐标为（2，m ），求m 的值及反比例函数的解析式；（3）若（2）中的反比例函数的图象与CD 相交于点F ，连接EF ，在直线AB 上找一点P ，使得32PEF CEF S S D D =，求点P 的坐标．9．阅读材料：已知,a b 为非负实数，∵2220a b +-=+-=³，∴a b +³“a b =”时，等号成立．这个结论就是著名的“均值不等式”，“均值不等式”在一类最值问题中有着广泛的应用．例：已知0x >，求函数4y x x =+的最小值．解：令a x =，4b x =，则由a b +³44y x x =+³=．当且仅当4x x=，即2x =时，函数取到最小值，最小值为4．根据以上材料解答下列问题：(1)已知0x >，则当x =______时，函数3y x x=+取到最小值，最小值为______；(2)用篱笆围一个面积为2100m 的矩形花园，则当这个矩形花园的长、宽各为多少时，所用的篱笆最短？最短的篱笆的长度是多少米？(3)已知0x >，则自变量x 取何值时，函数229x y x x =-+取到最大值？最大值为多少？。

初中数学竞赛题型分析在初中数学的学习领域中，数学竞赛无疑是对学生综合能力的一场大考。

它不仅要求学生具备扎实的基础知识，更需要有出色的思维能力、解题技巧和创新意识。

竞赛题型丰富多样，每一种都有其独特的特点和解题思路。

接下来，我们就对常见的初中数学竞赛题型进行一番深入分析。

首先，代数类题型是竞赛中的常客。

其中，方程与不等式的问题常常让学生们绞尽脑汁。

这类题目通常会设置复杂的数量关系，需要学生通过巧妙设元、灵活变形来求解。

例如，给出一些关于未知数的条件，然后要求解出未知数的取值范围或者具体值。

在解决这类问题时，需要熟练掌握方程的性质、不等式的解法以及消元、换元等方法。

函数类题型也是重点之一。

一次函数、二次函数、反比例函数等，常常以综合题的形式出现。

可能会要求根据给定的条件确定函数的解析式，或者利用函数的性质来解决最值问题、图象交点问题等。

这就需要学生对函数的概念、图象和性质有深入的理解，能够将实际问题转化为函数问题，并通过绘制图象、分析代数表达式等手段来找到解题的关键。

几何类题型更是充满了挑战和乐趣。

三角形、四边形、圆等几何图形的相关问题常常让学生们眼前一亮。

比如三角形中的全等与相似证明，需要学生熟练运用各种定理和性质，通过严谨的推理和逻辑思维来完成证明过程。

四边形中的平行四边形、矩形、菱形、正方形等，可能会涉及到性质的综合运用以及面积计算等问题。

而圆的相关题目，则常常与圆心角、圆周角、切线等知识相结合，要求学生具备较强的空间想象力和图形分析能力。

数论类题型虽然在日常教学中涉及较少，但在竞赛中却时有出现。

例如质数与合数、因数与倍数、整除性等问题。

这类题目往往需要学生运用数学的基本原理和规律，通过推理和尝试来找出答案。

组合数学类题型也不容小觑。

像排列组合问题、抽屉原理等，需要学生具有较强的抽象思维和分类讨论能力。

例如计算从若干个元素中选取若干个元素的排列或组合数，或者通过抽屉原理来证明某个结论的存在性。

2019年“大梦杯”福建省初中数学竞赛试题参考答案考试时间2019年3月17日9∶00－11∶00满分150分一、选择题（共5小题，每小题7分，共35分）。

每道小题均给出了代号为A ，B ，C ，D 的四个选项，其中有且只有一个选项是正确的。

请将正确选项的代号填入题后的括号里，不填、多填或错填都得0分）1．若一次函数2y x =+与反比例函数4y x=的图像交于11()A x y ，，22()B x y ，两点，则1212x x y y +的值为（）A ．8B ．6C ．6-D ．8-【答案】D【解答】由24y x y x =+⎧⎪⎨=⎪⎩，得2240x x +-=……………①。

依题意，1x ，2x 是方程①的两根，于是122x x +=-，124x x =-。

∴121212121212441616484x x y y x x x x x x x x +=+⋅=+=-+=--。

2．如图，ABC △为圆O 的内接三角形，D 为BC 中点，E 为OA 中点，40ABC ∠=︒，80BCA ∠=︒，则OED ∠的大小为（）A ．15︒B ．18︒C ．20︒D ．22︒【答案】C【解答】如图，连结OC 。

由40ABC ∠=︒，80BCA ∠=︒，得60BAC ∠=︒。

∵D 为BC 中点，∴OD BC ⊥，1602DOC BOC BAC ∠=∠=∠=︒。

∴30OCD ∠=︒，12OD OC =。

又E 为OA 中点，∴12OE OA OD ==。

结合40ABC ∠=︒，知24060140EOD AOC COD ∠=∠+∠=⨯︒+︒=︒，（第2题图）（第2题答题图）11(180)(180140)2022OED EOD ∠=︒-∠=︒-︒=︒。

3．已知二次函数2()2f x x ax b =++，若()(1)f a f b =+，其中1a b ≠+，则(1)(2)f f +的值为（）A ．8B ．10C ．12D ．14【答案】A【解答】由已知条件及二次函数图像的对称性，知124a b a++=-。

反比例函数提高练习题一一、选择题1． 如图，点A 在双曲线6y x=上，且OA ＝4，过A 作AC ⊥x 轴，垂足为C ，OA 的垂直平分线交OC 于B ，则△ABC 的周长为()A. 47B.5C. 27 222．函数xky -=1与x y 2=的图象没有交点，则k 的取值范围为（ ） A ．0<k B ．1<k C ．0>k D ．1>k3．双曲线x 10y =与x6y =在第一象限内的图象依次是M 和N ，设点P 在图像M 上，PC 垂直于X 轴于点C 交图象N 于点A 。

PD 垂直于Y 轴于D 点，交图象N 于点B ，则四边形PAOB 的面积为（ ）A. 8B. 6C.4D. 2 4．若反比例函数y ＝xk，当x ＜0时，y 随x 的增大而减小，则一次函数y ＝k(x －k)的图象不经过( )A.第一象限B.第二象限C.第三象限D.第四象限 5.若反比例函数的图象经过点，其中，则此反比例函数的图象在（ ）A ．第一、二象限B ．第一、三象限C ．第二、四象限D ．第三、四象限6.如图，一次函数与反比例函数的图像相交于A 、B 两点，则图中使反比例函数的值小于一次函数的值的x 的取值范围是（ ） A ．x ＜－1 B ．－1＜x ＜0，或x ＞2 C ．x ＞2 D ．x ＜－1，或0＜x ＜27.函数m x y +=与)0(≠=m xmy 在同一坐标系内的图象可以ky x=(3)m m ，0m ≠ 2 x B－1 AO －1 2y 第6题O xyBO x yC. OxyD.O x yA ．8.在同一直角坐标系中，函数y=kx+k ，与y=xk-（k 0≠）的图像大致为（ ）9．若反比例函数ky x=的图象经过点（-1,2)，则这个函数的图象一定经过点（ ） A.(2,-1) B.(1,2) C.(-2,-1) D.(12,2) 10．若点A （－2，y 1）、B （－1，y 2）、C （1，y 3）在反比例函数xy 1-=的图像上，则（ ） Ａ． y 1＞y 2 ＞y 3 Ｂ．y 3＞ y 2 ＞y 1 Ｃ．y 2 ＞y 1 ＞y 3 Ｄ． y 1 ＞y 3＞ y 2 11．反比例函数xy 3=图象上有三个点)(11y x ，，)(22y x ，，)(33y x ，，其中3210x x x <<<，则1y ，2y ，3y 的大小关系是( )A ．321y y y <<B ．312y y y <<C ．213y y y <<D ．123y y y << 12．如图，矩形ABCD 的对角线BD 经过坐标原点，矩形的边分别平行于坐标轴，点C 在反比例函数ky x=的图象上.若点A 的坐标为（－2，－2），则k 的值为 （ ） A ．-2 B ．2 C ．3 D ．4 二、填空题1．一次函数1y x =-+与反比例函数2y x=-,x 与y 的对应值如下表： x3- 2- 1- 1 2 3 1y x =-+ 43 2 0 1- 2-2y x=-32 122-1--32 不等式1x -+>-x2的解为 ．2.如图，有反比例函数1y x =、1y x=-的图象和一个以原点为圆心，2为半径的圆，则S =阴影．3.如图，△OPQ 是边长为2的等边三角形，若反比例函 数的图象过点P ，则它的解析式是 .第2题4.如图，直角顶点P 1、P 2、 P 3、……在函数4y x=（x ＞0）图象上，点A 1、A 2、 A 3、……在x 轴的正半轴上，则点P 2010的横坐标为 .5．某中学要在校园内划出一块面积是 100m 2的矩形土地做花圃，设这个矩形的相邻两边的长分别为xm 和ym ，那么y 关于x 的函数解析式是_________________． 6.点P 既在反比例函数3(0)y x x=->的图像上，又在一次函数2y x =--的图像上，则P 点的坐标是___________. 7.已知反比例函数y ＝xk 的图象过点P(a ，b)，且a 、b 是方程x 2＋6x ＋4＝0的两个根，则函数式为 ；8.我们知道，根据二次函数的平移规律，可以由简单的函数通过平移后得到较复杂的函数，事实上，对于其他函数也是如此.如一次函数，反比例函数等。

2007年初中数学竞赛试题赏析2007年春末夏初，国内的初中数学竞赛基本告一段落，暑假期间，在放松避暑纳凉的同时，对数学爱好者来说，把玩一下新的试题，也是一件乐事．下面为大家选析一些试题，供同学们玩赏．一、代数问题例1 已知a ，b ，c 是实数，若2222b c a bc +-，2222c a b ac +-，2222a b c ab+-之和恰等于1，求证：这三个分数的值有两个为1，一个为-1．（2007年北京市初二数学竞赛试题三）证明 由题设2222b c a bc +-+2222c a b ac +-+2222a b c ab+-=1， 即（2222b c a bc +--1）+（2222a c b ac +--1）+（2222a b c ab+-+1）=0， 通分，分子部分因式分解，（请自己完成演算）可得()()()2a b c c a b c a b abc+-+--+=0． 所以，或者a+b-c=0或者c+a-b=0或者b+c-a=0．①若a+b-c=0，则222222222222222222()21;222()21;222()2 1.222b c a b c b c bc bc bc bcc a b c a c a ac ac ac cab c a a b a b ab bc ab ab+-+--===+-+--===+-+-+-===- ②若c+a-b=0，同理可得2222b c a bc +-=1，2222c a b ac +-=-1，2222a b c ab+-=1， ③若c+a-b=0，同理可得2222b c a bc +-=-1，2222c a b ac +-=1，2222a b c ab+-=1． 综合①、②、③可得，三个分数2222b c a bc +-，2222c a b ac +-，2222a b c ab+-的值有两个为1，一个为-1．评析：由题设2222b c a bc +-+2222c a b ac +-+2222a b c ab+-=1，要证这三个分数的值有两个为1，一个为-1，想到证（2222b c a bc +--1）+（2222a c b ac +--1）+（2222a b c ab+-+1）=0 是关键．其中分子部分的因式分解，可检验你的代数式恒等变形的基本功是否过硬． 例2 设a 是正整数，二次函数y=x 2+（a+17）x+38-a ，反比例函数y=56x，•如果这两个函数的图象的交点都是整点（横坐标和纵坐标都是整数的点），求a 的值．（2007年全国初中数学联合竞赛（B 组）试题第三大题）解 联立方程组2(17)38,56,y x a x a y x ⎧=+++-⎪⎨=⎪⎩消去y 得x 2+（a+17）x+38-a=56x， 即x 3+（a+17）x 2+（38-a ）x-56=0，分解因式得（x-1）[x 2+（a+18）x+56]=0． （1）显然x 1=1是方程（1）的一个根，（1，56）是两个函数的图象的一个交点， 因为a 是正整数，所以关于x 的方程x 2+（a+18）x+56=0 （2）的判别式△=（a+18）2-224>0，它一定有两个不同的实数根．而两个函数的图象的交点都是整点，所以方程（2）的根都是整数，•因此它的判别式△=（a+18）2-224应该是一个完全平方数．设（a+18）2-224=k 2（其中k 为非负整数），则（a+18）2-k 2=224，即（a+18+k ）（a+18-k ）=224．显然a+18+k 与a+18-k 的奇偶性相同，且a+18+k ≥8，而224=112×2=56×4=28×8，18112,1856,1828,182,184,188.39,12,0,55,26,10.a k a k a k a k a k a k a a a k k k ++=++=++=⎧⎧⎧⎨⎨⎨+-=+-=+-=⎩⎩⎩===⎧⎧⎧⎨⎨⎨===⎩⎩⎩所以或或解得或或 而a 是正整数，所以只可能39,12,55,26,a a k k ==⎧⎧⎨⎨==⎩⎩或 当a=39时，方程（2）即x 2+57x+56=0，它的两根分别为-1和-56，此时两个函数的图象还有两个交点（-1，-56）和（-56，-1）．当a=12时，方程（2）即x 2+30x+56=0，它的两根分别为-2和-28，此时两个函数的图象还有两个交点（-2，-28）和（-28，-2）．评析：这是初中数学的重点知识与方法高度综合的题目，要求会自行演算独立解答．二、几何问题在初中阶段，图形的运动主要是合同变换，包含平移、轴对称、旋转和中心对称．另外，在我国的几何教学中，对等积变换的知识日益普及，主要是利用“同底等高的两个三角形面积相等”和三角形面积公式来证题、计算，包括解决线段的比例问题．例3 如图1所示，△ABC 中，∠ABC=46°，D 是BC 边上一点，DC=AB ，∠DAB=21°，•试确定∠CAD 的度数．（2007年北京市中学生数学竞赛初二年级试题四）图1 图2解如图2，作△ABD关于AD的轴对称图形△AED，即∠EAD=21°，AE=AB，•所以DE=BD．易知∠ADC=21°+46°=67°，所以∠ADE=∠ADB=180°-67°=113°，∠CDE=113°-67°=46°，连接CE，DC=AB，△ABD≌△CDE≌△ADE．设O为AE与DC的交点，由于∠ODE=∠OED=46°，所以OD=OE．又DC=AE，所以AO=CO ∠OCA=∠OAC ∠COE=2∠ACO．易知∠COE=2×46°=92°，因此2∠ACO=∠COE=92°∠ACO=46°=∠OAC．所以∠DAC=∠DAE+∠EAC=21°+46°=67°．例4如图3，已知等腰△ABC中，AB=AC，P、Q分别为AC、AB上的点，且AP=PQ=•QB=BC，则∠PCQ=______．（2007年北京市中学生数学竞赛初二年级试题）图3 图4解：如图4，过P作AB的平行线，过B作PQ的平行线，二平行线相交于O，则PQBO•是个菱形．连接CO．由AB=AC，AP=QB，则PC=AQ，AP=QB=PO，∠CPO=∠PAQ，所以△PQC≌△APQ，因此CO=PQ=CB=OB，可知△BCO为等边三角形，∠BCO=∠CBO=60°，•设∠CAB=θ，•则∠PCO=∠QBO=θ，由三角形内角和定理，得3θ+2×60°=180°⇒θ=20°，因此∠PCQ=80°-•50°=30°．例5 如图5，四边形ABCD 是梯形，点E 是上底AD 边上一点，CE 的延长线与BA 的延长线交于点F ，过点E 作BA 的平行线CD 交的延长线于点M ，BM 与AD 交于点N ．证明：∠AFN=∠DME ．（2007全国初中数学联合竞赛试题）例5分析 延长BF ，CM 相交于Q ，因为EM ∥AF ，所以∠DME=∠DQA ．要证∠AFN=∠DME ，只需证∠AFN=∠DQA 即可．为此，只需证FN ∥MC ．证明 （面积法）连接FM ，BE ，CN ，因为EM ∥AF ，所以S △PFM =S △PBE ，因为AD ∥BC ，S △BNE =S △CNE ，因此S △BNE +S △PNE =S △CNE +S △PNE ．即S △PBE =S △PNC ，所以S △PFM =S △PNC ．两边同加S △PMC 得S △FMC =S △NMC ，所以FN ∥MC ，又已知FB ∥ME ，所以∠AFN=∠DME ．至于其它的证法我们就不再例举了．例6 试问：18能否表示为3个互异的正整数的倒数的和？18能否表示为3•个互异的完全平方数的倒数的和？如果能，请给出一个例子；如果不能，请说明理由． （第12届华杯赛初一组决赛试题14）解：（1）由于18=14×12=14×（112+16+14）=114824++116，所以18能表示为3个互异的正整数的倒数的和．（2）不妨设三个正整数a<b<c ，满足18=21a +21b +21c． 由于a ，b ，c 是互异的正整数，则21c <21b <21a， 从而18=21a +21b +21c <23a ，所以a 2>24．又18>21a，所以a 2>8，故a 2=9或16． 若a 2=9，则21b +21c =18-19=172，于是172>21b，有b 2>72； 又因为21c <21b ，所以172=21b +21c <22b ， 因此b 2<144，所以72<b 2<144．故b 2=81，100或121，将b 2=81，100，121分别代入c 2=227272b b -，没有一个是完全平方数，此时无解．若a 2=16，则21b +21c =18-116=116， 同上讨论可得：16<b 2<32，所以b 2=25，c 2=22161625169b b ⨯=-不是整数． 综上所述，18不能表示为3个互异的完全平方数的倒数之和． 例7 已知a ，b 都是正整数，试问关于x 的方程x 2-abx+12（a+b ）=0是否有两个整数解？如果有，请把它们求出来；如果没有，请给出证明．解 不妨设a ≤b ，且方程的两个整数根为x 1，x 2（x 1≤x 2），则有12121()2x x ab x x a b +=⎧⎪⎨=+⎪⎩ 所以x 1x 2-x 1-x 2=12a+12b-ab ，4（x 1-1）（x 2-1）+（2a-1）（2b-1）=5． 因为a ，b 都是正整数，所以x 1，x 2均是正整数．于是x 1-1≥0，x 2-1≥0，2a-1≥1，2b-1≥1，所以12(1)(1)0(21)(21)5x x a b --=⎧⎨--=⎩或12(1)(1)1(21)(21)1x x a b --=⎧⎨--=⎩ （1）当12(1)(1)0(21)(21)5x x a b --=⎧⎨--=⎩时，由于a ，b 都是正整数，且a ≤b ，可得a=1，b=3． 此时，一元二次方程为x 2-3x+2=0，它的两个根为x=1，x=2．（2）当12(1)(1)1(21)(21)1x x a b --=⎧⎨--=⎩时，可得a=1，b=1，此时，一元二次方程为x 2-x+1=0，它无整数解．综上所述，当且仅当a=1，b=3时，题设方程有整数解，且它的两个整数解为x 1=1，x 2=2．例8 （1）是否存在正整数m ，n ，使得m （m+2）=n （n+1）？（2）设k （k ≥3）是给定的正整数，是否存在正整数m ，n ，使得m （m+k ）=n （n+1）？ 解:（1）答案是否定的．若存在正整数m ，n ，使得m （m+2）=n （n+1）． 则（m+1）2=n 2+n+1，显然n>1．于是n 2<n 2+n+1<（n+1）2，所以n 2+n+1不是平方数，矛盾．（2）当k=3时，若存在正整数m ，n ，使得m （m+3）=n （n+1），则4m 2+12m=4n 2+4n ⇔（2m+3）2=（2n+1）2+8即（2m+3-2n-1）（2m+3+2n+1）=8⇔ （m-n+1）（m+n+2）=2， 而m+n+2>2，故上式不可能成立．当k ≥4时，若k=2t （t 是不小于2的整数）为偶数，取m=t 2-t ，n=t 2-1，则m （m+k ）=（t 2-t ）（t 2+t ）=t 4-t 2，n （n+1）=（t 2-1）t 2=t 4-t 2，因此这样的（m ，n ）满足条件．若k=2t+1（t是不小于2的整数）为奇数，取m=22t t-，n=222t t+-，则m（m+k）=22t t-（22t t-+2t+1）=14（t4+2t3-t2-2t）n（n+1）=222t t+-·22t t+=14（t4+2t3-t2-2t），因此这样的（m，n）满足条件．综上所述，当k=3时，答案是否定的；当k≥4时，答案是肯定的．（注：当k≥4时，构造的例子不是唯一的．）四、组合与极值组合问题对锻炼思维意义重大，初中只适宜分类计数、加法原理、乘法原理的简单运用，简单的包含排除原理，基本的抽屉原理也是重要的内容．但在初中阶段，不应提前引入排列组合的计算公式．特别是提前较大范围的培训高中的排列组合知识，会激起大范围超前学习的竞争热，从而影响基础教育，并且也影响竞赛的公平性．建议命一些以几何元素为背景的构造性的问题，容易引发学生兴趣，又使套用组合公式的人容易出错，这类问题的研制特别引人注目．例9 平面上有6个点，其中任何3个点不在同一条直线上，以这6个点为顶点可以构造多少个不同的三角形？从这些三角形中选出一些，如果要求其中任何两个三角形没有公共点，则最多可以选出多少个三角形？（第12届华杯赛初一组决赛试题12）解答:（1）先从6个点中选取1个做三角形的一个顶点，有6种取法；•再从余下的5点中选取1个做三角形的第二个顶点，有5种取法；再从余下的4个点中选取1个点做三角形的第三个顶点者，有4种取法．因为任何3个点不在同一条直线上，所以，这样选出的三个点可以做出一个三角形．但是，如果选出的三个点相同的话，则做出的三角形相同，•三个点相同的取法有3×2×1=6种，所以，以这6个点为顶点可以构造654321⨯⨯⨯⨯=20个不同的三角形．（2）每个三角形有3个顶点，所以，6个点最多只能做出2个三角形，•它们没有公共顶点，如图4（1）．（3）用英文大写字母A，B，C，D，E，F记这6个点，如果可以选出5个三角形，它们共有15个顶点，需要15个英文大写字母．但是，不同的英文大写字母仅有6个，因此，这5•个三角形中至少有三个三角形有同一个顶点，不妨设为点A．根据题目条件，这三个三角形没有公共边，即除去公共顶点A之外，其余6•个顶点互不相同，即表示这6个顶点的字母不相同．否则，根据题目条件，它们将有公共边．但是，除A之外，我们仅有5个不同的字母，所以，不可能存在5个三角形，它们没有公共边．如图4（2）所示，△ABC，△ADE，△BDF和△CEF这4个三角形没有公共边，所以，最多可以选出4个三角形，它们没有公共边．例10 若对于任意n个连续正整数中，总存在一个数的数字之和8是的倍数．试确定n的最小值，并说明你的理由．（2007北京市中学生数学竞赛初二年级试题五）解先证n≤14时题设的性质不成立．因为，当n=14时，对于9999993，9999994，…，999999，…，10000006这14个连续整数中，任意一个数字的数字之和均不能被8整除．所以n≤14时题设的性质不成立．因此要使题设的性质成立，应有n≥15．再证n=15时，题设的性质成立．设a1，a2，…，a15为任意的连续15个正整数，则这15个正整数中，个位数字为0•的整数最多有两个，最少有一个，可分为：（1）当a1，a2，…，a15中个位数字为0的整数有两个时，设a i<a j，且a i，a j的个位数字为0．则满足a i，a i+1，a i+2，…，a i+9，a j为连续的11个整数，其中a i，a i+1，a i+2，…，a i+9无进位设n i表示a i各位数字之和．则前10个数的各位数字之和分别为n i，n i+1，…，n i+9则这连续的10个数中至少有一个被8整除．（2）当a1，a2，…，a15中个位数字为0的整数只有一个时，设其中的a i的个位数字为0，•①若整数满足1≤i≤8，则在a i后面至少有7个连续整数，则a i，a i+1，a i+2，…，a i+7这8个连续整数的各位数字和也为8个连续整数，所以必有一个数能被8整除．②若整数i满足9≤i≤15，则在a前面至少有8个连续整数，不妨设为a i-8，a i-7，a i-5，a i-4，a i-3，a a-2，a a-2，a i-1，这8个连续整数的各位数字和也为8个连续整数，所以必有一个数能被8整除．由①、②可知，当a1，a2，…，a15中个位数字为0的整数只有一个时，必有一个数，其各位数字之和是8的倍数．综上（1）、（2）所述，对于任意15个连续整数中，必有一个数，•其各位数字之和是的倍数．而小于15个的任意连续整数不成立此性质，所以n的最小值是15．例11 平面上有若干个点，其中任意三点都不在同一直线上，将这些点分成三组，并按下面的规则用线段连接：①在同一组的任意两点都没有线段连接；②不在同一组的任意两点间一定有线段连接．（1）若平面上恰好有9个点，且平均分成三组，那么平面上有多少条线段？（2）若平面上恰好有9个点，且点数分成2，3，4三组，那么平面上有多少条线段？（3）若平面上共有192条线段，那么平面上至少有多少个点？（第十八届“希望杯”全国数学邀请赛初二第2试23题）解：（1）平面上恰好有9个点，且平均分成三组，每组3个点，•按题设规则用线段连接，可以连出3×3+3×3+3×3=27条线段．（2）平面上恰好有9个点，且点数分成2，3，4三组，按题设规则用线段连接，可以连出2×3+2×4+3×4=26条线段．（3）设平面上三组点数为m，n，p个，s=m+n+p，目标求s的最小值？按题设规则用线段连接，可以连出mn+mp+np=192条线段．由于s2=（m+n+p）2=m2+n2+p2+2mn+2mp+2np≥mn+mp+np+2mn+2mp+2np=3mn+3mp+3np=•3（mn+mp+np）=3×192=576=242所以s≥24．s的最小值是24．事实上，当这24个点平分为3组，每组8个点，按题设规则用线段连接，恰可以连出8×8+8×8+8×8=3×64=192条线段．因此平面上至少有24个点．- 11 -。

第三届潮汕 “星河杯”初中二年级数学竞赛试题(答案) 时间:120分钟 满分150分第Ⅰ卷(选择题、填空题)一.选择题 1.【答案】 C 2.【答案】 B 3.【答案】 B【解析】当0=++c b a 时,1-=+=+=+ba c ac b cb a由⎪⎩⎪⎨⎧=+=+=+bp a c ap c b cp b a , 得)()(2c b a p c b a ++=++, 当0≠++c b a 时,2=p ∴1-=p 或2=p ,代入直线可知直线一定过点()0,1-,故选B4.【答案】 C【解析】 当0>k 时,xk y =的图象关于直线x y =对称当0<k 时,xk y =的图象关于直线x y -=对称 故选C5.【答案】 D 【解析】将aa a x x 2122++=-+变形为 ()aa x x 2121+=-+-令1-=x t ,则aa t t 22+=+ ∴at a t 2,21==,即ax a x 21,121+=+=6.【答案】 A【解析】 设三角形三边长分别是,,,c b a 且c b a >>,则2c a b +=.又c a ch ah S ===∆2121,得ac h h ca =.∵0>>c a ∴1<ac ………①又∵三边要构成三角形, 且c b a >> ∴a c b >+,即a c c a >++2∴a c >3 ………② ∴由①②得131<<ac .7.【答案】 D【解析】 对正整数3≥n ,有)2121(41412+--=-n n n∴[])10216151()981211(4148 )41001441431(4148222+++-+++⨯=-++-+-⨯= A⎪⎭⎫⎝⎛----+++⨯=102110111001991413121112=)102110111001991(1225+++- ∵2199412)102110111001991(12<⨯<+++⨯ 故选D8.【答案】 C【解析】 二次购物的总商品价为 6389.0423168=÷+元若一次购入商品638元,则须付款4.5608.01389.0500=⨯+⨯元.9.【答案】A【解析】设这个相同的正整数为n ,则()[]341122=--+n n ,解得17=n10.【答案】D【解析】 如图把22D C ,33D C ,44D C ……通过平行平移移到O C 1上,最后各段长度之和等于O C 1=34二.填空题(本大题共6小题,每题5分,共30分) 11.【答案】402≤≤x 12.【答案】1【解析】∵a 是方程的一个正根, ∴020072=--a a ,∴a a a a =-=+2007,200722原式=1200720071200712007120072=-=+-=-++-aa aa aa a a13.【答案】249π【解析】设上与底面半径分别为R r , R BO r AO 2,2==,49)(222222==+=+ABR r BOAO249)(22ππ=+=+R r S S 下上14.【答案】ab ab -2【解析】设船速与水速分别是21,v v .则 b v v a v v )()(2121-=+,则ab a b v v -+=21.又所求时间()a b ab a a b a b a v v v av v -=⎪⎭⎫ ⎝⎛+-+=⎪⎪⎭⎫ ⎝⎛+=+21121221 15.【答案】12 【解析】作等边BCO ∆,连结AO,AC.ACO ∆≌DCB ∆ AO=BD,BO=BC. 在ABO Rt ∆中,122222===+BDAOBCAB16.【答案】2222cb a ++【解析】所求的点是1111,,,BD D B AC C A 和交点,交点到各顶点的距离是2222cb a ++.三.解答题(本大题共5小题, 共70分) 17.(本题10分)解方程0691014510129101=---+-x x x【解析】令2910-=x y ,则原方程变形为04021611=---+y y y, ---------------------------2分即0)40)(16()16(2)40()40)(16(=-----+--y y y y y y y y y ------------------4分64064=y ∴10=y -------------6分∴102910=-x 解得3=x ------------9分 经检验都是方程的根.--------------10分18. (本题12分)设P 为已知ABC ∆内部一点,记点P 到三角形三边c b a ,,的距离依次为z y x ,,求证:cz by ax ++是一个常数. 【证明】∵PAB PCA PBC ABC S S S S ∆∆∆∆++=---------2分 cz by ax 212121++=)(21cz by ax ++=---------------8分∴ABC S cz by ax ∆=++2-----------10分 又∵ABC S ∆是一个常数∴cz by ax ++是一个常数.---------------12分19. (本题15分)作图题: 如图长方形ABCD 中,点P 是BC 边的中点.若点N M ,分别是AC 与AB 上的一点,1) 在图中作出点N M ,, 使MN PM +的值最小. 在右边的长方形中作图,，且要保留作图的痕迹 ;-----------(作图)3分在下面写出作法:①作点P 关于AC 的对称点P '②过P '作x 轴的垂线交AC 于M,交AB 于N,连结MP , 则M,N 为所求的点.----------5分2)对上面作图证明.【证明】在AC 上取异于M 的另一点M ',连结P M P M ''',,过M '作N M ''垂直于AB 于N '.∵P M MP '= ∴N P MN P M MN MP '=+'=+ 又∵P M P M ''=' ∴N M P M N M P M ''+''=''+' ∵N P N M P M '>''+''∴MN MP N M P M +>''+'----------------8分3)在1)作出的三角形PMN ∆中, 三角形周长是否最小?若是,说明理由.若不是,再作出周长最小的三角形,也说 明理由. 【解析】1)中的三角形的周长不会最小.下面作出周长最小的三角形.设点P 关于AC 的对称点1P ,关于AB 的对称点2P , 连结21P P ,分别交AC 与AB 于N M ,两点,则N M ,为所求的点,使PMN ∆的周长最小. ----------------(作图)12分【证明】在AC 与AB 上分别取异于M,N 的点11,N M ,连结111,P M P M ,11N M ,P N 1,21P N . ∵21,NP NP MP MP == ∴PMN ∆的周长等于21P P又∵211111,P N P N P M P M == ∴11N PM ∆的周长等于折线211111P N N M M P ++ ∵21211111P P P N N M M P >++ ∴PMN ∆的周长最小. -----------(15分) 20.(本题15分)已知c b a ,,为整数,且c b a c b a 126448222++<+++,求abcc b a ⎪⎭⎫⎝⎛++111的值.【解析】由于c b a ,,为整数及已知条件的不等式有c b a c b a 126449222++≤+++----------------6分()0)3612()96(44222≤+-++-++-c c b b a a ---------------8分()0)6()3(2222≤-+-+-c b a -------------------10分而()0)6()3(2222≥-+-+-c b a∴()0)6()3(2222=-+-+-c b a∴6,3,2===c b a -----------------13分 故abcc b a ⎪⎭⎫⎝⎛++111=1613121632=⎪⎭⎫ ⎝⎛++⨯⨯------------15分21. (本题18分)一个三角形的三边长都是整数,且它的面积和周长的数值相等.1)如果这个三角形是直角三角形,这样的直角三角形是否存在?若存在,确定它的三边的长; 若不存在,说明理由.2)是否存满足条件的非直角三角形?若存在,把它们找出来.若不存在,说明理由.(注:若ABC ∆三边长分别是c b a ,,,设2cb a p ++=,则三角形的面积是))()((c p b p a p p S ABC ---=∆)【解析】1)假设存在符合条件的直角三角形,它的三边长分别为c b a ,,,其中c 是斜边. 由于c b a ,,均为正整数,所以b a ≠,(否则,若b a =,则a c 2=不是整数)不妨设b a >,则有222ab ba b a =+++,-------------------2分两边平方得 0242222=+--ab abb a b a∴024=+--b a ab∴()42818)4(4⨯=⨯==--b a ----------------4分∴⎩⎨⎧=-=-1484b a 或⎩⎨⎧=-=-2444b a -----------------------6分分别得13,5,12===c b a 或.10,6,8===c b a ---------------7分2)设三边长为z y x ,,,依题意,由海伦公式得 ()))()((41z y x z y x z y x z y x z y x ++-+--+++=++∴()))()(()(16z y x z y x z y x z y x z y x ++-+--+++=++------------8分∵右边的因子它们两两之差都是两条边长之差的两倍都是偶数,所以各因子它们的奇偶性相同. ∴右边的因子或者都是奇数或者都是偶数又∵左边是偶数 ∴右边的因子都是偶数.于是得: k z y x 2=-+, ()())4(422+--+=k kx k x ky , k y x z 2-+=---------------12分其中k 是正整数对于1=k 和2=k ,我们有下列的解13 ,12 ,5 ; 10 ,8 ,6; 29 ,25 ,6; 20 ,15 ,7; 17 ,10 ,9.对于k 的其他值,只是重复出现这些解.∴满足条件的三角形是 29 ,25 ,6; 20 ,15 ,7; 17 ,10 ,9.---------------18分。

八年级数学竞赛辅导之猜想、归纳与探索1、将x=23代入反比例函数y=-x1中，所得函数值记为y，又将x=y，+1代入原反比例函数中，所得函数值记为y2，再将x=y2+1代入原反比例函数中，所得函数值为y3，……，如此继续下去，则y2004= 。

2、若x2-x-2=0的值等于。

3、已知a、b、c为△ABC的三边，且满足a2c2-b2c2=a4-b4，试判断△ABC的形状。

4、如图1，将边长为8cm的正方形纸片ABCD折叠，使点D落在BC边中点上处，点A落在点下处，折痕为MN，则线段CN的长是。

5、小说《达·芬奇密码》中的一个故事里出现了一串神秘排列的数，按从小到大顺序排列为：1，1，2，3，5，8……则这组数的第8个数是 .6、按如图2所示的程序计算，若开始输入的x值为48，我们发现第一次提到的结果为24，第2次得到……结果为7、符号“f”表示一运算，它对一些数的运算结果如下：（1）f(0)=0，f(2)=1，f(3)=2，f(4)=3……（2）f（12）=2，f（13）=3，f（14）=4，f（15）=5，……利用以上规律计算：f12008-f(2008)=8、求出所有以12为勾股的勾股数组：9、西瓜论千克计价，购买西瓜时，总是希望可以食用的部分占整个西瓜的比例越大越好。

如果一批西瓜的皮厚都是d，试问购买大西瓜合算还是小西瓜合算？（把西瓜看作球形，V球=43πR3）10、矩形ABCD的边AB=8，AD=6，现将矩形ABCD放在直线t上，且沿着t向右作无滑动的翻滚，当它翻滚至类似于开始的位置A1B1C1D1时，如图所示，则顶点A所经过的路线长是11、在△ABC中，AB=AC=12cm，BC=6cm，D为BC的中心，动点P从B点出发，以每秒1cm的速度沿B→A→C的方向运动，运动时间为t，当t时，过D、P两点，直线将△ABC的周长分成两个部分，使其中一部分是另一部分的2倍。

12、把一个正方形分成面积相等的四个三角形的方法有很多，除以可以分成相互全等的四个三角形外，你还能用三种不同的方法将正方形分成面积相等的四个三解形吗？请分别画出图。

全国初中数学竞赛试题及答案This manuscript was revised on November 28, 2020中国教育学会中学数学教学专业委员会全国初中数学竞赛试题一、选择题（共5小题，每小题6分，共30分.）1（甲）．如果实数a ，b ，c 在数轴上的位置如图所示，那么代数式22||()||a a b c a b c -++-++可以化简为（ ）．（A ）2c a - （B ）22a b - （C ）a - （D ）a 1（乙）．如果22a =-+11123a+++的值为（ ）．（A ）2- （B 2（C ）2 （D ）22（甲）．如果正比例函数y = ax （a ≠ 0）与反比例函数y =x b（b ≠0 ）的图象有两个交点，其中一个交点的坐标为（－3，－2），那么另一个交点的坐标为（ ）．（A ）（2，3） （B ）（3，－2） （C ）（－2，3） （D ）（3，2）2（乙）． 在平面直角坐标系xOy 中，满足不等式x 2＋y 2≤2x ＋2y 的整数点坐标（x ，y ）的个数为（ ）．（A ）10 （B ）9 （C ）7 （D ）53（甲）．如果a b ，为给定的实数，且1a b <<，那么1121a a b a b ++++，， ，这四个数据的平均数与中位数之差的绝对值是（ ）． （A ）1 （B ）214a - （C ）12（D ）143（乙）．如图，四边形ABCD 中，AC ，BD 是对角线，△ABC 是等边三角形．30ADC ∠=︒，AD = 3，BD = 5，则CD 的长为（ ）． （A ）23 （B ）4 （C ）52 （D ）OAB CED4（甲）．小倩和小玲每人都有若干面值为整数元的人民币．小倩对小玲说：“你若给我2元，我的钱数将是你的n 倍”；小玲对小倩说：“你若给我n 元，我的钱数将是你的2倍”，其中n 为正整数，则n 的可能值的个数是（ ）． （A ）1 （B ）2 （C ）3 （D ）44（乙）．如果关于x 的方程 20x px q p q --=（，是正整数）的正根小于3， 那么这样的方程的个数是（ ）．（A ） 5 （B ） 6 （C ） 7 （D ） 85（甲）．一枚质地均匀的正方体骰子的六个面上的数字分别是1，2，3，4，5，6．掷两次骰子，设其朝上的面上的两个数字之和除以4的余数分别是0，1，2，3的概率为0123p p p p ，，，，则0123p p p p ，，，中最大的是（ ）． （A ）0p （B ）1p （C ）2p （D ）3p5（乙）．黑板上写有111123100，　， ，，　共100个数字．每次操作先从黑板上的数中选取2个数a b ，，然后删去a b ，，并在黑板上写上数a b ab ++，则经过99次操作后，黑板上剩下的数是（ ）．（A ）2012 （B ）101 （C ）100 （D ）99 二、填空题（共5小题，每小题6分，共30分） 6（甲）．按如图的程序进行操作，规定：程序运行从“输入一个值x ”到“结果是否>487”为一次操作. 如果操作进行四次才停止，那么x 的取值范围是 . 6（乙）.如果a ，b ，c 是正数，且满足9a b c ++=，111109a b b c c a ++=+++，那么a b cb c c a a b+++++的值为 ．7（甲）．如图，正方形ABCD 的边长为215，E ，F 分别是AB ，BC 的中点，AF 与DE ，DB 分别交于点M ，N ，则△DMN 的面积是 . 7（乙）.如图所示，点A 在半径为20的圆O 上，以OA为一条对角线作矩形OBAC ，设直线BC 交圆O 于D 、E 两点，xyO ECABD若12OC =，则线段CE 、BD 的长度差是 。