当前位置：文档之家 › 邮递员问题最短路径的解法

邮递员问题最短路径的解法

  • 格式：doc
  • 大小：11.97 KB
  • 文档页数：2

下载文档原格式

  / 2

合集下载

中国邮路问题

中国邮路问题
3 5 1 2 2 3 1 2 3 6 3 5 1 2 2
3 1 2 3 6
思考： 思考：如何求恰好有 2k (k > 0) 个奇点的赋权图的最优 环游？ 环游？ 中国邮路问题的一个好算法是Edmonds Edmonds提出的最小 注：中国邮路问题的一个好算法是Edmonds提出的最小 匹配算法。 匹配算法。
例1 下图(a)给出赋权图G ， , x, l和m 是G 的四个奇点。根据 v 上述算法,求下图的最优环游。
u
1
v
5
1
w
7
5
x
6
2
y
2
z
8
4
m
6
3
t
l
4
k
(a)
v 解：根据上述算法(1)，把x 和 m 配对，和l 配对，取 P = xtlkzm ， 1 并对 P 中每条边各添加一条边；又取P2 = vwzkl ，并对 P2 中每条 1 边各添加一条边。得图(b).依次按算法，得到图(c),(d),(e)
u
1
v
5
1
w
7
u
1
v
5
1
w
7
5
5
4
m
x
6
2
y
2
z
8
x
6
2
y
2
z
8
4
m
6
3
6
3
1
t
u
l
4
1
k
t
u
l
4
1
k
1
(b) v
5
w
7
(c ) v
5
w
7

邮递员问题

邮递员问题

邮递员问题简介邮递员问题（Travelling Salesman Problem，TSP）是一个著名的组合优化问题，被称为计算机科学中的经典问题之一。

该问题起源于邮递员在一天内送货的最短路径问题。

邮递员需要从一个起点出发，经过所有的目标点，最后回到起点。

问题的目标是找到一条最短的路径，使得所有目标点都被访问，同时回到起点。

TSP问题涉及到组合爆炸，通常在计算上是NP难的。

问题描述给定一个有向图和一个起点，邮递员需要从起点出发经过所有的节点，最后回到起点。

每条边的权重表示从一个节点到另一个节点的距离。

找到一条最短路径，使得所有的节点都被访问且回到起点。

解决方法1. 枚举法枚举法是最简单的解决TSP问题的方法。

它通过遍历所有可能的路径，计算每条路径的总长度，并返回最短路径的长度和路径本身。

然而，由于TSP问题是NP难的，当图的规模增加时，枚举法的计算复杂度呈指数增长，很难在合理的时间内求解。

2. 动态规划法动态规划法是解决TSP问题的常用方法之一。

该方法通过将问题划分为子问题，并使用递归的方式求解。

具体而言，我们可以定义一个状态数组dp，其中dp[S][i]表示从起点到节点i，经过节点集合S中的所有节点，最后回到起点的最短路径长度。

那么，我们可以使用如下的递推关系来计算dp数组：dp[S][i] = min(dp[S-{i}][j] + dis(j, i))，其中j∈S，j≠i通过不断更新dp数组，最终可以得到从起点出发经过所有节点并回到起点的最短路径长度。

3. 遗传算法遗传算法是一种启发式优化算法，被广泛应用于解决TSP问题。

它模拟生物进化的过程，通过基因交叉、变异等操作，生成新的个体，并通过评估函数对个体进行选择。

遗传算法的优点是能够在较短的时间内找到接近最优解的解，但不能保证找到全局最优解。

4. 改进算法针对TSP问题，还有一些改进的算法，如蚁群算法、模拟退火算法、禁忌搜索等。

这些算法在不同的问题实例上可能会有更好的表现。

快递员派送货物最短路径的模型研究

快递员派送货物最短路径的模型研究

快递员派送货物最短路径的模型研究2 河北经贸大学管理科学与工程学院 063210摘要：网上购物的日益普及使消费者们对于快递物流的要求不断提高，这一趋势生出了关于快递配送的路线选择问题，如何规划路线从而使得耗费时间最少、路径最短成为待解决的问题模型。

本文关于配送路径的规划提出了两个解答方法，即Dijkstra方法和Lingo模型。

类似快递配送的路线规划的问题也普遍存在于现实生活中，而使用Dijkstra方法和Lingo模型可以便捷地解决这类问题。

关键词：最短路径；Dijkstra；Lingo；快递配送一、前言伴随着人们物质精神水平的不断提高以及互联网技术应用的飞速发展，在当今社会中，网上购物已经逐渐成为人们日常消费的主要手段之一，人们足不出户就能浏览店家、挑选心仪的商品、货比三家、下单购物。

这种相比传统的实体店购物方式更为便捷的网络购物方式，也催生了一大批相关产业的发展，比如物流、快递。

尤其在前段时期的新冠疫情爆发、扩散、情势严峻的时期，由于所居住的村庄、居民区的全方位封闭隔离，以及对人与人之间的近距离接触的杜绝，人们对于日常生存、生活用品的需求只能通过从网上的渠道购得。

这使大家对物流快递公司的要求也越来越高。

快递公司出于节省时间、提高效率进而节约成本、满足客户要求的迫切需求，不得不面临着优化派送路线的问题。

二、对快递派送路径问题的提出消费者们拍下消费订单后，除了对商家货物质量优劣的关注外，最大的担忧便是快递派送的问题。

这家快递公司的物流配送速度快不快？物流信息的更新及不及时？配送过程的安全保障怎么样？如果因为市场问题而发生货物的损毁灭失谁来向我承担损害赔偿？公司的配送效率高不高？快递工具是火车还是飞机？到达我市后市内的配送路线是什么样的？我的货物会被优先配送吗？消费者与快递公司间的信任关系常常受到一系列类似以上的问题的挑战。

就我本人的真实经历来说，某天上午8点钟物流信息显示包裹到达了我们市里并且正在派送中，按惯例一般1小时左右就能到达快递驿站，而我却一直等到傍晚都依然没有接收到包裹到达的消息通知。

中国邮路问题

中国邮路问题

定理：设P是加权连通图G中一条包含G的所有边 至少一次的闭链，则P最优的充要条件是 （1）P中没有二重以上的边； （2）在G的每条圈C中，重复边集E的长度之和不超过这 个圈长度的一半。
f： " "
（ 1 ）若P中存在重数大于 2的边，则删去 2条后得到的图仍为欧拉 图， 一直做下去，最终得到 的边数一定为 1条或2条。
②如果连通图不是欧拉图。 由于图G有偶数个奇度数顶点，对于任两个奇度数顶点x 和y，在G中必有一条路连接。 将这条路上的每条边改为二重边得到的新图 H1 ，则x 和y就变为H1 的偶度数顶点，在这条路上的其他顶点的度 数均增加2，即奇偶性不变。 于是 H1 的奇顶点个数比G的奇顶点个数少2，对H1 重 复上述过程得H 2 ，再对H 2 重复上述过程得H 3 ，……，经 若干次后，可将G中所有奇度数顶点变为偶度数顶点，从 而得到多重欧拉图G'。 这个欧拉图G'的一条欧拉回路就相应于中国邮递员问题 的一个可行解，且欧拉回路的长度等于G的所有边的长 度加上每次连奇度数顶点的路的长度。
2.3.3 中国邮递员问题
• 一名邮递员负责投递某个街区的邮件。如何为他（她）设 计一条最短的投递路线（从邮局出发，经过投递区内每条 街道至少一次，最后返回邮局）？
描述为图论语言：
在连通加权无向图G中，寻找一条经过每边至少一次 且权和最小的闭链，即G的最优环游。
①如果对应的图G是欧拉图，那么对应于邮局的顶点出发的 任何一条欧拉回路都是符合上述要求的投递员的最优投递 路线。 如果图G只有两个奇度数顶点x和y，则存在一条以x和 y为端点的欧拉路。因此，所要求的最优投递路线是由这 条欧拉路+边{x，y}。
奇偶点图上作业法
• 把G 中的所有奇度数顶点配成对，将每对奇度数顶点之间 的路上的每边改为二重边，得到一个新图G1 ，新图 G1 中没 有奇度数顶点，即 G1为欧拉图。 • 若 G1中某一对顶点之间有多于2两条边连接，则去掉其中 的偶数条边，留下1条或2条边连接这两个顶点，直到每一 对相邻顶点至多由2条边连接，得到图G2 。 • 检查G2 的每一个圈C，若某一个圈上重复边的权和超过此 圈权和的一半，则将C按定理1必要性的证明过程进行调 整，重复这一过程，直到对G2 的所有圈，其重复边的权和 不超过此圈权和的一半，得到G 。 3 • 用Fleury算法求G3 的欧拉回路。

中国邮递员数学问题

中国邮递员数学问题

中国邮递员数学问题
中国邮递员数学问题是一个著名的数学问题，也称为"中国邮递员问题"。

这个问题源于邮递员在担任邮递员工作时，需要沿着不同的街道进行投递。

邮递员必须走遍每一条街道至少一次，然后回到出发地点。

问题的目标是寻找一条最短的路径，使得邮递员能够满足投递的要求。

具体问题描述如下：给定一个城市的街道网络图，每条街道上都有一个正整数表示街道的长度。

邮递员需要从一个特定地点出发，沿着街道网络进行投递，然后回到出发地点。

要求邮递员经过的路径总长度最短。

这个问题属于旅行商问题的变种，是一个NP-完全问题。

因为问题规模较大，难以找到一个最优解。

因此，通常采用近似算法进行求解，如TSP（Traveling Salesman Problem）等。

邮递员问题在实际中有很多应用，比如快递员的路线规划、物流配送等。

解决这个问题可以提高物流效率，减少成本。

中国邮递员问题解法

中国邮递员问题解法

中国邮递员问题解法中国邮递员问题是一个著名的组合优化问题，实际上是一个旅行商问题（Traveling Salesman Problem，TSP）的变种。

问题描述：给定一个城市集合和城市之间的距离矩阵，求解一个最短的邮递员路径，使邮递员能够从出发城市出发，经过每个城市恰好一次，最后回到出发城市。

解法：1.暴力搜索暴力搜索是最简单直观的解法。

遍历所有可能的路径，计算每个路径的总距离，最后选择最短的路径。

这种解法的时间复杂度为O(n!)，随着城市数量的增加而急剧增加，效率非常低，只适用于小规模问题。

2.动态规划动态规划是一个更高效的解法。

使用一个二维数组dp[i][j]表示从城市i出发经过城市集合j的最短路径长度，其中j是一个二进制数，表示哪些城市已经访问过。

动态规划的转移方程为：dp[i][j] = min{dp[k][j XOR (1 << k)] + distance[i][k]}，其中k表示已经访问的最后一个城市。

利用这个递推关系，可以逐步计算出dp[0][1<<n-1]，即从城市0出发经过所有城市的最短路径。

最后，将此路径与每个城市的距离相加，得到最终的最短路径长度。

3.贪心算法贪心算法是一种更简单的解法。

首先选择一个起始城市，然后每次选择距离最近且未被访问过的城市，将其加入路径中。

重复此过程，直到访问完所有城市，然后回到起始城市。

这种解法的时间复杂度为O(n^2)，但由于贪心策略的局限性（可能会出现回头或死胡同），所以得到的解并不一定是最优解。

以上是三种常用的解决中国邮递员问题的方法，具体可以根据实际情况选择合适的算法进行求解。

中国邮递员问题的求解实例

中国邮递员问题的求解实例前面已经讲过，对于欧拉图，可以直接用Fleury算法找出一条欧拉巡回路线；对于半欧拉图，可以先求出奇点u和v之间的最短路径P,令G =G P，贝U G *为欧拉图，然后用Fleury算法来确定一个G *的欧拉巡回，它就是G的最优巡回。

当G有2n个奇点(n>1),可以用Edmonds算法解决，步骤如下：(1) 用Floyd算法求出所有奇点之间的最短路径和距离矩阵。

(2) 用匈牙利法或0-1规划法求出所有奇点之间的最佳配对。

(3) 在原图上添加最佳配对所包含的两两顶点之间的最短路得到欧拉图G *。

⑷用Fleury算法确定一个G *的欧拉巡回，这就是G的最优巡回。

以上步骤的关键是找出2n个奇点的最佳配对，举例如下。

例图3是某区街道示意图，各边的长度数据如下表所示。

现在需要对每条街道找最优巡回，需要先求26个奇点的最佳配对。

先用Floyd算法求出所有42个顶点之间的最短路距离和路径。

程序如下：E=[1 2 10261 4 402........ 注：每一行代表一条边(两个顶点和边长)，此处省略59行40 39 198];for i=1:42for j=1:42if j==ia(i,j)=0; elsea(i,j)=inf; end end endfor k=1:62 i=E(k,1);j=E(k,2);a(i,j)=E(k,3);a(j,i)=E(k,3); end[D,R]=floyd(a);图3某区街道示意图然后求26个奇点的最优配对，这可以用Lin go 求解，编写程序如下:MODEL: SETS:4U12°26"30 O3539 40413*27 21 4128* 3338仆2934O114251015• 1724，25201922 23 32313637dot/2,4,5,6,8,9,10,11,12,13,14,15,17,18,19,20,22,24,25,26,28,29,30,36,40,41/;LINKS(dot,dot)| &2 # GT # & 1:C,X;ENDSETSDATA:C=1319 1065 651 650 939 1228 1463 1500 1213 617 895 1590 1709 1377 1033 1112 1652 1761 1853 1418 1832 2124 2151 2479 1687254 668 1173 1462 1751 198 181 402 1140 1418 2113 453 601 945 1635 2175 2284 597 1941 2355 868 1463 1498 2104414 919 1208 1497 1732 435 148 886 1164 1859 679 347 691 1381 1921 2030 823 1687 2101 1094 1689 1724 1850505 794 1083 1318 849 562 472 750 1445 1058 726 382 967 1507 1616 1202 1273 1687 1473 2005 2103 1541289 578 813 1354 1067 471 245 940 1563 1231 887 462 1002 1111 1707 768 1182 1978 2005 2333 1541 289 524 1643 1356 760 534 651 1852 1520 1176 504 828 886 1996 594 1008 2267 2197 2525 1733235 1932 1645 1049 823 362 2141 1809 1465 793 706 597 2285 883 890 2556 2486 2814 20222167 1880 1284 1058 163 2376 2044 1700 1028 507 398 2520 1105 691 2766 2658 2986 2194306 1321 1599 2294 272 505 849 1571 2111 2220 416 1877 2291 687 1282 1317 20081034 1312 2007 531 199 543 1265 1805 1914 675 1571 1985 946 1541 1576 1702360 1411 1203 871 527 577 1117 1226 1347 883 1297 1618 1534 1862 10701101 1563 1231 887 217 757 866 1707 523 937 1978 1894 2222 14302282 1950 1606 884 344 235 2426 942 528 2603 2495 2823 2031332 676 1398 1938 2047 144 1704 2118 415 1010 1045 1824344 1066 1606 1715 476 1372 1786 747 1342 1377 1503722 1262 1371 820 1028 1442 1091 1623 1721 1159540 649 1542 306 720 1813 1729 2057 1265109 2082 598 184 **** **** 2479 16872191 707 293 2368 2260 2588 17961848 2262 271 866 901 1680414 1711 1603 1931 11392075 1967 2295 1503595 630 1409360 832792;ENDDATA图4 26个奇点的最优配对MIN=@SUM(LINKS:C *X);@FOR(LINKS:@BIN(X));@FOR(dot(l):@SUM(LINKS(J,K)| J #EQ# I #OR# K #EQ# I:X(J,K))=1);END运行以上程序，得到最优配对结果为：2与6、4与12、5与13、8与9、10与11、14 与15、17 与25、18 与26、19 与20、22 与28、24 与29、30 与36、40 与41。

中国邮递员问题


– 第四步：检查有重复边的线路是否是多余的。即检查重复边的两端是 否已有其他线路相连通，如有的话，可将重复边连同原边从线路图中 删去。发现重复边V4V5的两端可通过其他线路相连，可将V4V5及重复 边一起从线路图中删去。即可得送货线路如下：V0—V1—V2—V3— V5—V6—V10—V9—V12—V7—V8—V12—V9—V4—V11—V1—V0。线 路的总长度减少为215千米。总长度较前减少了20千米。
A
6
2 2 I 5 4
H 1
4
G 1 F 5
J 3 K 2
D
3
B 3 C
5
E
图中重复边的总距离W1为18＜23(总距离的一半），为可行解； 检查是否每一个闭合圈的重复边的总距离都小于该闭合圈的总距离 的一半。 在圈（A,B,K,J,I,H)中，重复边总距离为8，小于该圈总距离19 的一半，满足要求，不需改进；在圈（B,C,D,K)中，不需改进； 在圈（D,E,F,J)中，不满足要求需改进
A 6 B 3 C 4 5
2
2 I
H 1 J 3 K 2 D
4 3
G 1 F 5
5
E
阅读推荐
1、《物流管理实务》，梁金萍 主编，清华大学出 版社，2010。 2、《运筹学》
– 第二步：考虑到从配货中心出发的送货车辆，在送完所有的门店货物 后，仍需要返回配货中心，故再需对生成的最小树采用中国邮递员线 路的算法进行扩充。 奇点有：V0，V1，V3，V4，V6，V7，V8，V9，V10，V12。故需增加边 V3V5，重复边V0V1，V5V6，V4V9，V9V10，V7V12，V8V12，V9V12等 7条。 粗线部分已给出了送货车量从配送中心出发，送货到10家门店后返回 配货中心的具体路线。即可为：V0—V1—V2—V3—V5—V6—V5—V4— V9—V10—V9—V12—V7—V12—V8—V12—V9—V4—V11—V1—V0。线 路的总长度为251千米。

最短路径的算法标号法


5.2.1 配送的类型和形式
（3) 定时定量配送
•定时定量配送指按照规定的配送时间和配送数量进行配送，兼有定时、 定量两种方式的优点，是一种精密的配送服务方式。 •这种方式要求有较高的服务质量水平，组织工作难度很大，通常针对固 定客户进行这项服务。 •成本较高，在用户有特殊要求时采用，不是一种普遍适用的方式。 •它兼有定时和定量配送方式的特点，对配送企业的要求比较严格，管理 和作业的难度较大。 •需要配送企业有较强的计划性和准确度。 •定时定量配送方式在大量而且稳定生产的汽车、家用电器、机电产品的 供应物流里面取得了成功。 •这种方式的管理和运作，是靠配送双方事先的一定时期的协议为依据来 执行，也常常采用“看板方式”来决定配送的时间和数量。
5.1.2 配送的产生和发展史
1. 配送制的形成
配送是由送货逐渐发展过来的，随着社会化大生产走向健全。 第二次世界大战之后，日本的经济得到迅速的复苏，但随后就出现 了物流分散,生产企业自备车辆，出行混乱，道路拥挤，使企业收集 和发送货物的效率明显降低，物流成本增加。日本政府为了解决这 个矛盾，政府和企业一起筹划建立物流中心和“物流团地”(节点) 的同时，还积极推行“共同配送制度”。经过不断的尝试和改革， 一种被日本实业界称为“配送”的运营体制诞生了。 美国企业把曾在“二战”时应用在军事战争中的“军事后勤”的思 想引入到企业的经营管理中来，把原来的旧式的仓库改造成现代的 配送中心，统一了装卸、分拣、包装，运输等物流作业标准。不少 的公司还设立了新的流通机构，将独立、分散的物流活动统一集中， 促成了新的送货方式。这不仅降低了物流成本，而且节约了社会资 源。
思考题
1.沃尔玛的经营优势在哪些方面？ 2.沃尔玛的物流配送方式属于什么方式？
同 行观 摩

中国邮路问题介绍及解答

中国邮路问题介绍及解答中国学者于20世纪50年代提出的一种典型的组合优化问题，后在国际上被称为中国邮路问题(Chinese postman problem)。

已知图G=(V，E)，对于每条边e∈E，有距离d(e)，从G的某节点出发，走过G的所有边(允许重复穿过)，回到原出发点，使其总行程最短，这个问题是P问题。

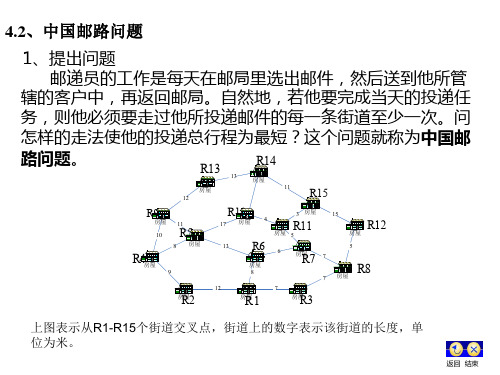
基本介绍一个邮递员送信，要走完他负责投递的全部街道，完成任务后回到邮局，应按怎样的路线走，他所走的路程才会最短呢?如果将这个问题抽象成图论的语言，就是给定一个连通图，连通图的每条边的权值为对应的街道的长度(距离)，要在图中求一回路，使得回路的总权值最小。

显然，若图为欧拉图，只要求出图中的一条欧拉回路即可。

否则，邮递员要完成任务就得在某些街道上重复走若干次。

如果重复走一次，就加一条平行边，于是原来对应的图就变成了多重图。

只是要求加进的平行边的总权值最小就行了。

于是问题就转化为：在一个有奇度数结点的赋权连通图中，增加一些平行边，使得新图不含奇度数结点，并且增加的边的总权值最小。

问题的解答要解决上述问题，应分下面两大步骤。

首先，增加一些边，使得新图无奇度数结点，称这一步为可行方案：其次，调整可行方案，使其达到增加的边的总权值最小，称这个最后的方案为最佳方案 [2] 。

【例1】在图1中，确定一条从到的回路，使它的权值最小。

事实上，所确定的回路从任何一个结点出发都可以。

(1)一个可行方案的确定。

由于图中奇度结点为偶数个，所以图中奇度数结点可以配对。

又由于图的连通性，每对奇度数结点之间均存在基本通路，在配好对的奇度数结点之间各确定一条基本通路，然后将通路中的所有边均加一条平行边，这样产生的新图中无奇度数结点，因而存在欧拉回路。

在图1(a)中，奇度数结点有4个：。

任意将它们配2对：与配对，v3与v6配对，选v1与v4之间的基本通路为，v3与v6之间的基本通路为。

每条通路中所含的边均加一条平行边。

增加平行边后如图1(b)所示，它无奇度数结点，因而是欧拉图。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

邮递员问题最短路径的解法
邮递员问题，又称旅行商问题（Traveling Salesman Problem，TSP），是一个著名的组合优化问题。

它要求找到一条路径，使得邮递员从出发点出发，经过所有的城市且仅经过一次，最后回到出发点，同时路径长度最短。

由于邮递员问题是NP-hard问题，没有多项式时间的解法。

然而，存在一些启发式和近似算法可以在可接受的时间内找到较好的解决方案：
1. 蛮力法：尝试所有可能的路径组合，计算每条路径的长度，最终选择最短路径作为解。

这种方法的时间复杂度为O(n!)，适用于较小规模的问题。

2. 最近邻算法：从一个起始点开始，每次选择离当前点最近的未访问过的城市作为下一个访问点，直到所有城市都被访问过，然后回到起始点。

该算法的时间复杂度为O(n^2)，虽然不能保证找到最优解，但是可以在较短的时间内找到较好的解。

3. 2-opt算法：先使用最近邻算法得到一个初始解，然后对路径进行优化。

2-opt算法通过不断交换路径中的两个边来减小路径的长度，直到没有可改进的交换。

该算法可以较快地优化路径，但无法保证找到全局最优解。

4. 遗传算法：使用进化计算的思想来解决TSP问题。

通过生成初始种群，交叉、变异等操作进行迭代优化，逐渐找到更好的路径。

遗传算法可以在较短时间内找到较好的解，但是无法保证找到最优解。

上述算法只是解决TSP问题的一部分方法，具体使用哪种方法取决于问题规模和时间要求。

对于较小规模的问题，可以使用蛮力法或者最近邻算法得到较好的解。

对于更大规模的问题，可以考虑使用启发式算法，如遗传算法等。

此外，还存在其他算法和优化技术用于处理TSP问题，根据具体情况选择合适的方法。