廖承恩《微波技术基础》第四-第六章答案

《微波技术基础》课程复习知识要点(2007版)第一章 “微波技术基础引论”知识要点廖承恩主编的《微波技术与基础》是国内较为经典的优秀教材之一，引论部分较为详细的介绍了微波的工作波段、特点及其应用，大部分应用背景取材于微波通讯占主导地位的上世纪80’s / 90’s 年代。

在科技迅猛发展的今天，建议同学们关注本网站相关联接给出的最新发展动态，真正做到学以致用，拓展自己的知识面，特别是看看微波在现代无线和移动通信、射频电路设计（含RFID ）、卫星定位、宇航技术、探测技术等方面的应用，不要局限于本书的描述。

(Microwaves have widespread use in classical communication technologies, from long-distance broadcasts to short-distance signals within a computer chip. Like all forms of light, microwaves, even those guided by the wires of an integrated circuit, consist of discrete photons ….. NATURE| Vol 449|20 September 2007)1本章的理论核心是在对导行波的分类的基础上推导了导行系统传播满足的微波的波段分类、特点与应用（TE 、TM 、TEM ）和基本求解方法，给出了导行系统、导行波、导波场满足的方程；（Halmholtz Eq 、横纵关系）、本征值---纵向场法、非本征值---标量位函数法（TEM ）。

{重点了解概念、回答实际问题，比如考虑一下如按如下的份类，RFID 涉及那些应用？全球定位系统GPS 呢？提高微波工作频率的好处及实现方法？}1．微波的定义 把波长从1米到1毫米范围内的电磁波称为微波。

微波波段对应的频率范围为: 3×108Hz ～3×1011Hz 。

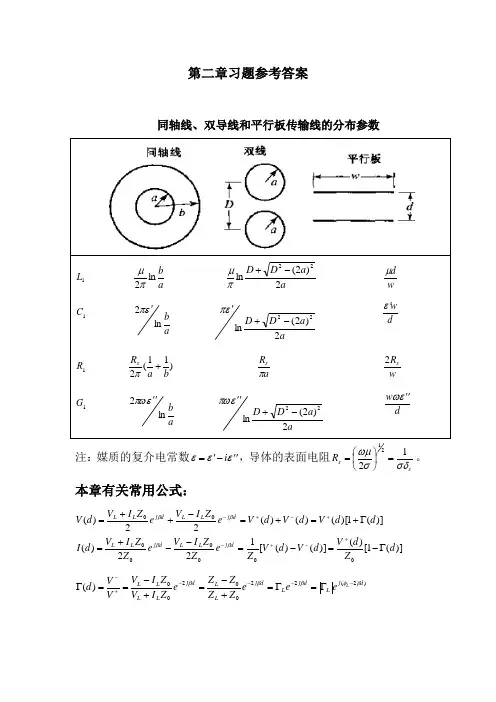
第二章习题参考答案同轴线、双导线和平行板传输线的分布参数注：媒质的复介电常数εεε''-'=i ，导体的表面电阻ss R σδσωμ1221=⎪⎭⎫⎝⎛=。

本章有关常用公式：)](1[)()]()([122)()](1)[()()(22)(00000000d Z d V d V d V Z e Z Z I V e Z Z I V d I d d V d V d V e Z I V e Z I V d V d j L L d j L L dj L L d j L L Γ-=-=--+=Γ+=+=-++=+-+-+-+-ββββ )2(2200200)(d j L d j L dj L L d j L L L L L e e e Z Z Z Z e Z I V Z I V VV d βφβββ----+-Γ=Γ=+-=+-==ΓL Lj L j L L L L L e e Z Z Z Z Z Z Z Z φφΓ=+-=+-=Γ0000dtg jZ Z dtg jZ Z Z d Z L L in ββ++=000)()(1)(1)()()(0d d Z d I d V d Z in Γ-Γ+==LL VV VSWR Γ-Γ+==11minmax2.1无耗或者低耗线的特性阻抗为110C L Z = 平行双导线的特性阻抗：aDa a D D a a D D Z r r rln 11202)2(ln 11202)2(ln 112222000εεεμεπ≈-+=-+=已知平行双导线的直径mm a 22=，间距cm D 10=，周围介质为空气（1=r ε），所以特性阻抗)(6.5521100ln 120ln11200Ω==≈a D Z rε 同轴线的特性阻抗：ab a b Z r rln 60ln 121000εεμεπ==已知同轴线外导体的内直径2mm b 23=，内导体的外直径2mm a 10=，中间填充空气(1=r ε)：特性阻抗)(50210223ln 60ln 600Ω===abZ r ε中间填充介质(25.2=r ε)：特性阻抗)(3.33210223ln 25.260ln 600Ω===a b Z r ε2.2对于无耗传输线线有相位常数μεωωβ===k C L 11，所以可求出相速度v k C L v p =====μεωβω1111，等于电磁波的传播速度。

微带电路的原理------------------------------------------------------------------------------------------------微带电路的原理一、微带线简介微带线是制作微波集成电路的平面结构传输线。

可用光刻程序制作，且容易与其他无源微波电路和有源微波器件集成，实现微波部件和系统的集成化。

与金属波导相比，其体积小、重量轻、使用频带宽、可靠性高和制造成本低等;但损耗稍大，功率容量小。

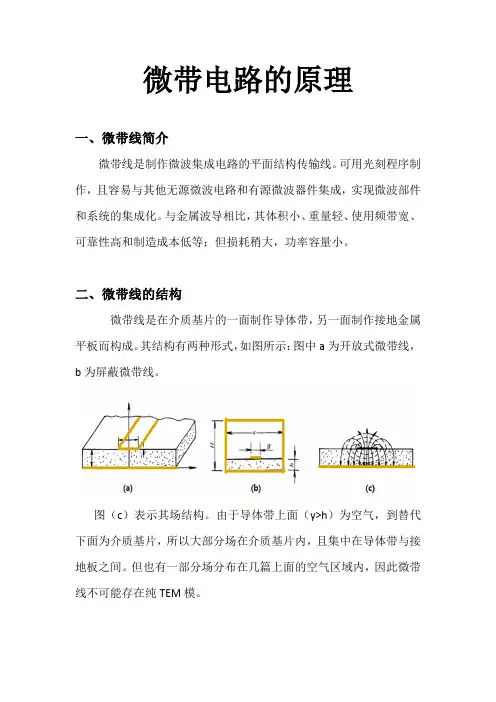
二、微带线的结构微带线是在介质基片的一面制作导体带，另一面制作接地金属平板而构成。

其结构有两种形式，如图所示:图中a为开放式微带线，b为屏蔽微带线。

图(c)表示其场结构。

由于导体带上面(y>h)为空气，到替代下面为介质基片，所以大部分场在介质基片内，且集中在导体带与接地板之间。

但也有一部分场分布在几篇上面的空气区域内，因此微带线不可能存在纯TEM模。

三、微带线的制作及工艺60年代前期，由于微波低损耗介质材料和微波半导体器件的发展，形成了微波集成电路，使微带线得到广泛应用，相继出现了各种类型的微带线。

一般用薄膜工艺制造。

介质基片选用介电常数高、微波损耗低的材料。

导体应具有导电率高、稳定性好、与基片的粘附性强等特点。

微带线介质基片的种类:常用的有99%的氧化铝陶瓷、石英、蓝宝石、聚四氟乙烯玻璃纤维等。

——————————————————————————————————————------------------------------------------------------------------------------------------------传统的微带线制作工艺过程首先要用真空蒸发的方法在抛光的介质几面正面镀上一层厚度为20~40mm的铬，再在铬层上镀上厚度约1um的金、铜或银等，然后在表面涂感光胶并贴上所需电路图形照片的底片，置于紫外光下进行光刻，经腐蚀后，只留下感光部分的电路图形。

微带电路的原理一、微带线简介微带线是制作微波集成电路的平面结构传输线。

可用光刻程序制作，且容易与其他无源微波电路和有源微波器件集成，实现微波部件和系统的集成化。

与金属波导相比，其体积小、重量轻、使用频带宽、可靠性高和制造成本低等；但损耗稍大，功率容量小。

二、微带线的结构微带线是在介质基片的一面制作导体带，另一面制作接地金属平板而构成。

其结构有两种形式，如图所示：图中a为开放式微带线，b为屏蔽微带线。

图（c）表示其场结构。

由于导体带上面（y>h）为空气，到替代下面为介质基片，所以大部分场在介质基片内，且集中在导体带与接地板之间。

但也有一部分场分布在几篇上面的空气区域内，因此微带线不可能存在纯TEM模。

三、微带线的制作及工艺60年代前期，由于微波低损耗介质材料和微波半导体器件的发展，形成了微波集成电路，使微带线得到广泛应用，相继出现了各种类型的微带线。

一般用薄膜工艺制造。

介质基片选用介电常数高、微波损耗低的材料。

导体应具有导电率高、稳定性好、与基片的粘附性强等特点。

微带线介质基片的种类：常用的有99%的氧化铝陶瓷、石英、蓝宝石、聚四氟乙烯玻璃纤维等。

传统的微带线制作工艺过程首先要用真空蒸发的方法在抛光的介质几面正面镀上一层厚度为20~40mm的铬，再在铬层上镀上厚度约1um的金、铜或银等，然后在表面涂感光胶并贴上所需电路图形照片的底片，置于紫外光下进行光刻，经腐蚀后，只留下感光部分的电路图形。

表面金属也要有一定厚度，也就是微带导体带的厚度t，导体带的宽度和长度视电路需要而定。

三、微带电路的实现有两种实现方法：1.在基片上沉淀金属导带，这类材料主要是陶瓷刚性材料。

这种方法工艺复杂，加工周期长，性能指标好，在毫米波或要求高的场合使用。

2.在现成介质覆铜板上光刻腐蚀成印制板电路，这类材料主要是复合介质类材料。

这种方法加工方便，成本低，是目前使用最广泛的方法，又称微波印制直板电路。

四、主要技术参数：1、特性阻抗2、衰减常数衰减常数表示微带的损耗，包括导体损耗、介质损耗和辐射损耗。

4-1 谐振腔有哪些主要的参量？这些参量与低频集总参数谐振回路有何异同点？答：谐振腔的主要特性参数有谐振频率、品质因数以及与谐振腔中有功损耗有关的谐振电导，对于一个谐振腔来说，这些参数是对于某一个谐振模式而言的，若模式不同，这些参数也是不同的。

谐振频率具有多谐性，与低频中的回路，当其尺寸、填充介质均不变化时，只有一个谐振频率是不相同的。

在谐振回路中，微波谐振腔的固有品质因数要比集总参数的低频谐振回路高的多。

一般谐振腔可以等效为集总参数谐振回路的形式。

4-2 何谓固有品质因数、有载品质因数？它们之间有何关系？答：固有品质因数是对一个孤立的谐振腔而言的，或者说，是谐振腔不与任何外电路相连接（空载）时的品质因数。

当谐振腔处于稳定的谐振状态时，固有品质因数0Q 的定义为02TWQ W π=，其中W 是谐振腔内总的储存能量，T W 是一周期内谐振腔内损耗的能量。

有载品质因数是指由于一个腔体总是要通过孔、环或探针等耦合机构与外界发生能量的耦合，这样不仅使腔的固有谐振频率发生了变化，而且还额外地增加了腔的功率损耗，从而导致品质因数下降，这种考虑了外界负载作用情况下的腔体的品质因数称为有载品质因数l Q 。

对于一个腔体，01l Q Q k=+，其中k 为腔体和外界负载之间的耦合系数。

4-4 考虑下图所示的有载RLC 谐振电路。

计算其谐振频率、无载Q 0和有载Q L 。

谐振器负载1800Ω解：此谐振电路属于并联谐振电路，其谐振频率为：0356f MHz ===无载时，017.9R Q w L====有载时，040.25L e R Q w L ====根据有载和无载的关系式111L e Q Q Q=+得： 1112.5111140.2517.9L e Q Q Q===++4-5 有一空气填充的矩形谐振腔。

假定x 、y 、z 方向上的边长分别为a 、b 、l 。

试求下列情形的振荡主模及谐振频率：（1）a b l >>；（2）a l b >>；（3）l a b >>；（4）a b l ==。

第四章习题参考答案带状线为双导体结构，中间填充均匀介质，所以能传输TEM 导波，且为带状线的工作模式。

4.1可由P.107:4.1-7式计算特性阻抗0Z 由介质r ε，导体带厚度与接地板高度的比bt ，以及导体带宽度与接地板高度的比bW确定。

Ω=45.690Z4.5可由P.107:4.1-6式计算⎪⎩⎪⎨⎧>--<=1206.085.012000Z x Z x b W r r εε 其中： 441.0300-=Z x r επ已知：1202.74502.20<=⨯=Z r ε 83.0441.02.7430441.0300=-=-=πεπZ x r 所以： )(66.283.02.3mm bx W =⨯==衰减常数P.109:4.1-10：d c ααα+=c α是中心导体带和接地板导体的衰减常数，d α为介质的衰减常数。

TEM 导波的介质损耗为：)/(2m Np ktg d δα=，其中εμω'=k 由惠勒增量电感法求得的导体衰减常数为)/(m Np ：P.111:4.1-11⎪⎪⎩⎪⎪⎨⎧Ω>Ω<-⨯=-12016.0120)(30107.200003Z B b Z R Z A t b Z R r s r r s c εεπεα 其中：⎪⎭⎫⎝⎛--++-+=t t b t b t b t b W A 2ln 121π ⎪⎭⎫⎝⎛++-++++=t W W t t b t b t W b B πππ4ln 21414.05.01)7.05.0(1)/(155.02001.0100.32.21010222289m Np tg c f ktg r d =⨯⨯===πδεπδα 铜的表面电阻在10GHz 下Ω==026.02σωμs R ，74.4=A m Np A t b Z R r s c /122.0)(30107.203=-⨯=-πεαm Np d c /277.0=+=αααdB e Np 686.8lg 1012==m dB m Np d c /41.2/277.0==+=ααα4.6可由P.107:4.1-6式计算⎪⎩⎪⎨⎧>--<=1206.085.012000Z x Z x b W r r εε 其中: 441.0300-=Z x r επ已知：1204.1481002.20>=⨯=Z r ε 194.0441.04.14830441.0300=-=-=πεπZ x r 所以： )(67.02128.016.3)6.085.0(mm x b W =⨯=--= 在10GHz ，带状线的波长为：cm fcr 02.210102.210398=⨯⨯⨯==ελ4.16可由P.130:4.3-27式计算已知Ω=700e Z ，Ω=300o Z ，mm b 4=，1.2=r ε3813.3300==re e Z A ε648.02212212143813.33813.3214=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫⎝⎛+--=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+--=e e e e k e eA A e45.1300==ro o Z A ε99.022222=⎪⎪⎪⎭⎫⎝⎛+-=o o A A o e e k ππ68.02==o e k k arctg b W π015.0112=⎪⎪⎭⎫⎝⎛--=oee o k k k k arctg b S π mm b 4=mm W 7.268.04=⨯= mm S 06.0015.04=⨯=廖承恩第6章习题6－5 求图6－1 所示的对称二端口网络的归一化ABCD 矩阵，并求不引起附加反射的条件。

《微波技术与天线》习题答案章节 微波传输线理路1.1设一特性阻抗为Ω50的均匀传输线终端接负载Ω=1001R ，求负载反射系数1Γ，在离负载λ2.0，λ25.0及λ5.0处的输入阻抗及反射系数分别为多少？ 解：31)()(01011=+-=ΓZ Z Z Zπβλ8.02131)2.0(j z j e e --=Γ=Γ31)5.0(=Γλ （二分之一波长重复性）31)25.0(-=ΓλΩ-∠=++= 79.2343.29tan tan )2.0(10010ljZ Z ljZ Z Z Z in ββλΩ==25100/50)25.0(2λin Z （四分之一波长阻抗变换性） Ω=100)5.0(λin Z （二分之一波长重复性）1.2求内外导体直径分别为0.25cm 和0.75cm 的空气同轴线的特性阻抗；若在两导体间填充介电常数25.2=r ε的介质，求其特性阻抗及MHz f 300=时的波长。

解：同轴线的特性阻抗abZ r ln 600ε= 则空气同轴线Ω==9.65ln 600abZ 当25.2=r ε时，Ω==9.43ln600abZ rε 当MHz f 300=时的波长：m f c rp 67.0==ελ1.3题设特性阻抗为0Z 的无耗传输线的驻波比ρ，第一个电压波节点离负载的距离为1min l ，试证明此时的终端负载应为1min 1min 01tan tan 1l j l j Z Z βρβρ--⨯=证明：1min 1min 010)(1min 101min 010in tan l tan j 1/tan tan 1min 1min l j Z Z Z Z l j Z Z l j Z Z Z Z l in l βρβρρββ--⨯=∴=++⨯=由两式相等推导出：对于无耗传输线而言：）（1.4传输线上的波长为：m fr2cg ==ελ因而，传输线的实际长度为：m l g5.04==λ终端反射系数为： 961.0514901011≈-=+-=ΓZ R Z R输入反射系数为： 961.0514921==Γ=Γ-lj in eβ 根据传输线的4λ的阻抗变换性，输入端的阻抗为：Ω==2500120R ZZ in1.5试证明无耗传输线上任意相距λ/4的两点处的阻抗的乘积等于传输线特性阻抗的平方。

第六章习题参考答案6.5: 已知并联导纳的ABCD 矩阵⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡101Y D C B A 和一段传输线的ABCD 矩阵l ch V l V V V A L I L I γ=====021)(2 l Z s h I l V I V B L V L V γ=====021)(2Z lsh V l I V I C L I LI γ=====021)(2 l ch I l I I I D L V LV γ=====021)(2对于无耗线:l j l ch A ββγγcos )(=== l jZ j l Zsh B ββγγsin )(=== l Zj j Z l sh C ββγγsin 1)(===l j l ch D ββγγcos )(=== 总的ABCD 矩阵为三个二端口网络ABCD 矩阵的乘积⎥⎥⎦⎤⎢⎢⎣⎡--+-=⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡θθθθθθθθθθθsin cos sin 1cos 2sin sin cos 101cos sin 1sin cos 10122BZ i Z Z B jB jZ BZ jB Zj jZ jB D C B A 则总的归一化ABCD 矩阵为：⎥⎥⎦⎤⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡D CZ Z BAd c b a 00 由S 矩阵ABCD 矩阵的关系式⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+-+----++++=D CZ B Z A BC AD D CZ B Z A D CZ B Z A S 00000012)(2111][ 可求出S 矩阵。

对于本题目求出不引起附加反射的条件，只需求θθcos 2sin )1(00220011B Z Z B Z Z Z Z S =⎥⎦⎤⎢⎣⎡--⇒=由上式可得各参数满足的关系式02)1(20202202=--+Z tg BZ Z Z tg Z B θθ6.9由题意知(a)和(c)图均为右端或中断开路的一端口网络，求S 矩阵只需求始端反射系数即可（略）(b)图为并联导纳的S 矩阵（参考6.5）（略） 6.14 推导：原来第i 个参考面位于0=i z ，归一化入射和反射波为：i i b a , 当第i 个参考面移到i i l z =时，归一化入射和反射波为：i i j i i j i i e b b e a a θθ='='-,，其中giii l λπθ2=（p.21，2.1-14）j i j i j j ij j j ji j i ije S e a b a b S θθθθ----==''=' 写成矩阵形式为：]][][[][P S P S ='其中： ⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=---N j j j e e e P θθθ0000][21已知：参考面21,T T 处的S 矩阵⎥⎦⎤⎢⎣⎡=22211211S S S S S⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎦⎤⎢⎣⎡=--221121220000][g g l j l j j j e e e e P λπλπθθ 则由公式]][][[][P S P S ='可求出][S '。

《微波技术基础》期末复习题第2章传输线理论1. 微波的频率范围和波长范围频率范围300MHz ~ 3000 300MHz ~ 3000 GHz GHz 波长范围 1.0 m ~ 0.1mm ；2. 微波的特点⑴拟光性和拟声性；⑵频率高、频带宽、信息量大；⑶穿透性强；⑷微波沿直线传播；3. 传输线的特性参数⑴特性阻抗的概念和表达公式特性阻抗＝传输线上行波的电压／传输线上行波的电流11011R j L Z G j C w w +=+⑵传输线的传播常数传播常数j g a b =+的意义，包括对幅度和相位的影响。

4. 传输线的分布参数：⑴分布参数阻抗的概念和定义⑵传输线分布参数阻抗具有的特性()()()in V d Z d I d =00ch sh sh ch L L L L V d I Z d V d I d Z g g g g +=+000th th L L Z Z d Z Z Z d g g +=+① 传输线上任意一点传输线上任意一点 d 的阻抗与该点的位置d 和负载阻抗Z L 有关；有关； ② d 点的阻抗可看成由该点向负载看去的输入阻抗；点的阻抗可看成由该点向负载看去的输入阻抗；③ 传输线段具有阻抗变换作用；传输线段具有阻抗变换作用；由公式由公式 ()in Z d 000th th L L Z Z d Z Z Z d g g +=+ 可以看到这一点。

可以看到这一点。

④ 无损线的阻抗呈周期性变化，具有λ/4的变换性和的变换性和 λ/2重复性；重复性； ⑤ 微波频率下，传输线上的电压和电流缺乏明确的物理意义，不能直接测量；接测量；⑶ 反射参量反射参量① 反射系数的概念、定义和轨迹；反射系数的概念、定义和轨迹；② 对无损线，其反射系数的轨迹？；对无损线，其反射系数的轨迹？；③ 阻抗与反射系数的关系；阻抗与反射系数的关系； [][]in ()1()()()1()V d d Z d I d d +++G =-G [][]01()1()d Z d +G =-G ⑷ 驻波参量驻波参量① 传输线上驻波形成的原因？传输线上驻波形成的原因？② 为什么要提出驻波参量？为什么要提出驻波参量？③ 阻抗与驻波参量的关系；阻抗与驻波参量的关系；5. 无耗传输线的概念和无耗工作状态分析无耗传输线的概念和无耗工作状态分析⑴ 行波状态的条件、特性分析和特点；行波状态的条件、特性分析和特点；⑵ 全反射状态的条件、特性分析和特点；全反射状态的条件、特性分析和特点；⑶ 行驻波状态的条件、特性分析和特点；行驻波状态的条件、特性分析和特点；6. 有耗传输线的特点、损耗对导行波的主要影响和次要影响有耗传输线的特点、损耗对导行波的主要影响和次要影响7. 引入史密斯圆图的意义、圆图的构成；引入史密斯圆图的意义、圆图的构成；8. 阻抗匹配的概念、重要性阻抗匹配的概念、重要性9. 阻抗匹配的方式及解决的问题阻抗匹配的方式及解决的问题⑴ 负载负载 — 传输线的匹配传输线的匹配⑵ 信号源信号源 — 传输线的匹配传输线的匹配⑶ 信号源的共轭匹配信号源的共轭匹配10. 负载阻抗匹配方法负载阻抗匹配方法⑴ λ/4阻抗匹配器阻抗匹配器⑵ 并联支节调配器并联支节调配器⑶ 串联支节调配器串联支节调配器第3章 规则金属波导1. 矩形波导的结构特点、主要应用场合；矩形波导的结构特点、主要应用场合；2. 矩形波导中可同时存在无穷多种TE 和TM 导模；导模；3. TE 和TM 导模的条件；导模的条件；TE 导模的条件：00(,,)(,)0j z z z z E H x y z H x y eb -==¹ TE 导模的条件：00(,,)(,)0j zz z z H E x y z E x y eb -==¹ 4. 关于矩形波导的5个特点；个特点；5. 掌握矩形波导TE 10模的场结构，并在此基础上掌握TE m0模的场结构；模的场结构；6. 管壁电流的概念；管壁电流的概念；7. 管壁电流的大小和方向；管壁电流的大小和方向；8. 矩形波导的传输特性（导模的传输条件与截止）；9. 圆形波导主模TE11模的场结构。

4-1[解]远区场条件：k r＞＞11/kr＞＞1/( k r)2＞＞1/( k r)3 →只保留1/rrE≈（＜＜Eθ，忽略）近区场条件：k r＜＜1，r＜＜λ→r＜＜λ/2∏1/kr＜＜1/( k r)2＜＜1/( k r)3∴忽略1/r项jkre-→14-2[解]：f=3Mhz, ∴λ=100mr=10km,r＞＞λ/2π即A、B、C、D、E各点在电基本振子远区场（1）∴60sinA jkrI lE jre θπθλ-=A点：θ=00，E A=0 v/mB点：θ=300，| E A|= 9.42 ⨯10-5 v/mC点：θ=900，| E c|=| E max|=1.884⨯10-4v/m D点：θ=1500，| E D|=| E B | =9.42 ⨯10-5 v/mE点：θ=1800，E E =E A =0 v/m（2）若电流元垂直纸面，则A、B、C、D、E各点在H平面上，则各点场强相同，且为最大值| E max|=1.884⨯10-5v/m，极化方向均垂直于纸面。

4-4[解]：2l=λ/2 E面xoz面极值：θ=900，2700，零值：θ=00，18002l=1.5λ 六个极值： 900，500，1300，2300，2700，3100零值：00，70.50，109.50，1800，250.50，289.502l=2λ 四个最大值：θ=600，1200，2100，3300四个零值：θ=00，1800，900，4-6[解]：电流元：F （0）=f （θ）=sin θ半功率波瓣宽度：BW 为F 2（θ0.5）=1/2夹角。

所以，θ0.5 =450 则BW=2θ0.5=900 4-7[解]：l=0.25λ→2l=λ/2 半波振子 c o s (/2c o s )f ()s i n πθθθ=F 2（θ0.5）=1/2，θ0.5≈390，则BW=2θ0.5=780l=1λ→2l=2λ，cos(2cos )f ()sin πθθϕθ=∴ F 2（θ0.5）=1/2 4-8 [解]：2042(,)sin D d F d πππϕθϕθθ=⎰⎰电流元：22(,)=sin Fθϕθ 代入积分，得电流元方向系数D=1.5 4-9[解]： max| E'|FSLL=20lg| E|db =20lg0.01 db=-40db 又因为，D=100则任意方向 ：D （θ）=(,)D F θϕ∙，max| (,)|(,)=| E|E F θϕθϕ副瓣max| E'|(,)=0.01| E|Fθϕ= 则第一副瓣：()=0.01100=1D θ⨯ 4-13[解]：2L=2m ，λ1=10m ，λ2=4m 有效长度：e l =2kl tg λπ代入： λ1=10m ，e1l = 1.032kltg m λπ= λ2=4m ，为半波偶极子，e2l 1.27m λπ≈= 4-25[解]： 1()=()=()g f f f ∆∆∆E 面方向图（纸平面）4-10 [解]： 由()f θ→()f θmax=1.414，θ=900所以由图：200.5( )0.4142sin 90 1.4142θ-+=，由max| |()=| E|E F θ定义4-11[解]： 由max 60D| E|=P r∑ 22max | E|r =60DP ∑且电流元D1=1.76db=1.5，半波振子D2=2.15db=1.64（a ）1121max 2max 12260D | E || E |60D P r r P ∑∑=∙ （b ）2221max 1122212max 260D | E |r 60D | E |r P P ∑∑=4-14[解]：对称振子的电流分布——近似认为与开路双线电流分布一致 4-16 已知电流元在、r=5km ，处电场为2mv/m ，求其辐射功率P ∑ [解]： 由max| E|(,)=| E|Fθϕ max | E|| E|(,)F θϕ∙=电流元(,)=sin Fθϕθ m a x 0| E |2| E|4m v /m s i n (,)30Fθϕ∴=== 由22max | E|r 60DP ∑=电流元D=1.5，22max | E|r 4.4w 60DP ∑== 4-17 已知P in =10w ，D=3，效率a 0.5η=求（1）r=10km 处电场值（2）若欲使r=20km 处电场和（1）中10km 处相同，方向系数应增加多大？[解]： a G D 30.5=1.5η==⨯由in max 60P G| E|r=得 （1） r =10km 处，-3max 36010 1.5| E|3v/m=3mv/m 101010⨯⨯==⨯⨯ （2） 设天线效率相同，输入功率相同由in amax 60P D | E|rη=4-18 设天线归于输入电流的辐射电阻和损耗电阻分别为r0R =4Ω，10R =1Ω，方向系数D=3，求其输入电阻R 0和增益G 。

紧凑型高方向大功率耦合器的设计摘要；紧凑型高方向大功率耦合器是由两种传输线组成，一种是矩形波导传输线，为信号传输主通道，传输微波大功率信号，一种是带状线，为信号传输耦合通道，传输微波低功率信号。

根据Bethe小孔耦合理论，设计工作在S频段，电磁波通过矩形波导宽边中心窄槽缝隙耦合的波导耦合器。

根据预定的技术指标,初步设计出波导耦合器的有关参数，再利用仿真软件CST对窄槽缝隙和带状线进行优化，大大提高波导耦合器的整体性能。

产品加工完成，通过实物电参数测试，在3.68GHz-3.72GHz内，方向性≥35dB，外形尺寸为188mm×119mm×128mm。

关键词: 紧凑型高方向大功率S频段耦合器0 引言近几年来，为了不断满足市场的需求，微波器件不断发展，耦合器种类繁多，主要分为波导定向耦合器和微带线定向耦合器。

普通的波导定向耦合器虽然能测量低功率及高功率微波信号，但加工出的实物体积大，不利于运输、携带和测量系统的设计安装；而且普通波导定向耦合器方向性一般只能达到25dB，影响测量结果的准确性；微带线定向耦合器虽然体积小巧，但大多只能准确测量功率较低的微波信号。

1 工作原理大多数定向耦合器一般都是只有四个端口的无源器件。

其实质就是输入功率P1按照一定的耦合机制，将其中一部分功率P3输送到耦合端口，剩余的功率输送到直通端口P2，理想情况下隔离端口没有输出功率，但实际上还是会有功率P4从隔离端口输出。

波导耦合器原理图如图1所示。

图1 波导耦合器原理图2 技术指标及设计方案分析2.1技术指标某高功率传输系统需要进行功率测量和指示，需要波导定向耦合器提取微波信号进行监测，工作频率在3.68GHz-3.72GHz内，耦合度为60dB±1 dB，方向性≥30dB，主路通道为BJ32矩形波导，耦合通道为同轴线N-KFD接口，外形尺寸小于200mm×120mm×130mm。