微波技术习题解答(部分)
- 格式:ppt
- 大小:984.50 KB
- 文档页数:15

1-1什么是行波,它的特点是什么,在什么情况下会得到行波;什么是纯驻波,它有什么特点,在什么情况下会产生纯驻波?解:当传输线是无限长,或其终端接有等于线的特性阻抗的负载时,信号源传向负载的能量将被负载完全吸收,而无反射,此时称传输线工作于行波状态,或者说,传输线与负载处于匹配状态。
在行波状态下,均匀无耗线上各点电压复振幅的值是相同的,各点电流复振幅的值也是相同的,即它们都不随距离z 而变化;而且,电压和电流的瞬时值是相同的。
当负载l c Z Z =时,反射波为零,由此得到行波。
从信号传向负载的入射波在终端产生全反射,线上的入射波和反射波相叠加,从而形成了纯驻波状态。
对于任意的电抗性负载都可以用一个有限长的短路线或开路线的输入阻抗来代替。
当传输线终端是短路、开路,或接有纯电抗性(电感性和电容性)负载时。
1-2传输线的总长为5/8λ,终端开路,信号源内阻等于特性阻抗。
终端的电压为15045∠ ,试写出始端、以及与始端相距分别为/8λ和/2λ等处电压瞬时值的表达式。
解:(1) 求终端电压L U终端开路,将产生全反射,线上为纯驻波状态。
终端电压L U 应等于入射电压加反射电压,即+L U U (0)U (0)-=,开路处+U (0)U (0)-=,即L U 2U (0)+=。
而开路线上任一处z 的电压,由下式求出L U z U cos z β()=题中,始端z 5/8λ=处有 0U (z )U (5/8)150/45λ== 故有 0j 45L5150e U c o s ()8βλ=⋅ 即00j45j45j(45)L 150e U 5cos()8πλβ±==-=⋅因此,线上任一处的电压复振幅为0+j (45)LU (z )U c o s z =2U (0)c o 1502c o sz eπβββ±== (2)开路状态下,沿线各处的瞬时电压为j w tu (z ,t )R e [U (z )e1502c o s z c o s (w t 45)βπ==+± 故始端瞬时电压j(45)jwt055u(,cos()e]=100cos zcos(wt+45)88πλλββ±⋅据终端8λ处,则距终端为z2λ=j(45)jwt0u(,)e e)22πλλβ±⋅据终端2λ处,则距终端为z8λ=j(45)jwt0u(,)e e]=150cos(wt+45)88πλλβπ±⋅±1-3传输线的特性阻抗为cZ,行波系数为K,终端负载为LZ,第一个电压最小点距终端的距离为l mi m,试求LZ的表达式。

第 1 章 习 题1、 求函数()D Cz By Ax u +++=1的等值面方程。
解:根据等值面的定义:标量场中场值相同的空间点组成的曲面称为标量场的等值面,其方程为)( ),,(为常数c c z y x u =。
设常数E ,则,()E D Cz By Ax =+++1, 即:()1=+++D Cz By Ax E针对不同的常数E (不为0),对应不同的等值面。
2、 已知标量场xy u =,求场中与直线042=-+y x 相切的等值线方程。
解:根据等值线的定义可知:要求解标量场与直线相切的等值线方程,即是求解两个方程存在单解的条件,由直线方程可得:42+-=y x ,代入标量场C xy =,得到: 0422=+-C y y ,满足唯一解的条件:02416=⨯⨯-=∆C ,得到:2=C ,因此,满足条件的等值线方程为:2=xy3、 求矢量场z zy y y x xxy A ˆˆˆ222++=的矢量线方程。
解:由矢量线的微分方程:zy x A dz A dy A dx ==本题中,2xy A x =,y x A y 2=,2zy A z =, 则矢量线为:222zy dzy x dy xy dx ==,由此得到三个联立方程:x dy y dx =,z dz x dx =,zy dz x dy =2,解之,得到: 22y x =,z c x 1=,222x c y =,整理, y x ±=,z c x 1=,x c y 3±=它们代表一簇经过坐标原点的直线。
4、 求标量场z y z x u 2322+=在点M (2,0,-1)处沿z z y xy xx t ˆ3ˆˆ242+-=方向的方向导数。
解:由标量场方向导数的定义式:直角坐标系下,标量场u 在可微点M 处沿l 方向的方向导数为γβαcos cos cos zu y u x u l u ∂∂+∂∂+∂∂=∂∂α、β、γ分别是l 方向的方向角,即l 方向与z y xˆˆˆ、、的夹角。

《微波技术》习题解(一、传输线理论)(共24页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--机械工业出版社《微 波 技 术》(第2版) 董金明 林萍实 邓 晖 编著习 题 解一、 传输线理论1-1 一无耗同轴电缆长10m ,内外导体间的电容为600pF 。
若电缆的一端短路, 另一端接有一脉冲发生器及示波器,测得一个脉冲信号来回一次需s ,求该电缆的特性阻抗Z 0 。
[解] 脉冲信号的传播速度为tlv 2=s /m 102101.010286⨯=⨯⨯=-该电缆的特性阻抗为 00C L Z =00C C L =lC εμ=Cv l =8121021060010⨯⨯⨯=-Ω33.83= 补充题1 写出无耗传输线上电压和电流的瞬时表达式。
[解] (本题应注明z 轴的选法)如图,z 轴的原点选在负载端,指向波源。
根据时谐场传输线方程的通解()()()()()())1()(1..210...21.⎪⎪⎩⎪⎪⎨⎧+=-=+=+=--z I z I e A e A Z z I z U z U e A e A z U r i zj z j r i zj z j ββββ 。
为传输线的特性阻抗式中02.22.1;;,Z U A U A r i ==:(1),,212.2.的瞬时值为得式设ϕϕj r j i e U U eU U -+==⎪⎩⎪⎨⎧+--++=+-+++=-+-+)()cos()cos([1),()()cos()cos(),(21021A z t U z t U Z t z i V z t U z t U t z u ϕβωϕβωϕβωϕβω1-2 均匀无耗传输线,用聚乙烯(εr =作电介质。
(1) 对Z 0=300 Ω的平行双导线,导线的半径 r =,求线间距D 。
(2) 对Z 0 =75Ω的同轴线,内导体半径 a =,求外导体半径 b 。
[解] (1) 对于平行双导线(讲义p15式(2-6b ))0C L Z =rD r D ln ln πεπμ=r D ln 1εμπ=r D rln 120ε=300= Ω 得52.42=rD, 即 m m 5.256.052.42=⨯=D (2) 对于同轴线(讲义p15式(2-6c ))Z LZ 0○ ~ z补充题1图示0C L Z =dD d D ln 2ln2πεπμ=d D r ln 60ε=ab r ln 60ε=75= Ω 得52.6=ab, 即 mm 91.36.052.6=⨯=b 1-3 如题图1-3所示,已知Z 0=100Ω, Z L =Z 0 ,又知负载处的电压瞬时值为u 0 (t)=10sin ωt (V), 试求: S 1 、S 2 、S 3 处电压和电流的瞬时值。

微波技术习题解答第1章练习题1.1 无耗传输线的特性阻抗Z0= 100()。
根据给出的已知数据,分别写出传输线上电压、电流的复数和瞬时形式的表达式:(1) R L= 100 (),I L = e j0(mA);(2) R L = 50(),V L = 100e j0(mV);(3) V L = 200e j0 (mV),I L = 0(mA)。
解:本题应用到下列公式:(1)(2)(3)(1) 根据已知条件,可得:V L = I L R L = 100(mV),复数表达式为:瞬时表达式为:(2) 根据已知条件,可得:复数表达式为:瞬时表达式为:(3) 根据已知条件,可得:复数表达式为:瞬时表达式为:1.2 无耗传输线的特性阻抗Z0 = 100(),负载电流I L = j(A),负载阻抗Z L = j100()。
试求:(1) 把传输线上的电压V(z)、电流I(z)写成入射波与反射波之和的形式;(2) 利用欧拉公式改写成纯驻波的形式。
解:根据已知条件,可得:V L = I L Z L = j(j100) = 100(V),1.3 无耗传输线的特性阻抗Z0 = 75(),传输线上电压、电流分布表达式分别为试求:(1) 利用欧拉公式把电压、电流分布表达式改写成入射波与反射波之和的形式;(2) 计算负载电压V L、电流I L和阻抗Z L;(3) 把(1)的结果改写成瞬时值形式。
解:根据已知条件求负载电压和电流:电压入射波和反射波的复振幅为(1) 入射波与反射波之和形式的电压、电流分布表达式(2) 负载电压、电流和阻抗V L = V(0) = 150j75,I L = I(0) = 2 + j(3) 瞬时值形式的电压、电流分布表达式1.4 无耗传输线特性阻抗Z0 = 50(),已知在距离负载z1= p/8处的反射系数为 (z1)= j0.5。
试求(1) 传输线上任意观察点z处的反射系数(z)和等效阻抗Z(z);(2) 利用负载反射系数 L计算负载阻抗Z L;(3) 通过等效阻抗Z(z)计算负载阻抗Z L。

3-1 一根以聚四氟乙烯 2.10r ε=为填充介质的带状线,已知其厚度b =5mm ,金属导带厚度和宽度分别为0t =、W =2mm ,求此带状线的特性阻抗及其不出现高次模式的最高频率。
解: 由于/2/50.40.35W b ==>,由公式20(0.35/)eW Wb b W b ⎧=-⎨-⎩ /0.35/0.35W b W b <> 得中心导带的有效宽度为:2e W W m m ≈=,077.3Z ==Ω带状线的主模为TEM 模,但若尺寸不对也会引起高次模,为抑止高次模,带状线的最短工作波长应满足:1010m ax (,)cT E cT M λλλ>102 5.8c T E W m m λ== mmbr cTM5.14210==ελ所以它的工作最高频率GHzc f 20105.1410338=⨯⨯==-λ3-2 对于特性阻抗为50Ω的铜导体带状线,介质厚度b =0.32cm ,有效相对介电常数2.20r ε=,求线的宽度W 。
若介质的损耗角正切为0.001,工作频率为10GHz ,计算单位为dB /λ的衰减,假定导体的厚度为t =0.01mm 。
解:00)74.2120==<和030)0.4410.830x π=-=,所以 由公式00,1200.85120x Wb ⎧<⎪=⎨->⎪⎩其中,300.441x =-计算宽度为(0.32)(0.830)0.266W b x cm ===。
在10GHz ,波数为1310.6k mc-==由公式)(/2tan 波TEM m Np k d δα=介电衰减为mNp k d /155.02)001.0)(6.310(2tan ===δα在10GHz 下铜的表面电阻为0.026s R =Ω。
于是,根据公式300002.710120,30()/0.16120,s r cs R Z A b t N p m R B Z b επα-⎧⨯<⎪-⎪=⎨>⎪⎪⎩其中2121ln ()W b tb t A b tb tt π+-=++--0.414141(0.5ln)(0.50.7)2bt W B W t Wtππ=++++得出的导体的衰减为mNp A t b Z R r s c /122.0)(30107.203=-⨯=-πεα因为 4.74A =。

题 解第 一 章1-1 微波是频率很高,波长很短的一种无线电波。
微波波段的频率范围为 8103⨯Hz~12103⨯Hz ,对应的波长范围为1m~0.1mm 。
关于波段的划分可分为粗分和细分两种。
粗分为米波波段、分米波波段、厘米波波段、毫米波波段、亚毫米波段等。
细分为Ka K Ku X C S L UHF 、、、、、、、…等波段,详见表1-1-2。
1-2 简单地说,微波具有下列特点。
(1) 频率极高,振荡周期极短,必须考虑系统中的电子惯性、高频趋肤效应、辐射效应及延时效应;(2) 波长极短,“反射”是微波领域中最重要的物理现象之一,因此,匹配问题是微波系统中的一个突出问题。
同时,微波波长与实验设备的尺寸可以比拟,因而必须考虑传输系统的分布参数效应;(3) 微波可穿透电离层,成为“宇宙窗口”;(4) 量子特性显现出来,可用来研究物质的精细结构。
1-3 在国防工业方面:雷达、电子对抗、导航、通信、导弹控制、热核反应控制等都直接需要应用微波技术。
在工农业方面,广泛应用微波技术进行加热和测量。
在科学研究方面,微波技术的应用也很广泛。
例如,利用微波直线加速器对原子结构的研究,利用微波质谱仪对分子精细结构进行研究,机载微波折射仪和微波辐射计对大气参数进行测量等等。
第 二 章2-1 解 ∵01011Z Z Z Z +-=Γ ∴)(82.811Ω=Z2-2 解图(a )的输入阻抗021Z Z ab =; 图(b )的输入阻抗0Z Z ab =;图(c )的输入阻抗0Z Z ab =;图(d )的输入阻抗052Z Z ab =; 其等效电路自绘。
2-3 解 ∵01011Z Z Z Z +-=Γ ∵e j j 4121)1(21π=+=Γ 2-4 解(1) ∵e j Z Z Z Z 40101122π=+-=Γ ∴83.511ρ11=Γ-Γ+= (2) ∵π2 =l β∴e e j l -j l 4π)β2(11022=Γ=Γϕ 2-5 解 ∵ljZ Z l jZ Z Z Z tg βtg β10010++= ∴)(39.673.8Ω+=j Z in)(24.6009.2201Ω+=j Z)(1005003Ω+=j Z2-6 证明∵)(00ββe e lj l j U U Γ+=-+ )(00ββ0e e l j l j Z U I Γ-=-+ 而I Z E I Z E U g 0-=-=∴e U E l j 0β2-+= 故2EU =+2-7 证明lZ j l j Z l jZ Z l jZ Z Z in tg β1tg βtg βtg β111001++=++= 而 ρ11min =Z ,对应线长为1min l 故 1min 11min 1tg β1tg βρ1l Z j l j Z ++= 整理得 1min 1min 1tg βρρtgβ1l j l j Z --=2-8 解 ∵38.001011=+-=ΓZ Z Z Z而给定的1Z 是感性复阻抗,故第一个出现的是电压腹点,即λ/4线应接在此处。



习题课1.1设一特性阻抗为50 Q 的均匀传输线终端接负载Ri=100Q,求负载反射系数门,在 离负载0.2 X 、0.25 X 及0.5 X 处的输入阻抗及反射系数分别为多少?解:根据终端反射系数与终端阻抗的关系r_ 乙-Z° _ 100-50 _ 1厂乙 + Z 。
一 100 + 50 一亍根据传输线上任一点的反射系数与输入阻抗的关系r (z )= f 严二 z =z i + D m°i-ra )得到离负载0.2 x 、0.25 x 及0.5 x 处的输入阻抗及反射系数分别为-j2—O.2X1 “ Qr (0.2X ) = r,e 入 =-e~)0SnZ,r (0.2X ) = 29.43Z-23.79°£2 -j2^O.25Xr (0・25 入) = iy xZ 加(0.25 入)= 25G-j2—0.5X]r (o.5入)= ry 1=-(反射系数具有x/2周期性)Z,r (0.5A ) = 100Q (输入阻抗具有入/2周期性)1.2求内外导体直径分别为0.25cm 和0.75cm 的空气同轴线的特性阻抗;若在两导体间 填充介电常数£ r=2.25的介质,求其特性阻抗及300MHz 时的波长。
解:空气同轴线的特性阻抗为Z o = 601ii- = 601ii —= 65.9Q° a 0.25填充相对介电常数e 1-2.25的介质后,其特性阻抗为戶300Mhz 时的波长J. 3络站=启InM 屆 a V2250.25 = 43・9GA=^X = 0.67m1.4有一特性阻抗Zo=5OQ 的无耗均匀传输线,导体间的媒质参数£r=2.25, m=l,终 端接有R1=1Q 的负载。
当尸100MHz 时,其线长度为X/40试求:① 传输线实际长度; ② 负载终端反射系数: ③ 输入端反射系数: ④ 输入端阻抗。
解:①传输线上的波长为入= # = 2m所以,传输线的实际长度为l-Xs = 0.5m4② 根据终端反射系数与终端阻抗的关系r _Z I -Z o _l-5O_ 49 1_Z 1 + Z 0 _1 + 50__51③ 根据传输线上任一点的反射系数与终端反射系数的关系④ 传输线上任一点的反射系数与输入阻抗的关系1 + 49Z m = Z o 1 + 1 U )- = 50一= 2500Gm °i-ru ) i_49511.10特性阻抗为Zo=150Q 的均匀无耗传输线,终端接有负载Z1=25O+J1OOQ,用X/4 阻抗变换器实现阻抗匹配(如图所示),试求八/4阻抗变换器的特性阻抗Z 。
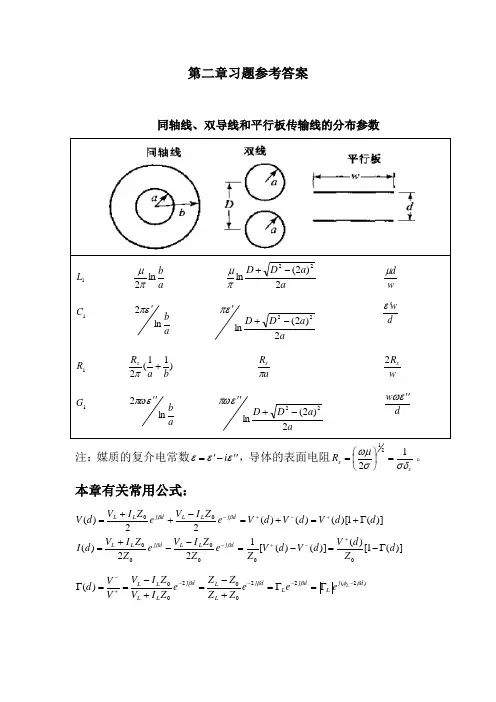
第二章习题参考答案同轴线、双导线和平行板传输线的分布参数注:媒质的复介电常数εεε''-'=i ,导体的表面电阻ss R σδσωμ1221=⎪⎭⎫⎝⎛=。
本章有关常用公式:)](1[)()]()([122)()](1)[()()(22)(00000000d Z d V d V d V Z e Z Z I V e Z Z I V d I d d V d V d V e Z I V e Z I V d V d j L L d j L L dj L L d j L L Γ-=-=--+=Γ+=+=-++=+-+-+-+-ββββ )2(2200200)(d j L d j L dj L L d j L L L L L e e e Z Z Z Z e Z I V Z I V VV d βφβββ----+-Γ=Γ=+-=+-==ΓL Lj L j L L L L L e e Z Z Z Z Z Z Z Z φφΓ=+-=+-=Γ0000dtg jZ Z dtg jZ Z Z d Z L L in ββ++=000)()(1)(1)()()(0d d Z d I d V d Z in Γ-Γ+==LL VV VSWR Γ-Γ+==11minmax2.1无耗或者低耗线的特性阻抗为110C L Z = 平行双导线的特性阻抗:aDa a D D a a D D Z r r rln 11202)2(ln 11202)2(ln 112222000εεεμεπ≈-+=-+=已知平行双导线的直径mm a 22=,间距cm D 10=,周围介质为空气(1=r ε),所以特性阻抗)(6.5521100ln 120ln11200Ω==≈a D Z rε 同轴线的特性阻抗:ab a b Z r rln 60ln 121000εεμεπ==已知同轴线外导体的内直径2mm b 23=,内导体的外直径2mm a 10=,中间填充空气(1=r ε):特性阻抗)(50210223ln 60ln 600Ω===abZ r ε中间填充介质(25.2=r ε):特性阻抗)(3.33210223ln 25.260ln 600Ω===a b Z r ε2.2对于无耗传输线线有相位常数μεωωβ===k C L 11,所以可求出相速度v k C L v p =====μεωβω1111,等于电磁波的传播速度。
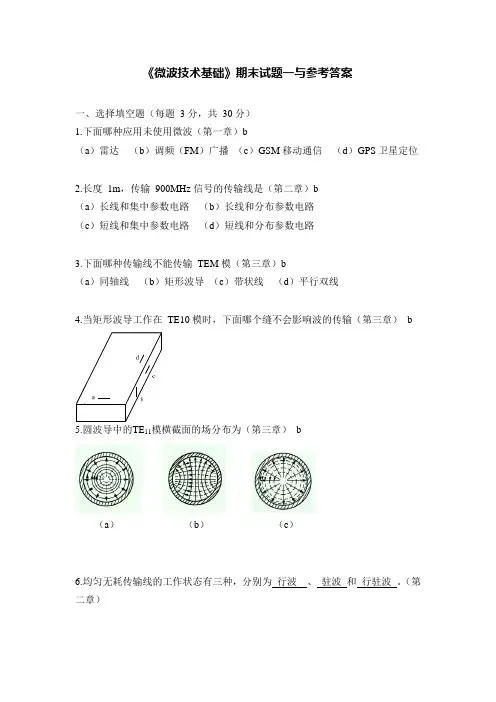
《微波技术基础》期末试题一与参考答案一、选择填空题(每题 3 分,共30 分)1.下面哪种应用未使用微波(第一章)b(a)雷达(b)调频(FM)广播(c)GSM 移动通信(d)GPS 卫星定位2.长度1m,传输900MHz 信号的传输线是(第二章)b(a)长线和集中参数电路(b)长线和分布参数电路(c)短线和集中参数电路(d)短线和分布参数电路3.下面哪种传输线不能传输TEM 模(第三章)b(a)同轴线(b)矩形波导(c)带状线(d)平行双线4.当矩形波导工作在TE10 模时,下面哪个缝不会影响波的传输(第三章)b5.圆波导中的TE11模横截面的场分布为(第三章)b(a)(b)(c)6.均匀无耗传输线的工作状态有三种,分别为行波、驻波和行驻波。
(第二章)Z L 0L 7.耦合微带线中奇模激励的对称面是 电 壁,偶模激励的对称面是 磁 壁。
(第三章)8.表征微波网络的主要工作参量有阻抗参量、 导纳 参量、 传输 参量、散射参量和 转移参量。
9.衰减器有吸收衰减器、 截止衰减器和 极化衰减器三种。
10.微波谐振器基本参量有 谐振波长 、 固有品质因数 和等效电导衰减器三种。
二、传输线理论工作状态(7 分)(第二章)在特性阻抗Z 0=200Ω的传输线上,测得电压驻波比ρ=2,终端为电压波节点,传输线上电压最大值 U max =10V ,求终端反射系数、负载阻抗和负载上消耗的功率。
解: Γ = ρ -1 = 12ρ +1 3由于终端为电压波节点,因此Γ =- 123由Γ =Z L - Z 0= - 12+ Z 3 可得,Z L =100Ω 负载吸收功率为P 2Z 0 ρ三、Smith 圆图(10 分)(第二章)已知传输线特性阻抗Z 0=75Ω,负载阻抗Z L =75+j100Ω,工作频率为 900MHz ,线长l =0.1m ,试用Smith 圆图求距负载最近的电压波腹点与负载的距离和传输线的输入阻抗Z 0Z L解:由工作频率为900 MHz,可得λ=1 m 3而线长为l=0.3λ1.计算归一化负载阻抗ZL=ZLZ= 1+j1.33在阻抗圆图上找到 A 点。
《微波技术基础》题集一、选择题(每题2分,共20分)1.微波是指频率为()的电磁波。
A. 300MHz-300GHzB. 300Hz-300MHzC. 300GHz-300THzD. 300kHz-300MHz2.微波在真空中的传播速度与()相同。
A. 光速B. 声速C. 电场传播速度D. 磁场传播速度3.微波的主要特性不包括()。
A. 直线传播B. 穿透性强C. 反射性D. 绕射能力强4.微波传输线主要包括()。
A. 同轴电缆和光纤B. 双绞线和同轴电缆C. 光纤和波导D. 双绞线和波导5.在微波通信中,常用的天线类型是()。
A. 偶极子天线B. 抛物面天线C. 环形天线D. 螺旋天线6.微波谐振腔的主要作用是()。
A. 储存微波能量B. 放大微波信号C. 转换微波频率D. 衰减微波信号7.微波加热的原理是()。
A. 微波与物体内部的分子振动相互作用B. 微波使物体表面温度升高C. 微波直接转化为热能D. 微波引起物体内部化学反应8.微波在介质中的传播速度与介质的()有关。
A. 密度B. 介电常数C. 磁导率D. 温度9.微波通信中,为了减少信号的衰减,通常采取的措施是()。
A. 增加信号频率B. 减小信号功率C. 使用中继站D. 改用光纤通信10.微波测量中,常用的仪器是()。
A. 示波器B. 微波功率计C. 万用表D. 频谱分析仪(部分功能重叠,但更专用于频率分析)二、填空题(每题2分,共20分)1.微波的频率范围是_________至_________。
2.微波在真空中的传播速度约为_________m/s。
3.微波的_________特性使其在雷达和通信系统中得到广泛应用。
4.微波传输线中,_________具有宽频带、低损耗的特点。
5.微波天线的作用是将微波能量转换为_________或相反。
6.微波加热过程中,物体吸收微波能并将其转化为_________。
7.微波在介质中的衰减主要取决于介质的_________和频率。
微波技术期末试题及答案以下是微波技术的一些期末试题以及对应的答案,供参考。
试题一:什么是微波技术?请简要介绍微波技术的应用领域。
答案一:微波技术是一种利用微波频段(300MHz-300GHz)进行通信、雷达、天文学和其他相关应用的技术。
其应用领域包括但不限于通信领域的无线电波传输、雷达系统、卫星通信、微波炉等。
试题二:请简要解释什么是微波谐振腔回路?答案二:微波谐振腔回路是指在微波电路中的一个闭合回路,由电感、电容和/或其他元件构成。
当该回路的电感和电容的数值合适时,可以使得微波信号在该回路内反射和传输的特性达到最佳的谐振状态。
试题三:简述微波网络分析器的原理及其主要应用。
答案三:微波网络分析器是一种用于测量微波电路的参数和性能的仪器。
其原理是将测试信号送入待测电路并测量其在不同频率和功率下的传输和反射特性,从而获取电路的参数和性能指标。
主要应用包括电路设计、信号分析、无线通信系统测试等。
试题四:解释微波导的概念和特点。
答案四:微波导是一种专门传输和导引微波信号的传输线路,具有一定的截止频率和传输特性。
其特点包括低传播损耗、高载波容量、较小的尺寸、较高的频率响应等。
试题五:简要解释集成电路在微波技术中的应用。
答案五:集成电路在微波技术中的应用主要是利用微波集成电路的高度集成性和小尺寸优势,实现微波频段上的信号处理和通信功能。
常见的应用领域包括通信系统中的低噪声放大器、混频器、振荡器等。
试题六:什么是微波功率管?请简要描述其原理和应用。
答案六:微波功率管是一种用于放大微波信号并提供较大功率输出的高频电子器件。
其原理是通过电子束与电磁场的相互作用来实现信号放大。
主要应用于雷达、通信系统等需要较高功率输出的场合。
试题七:简述微波天线的作用及其常见类型。
答案七:微波天线用于接收和发射微波信号,在微波通信和雷达系统中起到关键的作用。
常见的微波天线类型包括方向性天线、宽角度天线、偶极子天线等,用于满足不同的应用需求。
1、1,2,5,6解题2.1、解:①工作波长由工作频率唯一决定,εμωππλ22==k②k 分为纵向分量β和横向分量c k ,临界状态下,0=β,此时,k 全部分配给c k ,相应的波长即截止波长:εμπλc cc f k 12==它由横截面尺寸、波型决定③在传输状态下,0>>βk ,纵向传输时每π2相位变化时,对应的长度即波导波长:()()221122c c g k k k λλλπβπλ-=-==对于给定尺寸的波导,传输一定波型时,其c k 就定下来了,相应的截止波长被决定了, 工作波长如果大于它,k 不够分配给c k ,导致纵向β为虚数,纵向衰减; 工作波长=截止波长时,仅横向谐振;工作波长<截止波长时,提供分量β供纵向传输,分量β<k 导致波导的相波长>工作波长。
简而言之,三种波长分别对应 其波数k 、横向波数c k 、及纵向波数β。
它们通过222β+=ck k2.2、解:已知:()z t j x ey b A x E xE βωπ-⎪⎭⎫ ⎝⎛==sin ˆˆ,TE 波 ()()()()⎪⎪⎩⎪⎪⎨⎧⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛⨯⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=⨯∇=----z t j z t j z t j z t j e y b A y e y b b jA z e y b j y y b b z jA e y b A x z z y y j E jH βωβωβωβωπωμβππωμπβππωμπωμωμsin ˆcos ˆsin ˆcos ˆsin ˆˆˆ 其中 222222⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛-=-=b c b k kk cπωπβ c 是光速。
2.5、解: (1)mm b n a m c 60222=>⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=λλ30122<⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛b n a m 900104.3414.7222<⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛n m 上式如右图所示,所以可传输的波型有:TE 10,TE 20,TE 11,TM 11,和TE 01。