可靠性加速试验阿氏模型讲解

阿氏模型的原理及应用引言阿氏模型（Austin模型）是一种常用的流体物理模型，用于描述流体内部的微观结构和宏观性质。

本文将介绍阿氏模型的原理和应用，通过列举实例，解释其在不同领域的应用。

原理阿氏模型基于高分子溶液中的输运过程和聚合物网络结构来描述流体的性质。

该模型主要基于以下几个原理：1.聚合物网络结构：阿氏模型假设流体中存在一个立体网络结构，由聚合物链形成。

聚合物链之间的交联点决定了流体的黏性、弹性等性质。

2.聚合物链的输运：阿氏模型考虑了聚合物链在流体中的输运过程。

通过考虑聚合物的扩散、转动和运动等行为，模型可以描述聚合物在流体中的运动性质。

3.动态平衡：阿氏模型假设流体中的聚合物链处于动态平衡状态，即聚合物链的运动速率与聚合物链的重排速率相等。

应用阿氏模型在流体力学、生物学、材料科学等领域有着广泛的应用。

下面列举了一些具体的应用案例：1. 生物学中的应用•红细胞变形：阿氏模型被用来描述红细胞在血液流动中的变形行为。

通过模拟红细胞的弹性和粘性特性，可以研究血流动力学和相关疾病。

•细胞骨架：阿氏模型可以用来描述细胞内骨架网状结构的弹性和形变特性。

这对于研究细胞的力学特性和细胞迁移等生物学过程具有重要意义。

2. 材料科学中的应用•纳米材料：阿氏模型可以用来描述纳米颗粒间的相互作用和流体力学行为。

这对于研究纳米材料的力学性质和流变行为具有重要意义。

•液晶材料：阿氏模型可以用来描述液晶材料的分子结构和相互作用。

通过模拟分子中各向异性和远程相互作用，可以提高液晶材料的性能。

3. 化学工程中的应用•聚合物溶液：阿氏模型可以用来描述聚合物在溶液中的输运行为和流变性质。

这对于优化聚合物合成和溶液处理过程具有重要意义。

•复合材料：阿氏模型可以用来描述复合材料的微观结构和力学性质。

通过仿真不同填料颗粒和基质材料之间的相互作用，可以提高复合材料的强度和韧性。

结论阿氏模型是一种描述流体的物理模型，基于聚合物网络结构和输运过程。

产品可靠性试验6.2.1 可靠性试验的意义与分类可靠性试验是为分析、评价、提高或保证产品的可靠性水平而进行的试验。

产品的研制者通过试验获得产品设计、鉴定所需的可靠性数据（可靠性测定试验）。

通过试验暴露产品缺陷，改进设计并获得可靠性增长信息（可靠性增长试验）。

产品的制造者通过试验剔除零件批中的不合格品或暴露整机缺陷，消除早期故障（可靠性筛选或老化试验老化试验不是消除早期故障的）产品使用者通过试验验证产品批可靠性水平以保证接收的产品批达到规定要求（可靠性接收试验）。

政府或行业管理部门通过试验获得数据库所需基础可靠性数据（可靠性测定试验），认证产品可靠性等级（可靠性验证试验），进行产品的可靠性鉴定与考核（可靠性鉴定试验）。

本节主要介绍可靠性测定试验，这是为获得产品可靠性特征量的估计值而进行的试验，根据需要可由试验结果给出可靠性特征量的点估计值和给定置信度下的区间估计。

由于可靠性试验往往是旷日持久的试验，为节省时间与费用常采用加速试验的方式。

本节将介绍某些加速寿命试验的理论模型与试验方法。

6.2.2 指数分布可靠性测定试验大多数电子元器件、复杂机器及系统的寿命都服从指数分布。

其待估参数为故障率λ，其他可靠性指标可利用估计值进行计算MTBF 已经有平均的意思了1．定时截尾试验（1）点估计试验进行至事先规定的截尾时间t c停止试验，设参与试验的n个样本中有r个发生关联故障，则由极大似然估计理论得出的故障率点估计值为式中t i——第I个关联故障发生前工作时间（i=1，…，r）。

若在试验过程中及时将已故障产品修复或替换为新产品继续试验，则为有替换的定时截尾试验。

此时λ的点估计为（2）区间估计对于无替换和有替换的定时截尾试验，其给定置信度为1－α的双侧置信区间为[λL，λU]，则式中——自由度为υ的分布的概率为的下侧分位点；T——总试验时间（3）零故障数据的区间估计当定时截尾试验在（0，t c）内的故障数r=0时，可由式（4）给出。

透过MTBF，去发现其背后的故事！奉旨出征Reliability Testing作为Solid State Drive（简称固态硬盘）SIT测试阶段最重要的测试项，推动着产品质量的不断提升。

UBER、Endurance、Retention、Temperature Extreme、MTBF 等可靠性指标值也作为产品竞争力的一部分体现在产品规格书中。

马克思先生指导我们：“See through the appearance to perceive the essence”，这期让我们透过MTBF，去发现其背后的故事！战前准备古人有云：兵马未动，粮草先行；宜未雨而绸缪，毋临渴而掘井；足不强则迹不远，锋不铦则割不深！不错，总结就是：开战前，我们先把几个基本概念理清楚（敲黑板，划红线）！Failure Rate：failure Rateλ，λ定义为失效个数r与n测试样品在指定测试条件下运行t 时间的比值，即λ= r / n*t 。

针对电子产品，通常我们用FIT（Failure In Time）体现，如1 FIT 代表运行10 小时，出现1个失效设备。

例子：4000个测试设备，同时持续运，指新的产品在规定的工作环境条件下开始工作到出现第一个故障的时间的平均值。

MTBF越长表示可靠性越高，保持正确工作能力越强，单位为“小时”。

通常也指相邻两次故障之间的平均工作时间，也称为平均故障间隔。

它仅适用于可维修产品（不可维修产品我们用MTTF定义）。

当产品的寿命服从指数分布时，失效率的倒数表示两个失效之间的时间间隔。

λ=1/MTBF例子：某产品SSD MTBF值标称为150万小时，保修5年；150万小时约为171年，并不是说该产品SSD每块盘均能工作171年不出故障。

由MTBF=1/λ可知λ=1/MTBF=1/171年，即该固态硬盘的平均年故障率约为0.6%，一年内，平均1000块固态硬盘有6块会出故障。

综上所述，FIT/MTBF值是产品设计时要考虑的重要参数，测试工程师经常使用各种不同的方法与标准来估计产品的MTBF值，其目的就是为了找出产品设计中的薄弱环节。

可靠性试验中三大加速模型的研究与应用摘要：本文从国内外可靠性领域中常用的加速模型出发,从宏观的角度说明了阿伦尼斯Arrhenius,科芬-曼森Coffin-Manson和劳森Lawson这三大加速模型的应用范围,然后重点采用实例的方式介绍了这几大模型在汽车领域的可靠性试验中的应用。

关键词：可靠性；加速模型；阿伦尼斯Arrhenius；科芬-曼森Coffin-Manson；劳森Lawson高温寿命试验，湿度试验以及温度循环试验是几个最基本的可靠性环境试验，用于评估产品的各种可靠性特征。

但对寿命特别长的产品来说不太合适。

因为它需要花费很长的试验时间，甚至来不及作完相关试验，新的产品又设计出来，老产品就要被淘汰了。

因此，了解怎样对这些方法进行适当的加速可以大大缩短试验周期，提高试验效率，降低试验耗损。

本文就是以汽车仪表为例来详细说明这些加速模型。

一、阿伦尼斯模型Arrhenius Mode1.适用范围阿伦尼斯模型是适用于高温耐久试验的加速模型。

通常汽车主机厂先给出他们对产品的质量要求，或称为产品生命周期的要求，比如大众，对此要求是15年，按照平均一天1.5h 的用车时间，则总的生命周期转换为小时数的要求则为8212.5（15(年)*365（天）*1.5（h））小时。

此外主机厂的研究部会测出汽车内各零部件在整个生命周期内的温度谱图，用来描述产品遭受到的主要温度点，以及各自所占的比例。

2.应用实例以大众汽车为例，下图就是针对汽车仪表的温度谱图，并要求我们据此做一个高温耐久的试验。

如果按照非加速的方法则意味着总的时间为8212.5个小时，将近一年的时间，所以我们必须采用阿伦尼斯加速模型进行换算。

这里我先附上阿伦尼斯模型的计算公式并对其中各因子做一个简单说明：其中：A T,i: 就是我们要算出来的每个温度点下的加速因子，比如i为1，则根据谱图第一行来算出该条件下的加速因子，具体的含义就是比如说A T,1算出来为5000,则意味着如果想代替在-40°C 下工作的占6%比例的这段寿命时间，则等价的试验就是在T prüf下工作8212.5 / 5000个小时。

阿伦尼斯(Arrhenius)模型加速寿命试验的基本思想是利用高应力下的寿命特征去外推正常应力水平下的寿命特征。

实现这个基本思想的关键在于建立寿命特征与应力水平之间的关系，即加速模型。

阿伦尼斯(Arrhenius)模型是最典型、应用最广的加速模型，其表达式为式中，M为产品某特性值的退化量；δM/δt表示温度在T(热力学温度)时的退化速率，退化速率是时间t的线性函数；玻耳兹曼常数k=8.617×10-5eV/℃；T 为绝对温度；A0为常数；t为反应时间；ΔE为失效机理激活能，以eV为单位，对同一类产品的同一种失效模式为常数。

令产品初始状态的退化量为M1，对应时间为t1；另一状态的退化量为M2，对应时间为t2。

那么，当温度T为常数时，从t1~t2的累积退化量得令t=t2-t1，得t=[(m2-m1)/A0]exp(ΔE/kT)。

当退化量M2达到某个值Mp时，则认为该器件失效，而影响到由产品构成设备的性能参数或工作。

这时的时间差(t2-t1)就是产品从t1开始延续的寿命L。

即令A=ln[(Mp-M1)/A0]，B=ΔE/k，得lnL=A+(B/T)。

式中，A，B是待定参数；L为某寿命特征，如中位寿命，平均寿命等。

lnL=A+(B/T)是线性化的寿命与温度的关系模型，它符合化学反应器件的寿命L与温度T的关系。

该模型表明，寿命特征的对数是温度倒数的线性函数。

当在不同温度T1，T2下，经过时间t1，t2后特性值或退化量相同，可利用(1)式推出加速系数即加速因子公式上式是基于退化量相同导出的。

目前，国内外比较成熟的加速寿命试验数据处理方法都是基于失效数据的。

对于长寿命产品，在很长的时间内极少出现失效现象，因此传统的基于失效数据的试验数据处理方法在应用时会遇到很多困难。

阿伦尼斯模型有下述特点：(1)该模型反映的是产品某特性量与激活能和所施加应力的关系；(2)阿伦尼斯模型使用的寿命与温度的表达形式及加速因子都是基于退化量相同导出的。

阿伦尼斯(Arrhenius)模型林 震加速寿命试验的基本思想是利用高应力下的寿命特征去外推正常应力水平下的寿命特征。

实现这个基本思想的关键在于建立寿命特征与应力水平之间的关系，即加速模型。

阿伦尼斯(Arrhenius)模型是最典型、应用最广的加速模型，其表达式为)Δexp(0kT E A t M -=∂∂ (1)式中，M 为产品某特性值的退化量；∂M /∂t 表示温度在T (热力学温度)时的退化速率，退化速率是时间t 的线性函数；玻耳兹曼常数k =8.617×10-5 eV/℃；T 为绝对温度；A 0为常数；t 为反应时间；ΔE 为失效机理激活能，以eV 为单位，对同一类产品的同一种失效模式为常数。

令产品初始状态的退化量为M 1，对应时间为t 1；另一状态的退化量为M 2，对应时间为t 2。

那么，当温度T 为常数时，从t 1~t 2的累积退化量t kT E A m M M t t t t d )Δexp(d 2121021⎰⎰==-得()12021)Δexp(t t kT E A M M --=-令t =t 2-t 1，得t =[(m 2-m 1)/A 0]exp(∆E /kT )。

当退化量M 2达到某个值M p 时，则认为该器件失效，而影响到由产品构成设备的性能参数或工作。

这时的时间差(t 2-t 1)就是产品从t 1开始延续的寿命L 。

即kT E A M M L p ∆+-=01ln ln令A =ln[(M p -M 1)/A 0]，B =∆E /k ，得ln L =A +(B/T )。

式中，A ，B 是待定参数；L 为某寿命特征，如中位寿命，平均寿命等。

ln L =A +(B/T )是线性化的寿命与温度的关系模型，它符合化学反应器件的寿命L 与温度T 的关系。

该模型表明，寿命特征的对数是温度倒数的线性函数。

当在不同温度T 1，T 2下，经过时间t 1，t 2后特性值或退化量相同，可利用(1)式推出加速系数公式)]11(Δexp[1211kT kT E t t --==τ上式是基于退化量相同导出的。

产品可靠性试验6.2.1 可靠性试验的意义与分类可靠性试验是为分析、评价、提高或保证产品的可靠性水平而进行的试验。

产品的研制者通过试验获得产品设计、鉴定所需的可靠性数据（可靠性测定试验）。

通过试验暴露产品缺陷，改进设计并获得可靠性增长信息（可靠性增长试验）。

产品的制造者通过试验剔除零件批中的不合格品或暴露整机缺陷，消除早期故障（可靠性筛选或老化试验老化试验不是消除早期故障的）产品使用者通过试验验证产品批可靠性水平以保证接收的产品批达到规定要求（可靠性接收试验）。

政府或行业管理部门通过试验获得数据库所需基础可靠性数据（可靠性测定试验），认证产品可靠性等级（可靠性验证试验），进行产品的可靠性鉴定与考核（可靠性鉴定试验）。

本节主要介绍可靠性测定试验，这是为获得产品可靠性特征量的估计值而进行的试验，根据需要可由试验结果给出可靠性特征量的点估计值和给定置信度下的区间估计。

由于可靠性试验往往是旷日持久的试验，为节省时间与费用常采用加速试验的方式。

本节将介绍某些加速寿命试验的理论模型与试验方法。

6.2.2 指数分布可靠性测定试验大多数电子元器件、复杂机器及系统的寿命都服从指数分布。

其待估参数为故障率λ，其他可靠性指标可利用估计值进行计算MTBF已经有平均的意思了1．定时截尾试验（1）点估计试验进行至事先规定的截尾时间t c停止试验，设参与试验的n个样本中有r个发生关联故障，则由极大似然估计理论得出的故障率点估计值为式中t i——第I个关联故障发生前工作时间（i=1，…，r）。

若在试验过程中及时将已故障产品修复或替换为新产品继续试验，则为有替换的定时截尾试验。

此时λ的点估计为12（2）区间估计 对于无替换和有替换的定时截尾试验，其给定置信度为1－α的双侧置信区间为[λL ，λU ]，则式中——自由度为υ的分布的概率为的下侧分位点；T ——总试验时间（3）零故障数据的区间估计 当定时截尾试验在（0，t c ）内的故障数r=0时，可由式（4）给出。

Arrhenius阿氏加速壽命計算
正常使用的溫度(℃)正常使用的濕度(RH)
4395
加速試驗溫度(℃)1加速試驗濕度(RH)1試驗時間(h)
8585168 Ea活化能(eV)1
加速因數AF=52.89 4.301979984實際使用時間(h)tu= tt*AF =8886.3小時
實際使用時間(年)=1年
實際使用時間(月)=0.2月
加速試驗溫度(℃)2加速試驗濕度(RH)2加速試驗溫度('K)
11085383試驗2加速因數AF=437.49 6.414726588試驗2所需試驗時間(h)=20.3小時
Ea:
ev=0.3，多層陶瓷電容器1.15~1.20eV，無刷直流風扇1.7eV，車燈用
LED0.84eV
R:波爾茲曼常數(8.63*10-5eV/K)
RHu:器件正常使用時的相對濕度(%)
RHt:器件在加速實驗過程的相對濕度(%)
Tu:器件正常使用時的溫度 (0K)
Tt:器件在加速實驗過程的溫度(0K)
正常使用的溫度('K)316
加速試驗溫度('K)358 ('K)。

产品可靠性加速试验的加速试验有关标准加速试验有关标准阿伦尼斯模型是化学家阿列尼乌斯于1880年在大量的化学反应数据基础上总结出来的，它表明在化学反应过程中反应速率与反应温度的关系kT E a Ae dtdM /-=——化学反应速率 ——常数 ——引起失效或退化过程的激活能 ——玻尔兹曼常数——热力学温度dtdMAaE k T令t=t 1-t 0阿伦尼斯斯模型的变换dtAe dM Ae dt dM kTE kT E a a //--=⇒=⎰⎰-=110/t t kT E M M dt Ae dM a 当器件在t 0时刻处于正常状态数M 0，t 1时刻处于失效状态数为M 1，如果温度与时间无关，则积分上式得：)(01/01t t Ae M M kT E a -=--kTE a e A M M t /01-=Tb a T e k E A M M t a //)lg /(lg lg 01+=+-=寿命与温度关系—阿列尼乌斯模型激活能与温度、寿命的关系T b a T e k E AM M t a //)lg /(lg lg 01+=+-=激活能越大、曲线倾斜越大、与温度的关系越密切！！加速系数加速系数的计算方法：]1exp[)()(101100T T k E F t F t a -==τ设在基准应力条件下做试验达到累积失效概率F 0所需要的时间为t 0（F 0），施加某种应力条件下进行加速寿命试验达到相同的累积失效概率所需的时间为t 1（F 0），则两者的比值即为加速系数。

激活能越大、加速系数越大、越容易被加速失效，加速试验效果越明显。

激活能与加速系数的关系]1exp[)()(101100T T k E F t F t a -==τ阿列尼乌斯模型的局限：只考虑了温度应力对物质的化学与物理性质变化的影响。

实际上，很多的物理理象和化学反应过程，除了与温度有关之外，还与此时很多非温度应力因素如电压、湿度、机械应力等密切相关。

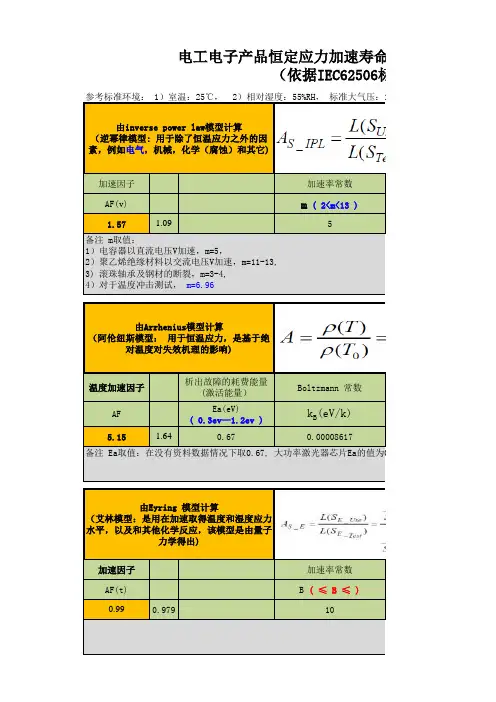
可靠性加速试验阿氏模型讲解阿氏模型讲解3.1 阿氏模型反应方程式DMTBF测试均采用阿氏模型进行计算,其反应方程式为:R 为反应速度其中A 为温度常数EA 为活化能(eV)K 为Boltzmann常数,等于8.623*10-5 eV/K.T 为绝对温度(Kelvin)3.2 阿氏模型中的加速因子加速因子AF即为产品在使用条件下的寿命和高测试应力条件下的寿命的比值.在阿氏模型中:其中:Vu为使用条件下的绝对温度Va为加速条件下的绝对温度B=EA/K由上式可得,温度加速因子为:A=Exp((Ea/K)(1/Tspec-1/Telev)) Ftemp3.3 加速因子中活化能Ea活化能是分子与化学或物理作用中需具备的能量,单位是电子伏特Ev. 当试验的温度与使用温度差距范围不大时,则Ea可设为常数.Ea= K* (Inλa –Inλ)/(1/Tn-1/Ta) n其中,Tn,Ta均为绝对温度0Kλa为加速温度时的失效率λn为正常温度时的失效率(λa和λn可以以试验的方式的得出,但需要较长的试验时间.而且新机种的失效率很难在短时间内得出.)3.4 活化能Ea的取值一般电子产品在早夭期失效之Ea为0.2~0.6eV,正常有用期失效之Ea趋近于1.0eV;衰老期失效之Ea大于1.0eV.新机种的Ea无法计算，一般为0.67eV.3.5 参数估计为了解产品可靠度水准,须先对其失效时间分布做某种程度的推定.通常有参数点估计及参数信赖区间估计推定3.5.1参数点估计点估计,是寻求一个统计量,作为参数的估计,它是一随机变量,其好坏只能以其期望值及变异数来衡量(当然最好的结果是其期望值要等于母体参数,即不偏性,且其变异数愈小愈好).平均值的点估计量(Estimator)为样本数之平均值: μ即称为点估计值(Estimate).不管f(x)属于不偏性还是可偏性,只要n(>=30)足够大,则的μ分布将呈常态分布(如图3.1所示)。

可靠性试验中三大加速模型的研究与应用摘要：本文从国内外可靠性领域中常用的加速模型出发,从宏观的角度说明了阿伦尼斯Arrhenius,科芬-曼森Coffin-Manson和劳森Lawson这三大加速模型的应用范围,然后重点采用实例的方式介绍了这几大模型在汽车领域的可靠性试验中的应用。

关键词：可靠性；加速模型；阿伦尼斯Arrhenius；科芬-曼森Coffin-Manson；劳森Lawson高温寿命试验，湿度试验以及温度循环试验是几个最基本的可靠性环境试验，用于评估产品的各种可靠性特征。

但对寿命特别长的产品来说不太合适。

因为它需要花费很长的试验时间，甚至来不及作完相关试验，新的产品又设计出来，老产品就要被淘汰了。

因此，了解怎样对这些方法进行适当的加速可以大大缩短试验周期，提高试验效率，降低试验耗损。

本文就是以汽车仪表为例来详细说明这些加速模型。

一、阿伦尼斯模型Arrhenius Mode1.适用范围阿伦尼斯模型是适用于高温耐久试验的加速模型。

通常汽车主机厂先给出他们对产品的质量要求，或称为产品生命周期的要求，比如大众，对此要求是15年，按照平均一天1.5h 的用车时间，则总的生命周期转换为小时数的要求则为8212.5（15(年)*365（天）*1.5（h））小时。

此外主机厂的研究部会测出汽车内各零部件在整个生命周期内的温度谱图，用来描述产品遭受到的主要温度点，以及各自所占的比例。

2.应用实例以大众汽车为例，下图就是针对汽车仪表的温度谱图，并要求我们据此做一个高温耐久的试验。

如果按照非加速的方法则意味着总的时间为8212.5个小时，将近一年的时间，所以我们必须采用阿伦尼斯加速模型进行换算。

这里我先附上阿伦尼斯模型的计算公式并对其中各因子做一个简单说明：其中：A T,i: 就是我们要算出来的每个温度点下的加速因子，比如i为1，则根据谱图第一行来算出该条件下的加速因子，具体的含义就是比如说A T,1算出来为5000,则意味着如果想代替在-40°C 下工作的占6%比例的这段寿命时间，则等价的试验就是在T prüf下工作8212.5 / 5000个小时。

电子元器件加速寿命试验方法的比较介绍1 引言加速寿命试验分为恒定应力、步进应力和序进应力加速寿命试验。

将一定数量的样品分成几组，对每组施加一个高于额定值的固定不变的应力，在达到规定失效数或规定失效时间后停止，称为恒定应力加速寿命试验（以下简称恒加试验）；应力随时间分段增强的试验称步进应力加速寿命试验（以下简称步加试验）；应力随时间连续增强的试验称为序进应力加速寿命试验（以下简称序加试验）。

序加试验可以看作步进应力的阶梯取很小的极限情况。

加速寿命试验常用的模型有阿伦尼斯（Arrhenius）模型、爱伦（Eyring）模型以及以电应力为加速变量的加速模型。

实际中Arrhenius模型应用最为广泛，本文主要介绍基于这种模型的试验。

Arrhenius模型反映电子元器件的寿命与温度之间的关系，这种关系本质上为化学变化的过程。

方程表达式为式中：为化学反应速率；E为激活能量（eV）； k为波尔兹曼常数0.8617×10-4 eV/K；A为常数；T为绝对温度（K）。

式⑴可化为式中：式中：F0为累计失效概率； t(F0)为产品达到某一累计失效概率 F(t)所用的时间。

算出b后，则式⑵是以Arrhenius方程为基础的反映器件寿命与绝对温度T之间的关系式，是以温度T为加速变量的加速方程，它是元器件可靠性预测的基础。

2 试验方法2.1 恒定应力加速寿命试验目前应用最广的加速寿命试验是恒加试验。

恒定应力加速度寿命试验方法已被IEC标准采用[1] 。

其中3.10加速试验程序包括对样品周期测试的要求、热加速电耐久性测试的试验程序等，可操作性较强。

恒加方法造成的失效因素较为单一，准确度较高。

国外已经对不同材料的异质结双极晶体管（HBT）、CRT 阴极射线管、赝式高电子迁移率晶体管开关（PHEMT switch）、多层陶瓷芯片电容等电子元器件做了相关研究。

和InP PHEMT单片微波集成电路（MMIC）放大器进行了恒加试验 [2]。

accerlerate failture model结果解读
Accelerate Failure Model (加速失效模型) 是一种统计模型，用于描述在加速应力
或应变速率下材料的失效行为。

这种模型通常用于预测在非正常工作条件下，例如高温度、高压力或高辐射等极端环境下的产品或材料的寿命。

结果解读可能包括以下内容：
1.参数估计：模型中可能会估计某些参数，例如失效时间、加速因子等。

这
些参数提供了对产品或材料性能的定量描述。

2.拟合度检验：为了验证模型的适用性，可能会进行拟合度检验。

这可以通
过比较理论预测与实际观测数据来完成。

3.预测：基于所估计的参数和给定的加速条件，模型可以预测产品或材料在
正常工作条件下的寿命。

4.可靠性分析：加速失效模型的结果也可以用于可靠性分析。

这涉及到估计
产品在给定置信水平下能够正常工作的概率。

5.优化：如果已知加速因子和材料性能之间的关系，可以通过调整加速条件
来优化产品的寿命或性能。

6.不确定性分析：模型的不确定性可能来源于多个方面，例如数据的不确定
性、模型参数的不确定性等。

结果解读应包括对这些不确定性的评估。

7.建议和改进：基于分析结果，可以提出针对产品或材料的改进建议，以增
强其可靠性和寿命。

总之，解读加速失效模型的结果需要综合考虑多个方面，包括模型的参数估计、拟合度、预测能力、可靠性分析、优化建议以及不确定性评估等。

这些信息有助于更好地理解产品或材料的性能，并为其在实际应用中的表现提供指导。