最大时间间隔误差计算方法及其分析

实验名称：时间测量中随机误差的分布规律实验目的：用常规仪器（如电子秒表，频率计等）测量时间间隔，通过对时间和频率测量的随机误差分布，学习用统计方法研究物理现象的过程和研究随机误差的分布规律。

实验器材及规格：秒表0.01s实验原理：1常用时间测量仪器的简要原理：机械节拍器：由齿轮带动摆做周期性运动，摆动周期可以通过改变摆锤的位置来连续调节。

电子节拍器：由石英晶体震荡器，计数器，译码器，电源，分档控制及显示部分组成。

按一定频率发出有规律的声音和闪光。

电子秒表：机心由CMOS集成电路组成，石英晶体震荡器做时标，一般用6位液晶数字显示。

连续累积时间59min,59.99s,分辨频率为0.01s。

V AFN多用数字测试仪：由PMOS集成元件和100kHs石英晶体震荡器构成。

可测量记数，震动，累计，速度，加速度，碰撞，频率，转速，角速，脉宽等。

时标由DC10集成电路和100kHs石英晶体震荡器构成。

2在不考虑系统误差的前提下，用时间测量仪器，测量同一时间N次，统计时间分布规律，并且分析误差。

当N趋于无穷时，各测量值出现的概率密度可用正态分布的概率密度函数表示：221()/21()niiX Xf x eσ=⎡⎤--⎢⎥⎢⎥⎣⎦∑=平均值计算公式：1/niiX X n==∑标准差计算公式：Xσ=（1）统计直方图方法在一组等精度测量的N个结果中，找出最大最小值，再有此得到极差max minR X X=-。

将极差分为K 个部分。

每个区间长度x ∆MAX MINX X R x K K-∆==将落在每个区间的次数称为频数，i n N 称为频率。

最后以X 为横轴i nN为纵轴做图。

（2）密度分布曲线利用直方图中得到的概率密度值，以概率密度值为纵坐标，x 为横坐标可的密度分布曲线，数据处理:最小值min 2.84X s=最大值max 3.64X s=平均值 3.23X s=标准差0.15sσ=A 类不确定度0.01s Ua σ==因为人反应时间约为0.2s,秒表仪器误差约为0.01s,所以取 B 类不确定度 0.20Ub s =误差合成0.25s ∆== P ≥0.95 测量结果为(3.230.25)T s =± 置信概率 0.95P ≥图表统计如下:取区间数K=17，区间长0.05s 。

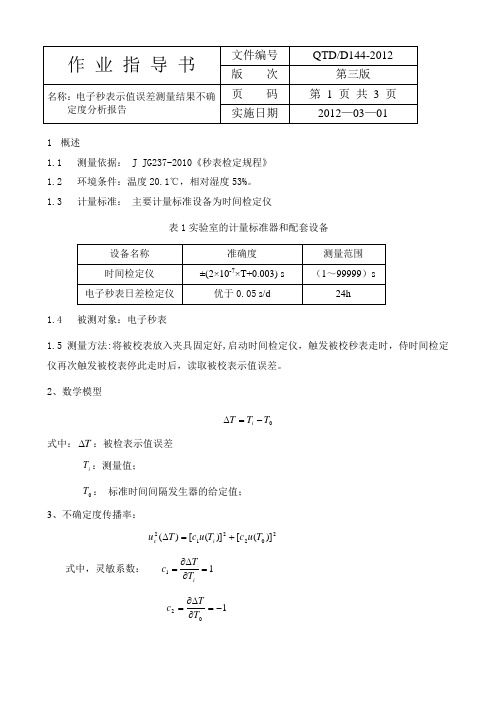
1 概述1.1 测量依据： J JG237-2010《秒表检定规程》 1.2 环境条件：温度20.1℃，相对湿度53%。

1.3 计量标准： 主要计量标准设备为时间检定仪表1实验室的计量标准器和配套设备1.4 被测对象：电子秒表1.5 测量方法:将被校表放入夹具固定好,启动时间检定仪，触发被校秒表走时，侍时间检定仪再次触发被校表停此走时后，读取被校表示值误差。

2、数学模型0T T T i -=∆式中：T ∆：被检表示值误差 i T ：测量值；0T ： 标准时间间隔发生器的给定值；3、不确定度传播率：202212)]([)]([)(T u c T u c T u i c +=∆式中，灵敏系数： 11=∂∆∂=iT Tc 102-=∂∆∂=T Tc4 输入量标准不确定度分析：4.1 被校秒表测量时间间隔重复性引入的标准不确定度)(i T u ，用A 类不确定度评定以校准一跳动量为0.01s 的电子秒表的3600s 为例，将被校秒表与时间检定仪连接好后，重复性测量10次，得到系列测量值3600.01、3600.01、3600.01、3600.01、3600.01、3600.01、3600.01、3600.01、3600.01、3600.02。

i T =3600.011 s ，单次实验标准差)(i T s =0.0032s 。

在实际检定中，只取一次测量值(其中误差最大的)作为测量结果，故标准不确定度：)(i T u =)(i T s =0.0032 s4.2 时间检定仪引入的标准不确定度分量)(0T u ，用B 类标准不确定度评定。

时间检定仪送一级计量检定合格，按使用说明书得知时间检定仪检定秒表准确度为±(2×10-7×T+0.003) s ，在输出时段为3600s 时，走时误差为均匀分布， 3=k ，)(0T u =0.00215 合成标准不确定度 5.1 标准不确定度汇总表5.2合成标准不确定度计算以上各项标准不确定度分量彼此独立不相关，所以合成不确定度为。

最全面的实验室误差分析，一篇文章帮您搞懂实验室误差！问题：怎样才能每天都收到这种文章呢？？答案：只需要点击图片上边蓝字药源网制药在线即可！误差理论简介在日常检测工作中，我们虽然有最好的检验方法、有检定合格的仪器设备、有满足检验要求的环境条件和熟悉检验工作的操作人员，但是，得到的检验结果却往往不可能是绝对准确的，即使是同一检测人员对同一检测样品、对同一项目的检测，其结果也不会完全一样，总会产生这样或那样的差别，也就是说，任何物理量的测定，都不可能是绝对准确的，在测得值与真实值之间总是或多或少的存在着差别，这就是误差。

误差是客观存在的，用它可以衡量检测结果的准确度，误差越小，检测结果的准确度越高。

一、术语和定义1.准确度准确度指，检测结果与真实值之间相符合的程度。

(检测结果与真实值之间差别越小，则分析检验结果的准确度越高)。

2.精密度精密度指，在重复检测中，各次检测结果之间彼此的符合程度。

(各次检测结果之间越接近，则说明分析检测结果的精密度越高)3.重复性重复性指，在相同测量条件下，对同一被测量进行连续、多次测量所得结果之间的一致性。

重复性条件包括：相同的测量程序、相同的测量者、相同的条件下，使用相同的测量仪器设备，在短时间内进行的重复性测量。

4.再现性(复现性)在改变测量条件下，同一被测量的测定结果之间的一致性。

改变条件包括：测量原理、测量方法、测量人、参考测量标准、测量地点、测量条件以及测量时间等。

如：实验室资质认定现场操作考核的方法之一：样品复测即是样品再现性(复现性)的一种考核、样品复测包括对盲样(即标准样品)的检测，也可以是对检验过的样品、在有效期内的再检测。

或是原检测人员或是重新再安排检测人员。

※ 通常再现性或复现性好，意味着精密度高。

精密度是保证准确度的先决条件，没有良好的精密度就不可能有高的的准确度，但精密度高准确度不一定高;反之，准确度高，精密度必然好。

二、误差的种类、来源和消除根据误差的来源和性质，误差可以分为以下几种：1.系统误差(又称规律误差)1.1系统误差的定义系统误差是指，在偏离检测条件下，按某个规律变化的误差。

秒表示值误差测量不确定度的评定1 概述1.1 测量方法：参照JJG237-95《指针式时间间隔测量仪(试行)检定规程》1.2 环境条件：温度（20±5）℃相对湿度≤80%1.3 测量标准：SJY-5型时间检定仪测量秒表时最大允许误差为±（1×10-7×输出时段+2ms）1.4被测对象：各型号的秒表，最大走时差60s，最大允许误差为±0.4s1.5 测量方法：采用标准装置输出标准时间，启动秒表计时，结束时秒表停计，读出秒表记录时间，计算出误差。

2 数学模型δ=A－As式中：A——秒表指示值As——标准装置的标准时间δ——被测秒表的示值误差3 输入量的标准不确定度评定3.1输入量A的标准不确定度u（A）的评定输入量A的不确定度主要来源于被测秒表的测量不重复性，可通过连续测量得到测量列，采用A类方法进行评定。

对一只504型的秒表，选择30秒时间连续测量10次，得到测量列：30.2、30.1、30.1、30.0、29.9、30.2、30.1、30.2、30.1、29.9s，计算的：平均值：单次测量标准差：故，u(A)=s=0.11s3.2输入量As的标准不确定度u(As) 的评定输入量As的不确定度主要来源于秒表检定仪的偏差，可根据出厂说明书的允许误差来评定，采用B类方法进行评定。

出厂说明书给出测量秒表时的最大允许误差为±（1×10-7×输出时段+2ms），当输出时段为30s时，最大允许误差为±2.003×10-3s,半宽为a=2.003×10-3s，可认为在区间内是均匀分布的，取包含因子k=2，则标准不确定度为：u(As)= 1.2×10-3s4 合成标准不确定度的评定4.1 灵敏系数数学模型：δ=A－As灵敏系数：4.2合成标准不确定度的计算输入量As与A彼此独立互不相关，所以合成标准不确定度可按下式计算得：5 扩展不确定度的评定取包含因子k=2，扩展不确定度为U= k×uc(δ)=2×0.11=0.22s6 测量不确定度的报告与表示秒表在测量30s时的扩展不确定度为：U=0.22s k=2。

半偏法及其系统误差分析
半偏法（Half-Period Method）是一种测量时间间隔误差的方法，常用于测量钟表、计时器、震荡器等时间测量设备的精度，以及物理实验中的时间测量误差等。

该方法通过比较两个相邻时间间隔的平均值和系统误差的差异，以及其方差，来评估测量设备的准确度和稳定性。

半偏法的基本原理是将一段时间分成若干个相邻的时间间隔，并记录下每个时间间隔的测量结果。

然后将相邻的两个时间间隔的平均值与系统误差进行比较，以评估系统误差对测量结果的影响。

具体步骤如下：
1.选择测量时间段，并将其等分成n个时间间隔（至少3个）。

对于物理实验中的时间测量误差，一般需要保证时间跨度足够长，以便观察系统误差的影响。

2.进行测量，记录下每个时间间隔的测量结果。

3.计算相邻两个时间间隔的平均值，并计算平均值的标准差。

1.仪器固有误差：包括仪器的刻度不准确、零位偏移、灵敏度不一致等问题。

这些误差会导致测量结果整体上的偏差。

2.环境变化：例如温度变化、气压变化等都可能对测量结果产生一定的影响。

3.操作误差：例如使用不正确的操作方式、技术人员疏忽等都可能导致系统误差的增加。

分析系统误差可以采取以下几种方法：
1.重复测量：多次进行相同测量，查看测量结果的稳定性和一致性。

若结果变化较大，则可能存在系统误差。

2.与参考标准比较：将被测量设备与已知准确度较高的参考标准进行比较，评估其误差大小。

3.分析实验数据：根据测量结果和已知条件，运用统计学方法进行数据分析，以判断系统误差的大小。

时间间隔测量方法及误差分析作者：李新声来源：《中国科技博览》2013年第36期[摘要]本文针对电子计数法测量时间间隔存在原理误差、时标误差和触发误差的问题进行了分析，并且提出了减小电子计数法测量误差的方法。

[关键词]时间间隔电子计数中图分类号：F416.63 文献标识码：A 文章编号：1009-914X（2013）36-0349-01引言：电磁信号的时间测量主要是指时间间隔的测量，时间间隔是起始信号和终止信号之间所经历的时间，广义上也包括周期测量。

时间间隔测量技术在通信、雷达、卫星及导航定位等领域起着非常重要的作用，因此提高测量时间间隔测量准确度是测量领域一直关注的问题。

1 时间间隔测量原理（如图1）随着科学技术的发展，电子计数器的使用越来越广泛，特别是在时间间隔测量中，它已成为通用的测量设备。

电子计数器通常由时基，控制单元，计数及显示单元等部分组成。

电子计数器机内晶振输出的信号（周期为T0）经分频倍频后，以脉冲列的形式（时基T0）通过主闸门进入计数器。

由被测信号控制主闸门，而用时基脉冲进行计数。

在时间间隔测量中设置了B，C两个输入通道，分别送出起始信号和终止信号去控制门控双稳电路以形成闸门信号。

根据被测时间间隔TX内进入计数器的时标脉冲T0的个数N，得到两个被测信号之间的时间间隔Tx，即Tx=T0*N。

利用电子计数器的时间间隔测量功能既可以对周期信号进行测量，也可以对非周期信号进行测量，可以方便的实现脉冲宽度，上升时间，下降时间的脉冲参数的测量。

例如要实现上升时间的测量，只需将脉冲同时接入B，C两个通道，B通道触发电平设置为信号幅度的10%（正极性），C通道触发电平设置为信号幅度的90%（正极性）。

2 时间间隔误差分析及减小办法在测量精度要求不高的情况，电子计数法是一种非常好的时间间隔测量方法，已经在许多领域获得了广泛应用，测量时序图如图1：引起电子计数器出现测量误差的因素很多，但是主要是量化误差、时基误差和触发误差三种误差。

最大时间间隔误差摘要：1.最大时间间隔误差的定义和重要性2.最大时间间隔误差的计算方法3.最大时间间隔误差的应用领域4.最大时间间隔误差的实际案例分析正文：【1.最大时间间隔误差的定义和重要性】最大时间间隔误差（Maximum Time Interval Error，简称MTIE）是指在一定时间范围内，系统或设备所能容忍的最大时间间隔误差。

在工程技术、科学研究和日常生活中，时间间隔误差的存在会对系统的稳定性和精确性产生影响，因此研究和控制最大时间间隔误差具有重要意义。

【2.最大时间间隔误差的计算方法】最大时间间隔误差的计算方法取决于具体的应用场景和需求。

一般来说，可以通过以下公式来计算最大时间间隔误差：MTIE = （最大允许误差+ 最小采样间隔）/ 2其中，最大允许误差是指系统或设备所能容忍的最大误差，最小采样间隔是指系统或设备进行采样的最短时间间隔。

【3.最大时间间隔误差的应用领域】最大时间间隔误差在多个领域具有广泛的应用，包括但不限于以下几个领域：1.通信系统：在通信系统中，最大时间间隔误差会影响数据传输的速率和稳定性。

因此，通信系统需要根据具体需求，合理设定最大时间间隔误差，以保证数据传输的准确性。

2.控制系统：在控制系统中，最大时间间隔误差会影响控制系统的响应速度和精度。

为了保证控制系统的稳定性，需要对最大时间间隔误差进行严格的控制。

3.测量系统：在测量系统中，最大时间间隔误差会影响测量结果的准确性。

因此，测量系统需要根据具体需求，合理设定最大时间间隔误差，以提高测量结果的精度。

【4.最大时间间隔误差的实际案例分析】以某通信系统为例，假设其最大允许误差为1 微秒，最小采样间隔为5 微秒。

则可以通过以下公式计算最大时间间隔误差：MTIE = （1 微秒+ 5 微秒）/ 2 = 3 微秒这意味着在该通信系统中，最大时间间隔误差为3 微秒。

如果系统的时间间隔误差超过3 微秒，将会影响通信的稳定性和数据传输的准确性。

最大时间间隔误差最大时间间隔误差是指在进行时间测量时，所能达到的最大误差范围。

在许多领域，如科学实验、电子工程、物理测量等，时间间隔测量的准确性和稳定性是非常重要的。

而最大时间间隔误差则限制了时间测量的准确性，因此需要采取一系列措施来降低最大时间间隔误差。

首先，最大时间间隔误差与测量设备的精度和稳定性密切相关。

为了降低最大时间间隔误差，需要选择精度高、稳定性好的测量设备。

例如，在科学实验中常常使用高精度的计时器或天文钟来进行时间测量，而在电子工程中则常常使用精密的时钟电路和计时器来进行时间测量。

其次，环境条件的稳定性也对最大时间间隔误差有较大影响。

温度、湿度、空气压力等环境因素的变化都会对测量设备的性能产生影响。

为了降低最大时间间隔误差，需要将测量设备放置在稳定的环境中，并采取相应的措施来保持环境条件的稳定性。

例如，在实验室中可以使用恒温恒湿设备来控制实验环境的温度和湿度，以保证测量的准确性。

此外，最大时间间隔误差还与测量方法和测量过程的规范性有关。

在进行时间测量时，需要严格按照相关标准和规范来进行操作，避免人为因素对测量结果的影响。

例如，在科学实验中，需要按照实验方案来进行时间测量，并记录实验过程中的各项操作和条件，以便分析和验证测量结果的可靠性。

另外，最大时间间隔误差还与测量数据处理和分析方法有关。

在进行时间测量后，需要对测量数据进行处理和分析，以得到符合实际需求的结果。

在进行数据处理和分析时，需要选择适合的方法和算法，并结合实际情况进行合理的处理。

例如，在实验数据处理中常常使用统计学方法来进行数据的平均、方差和标准差等计算，以评估测量结果的准确性和稳定性。

总结起来，降低最大时间间隔误差需要选择精度高、稳定性好的测量设备，保持环境条件的稳定性，严格按照规范进行测量操作，合理选择数据处理和分析方法。

通过综合考虑这些因素，可以有效降低最大时间间隔误差，提高时间测量的准确性和稳定性。