类比推理和假说演绎法的比较

第10课时基因在染色体上[目标导读] 1.理解“类比推理法”，通过比较基因和染色体的平行关系，把握萨顿的假说。

2.结合教材P29图2－9、图2－10，理解“基因在染色体上”的试验证据。

3.运用有关基因和染色体的学问，阐明孟德尔遗传规律的细胞学基础和实质。

[重难点击] 1.萨顿推想基因在染色体上的“类比推理法”。

2.摩尔根的试验过程。

3.孟德尔遗传规律的实质。

1．减数分裂中染色体的行为(1)减数分裂和受精作用中，染色体有相对稳定的形态和结构。

(2)体细胞中的染色体成对存在，称为同源染色体，一条来自父方，一条来自母方。

(3)减数第一次分裂后期，同源染色体分别，非同源染色体自由组合。

(4)减数分裂产生的配子中染色体数目只有亲本的一半，经过受精作用子代的染色体数目和亲代相同。

2．孟德尔对分别现象的缘由提出的假说内容(1)生物的性状是由遗传因子打算的。

(2)体细胞中遗传因子是成对存在的。

(3)在形成配子时，成对的遗传因子彼此分别，分别进入不同的配子中；不同对的遗传因子自由组合。

(4)受精时，雌雄配子的结合是随机的。

3．将下列假说—演绎法的基本步骤排序：②④①③⑤⑥。

①分析推理②观看现象③提出假说④提出问题⑤试验验证⑥总结规律课堂导入师：回顾减数分裂学问，思考：某生物体细胞含有一对同源染色体，它进行减数分裂，可以产生几种类型的配子？含有两对同源染色体的呢？(2种，4种)师：一个基因型为Aa的个体，能产生几种类型的配子？AaBb的个体呢？(2种、4种)师：大家比较一下在配子的形成过程，即减数分裂过程中染色体和基因的行为变化，你们有什么发觉？可以提出什么样的假说？探究点一萨顿的假说1．类比推理是依据两个或两类对象有部分属性相同，从而推出它们的其他属性也相同的推理。

2．萨顿推论：基因是由染色体携带着从亲代传递给下一代的，也就是说，基因就在染色体上。

缘由：基因和染色体在传递行为上有很多相像之处，存在着明显的平行关系，可以归纳如下：类别项目基因的行为染色体的行为传递中的性质在杂交过程中保持完整性和独立性在配子形成和受精过程中，保持相对稳定的形态结构存在形式体细胞中的存在形式成对成对配子中的存在形式成单，只有成对的基因中的一个成单，只有成对的染色体中的一条在体细胞中的来源等位基因中一个来自父方，一个来自母方同源染色体中一条来自父方，一条来自母方形成配子时等位基因分别，非等位基因自由组合同源染色体分别，非同源染色体自由组合3.结合萨顿的类比推理法，在下图中的横线处填上合适的基因(用D、d表示一对基因)，来解释一对相对性状的杂交试验。

高中生物中的假说演绎法与类比推理法假说一演绎法是现代科学研究中常用的一种科学方法。

在观察和分析基础上提出问题以后，通过推理和想像提出解释问题的假说，根据假说进行演绎推理，再通过实验检验演绎推理的结论。

如果实验结果与预期结论相符，就证明假说是正确的，反之，则说明假说是错误的。

高中生物中，那些科学家用了假说演绎法1、孟德尔的豌豆杂交实验。

19世纪中期，孟德尔用豌豆做了大量的杂交实验，在对实验结果进行观察、记载和进行数学统计分析的过程中，发现杂种后代中出现一定比例的性状分离，两对及两对以上相对性状杂交实验中子二代出现不同性状自由组合现象。

他通过严谨的推理和大胆的想象而提出假说，并对性状分离现象和不同性状自由组合现象作出尝试性解释。

然后他巧妙地设计了测交实验用以检验假说，测交实验不可能直接验证假说本身，而是验证由假说演绎出的推论，即:如果遗传因子决定生物性状的假说是成立的，那么，根据假说可以对测交实验结果进行理论推导和预测;然后，将实验获得的数据与理论推导值进行比较，如果二者一致证明假说是正确的，如果不一致则证明假说是错误的。

当然，对假说的实践检验过程是很复杂的，不能单靠一两个实验来说明问题。

事实上，孟德尔做的很多实验都得到了相似的结果，后来又有数位科学家做了许多与孟德尔实验相似的观察，大量的实验都验证了孟德尔假说的真实性之后，孟德尔假说最终发展为遗传学的经典理论。

我们知道，演绎推理是科学论证的一种重要推理形式，测交实验值与理论推导值的一致性为什么就能证明假说是正确的呢?原来，测交后代的表现型及其比例真实地反映出子一代产生的配子种类及其比例，根据子一代的配子型必然地可以推导其遗传组成，揭示这个奥秘为演绎推理的论证过程起到画龙点睛的作用，不揭示这个奥秘学生则难以理解“假说一演绎法”的科学性和严谨性，对演绎推理得出的结论仍停留在知其然的状况。

2、1900年，3位科学家分别重新发现了孟德尔的工作，遗传学界开始认识到孟德尔遗传理论的重要意义。

高中生物中的假说演绎法与类比推理法假说一演绎法是现代科学研究中常用的一种科学方法。

在观察和分析基础上提出问题以后，通过推理和想像提出解释问题的假说，根据假说进行演绎推理，再通过实验检验演绎推理的结论。

如果实验结果与预期结论相符，就证明假说是正确的，反之，则说明假说是错误的。

高中生物中，那些科学家用了假说演绎法1、孟德尔的豌豆杂交实验。

19世纪中期，孟德尔用豌豆做了大量的杂交实验，在对实验结果进行观察、记载和进行数学统计分析的过程中，发现杂种后代中出现一定比例的性状分离，两对及两对以上相对性状杂交实验中子二代出现不同性状自由组合现象。

他通过严谨的推理和大胆的想象而提出假说，并对性状分离现象和不同性状自由组合现象作出尝试性解释。

然后他巧妙地设计了测交实验用以检验假说，测交实验不可能直接验证假说本身，而是验证由假说演绎出的推论，即:如果遗传因子决定生物性状的假说是成立的，那么，根据假说可以对测交实验结果进行理论推导和预测;然后，将实验获得的数据与理论推导值进行比较，如果二者一致证明假说是正确的，如果不一致则证明假说是错误的。

当然，对假说的实践检验过程是很复杂的，不能单靠一两个实验来说明问题。

事实上，孟德尔做的很多实验都得到了相似的结果，后来又有数位科学家做了许多与孟德尔实验相似的观察，大量的实验都验证了孟德尔假说的真实性之后，孟德尔假说最终发展为遗传学的经典理论。

我们知道，演绎推理是科学论证的一种重要推理形式，测交实验值与理论推导值的一致性为什么就能证明假说是正确的呢?原来，测交后代的表现型及其比例真实地反映出子一代产生的配子种类及其比例，根据子一代的配子型必然地可以推导其遗传组成，揭示这个奥秘为演绎推理的论证过程起到画龙点睛的作用，不揭示这个奥秘学生则难以理解“假说一演绎法”的科学性和严谨性，对演绎推理得出的结论仍停留在知其然的状况。

2、1900年，3位科学家分别重新发现了孟德尔的工作，遗传学界开始认识到孟德尔遗传理论的重要意义。

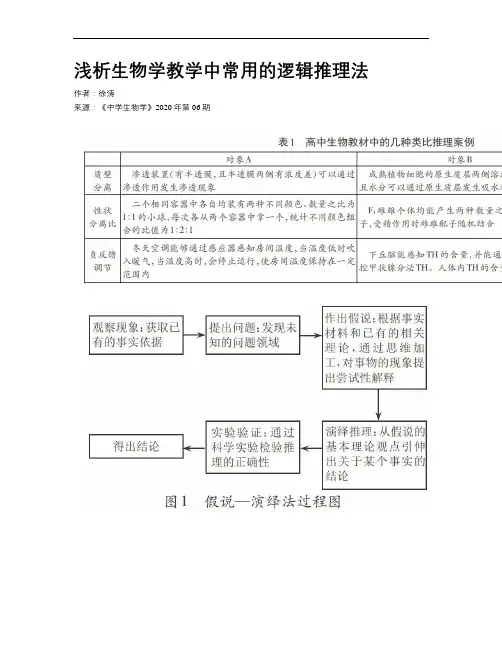
浅析生物学教学中常用的逻辑推理法作者：徐涛来源：《中学生物学》2020年第06期摘要列举了高中生物教学中涉及到的逻辑学相关内容，举例阐述了类比推理、求异法、概率统计推理和假说演绎法在高中生物教学中的应用。

关键词高中生物逻辑学推理法中图分类号 C633. 91文献标志码B“逻辑”是一个外来词，它是英文Logic的音译，其原意是指思想、言辞、理性、规律性等。

逻辑学研究的主体是推理，推理是从一个或一些陈述得出另一个陈述的思维过程。

生物学在发展过程中，实验的设计、科学的发现、理论的提出等均涉及到了逻辑学的应用。

《普通高中生物学课程标准（2017年版）》提出，高中生物学学科核心素养之一是科学思维，培养学生能够掌握归纳与概况、演绎与推理等方法。

因此，教师应当在生物学教学中培养学生的逻辑思维能力，并使其能熟练的运用到实验分析、假设提出、模型建构、科学解释中去。

学习逻辑学的规律、方法不仅可以提高学生的认知能力，使思维更加严谨，还能让学生掌握科学研究的工具，有利于创新能力的提高。

下面介绍几种高中生物教学中常用的逻辑推理法。

1 类比推理类比推理指根据两个对象A和B都有若干相同属性，并且A还有另外某个属性，推出对象B也具有这个属性。

它的推理过程为：A对象具有属性a、b、c、d;B对象具有属性a、b、c。

所以，B对象也具有属性d。

所以，类比推理是根据2个或2类事物在一系列属性上的相似，推出它们在另一个或另一类属性上也相似的推理形式。

类比推理是一种重要的说明方法，方便教师通过列举学生熟悉的相似的事实或原理来解释问题。

生物学很多现象微观而抽象，为此教师要能从身边的事例中，找到与要解释的对象相似的例子，即为了更通俗地讲解“B”的属性，教师要善于去寻找相似物“A”。

高中生物教材中的几种类比推理案例见表l。

教师利用类比推理法，可以将抽象的知识形象化、将深奥的知识通俗化，有利于学生对问题的理解，进而探究思考后，达到抽象知识的提升。

高中生物实验方法、学过的酶、常见英文缩写和高中生物课程中的“一般”与“例外1、显微观察法：观察细胞有丝分裂｜观察叶绿体和细胞质流动｜用显微镜观察多种多样的细胞2、假说演绎法：发现问题→提出假说→实验检验→验证假说→得出结论。

孟德尔的豌豆杂交实验【孟德尔】｜DNA复制方式的提出与证实（以及整个中心法则的提出与证实）【沃森、克里克大肠杆菌为实验材料】｜DNA双螺旋结构模型【克里克以T4噬菌体为实验】3、类比推理法：指是根据两个或两类对象在某些属性上相同，推断出它们在另外的属性上（这一属性已为类比的一个对象所具有，另一个类比的对象那里尚未发现）也相同的一种推理。

基因和染色体行为之间明显的平行关系【萨据提出假说：基因是由染色体携带着从亲代传递给子代的，也就是说，基因位于染色体上】｜摩尔根果蝇杂交实验｜细胞学说的建立【施旺由植物推挤动物】｜DNA模型建立【沃森、克里克由蛋白质的空间结构呈螺旋型推挤DNA结构也是螺旋型】4、种群密度的取样调查①黑灯光诱捕计数法：对紫外线敏感的夜间活动的昆虫②样方法：植物或活动范围小的动物和虫卵③标记重捕法：对于活动范围较大，活动能力较强的动物④显微计数法／计数板计数：肉眼看不见的细菌、酵母菌等微生物或细胞⑤取样器取样法：活动能力强（不适合样方法）、身体微小（不适合标志重捕法）的土壤小动物，包括记名计算法和目测标记法。

5、荧光标记法：动物细胞融合／细胞杂交（骨髓瘤细胞）6、水培法：完全培养液与缺素完全培养液对照7、饲喂法，切除注射法，阉割移植法：给生物添加激素的方法8、手握法、电刺激法、假台畜法：收集动物精子9、观色法：生物组织中还原糖、脂肪和蛋白质的鉴定｜观察动物毛色和植物花色的遗传｜DNA和RNA的分布10、同位素标记法（元素示踪法）：分泌蛋白的分泌过程｜卡尔文循环｜光合作用中氧气中氧的来源的确定｜噬菌体浸染细菌的实验｜恩格尔曼实验11、补充法：用饲喂法研究甲状腺激素｜用注射法研究动物胰岛素和生长激素｜用移植法研究性激素12、摘除法：用“阉割法、摘除法研究性激素｜甲状腺激素或生长激素的作用｜雌蕊受粉后除去正在发育着的种子13、杂交法：植物的杂交、测交实验14、化学分析法：番茄对Ca和Si的选择吸收｜叶绿体中色素的提取和分离15、理论分析法：大、小两种草履虫的竞争实验｜植物向性动物的研究16、模拟实验法：渗透作用的实验装置｜分离定律的模拟实验17、引流法：临时装片中液体的更换，用吸水纸在一侧吸引，于另一侧滴加换进的液体。

2021届高三生物一轮复习——基因在染色体上的假说与证据
知识梳理
1.萨顿的假说
(1)研究方法：类比推理。

(2)内容：基因是由染色体携带着从亲代传递给下一代的，即基因就在染色体上。

2.基因位于染色体上的实验证据(实验者：摩尔根)
(1)果蝇的杂交实验——问题的提出
(2)对实验现象的解释——提出假设
①假设：控制果蝇红眼、白眼的基因只位于X染色体上，Y染色体上无相应的等位基因。

②对杂交实验的解释(如图)
(3)测交验证：亲本中的白眼雄蝇和F1中的红眼雌蝇交配→子代中雌性红蝇∶雌性白蝇∶雄性红蝇∶雄性白蝇＝1∶1∶1∶1。

(4)结论：控制果蝇红眼、白眼的基因只位于X染色体上→基因位于染色体上。

(5)研究方法——假说—演绎法。

(6)基因与染色体的关系：一条染色体上有多个基因，基因在染色体上呈线性排列。

1.类比推理法与假说—演绎法的比较。

归纳论证对比演绎论证
归纳论证和演绎论证是两种不同的推理方法，它们在逻辑推理中起着重要的作用。

归纳论证是从特殊到一般的推理方法。

它通过观察和分析一系列具体的例子或事实，从中总结出一般规律或结论。

归纳论证的优点是可以从具体的经验中得出普遍的结论，帮助我们发现新的知识和规律。

但是，归纳论证的结论并不一定是绝对正确的，因为它基于有限的观察和样本，可能存在例外情况。

演绎论证则是从一般到特殊的推理方法。

它从一个已知的一般性原则或前提出发，通过逻辑推理得出具体的结论。

演绎论证的优点是结论具有必然性，如果前提是正确的，那么结论也一定是正确的。

演绎论证常用于数学、科学和法律等领域，因为这些领域需要精确和确定的结论。

对比起来，归纳论证和演绎论证各有优缺点。

归纳论证可以帮助我们从具体的经验中得出普遍的结论，但结论的可靠性相对较低。

而演绎论证则可以从一般性原则出发得出确定的结论，但前提的正确性至关重要。

在实际的推理过程中，我们通常会综合运用这两种论证方法，以提高结论的可靠性和准确性。

总的来说，归纳论证和演绎论证是逻辑推理中常用的两种方法，它们相互补充，帮助我们从不同的角度进行思考和推断。

演绎法归纳法类比法一、演绎法从一般性的原理出发，推出某个特殊情况下的结论，这种推理就是演绎推理，也叫逻辑推理。

简而言之，演绎推理是由一般到特殊的推理。

演绎推理的一般模式为“三段论”，即：（1）大前提：已知的一般原理；（2）小前提：所研究的特殊情况；（3）结论：根据一般原理，对特殊情况做出的判断。

【例题】证明函数），在（12)(2∞-+-=x x x f 内是增函数。

分析：本题中大前提为：在某个区间),(b a 内，如果0)(>'x f ，那么函数)(x f y =在这个区间内单调递增。

小前提为：x x x f 2)(2+-=的导数在区间)1,(-∞内满足0)(>'x f ，是证明本题的关键。

证明：22)(+-='x x f当)1,(-∞∈x 时，有01>-x所以0)1(222)(>-=+-='x x x f即根据“三段论”得，)1,(2)(2-∞+-=在x x x f 内是增函数. 在演绎推理中，只要前提和推理形式是正确的，结论必定是正确的.二、归纳法由某类事物的部分对象具有某些特征，推出该类事物的全部对象都具有这些特征的推理，或者由个别事实概括出一般结论的推理，称为归纳推理（简称归纳）。

简而言之，归纳推理是由部分到整体、由个别到一般的推理。

归纳推理的思维过程大致是：实验、观察→概括、推广→猜测一般性结论。

该过程包括两个步骤：（1）通过观察个别对象发现某些相同的性质；（2）从已知的相同性质中推出一个明确表述的一般性命题（猜想）。

【例题】已知数列11}{1=a a n 项的第，且),3,2,1(11 =+=+n a a a nn n ，试归纳除这个数列的通项公式。

解：当1=n 时，数列的第1项11=a ；当2=n 时，数列的第2项211112=+=a ； 当3=n 时，数列的第3项31211213=+=a ； 当4=n 时，数列的第4项41311314=+=a . 观察可知，数列的前4项都等于相应序号的倒数. 由此猜想，这个数列的通项公式为na n 1=.三、类比法由两类对象具有某些类似特征和其中一类对象的某些已知特征，推出另一类对象也具有这些特征的推理称为类比推理（简称类比）。