1.2库仑定律

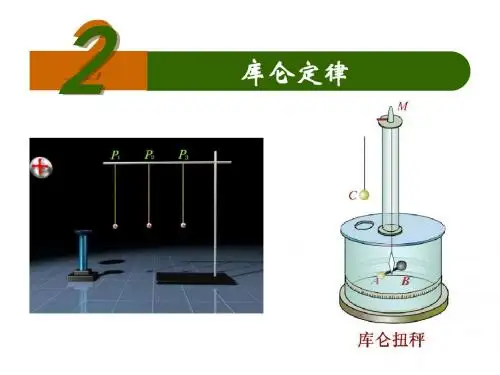
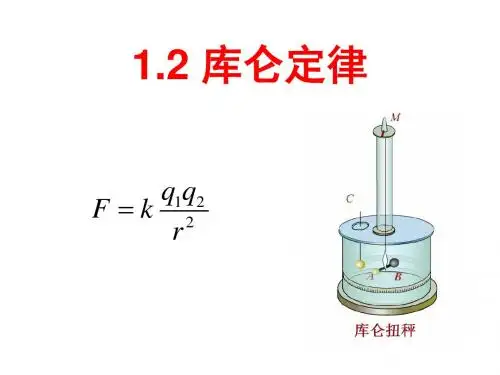
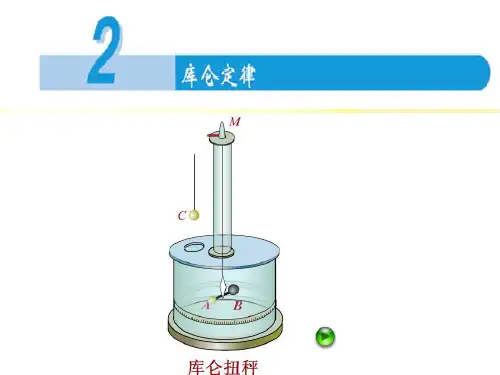
1.2 库仑定律简介库仑定律是电磁学中的基本定律之一，描述了带电物体之间相互作用力的大小与它们之间距离、电荷量的关系。

该定律是由法国物理学家库仑于18世纪末提出的，被认为是电磁学的基石之一，对于理解电荷之间的相互作用以及电磁现象的发生和演化具有重要意义。

定义库仑定律可以表述如下：两个电荷之间的静电力的大小与它们之间直线距离的平方成反比，在恒定吸引或排斥力的情况下，与这两个电荷的数量成正比。

公式表示为：F = k * (q1 * q2) / r^2其中，F表示两个电荷之间的静电力，k是库仑常数，q1和q2分别表示两个电荷的电荷量，r表示它们之间的距离。

库仑常数库仑常数是一个物理常数，用于计算两个电荷之间的静电力。

它的数值约为9.0 x 10^9 Nm2/C2，其中Nm2/C2是国际单位制中的单位。

电荷的性质根据库仑定律，电荷有两种性质：正电荷和负电荷。

正电荷尽可能地排斥彼此，而负电荷也尽可能地排斥彼此。

正电荷和负电荷之间会产生吸引力，这是导致电荷之间相互作用的原因。

实例分析下面我们通过一个实例来分析和应用库仑定律。

假设有两个电荷，电荷q1的电荷量为2C，电荷q2的电荷量为-4C，它们之间的距离r为1m。

我们可以使用库仑定律来计算它们之间的静电力。

根据库仑定律的公式，我们有：F = k * (q1 * q2) / r^2代入具体数值得到：F = (9.0 x 10^9 Nm2/C2) * (2C * -4C) / (1m)^2简化计算得到：F = -7.2 x 10^9 N由此可见，这两个电荷之间的静电力是-7.2 x 10^9 N（牛顿）。

负号表示这两个电荷之间的力是吸引力，而不是排斥力。

应用库仑定律在众多领域中都有广泛的应用。

以下是一些常见的应用场景：1.静电学：库仑定律对于描述静电现象和静电力的大小提供了基本的理论基础。

2.电荷的分布与运动：在电荷的分布和运动方面，库仑定律有很多应用，比如计算静电场的大小、电荷在电场力作用下的运动等。

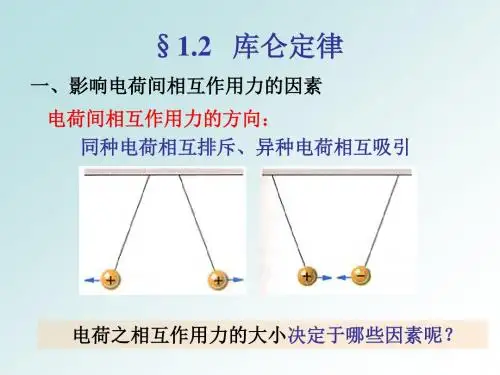
第一章 静电场课时2 库仑定律一、库仑定律 1．内容真空中两个静止 之间的相互作用力，与它们的电荷量的 成正比，与它们的距离的二次方成 ，作用力的方向在它们的连线上。

电荷间的这种相互作用力叫做静电力或库仑力。

2．适用范围（1）真空中 （2）静止的 （3）点电荷 二、点电荷当带电体间的距离比它们自身的大小 得多，以致带电体的形状、大小及电荷分布状况对它们之间的作用力的影响可以 时，这样的带电体就可以看作带电的点，叫做 。

注意：点电荷类似于力学中的质点，也是一种 的模型。

库仑定律的表达式 。

式中的k 是比例系数，叫做静电力常量。

k = 。

注意：计算大小时只需将电荷量的绝对值代入。

静电力与万有引力的比较1．相同点：公式形式相同，应用时都有条件 都是不接触力，且与距离的二次方成反比2．不同点：万有引力只是相互吸引，而静电力可以是引力，也可以是斥力 3．在求静电力时，万有引力可以忽略点电荷 乘积 反大 忽略 点电荷 理想化 122=q q F kr9229.010N m C ⨯⋅一、对库仑定律的理解和应用库仑定律的适用条件是真空中的静止点电荷。

点电荷是一种理想化的物理模型，当带电体间的距离远大于带电体的自身大小时，可以视其为点电荷，可以用库仑定律，否则不能用。

【例题1】如图所示，两个质量均为m的完全相同的金属球壳a与b，其壳层的厚度和质量分布均匀，将它们固定于绝缘支架上，两球心间的距离为l，为球壳外半径r的3倍，若使它们带上等量的异种电荷，使其所带电荷量的绝对值均为Q，那么a、b两球间的万有引力F1与库仑力F2为A．212mF Gl=，222QF kl=B．212mF Gl≠，222QF kl≠C．212mF Gl≠，222QF kl=D．212mF Gl=，222QF kl≠参考答案：D二、三个自由点电荷仅在它们系统的静电力作用下处于平衡状态时，满足的规律1．“三点共线”——三个点电荷分布在同一直线上。