静磁场习题7.1

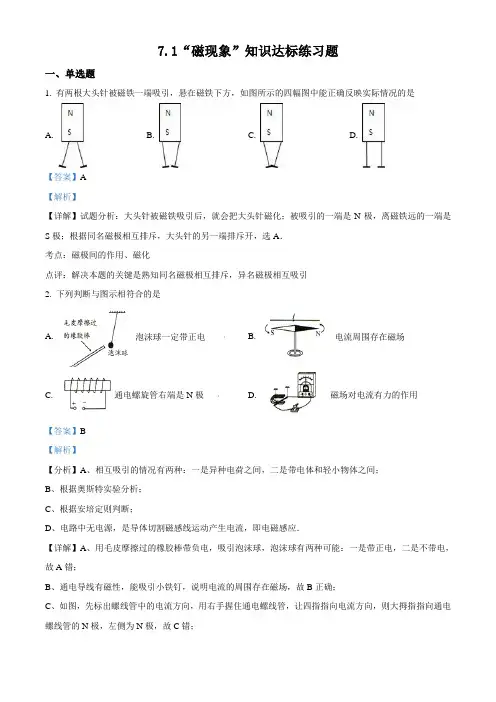
7.1“磁现象”知识达标练习题一、单选题1. 有两根大头针被磁铁一端吸引，悬在磁铁下方，如图所示的四幅图中能正确反映实际情况的是A. B. C. D.【答案】A【解析】【详解】试题分析：大头针被磁铁吸引后，就会把大头针磁化；被吸引的一端是N极，离磁铁远的一端是S极；根据同名磁极相互排斥，大头针的另一端排斥开，选A．考点：磁极间的作用、磁化点评：解决本题的关键是熟知同名磁极相互排斥，异名磁极相互吸引2. 下列判断与图示相符合的是A. 泡沫球一定带正电B. 电流周围存在磁场C. 通电螺旋管右端是N极D. 磁场对电流有力的作用【答案】B【解析】【分析】A、相互吸引的情况有两种：一是异种电荷之间，二是带电体和轻小物体之间；B、根据奥斯特实验分析；C、根据安培定则判断；D、电路中无电源，是导体切割磁感线运动产生电流，即电磁感应．【详解】A、用毛皮摩擦过的橡胶棒带负电，吸引泡沫球，泡沫球有两种可能：一是带正电，二是不带电，故A错；B、通电导线有磁性，能吸引小铁钉，说明电流的周围存在磁场，故B正确；C、如图，先标出螺线管中的电流方向，用右手握住通电螺线管，让四指指向电流方向，则大拇指指向通电螺线管的N极，左侧为N极，故C错；D 、本图为研究电磁感应现象的实验，故D 错．故选B ．3. 指南针是我国四大发明之一，《论衡》记载：司南之杓，投之于地，其柢指南．如图所示的司南放在水平光滑的“地盘”上，静止时它的长柄指向南方．司南长柄所指方向是（ ）A. 地理南极，地磁北极B. 地理南极，地磁南极C. 地理北极，地磁北极D. 地理北极，地磁南极【答案】A【解析】 【分析】指南针是根据磁体的指向性工作的，地球本身是一个巨大的磁体，地球周围的磁场叫做地磁场，地磁的南极在地理的北极附近，而地磁的北极在地理的南极附近．【详解】地球本身是一个大磁体，司南实质就是一块磁铁，在地球的磁场中受到磁力的作用，其静止时它的长柄指向南方，即地理上的南极；地理上的南极是地磁的北极，故BCD 错误、A 正确．故选A ．【点睛】磁场是一种看不见摸不着的物质，是真实存在的，对于磁场的认识，我们是通过它对其他物体的作用来认识的．4. 如图是有关电与磁实验的装置图，其中应用与所对应的原理图错误的一组是A. B. C.D.【答案】C【解析】【分析】首先要弄清楚每一选项的物理原理，再看应用是否和原理相对应，最后进行判断．【详解】A、如图原理是通电导体在磁场中受力．电动机就是利用这一原理来工作的．故A正确；B、实验原理为：通电导体周围存在磁场．电铃就是应用该原理来工作的．故B正确；C、实验说明：同名磁极相互排斥．不是光盘的工作原理．故C错误；D、实验原理：电磁感应现象．发电机就是应用该原理来工作的．故D正确．故选C．5. 下列说法中正确的是A. 用干燥的毛刷刷毛料衣服，毛刷上会附着许多细小脏物B. 两球相互吸引，则它们都带电荷C. 把钢针沿磁铁摩擦，钢针能吸铁，则说明钢针带了电D. 验电器可显示物体所带电荷的种类【答案】A【解析】【分析】（1）由于不同物质的原子核对核外电子的束缚本领不同，不同的物体在摩擦的过程中束缚本领强的得电子带负电，束缚本领弱的失电子带正电，这就是摩擦起电现象．（2）同种电荷相互排斥，异种电荷相互吸引，带电体有吸引轻小物体的性质；（3）钢铁等物质会被磁化，磁化后能吸引铁钴镍等物质；（4）验电器是检验物体是否带电的仪器．【详解】A、用干燥的毛刷刷毛料衣服，由于摩擦起电而带了电，所以毛刷上会附着许多细小脏物，故A 正确；B、两球相互吸引，则它们可能带异种电荷，也可能有一个不带电，故B错误；C、把钢针沿磁铁摩擦，钢针能吸铁，则说明钢针有磁性，故C错误；D、验电器可以检验物体是否带电，不能显示物体所带电荷的种类，故D错误．故选A．6. 如图所示，下列作图正确的是A. 物体所受重力的示意图B. 凹透镜对平行光线的作用C. 异名磁极间的磁感线D. 力F1的力臂L1【答案】C【解析】【分析】A、压力是指垂直作用在物体表面上的力，重力竖直向下；B、根据凹透镜的三条特殊光线分析判断；C、异名磁极之间的磁场的磁感线从N极到S极；D、力臂是支点到力的作用线的距离，力臂与力的作用线垂直．【详解】A、压力是指垂直作用在物体表面上的力，而重力的方向始终竖直向下，故A错；B、平行于凹透镜主光轴的入射光线，经凹透镜折射后，折射光线反向延长线过焦点，故B错．C、异名磁极之间的磁场的磁感线从N极到S极，故C正确；D、F1的力臂是支点到力的作用线的距离，故D错．故选C．7. 如图所示实验装置，弹簧测力计下面挂着条形磁铁，螺线管中插有铁芯，开关S接在触点②位置．要使弹簧测力计的示数变大，下列操作方法能够实现的是A. 滑片P向b端滑动B. 将S拨到①位置C. 将螺线管往上移动D. 将铁芯从螺线管中取出【答案】D【解析】【详解】A．根据安培定则可知，螺线管的上端是N极，滑片P向b端滑动，电阻变小，电流变大，螺线管磁性变强，同名磁极相互排斥．排斥力增大，则弹簧测力计示数变小，不符合题意；B．将S拨到①位置，线圈匝数增加，螺线管磁性增强，排斥力增大，则弹簧测力计示数变小，不符合题意；C．将螺线管往上移动，磁极间的作用会变强，排斥力变大，则弹簧测力计示数变小，不符合题意；D．将铁芯从螺线管中抽出，螺线管的磁性就会变弱，排斥力减小，则弹簧测力计示数变大，符合题意．8. 如图所示，晓彤和小雪自制了一些实验器材，关于它们的工作原理，下列说法正确的是A. 图甲是简易的热机，它是利用机械能转化为内能来工作的B. 图乙是电磁秋千，它是利用磁极间的相互作用来工作的C. 图丙是皮筋动力小车，它是利用平衡力来使车前进的D. 图丁是泡沫塑料切割机，它是利用电流的磁效应来工作的【答案】B【解析】【分析】（1）利用内能做功的机器叫做热机，在做功时内能转化为机械能．（2）同名磁极相互排斥，异名磁极相互吸引．（3）转动螺旋桨，与其连接的皮筋扭转并绷紧，橡皮筋的弹性势能增大；松手后，橡皮筋的弹性势能转化为螺旋桨的动能；由于力的作用相互，空气对小车的力使车前进．（4）泡沫塑料切割机利用电流的热效应工作．【详解】A、热机是利用内能来工作的机器，将内能转化为机械能，故A错误；B、电磁秋千是利用同名磁极相互排斥原理工作的，故B正确；C、转动螺旋桨，与其连接的皮筋扭转并绷紧，橡皮筋的弹性势能增大，松手后，橡皮筋的弹性势能转化为螺旋桨的动能，小车的前进利用了力的作用相互，不是利用平衡力来使车前进的，故C错误；D、泡沫塑料切割机，它是利用电流的热效应工作的，故D错误．故选B．9. 如图所示，一条形磁铁的周围放着能自由转动的小磁针甲、乙、丙、丁四根小磁针，静止时，画错的是A. 甲B. 乙C. 丙D. 丁【答案】A【解析】【详解】试题分析:磁场的性质是对放入其中的磁体有力的作用．一条形磁铁的周围放着能自由转动的小磁针甲、乙、丙、丁四根小磁针，这四个小磁针受条形磁体的吸引作用而静止．和条形磁体N极相接触的磁针的极性是S极，和条形磁体S极相接触的磁针的极性是N极．画错的是选A．考点:本试题考查的是磁体的相互作用．点评：对于此类试题，学生应把握和条形磁体N极相接触的磁针的极性是S极，和条形磁体S极相接触的磁针的极性是N极．10. 一条磁铁从中间折成两段后A. S极的那一半只有S极，N极的那一半只有N极B. 两半都有N极和S极C. S极的那一半只有N极，N极的那一半只有S极D. 两半都不再有磁性【答案】B【解析】【分析】任意磁铁均有两个磁极，一个为N极另一个为S极．【详解】磁铁从中间断开后，每一段均仍然有两个磁极，一个是N极，一个是S极，即磁极一定是成对出现的．故选B．11. 司南是我国早期的指南针，它是把天然磁石琢磨成勺子的形状，然后放在一个水平光滑的地盘上制成的．静止时，它的长柄指向南方．在得知指南针的制作原理后，小明自己也制作了一个指南针．当他将指南针和一块条形磁体放在一起时，下列四个指南针中指向正确的是（指南针与条形磁体颜色深得一极为N 极）A. B. C. D.【答案】C【解析】【详解】试题分析：利用磁极间的作用规律分析判断．解：A、根据同名磁极相互排斥，异名磁极相互吸引可知，小磁针S极应该向下，故A错误；BCD、根据同名磁极相互排斥，异名磁极相互吸引可知，小磁针的N极在条形磁体的S极附近，S极在N 极附近，故只有C正确．故选C12. 下列各图描述磁场的磁感线中，正确的是A. B.C. D.【答案】B【解析】【详解】解：A、由图可知，螺线管左端为N极，右端为S极，在磁体的外部，磁体周围的磁感线从磁体的N极出发，回到磁体的S极，而图中正好相反，故A错误；B、由图可知，小磁针上端为N极，下端为S极，在磁体的外部，磁体周围的磁感线从磁体的N极出发，回到磁体的S极，故B正确；C、由图可知，螺线管左端为N极，右端为S极，在磁体的外部，磁体周围的磁感线从磁体的N极出发，回到磁体的S极，而图中下边的那根磁感线正好相反，故C错误；D、在磁体的外部，磁体周围的磁感线从磁体的N极出发，回到磁体的S极，而图中右端磁感线错误，故D故选B．13. 以下探究实验装置中，不能完成探究内容的是（）A. 磁极间相互作用规律B. 通电直导线周围存在磁场C. 磁性强弱与电流大小的关系D. 产生感应电流的条件【答案】C【解析】【详解】A．同名磁极相互吸引，异名磁极相互排斥，A可以完成；B．小磁针在磁场中受力会转动，所以B能完成；C．由于没有滑动变阻器，电流大小无法改变，所以C不能完成；D．磁场方向和导体运动方向可以改变，所以D能完成。

物理学简明教程第七章课后习题答案高等教育出版社第七章 恒定磁场和电磁感应7－1 两根长度相同的细导线分别多层密绕在半径为R 和r 的两个长直圆筒上形成两个螺线管，两个螺线管的长度相同，R ＝2r ，螺线管通过的电流相同为I ，螺线管中的磁感强度大小r R B B 、满足（ ）（A ） r R B B 2= （B ） r R B B = （C ） r R B B =2 （D ）r R B B 4=分析与解 在两根通过电流相同的螺线管中，磁感强度大小与螺线管线圈单位长度的匝数成正比．根据题意，用两根长度相同的细导线绕成的线圈单位长度的匝数之比21==R r n n r R 因而正确答案为（C ）7－2 一个半径为r 的半球面如图放在均匀磁场中，通过半球面的磁通量 为（ ）（A ）B r 2π2 （B ） B r 2π（C ）αB r cos π22 （D ） αB r cos π2题 7-2 图分析与解 作半径为r 的圆S ′与半球面构成一闭合曲面，根据磁场的高斯定理，磁感线是闭合曲线，闭合曲面的磁通量为零，即穿进半球面S 的磁通量等于穿出圆面S ′的磁通量；S B ⋅=m Φ．因而正确答案为（D ）．7－3 下列说法正确的是（ ）（A ） 闭合回路上各点磁感强度都为零时，回路内一定没有电流穿过（B）闭合回路上各点磁感强度都为零时，回路内穿过电流的代数和必定为零（C）磁感强度沿闭合回路的积分为零时，回路上各点的磁感强度必定为零（D）磁感强度沿闭合回路的积分不为零时，回路上任意一点的磁感强度都不可能为零分析与解由磁场中的安培环路定律，磁感强度沿闭合回路的积分为零时，回路上各点的磁感强度不一定为零；闭合回路上各点磁感强度为零时，穿过回路的电流代数和必定为零.因而正确答案为（B）．7－4一根无限长平行直导线载有电流I，一矩形线圈位于导线平面内沿垂直于载流导线方向以恒定速率运动（如图所示），则（）（A）线圈中无感应电流（B）线圈中感应电流为顺时针方向（C）线圈中感应电流为逆时针方向（D）线圈中感应电流方向无法确定题 7-4 图分析与解由右手定则可以判断，在矩形线圈附近磁场垂直纸面朝里，磁场是非均匀场，距离长直载流导线越远，磁场越弱．因而当矩形线圈朝下运动时，在线圈中产生感应电流，感应电流方向由法拉第电磁感应定律可以判定．因而正确答案为（B）．7－5将形状完全相同的铜环和木环静止放置在交变磁场中，并假设通过两环面的磁通量随时间的变化率相等，不计自感时则（）（A）铜环中有感应电流，木环中无感应电流（B）铜环中有感应电流，木环中有感应电流（C）铜环中感应电动势大，木环中感应电动势小（D）铜环中感应电动势小，木环中感应电动势大分析与解 根据法拉第电磁感应定律，铜环、木环中的感应电场大小相等， 但在木环中不会形成电流．因而正确答案为（A ）．7－6 对位移电流，下述说法正确的是（ ）（A ） 位移电流的实质是变化的电场（B ） 位移电流和传导电流一样是定向运动的电荷（C ） 位移电流服从传导电流遵循的所有定律（D ） 位移电流的磁效应不服从安培环路定理分析与解 位移电流的实质是变化的电场．变化的电场激发磁场，在这一点位移电流等效于传导电流，但是位移电流不是走向运动的电荷，也就不服从焦耳热效应、安培力等定律．因而正确答案为（A ）．7－7 已知地球北极地磁场磁感强度B 的大小为6.0×10－5T ．如图所示，如设想此地磁场是由地球赤道上一圆电流所激发的，此电流有多大？ 流向如何？解 设赤道电流为I ，则由教材第11－4节例2 知，圆电流轴线上北极点的磁感强度 ()R IR R IR B 24202/32220μμ=+=因此赤道上的等效圆电流为A 1073.12490⨯==μRB I 由于在地球地磁场的Ｎ 极在地理南极，根据右手螺旋法则可判断赤道圆电流应该是由东向西流，与地球自转方向相反．题 7-7 图7－8 如图所示，有两根导线沿半径方向接触铁环的a 、b 两点，并与很远处的电源相接.求环心O 的磁感强度．题 7-8 图分析 根据叠加原理，点O 的磁感强度可视作由ef 、be 、fa 三段直线以及acb 、a d b 两段圆弧电流共同激发．由于电源距环较远，0=ef B ．而be 、fa 两段直线的延长线通过点O ，由于0Idl r ⨯=，由毕奥－萨伐尔定律知0be fa ==B B ．流过圆弧的电流I 1 、I 2的方向如图所示，两圆弧在点O 激发的磁场分别为21101π4r l I μB =,22202π4r l I μB = 其中l 1 、l 2 分别是圆弧acb 、a d b 的弧长，由于导线电阻R 与弧长l 成正比，而圆弧acb 、a d b 又构成并联电路，故有2211l I l I =将21B B 、叠加可得点O 的磁感强度B ．解 由上述分析可知，点O 的合磁感强度0π4π42220211021=-=-=r l I μr l I μB B B 7－9 如图所示，几种载流导线在平面内分布，电流均为I ，它们在点O 的磁感强度各为多少？题 7-9 图分析 应用磁场叠加原理求解．将不同形状的载流导线分解成长直部分和圆弧部分，它们各自在点O 处所激发的磁感强度较容易求得，则总的磁感强度∑=i B B 0.解 （ａ） 长直电流对点O 而言，有0d =⨯r l I ，因此它在点O 产生的磁场为零，则点O 处总的磁感强度为1/4 圆弧电流所激发，故有RI μB 800= B 0 的方向垂直纸面向外．（ｂ） 将载流导线看作圆电流和长直电流，由叠加原理可得RI μR I μB π22000-= B 0 的方向垂直纸面向里．（c ） 将载流导线看作1/2 圆电流和两段半无限长直电流，由叠加原理可得RI μR I μR I μR I μR I μB 4π24π4π4000000+=++= B 0 的方向垂直纸面向外．7－10 已知10 mm 2 裸铜线允许通过50 A 电流而不会使导线过热．电流在导线横截面上均匀分布．求导线内、外磁感强度的分布.题 7-10 图分析 可将导线视作长直圆柱体，电流沿轴向均匀流过导体，故其磁场必然呈轴对称分布，即在与导线同轴的圆柱面上的各点，B 大小相等、方向与电流成右手螺旋关系．为此，可利用安培环路定理，求出导线表面的磁感强度．解 围绕轴线取同心圆为环路L ，取其绕向与电流成右手螺旋关系，根据安培环路定理，有∑⎰=⋅=⋅I μB 0πr 2d l B在导线内r ＜R ， 2222ππRIr r R I I ==∑，因而 202πRIr μB = 在导线外r ＞R ，I I =∑，因而rI μB 2π0= 磁感强度分布曲线如图所示．7－11 有一同轴电缆，其尺寸如图（ａ）所示．两导体中的电流均为I ，但电流的流向相反，导体的磁性可不考虑．试计算以下各处的磁感强度：（1） r ＜R 1 ；（2） R 1 ＜r ＜R 2 ；（3） R 2 ＜r ＜R 3 ；（4） r ＞R 3 ．画出B －r 图线．题 7-11 图分析 同轴电缆导体内的电流均匀分布，其磁场呈轴对称，取半径为r 的同心圆为积分路径， πr 2d ⋅=⋅⎰B l B ，利用安培环路定理∑⎰=⋅I μ0d l B ，可解得各区域的磁感强度．解 由上述分析得r ＜R 122101ππ12πr R μr B =⋅ 21012πR Ir μB = R 1 ＜r ＜R 2I μr B 022π=⋅rI μB 2π02= R 2 ＜r ＜R 3()()⎥⎦⎤⎢⎣⎡---=⋅I R R R r I μr B 22232203ππ2π 2223223032πR R r R r I μB --= r ＞R 3()02π04=-=⋅I I μr B04=B磁感强度B （r ）的分布曲线如图（ｂ）．7－12 一铁心上绕有线圈100匝，已知铁心中磁通量与时间的关系为t Φπ100sin 100.85⨯=，式中Φ的单位为Wb ，t 的单位为s ，求在s 100.12-⨯=t 时，线圈中的感应电动势．分析 由于线圈有N 匝相同回路，线圈中的感应电动势等于各匝回路的感应电动势的代数和，在此情况下，法拉第电磁感应定律通常写成tψt ΦNξd d d d -=-=，其中ΦN ψ=称为磁链．解 线圈中总的感应电动势 ())V (π100cos 51.2d d t tΦN =-=ξ 当s 100.12-⨯=t 时，V 51.2=ξ．7－13 载流长直导线中的电流以tI d d 的变化率增长.若有一边长为d 的正方形线圈与导线处于同一平面内，如图所示.求线圈中的感应电动势.分析 本题仍可用法拉第电磁感应定律tΦd d -=ξ，来求解.由于回路处在非均匀磁场中，磁通量就需用⎰⋅=S S B Φd 来计算.为了积分的需要，建立如图所示的坐标系.由于B 仅与x 有关，即B =B (x )，故取一个平行于长直导线的宽为d x 、长为d 的面元d S ，如图中阴影部分所示，则d S =d d x ，所以，总磁通量可通过线积分求得（若取面元d S =d x d y ，则上述积分实际上为二重积分）.本题在工程技术中又称为互感现象，也可用公式tI M d d -=ξ求解. 解1 穿过面元d S 的磁通量为x d x I S B Φd π2d d 0μ=⋅=因此穿过线圈的磁通量为2ln π2d π2d 200⎰⎰===d d Id x x Id ΦΦμμ再由法拉第电磁感应定律，有 tI d t Φd d 21ln π2d d 0）（μξ=-= 解2 当两长直导线有电流I 通过时，穿过线圈的磁通量为2ln π20dI Φμ=线圈与两长直导线间的互感为 2ln π20d I ΦM μ== 当电流以tI d d 变化时，线圈中的互感电动势为 tI d t I M d d 21ln π2d d 0）（μξ=-=题 7-13 图7－14 如图所示，把一半径为R 的半圆形导线OP 置于磁感强度为B 的均匀磁场中，当导线以速率v 水平向右平动时，求导线中感应电动势E 的大小，哪一端电势较高？题 7-14 图分析 本题及后面几题中的电动势均为动生电动势，除仍可由t ΦE d d -=求解外（必须设法构造一个闭合回路），还可直接用公式()l B d ⋅⨯=⎰l E v 求解．在用后一种方法求解时，应注意导体上任一导线元ｄl 上的动生电动势()l B d d ⋅⨯=v E .在一般情况下，上述各量可能是ｄl 所在位置的函数．矢量（v ×B ）的方向就是导线中电势升高的方向．解1 如图（ｂ）所示，假想半圆形导线OP 在宽为2R 的静止形导轨上滑动，两者之间形成一个闭合回路．设顺时针方向为回路正向，任一时刻端点O 或端点P 距 形导轨左侧距离为x ，则B R Rx Φ⎪⎭⎫ ⎝⎛+=2π212 即B R tx RB t ΦE v 2d d 2d d -=-=-= 由于静止的 形导轨上的电动势为零，则E ＝－2RvB ．式中负号表示电动势的方向为逆时针，对OP 段来说端点P 的电势较高．解2 建立如图（c ）所示的坐标系，在导体上任意处取导体元ｄl ，则()θR θB l θB E o d cos d cos 90sin d d v v ==⋅⨯=l B vB R θθBR E v v 2d cos d E π/2π/2===⎰⎰- 由矢量（v ×B ）的指向可知，端点P 的电势较高．解3 连接OP 使导线构成一个闭合回路．由于磁场是均匀的，在任意时刻，穿过回路的磁通量==BS Φ常数.由法拉第电磁感应定律tΦE d d -=可知，E ＝0又因 E ＝E OP ＋E PO即 E OP ＝－E PO ＝2RvB由上述结果可知，在均匀磁场中，任意闭合导体回路平动所产生的动生电动势为零；而任意曲线形导体上的动生电动势就等于其两端所连直线形导体上的动生电动势．上述求解方法是叠加思想的逆运用，即补偿的方法．7－15 长为L 的铜棒，以距端点r 处为支点，以角速率ω绕通过支点且垂直于铜棒的轴转动.设磁感强度为B 的均匀磁场与轴平行，求棒两端的电势差．题 7-15 图分析 应该注意棒两端的电势差与棒上的动生电动势是两个不同的概念，如同电源的端电压与电源电动势的不同．在开路时，两者大小相等，方向相反（电动势的方向是电势升高的方向，而电势差的正方向是电势降落的方向）．本题可直接用积分法求解棒上的电动势，亦可以将整个棒的电动势看作是OA 棒与OB 棒上电动势的代数和，如图（ｂ）所示．而E OA 和E OB 则可以直接利用第12－2 节例1 给出的结果．解1 如图（ａ）所示，在棒上距点O 为l 处取导体元ｄl ，则()()r L lB ωl lB ωE L-rr ABAB 221d d --=-=⋅⨯=⎰⎰-l B v因此棒两端的电势差为()r L lB ωE U AB AB 221--==当L ＞2r 时，端点A 处的电势较高解2 将AB 棒上的电动势看作是O A 棒和O B 棒上电动势的代数和，如图（ｂ）所示．其中221r ωB E OA =,()221r L B ωE OB -= 则()r L BL ωE E E OB OA AB 221--=-=7－16 如图所示，在“无限长”直载流导线的近旁放置一个矩形导体线框，该线框在垂直于导线方向上以匀速率v 向右移动，求在图示位置处，线框中感应电动势的大小和方向．题 7-16 图分析 本题亦可用两种方法求解．其中应注意下列两点：（1）当闭合导体线框在磁场中运动时，线框中的总电动势就等于框上各段导体中的动生电动势的代数和．如图（ａ）所示，导体eh 段和fg 段上的电动势为零［此两段导体上处处满足()0l B =⋅⨯d v ］，因而线框中的总电动势为()()()()hg ef hgefghefE E E -=⋅⨯-⋅⨯=⋅⨯+⋅⨯=⎰⎰⎰⎰l B l B l B l B d d d d v v v v 其等效电路如图（ｂ）所示．（2）用公式tΦE d d -=求解，式中Φ是线框运动至任意位置处时，穿过线框的磁通量．为此设时刻t 时，线框左边距导线的距离为ξ，如图（c ）所示，显然ξ是时间t 的函数，且有v =tξd d ．在求得线框在任意位置处的电动势E （ξ）后，再令ξ＝d ，即可得线框在题目所给位置处的电动势．解1 根据分析，线框中的电动势为hg ef E E E -=()()⎰⎰⋅⨯-⋅⨯=hgefl B l B d d v v()⎰⎰+-=2201000d 2πd 2πl l l l d I μl d I μvv ()1202πl d d l I +=1vl μ由E ef ＞E hg 可知，线框中的电动势方向为efgh ．解2 设顺时针方向为线框回路的正向．根据分析，在任意位置处，穿过线框的磁通量为()ξξμξμ120020lnπ2d π21l Il x x Il l +=+=Φ⎰ 相应电动势为()()1120π2d d l ξξl l I μt ΦξE +=-=v 令ξ＝d ，得线框在图示位置处的电动势为()1120π2l d d l l I μE +=v由E ＞0 可知，线框中电动势方向为顺时针方向．7－17 在半径为R 的圆柱形空间中存在着均匀磁场，B 的方向与柱的轴线平行．如图（ａ）所示，有一长为l 的金属棒放在磁场中，设B 随时间的变化率tBd d 为常量．试证：棒上感应电动势的大小为2222d d ⎪⎭⎫ ⎝⎛-=l R l t B ξ题 7-17 图分析 变化磁场在其周围激发感生电场，把导体置于感生电场中，导体中的自由电子就会在电场力的作用下移动，在棒内两端形成正负电荷的积累，从而产生感生电动势．由于本题的感生电场分布与上题所述情况完全相同，故可利用上题结果，由⎰⋅=lk l E d ξ计算棒上感生电动势．此外，还可连接OP 、OQ ，设想PQOP构成一个闭合导体回路，用法拉第电磁感应定律求解，由于OP 、OQ 沿半径方向，与通过该处的感生电场强度E k 处处垂直，故0d =⋅l E k ，OP 、OQ 两段均无电动势，这样，由法拉第电磁感应定律求出的闭合回路的总电动势，就是导体棒PQ 上的电动势．证1 由电磁感应定律，在r ＜R 区域，⎰⎰⋅-=⋅=S B t l E k d d dd ξ tB r E r k d d ππ22-=⋅ 解得该区域内感生电场强度的大小tBr E k d d 2=设PQ 上线元ｄx 处，E k 的方向如图（b ）所示，则金属杆PQ 上的电动势为()()222202/2d d d 2/d d 2d cos d l R l t B x r l R tB r xE lk k PQ -=-==⋅=⎰⎰θξx E证2 由法拉第电磁感应定律，有22Δ22d d d d d d ⎪⎭⎫⎝⎛-==-==l R l t B t B S t ΦE E PQ讨论 假如金属棒PQ 有一段在圆外，则圆外一段导体上有无电动势？ 该如何求解？。

第三章 静磁场1. 试用A 表示一个沿z 方向的均匀恒定磁场0B ，写出A 的两种不同表示式，证明二者之差为无旋场。

解：0B 是沿 z 方向的均匀恒定磁场，即 z B e B 00=，由矢势定义B A =⨯∇得0//=∂∂-∂∂z A y A y z ；0//=∂∂-∂∂x A z A z x ；0//B y A x A x y =∂∂-∂∂三个方程组成的方程组有无数多解，如：○10==z y A A ，)(0x f y B A x +-= 即：x x f y B e A )]([0+-=； ○20==z x A A ，)(0y g x B A y += 即：y y g x B e A )]([0+= 解○1与解○2之差为y x y g x B x f y B e e A )]([)]([00+-+-=∆ 则 0)//()/()/()(=∂∂-∂∂+∂∂+∂-∂=∆⨯∇z x y y x x y y A x A z A z A e e e A 这说明两者之差是无旋场2. 均匀无穷长直圆柱形螺线管，每单位长度线圈匝数为n ，电流强度I ，试用唯一性定理求管内外磁感应强度B 。

解：根据题意，取螺线管的中轴线为 z 轴。

本题给定了空间中的电流分布，故可由⎰⨯='430dV r rJ B πμ 求解磁场分布，又 J 只分布于导线上，所以⎰⨯=304r Id r l B πμ1)螺线管内部：由于螺线管是无限长理想螺线管，所以其内部磁场是均匀强磁场，故只须求出其中轴 线上的磁感应强度，即可知道管内磁场。

由其无限长的特性，不z y x z a a e e e r ''sin 'cos ---=φφ， y x ad ad d e e l 'cos ''sin 'φφφφ+-= )''sin 'cos ()'cos ''sin '(z y x y x z a a ad ad d e e e e e r l ---⨯+-=⨯φφφφφφz y x d a d az d az e e e '''sin '''cos '2φφφφφ+--=取''~'dz z z +的一小段，此段上分布有电流'nIdz⎰++--=∴2/32220)'()'''sin '''cos '('4z a d a d az d az nIdz z y x e e e B φφφφφπμ ⎰⎰⎰+∞∞-+∞∞-=+=+=z z I n a z a z d nI nI z a dz a d e e 02/3202/3222200])/'(1[)/'(2)'(''4μμφπμπ2)螺线管外部：由于螺线管无限长，不妨就在过原点而垂直于轴线的平面上任取一点)0,,(φρP 为场点，其中a >ρ。

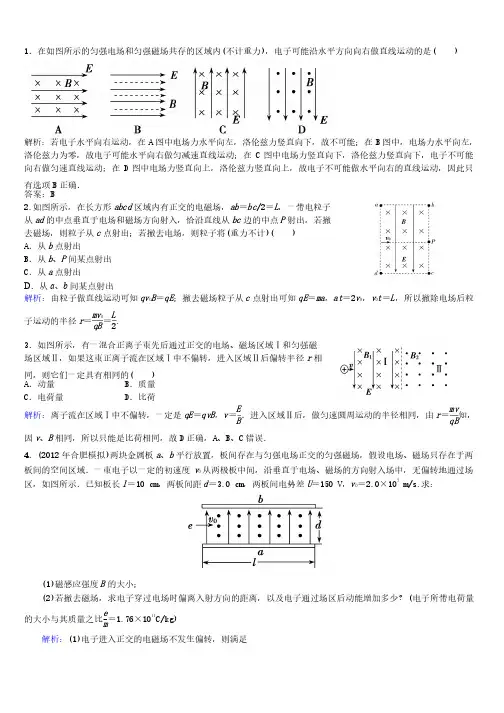
1．在如图所示的匀强电场和匀强磁场共存的区域内．在如图所示的匀强电场和匀强磁场共存的区域内((不计重力不计重力))，电子可能沿水平方向向右做直线运动的是，电子可能沿水平方向向右做直线运动的是( ( )解析：若电子水平向右运动，在A 图中电场力水平向左，洛伦兹力竖直向下，故不可能；在B 图中，电场力水平向左，洛伦兹力为零，故电子可能水平向右做匀减速直线运动；在C 图中电场力竖直向下，洛伦兹力竖直向下，电子不可能向右做匀速直线运动；在D 图中电场力竖直向上，洛伦兹力竖直向上，故电子不可能做水平向右的直线运动，因此只有选项B 正确．正确．答案：答案：B B2.2.如图所示，在长方形如图所示，在长方形abcd 区域内有正交的电磁场，ab ＝bc /2/2＝＝L ，一带电粒子，一带电粒子从ad 的中点垂直于电场和磁场方向射入，恰沿直线从bc 边的中点P 射出，若撤射出，若撤去磁场，则粒子从c 点射出；若撤去电场，则粒子将点射出；若撤去电场，则粒子将((重力不计重力不计)( )( )A ．从b 点射出点射出B ．从b 、P 间某点射出间某点射出C ．从a 点射出点射出D ．从a 、b 间某点射出间某点射出解析：由粒子做直线运动可知qv 0B ＝qE ；撤去磁场粒子从c 点射出可知qE ＝ma ，at ＝2v 0，v 0t ＝L ，所以撤除电场后粒子运动的半径r ＝mv 0qB ＝L 2. 3．如图所示，有一混合正离子束先后通过正交的电场、磁场区域Ⅰ和匀强磁．如图所示，有一混合正离子束先后通过正交的电场、磁场区域Ⅰ和匀强磁场区域Ⅱ，如果这束正离子流在区域Ⅰ中不偏转，进入区域Ⅱ后偏转半径r 相同，则它们一定具有相同的同，则它们一定具有相同的( ( ) A ．动量．动量 B B．质量．质量．质量C ．电荷量．电荷量D D D．比荷．比荷．比荷解析：离子流在区域Ⅰ中不偏转，一定是qE ＝qvB ，v ＝E B ．进入区域Ⅱ后，做匀速圆周运动的半径相同，由r ＝mv qB知，因v 、B 相同，所以只能是比荷相同，故D 正确，正确，A A 、B 、C 错误．错误．4．(2012年合肥模拟年合肥模拟))两块金属板a 、b 平行放置，板间存在与匀强电场正交的匀强磁场，假设电场、磁场只存在于两板间的空间区域．一束电子以一定的初速度v 0从两极板中间，沿垂直于电场、磁场的方向射入场中，无偏转地通过场区，如图所示．已知板长l ＝10 cm 10 cm，两板间距，两板间距d ＝3.0 cm 3.0 cm，两板间电势差，两板间电势差U ＝150 V 150 V，，v 0＝2.0×107 m/s. m/s.求：求：求：(1)(1)磁感应强度磁感应强度B 的大小；的大小；(2)(2)若撤去磁场，求电子穿过电场时偏离入射方向的距离，以及电子通过场区后动能增加多少？若撤去磁场，求电子穿过电场时偏离入射方向的距离，以及电子通过场区后动能增加多少？若撤去磁场，求电子穿过电场时偏离入射方向的距离，以及电子通过场区后动能增加多少？((电子所带电荷量的大小与其质量之比e m ＝1.76×1011C/kg)解析：(1)(1)电子进入正交的电磁场不发生偏转，则满足电子进入正交的电磁场不发生偏转，则满足电子进入正交的电磁场不发生偏转，则满足Bev 0＝e U dB ＝U v 0d＝2.5×10－4T.(2)(2)设电子通过场区偏转的距离为设电子通过场区偏转的距离为y l ＝v 0t ，a ＝eU mdy ＝12at 2＝12×eU md·(l v 0)2＝1.1×10－2m. ΔE k ＝eEy ＝e U dy ＝8.8×10－18J ＝55 eV. [例1] 在平面直角坐标xOy 中，第Ⅰ象限存在沿y 轴负方向的匀强电场，第Ⅳ象限存在垂直于坐标平面向外的匀强磁场，磁感应强度为磁感应强度为 B ．一质量为m 、电荷量为q 的带正电的粒子从y 轴正半轴上的M 点以速度v 0垂直于y 轴射入电场，经x 轴上的N 点与x 轴正方向成θ＝60°角射入磁场，最后从y 轴负半 轴上的P 点垂直于y 轴射出磁场，如图所示．不计粒子重力，求：轴射出磁场，如图所示．不计粒子重力，求：(1)M 、N 两点间的电势差UMN ；(2)(2)粒子在磁场中运动的轨道半径粒子在磁场中运动的轨道半径r ；(3)(3)粒子从粒子从M 点运动到P 点的总时间t .[思路点拨思路点拨] ] 根据粒子在不同区域内的运动特点和受力特根据粒子在不同区域内的运动特点和受力特点画出轨迹，分别利用类平抛和圆周运动的分析方法列方程求解．点画出轨迹，分别利用类平抛和圆周运动的分析方法列方程求解．[自主解答] (1)(1)设粒子过设粒子过N 点时的速度大小为点时的速度大小为 v ，有v 0v＝cos θ,v ＝2v 0粒子从M 点运动到N 点的过程，有qu MN ＝12mv 2－12mv 20，U MN ＝3mv 202q . (2)(2)粒子在磁场中以粒子在磁场中以O ′为圆心做匀速运动，半径为O ′N ，有qvB ＝mv 22r ，r ＝2mv 0qB . (3)(3)由几何关系得由几何关系得ON ＝r sin θ设粒子在电场中运动的时间为t 1，有ON ＝v 0t 1t 1＝3mqB粒子在磁场中做匀速圆周运动的周期T ＝2πm qB设粒子在磁场中运动的时间为t 2，有，有t 2＝π－θ2πT ，故t 2＝2πm 3qBt ＝t 1＋t 2，t ＝33＋2πm 3qB .1．如图所示．如图所示 ，匀强电场区域和匀强磁场区域是紧邻的，且宽度相等均为d ，电场方向在纸平面内竖直向下，而磁场方向垂直于纸面向里，一带正电的粒子从O 点以速度v 0沿垂直电场方向进入电场，从A 点射出电场进入磁场，离开电场点时的速度方向一致，已知d 、v 0(带电粒子重力不计带电粒子重力不计))，求：，求：(1)(1)(1)粒子从粒子从C 点穿出磁场时的速度大小v ；(2)(2)电场强度电场强度E 和磁感应强度B 的比值E B .解析：(1)(1)粒子在电场中偏转时做类平抛运动，则粒子在电场中偏转时做类平抛运动，则粒子在电场中偏转时做类平抛运动，则垂直电场方向d ＝v 0t ，平行电场方向d 2＝v y2t 得v y ＝v 0，到A 点速度大小为v ＝2v 0在磁场中速度大小不变，所以从C 点出磁场时速度大小仍为2v 0.(2)(2)在电场中偏转时，出在电场中偏转时，出A 点时速度与水平方向成45°45° v y ＝qE m t ＝qEd mv 0，并且v y ＝v 0得E ＝mv 20qd在磁场中做匀速圆周运动，如图所示在磁场中做匀速圆周运动，如图所示由几何关系得R ＝2d又qvB ＝mv 22R ，且v ＝2v 0 得B ＝mv 0qd 解得E B ＝v 0.[例2] 如右图所示，在磁感应强度为B 的水平匀强磁场中，有一足够长的绝缘细棒OO ′在竖直面内垂直于磁场方向放置，细棒与水平面夹角为α.一质量为m 、带电荷量为＋q 的圆环A 套在OO 圆′棒上，圆环与棒间的动摩擦因数为μ，且μ<tan α.现让圆环A 由静止开始下滑，试问圆环在下滑过程中：由静止开始下滑，试问圆环在下滑过程中：(1)(1)圆环圆环A 的最大加速度为多大？获得最大加速度时的速度为多大？的最大加速度为多大？获得最大加速度时的速度为多大？(2)(2)圆环圆环A 能够达到的最大速度为多大？能够达到的最大速度为多大？[思路点拨][自主解答] (1)(1)由于由于μ<tanα，所以环将由静止开始沿棒下滑．环A 沿棒运动的速度为v 1时，受到重力mg 、洛伦兹力qv 1B 、杆的弹力F N1和摩擦力F f 1＝μF N1.根据牛顿第二定律，对圆环A 沿棒的方向：沿棒的方向：mg sin α－F f 1＝ma垂直棒的方向：F N1＋qv 1B ＝mg cos α所以当F f 1＝0(0(即即F N1＝0)0)时，时，a 有最大值a m ，且a m ＝g sin α此时qv 1B ＝mg cos α解得：v 1＝mg cos αqB. (2)(2)设当环设当环A 的速度达到最大值v m 时，环受杆的弹力为F N2，摩擦力为F f 2＝μF N2.此时应有a ＝0，即mg sin α＝F f 2在垂直杆方向上：F N2＋mg cos α＝qv m B解得：v m ＝mg sin α＋μcos αμqB. 2．如图所示，套在很长的绝缘直棒上的小球,质量为 1.0×10－4 kg ，带 4.0×10－4 C 正电荷，小 球在棒上可以滑动，将此棒竖直放置在沿水平方向的匀强电场和球在棒上可以滑动，将此棒竖直放置在沿水平方向的匀强电场和匀强磁场中．匀强电场的电场强度E ＝10 N/C 10 N/C，方向水平向右，，方向水平向右，，方向水平向右，匀强磁场的磁感应强度B ＝0.5 T 0.5 T，方向为垂直纸面向里，小球与棒，方向为垂直纸面向里，小球与棒，方向为垂直纸面向里，小球与棒间动摩擦因数为μ＝0.20.2，求小球由静止沿棒竖直下落的最大加速度，求小球由静止沿棒竖直下落的最大加速度，求小球由静止沿棒竖直下落的最大加速度和最大速度．和最大速度．((设小球在运动过程中所带电荷量保持不变，g 取10 m/s2)解析：带电小球沿绝缘棒下滑过程中，受竖直向下的重力，竖直向上的摩擦力，水平方向弹力和洛伦兹力及电场力作用．当小球静止时，弹力等于电场力，小球在竖直方向所受摩擦力最小，小球加速度最大，小球运动过程中，弹力等于电场力与洛伦兹力之和，随着小球运动速度的增大，小球所受洛伦兹力增大，小球在竖直方向的摩擦力也随之增大，小球加速度减小，速度增大，当球的加速度为零时，速度达最大．小球刚开始下落时，加速度最大，设为a m ，这时竖直方向有mg －F f ＝ma ①在水平方向上有qE －F N ＝0②又F f ＝μF N ③由①②③解得a m ＝mg －μqE m，代入数据得a m ＝2 m/s 2. 小球沿棒竖直下滑，当速度最大时，加速度a ＝0在竖直方向上mg －F ′f ＝0④在水平方向上qv m B ＋qE －F N ′＝′＝00⑤又F ′f ＝μF N ′⑥′⑥ 由④⑤⑥解得v m ＝mg －μqE μqB， 代入数据得v m ＝5 m/s.[例3] 如图所示 ，在磁感应强度为B 的匀强磁场中，有一与磁感线垂直且水平放置的、长为L 的摆线，拴一质量为m 、带有＋q 电荷量的摆球，若摆球始终能在竖直平面内做圆弧运动．试求 摆球通过最低位置时绳上的拉力F 的大小．的大小．[思路点拨思路点拨] ] 解答此题应把握以下两点：解答此题应把握以下两点：(1)(1)弹力和洛伦兹力都随小球速度改变而改变，但这两力不做功，只有重力做功．弹力和洛伦兹力都随小球速度改变而改变，但这两力不做功，只有重力做功．弹力和洛伦兹力都随小球速度改变而改变，但这两力不做功，只有重力做功．(2)(2)在最低点应用牛顿第二定律求解．在最低点应用牛顿第二定律求解．在最低点应用牛顿第二定律求解．[自主解答] 以摆球为研究对象．以摆球为研究对象．根据机械能守恒定律得：mgL ＝12mv 2m ， 当向左摆动，到最低点速度向左时F 洛的方向向下．的方向向下．由牛顿第二定律得：F －mg －F 洛＝mv 2m /L ，且：F 洛＝qv m B ，联立以上各式解得：F ＝3mg ＋qB 2gL .当向右摆动，到最低点的速度向右时，F 洛的方向则向上．的方向则向上．由牛顿第二定律得：F ＋F 洛－mg ＝mv 2m /L ，联立解得：F ＝3mg －qB 2gL .3．在竖直平面内半圆形光滑绝缘管处在如图所示的匀强磁场中，B ＝1.1 T ，半径R ＝0.8 m ，其直径AOB 在竖直线上．圆环平面与磁场方向垂直，在管口A 处以2 m/s 水平速度射入一个直径略小于管内径的带电小球，其电荷量为＋10－4 C ，问：(1)小球滑到B 处的速度为多少？(2)若小球从B 处滑出的瞬间，管子对它的弹力恰好为零，小球质量为多少？(g ＝10 m/s2)解析：(1)(1)小球从小球从A 到B ，利用动能定理得，利用动能定理得mg 2R ＝12mv 2B －12mv 2A得v B ＝v 2A ＋4gR ＝22＋4×10×0.8＋4×10×0.8 m/s m/s m/s＝＝6 m/s. (2)(2)在在B 点，小球受到的洛伦兹力方向指向圆心，由于小球做圆周运动，所以有qv B B －mg ＝mv 22B R 即：即：1010－4×6×1.1－×6×1.1－1010m ＝36m 0.8得m ＝1.2×10－－55 kg.2.(2012年淮北模拟年淮北模拟))如图所示，空间存在正交的匀强电场和匀强磁场，匀强电场方向竖直向上，匀强磁场的方向垂直纸面向里．有一内壁光滑、底部有带正电小球的试管．在水平拉力F 作用下，试管向右匀速运动，带电小球能从试管口处飞出．口处飞出．已知小球质量为已知小球质量为m ，带电量为q ，场强大小为E ＝mg q.关于带电小球及其在离开试管前的运动，关于带电小球及其在离开试管前的运动，下列说法中不下列说法中不正确的是正确的是( ( )A ．洛伦兹力对小球不做功．洛伦兹力对小球不做功B ．洛伦兹力对小球做正功．洛伦兹力对小球做正功C ．小球的运动轨迹是一条抛物线．小球的运动轨迹是一条抛物线D ．维持试管匀速运动的拉力F 应逐渐增大应逐渐增大解析：洛伦兹力方向始终与小球运动速度方向垂直，不做功，故A 正确、正确、B B 错误；小球在竖直方向受向上的电场力与向下的重力，二者大小相等，试管向右匀速运动，小球的水平速度保持不变，则竖直向上的洛伦兹力分量大小不变，小球竖直向上做匀加速运动，即小球做类平抛运动，故C 正确；小球竖直分速度增大，受水平向左的洛伦兹力分量增大，为维持试管匀速运动拉力F 应逐渐增大，应逐渐增大，D D 正确．正确．答案：答案：B B3．(2012年铜陵模拟年铜陵模拟))如图所示的装置，左半部分为速度选择器，右半部分为匀强的偏转电场．一束同位素离子流从狭缝S 1射入速度选择器，能够沿直线通过速度选择器并从狭缝S 2射出的离子，又沿着与电场垂直的方向，立即进入场强大小为E 的偏转电场，最后打在照相底片D 上．已知同位素离子的电荷量为q (q >0)>0)，速度选择器内部存在着相互垂，速度选择器内部存在着相互垂直的场强大小为E 0的匀强电场和磁感应强度大小为B 0的匀强磁场，照相底片D 与狭缝S 1、S 2的连线平行且距离为L ，忽略重力的影响．忽略重力的影响．(1)(1)求从狭缝求从狭缝S 2射出的离子速度v 0的大小；(2)(2)若打在照相底片上的离子在偏转电场中沿速度若打在照相底片上的离子在偏转电场中沿速度v 0方向飞行的距离为x ，求出x 与离子质量m 之间的关系式之间的关系式((用E 0、B 0、E 、q 、m 、L 表示表示))．解析：(1)(1)能从速度选择器射出的离子满足能从速度选择器射出的离子满足能从速度选择器射出的离子满足qE 0＝qv 0B 0①故v 0＝E 0B 0② (2)(2)离子进入匀强偏转电场离子进入匀强偏转电场E 后做类平抛运动，则后做类平抛运动，则x ＝v 0t ③L ＝12at 22④ 由牛顿第二定律得qE ＝ma ⑤由②③④⑤解得x ＝E 0B 0 2mL qE4.(2010年高考课标全国卷年高考课标全国卷))如图所示，在0≤x ≤a 、0≤y ≤a2范围内垂直于xOy 平面向外的匀强磁场，磁感应强度大小为B 坐标原点O 处有一个粒子源，在某时刻发射大量质量为m 、电荷量为q 的带正电粒子，它们的速度大小相同，速度方向均在xOy 平面内，与y 轴正方向的夹角分布在0～90°范围内．已知粒子在磁场中做圆周运动的半径介于a /2到a 之间，从发射粒子到粒子全部离开磁场经历的时间恰好为粒子在磁场中做圆周运动周期的四分之一．求最后离开磁场的粒子从粒子源射出时的磁场的粒子从粒子源射出时的(1)(1)速度的大小；速度的大小；速度的大小；(2)(2)速度方向与速度方向与y 轴正方向夹角的正弦．轴正方向夹角的正弦．解析：(1)(1)设粒子的发射速度大小为设粒子的发射速度大小为v ，粒子做圆周运动的轨道，粒子做圆周运动的轨道半径为R ，由牛顿第二定律和洛伦兹力公式得：，由牛顿第二定律和洛伦兹力公式得： qvB ＝mv 2R① 由①式得R ＝mv qB ②当a 2<R <a 时，在磁场中运动时间最长的粒子，其轨迹是圆心为C 的圆弧，圆弧与磁场的上边界相切，如图所示．的圆弧，圆弧与磁场的上边界相切，如图所示． 设该粒子在磁场中运动的时间为t ，依题意t ＝T 4，得，得 ∠OCA ＝π2③设最后离开磁场的粒子的发射方向与y 轴正方向的夹角为α，由几何关系得，由几何关系得R sin α＝R －a 2④ R sin α＝a －R cos α⑤又sin 2α＋cos 2α＝1⑥由④⑤⑥式得R ＝(2(2－－62)a ⑦ 由②⑦式得v ＝(2(2－－62)aqB m(2)(2)由④⑦式得：由④⑦式得：由④⑦式得：sin sin α＝6－610. [例1] 在真空中，半径r ＝3×10－2m 的圆形区域内有匀强磁场，方向如图所示，磁感应强度B ＝0.2 T ，一个带正电的粒子以初速度v 0＝106 m/s 从磁场边界上直径ab 的一端a 射入磁场，已知该粒子的比荷q m ＝108C/kg C/kg，不计粒子重，不计粒子重力．(1)(1)求粒子在磁场中做匀速圆周运动的半径；求粒子在磁场中做匀速圆周运动的半径；(2)(2)若要使粒子飞离磁场时有最大偏转角，若要使粒子飞离磁场时有最大偏转角，求入射时v 0与ab 的夹角θ及粒子的最大偏转角．及粒子的最大偏转角．[解析] (1)(1)粒子射入磁场后，由于不计重力粒子射入磁场后，由于不计重力粒子射入磁场后，由于不计重力,,所以洛伦兹力提供圆周运动需要的向心力，根据牛顿第二定律有：qv 0B ＝m v 220R ， R ＝mv 0qB ＝5×10－2m. (2)(2)粒子在圆形磁场区域运动轨迹为一段半径粒子在圆形磁场区域运动轨迹为一段半径R ＝5 cm 的圆弧，要使偏转角最大，就要求这段圆弧对应的弦最长，即为圆形区域的直径，粒子运动轨迹的圆心O ′在ab 弦中垂线上，如上图所示．由几何关系可知：知：sin θ＝r R ＝0.60.6，，θ＝37°＝37°最大偏转角β＝2θ＝74°.＝74°.[例2] 如图所示，半径为r ＝0.1 m 的圆形匀强磁场区域边界跟y 轴相切于坐标原点O ，磁感应强度B ＝ 0.332 T 方，方向向垂直纸向面向里里．在O 有处有一一射放射源源，可沿纸向面向各各方个方向向射出速率均为v ＝3.2×106 m/s 的α粒子．已知α粒子质量m ＝6.646.64××1010－－27kg 27kg，电荷量，电荷量q ＝3.23.2××1010－－19C 19C，不计，不计α粒子的重力．求α粒子在磁场中运动的最长时间．动的最长时间．m v R 得＝mv ＝粒子在磁场中运动的圆弧所对应的弦长最长，从右图可以看出，粒子在磁场中运动的时间最长．粒子在磁场中运动的时间最长．＝2πm qB ，运动时间＝2θ2π·＝r R ＝y 轴上的a 点射入右图中第可在适当的地方加一个垂直于的匀强磁场，若此磁场分布在一个圆形区域内，试求这个圆形磁场区域的最小面积．的匀强磁场，若此磁场分布在一个圆形区域内，试求这个圆形磁场区域的最小面积．[解析] 质点在磁场中做半径为＝mv 0qB 的圆周运动，根据题意，质点在磁场区域中的轨道为半径等于的圆上的的圆上的113圆周，这段圆弧应与入射方向的速度，出射方向的速度相切，如右图所示．则到入射方向所在直线和出射方向所在直线相距为R 的O ′点就是圆周的圆心．质点在磁场区域中的轨道就是以和f 点应在所求圆形磁场区域的边界上，在通过即得圆形磁场区域的最小半径sin 60°＝3mv 02qB＝34π(mv 0qB )。

磁场补充练习题题组一1．如图所示，在xOy 平面内，y ≥ 0的区域有垂直于xOy 平面向里的匀强磁场，磁感应强度为B ，一质量为m 、带电量大小为q 的粒子从原点O 沿与x 轴正方向成60°角方向以v 0射入，粒子的重力不计，求带电粒子在磁场中运动的时间和带电粒子离开磁场时的位置。

2．如图所示，abcd 是一个正方形的盒子，在cd 边的中点有一小孔e ，盒子中存在着沿ad 方向的匀强电场，场强大小为E ，一粒子源不断地从a 处的小孔沿ab 方向向盒内发射相同的带电粒子，粒子的初速度为v 0，经电场作用后恰好从e 处的小孔射出，现撤去电场，在盒子中加一方向垂直于纸面的匀强磁场，磁感应强度大小为B （图中未画出），粒子仍恰好从e 孔射出。

（带电粒子的重力和粒子之间的相互作用均可忽略不计） （1）所加的磁场的方向如何？（2）电场强度E 与磁感应强度B 的比值为多大？题组二3．长为L 的水平极板间，有垂直纸面向里的匀强磁场，磁感应强度为B ，板间距离也为L ，极板不带电。

现有质量为m ，电荷量为q 的带正电粒子(重力不计)，从左边极板间中点处垂直磁场以速度v 水平射入，如图所示。

为了使粒子不能飞出磁场，求粒子的速度应满足的条件。

4．如图所示的坐标平面内，在y 轴的左侧存在垂直纸面向外、磁感应强度大小B 1 = 0.20 T 的匀强磁场，在y 轴的右侧存在垂直纸面向里、宽度d = 0.125 m 的匀强磁场B 2。

某时刻一质量m = 2.0×10-8 kg 、电量q = +4.0×10-4 C 的带电微粒（重力可忽略不计），从x 轴上坐标为（-0.25 m ，0）的P 点以速度v = 2.0×103 m/s 沿y 轴正方向运动。

试求： （1）微粒在y 轴的左侧磁场中运动的轨道半径；（2）微粒第一次经过y 轴时速度方向与y 轴正方向的夹角； （3）要使微粒不能从右侧磁场边界飞出,B 2应满足的条件。

第七章 稳恒磁场习题7-1 一个半径为r 的半球面如图放在均匀磁场中，通过半球面的磁通量为多少？解：取平面S ’与半球面S 构成闭合曲面，根据高斯定理有 0m mS mS ΦΦΦ'=+=2cos mS mS r E ΦΦπα'=-=-球面外法线方向为其正方向7-2 如图所示，几种载流导线在平面内分布，电流均为I ，它们在点O 的磁感应强度各为多少？08IR μ垂直画面向外0022II RR μμπ-垂直画面向里 00+42I IR Rμμπ垂直画面向外 7-3 如图所示，两根导线沿半径方向引向铁环上的A ，B 两点，并在很远处与电源相连。

已知圆环的粗细均匀，求环中心O 的磁感应强度。

解： 如图所示，圆心O 点磁场由直电流∞A 和∞B 及两段圆弧上电流1I 与2I 所产生，但∞A 和∞B 在O 点产生的磁场为零。

且θ-πθ==21221R R I I 电阻电阻 1I 产生1B 方向⊥纸面向外πθπμ2)2(2101-=R I B2I 产生2B 方向⊥纸面向里πθμ22202R I B =∴1)2(2121=-=θθπI I B B 有0210=+=B B B7-4 如图所示，已知地球北极地磁场磁感强度B 的大小为6.0×10－5T 。

如设想此地磁场是由地球赤道上一圆电流所激发的，此电流有多大？流向如何？（已知圆电流轴线上北极点的磁感强度()R IRR IR B 24202/32220μμ=+=）解：9042 1.7310A RBI μ==⨯方向如图所示7-5 有一同轴电缆，其尺寸如题图所示．两导体中的电流均为I ，但电流的流向相反，导体的磁性可不考虑。

试计算以下各处的磁感应强度：（1）r<R 1；（2）R 1<r<R 2；（3）R 2<r<R 3；（4）r>R 3。

解：同轴电缆的电流分布具有轴对称性在电缆各区域中磁感应线是以电缆轴线为对称轴的同心圆。

穩恒磁場鞏固練習題§1Biot-Savart'law1.无限长的直导线载流I，距离导线x处的磁感应强度大小为；沿着直线运动的电荷，其运动的正前方的磁感应强度大小为2.相互平行的直导线之间距离为d；电流大小都是I，方向相反；则两导线中点位置的磁场B=3.半径为R的单匝环形导线载有电流I，环心处的磁感应强度为；该电流的磁矩为4.半径为R的两个单匝圆形线圈正交放置，其圆心重合。

若两个线圈中的电流大小都是I，则圆心处的磁场B=，两个电流环的总磁矩大小为5.边长为0.1m，匝数为1000的正方形线圈，通电0.5A，其磁矩大小为6.如下图所示，几种载流导线在平面内分布，电流均为I，它们在O点的磁感应强度各为多少？§2磁場的高斯定理、安培環路定理7.下图中两导线中的电流绝对值分别为I 1，I 2，写出下列环路积分的值˛L 1B ·d l =˛L 2B ·d l =˛L 3B ·d l =8.如下图所示，直线电流I 从立方体的两个相对表面的中心穿过，则˛abcda B ·d l =¨abcd B ·d S =˛bcgfbB ·d l =¨bcgfB ·d S =9.无限长的空心直螺线管，线圈数密度为n ，横截面积为S ，载流I ，则其管内的磁场B =，横截面上的磁通量为§3洛侖茲力、安培力10.一个电子以速度v=(5×104j)m/s的速度射入均匀磁场B=(0.4i+0.5j)T 中，受到的洛仑兹力F=11.一电荷q在均匀磁场B中运动，判断下列说法是否正确，并说明理由。

(1)只要速度大小相同，所受的洛仑兹力就相同。

(2)在速度不变的前提下，电荷q改为−q，受力的方向逆转，数值不变。

(3)电荷q改变为−q，速度方向也反向，则受力的方向逆转，数值不变。

(4)v,B,F三个矢量，已知任意两个，就能确定第三个量。