当前位置：文档之家 › §2 共轴球面光学系统

§2 共轴球面光学系统

  • 格式：ppt
  • 大小：489.00 KB
  • 文档页数：13

下载文档原格式

  / 13

合集下载

第二章_共轴球面系统的物像关系

第二章_共轴球面系统的物像关系

uk
u1 , h1 解法二
u ' n' un
' un
l1
解法三
h n' n r
' un 1 un
' ' un , ln
' un 1 un ' ln 1 ln d n
ri ' u'
同样可得：
l' r
l 'u ' u ' i ' r
' 显然 h lu l 'u,代入上式，并在第一式两边同乘以n， 第二式两侧同乘以n '
nh nu ni r
n' h n' u ' n' i ' r
将以上二式相减，并考虑到
n sin I n' sin I '
d—由前一面顶点算起到下一面顶点。
2．角度： 一律以锐角度量，顺时针转为正，逆时针转为负。 角度也要规定起始轴： U、U'—由光轴起转到光线； I、I'—由光线起转到法线； ψ—由光轴起转到法线，
应用时，先确定参数的正负号，代入公式计算。 算出的结果亦应按照数值的正负来确定光线的相对位置。 推导公式时，也要使用符号规则。
注意 为了使导出的公式具有普遍性，推导公式时，几何 图形上各量一律标注其绝对值，永远为正
反射情形 看成是折射的一种特殊情形： n’= －n 把反射看成是n’= －n 时的折射。 往后推导公式时，只讲折射的公式；对于反射情形， 只需将n’用－n代入即可，无需另行推导。
Q
P
I
I’
-U A O φ C Uˊ Aˊ
l ' f (n, n' , r , l )

第二章 共轴球面系统(二)

第二章 共轴球面系统(二)
= l2u2 l'1 u'1d1u'1 ,l3u3 l'2 u'2 d2u'2 , lkuk l'k1 uk1 dk1uk1
共轴球面系统的过渡公式（3-2）
lu l'u' h
l1u1 l'1 u'1 h1 ,l2u2 l'2 u'2 h2 ,
l2u2 l'1 u'1d1u'1 ,l3u3 l'2 u'2 d2u'2 , lkuk l'k1 uk1 dk1uk1
拉格朗日- 赫姆霍兹恒等式
y' nl'
y n'l
lu l'u'
J为拉赫不变量 nuy n'u' y' J
题 例 1：在一直径为30cm的球形玻璃鱼缸内盛满水，鱼缸中
心处有一条小鱼，求缸外观察者看到鱼的位置及放大率！
解： n n n n l' l r
n' 4 ,l 15, r 15代入 3
定义：通过一定光学系统所成的像对光轴的 垂直高度与物本身对光轴的垂直高度的比。
公式：
y'
y
近轴区的放大率
-u
u’
近轴区的放大率----横向放大率
y'
y
y' l'r y l r
n(1 1) n'(1 1)
rl
r l'
物像位置关系式
n l r n' l' r
rl
rl'
l r l' r n' l nl'
n'k 2

第2章 共轴球面系统的物像关系

第2章 共轴球面系统的物像关系
12
• 二、轴向放大率（倍率）α 轴向放大率（倍率） • 如果轴上物点移动，那么，像点也必然移动。 如果轴上物点移动，那么，像点也必然移动。
如图2.3-2，设物点A沿轴移动 dl ，那么像点移 如图 ，设物点 沿轴移动 动dl' ，则沿轴放大率定义为 dl'
α=
对式(2-12)进行微分得 进行微分得 对式
5
• 当角度足够小时，上述角度的正弦值与弧度值 几乎没有差别，此时角度U,I,U',I' 的正弦值可 以用相应的弧度值u,i,u',i' 来代替。为了区别， 也用小写字母 表示，见图2.2-1。因为这种光线 很靠近光轴，所以称为近轴光线。
6
对于近轴光线， 对于近轴光线，其光路计算公式可以直接由上 节公式得到， 节公式得到，这只要将其中的角度的正弦值用弧 度值来代替即可
9
§2-3 单个折射球面的成像放大率及拉赫不变量
折射面对有限大小的物体成像时， 折射面对有限大小的物体成像时，就产生了 像的放大率问题，像的虚实、正倒的问题， 像的放大率问题，像的虚实、正倒的问题，下 面在近轴区内予以讨论。 面在近轴区内予以讨论。 • 一、垂轴放大率（倍率）β 垂轴放大率（倍率） • 在折射球面的近轴区，如图2.3-1，垂轴小线 在折射球面的近轴区，如图 ， 如果由点B作 段AB，通过折射球面成像 ，通过折射球面成像A'B' 。如果由点 作 一通过曲率中心C的直线 的直线BC，显然， 一通过曲率中心 的直线 ，显然，该直线应 通过点B' 对于该球面来说也是一个光轴， 通过点 。BC对于该球面来说也是一个光轴， 对于该球面来说也是一个光轴 称为辅轴。由辅轴上点B发出沿轴光线必然不 称为辅轴。由辅轴上点 发出沿轴光线必然不 近轴区的物高AB以 表 发生折射地到达像点 。近轴区的物高 以y表 像高以- 。 示，像高以 y'。像的大小和物的大小的比值 称为垂轴放大率 垂轴放大率β 称为垂轴放大率 y' •

工程光学第2章 共轴球面光学系统

工程光学第2章 共轴球面光学系统
10
共轴球面光学系统
§2.4
共轴球面系统的成像
11
1. 过渡公式
共轴球面光学系统
, n3 n2 , , nk nk 1 n2 n1 , u3 u2 , , uk uk 1 u2 u1 , y3 y2 , , yk yk 1 y2 y1
a b 2
单个反射球面成像
1 1 2 l l r f f r 2
b 1
物点位于球心时
a 1
g 1 b
g 1
9
共轴球面光学系统
b l l
a b 2
g 1 b
J uy uy
球面镜的拉赫不变量
结论
a<0，物体沿光轴移动时，像总是以相反方向移动。 通过球心的光线沿原光路反射。 反射球面镜的焦距等于球面半径的1/2。
3、角放大率g
g
u l n n' l n 1 u l n' nl n' b
n
ag b
n
h
I
nuy nuy J
单折射球面光学系统 拉赫不变量
I
y
U
o

U
r
l'
y
-l
7
共轴球面光学系统
结论：
1.

b是有符号数，具体表现为
成像正倒：当b>0时，表明y’、y同号，成正像；否则，成倒像。 成像大小：当|b|＝1时，表明|y’|=|y|，像、物大小一致；|b|>1时， 表明|y’|>|y|，成放大的像；反之，成缩小的像。 成像虚实：当b>0时，表明l’、l同号，物像同侧，虚实相反；否 则，物像异侧，虚实相同。

应用光学 第二章 球面和球面系统

应用光学 第二章 球面和球面系统

一.符号规则
1、沿轴线段：L、 L 、r以折射球面（或反射面）
顶点O为原点，到光线与光轴交点或球心的方向 与光线的传播方向相同，其值为正，反之为负；
2、垂轴线段：以光轴为基准，在光轴上为正，反 之为负； 3、孔径角U和U′ ：光轴以锐角方向转到光线，顺 时针为正，逆时针为负； 4、光线与法线的夹角：I 和I′ ，光线以锐角方向 转到法线，顺时针为正，逆时针为负； 5、光轴与法线的夹角 ：光轴以锐角方向转向法 线，顺时针为正，逆时针为负； 6、折射面之间的间隔：在折射系统中，d恒为正。
3：已知一个光学系统的结构参数，r = 36.48mm, n=1, n’=1.5163 l = - 240mm, y=20mm 已求出：l’=151.838mm，现求 β, y’ （横向放大率与像的大小）
l2 l'1 d1 ,l3 l'2 d 2 ......lk l'k 1 d k 1
当只关心物像位置且折射面很少时，用方法2较为 方便。如需知道一些中间量且折射面较多时，多 采用方法1。
第五节 球面反射镜
一.球面反射镜的物像位置
1 1 2 l' l r
实物成实像
三个放大率之间的关系：

第四节 共轴球面系统
※光学系统一般是轴对称的，有一条公共轴线， 称为光轴。这种系统被称为“共轴系统”
光轴
一个共轴球面系统的结构参数由下列数值确定 （如有 k 个折射面）：各个折射面的曲率半 径 r1 ,r2 ,r3 rk ；各个折射球面的顶点之间的间 隔 d1 , d 2 , d3 dk-1 。各球面间的介质折射 率 n1 , n2 , n3 nk+1 ，其中 nk+1 nk

第二章 共轴球面系统中的光路计算公式汇总

第二章 共轴球面系统中的光路计算公式汇总
What’s the use of paraxial optics 1. As a criterion to scale the factual optical system. Paraxial optics is a perfect optical system so it images perfectly.
r1 10
r2 50
d 1 5 n2 1.5163 K9
空气
L1 100 L1 100 L1 100
U1 1 U1 2 U1 3
L1 ' 35.969 L1 ' 34.591 L1 ' 32.227
§2-3 球面近轴范围内的成像性质和近轴光路计算公式
Optical path calculation formula
Known:
n，n'，r，L，U
1. sin I
Lr sinU r n 2. sin I ' sin I n' 3. U ' I U I ' sin I ' 4. L' r r sin U '
L '，U '
n2 n1 '
u2 u1 '
1
2
u1
h1
d1 n1
n2 n1 '
h2
u2 u1 '
n2 '
1. Positional relations of object and image
h n' u 'nu (n'n) r
u' u l', l h h
n' n n' n l' l r

共轴球面光学系统特点

共轴球面光学系统特点

共轴球面光学系统特点
共轴球面光学系统是一种采用球面反射镜的光学系统，它由一个球面
反射镜和一个准直物镜组成，它可以聚焦起一束高度集中的光束来实现观
测或其他应用目的。

共轴球面光学系统能够提供高度集中的光束，使其能
够在极短的像差范围内获得高质量的图像，在科学、工业、医学、检测等
领域有着广泛的应用。

其主要特点有：
1、透射特性卓越：由于共轴球面光学系统采用的球面反射镜是镀铬
或钎焊的，具有良好的光学性能，其较高的反射率可以使光的各种波长的
透射率都达到较高的水平。

2、聚焦效果好：由于共轴球面光学系统采用的设计原理是根据透镜
来实现聚焦，因此可以较好的实现视野的高度放大，使其能够有效聚焦。

3、维护方便：共轴球面光学系统采用的是球面反射镜，它只需要定
期清洁即可，而且它没有润滑要求，所以维护非常方便。

4、耐用性强：共轴球面光学系统采用的是优质的、耐用的球面反射镜，可以保证长期使用的稳定性，耐用性也很强。

5、体积小：共轴球面光学系统采用的是非折射性镜片，所以体积小，可以更容易地应用于有空间限制的系统中。

第二章球面和共轴球面系统分析

第二章球面和共轴球面系统分析
要讨论成像规律，即像的虚实，成像的位置、正倒和大 小问题，必须计算出光线的走向，所以我们先讨论计算公式。 光线经过单个折射球面的情况如图所示。 包含光轴和物点的平面称为含轴面（纸面）或子午面。 计算的目的：光从何处来，经何处到哪里去（由此得出由物 点发出的光线经过系统后能否交到一点完善成像）？
首要问题：用什么量（怎样）来决定光线在空间中的位置？
对AEC应用正弦定理得 L r r Lr 即 sin I sin U 可求出I sin I sin （ U） r n 据折射定律 sin I ` sin I 可求出I ` n` 对AEC和A`EC应用外角定理 U I U ` I ` U ` U I I ` 可得到U ` sin I ' sin U ' sin I 在A ' EC中 ，利用正弦定律 L ' rr L ' r r sin U
从光轴起算，光轴转向光线（按锐角方向）， 顺时针为正，逆时针为负。
入射角、折射角 从光线起算，光线转向法线（按锐角方向）， 顺时针为正，逆时针为负。 ③ 光轴与法线的夹角（如） 从光轴起算，光轴转向法线（按锐角方向）， 顺时针为正，逆时针为负。
二、实际光线经过单个折射球面的光路计算
已知：折射球面曲率半径r，介质折射率n和n′，及物方坐标L和U。 求：像方L ′和 U ′。
共轴球面系统由许多单个球面构成，当计算出第一面后， 其折射光线就是第二面的入射光线。
U 2 U1; L2 L1 d1
再由相邻两折射球面间的关系，求出下一个球面的折 射光线。
第四节 球面反射镜成像
n n n n 成像公式： l l r

n n
1 1 2 l l r

应用光学第二章共轴球面系统的物像关系

应用光学第二章共轴球面系统的物像关系
I’=-I • 往后推导公式，都只讲折射，对反射
情形，只需将n’=-n代入即可无须另行 推导。
第3节 球面近轴范围内的成像性质 和近轴光路计算公式
• 研究光线通过球面后成像规律和特性，找出理想成像范围
• 例子：对一个单透镜进行三条光线的实际计算，透镜结构 参数为：
– r1=10
n1=1.0
空气
–
d1=5 n1’=n2=1.5163 玻璃（K9）
5.90945
24.5908
34.5908
22.57512 14.66568
34.5908 5.90945
-3°
-100 10
-11 -0.05234
0.57570 35.14835
0.37967 22.31332
9.83503
22.22743
32.22743
35.14835 22.31332
32.22743 9.83503
P1
P2 U1’=U2
A
O1
O2L1’ A2’
A1’(A2)
d1
L2
第2节 符号规则
• 符号规则
• 在实际光学系统中，光线和球面位置可能是各种各样的， 为了是光路计算公式普遍适用于各种情况，必须规定一套 符号规则。符号规则直接影响公式的形式。
• 各参量的符号规则规定如下：
– 线段：规定从左到右为正，从下到上为正，反之为负。
L’ L
第1节 共轴球面系统中的光路计算公式
• 转面公式：
• 计算完第一面后，其折射光线就是第二面的入射光线。
L2 L1 ' d1
U2 U1 ' (2-5)
sin I L r sinU r
sin I ' n sin I n'

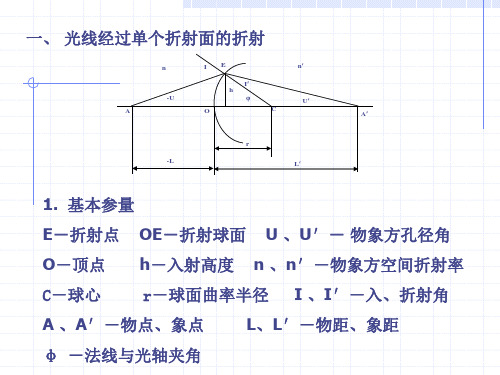
应用光学第二章球面与共轴球面系统

应用光学第二章球面与共轴球面系统

sin I L r sinU r
n
IE
n′
I′
sin I n sin I n
h
-U
φ
U′
A
O
C
A′
U U I I r
L r r sin I
-L
L′
sinU
说明：
1）L′＝f (U、L、n、n′、r) 2）当L为定值时，L′随U变化而变化，象方光束失去同心性， 成不完善象，形成球差。
d）光线与法线夹角I、I′ 以光线转向法线成的锐角来度量，顺时针为“＋”
逆时针为“－” e）光轴与法线的夹角φ 以光轴转向法线成的锐角来度量，顺时针为“＋”
逆时针为“－” f）折射面的间隔d，一般取“＋” g）所有参量是含符号的量，但图示标为参量的大小。
二、 远轴光的计算公式（实际光线光路计算） 给定n、 n′、r，已知L、U，求解L′、 U′ 其中U、 U′较大，远轴光线成像（大光路）
1
4）三者关系：
nk 2 n1 1 n1 nk
4. 拉赫不变量： J n1u1 y1 nk uk yk
意义： J对整个光学系统的每个折射面的物象空间都是不变量，可用J来
校对光路计算是否正确。
例：厚透镜：
例：一玻璃棒（n=1.5），长500mm，两端面为半球 面，半径分别为50mm和100mm，一箭头高1mm，垂 直位于左端球面顶点之前200mm处的轴线上，求箭头 经玻璃棒成像后像的位置、大小、正倒、虚实。
§ 2－3 共轴球面系统
探讨方法— 将光线的光路计算公式及放大率公式反复应 用于各个折射面，分别求出各面的u、 u′、l 、 l′、 β、α、γ、y、y′J、J′、Q、 Q′。 转面公式— 前后相邻面之间的基本量的转化关系。

工程光学 章节2 球面系统

工程光学 章节2 球面系统
3. 光路计算是根据给定的光学系统，由物求像或由像 求物的过程。 4. 光路计算是根据几何光学的基本定律利用成像光路 图建立起的物象计算式。
光线经球面折射时的光路计算
要讨论成像规律，即像的虚实，成像的位置、正倒和大小问题，必须 计算出光线的走向，所以我们先讨论计算公式。 包含光轴和物点的平面称为含轴面（纸面）或子午面。
第一种情况
求光束经过两次成像后的会聚，图 已知系统 r1 R r2 R n1 1 n2 1.5 n3 1
•第一次成像
n1 1
n'1 1.5
r R
l1
1.5 1 1 .5 1 l '1 R
l1 '求得
A′ -Y′ B′
规则： 以球面的顶点为原点 2-1 沿轴量向右取正，向左取负 垂轴量向上取正，向下取负
单个球面的折射光路
B Y
A -U -L n E I
h I′ O C U′ r L′
n′
A′ -Y′ B′
2-1
角度的符号
• 角度量：U、U′、I、 I ′、φ
规则： 角度正切值为正时该角度为正，反 之为负
第二章 共轴球面光学系统
第一节 光路计算
• • • • 一、概述 二、符号规则 三、单个球面的成像计算 四、共轴球面的成像计算
一、概述
1. 绝大多数光学系统由球面、平面或非球面组成，如 果各曲面的曲率中心在一条直线上，则称该光学系 统为共轴光学系统，该直线为光轴。
2. 非球面, 如抛物面、椭球面等对某些位置等光程的 像质不错, 但加工检验有一定困难。因此，后面的讨 论主要是由球面和平面组成的光学系统。
• 实际光线的光路计算
严格按照几何光学基本定律的光线计算，这类 光线称为实际光线

第二章共轴球面系统

第二章共轴球面系统
dx' x' α= = dx x
讨论: ① α恒为正,当物点沿轴向移动时,像点沿轴同 向移动 ②一般α≠ β,即空间物体成像后要变形,如正方 体. ③只有在dl 很小时才适用
3. 角放大率
共轭光线与光轴夹角u ′和u 的比值,称为角放大率.
B' K B K'
H
A F
H'
F'
A'
对共轴理想光学系统性质第三点的解释: 一个共轴理想光学系统,如果已知两对共轭面的位置和放 大率,或者一对共轭面的位置和放大率,以及轴上两对共 轭点的位置,则其他一切物点的像点都可以根据这些已知 的共轭面和点确定
§2.8 理想光学系统的物像关系式
I I' B'
2.近轴光路计算公式 在近轴几何光学中,经常用到以下近似公式(一 级泰勒展开)
sin U ≈ U ≈ tan U
1 1 (sin θ = θ θ 3 + θ 5 ......) 3! 5!
U为物方孔径角,是个很小值(<<1rad),当 U<5°,近似代替误差大约为1%.
代入到(2-1)-(2-3),并用小写字母表示,得到以下公式:
dl ′ α = dl
(1)高斯公式求解:
f' f + =1 l' l
f ' dl ' fdl '2 2 = 0 l l
fl ' α = 2 f 'l
dl ′ nl ′2 n′ 2 = 2 = β α= dl n′l n
2
(2)牛顿公式求解:
xx' = ff '
xdx'+ x' dx = 0

第二章 球面和共轴球面系统

第二章 球面和共轴球面系统
2）物体移动有限距离
此时轴向倍率可以表示为：
α＝
l2 '− l1 ' l2 − l1
高斯公式
β1为第一位置处的垂轴放大率；β2为第二位置处的垂轴放大率。
2.2.3 角倍率γ
角放大率γ ：近轴区内，一对共轭光线的像方孔径 角u与物方孔径角u’之比， 即：
2.2.4
三个倍率之间的关系
即轴向放大率与角放大率之积与垂轴放大率相等。 即轴向放大率与角放大率之积与垂轴放大率相等。
2.2.1 垂轴倍率β 2.2.2 轴向倍率α 2.2.3 角倍率γ 2.2.4 三个倍率之间的关系 2.2.5 拉格朗日-赫姆霍兹不变量
2.2.1 垂轴倍率β
定义：像的大小与物的大小比值。 其数学表示形式为：β=y' /y
近轴区有限大小的物体 经过单个折射球面的成像
从图中可见，根据三角形ABC与A’B’C相似有：
现在对于已知的现在对于已知的ll和和uu值无论值无论uu为何值为何值l表明表明轴上点在近轴区成像轴上点在近轴区成像时其像可认为是时其像可认为是完善完善的称为称为高斯像点高斯像点过高斯像点垂直于光轴的面称为过高斯像点垂直于光轴的面称为高斯像面高斯像面构成物像关系的一对点称为构成物像关系的一对点称为共轭点共轭点
2.4 球面反射镜
前面指出，反射定律可认为是折射定律在n’=-n时的 特例，因此，将之前的折射球面的计算公式代以 n’=-n，可以得到相应的反射球面计算公式。 2.4.1 球面反射镜的物像位置公式 2.4.2 球面反射镜的成像倍率 2.4.3 球面反射镜的拉赫不变量
2.4.1 球面反射镜的物像位置公式
以上三式是我们计算单折射球面物像之间关系的基本公式
2.1.3 近轴光的光路计算公式

应用光学-共轴球面系统(II)共23页文档

应用光学-共轴球面系统(II)共23页文档
J 不变量对光学系统的每个面每个空间都是不变量。
8
3. 共轴球面系统的放大率
a） 垂轴放大率
Applied optics

k
i
i 1
n l1 ' l2 ' lk ' n ' l1l2 lk
yk ' n1u1 y1 nk 'uk '
9
3. 共轴球面系统的放大率
b） 轴向放大率
Applied optics
22
6、最大的骄傲于最大的自卑都表示心灵的最软弱无力。——斯宾诺莎 7、自知之明是最难得的知识。——西班牙 8、勇气通往天堂，怯懦通往地狱。——塞内加 9、有时候读书是一种巧妙地避开思考的方法。——赫尔普斯 10、阅读一切好书如同和过去最杰出的人谈话。——笛卡儿
Thank you
15
3.讨论
1).几条特殊成像光线
Applied optics
2).垂轴放大率
Applied optics
-l’
l’
l' l
实物 实像，物像距同号，β < 0 实物 虚像, 物像距反号, β > 0
Applied optics
例2. 凹面反射镜半径为-400mm，物体放在何处成放 大两倍的实像？放在何处成放大两倍的虚像？
Applied optics
例3：玻璃球中心有一图案，观察此图案时，像的位置及
大小？若将玻璃球用作透镜，其主平面位于何处？
21
Applied optics
例 4 ： 双 球 面 反 射 镜 系 统 由 主 镜 O1 和 次 镜 O2 构 成 ， 总 焦 距
f’=500mm. 若要求将无限远目标成像在主镜后20mm处，且次 镜垂轴放大率为β2=5，求主镜次镜曲率半径及两镜间隔。

第2章 共轴球面系统.ppt

第2章 共轴球面系统.ppt
二、符号规则 1.光线传播方向：规定光线从左向右传播为正。
2.线段： 沿轴线段:以顶点O为基准，左负右正；
垂轴线段:(h)以光轴为准，上正下负；
间隔d：以前一个面为基准，左负右正。
2.1光线经单个折射球面的折射
3.角度： 光轴与光线组成角度：光轴以锐角方向转到光
线，顺时针正逆时针负； 光线与法线组成角度：光线以锐角方向转到法
2.1光线经单个折射球面的折射
2.近轴光线的光路计算公式：
sin I L r sinU sin I n sin I
r
n
U U I I L r(1 sin I ) sinU
光线平行于光轴:光线的入射角用光线的入射高度
表示为： i h / r
2.1光线经单个折射球面的折射
不变量公式，它表示单个折射球面物方和像方的
Q值相等；（3）式表示近轴光线经球面折射后物
像方孔径角的关系。
例题：有一折射球面，其参数为 r 20mm,n 1,n 1.5163,
物距为 l 60mm ，求像距的值。
2.2单个折射球面的成像放大率 及拉赫不变量
主要内容： 垂轴平面物体以细光束经折射球面成像 单个折射球面的近轴光线成像放大率 三种放大率的关系 拉赫不变量
2.1光线经单个折射球面的折射
一、概念
1.子午平面：包含光轴的平面。 2.截距：物方截距——物方光线与光轴的交点到顶
点的距离；像方截距——像方光线与光轴的交点 到顶点的距离。 3.孔径角：物方孔径角——物方光线与光轴的夹角； 像方孔径角——像方光线与光轴的夹角。
2.1光线经单个折射球面的折射
分界面有左右，球面有凹凸，光轴有上方下方，如 何区别？

工程光学第二章知识点

工程光学第二章知识点

第二章共轴球面光学系统第一节符号规则●常见的光学系统有多个光学零件组成，每个光学零件往往由多个球面组成●这些球面的球心在一条直线上即为“共轴球面系统”●这条直线称为“光轴”●折射球面的结构参数：曲率半径r、物方折射率n、像方折射率n'●入射光线的参数：物方截距L、物方孔径角U●像方量在相应的物方量字母旁加“ ’ ”区分●光线的传播方向为自左向右●规定符号规则如下：●1）沿轴线段（如L、L’和r）●以顶点为原点，与光线方向相同为正，相反为负●2）垂轴线段（如h、y和y’）●以光轴为基准，光轴以上为正，以下为负●3）光线与光轴的夹角（如U、U’）●光轴转向光线；角量均以锐角计、顺时针为正、逆时针为负●4）光线与法线的夹角（如I、I’、I”）●光线转向法线●5）光轴与法线的夹角（如φ）●光轴转向法线●6）折射面间隔d●前一面顶点到后一面顶点，与光线方向相同为正，相反为负；在折射系统中，d恒为正●物方截距、像方截距、物方孔径角、像方孔径角等物理量是可以有正负的，但作为几何量AO、OA’、∠EAO、∠EA’O等应为正值；在负值物理量前加负号，以保证相应几何量为正●根据物像的位置判断物像的虚实●负（正）物距对应实（虚）物●正（负）像距对应实（虚）像第二节物体经过单个折射球面的成像1，单球面成像的光路计算已知折射球面的结构参数曲率半径r ，物方折射率n ，像方折射率n ’已知入射光线AE 的参数物方截距L ，物方孔径角U （轴上物点）求出射光线参数像方截距L ’，像方孔径角U ’（轴上像点）光路计算2在ΔAEC 中用正弦定律，有 sin sin()I U r L r -=-导出求入射角I 的公式sin sin L r I U r -=（2-1）由折射定律可以求得折射角I ’sin sin n I I n '=='（2-2）由角度关系，可以求得像方孔径角U ’U U I I ''=+-（2-3） 在ΔA ’EC 中应用正弦定律，得像方截距L ’ sin sin I L r r U ''=+' （2-4）式（2-1）至（2-4）就是子午面内实际光线的光路计算公式，利用这组公式可以由已知的L 和U 求L ’和U ’ sin sin L r I U r -= sin sin n I I n '=='U U I I ''=+-sin sin I L r r U ''=+'当物点A 位于轴上无限远处时，相应的L=∞，U=0，则式（2-1）须改变为sin hI r =（2-5）●若L 是定值，L ’是U 的函数，即从同一点发出的光线，孔径角不同，将在像方交在不同的点上 ● 同心光束经过单球面后不再是同心光束●这种误差被称为“球差” ●球差是各种像差中最常见的一种●如果把孔径角U 限制在很小的范围内，光线距光轴很近，称为“近轴光”，U 、U ’、I 和I ’都很小，式（2-1）~（2-4）中的正弦值用弧度来表示 ● 用小写字母u 、u ’、i 、i ’、l 和l ’表示近轴量● l r i u r n ii n u u i i i l r r u -='='''=+-''=+'（2-6）~（2-9） ● 当入射光线平行于光轴时，也以h 作为入射光线的参数，有●h i r =（2-10） ●近轴光线l ’与u 无关，即当物点位置确定后，其像点位置与孔径角u 无关，物点发出的同心光束经折射后在近轴区仍为同心光束 ●在近轴区成的是完善像，这个完善像通常称为“高斯像” ● 近轴区最常用的物像位置公式●n n n n l l r ''--='（2-14） ●已知物点位置l 求像点位置l ’时（或反过来）十分方便 ●1、轴上物点：轴上同一物点发出的近轴光线，经过球面折射以后聚交一点，即轴上物点近轴成像时是符合理想成像条件的。

第二章-共轴光学系统

第二章-共轴光学系统
物点参数为 (l1,u1, y1)
（1）对第一面做单个球面成像计算求得 (l1,u1, y1)
（2）用过渡公式由 (l1,u1, y1) 求得 (l2,u2, y2 ) （3）对第二面做单个球面成像计算求得 (l2 ,u2 , y2 )
……
（4）对第K面做单个球面成像计算求得(lk ,uk , yk )
I I '也U非' 常小。
sin x x x 为弧度值
用弧度值代替正弦值
u ~ sinU i ~ sin I l~L
u'~ sinU ' i ~ sin I l'~ L'
（2－1）～（2－4）式变为：
i (l r)u / r i n i / n u u i i l r r i/ u
处，如下图所示。
试求：像距、像高和垂轴放大率。
C
A
O
§2.4 共轴球面系统的成像
过渡公式luny2222l1uny111,,,undy3313,l3uny222l2d2 h2 h1 d1u1, h3 h2 d2u2
K个折（反）射面，系统参数为 r1, r2 , rk ; n1, n2 , nk1; d1, d2 dk1
dl
利用（2-14）式
n n n n l l r
对其求导
ndl l2
ndl l2
0
dl dl
nl2 nl 2
dl n (nl)2 n 2
dl n nl n
由上式可见：
n n
2
0
所以物和像同方向移动。
且一般： （除非 、1 n ） n
提问：立方体成像还是立方体吗？
③、角放大率
sin(180o I ) sin(U )

工程光学第二章

工程光学第二章

近轴区的特点
l u lu h
和 （1）-（4）式说明：
对于一个确定位置的物体，无论 u 为何值，l’ 均为定值，即近轴光路
能获得唯一像。即： l’ 与 u 无关，与 l 有关。 证明做为作业
近轴区内以细光束成像都是完善的，该像称为高斯像，通过高斯像点且垂
直于光轴的平面称为高斯像面，A 与 A’ 点称为共轭点。

练习：推倒垂轴放大率公式，寻找 p17推倒中的错误

近轴区成像的放大率和传递不变量 轴向放大率
dl nl 2 n 2 2 dl nl n
两放大率关系
α 恒为正，物点沿轴向移动时，其像点沿同方向
移动。

近轴区成像的放大率和传递不变量 角放大率
u l n n' l n 1 u l n' nl n'
物方焦距

例题
已知一折射球面其r =36.48mm，n =1， n’ =1.5163。轴上点A的截距 L=-240mm，由它 发出一同心光束，今取U为-1°、-2 °、 -3 °的三条光线，分别求它们经折射球面后的 光路。（即求像方截距L’ 和像方倾斜角U’ E n n’ ）
A O -240mm C
U U I I
l r i u r n l r i i u n r
第四式 轴上点 无限远
h r n l r i i u n r i
u u i i
i l r (1 ) u
u u i i
l r (1 i ) u
第二章：共轴球面光学系统
2.1 基本概念与符号规则 2.2 单个折射球面成像
2.3 单个反射球面成像 2.4 共轴球面光学系统成像
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
y
光焦度
n
n
h
U
n n r
I
n n l n n f' f
n n l

o
I
U
r
l'
y
-l
6
共轴球面光学系统
三、近轴区域的物像放大率
1、垂轴放大率b
y nu nl b y nu' nl
dl nl 2 n 2 2、轴向放大率a a b 2 dl nl n


当物体位于不同的位置时， b不同。
2.
因a恒为正，故当物点沿轴向移动时，其像点沿光轴同 向移动；且因a ≠ b，故空间物体成像时要变形，例如一 正方体成像后将不再是正方体。 g只与共轭点的位置有关，而与光线的孔径角无关。
8
位置公式 2、成像放大率
b l l
3、角放大率g
g
u l n n' l n 1 u l n' nl n' b
n
ag b
n
h
nuy nuy J
单折射球面光学系统 拉赫不变量
I
y
U

I
U
o
-l
r
l'
y
7
共轴球面光学系统
结论：
1.

b是有符号数，具体表现为
成像正倒：当b>0时，表明y’、y同号，成正像；否则，成倒像。 成像大小：当|b|＝1时，表明|y’|=|y|，像、物大小一致；|b|>1时， 表明|y’|>|y|，成放大的像；反之，成缩小的像。 成像虚实：当b>0时，表明l’、l同号，物像同侧，虚实相反；否 则，物像异侧，虚实相同。
,U 3 U 2 , ,U k U k 1 U2 U1 d 1 , L3 L2 d 2 , , Lk Lk 1 d k 1 L2 L1
d1 , l3 l2 d 2 , , l k l k 1 d k 1 l 2 l1 , h3 h2 d 2 u h2 h1 d 1 u1 2 , , hk hk 1 d k 1 uk 1 n1 u1 y1 n2 u2 y 2 nk uk yk n k uk y k J
U
y
L
1
共轴球面光学系统
2、符号规则
（一）光线行进方向：从左向右。 （二）线量符号： (1)沿轴线段：以球面顶点O为原点，与光线行进方向相 同者为正，与光线行进方向相反者为负。 (2)垂轴线段：以光轴为界，在光轴之上为正，在光轴之 下为负。 (三）角度符号（一律以锐角来衡量）： (1) 光线与光轴的夹角：光轴转向光线，顺时针为正，逆 时针为负。 (2) 光线与法线的夹角：光线转向法线，顺时针为正，逆 时针为负。 (3) 光轴与法线的夹角：光轴转向法线，顺时针为正，逆 时针为负。
U U I I
L r ( 1
sin I ) sin U
4
共轴球面光学系统
sin U sin I ( L r ) r n sin I sin I n
i
U U I I
l r u r n l r i i u n r
10
共轴球面光学系统
§2.4
共轴球面系统的成像
11
1. 过渡公式
共轴球面光学系统
, n3 n2 , , nk nk 1 n2 n1 , u3 u2 , , uk uk 1 u2 u1 , y3 y2 , , y k y k 1 y 2 y1
u u i i
sin I L r ( 1 ) sin U
nl r i r 1 l r( 1 ) n' l nl r u
5
共轴球面光学系统
二、近轴区域的物像关系
l u lu h 1 1 1 1 n ( ) n( ) Q r l r l h nu nu ( n n ) r n n n n l l r
2
共轴球面光学系统
3、符号规则的意义：
清楚地描述物像的虚实和正倒：
n

物在左：负物距——实物； 右：正物距——虚物；
I
h
n
y
U

o
r
I
U
y

像在右：正像距——实像； 左：负像距——虚像；
-L
L

物高y像高y’代数值符号相反——倒像； 符号相同——正像；
4、光路图中符号标注：
图中标注几何量为正。
12
共轴球面光学系统
2. 成像放大率
单折射球面
y nl b y nl
dl nl 2 n 2 a b 2 dl nl n
u l n 1 g u l n' b
共轴球面系统
y'k y'1 y'2 y'k b b 1b 2 b k y1 y1 y 2 yk
a b 2
单个反射球面成像
1 1 2 l l r f f r 2
b 1
物点位于球心时
a 1
g 1 b
g 1
9
共轴球面光学系统
b l l
a b 2
g 1 b
J uy uy
球面镜的拉赫不变量
结论
a<0，物体沿光轴移动时，像总是以相反方向移动。 通过球心的光线沿原光路反射。 反射球面镜的焦距等于球面半径的1/2。
' dl'k dl1 dl'2 dl'k a a 1a 2 a k dl1 dl1 dl2 dlk
u'k u'1 u'2 u'k g g 1g 2 g k u1 u1 u2 uk
ag b
nuy nuy J
13
共轴球面光学系统
§2 共轴球面光学系统 §2.1 符号规则
1、常用符号：
n 、n’ ——折射率
n
y
I
h
I
n
r ——球面的曲率半径 U y—— 物体的大小 o r y’—— 像的大小 I——光线的入射角 L I’——光线的折射角 L——物体到折射面或反射面的距离（物方截距） L’ ——折射面或反射面到像的距离（像方截距） U——入射光线和光轴倾斜的角度（物方孔径角） U’ ——出射光线和光轴倾斜的角度（像方孔径角） ——光轴与法线的夹角
3
共轴球面光学系统
§2.2 物体经单个折射球面的成像
一、单折射球面成像的光路计算
n
y
U
I
h
n

o
I
U
I E
h

I
r
L
sin U sin I ( L r ) r n sin I sin I n
y
o
U
A’
-L
sinI h r ih r h l u lu