二次根式知识点总结及其应用

二次根式知识点总结二次根式是数学中的一种常见的根式表达式，它可以表示为$\sqrt{a}$ 的形式，其中 $a$ 是一个非负实数。

在学习二次根式时，常常会涉及到以下几个方面的知识点。

一、二次根式的性质：1. 非负性：对于任何非负实数 $a$，二次根式 $\sqrt{a}$ 都是非负实数。

2. 平方性：相对应的，对于任何非负实数 $a$，二次根式$\sqrt{a}$ 的平方等于 $a$，即 $(\sqrt{a})^2=a$。

3. 两个二次根式可以相等：如果两个二次根式 $\sqrt{a}$ 和$\sqrt{b}$ 相等，那么 $a$ 和 $b$ 必须相等，即$\sqrt{a}=\sqrt{b}$ 可推出 $a=b$。

二、二次根式的运算：1. 加减运算：两个二次根式可以进行加减运算，只要它们的被开方数相同即可。

即 $\sqrt{a} \pm \sqrt{b}=\sqrt{a \pm b}$。

2. 乘法运算：两个二次根式相乘，可以将它们的被开方数相乘并开方。

即 $\sqrt{a} \cdot \sqrt{b}=\sqrt{ab}$。

3. 除法运算：两个二次根式相除，可以将它们的被开方数相除并开方。

即 $\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}$。

4. 有理化分母：当二次根式的分母不含二次根式时，可以通过有理化分母的方法将其转化为含有二次根式的形式。

有理化分母的基本方法是将分母有理化，即乘以一个适当的形式为 $\sqrt{x}$ 的分子与分母相等的有理数，从而使得分母成为没有二次根式的有理数。

三、二次根式的化简：1.合并同类项：当二次根式相加或相减时，可以合并同类项，即将其中具有相同被开方数的二次根式相加或相减，并保持其他二次根式不变。

2.分解因式：当一个二次根式的被开方数可以分解成互质因子的乘积时，可以利用分解因式的方法进行化简。

3.化简根式：当二次根式的被开方数可以开方时，可以进行化简，即将其转化为整数、分数或者更简单的二次根式的形式。

二次根式知识点及其应用一、二次根式的概念：（1）形如 的式子叫做二次根式.（2）二次根式有意义的条件:被开方数大于或等于零。

二、二次根式化简:1、最简二次根式：满足下列两个条件的二次根式，叫做最简二次根式。

①被开方数不含分母；②被开方数中不含能开得尽方的因数或因式；2、同类二次根式：几个二次根式化成最简二次根式后，如果被开方数相同， 那么这几个二次根式叫做同类二次根式。

3、分母有理化：（1）有理化因式：两个含有二次根式的代数式相乘，如果他们的积不含有二次根式，那么这两个代数式叫做互为有理化因式。

（2）分母有理化：在分母含有根号的式子中，把分母中的根号化去。

方法：①分子与分母同乘以分母的有理化因式例如：②分子或分母分解因式，约去分母中含有二次根式的因式例如：三、二次根式的性质：（1） 非负性0()a ≥0 2(2)(0)a = ≥ 0()a ≥0(00)0,0,)a b a b a b ==≥>==≥≥≠ ,0,0)0,0)x y x y ==>>==>>四、二次根式的运算：二次根式乘法法则二次根式除法法则二次根式的加减：（1）将每个二次根式化为最简二次根式；（2）找出其中的同类二次根式；（3）合并同类二次根式。

五、二次根式的应用1.对二次根式的认识1．一个自然数的算术平方根为()0a a >，则与这个自然数相邻的两个自然数的算术平方根为（ ）（A ）1,1a a -+（BCD ）221,1a a -+2.若21x +的平方根是5±_____=．3.a 的被开方数相同，则_____ab +=．4．若xy____x =，_____y =．5=，且0x y <<，则满足上式的整数对(),x y 有_____．2、根据二次根式有意义的条件确定未知数的值：1有意义的x 的取值范围=(0,0)a b = ≥ ≥(00)a b = ≥>(0,0)a b = ≥≥(0,0)a b = ≥>2.若2)(11y x x x +=-+-，则y x -=_____________。

二次根式知识点总结二次根式是高中数学中重要的知识点之一，它在解决一元二次方程、求解勾股定理以及图形的面积计算等问题中起到了重要的作用。

本文将对二次根式的定义、性质以及相关的数学运算进行总结，并探讨其在实际问题中的应用。

一、二次根式的定义二次根式是指形如√a的代数式，其中a为非负实数。

它可以表示为一个单独的根号表达式，也可以是两个或多个二次根式之间的运算。

二、二次根式的性质1. 二次根式与有理数的关系：二次根式可以是有理数或无理数。

当根号内的数可以化简为有理数时，二次根式即为有理数；否则，二次根式为无理数。

2. 二次根式的相等性：两个二次根式相等的条件是它们的被开方数相等。

3. 二次根式的大小比较：对于非负实数a和b，若a > b，则有√a >√b。

4. 二次根式的运算性质：对于非负实数a和b，有以下运算性质：- 加法：√a + √b = √(a + b)- 减法：√a - √b = √(a - b)，其中a ≥ b- 乘法：√a * √b = √(a * b)- 除法：√a / √b = √(a / b)，其中b ≠ 0三、二次根式的化简当二次根式存在可以化简的情况时，可以通过以下方法进行化简：1. 提取因子法：将根号内的数分解为两个数的乘积，其中一个数是完全平方数，并提取出完全平方数的根号作为整体。

2. 有理化分母法：对于含有二次根式的分数，可以通过有理化分母的方法化简，即将分母有理化为一个有理数或二次根式。

四、二次根式的应用1. 解一元二次方程：一元二次方程的形如ax^2 + bx + c = 0，其中a ≠ 0。

通过二次根式的求解方法，可以求得方程的解，并通过图像分析得到方程的根的性质。

2. 求解勾股定理：在平面几何中，勾股定理是指在直角三角形中，直角边的平方等于两个其他边的平方之和。

通过二次根式的运算，可以准确计算出直角三角形的边长。

3. 计算图形的面积：在几何问题中，经常需要计算图形的面积，而某些图形的面积计算涉及到二次根式。

数学中的二次根式知识点一、定义与性质二次根式是指具有以下形式的数：√a，其中a为非负实数。

其中，√a被称为二次根式的根号形式，a被称为二次根式的被开方数。

二次根式的一些重要性质如下：1. 非负性质：对于任意非负实数a和b，如果a<b，则√a<√b。

2. 非负完全平方值：对于任意非负实数a，若存在非负实数b满足b^2=a，则称b为a的平方根，记作√a=b。

3. 非负根式相等：对于任意非负实数a和b，如果a≥0，b≥0且√a=√b，则a=b。

4. 非负根式与绝对值：对于任意实数a，有√(a^2)=|a|。

二、化简与运算1. 化简（1）合并同类项：对于形如√a±√b的二次根式，可以根据运算规则合并同类项。

（2）有理化分母：对于形如1/√a的二次根式，可以通过有理化分母的方法，将分母中的二次根式消去。

（3）去除分母内的二次根式：对于形如a/√b的二次根式，可以通过有理化分母的方法，去除分母内的二次根式。

2. 运算（1）加减运算：对于形如√a±√b的二次根式，可以根据运算规则进行加减运算。

（2）乘法运算：对于形如√a*√b的二次根式，可以根据运算规则进行乘法运算。

（3）除法运算：对于形如√a/√b的二次根式，可以根据运算规则进行除法运算。

（4）幂运算：对于形如(√a)^n的二次根式，可以根据运算规则进行幂运算。

三、应用与解题思路1. 求解二次根式的值：根据给定的被开方数，利用二次根式的定义和运算规则，可以求解二次根式的值。

2. 化简二次根式：根据给定的二次根式，利用化简的方法，将其化简为最简形式，以便于进行运算或比较大小。

3. 比较大小：根据二次根式的性质，可以通过比较被开方数的大小，来比较二次根式的大小关系。

4. 解方程与不等式：在数学中的各种问题中，经常会涉及到二次根式的方程或不等式，可以利用二次根式的性质以及运算规则，对方程或不等式进行求解。

综上所述，二次根式是数学中重要的知识点之一。

二次根式知识点总结及其应用二次根式是指形如√a的数，其中a为一个非负实数。

在学习二次根式的过程中，我们需要掌握以下几个重要的知识点。

1.二次根式的定义和性质二次根式是数学中的一种运算符号，表示一个非负实数的算术平方根。

如果a≥0，则√a是一个实数；如果a<0，则√a是一个虚数。

二次根式的性质有以下几点：（1）非负数的非负平方根是一个实数，记作√a，其中a≥0；（2）非负实数a的平方根必须满足：如果x是a的平方根，则-x也是a的平方根；（3）二次根式的运算规律：√ab=√a·√b，√(a/b)=√a/√b。

2.简化二次根式简化二次根式是指将一个二次根式写成最简形式。

其中的关键是将根号下的数分解成若干个因数的平方。

一般地，对于一个非负实数a，我们可以将其分解为质因数的乘积，然后将其中的每个质因数的平方提取出来写成一个二次根式。

例如，对于√12，我们可以将12分解为2×2×3，然后将2和3的平方根提取出来，得到√12=2√33.二次根式的四则运算对于二次根式的加、减、乘、除，我们需要根据运算规律来进行计算。

（1）加减：对于两个二次根式的加减，可以先化简，然后将其中的同类项合并。

例如，计算√3+2√3，可以化简得到3√3，再将3√3与2√3相加，得到5√3（2）乘法：对于两个二次根式的乘法，使用运算法则√ab=√a·√b，将根号下的数分解后相乘。

例如，计算(√2+√3)(√2-√3)，可以用分配律展开，得到2-3=-1（3）除法：对于两个二次根式的除法，也使用运算法则√(a/b)=√a/√b，将根号下的数分解后相除。

例如，计算(√8)/(√2)，可以化简得到√2，即(√8)/(√2)=√24.二次根式的应用二次根式在数学和实际生活中有广泛的应用。

（1）几何应用：二次根式常用于计算几何图形的面积和边长。

例如，计算正方形的对角线长度、矩形的对角线长度等。

（2）物理应用：二次根式常用于计算一些物理问题。

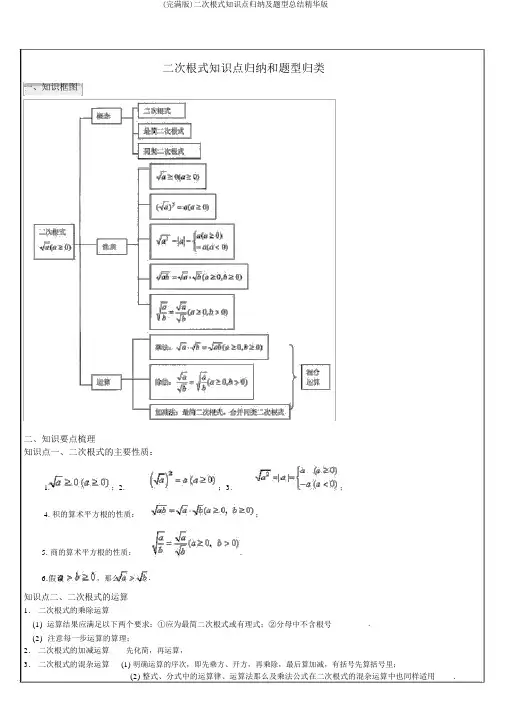
二次根式知识点归纳和题型归类一、知识框图二、知识要点梳理知识点一、二次根式的主要性质：1.；2.；3.；4.积的算术平方根的性质：；5. 商的算术平方根的性质：.6.假设，那么.知识点二、二次根式的运算1．二次根式的乘除运算(1) 运算结果应满足以下两个要求：①应为最简二次根式或有理式；②分母中不含根号.(2)注意每一步运算的算理；2．二次根式的加减运算先化简，再运算，3．二次根式的混杂运算(1) 明确运算的序次，即先乘方、开方，再乘除，最后算加减，有括号先算括号里；(2) 整式、分式中的运算律、运算法那么及乘法公式在二次根式的混杂运算中也同样适用.一. 利用二次根式的双重非负性来解题〔a0 〔a≥0〕，即一个非负数的算术平方根是一个非负数。

〕1.〕。

A、3；B、x ；C、x21；D、x1以下各式中必然是二次根式的是〔2．等式(x 1)2＝1－ x 成立的条件是 _____________ ．3．当 x____________ 时，二次根式2x 3 有意义．4.x 取何值时，以下各式在实数范围内有意义。

〔 1〕〔 2〕1〔3〕5x 2 x1x4〔 4〕假设x( x1)x x1，那么 x 的取值范围是〔 5〕假设x3x3，那么 x 的取值范围是。

x1x16.假设3m 1 有意义，那么m能取的最小整数值是；假设 20m 是一个正整数，那么正整数m的最小值是________．7.当 x 为何整数时，10x11有最小整数值，这个最小整数值为。

8. 假设2004 a a2005a ，那么a2004 2=_____________；假设y x33x 4 ，那么x y9．设 m、n 满足n m299m22mn =。

m 3，那么10. 假设三角形的三边a、 b、 c 满足a24a 4 b 3 =0，那么第三边c的取值范围是11. 假设|4x8 |x y m0 ，且 y 0 时，那么〔〕 A 、0m1 B 、m2C、m 2 D、 m 2利用二次根式的性质2a(a b)(即一个数的平方的算术平方根等于这个数的绝对值)来解题二． a =|a|=0(a0)a(a0)1.x33x2＝－x x 3 ，那么〔〕 A.x≤0 B. x≤－ 3Ｃ. x≥－ 3 D.－ 3≤x≤ 02.． a<b，化简二次根式 a 3b 的正确结果是〔〕A．a ab B ．a ab C． a ab D ．a ab3.假设化简 | 1-x |-28x16 的结果为2x-5 那么〔〕 A 、 x 为任意实数B、1≤ x≤ 4C、 x≥1 D 、x≤ 4 x4. a， b， c 为三角形的三边，那么(a b c)2(b c a) 2(b c a) 2=5.当 -3<x<5 时，化简26921025 =。

初中二次根式知识点总结二次根式是初中数学的一个重要内容，它涉及到实数的非负数平方根、根式的性质、根式的乘除法、根式的加减法等内容。

以下是关于二次根式的重要知识点总结：1. 二次根式的定义：形如√a（a≥0）的式子叫做二次根式。

其中，a是实数。

2. 非负数的平方根：对于任何非负数a，都有实数平方根，记作√a。

3. 根式的性质：√a² = a（a表示a的绝对值）。

√ab = √a × √b（当a≥0，b≥0时）。

√(a/b) = √a / √b（当a≥0，b>0时）。

4. 根式的乘除法：当两个根式相乘或相除时，可以直接对它们的被开方数进行乘除运算。

例如：√a × √b = √(a×b)，√a / √b = √(a/b)。

5. 根式的加减法：当两个根式相加或相减时，需要先将它们化为最简二次根式，然后再对被开方数进行加减运算。

例如：√a + √b 和√a - √b 不能直接合并，除非它们有相同的被开方数。

6. 最简二次根式：满足以下三个条件的二次根式被称为最简二次根式：被开方数的因数是整数，因式没有重复；被开方数中不含有分母；根号内没有剩余的被开方数。

7. 负数的平方根：负数没有实数平方根。

在实数范围内，只有非负数有实数平方根。

8. 无理数：无法表示为两个整数的比的数被称为无理数。

常见的无理数包括π和√2等。

9. 代数运算：在二次根式的运算中，经常需要使用代数的基本运算规则，如分配律、结合律等。

以上是关于二次根式的重要知识点总结。

在学习二次根式时，需要理解并掌握这些知识点，以便能够正确地进行二次根式的运算和化简。

二次根式知识点一：二次根式的定义二次根式：一般地，式子√a （a ≥0）叫做二次根式，a 叫做被开方数。

1）二次根式的定义必须包含二次根号“√”，尽管√9的结果为3，但由于√9满足二次根式的特征，所以√9是二次根式； 2）二次根式的被开方数可以使数字，亦可以是一代数式，但必须满足被开方数≥0，如√-x 2-1，由于被开方数＜0，所以它不是二次根式； 3） 根指数是2，此处的2可以省略不写； 4）形如b √a （a ≥0）的式子也是二次根式；知识点二：二次根式有意义的条件（被开方数是非负数） 知识点三：二次根式的性质性质1：双重非负性 性质2：(a )2＝a （a ≥0）性质3：a a a a a a 200==≥-<⎧⎨⎩||()()知识点四：同类二次根式与最简二次根式例1．下列式子，哪些是二次根式，哪些不是二次根式：2、33、1x 、x （x>0）、0、42、-2、1x y +、x y +（x ≥0，y •≥0）．例2. 求下列各式有意义的所有x 的取值范围。

（）；（）；（）；（）；（）；（）13221312411521645332-++-++-----x x x x x xx x x x例3.已知x,y 为实数，且335y x x =-+-+，求22x xy y -+的值。

例4. 已知y=2x -+2x -+5，求x y的值例5. 当a 取什么值时，代数式211a ++取值最小，并求出这个最小值例6. 已知2310x x -+=，求2212x x +-的值例7. 已知：,x y 为实数，且113y x x -+-+，化简：23816y y y ---+例8. 实数a 在数轴上的位置如图所示，化简：()2|1|2a a -+-例9.已知a 、b、c 满足2(8)5320a b c -+-+-=（1）a 、b 、c 的值；（2）试问以a 、b 、c 为边能否构成三角形？若能构成三角形，求出三角形的周长；若不能构成三角形，请说明理由巩固练习： 一、选择题1 2-1a1、函数13x y x +=-中，自变量x 的取值范围是（ ） A. 1x ≥- B. 3x ≠ C. 13x x ≥-≠且 D. 1x <- 2、()a a -=-112成立的条件是：A ．a ≠1B ．a ≥1C ．a <1D ．a ≤1 3、下列根式中，最简二次根式为： A ．4x B ．x 24- C ．x 4D ．()x +424、已知t <1，化简1212---+t t t 得：A ．22-tB ．2tC ．2D ．0 5、下列各式中，正确的是：A ．()-=-772B ．()-=07072..C ．()-=7722D ．()-=07072..6、下列命题中假命题是：A ．设()x x x <-=-02，则 B ．设x x x<=-012，则C ．设x x x <=02，则 D ．设()x xx <=0222，则7、与23是同类根式的是：A ．50B ．32C ．18D ．75二、解决问题 1、已知：x y =+=-123123， 求：x xy y 225-+2、若5的整数部分为a ，小数部分是b 求：a b-1的值。

二次根式的知识点的总结二次根式是高中数学中重要的一个内容，也是学习代数的基础。

在学习二次根式时，需要了解其定义、性质、运算法则等知识点。

下面是对二次根式知识的总结：一、二次根式的定义和性质：1. 定义：对于非负实数a，b，如果存在非负实数x使得$x^2=a$，则称x为a的平方根，记作$x=\sqrt{a}$。

简记作$\sqrt{a}$，a称为二次根式的被开方数。

2.性质：（1）非负实数的平方根是唯一的。

即对于非负实数a，其平方根也是非负实数且唯一（2）非负实数a的平方根如果记作±$\sqrt{a}$，则规定非负实数a的平方根仅指称为非负实数$\sqrt{a}$。

（3）非负实数a的平方根的平方等于a。

即$(\sqrt{a})^2=a$。

（4）非负实数的平方根存在且非负。

即对于非负实数a，总是存在非负实数x使得$x^2=a$，且x唯一（5）相等的二次根式具有相等的平方根。

即如果$\sqrt{a}=\sqrt{b}$，则有a=b。

（6）平方根的运算：$\sqrt{ab}=\sqrt{a}\sqrt{b}$、$\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}$。

二、二次根式的化简：1. 因式分解法：将二次根式的被开方数进行因式分解，然后利用性质$\sqrt{ab}=\sqrt{a}\sqrt{b}$和$\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}$对二次根式进行简化，最后利用性质$\sqrt{a^2}=，a，$化简。

2. 合并同类项法：对于同根号的二次根式，可以合并同类项进行简化。

如$\sqrt{2}+\sqrt{3}+\sqrt{2}=\sqrt{2}+\sqrt{2}+\sqrt{3}=2\sqrt{2}+\sqrt{3}$。

3.有理化法：对于含有分母的二次根式，可以通过有理化的方法将其化简为一个无理数。

三、二次根式的比大小：1. 利用性质$\sqrt{a^2}=，a，$，我们可以对二次根式的大小进行比较。