安徽省祁门县2011-2012学年度九年级数学第三次模考试题(无答案) 人教新课标版

九年级中考数学第三次模拟试卷1一．选择题（共6小题，满分18分，每小题3分）1．下列说法正确的是（）A．负数没有倒数B．正数的倒数比自身小C．任何有理数都有倒数D．﹣1的倒数是﹣12．下列几何体是由4个相同的小正方体搭成的，其中左视图与俯视图相同的是（）A．B．C．D．3．已知∠A为锐角，且sin A＝，那么∠A等于（）A．15°B．30°C．45°D．60°4．一组数据40、10、80、20、70、30、50、90、70．若这组数据的平均数为m，众数为n，中位数为p，则m、n、p之间的大小关系为（）A．m＝n＝p B．p＜m＜n C．p＜n＜m D．n＜m＜p5．如图，直线AB∥CD，∠1＝60°，∠2＝50°，则∠E＝（）A．80°B．60°C．70°D．50°6．如图，汽车在东西向的公路l上行驶，途中A，B，C，D四个十字路口都有红绿灯．AB之间的距离为800米，BC为1000米，CD为1400米，且l上各路口的红绿灯设置为：同时亮红灯或同时亮绿灯，每次红（绿）灯亮的时间相同，红灯亮的时间与绿灯亮的时间也相同．若绿灯刚亮时，甲汽车从A路口以每小时30千米的速度沿l向东行驶，同时乙汽车从D路口以相同的速度沿l向西行驶，这两辆汽车通过四个路口时都没有遇到红灯，则每次绿灯亮的时间可能设置为（）A．50秒B．45秒C．40秒D．35秒二．填空题（共6小题，满分18分，每小题3分）7．计算：（﹣1）0+（）﹣1＝．8．2008年9月27日，神舟七号航天员翟志刚完成中国历史上第一次太空行走，他相对地球行走了5 100 000米路程，用科学记数法表示为．9．关于x的一元二次方程x2﹣2x+m﹣3＝0有两个实数根，则m的取值范围是．10．在纸上剪下一个圆和一个扇形纸片，使它们恰好围成一个圆锥（如图所示），如果扇形的圆心角为90°，扇形的半径为4，那么所围成的圆锥的高为．11．如图，△ABO中，AO＝AB，点B（10，0），点A在第一象限，C，D分别为OB、OA的中点，且CD＝6.5，则A点坐标为．12．如图，在菱形ABCD中，对角线AC、BD相交于点O．AC＝8cm，BD＝6cm，点P为AC上一动点，点P以1cm/的速度从点A出发沿AC向点C运动．设运动时间为ts，当t＝s时，△PAB为等腰三角形．三．解答题（共5小题，满分30分，每小题6分）13．解方程：＝214．如图，正方形网格中的每个小正方形边长都是1，每个小格的顶点叫做格点，以格点为顶点分别按下列要求画三角形．（1）在图1中，画一个直角三角形，使它的三边长都是有理数；（2）在图2中，画一个直角三角形，使它们的三边长都是无理数；（3）在图3中，画一个正方形，使它的面积是5．15．先化简（1﹣）÷，然后从不等式2x﹣6＜0的非负整数解中选取一个合适的解代入求值．16．（1）已知，如图①，在△ABC中，∠BAC＝90°，AB＝AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E，求证：DE＝BD+CE．（2）如图②，将（1）中的条件改为：在△ABC中，AB＝AC，D、A、E三点都在直线m上，并且有∠BDA ＝∠AEC＝∠BAC＝α，其中α为任意钝角，请问结论DE＝BD+CE是否成立？若成立，请你给出证明：若不成立，请说明理由．17．小明家将于5月1日进行自驾游，由于交通便利，准备将行程分为上午和下午．上午的备选地点为：A﹣鼋头渚、B﹣常州淹城春秋乐园、C﹣苏州乐园，下午的备选地点为：D﹣常州恐龙园、E﹣无锡动物园．（1）请用画树状图或列表的方法分析并写出小明家所有可能的游玩方式（用字母表示即可）；（2）求小明家恰好在同一城市游玩的概率．四．解答题（共4小题，满分32分，每小题8分）18．现代营养学家用身体质量指数判断人体的健康状况，这个指数等于人体质量（千克）与人体身高（米）平方的商，一个健康人的身体质量指数在20～25之间，身体质量指数低于18，属于不健康的瘦；身体质量指数高于30，属于不健康的胖．（1）A同志的体重为90千克，身高为1.6米，A属于哪种类型的人？（2）B同志的体重在65～70之间，经测定该同志的身体质量指数为23，请估算B同志的身高．19．如图，已知反比例函数y＝的图象与一次函数y＝x+b的图象交于点A（1，4），点B（﹣4，n）．（1）求n和b的值；（2）求△OAB的面积；（3）直接写出一次函数值大于反比例函数值的自变量x的取值范围．20．为了配合数学课程改革，某县举行了初三年级“数学知识应用”竞赛（满分100分）．为了解初三年级参赛的1万名学生竞赛成绩情况，现从中随机抽取部分学生的竞赛成绩作为一个样本，整理后分成5组，绘制出频数分布直方图．已知图中从左到右的第一、第二、第四、第五小组的频数分别是50，100，200，25，其中第二小组的频率是0.2．（1）求第三小组的频数，并补全频数分布直方图；（2）抽取的样本中，学生竞赛成绩的中位数落在第几小组？（3）若成绩在90分以上（含90分）的学生获优胜奖，请你估计全县初三参赛学生中获优胜奖的人数．21．如图，抛物线y＝与x轴交于A，B（点A在点B的左侧）与y轴交于点C，连接AC、BC．过点A作AD∥BC交抛物线于点D（8，10），点P为线段BC下方抛物线上的任意一点，过点P 作PE∥y轴交线段AD于点E．（1）如图1．当PE+AE最大时，分别取线段AE，AC上动点G，H，使GH＝5，若点M为GH的中点，点N 为线段CB上一动点，连接EN、MN，求EN+MN的最小值；（2）如图2，点F在线段AD上，且AF：DF＝7：3，连接CF，点Q，R分别是PE与线段CF，BC的交点，以RQ为边，在RQ的右侧作矩形RQTS，其中RS＝2，作∠ACB的角平分线CK交AD于点K，将△ACK绕点C顺时针旋转75°得到△A′CK′，当矩形RQTS与△A′CK′重叠部分（面积不为0）为轴对称图形时，请直接写出点P横坐标的取值范围．五．解答题（共1小题，满分10分，每小题10分）22．如图，在矩形ABCD中对角线AC、BD相交于点F，延长BC到点E，使得四边形ACED是一个平行四边形，平行四边形对角线AE交BD、CD分别为点G和点H．（1）证明：DG2＝FG•BG；（2）若AB＝5，BC＝6，则线段GH的长度．六．解答题（共1小题，满分12分，每小题12分）23．如图，直角坐标系中，已知两点O（0，0），A（2，0），点B在第一象限且△OAB为正三角形．△OAB 的外接圆交y轴的正半轴于点C．（1）点B的坐标是，点C的坐标是；（2）过点C的圆的切线交x轴于点D，则图中阴影部分的面积是；（3）若OH⊥AB于点H，点P在线段OH上．点Q在y轴的正半轴上，OQ＝PH，PQ与OB交于点M．①当△OPM为等腰三角形时，求点Q的坐标；②探究线段OM长度的最大值是多少，直接写出结论．参考答案与试题解析一．选择题（共6小题，满分18分，每小题3分）1．【分析】根据倒数的定义可知．【解答】解：A、负数有倒数，例如﹣1的倒数是﹣1，选项错误；B、正数的倒数不一定比自身小，例如0.5的倒数是2，选项错误；C、0没有倒数，选项错误；D、﹣1的倒数是﹣1，正确．故选：D．【点评】本题主要考查了倒数的定义及性质．乘积是1的两个数互为倒数，除0以外的任何数都有倒数，倒数等于它本身的数是±1．2．【分析】分别画出四个选项中简单组合体的三视图即可．【解答】解：A、左视图为，俯视图为，主视图与俯视图不同，故此选项不合题意；B、左视图为，俯视图为，主视图与俯视图相同，故此选项符合题意；C、左视图为，俯视图为，主视图与俯视图不同，故此选项不合题意；D、左视图为，俯视图为，主视图与俯视图不同，故此选项不合题意；故选：B．【点评】此题主要考查了简单组合体的三视图，关键是掌握左视图和俯视图的画法．3．【分析】根据特殊角的三角函数值求解．【解答】解：∵sin A＝，∠A为锐角，∴∠A＝30°．故选：B．【点评】本题考查了特殊角的三角函数值，解答本题的关键是掌握几个特殊角的三角函数值．4．【分析】要求平均数只要求出数据之和再除以总个数即可；找中位数要把数据按从小到大的顺序排列，位于最中间的一个数或两个数的平均数为中位数；众数是一组数据中出现次数最多的数据，注意众数可以不止一个．【解答】解：平均数m＝≈51；在这组数据中，70出现的次数最多，故n＝70；将这组数据按从大到小的顺序排列（10，20，30，40，50，70，70，80，90），位于中间位置的数为50，故p＝50．由上可知：p＜m＜n，故选：B．【点评】此题考查了平均数、中位数和众数的意义，解题的关键是正确理解各概念的含义．5．【分析】由AB∥CD，根据两直线平行，同位角相等，可得∠2＝∠3，又因为对顶角相等，可得∠3＝∠4；再根据三角形的内角和为180°，可得∠E的度数．【解答】解：∵AB∥CD，∴∠3＝∠2＝50°，∴∠4＝∠3＝50°，∵∠1+∠2+∠E＝180°，∴∠E＝180°﹣∠1﹣∠4＝180°﹣60°﹣50°＝70°．故选：C．【点评】此题考查了平行线的性质：两直线平行，同位角相等．还考查了三角形内角和定理．比较简单，解题要细心．6．【分析】首先求出汽车行驶各段所用的时间，进而根据红绿灯的设置，分析每次绿灯亮的时间，得出符合题意答案．【解答】解：∵甲汽车从A路口以每小时30千米的速度沿l向东行驶，同时乙汽车从D路口以相同的速度沿l向西行驶，∴两车的速度为：＝（m/s），∵AB之间的距离为800米，BC为1000米，CD为1400米，∴分别通过AB，BC，CD所用的时间为：＝96（s），＝120（s），＝168（s），∵这两辆汽车通过四个路口时都没有遇到红灯，∴当每次绿灯亮的时间为50s时，∵＝1，∴甲车到达B路口时遇到红灯，故A错误；∴当每次绿灯亮的时间为45s时，∵＝3，∴乙车到达C路口时遇到红灯，故B错误；∴当每次绿灯亮的时间为40s时，∵＝5，∴甲车到达C路口时遇到红灯，故C错误；∴当每次绿灯亮的时间为35s时，∵＝2，＝6，＝10，＝4，＝8，∴这两辆汽车通过四个路口时都没有遇到红灯，故D正确；则每次绿灯亮的时间可能设置为：35秒．故选：D．【点评】此题主要考查了推理与论证，根据题意得出汽车行驶每段所用的时间，进而由选项分析是解题关键．二．填空题（共6小题，满分18分，每小题3分）7．【分析】根据零指数幂、负指数幂的运算法则解答即可．【解答】解：（﹣1）0+（）﹣1＝1+3＝4．故答案为：4．【点评】主要考查了零指数幂，负指数幂的运算，负指数为正指数的倒数；任何非0数的0次幂等于1．8．【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值大于1时，n是正数；当原数的绝对值小于1时，n是负数．【解答】解：将5 100 000用科学记数法表示为5.1×106．【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．9．【分析】由方程的系数结合根的判别式△≥0，即可得出关于m的一元一次不等式，解之即可得出m的取值范围．【解答】解：∵关于x的一元二次方程x2﹣2x+m﹣3＝0有两个实数根，∴△＝（﹣2）2﹣4×1×（m﹣3）＝16﹣4m≥0，解得：m≤4．故答案为：m≤4．【点评】本题考查了根的判别式，牢记“当△≥0时，方程有两个实数根”是解题的关键．10．【分析】设圆锥的底面圆的半径为r，根据圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长和弧长公式得到2πr＝，解得r＝1，然后利用扇形的半径等于圆锥的母线长和勾股定理计算圆锥的高．【解答】解：设圆锥的底面圆的半径为r，根据题意得2πr＝，解得r＝1，所以所围成的圆锥的高＝．故答案为．【点评】本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．也考查了弧长公式和勾股定理．11．【分析】连接AC，根据等腰三角形三线合一的性质可得AC⊥BC，根据线段中点的定义求出OC，再根据直角三角形斜边上的中线等于斜边的一半求出AO，利用勾股定理列式求出AC，然后写出点A的坐标即可．【解答】解：如图，连接AC，∵AO＝AB，点C是OB的中点，∴AC⊥BC，OC＝OB＝×10＝5，∵点D是AO的中点，∴AO＝2CD＝2×6.5＝13，由勾股定理得，AC＝＝＝12，所以，点A（5，12）．故答案为：（5，12）．【点评】本题考查了坐标与图形性质，直角三角形斜边上的中线等于斜边的一半的性质，勾股定理，等腰三角形的性质，熟记性质并作辅助线构造成直角三角形是解题的关键．12．【分析】求出BA的值，根据已知画出符合条件的三种情况：①当PA＝AB＝5cm时，②当P和C重合时，PB＝AB＝5cm，③作AB的垂直平分线交AC于P，此时PB＝PA，连接PB，求出即可．【解答】解：∵四边形ABCD是菱形，AC＝8cm，BD＝6cm，∴AC⊥BD，AO＝OC＝4cm，BO＝OD＝3cm，由勾股定理得：BC＝AB＝AD＝CD＝5cm，分为三种情况：①如图1，当PA＝AB＝5cm时，t＝5÷1＝5（s）；②如图2，当P和C重合时，PB＝AB＝5cm，t＝8÷1＝8（s）；③如图3，作AB的垂直平分线交AC于P，此时PB＝PA，连接PB，在Rt△BOP中，由勾股定理得：BP2＝BO2+OP2，AP2＝32+（4﹣AP）2，AP＝；t＝÷1＝（s），故答案为：5或8或．【点评】本题考查了菱形性质和等腰三角形的判定的应用，主要考查学生能否求出符合条件的所有情况．三．解答题（共5小题，满分30分，每小题6分）13．【分析】分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．【解答】解：去分母，得2x﹣（x﹣1）＝4（x﹣5），去括号，得2x﹣x+1＝4x﹣20，移项并合并同类项，得﹣3x＝﹣21，系数化为 1，得x＝7，经检验，x＝7是原方程的解，所以原方程的解是x＝7．【点评】此题考查了解分式方程，利用了转化的思想，解分式方程注意要检验．14．【分析】（1）画一个边长3，4，5的三角形即可；（2）利用勾股定理，找长为、2、的线段，画三角形即可．（3）利用勾股定理作一个边长为的正方形即可得．【解答】解：（1）如图1所示，Rt△ABC即为所求；（2）如图所示，Rt△DEF即为所求；（3）如图所示，正方形PQRS即为所求．【点评】此题主要考查了作图与应用作图．本题需仔细分析题意，结合图形，利用勾股定理即可解决．15．【分析】原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，求出x的值，代入计算即可求出值．【解答】解：原式＝•＝•＝，由不等式2x﹣6＜0，得到x＜3，∴不等式2x﹣6＜0的非负整数解为x＝0，1，2，则x＝0时，原式＝2．【点评】此题考查了分式的化简求值，以及一元一次不等式的整数解，熟练掌握运算法则是解本题的关键．16．【分析】（1）根据BD⊥直线m，CE⊥直线m得∠BDA＝∠CEA＝90°，而∠BAC＝90°，根据等角的余角相等得∠CAE＝∠ABD，然后根据“AAS”可判断△ADB≌△CEA，则AE＝BD，AD＝CE，于是DE＝AE+AD＝BD+CE；（2）利用∠BDA＝∠BAC＝α，则∠DBA+∠BAD＝∠BAD+∠CAE＝180°﹣α，得出∠CAE＝∠ABD，进而得出△ADB≌△CEA即可得出答案．【解答】证明：（1）∵BD⊥直线m，CE⊥直线m，∴∠BDA＝∠CEA＝90°，∵∠BAC＝90°，∴∠BAD+∠CAE＝90°，∵∠BAD+∠ABD＝90°，∴∠CAE＝∠ABD，∵在△ADB和△CEA中，∴△ADB≌△CEA（AAS），∴AE＝BD，AD＝CE，∴DE＝AE+AD＝BD+CE；（2）∵∠BDA＝∠BAC＝α，∴∠DBA+∠BAD＝∠BAD+∠CAE＝180°﹣α，∴∠CAE＝∠ABD，∵在△ADB和△CEA中，∴△ADB≌△CEA（AAS），∴AE＝BD，AD＝CE，∴DE＝AE+AD＝BD+CE．【点评】本题考查了全等三角形的判定与性质：判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”；得出∠CAE＝∠ABD是解题关键．17．【分析】（1）此题需要两步完成，所以采用树状图法或者采用列表法都比较简单，注意要不重不漏；（2）根据（1）求得所有情况与符合条件的情况，求其比值即可．【解答】解：（1）列表如下：或树状图；∴小明家所有可能选择游玩的方式有：（A，D），（A，E），（B，D），（B，E），（C，D），（C，E）；（2）小明家恰好在同一城市游玩的可能有（A，E），（B，D）两种，∴小明家恰好在同一城市游玩的概率＝＝．【点评】本题考查的是用列表法或树状图法求概率．注意列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件；树状图法适合两步或两步以上完成的事件．四．解答题（共4小题，满分32分，每小题8分）18．【分析】（1）根据已知条件列出算式，进行有理数的混合运算，再根据所给条件判断他的健康情况．（2）根据指数的计算公式，分别求出重量在65千克时的身高及重量在70千克的身高，从而可估算出B同志的身高．【解答】解：（1）A同志的指数＝＝35.16，身体质量指数高于30，所以A同志属于不健康的胖．（2）B同志的指数＝＝23，身高2＝，又∵B同志的体重在65～70之间，如果体重为65千克，则身高＝＝1.68米；如果体重为70千克，则身高＝＝1.74米，∴B同志的身高在1.68至1.74之间．【点评】本题考查了一元一次不等式的应用，题目涉及了身体质量指数这个概念，比较新颖，关键是掌握身体质量指数的计算方法，另外在第二问估算身高时要将两端的值算出来，这样才能进行估算．19．【分析】（1）把点A坐标分别代入反比例函数y＝，一次函数y＝x+b，求出k、b的值，再把点B 的坐标代入反比例函数解析式求出n的值，即可得出答案；（2）求出直线AB与y轴的交点C的坐标，分别求出△ACO和△BOC的面积，然后相加即可；（3）根据A、B的坐标结合图象即可得出答案．【解答】解：（1）把A点（1，4）分别代入反比例函数y＝，一次函数y＝x+b，得k＝1×4，1+b＝4，解得k＝4，b＝3，∵点B（﹣4，n）也在反比例函数y＝的图象上，∴n＝＝﹣1；（2）如图，设直线y＝x+3与y轴的交点为C，∵当x＝0时，y＝3，∴C（0，3），∴S△AOB＝S△AOC+S△BOC＝×3×1+×3×4＝7.5；（3）∵B（﹣4，﹣1），A（1，4），∴根据图象可知：当x＞1或﹣4＜x＜0时，一次函数值大于反比例函数值．【点评】本题考查了一次函数和反比例函数的交点问题，用待定系数法求函数的解析式，三角形的面积，一次函数的图象等知识点，题目具有一定的代表性，是一道比较好的题目，用了数形结合思想．20．【分析】（1）总数是100÷0.2＝500，所以第三组的频数是125，画图即可；（2）根据中位数的求算方法可知中位数落在第三组；（3）用样本来估计总体．【解答】解：（1）样本容量＝100÷2＝500，则第三小组的频数＝500﹣50﹣100﹣200﹣25＝125，补图（2）∵中位数是从小到大排列的第250，第251这两个数据和的平均数，又∵落在前三小组的频数分别为50，100，125∴抽取的样本中的中位数落在第三小组；（3）∵10000×＝500，∴估计全县初三参赛学生中获优胜奖的有500人．【点评】主要考查了频率的计算方法和如何画频率分布折线图，还考查了中位数的确定方法和用样本估计总体的能力．21．【分析】（1）先通过二次函数解析式求出点A，B的坐标，再求出AC，AB，CB的长度，用勾股定理逆定理证直角三角形，求出直线AD的解析式，用含相同字母的代数式分别表示E，Q，P的坐标，并表示出EP长度，求出AE长度，根据二次函数的性质求出EA+EP最大值时点E的坐标．最后作出点E关于CB的对称点，利用两点之间线段最短可求出结果；（2）由旋转的性质得到三角形CA′K与三角形CAK全等，且为等腰直角三角形，求出A′，K′的坐标，求出直线A′K′及CB的解析式，求出交点坐标，通过图象观察出P的横坐标的取值范围．【解答】解：（1）在抛物线y＝x2﹣x﹣6中，当y＝0时，x1＝﹣2，x2＝6，当x＝0时，y＝﹣6，∵抛物线y＝x2﹣x﹣6与x轴交于A，B（点A在点B左侧），与y轴交于点C，∴A（﹣2，0），B（6，0），C（0，﹣6），∴AB＝8，AC＝，BC＝，在△ABC中，AC2+BC2＝192，AB2＝192，∴AC2+BC2＝AB2，∴△ABC是直角三角形，且∠ACB＝90°，∵AD∥BC，∴∠CAD＝90°，过点D作DL⊥x轴于点L，在Rt△ADL中，DL＝10，AL＝10，tan∠DAL＝＝，∴∠DAB＝30°，把点A（﹣2，0），D（8，10）代入直线解析式，得，解得k＝，b＝2，∴y AD＝x+2，设点E的横坐标为a，EP⊥y轴于点Q，则E（a， a+2），Q（a，0），P（a， a2﹣a﹣6），∴EQ＝a+2，EP＝a+2﹣（a2﹣a﹣6）＝a2+a+8，∴在Rt△AEB中，AE＝2EQ＝a+4，∴PE+AE＝a+4+（a2+a+8）＝a2a+12＝（a﹣5）2+∴根据函数的性质可知，当a＝5时，PE+AE有最大值，∴此时E（5，7），过点E作EF⊥CB交CB的延长线于点F，则∠EAC＝∠ACB＝∠ACF＝90°，∴四边形ACFE是矩形，作点E关于CB的对称点E'，在矩形ACFE中，由矩形的性质及平移规律知，x F﹣x E＝x C﹣x A，y E﹣y F＝y A﹣y C，∵A（﹣2，0），C（0，﹣6），E（5，7），∴x F﹣5＝0﹣（﹣2），7﹣y F＝0﹣（﹣6），∴x F＝7，y F＝1，∴F（7，1），∵F是EE′的中点，∴，，∴x E′＝9，y E′＝﹣5，∴E'（9，﹣5），连接AE'，交BC于点N，则当GH的中点M在E′A上时，EN+MN有最小值，∴AE′＝＝2，∵M是Rt△AGH斜边中点，∴AM＝GH＝，∴EN+MN＝E′M＝2﹣，∴EN+MN的最小值是2﹣．（2）在Rt△AOC中，∵tan∠ACO＝＝，∴∠AOC＝30°，∵KE平分∠ACB，∴∠ACK＝∠BCK＝45°，由旋转知，△CA′K′≌△CAK，∠AC′A′＝75°，∴∠OCA′＝75°﹣∠ACO＝45°，∠AC′K′＝45°，∴OCK′＝90°，∴K′C⊥y轴，△CAK′是等腰直角三角形，∴A′C＝AC＝4，∴x A′＝＝2，y A′＝2﹣6，∴A′（2，2﹣6），∴K′（4，﹣6），将A′（2，2﹣6），K′（4，﹣6），代入一次函数解析式，得，解得k＝﹣1，b＝4﹣6，∴y A′K′＝﹣x+4﹣6，∵CB∥AD，∴将点C（0，﹣6），B（6，0）代入一次函数解析式，得，解得k＝，b＝﹣6，∴y CB＝x﹣6，联立y A′K′＝﹣x+4﹣6和y CB＝x﹣6，得﹣x+4﹣6＝x﹣6，∴x＝6﹣6，∴直线CB与A′K′的交点横坐标是6﹣6，∵当EP经过A′时，点P的横坐标是2，∴如图2，当2＜x P＜6﹣6时，重叠部分是轴对称图形；如图3，由于RS的长度为2，由图可看出当x P＝2﹣1时，重叠部分同样为轴对称图形；综上，当x P＝2﹣1或2＜x P＜6﹣6时，矩形RQRS和△A′CK′重叠部分为轴对称图形．【点评】本题考查了勾股定理的逆定理，三角函数，二次函数的性质，旋转的性质，两点之间线段最短等众多知识点，综合性非常强，解此题的关键是对初中阶段各知识点都要掌握熟练．五．解答题（共1小题，满分10分，每小题10分）22．【分析】（1）由已知可证得△ADG∽△EBG，△AGF∽△EGD，根据相似三角形的对应边成比例即可得到DG2＝FG•BG；（2）由已知可得到DH，AH的长，又因为△ADG∽△EBG，从而求得AG的长，则根据GH＝AH﹣AG就得到了线段GH的长度．【解答】解：（1）证明：∵ABCD是矩形，且AD∥BC，∴△ADG∽△EBG．∴＝．又∵△AGF∽△DGE，∴＝．∴＝．∴DG2＝FG•BG．（2）∵ACED为平行四边形，AE，CD相交点H，∴DH＝DC＝AB＝．∴在直角三角形ADH中，AH2＝AD2+DH2∴AH＝．又∵△ADG∽△BGE，∴＝＝．∴AG＝GE＝×AE＝×13＝．∴GH＝AH﹣AG＝﹣＝．【点评】此题主要考查学生对相似三角形的判定，平行四边形的性质及矩形的性质等知识点的掌握情况．六．解答题（共1小题，满分12分，每小题12分）23．【分析】（1）由于OA是等边三角形的边，又是圆的弦，过B点作OA的垂线，根据等边三角形的性质，可求B点坐标，连接AC，则∠OCA＝∠OBA＝60°，解直角△OCA可求OC．（2）因为∠COA＝90°，所以CA为直径，CD为圆的切线，∠OCA＝60°，所以∠DCO＝30°，解直角△OCD可求OD，取AC的中点（圆心）为O'，用阴影部分面积＝△OCD面积+△OO'C面积﹣扇形OO'C面积可求解．（3）①设点Q的坐标为（0，t），计算OH的长，△OPM为等腰三角形，有三种可能：OP＝OM，OM＝PM，OP＝PM，根据每一种情况下的图形特征，分别求解．【解答】解：（1）过点B作OA的垂线，垂足为G，∵A（2，0），∴OA＝2，OG＝OA＝1，设B点坐标为（1，t），则＝2，∴t＝，∴B（1，）（1分）连接AC，则∠OCA＝∠OBA＝60°，∴＝tan60°，OC＝＝＝，∴C（0，）．故答案为（1，），（0，）．（2）∵∠COA＝90°，∴CA为直径，又∵CD为圆的切线，∠OCA＝60°，∴∠DCO＝30°，∴OD＝tan∠DCO•OC＝×＝，∵AC是⊙O的直径，BG为△OAB的边OA的中线，∴O′为△ABC外接圆的圆心，∵∠OCA＝60°，∴∠OCA＝30°，∠OO′C＝60°，S阴影＝S△OCD+S△OO'C﹣S扇形OO'C＝××+××1﹣＝．故答案为：．（3）①设点Q的坐标为（0，t），OH＝OA×cos60°＝，（I）若OP＝OM，∠OPM＝∠OMP＝75°，∴∠OQP＝45°，过点P做PE⊥OA，垂足为E，则有：OE＝EP，即t﹣（﹣t）＝（t），解得：t＝1，即点Q的坐标为（0，1）．（II）若OM＝PM，则∠MOP＝∠MPO＝30°，∴PQ∥OA，从而OQ＝0.5OP，即t＝（﹣t），解得t＝即点的坐标为（0，），（III）若OP＝PM，∠POM＝∠PMO＝∠COB，此时PQ∥OC，不满足题意．②线段OM的长的最大值为．【点评】本题考查了正三角形与圆，圆的切线性质，等腰三角形条件的探求方法，面积求法及分类讨论的思想，具有较强的综合性．。

九年级上学期模拟考试数学试题考试时间120分钟 试卷满分150分一、选择题（下列各题的备选答案中，只有一个是正确的，请将正确答案的序号填入下面的表格内，每小题3分，满分30）1、下列图形属于中心对称图形的是（ ）A B C D ．2、已知k 、b 是一元二次方程（2x+1）（3x ﹣1）=0的两个根，且k ＞b ，则函数y=kx+b 的图象不经过（ ）A ．第一象限B ． 第二象限C ． 第三象限D ．第四象限3、某商品经过连续两次降价，销售单价由原来200元降到162元．设平均每次降价的 百分率为x ，根据题意可列方程为（ ）A ．200（1﹣x ）2=162B ．200（1+x ）2=162 ‘C ．162（1+x ）2=200D ．162（1﹣x ）2=2004. 设抛物线y=x 2-4x+k 的顶点在直线y=x 上，则k 的值为（ ） A. -6 B. -4 C. 4 D. 65．在同一直角坐标系中，函数y mx m =+和函数222y mx x =-++（m 是常数，且0m ≠）的图象可能是（）6、如图，⊙O是△ABC的外接圆，⊙O的半径为3，∠A=45°，则的长是（）A πB．πC． D π7．如图，在R t △ABC中，∠ACB=90°，∠BAC=60°．把△ABC绕点A按顺时针方向旋转60°后得到△AB'C'，若AB=4，则线段BC在上述旋转过程中所扫过部分的面积是（）A．πB．πC．2πD．4π6题图7题图8题图8．如图，电路图上有四个开关A、B、C、D和一个小灯泡，闭合开关D或同时闭合开关A、B、C 都可使小灯泡发光，则任意闭合其中两个开关，小灯泡发光的概率是（）A ．B ．C ．D ．9．已知点A （1， y 1）、B （2-，y 2）、C （2-，y 3）在函数212(1)2=+-y x 上，则 y 1、y 2、y 3的大小关系是 （ ） A ．y 1 ＞y 2 ＞y 3 B ． y 2 ＞y 1 ＞y 3 C ．y 3 ＞y 1 ＞y 2 D ．y 1 ＞y 3 ＞y 210．已知：⊙O 的半径为2cm ，圆心到直线l 的距离为1cm ，将直线l 沿垂直于l 的方向平移，使l 与⊙O 相切，则平移的距离是 （ ） A ．1 cm B ．3cm 或2 cm C ．3cm D ．1 cm 或3cm二、填空题（每小题3分，满分 24分）11、若一元二次方程（m ﹣1）x 2﹣4x ﹣5=0没有实数根，则m 的取值范围是 ．12.△ABC 内接于⊙O ，且∠BAC=100°，点P 为⊙O 上一点（P 不与A 、B 、C 重合），则∠BPC= .13.如图,在△ABC 中,AB=2 BC=3.6, ∠B=600,将△ABC 绕点A 按顺时针旋转一定角度得到 △ADE,当点B 的对应点D 恰好落在BC 边上时,则CD 的长为_____.1PAOyxP13题图 16题图 17题图14．已知圆锥的母线长为5cm ，底面圆的半径为3cm ，则圆锥的侧面展开图的面积 是 cm 2．15. 已知m 、n 是关于x 的一元二次方程x 2-2ax+a 2+a-2=0的两实根，那么m+n 的 是 ．16.如图，⊙O 是等腰三角形的外接圆，AB=AC ，∠A=45°，BD 为⊙O 的直径，BD=22，连结CD ，则BC= ．17．如图，二次函数y=ax 2+bx+c （a ≠0）的图象与x 轴交于A 、B 两点，与y 轴交于点C ， 点B 坐标是（﹣1，0），对称轴为直线x=1，下面的四个结论：①9a+3b+c=0；②a+b ＞0；③ac ＞0；④b 2﹣4ac ＞0．其中正确的结论序号是 ．18.如图，将边长为1的正三角形OAP 沿x 轴正方向连续翻转2015次，点P 依次落在点P 1，P 2，P 3，……P 2015的位置，则点P 2015的横坐标为 ．三、解答题（每题10分，满20分）19．先化简，再求值：144)131(2-+-÷--+x x x x x ，其中x 满足方程：x 2+x ﹣6=0．20.如图，在平面直角坐标系中，△ABC 的三个顶点坐 标分别为A(1，4)，B(4，2)，C(3，5)（每个方 格的边长均为1个单位长度）.（1）请画出△A 1B 1C 1，使△A 1B 1C 1与△ABC 关于x 轴对称；（2）将△ABC 绕点O 逆时针旋转90°，画出旋转后得到的△A 2B 2C 2，并直接写出点B 旋转到点B 2所经过的路径长.BCAy xO 第18题图21.一个不透明的口袋中装有4个分别标有数字-1，-2，3，4的小球，它们的形状、大小完全相同.小红先从口袋中随机摸出一个小球记下数字为x ；小颖在剩下的3个小球中随机摸出一个小球记下数字为y.（1）小红摸出标有数字3的小球的概率是 ；（2）请用列表法或画树状图的方法表示出由x ，y 确定的点P （x ，y ）所有可能的结果； （3）若规定：点P (x ，y)在第一象限或第三象限小红获胜；点P （x ，y ）在第二象限或第四象限则小颖获胜.请分别求出两人获胜的概率.22．一名男生推铅球，铅球行进高度 （单位：m ）与水平距离 （单位：m ）之间的关系是35321212++-=x x y ，铅球运行路线如图。

A BC D 第4题图2012年初三年级模拟考试数学试卷本卷满分：120分 考试时间：120分钟一 选择题（本大题共12小题，1~6题每小题2分，7~12题每小题3分，共30分） 1. 2-的3倍是 （ ） A.5- B.1 C 、6 D 、6-2．计算a 3·a 4的结果是 （ ） A ．a 5 B ．a 7 C ．a 8 D ．a 123. 如图, 点A 、B 、C 在⊙O 上, 若∠C =40︒, 则∠AOB 的度数为 （ ）A ．20︒B ．40︒C ．80︒D ．100︒第3题图4．如图：矩形ABCD 的对角线AC ＝10，BC ＝8，则图中五个小矩形的周长之和为 （ ）A ．14B ．16C ．20D ．284－2a ＋4b 5．已知a －2b ＝－2，值是则的 （ ） A ．0 B.2 C.4 D.86.如图，平行四边形ABCD 中，CE AB ⊥，E 为垂足．若125A =∠，则BCE =∠ Ａ．55Ｂ．35Ｃ．25Ｄ．307.某市环保检测中心网站公布的2012年3月31日的PM2.5研究性检测部分数据如下表:时间0:004:008:0012:0016:0020:00PM2.5(mg/m 3) 0.027 0.035 0.032 0.014 0.016 0.032 则该日这6个时刻的PM2.5的众数和中位数分别是 （ ）A. 0.032, 0.0295B. 0.026, 0.0295C. 0.026, 0.032D. 0.032, 0.027CBAOA E BCD6题图y 1y x2O -1 y 248．如图，在△ABC 中，∠C =90︒, 点D 在CB 上，DE ⊥AB 于E ，若DE=2， CA=4，则DBAB的值为 （ ）A ．41B ．31C ．12D ．329． 货车行驶25千米与小车行驶35千米所用时间相同,已知小车每小时比货车多行驶20千米,求两车的速度各为多少?设货车的速度为x 千米/小时,依题意列方程正确的是（ ） Ａ.203525-=x x Ｂ．x x 352025=-Ｃ．203525+=x x Ｄ．xx 352025=+ 10．十字路口的交通信号灯每分钟红灯亮30秒，绿灯亮25秒，黄灯亮5秒．当你抬头看信号灯时，是黄灯的概率是 （ ）A ．1 3B ．512C ．112D ．1 211．根据图象，判断下列说法错误的是（ ）A ．函数2y 的最大值等于4B ．当x ＞2 时， 1y ＞2yC ．当－1＜x ＜3时，2y ＞1yD ．当x 为－1或2时，1y = 2y12.如图，矩形ABCD 中，AB =3，BC =5，点P 是BC 边上的一个动点（点P 不与点B 、C 重合），现将△PCD 沿直线PD 折叠，使点C 落到点C’处；作∠BPC’的角平分线交AB 于点E ．设BP =x ，BE =y ，则下列图象中，能表示y 与x 的函数关系的图象大致是（ ） A ． B ． C ． D ．ED C BAE PC’A DBCO5yxO5yxOxy5O5y x2012年初三年级模拟考试数学试卷答题纸二 填空题（每题3分，共18分） 13． 分解因式：x 3 - 4x = ．14． 如果一个正多边形的一个外角是60°，那么这个正多边形的边数是 ．15. 不等式组 ⎪⎩⎪⎨⎧〉-〉+010121x x 的解集为 ．16．已知1x =-是关于x 的方程2220x ax a +-=的一个根，则a =____ __． 17．、某计算装置有一数据入口A 和运算结果输出口B ，下表是小明输入的一些数据和经该装置后输出的相应数据结果：A 0.5 1 1.5 3 …B6321…根据计算装置的计算规律，若输入的数是x ，输出的数是y ， 则y 与x 之间的函数关系式为___________.18．在数学校本活动课上，张老师设计了一个游戏，让电动娃娃在边长为1的正方形的四个顶点上依次跳动．规定：从顶点A 出发，每跳动一步的长均为1．第一次顺时针方向跳1步到达顶点D ，第二次逆时针方向跳2步到达顶点B ，第三次顺时针方向跳3步到达顶点C ，第四次逆时针方向跳4步到达顶点C ，… ，以此类推，跳动第2012次到达的顶点是 ． 三 解答题19.（1）（本题满分8分） 计算：已知a = -2，1-=b ，求2221a b a ab --+÷1a 的值．A输 入 B 输 出A D C B电视机月销量扇形统计图第一个月15% 第二个月30%第三个月 25%第四个月图①20.（本题满分8分）在平面直角坐标系中，△ABC 的顶点坐标分别是 A （-7，1），B （1，1），C （1，7）.线段DE 的端点坐标是D （7，-1） E （-1，-7）.（1）试说明如何平移线段AC ，使其与线段ED 重合；（2）将△ABC 绕坐标原点O 逆时针旋转，使AC 的对应边为DE ，请直接写出点B 的对应点F 的坐标；（3）画出（2）中的△DEF ，并和△ABC 同时绕坐标原点O 逆时针旋转90°，画出旋转后的图形.21. （本题满分8分）某商店在四个月的试销期内，只销售A ，B 两个品牌的电视机，共售出400台．试销结束后，只能经销其中的一个品牌，为作出决定，经销人员正在绘制两幅统计图，如图①和如图②． （1）第四个月销量占总销量的百分比是 ； （2）在图②中补全表示B 品牌电视机月销量的折线； （3）为跟踪调查电视机的使用情况，从该商店第四个月售出的电视机中，随机抽取一台，求抽到B 品牌电视机的概率；（4）经计算，两个品牌电视机月销量的平均水平相同， 请你结合折线的走势进行简要分析，判断该商店应经销 哪个品牌的电视机．时间/月10 20 30 50 40 60 图②销量/台 第一 第二 第三 第四 电视机月销量折线统计图A 品牌B 品牌80 7022.（本题满分8分）某厂家新开发一种摩托车如图所示，它的大灯A 射出的光线AB 、AC 与地面MN 的夹角分别为8°和10°，大灯A 与地面距离1 m ．（1）该车大灯照亮地面的宽度BC 约是多少m ？（2）一般正常人从发现危险到做出刹车动作的反应时间是0.2 s ，从发现危险到摩托车完全停下所行驶的距离叫做最小安全距离，某人以60km ／h 的速度驾驶该车，突然遇到危险情况，立即刹车直到摩托车停止，在这过程中刹车距离是314m ，请判断该车大灯的设计是否能满足最小安全距离的要求，请说明理由．（参考数据：2548sin ≈ ，718tan ≈ ，50910sin ≈ ，28510tan ≈ ）23．（本题满分9分）已知：△ABC 和△ADE 是两个不全等的等腰直角三角形，其中BA =BC ，DA =DE ，联结EC ，取EC 的中点M ，联结BM 和DM ．（1）如图1，如果点D 、E 分别在边AC 、AB 上，那么BM 、DM 的数量关系与位置关系是 ； （2）将图1中的△ADE 绕点A 旋转到图2的位置时，判断（1）中的结论是否仍然成立，并说明理由．M B C N ADCB AEMMEABCD24．（本题满分9分）今年4月18日，我国铁路第六次大提速，在甲、乙两城市之间开通了动车组高速列车．已知每隔1h有一列速度相同的动车组列车从甲城开往乙城．如图所示，OA是第一列动车组列车离开甲城的路程s（单位：km）与运行时间t（单位：h）的函数图象，BC是一列从乙城开往甲城的普通快车距甲城的路程s（单位：km）与运行时间t（单位：h）的函数图象．请根据图中信息，解答下列问题：（1）点B的横坐标0.5的意义是普通快车发车时间比第一列动车组列车发车时间 h，点B的纵坐标300的意义是。

一、选择题（下列各题给出的四个选项中，只有一个是正确的．每小题3分，满分24分） 1．是A ．2的相反数B ． 的相反数C ．的相反数D ． 的相反数 2．花果山风景区一年接待旅游者约876000人，这个数可以用科学记数法表示为 A ．0.876×106 B. 876×103 C. 8.76×106 D. 8.76×105 3．下列运算中，计算正确的是A ．3x 2+2x 2=5x 4B ．(－x 2)3＝－x 6C ．(2x 2y)2=2x 4y 2D ．(x+y 2)2=x 2+y 4 4．体育课上，体育委员记录了6位同学在25秒内连续垫排球的情况，6位同学连续垫球的个数分别为30、27、32、30、28、34，则这组数据的众数和极差分别是 A ．33，7B ．32，4C ．30，4D ．30，75．如右图所示的几何体是由一些小立方块搭成的，则这个几何体的左视图是 6．已知,那么在数轴上与实数x 对应的点可能是A ．B ．C ．或D ． 或7．如图，已知□ABCD ，∠A=45°，AD=4，以AD 为直径的半圆O 与BC 相切于点B ，则图中阴影部分的面积为 A ．4 B ．π+2C ．4D ．28．如图，在的正方形网格中，以AB 为边画直角△ABC ，使点C 在格点上，满足这样条件的点C 的个数 A ．6B ．7C ．8D ．9二、填空（每小题3分，共24分）9．写出一个小于0的无理数______ _______．10．函数y =－中自变量x 的取值范围_______ ________． 11．分解因式：= _______ ______．12．已知等腰梯形的面积为24cm 2，中位线长为6cm ，则等腰梯形的高为____ _____cm ． 13．如图，把一块直角三角板的直角顶点放在直尺的一边上，如果∠1=35°，那么∠2是 °．第5题AB D C14． 已知实数m 是关于x 的方程2x 2－3x －1=０的一根，则代数式4m 2－6m －2值为___ __．15．如图，△ABC 的三个顶点都在5×5的网格（每个小正方形的边长均为1个单位长度）的格点上，将△ABC 绕点B 顺时针旋转到△A’BC’的位置，则点A 经过的路径长为 .（结果保留π）．16．某中学在校内安放了几个圆柱形饮水桶的木制支架（如图①），若不计木条的厚度，其俯视图如图②所示，已知AD 垂直平分BC ，AD =BC =40cm ，则圆柱形饮水桶的底面半径的最大值是 cm.三、解答题：102分．请在答题卡指定区域．．．．．．．内作答，解答时应写出文字说明、证明过程或演算步骤） 17．(本题满分6分)计算：－18．(本题满分6分)先化简，再选取一个使原式有意义的的值代入求值． 19．(本题满分6分)解方程：20．（本题满分6分）如图，四边形ABCD 是正方形，点E 在BC 上，DF ⊥AE ，垂足为F ，请你在AE 上确定一点G ，使△ABG ≌△DAF ，请你写出两种确定点G 的方案，并就其中一种方案的具体作法证明△ABG ≌△DAF ．方案一：作法： ； 方案二：（1）作法： .(2) 证明：21．(本题满分6分)某手机专营店代理销售A 、B 两种型号手机．手机的进价、售价如下表：第16题 第20题用36000元购进A、B两种型号的手机，全部售完后获利6300元，求购进A、B两种型号手机的数量。

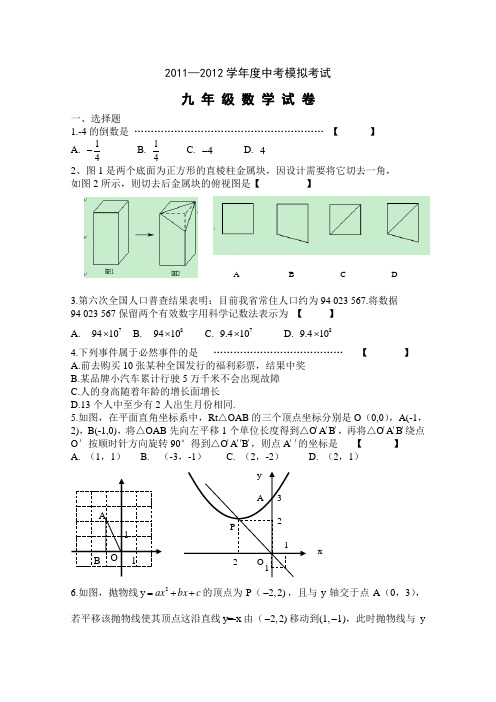
2011—2012学年度中考模拟考试九 年 级 数 学 试 卷一、选择题1.-4的倒数是 ………………………………………………… 【 】 A. 14-B.14C. 4-D. 42、图1是两个底面为正方形的直棱柱金属块，因设计需要将它切去一角， 如图2所示，则切去后金属块的俯视图是【 】A B C D3.第六次全国人口普查结果表明：目前我省常住人口约为94 023 567.将数据 94 023 567保留两个有效数字用科学记数法表示为 【 】 A. 79410⨯ B. 89410⨯ C. 79.410⨯ D. 89.410⨯4.下列事件属于必然事件的是 ………………………………… 【 】 A.前去购买10张某种全国发行的福利彩票，结果中奖 B.某品牌小汽车累计行驶5万千米不会出现故障 C.人的身高随着年龄的增长面增长 D.13个人中至少有2人出生月份相同.5.如图，在平面直角坐标系中，Rt △OAB 的三个顶点坐标分别是O （0,0），A(-1，2)，B(-1,0)，将△OAB 先向左平移1个单位长度得到△O ′A ′B ′，再将△O ′A ′B ′绕点O ′按顺时针方向旋转90°得到△O ′A ′′B ′，则点A ′′的坐标是 【 】 A. （1，1） B. （-3，-1） C. （2，-2） D. （2，1）6.如图，抛物线2y ax bx c=++的顶点为P （2,2)-，且与y轴交于点A （0，3），若平移该抛物线使其顶点这沿直线y=-x 由（2,2)-移动到(1,1-)，此时抛物线与yx轴交于点A ′，则AA ′的长度为 ………………………… 【 】 A. 124B. 334C.D. 3二、填空题（每小题3分，共27分）7.计算：03(2-++=___________8.在平面直角坐标系中，点P （2，3）关于y 轴对称的点坐标是_________ 9.按照如下的操作步骤 ，若输入x 的值为1-，则输出的值为____________10.如图，AB 为半圆O 的直径，点P 是BA 延长线上一点，PC 切半圆O 于点C ，弦CD ∥AB ，若∠P=28°，则∠D 的度数为________11.当x=__________时，代数式312x x -+-与32x-的值相等.12.抛掷两枚质地均匀的硬币，落地后两枚全部是正面朝上的概率是_______ 13.一次函数11y k x b =+与反比例函数22k y x=的图象在平面直角坐标系中的位置如图所示.当12x =-时，1y 与2y 的大小关系是1y ________2y14.如图，将矩形ABCD 沿着直线EF 折叠，使点C 与点A 重合，点D 落到D ′处，若AB=1，当BC 的长为___________时，△AEF 是等边三角形.15.如图，在直角梯形ABCD 中，AD ∥BC ，∠C=90°，BC=CD=6，E 是CD 的中点，AE=5，则∠ABE 的正切值是_______________. 三解答题（本题共8小题，共75分） 16.（8分）先化简，再求值：22224224424xx x x x x x x--÷+++++，其中x 满足x 2=x.P CDOAB17.(9分)已知∠MAN=30°，点B 是边AM 上一点. （1）尺规作图（不写作法，保留作图痕迹）；①作线段AB 的垂直平分线分别交AB 、AN 于点C 、D ； ②在DN 上截取DE ，使DE=DC ,连接BD 、BE ； （２）判断BE 和AE 的位置关系，并给出证明.18.（9分）下面的图象反映的过程是是：小明与朋友一起骑车从家出发到一个山水景区游玩，玩了一段时间后，又骑车回家，其中x(时) 表示时间.y(千米)表示他们离家的距离.请根据图中信息解答下列问题;(1)景区距小明家多少千米?他们在景区游玩了多长时间？（2）求他们回家途中y 与x 之间的函数解析式，并写自变量x 的取值范围； （3）若他们是上午8：00从家出发，求整个旅途中他们离家10千米时的时间刻19.（9分）某实践活动小组为了解本校九年级600名同学投掷实心球的成绩，随机抽取了120名同学的测试成绩(满分10分)，统计整理并绘制了如下的统计图：时M N根据以上信息解答下列问题（1）所抽取成绩的中位数是____________分，扇形统计图中的m=__________.(2)估计该校九年级同学大约有多少人得满分？(3)若从该校九年级得满分的同学中，随机选出20名同学作为小教练，则得满分的小刚被选中的概率是多少？20.（9分）小林家要在卫生间墙壁（AB）上安装一个淋浴装置，要求淋浴头放至插槽中正常情况下使用时，水不能喷洒到对面墙壁（MN）上，小林经过研究和测量，将其简化成下面的问题：已知淋浴头放入插槽后，喷射最远的水线DE与CD 的夹角∠CDE＝８７°，CD＝０.２ｍ，∠BCD＝４５°，两墙壁之间的距离为２ｍ，请计算插槽安装的最大高度AC，（参考数据： 1.414≈，00≈≈，结果保留两个有效数字）tan48 1.111,tan420.900２１.（１０分）小红和小丽去某商店购买学习用品，小红用２２元买了１文具袋和２本笔记本；小丽用５６元买了同样的文具袋２个和笔记本６本.（１）求文具袋和笔记本的单价；（２）小红和小丽所在的班级共捐款７４０元，准备购买上述的文具袋和笔记本，赠给本市的一所进城务工子弟学校，若购买的文具袋和笔记本共１００件，，共有多少种购买方案？且要求文具袋数量不少于笔记本数量的12２２.（１０）如图１.△ABC和△DEC是两个完全重合在一起的等腰直角三角形，现将△ABC固定，将△DEC绕点C按顺时针方向旋转，旋转角为a（0°＜a≤135°）,过点D作DF∥AB交BE的延长线于点F，连接AF，BD.（１）如图２.当a＝９０°时，四边形ABDF的形状为____________（2）如图3.当0°＜a≤135°时，（1）中的结论是否仍然成立？说明理由；（3）若AB=1，当a从45°变化到135°的过程中，线段DF扫过区域的面积是多少？试说明理由；23.（11分）如图，在直角梯形OABC中，CB∥OA，∠AOC=90°，OA=OC=5,BC=3.以O为原点，OA、OC所在的直线为坐标轴建立平面直角坐标系，过A、B、C三点的抛物线交x轴的负半轴于点D.（1）求抛物线的解析式；（2）连接BD交y轴于点E，连接AC交BD于点F，比较AE和AB的大小，并说明理由；（３）点P是抛物线上一点，判断有几个位置能够使点P到直线AC的距离等于BF的长，直接写出相应的点P的坐标；。

九年级第三次模拟考试数学一、选择题（本大题共10小题，每小题4分，满分40分） 1. 下列运算正确的是（ ） A. 331-=- B.39±= C. 6332)(b a ab = D. 532a a a =+2. 如图是由6个相同的小正方体搭成的立体图形，若由图①变到图②，则（ ） A. 主视图改变，俯视图改变 B. 主视图不变，俯视图改变 C. 主视图不变，俯视图不变 D. 主视图改变，俯视图不变3. 物理某一实验的电路图如图所示，其中1K 、2K 、3K 为电路开关，1L 、2L 为能正常发光的灯泡，任意闭合开关1K ，2K ，3K 中的两个，那么能让两盏灯泡同时发光的概率为（ ） A.61 B. 32 C.21 D.31 4. 把代数式32b b a -分解因式，结果正确的是（ ）A. )(2b a b +B. )(b a b -C. )(22b a b - D. ))((b a b a b -+5. 2502015）（-的值等于（ ）A. ()502015-±B.()502015± C.502015- D. 201550-6. 桌面上有甲、乙、丙三个圆柱形的杯子，杯子的深度都是为15cm ，各装有10cm 高的水，且表格记录了甲、乙、丙三个杯子的底面积。

小明将甲、乙两杯内的一些水倒入丙杯，在这个过程中水没溢出，使得甲、乙、丙三杯内水的高度比变为3:4:5，若不记杯子厚度，则甲杯内水的高度变为多少cm ？（ ） A. 5.4 B. 5.7 C.7.2 D. 7.5第6题图 第7题图 7. 如图，在矩形ABCD 中，9=AB ，12=BC ，点E 是BC 中点，点F 是边CD 上的任意一点，当AEF ∆的周长最小时，则DF 的长为（ ）A. 3B. 6C. 8D. 98. 已知0132=+-a a ，则分式142+a a 的值是（ ）A. 3B.31 C. 7 D. 71 9. ABC ∆的三边AB ，BC ，CA 的长分别为6cm ，4cm ，4cm ，P 为三条内角平分线的交点，则ABP ∆，BCP ∆，ACP ∆的面积比等于（ ）A . 1:1:1B . 3:2:2C . 2:3:2D . 2:2:310. 直线4+-=x y 与x 轴交于点A ，与y 轴交于点B ，O 是原点。

2011年安徽省中考摸底考试卷数 学 试 题考生注意：本卷共八大题，计23小题，满分150分，考试时间120分钟一、选择题（本大题共10小题，每小题4分，满分40分）1、2-的相反数是…………………………………………………（ ）A 、2B 、－2C 、4D 2、2009年我省GDP 突破万亿达到10052.9亿元，这意味着安徽已经成为全国GDP 万亿俱乐部的第14个成员，10052.9亿元用科学记数法表示为（保留三个有效数字）………………（ ）元A 、121.0010⨯B 、121.00510⨯C 、121.0110⨯D 、121.0052910⨯3、如图，把矩形直尺沿直线断开并错位，点E 、D 、B 、F 在同一条直线上，若∠ADE=125°，则∠DBC 的度数为……………………………………………………………………（ ）A 、55°B 、65°C 、125°D 、135°4、如图是一个几何体的三视图，根据图中标注的数据求出这个几何体的体积为……（ ）A 、24πB 、32πC 、36πD 、48π5、小明正在玩飞镖游戏，如果小明将飞镖随意投中如图所示的正方体木框中，那么投中阴影部分的概率为……………………………………………………………………………（ ）A 、16B 、18C 、19D 、5186、已知⊙O 1和⊙O 2的半径是方程2560x x -+=两根，且两圆的圆心距等于5，则⊙O 1和⊙O 2的位置是……………………………………………………………………………（ ）A 、相交B 、外离C 、外切D 、内切7、将量角器按如图所示的方式放置在三角形纸板上，使点C 在半圆上，点A 、B 的读数分别为86°、30°，则∠ACB 的大小为………………………………………………（ ）A 、15°B 、28°C 、29°D 、34°8、如图，CD 是平面镜，光线从A 点出发经CD 上点E 反射照到B 点，若入射角为α，AC ⊥CD ，BD ⊥CD ，且AC=3，BD=6，CD=12，则tan α值为…………………（ ）A 、35B 、43C 、45D 、349、如图所示是二次函数2y ax bx c =++图象的一部分，图象过A 点（3，0），对称轴为1x =，给出四个结论：①240b ac ->；②20a b +=；③0a b c ++=；④当1x =-或3x =时，函数y的值都等于0。

2011—2012学年度下学期学业考试初三数学试题一、单项选择题(每小题3分，满分30分)1.下列运算正确的是( )(A) a 2-c^(B) -x-x = 0(C)(6f 3)4=a 7(D) (-2x )02 =4x 2y 23•如果两个相似多边形的面积比为9:4,那么这两个相似多边形的相似比为( )7.已知△ ABC 屮，AB=10, AC=17, BC 边上的高AD=8,则厶ABC 的面积为( )(A) 9:4(B)2:3 (03:2 (D )81:16身高(cm)180 186188 192 195 人数(人)4 6 542(A) 186 J 88 (B) 186,187(C) 186 J 86 (D) 195,1885. 如图，以O 为圆心的两个同心圆中，大圆的弦AB 切小圆于点C,若ZAOB=120° ,则大圆半径/?与小圆半径厂之间满足((A) R = y/3r (B) R = 3r(0 R = 2r (D) R = V2r6. 己知函数y = (x-aXx-b)(其中a>b)的图象如下面左图所示，则函数y = ax + b2.在下面的四个儿何体中，左视图与主视图不一定相同的儿何体是4.某校篮球队21名队员的身高如下表: 则该校篮球队21名同学身高的众数和中位数分别是(单位：cm) ( )的图象可能正确的是)(A) 168 (B) 84 (C) 84 或36 (D) 168 或72\x — m<Oj8若关于询不等式7_2Z 的整数解共有4个皿的取值范围是((A) 6 < < 7 (B)6W 〃2V7 (C)6W 〃W7 (D) 6 < m 79. 如图，梯形ABCD 中，AB 〃DC,点E 、F 、G 分别是BD 、 AC 、DC 的中点.已知两底差是6,两腰和是12,则AEFG的周长是()(A) 8 (B)9 (C)10 (D) 1210. 如图，一次函数y = ax-^b 的图象与x 轴，y 轴交于A 、B两点，与反比例函数y = ±的图象相交于C 、D 两点，分别过XC 、D 两点作y 轴、x 轴的垂线，垂足为E 、F,连接CF 、DE 、 EF.写出下列五个结论：©ACEF 与Z\DFE 的面积相等;②EF 〃CD ；③△DCEMACDF ；④△AOB S /XF OE ： ⑤ AC=BD ・ (第 1 隠)其中正确的结论的个数为()(A) 2 (B) 3 (0 4 (D) 5二、填空题(每小题3分，满分30分)11. 我国以2011年11月1日零时为标准记时点，进行了第六次全国人口普查，查得全国总人口约为1 370 000 000人，请将总人口用科学记数法表示为 ____________________12. 函数y 二 一中自变量兀的取值范围是 _________________ .x — 313. 甲盒子中有编号为1、2、3的3个白色乒乓球，乙盒子中有编号为4、5、6的3个黄色乒乓球.现分别从每个盒子中随机地取出1个乒乓球，则取出乒乓球的编号之和大 于6的概率为 ______________ .14. 分解因式：Fy_4xy + 4y = ____________________ .15. 已知G>0|与002交于点A 、点B,点O2在OO|±,且ZAO|B=80° ZAO.B 二 ______________ . 16. 如图，是二次函数)=心2+分+。

2011-2012年第二学期第三次质量检测九年级数学试题第I 卷 （选择题 共42分）一、选择题（本大题共14小题，每小题3分，共42分） 在每小题所给的四个选项中，只有一项是符合题目要求的.题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 答案1．下列计算正确的是 （ ）A ．030=B ．33-=--C ．331-=-D ．39±= 2． 自上海世博会开幕以来,中国馆以其独特的造型吸引了世人的目光.据预测, 在会展期间,参观中国馆的人数估计可达到14 900 000,此数（保留两个有效 数字）用科学记数法表示是（ ）A. 61.5010⨯B.810149.0⨯C.7109.14⨯D. 71.510⨯3．下面四个几何体中，主视图、左视图、俯视图是全等图形的几何图形是（ ） Ａ．圆柱 Ｂ．圆锥 Ｃ．三棱柱 Ｄ．正方体4. 不等式组2133x x +⎧⎨>-⎩≤的解集在数轴上表示正确的是 （ ）5. 菱形OABC 在平面直角坐标系中的位置如图所示，452AOC OC ∠==°，，则点B 的坐标为（ ）A ．(21)，B ．(12)，C ．(211)+，D ．(121)+，5题图 6题图 8题图6. 如图，D E ，分别为ABC △的AC ，BC 边的中点，将此三角形沿DE 折叠，使点C 落在AB 边上的点P 处．若48CDE ∠=°，则APD ∠等于（ ）A ．42°B ．48°C ．52°D ．58°7. ()24-的算术平方根是: （ ）A. 4B. 4±C. 2D. 2±8. 如图，为估计池塘岸边A B 、的距离，小方在池塘的一侧选取一点O ，测得15OA =米，OB =10米，A B 、间的距离不可能是（ ）A ．20米B ．15米C ．10米D ．5米OABA ．B ．C ．D ．xyO C B A9. 如图，火车匀速通过隧道（隧道长大于火车长）时，火车进入隧道的时间x 与火车在隧道内的长度y 之间的关系用图象描述大致是（ ）A ．B ．C ．D ．10. 如图，PA 、PB 是⊙O 的切线，切点分别是A 、B ，如果∠P ＝60°, 那么∠AOB 等于（ ） A. 60° B. 90° C. 120° D. 150°11. 如图，点A ，B 的坐标分别为（1, 4）和（4, 4）,抛物线n m x a y +-=2)(的 顶点在线段AB 上运动，与x 轴交于C 、D 两点（C 在D 的左侧），点C 的横坐标 最小值为3-，则点D 的横坐标最大值为（ ） A ．－3 B ．1 C ．5 D ．812. 把代数式322363x x y xy -+分解因式，结果正确的是（ ）A ．(3)(3)x x y x y -B ．223(2)x x xy y -+C ．2(3)x x y -D ．23()x x y -13. 为了解某班学生每天使用零花钱的情况，小红随机调查了15名同学，结果如下表：则这15A ．3，14. 如图，△点C 原来的2倍，B 的横坐标是（ ）A ．12a -B ．1(1)2a -+C ．1(1)2a --D ．1(3)2a -+每天使用零花钱（单位：元）1 2 3 5 6 人 数 2 5 4 3 1火车隧道oyxoy xoy xoy xy xOD CB (4,4)A (1,4)第Ⅱ卷 (非选择题 共78分)二、填空题：（本大题共5个小题，每小题4分，共20分 把答案填写在题中的横线上.15. 已知圆锥的底面直径为4，母线长为6，则它的侧面展开图的圆心角为_____. 16. 有一组数据如下：2，3，a ，5，6，它们的平均数是4，则这组数据的方差是 ．17. 如图，直角梯形ABCD 中，AD ∥BC ，AB ⊥BC ，AD = 2，将腰CD 以D 为中心逆 时针旋转90°至DE ，连接AE 、CE ，△ADE 的面积为3，则BC 的长为 ． 18. 某校举行以“保护环境，从我做起”为主题的演讲比赛．经预赛，七、八年 级各有一名同学进入决赛，九年级有两名同学进入决赛．前两名都是九年级同学 的概率是 .19. 如图，正方形ABCD 边长为4，以BC 为直径的半圆O 交对角线BD 于E ．则直线CD 与⊙O 的位置关系是 _____，阴影部分面积为(结果保留π) _______．三、解答题：（共58分）20. （本题7分）计算：（π－2011）0 +（sin60︒）-1－︱tan30︒－3︱+38．ABCDOE19题图21.（本题7分）化简: )212(112aa a a a a +-+÷--.22. （本题15分）如图，BD 为⊙O 的直径，点A 是弧BC 的中点，AD 交BC 于E 点，AE=2，ED=4. （1）求证: ABE ∆～ABD ∆；(2) 求tan ADB ∠的值；（3）延长BC 至F ，连接FD ，使BDF ∆的面积等于求EDF ∠的度数.23.（本题15分）某市政府大力扶持大学生创业．李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯．销售过程中发现，每月销售量y（件）与销售单价x（元）之间的关系可近似的看作一次函数：10500=-+．y x（1）设李明每月获得利润为w（元），当销售单价定为多少元时，每月可获得最大利润？（2）如果李明想要每月获得2000元的利润，那么销售单价应定为多少元？（3）根据物价部门规定，这种护眼台灯的销售单价不得高于32元，如果李明想要每月获得的利润不低于2000元，那么他每月的成本最少需要多少元？（成本＝进价×销售量）24.（本题14分）如图，二次函数c x y +-=221的图象经过点D ⎪⎭⎫ ⎝⎛-29,3，与x 轴交于A 、B 两点．⑴求c 的值；⑵如图①，设点C 为该二次函数的图象在x 轴上方的一点，直线AC 将四边形ABCD 的面积二等分，试证明线段BD 被直线AC 平分，并求此时直线AC 的函数解析式；⑶设点P 、Q 为该二次函数的图象在x 轴上方的两个动点，试猜想：是否存在这样的点P 、Q ，使△AQP ≌△ABP ？如果存在，请举例验证你的猜想；如果不存在，请说明理由．（图②供选用）。