落石冲击力计算表
- 格式:xlsx
- 大小:234.29 KB
- 文档页数:2
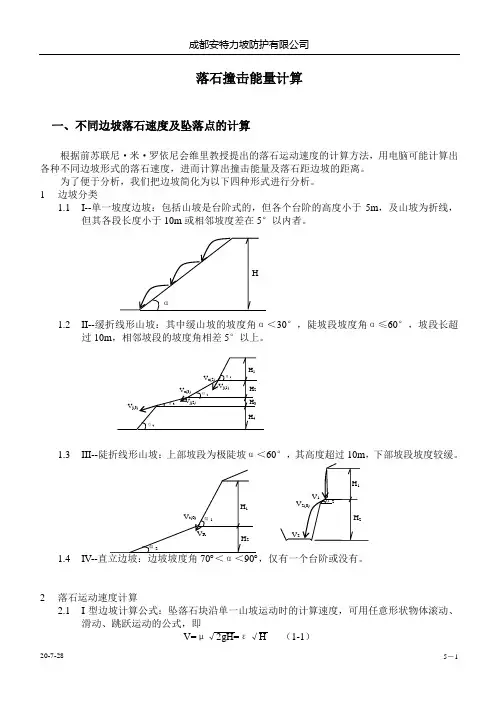
落石撞击能量计算一、不同边坡落石速度及坠落点的计算根据前苏联尼·米·罗依尼会维里教授提出的落石运动速度的计算方法,用电脑可能计算出各种不同边坡形式的落石速度,进而计算出撞击能量及落石距边坡的距离。
为了便于分析,我们把边坡简化为以下四种形式进行分析。
1 边坡分类1.1 I--单一坡度边坡:包括山坡是台阶式的,但各个台阶的高度小于5m ,及山坡为折线,但其各段长度小于10m 或相邻坡度差在5°以内者。
1.2 II--缓折线形山坡:其中缓山坡的坡度角α<30°,陡坡段坡度角α≤60°,坡段长超过10m ,相邻坡段的坡度角相差5°以上。
1.3 III--陡折线形山坡:上部坡段为极陡坡α<60°,其高度超过10m ,下部坡段坡度较缓。
1.4 IV--,仅有一个台阶或没有。
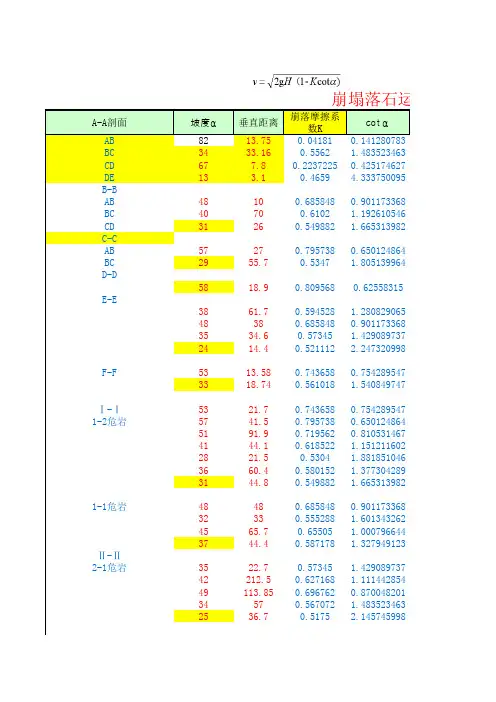
2 落石运动速度计算2.1 I 型边坡计算公式:坠落石块沿单一山坡运动时的计算速度,可用任意形状物体滚动、滑动、跳跃运动的公式,即V=μ√2gH=ε√H(1-1)ε=μ√2g (1-2)式中H---石块坠落高度(m);g---重力加速度(m/s2);α---山坡坡度角(度);K---石块沿山坡运动所受一切有关因素综合影响的阻力特性系数。
μ、ε值见表1。
2.2II型边坡计算公式:最高一个坡段坡脚的速度按公式(1-1)(1-2)计算,其余坡段终端的速度为:V j(i)= √V0(i)+2gH i(1-K i ctgαi) =√V0(i) 2+ εi2H i (1-3)式中V0(i)---石块运动所考虑坡段的起点的初速度,可按下列不同情况考虑,若α(i-1)>αi时,则V0(i)=V j(i-1)cos(α(i-1)-αi);若α(i-1)<αi时,则V0(i)=V j(i-1)。
αi---所考虑坡段的坡度角(度);α(i-1)---为相邻的前一坡段的坡度角(度);V j(i-1)---石块在前一坡段终端的运动速度(m/s);系数εi值可查表1,若αi<30°,则系数K i值可用表2中公式1计算。

落石冲击力计算方法的比较研究落石冲击力是一种重要的山坡稳定因素,直接影响着人们的安全。
目前,计算落石冲击力的方法有很多,比如动力学方法、静力学方法、复合动力学方法、离散元方法等。
本文通过比较不同计算方法,以期找出最佳计算方法。
首先,对于动力学方法,我们知道它是依据物理学中的动力学原理来计算冲击力的。
在实际的计算过程中,它可以准确的预测落石的瞬时冲击力,以及它对山坡的变形情况。
然而,由于动力学原理的复杂性,很难计算出准确的落石冲击力值,且计算时间较长,因此本文并不推荐使用动力学方法来计算落石冲击力。
其次,静力学方法是依据物理学中的静力学原理,即牛顿定律及弹力学原理,来计算冲击力的。
它在计算过程中,利用弹力学原理,能够精确地计算出落石冲击力的大小和分布状况,同时避免了动力学计算的时间延迟问题。
因此,静力学方法可以准确的预测不同类型落石冲击力的大小,因此本文比较推荐使用静力学方法来计算落石冲击力。
第三,复合动力学方法是将动力学和静力学相结合,充分发挥他们的优势,从而更好地计算冲击力的。
在实际应用过程中,它结合了动力学方法和静力学方法的优势,能够准确的预测落石冲击力的大小及分布,并能够较快地得出结果,是一种很有用的计算方法。
最后,离散元方法是一种将物体划分为多个小元素来进行运算的方法。
它可以有效的解决落石冲击力计算的全局优化问题,计算出更有效的结果,但同时其计算过程较为复杂,需要大量的数据和时间,因此在实际应用中只能在部分情况下使用。
综上所述,最佳的计算方法是基于静力学原理的静力学方法。
尽管这些计算方法各有特点,但本文推荐使用静力学方法,因为它可以准确的计算出落石冲击力的大小,同时能够较快地得出结果。
此外,本文也建议在计算落石冲击力的过程中,最好结合使用复合动力学和离散元方法,以获得最准确的计算结果。
论文的最后,在计算落石冲击力的过程中,应当充分考虑落石的特性和结构,以确保最佳的计算结果。
在此基础上,加强落石冲击力计算方法的科学研究,对于确保人们的山坡安全具有重要意义。

泥石流防治工程设计计算1.泥石流防治工程设计主要参数的选取 (1)泥石流体重度按照《泥石流灾害防治工程勘察规范》附录G 进行易发程度评分,按照表G.2查表确定泥石流重度和泥沙修正系数,其结果如下表1所示:表1 泥石流重度及泥沙修正系数表U C =γH φ+1n C 2/3I C 1/2 式中,γH 为泥浆体容重,γH =2.65t /m 3;n 河床糙率系数,n =0.33;H C 为计算断面的平均泥深,根据病害现场照片,取H C =1.5m ;I C 为泥石流水力坡度,取沟床纵率0.268。
计算得U C =5.3m/s 。
(3)泥石流流量用雨洪修正法计算泥石流流量Q C =Q B (1+φ)D式中,Q B 为青水洪峰流量。
按云南省水文手册计算公式算得Q 0.2=11.21m 3/s ,D 为泥石流堵塞系数,取1.2。
计算得Q C =21.05m 3/s 。
(4)一次泥石流过程总量计算根据泥石流历时T(s)和最大流量Q C (m 3/s ),按泥石流暴涨暴落的特点,将其过程线概化为五角形,其计算式为:Q=KTQ C 式中,K =0.264,T=22.4s 。
计算得Q =124.5m 3。
一次泥石流冲出的固体物质总量Q H :Q H =Q (γC −γW )/(γH −γW )式中,γC 为泥石流重度,γC =1.593t/m 3;γW 为水的重度,γW =1.0t/m 3;γH 为固体物质重度,γH =2.65t/m 3。
计算得Q H =44.8m 3。
(5)泥石流整体冲击力σ=λγc g V C 2sina式中,λ为建筑物形状系数,λ=1.33;a 为建筑物受力面与泥石流冲压力方向的夹角,a =90°。
σ=0.37kPa 。
2. 结构抗泥石流灾害的设计计算 (1)设计要求及计算参数:结构安全等级: 一级 混凝土强度等级: C50 钢筋等级: HRB335 单元类型:SOLID95材料特性:柱子:线弹性;顶板:材料非线性;填土:DP 特性初拟几何尺寸:边柱高32.0m ,截面2.0m ×3.0m ;顶板厚1.0m ;填土厚0.45+0.30×L 边界条件:基础:D ,ALL ,ALL ,0;靠山侧填土:D,ALL,UX,0 荷载组合:自重+泥石流固体物质+泥石流整体冲击(2)结构承载力验算C50砼抗压强度标准值:32.4MPa;抗拉强度标准值:2.64MPa;抗剪强度标准值:4.0MPa。

冲击地面过程中落石特征参量的理论分析落石是一种常见的地质过程,也是地质灾害最危险的因素之一。
它能够在地表产生巨大的破坏力,并且通常伴随着地面微地貌的变化。
因此,研究落石的特征参量对于清楚地质灾害动力机制具有重要的意义。
本文旨在从理论上对冲击地面过程中落石特征参量进行深入分析,以期为认识落石提供一些理论支持。
首先,落石是一种复杂的物理现象,它的发生主要取决于石头碰撞地面时产生的冲击力。
据了解,碰撞地面冲击力与碰撞角、碰撞速度、石头尺寸、石头重量、空气压力等因素有关。
因此,在探讨冲击地面过程中落石特征参量的理论模型时,应当从这些因素出发进行分析。
其次,已有研究表明,石头尺寸和重量是影响落石特性参量的重要因素。
一方面,石头的尺寸和重量会影响冲击力大小以及落石的形状,从而影响落石的运动特性和破坏程度。
另一方面,石头的尺寸和重量也会影响落石发生位置,也就是说,石头落到不同的地方会产生不同的破坏情况。
此外,空气压力也是影响落石特性参量的一个重要因素。
空气压力会影响落石冲击力大小,因此会影响石头对地面的冲击强度,从而影响落石破坏程度。
根据实验研究,当空气压力下降时,落石破坏的程度会增加。
此外,落石的破坏程度还受到周围环境条件的影响。
当地面受到水浸时,落石造成的破坏程度会减弱;当地面受到高温环境时,落石破坏程度会增强。
因此,落石破坏程度的变化还受到空气温度、地表湿润度等外部条件的影响。
最后,冲击地面的过程中落石特征参量的变化与时间有关。
研究表明,落石的大小、形状和速度与时间有一定的关系,这反映了冲击力的大小会随着时间的推移而发生变化,从而对落石的特征参量造成不同程度的影响。
总之,以上分析表明,碰撞角、碰撞速度、石头尺寸、石头重量、空气压力以及外界环境条件和时间等因素,都能够影响冲击地面过程中落石特征参量的变化,具有重要的意义。
因此,未来研究应重点探讨这些因素之间的联系,以期望能够更好地了解落石运动特征参量,更好地预测落石灾害的影响。
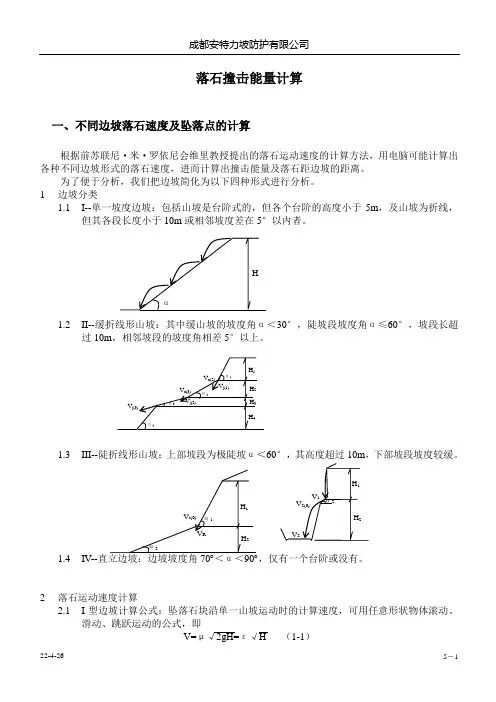
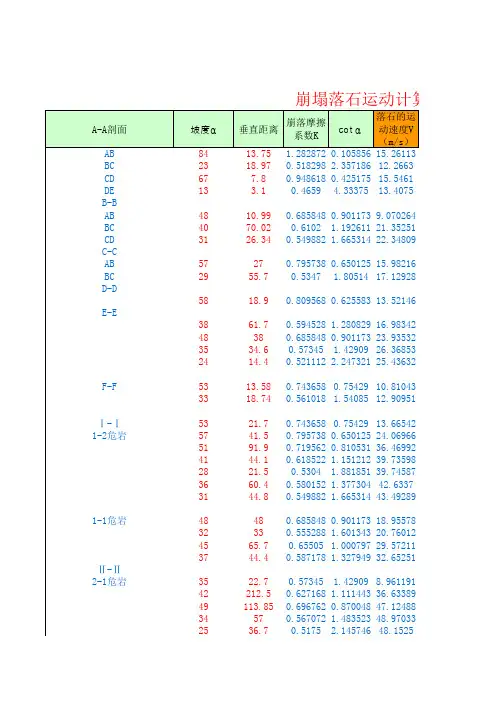
落石撞击能量计算一、不同边坡落石速度及坠落点的计算根据前苏联尼·米·罗依尼会维里教授提出的落石运动速度的计算方法,用电脑可能计算出各种不同边坡形式的落石速度,进而计算出撞击能量及落石距边坡的距离。
为了便于分析,我们把边坡简化为以下四种形式进行分析。
1 边坡分类1.1 I--单一坡度边坡:包括山坡是台阶式的,但各个台阶的高度小于5m ,及山坡为折线,但其各段长度小于10m 或相邻坡度差在5°以内者。
1.2 II--缓折线形山坡:其中缓山坡的坡度角α<30°,陡坡段坡度角α≤60°,坡段长超过10m ,相邻坡段的坡度角相差5°以上。
1.3 III--陡折线形山坡:上部坡段为极陡坡α<60°,其高度超过10m ,下部坡段坡度较缓。
1.4 IV--,仅有一个台阶或没有。
2 落石运动速度计算2.1 I 型边坡计算公式:坠落石块沿单一山坡运动时的计算速度,可用任意形状物体滚动、滑动、跳跃运动的公式,即V=μ√2gH=ε√H(1-1)μ=√1-Kctgαε=μ√2g (1-2)式中H---石块坠落高度(m);g---重力加速度(m/s2);α---山坡坡度角(度);K---石块沿山坡运动所受一切有关因素综合影响的阻力特性系数。
μ、ε值见表1。
2.2II型边坡计算公式:最高一个坡段坡脚的速度按公式(1-1)(1-2)计算,其余坡段终端的速度为:V j(i)= √V0(i)+2gH i(1-K i ctgαi) =√V0(i) 2+ εi2H i (1-3)式中V0(i)---石块运动所考虑坡段的起点的初速度,可按下列不同情况考虑,若α(i-1)>αi时,则V0(i)=V j(i-1)cos(α(i-1)-αi);若α(i-1)<αi时,则V0(i)=V j(i-1)。
αi---所考虑坡段的坡度角(度);α(i-1)---为相邻的前一坡段的坡度角(度);V j(i-1)---石块在前一坡段终端的运动速度(m/s);系数εi值可查表1,若αi<30°,则系数K i值可用表2中公式1计算。

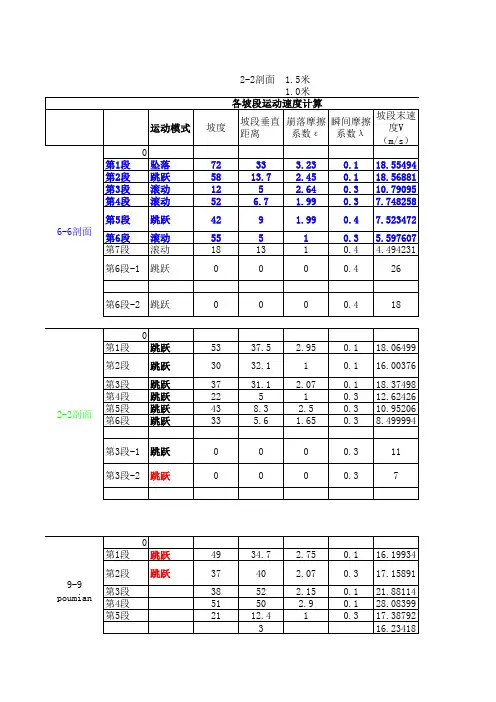
1--1(WS01)速度计算h1gα1cotα1k k*cotα116.39.8157.20.6444560230.7984780.514584008 h2gα2cotα2k k*cotα2 309.8144.4 1.021*******.649240.662982386 h3gα3cotα3k k*cotα36.59.8128.7 1.8265373690.5386780.983915095 h4gα4cotα3k k*cotα316.49.8145.90.9690674170.6639830.643444504落石腾跃(手算)α2V20(V2)1/32α2(1-α2/45)β44.48.504906 2.543403 1.18479.10031g cotβtanα2(tanα2-cotβ)2V202V202(tanα2-cotβ)29.810.1925640.9792720.61891002772.3334344.76788336撞击能量ρV(m3)m v2E2(j)28000.8224016.45302387363823.5落石腾跃(手算)α3V30(V3)1/32α3(1-α3/45)β3011.08743 2.2360162098.38929g cotβtanα3(tanα3-cotβ)2V302V302(tanα3-cotβ)29.81-0.147480.577350.525373326122.931264.58476027撞击能量ρV(m3)m v3E3(j)28000.8224011.0874332165219.5落石腾跃(手算)α4V40(V4)1/32α4(1-α4/45)β45.97.475712 2.355063-1.83684.1438gcot βtan α4(tan α4-cot β)2V402V402(tan α4-cot β)29.810.102567 1.031920.86369629255.8862748.26876249撞击能量ρV(m 3)mv4E(j)28000.8224013.06194537229305.8速度计算h1gα1cot α1k k*cot α13.39.8136.1 1.3713422930.580840.796530485h2gα2cot α2k k*cot α2139.8153.10.7508212380.7448970.559284353落石腾跃(手算)α2V20(V2)1/32α2(1-α2/45)β53.1 2.429688 2.21567-19.11681.63853gcot βtan α2(tan α2-cot β)2V202V202(tan α2-cot β)29.810.14698 1.331875 1.403975726 5.9033848.288207269撞击能量ρV(m 3)mv2E2(j)2800 1.54200 3.62957810433198.07速度计算1--1(ws02)2--2(WSⅠ区)18.99.8134.8 1.4388114380.5721480.823213777 h2gα2cotα2k k*cotα225.89.8144.6 1.0140610270.6511640.660319953 h3gα3cotα3k k*cotα337.19.8154.20.7212227460.7587380.547218873落石腾跃(手算)α2V20(V2)1/32α2(1-α2/45)β44.6 5.584942 2.4245510.79288888982.81654g cotβtanα2(tanα2-cotβ)2V202V202(tanα2-cotβ)29.810.1260360.9861340.73976831431.1915823.07454292撞击能量ρV(m3)m v2E2(j)2800 1.2336014.25258788409522.7落石腾跃(手算)α3V30(V3)1/32α3(1-α3/45)β54.29.837097 2.743432-22.1617777864.82327g cotβtanα3(tanα3-cotβ)2V302V302(tanα3-cotβ)29.810.470068 1.3865340.83990976196.7684781.2767824撞击能量ρV(m3)m v3E3(j)2800 1.2336020.64821439859519.14--4(WY01)速度计算h1gα1cotα1k k*cotα111.49.8135.3 1.4123506480.5754270.81270410331.99.8142.2 1.1028463440.6289360.693619857 h3gα3cotα3k k*cotα315.99.8149.80.8450655190.7057260.596385114 h4gα4cotα3k k*cotα319.79.81590.6008606190.8237220.494942111落石腾跃(手算)α2V20(V2)1/32α2(1-α2/45)β42.2 4.497873 2.441847 5.25155555684.05588g cotβtanα2(tanα2-cotβ)2V202V202(tanα2-cotβ)29.810.1041180.9067450.64420905920.2308613.03290533撞击能量ρV(m3)m v2E2(j)280051400014.559788961780695落石腾跃(手算)α3V30(V3)1/32α3(1-α3/45)β49.810.10232 2.471604-10.62476.62068g cotβtanα3(tanα3-cotβ)2V302V302(tanα3-cotβ)29.810.237852 1.183340.893947622102.056991.23353822撞击能量ρV(m3)m v3E3(j)280051400010.10232236857278.1落石腾跃(手算)α4V40(V4)1/32α4(1-α4/45)β5910.43306 2.593145-36.7111111162.96945g cotβtanα4(tanα-cotβ)2V402V402(tanα4-cotβ)249.810.510197 1.664279 1.331905765108.8488144.9764026撞击能量ρV(m3)m v4E(j)280051400017.4373389325541115--5(WYⅠ区)速度计算h1gα1cotα1k k*cotα117.49.8154.70.7080394670.7651590.541762473撞击能量ρV(m3)m v2E(j)28000.6168012.50746948157688.36--6(WY02)速度计算h1gα1cotα1k k*cotα140.19.8142.4 1.0951397390.6307170.690723382 h2gα2cotα2k k*cotα226.19.8153.10.7508212380.7448970.559284353落石腾跃(手算)α2V20(V2)1/32α2(1-α2/45)β53.110.72941 2.642919-19.11668.44099g cotβtanα2(tanα2-cotβ)2V202V202(tanα2-cotβ)29.810.395101 1.3318750.877546209115.1202101.0232577撞击能量ρV(m3)m v1E2(j)28002560015.59894517817579撞击能量ρV(m3)m v2E3(j)28000.5140018.46084255286274.37--7(WS03)速度计算h1gα1cotα1k k*cotα1 119.81710.3443276130.1751030.060292626 h2gα2cotα2k k*cotα259.8136 1.376381920.5801520.798510724 h3gα3cotα3k k*cotα38.79.81540.7265425280.7561920.549405647 h4gα4cotα3k k*cotα315.39.8144.8 1.00700580.65310.657675972落石腾跃(手算)α2V20(V2)1/32α2(1-α2/45)β368.165912 2.10277414.4101.9605g cotβtanα2(tanα2-cotβ)2V202V202(tanα2-cotβ)29.81-0.211840.7265430.8805556466.6821358.71732268撞击能量ρV(m3)m v2E2(j)2800 1.850409.29775374261419.4落石腾跃(手算)α3V30(V3)1/32α3(1-α3/45)β300 2.06221520106.6814g cotβtanα3(tanα3-cotβ)2V302V302(tanα3-cotβ)29.81-0.299660.577350.76914778700撞击能量ρV(m3)m v3E3(j)28000.616808.77004859977529.06落石腾跃(手算)α4V40(V4)1/32α4(1-α4/45)β44.8 6.060063 2.2773060.39822222287.99794g cotβtanα4(tanα-cotβ)2V402V402(tanα4-cotβ)249.810.0349570.9930430.9179289836.7243633.71035883撞击能量ρV(m3)m v4E(j)28000.6168011.8103872140601.13--3(WYⅠ区)速度计算h1gα1cotα1k k*cotα122.59.8154.50.7132930680.7625810.543943384撞击能量ρV(m3)m v3E3(j)2800 1.5420014.188946155073422gh1(1-k*cotα1)V1V20λ155.238946812.4594928.5049060.32gh2(1-k*cotα2)V202+2gh2(1-k*cotα2)V2V30198.3685674270.701994616.45302411.087430.32gh3(1-k*cotα3)V302+2gh3(1-k*cotα3)V3V402.0513*******.982482911.1795567.4757120.32gh3(1-k*cotα3)V302+2gh3(1-k*cotα3)V4V50114.7281488170.614416913.0619450.3ρ2800 1+cot2β2g(1+cot2β)Lmax Hmax1.0370*******.347527152.2467328 2.2001631+cot2β2g(1+cot2β)Lmax Hmax1.021********.046719555.5801692 3.2217121+cot2β2g(1+cot2β)Lmax Hmax1.010********.826403522.3592622 2.434572gh1(1-k*cotα1)V1V20λ13.17383721 3.6295781 2.4296880.32gh2(1-k*cotα2)V202+2gh2(1-k*cotα2)V2112.408933118.312316610.8771470.3 1+cot2β2g(1+cot2β)Lmax Hmax1.021*******.0438540.31046730.4135042gh1(1-k*cotα1)V1V20λ65.55551358.0966359 5.5849420.32gh2(1-k*cotα2)V202+2gh2(1-k*cotα2)V2V30171.9446809203.136261414.2525889.8370970.32gh3(1-k*cotα3)V302+2gh3(1-k*cotα3)V3329.5802877426.348757620.648214ρV(m3)m2800 1.23360 1+cot2β2g(1+cot2β)Lmax Hmax1.01588509719.93166561.1739608 1.1576831+cot2β2g(1+cot2β)Lmax Hmax1.22096419423.955317492.44700013.3928492gh1(1-k*cotα1)V1V20λ41.8920987 6.4724106 4.4978730.32gh2(1-k*cotα2)V202+2gh2(1-k*cotα2)V2V30191.7565914211.987454614.55978910.102320.32gh3(1-k*cotα3)V302+2gh3(1-k*cotα3)V3V40125.9108925227.967809515.09860310.433060.32gh3(1-k*cotα3)V302+2gh3(1-k*cotα3)V4V50195.211945304.060788817.437339ρV(m3)m v2E2(j)28000.51400 6.47241135189.361+cot2β2g(1+cot2β)Lmax Hmax1.010********.832692890.72472720.6571421+cot2β2g(1+cot2β)Lmax Hmax1.0565*******.729975063.7191708 4.4010441+cot2β2g(1+cot2β)Lmax Hmax1.26030124924.727110513.5228787 5.8630552gh1(1-k*cotα1)V1V20λ156.436792812.5074690.12gh1(1-k*cotα1)V1V20λ243.327090515.59894510.729410.32gh2(1-k*cotα2)V202+2gh2(1-k*cotα2)V2225.6825502340.802707518.4608430.3ρV(m3)m v1E2(j)28000.5140015.59895204394.81+cot2β2g(1+cot2β)Lmax Hmax1.15610447422.682769783.34396584.4537442gh1(1-k*cotα1)V1V20λ202.807645514.2410558.1659120.32gh2(1-k*cotα2)V202+2gh2(1-k*cotα2)V2V3019.7660979886.448224629.29775370.32gh3(1-k*cotα3)V302+2gh3(1-k*cotα3)V3V4076.9137524376.913752438.7700486 6.0600630.32gh3(1-k*cotα3)V302+2gh3(1-k*cotα3)V4V50102.7608808139.485245711.8103870.3ρV(m3)m v2E2(j)28000.5140014.24105170358.41+cot2β2g(1+cot2β)Lmax Hmax1.04487480220.500443613.94222992.8641981+cot2β2g(1+cot2β)Lmax Hmax1.0897963821.38180498001+cot2β2g(1+cot2β)Lmax Hmax1.0012219819.643975261.7280885 1.716066 2gh1(1-k*cotα1)V1201.32619314.1889465385.350042.652214.865007.431910.46500 5.23 V(m3)m v2E2(j)3840012.45949782404.32925.550012.75 6136.450018.2 11 6.4500 3.2v2E2(j)8.096636132159.93825.250012.63 1.95000.955589.550044.752624.150012.05149.3500 4.654442.7 3445 3078.5 2247.54075 3190 2770 5857 3130。

边坡落石运动轨迹计算新方法边坡落石是指悬崖或陡坡上个别岩块在自重或外力作用下突然脱离母体而急剧下落的现象。
落石是一种突发的地质灾害,虽然规模不如滑坡巨大,但落石发生往往很突然,同样会造成巨大损失。
落石运动是一种复杂的运动,影响边坡坡面的地质与性质、落石大小、形状等。
落石本身及地面条件是多样的,落石的运动形式也是多种多样,要实现对落石的运动轨迹精确计算有很大的困难。
现实中落石与边坡碰撞的受力情况有很大的不确定性。
落石运动可分为5种形式:自由落体、斜抛运动、碰撞、滑动和滚动等运动方式的一种或多种组合沿着坡面向下快速运动。
最后在较平缓的地带或有障碍物附近静止下来的一个动力学过程。
1.自由落体当岩块脱离母体,只在重力作用下自由坠落时,或者在只有一个初始角速度时,危石突然倾倒破坏后坠落,忽略空气阻力作用,角速度在坠落过程中保持不变,则落石的速度为v。
式中:1H为自1由落体高度,g为重力加速度。
2.斜抛运动阶段当落石在碰撞后法向恢复系数和切向恢复系数>0时,落石将离地做斜抛运动,落石做斜抛运动的危害极大。
工程设计时常采用阻挡拦截结构物。
因此;需要确定落石做斜抛运动的弹跳最大高度和最大水平运动距离。
落石做斜抛运动时没有和地面接触,忽略空气阻力影响,可以根据能量守恒得到弹跳的最大高度为:23r 1t211h =v cos -v sin 2gθθ() 式中3h 为弹跳最高点与坡面碰撞点的竖直距离。
最大水平运动距离为→2r 1v vt gL ⎡=⎢⎣ 式中1L 为起跳点与下一个碰撞点的水平距离。
3. 滑动阶段当落石与坡面碰撞都得法向速度为0时而切向速度不为0,且r d =0时,落石会沿坡面滑动,下滑速度为4vt 式中:f 为滑动摩擦系数;2l 为滑动的距离;3vt 为碰撞后的切向初速度;4vt 为滑动后的切向速度。
如果已知滑动后坡面的坡度不变且坡面较长时,可根据上式计算出落石滑动停止时所经过的切向距离。
4. 滚动阶段(椭圆落石)当落石与坡面碰撞后法向速度为0,而r d ﹤0,切向速度反向时,落石会向后滚动。
落石冲击力的颗粒流计算方法摘要:目前我国落石冲击力的计算主要有《铁路工程设计技术手册》推荐方法和《公路路基设计规范( JTJ13-95 ) 》推荐方法两种,但由于其计算的是落石的平均冲击力,其计算值比实际值小几倍甚至上百倍,从而导致了实际工程中被动防护结构的失效。
本文通过对比与实际冲击力较符合的日本道路公团推荐算法的计算值、现场实测值、颗粒流模拟值,得出结论:通过PFC3D颗粒流计算落石冲击力,比公式法更精确,同时适用性也更广。
关键词:落石;冲击力;颗粒流引言珠海主要为剥蚀残丘地貌,再加上雨季台风频繁,因此,边坡的崩塌落石灾害时有发生。
落石冲击力是设置被动防护结构的主要依据,国内求解落石冲击力的方法主要有路基规范法、隧道手册法、杨其新方法等,国外计算方法主要有日本道路协会方法、瑞士方法等。
前两种方法是利用功能原理和冲量定理获得,杨其新法是根据室内试验进行拟合得到的计算公式,日本法和瑞士法是根据现场试验拟合得到的计算公式。
文献[1]对比了各类落石冲击力算法,发现国内几种算法的计算的仅仅是落石中的平均冲击力,从而导致计算出的落石冲击力严重偏小,而日本法和瑞士是基于现场试验所进行拟合得到的,相对来说更精确。
其中特别值得注意的是,规范法的计算结果往往仅是日本法计算结果的几分之一甚至百分之一,从而导致按相关规范所建成防护结构不够安全,常常被落石损坏、从而丧失了保护作用。
从Pichler[2]的现场试验结果来看,与真实落石冲击力符合的最好的算法是日本道路公团法。
但对比发现,日本法比实测值仍小30%—60% ,也就是说,它的计算结果也仅仅是可以参考而已,我们需要寻找更精确的算法。
1PFC3D算法、日本算法和Pichler现场试验结果的对比1.1PFC3D力学原理作为离散元的一种,三维颗粒流程序(Particle Follow Code PFC3D)的理论基础是Cundall [1979]提出的离散单元法,用微观颗粒及颗粒之间的接触关系,模拟宏观物体的物理性质,PFC3D有ball(颗粒)单元和wall(墙)单元,通过ball之间的组合,可以模拟岩土体的弹性模量,内聚力,内摩擦角,泊松比,单轴抗压强度等等;通过wall之间的组合,可以模拟三维地形及相关地形的力学参数,因此,对落石运动可以进行模拟。