流体力学 第五章 压力管路的水力计算资料

流体力学孔口管嘴出流与管路水力计算流体力学是研究流体运动和力学性质的物理学科。

在水力学中，孔口管嘴出流和管路水力计算是流体力学的一个重要应用。

1.孔口管嘴出流孔口管嘴出流是指在一定压力差下，流体从孔口或管嘴中流出的现象。

它是一种自由射流，不受管道限制，流速和流量可以自由变化。

对于理想流体来说，根据贝努利定律和连续性方程，可以得出孔口管嘴出流速度的计算公式：v = √(2gh)其中，v为出流速度，g为重力加速度，h为液面距离孔口或管嘴的高度差。

可以看出，出流速度与液面高度差成正比，与重力加速度的平方根成正比。

对于真实流体来说，考虑到粘性和摩擦等因素，出流速度会稍有减小。

此时，可以使用液体流量系数进行修正。

液体流量系数是指实际流量与理论流量之比，一般使用实验数据来确定。

根据实验结果，可以通过乘以液体流量系数来修正出流速度的计算。

管路水力计算是指在给定管道材料、管径和流体性质的条件下，计算流体在管路中的流动状态、压力损失以及流量等参数。

管路水力计算是实际工程中常见的问题，它可以帮助我们了解管道的输送性能和节能问题。

管道中的流体运动受到多个因素的影响，包括管道长度、管道粗糙度、流速、流量等。

在水力学计算中，一般常用的公式有达西公式和罗斯诺-魏谢巴赫公式。

达西公式可以用来计算管道中流体的摩阻损失，它的计算公式为：ΔP=λ(L/D)(v^2/2g)其中，ΔP为管道中的压力损失，L为管道长度，D为管道直径，v为流速，g为重力加速度，λ为摩阻系数，也称为达西摩阻系数。

罗斯诺-魏谢巴赫公式则可以用来计算管路中流体的水力损失，它的计算公式为：ΔP=ρ(h_f+h_m)其中，ΔP为管路中的总压力损失，ρ为流体密度，h_f为摩阻压力损失，也称为莫阿P（Moody）摩阻，h_m为各种表面或局部的附加压力损失。

除了达西公式和罗斯诺-魏谢巴赫公式，还有一些经验公式和图表可以用来计算管路的压力损失和流量。

这些公式和图表都是根据实验数据和经验总结得出的，可以帮助工程师在实际应用中进行快速计算。

流体力学管路水力的计算一.问题提出为了实现在已知参数（总流量、粘度、管长、管径、粗糙度、总作用水头等）的情况下，能直接算出已知管路系统的基本流动参数（流速、分流量、损失因数、雷诺数、沿裎损失因数等）的目的，为此特别编写了简单管路系统流动参数计算的程序。

该程序能实现串联和并联管路系统流动参数的计算。

需要指明的是，由于本人编程能力有限，且为了能计算书上例题的管路系统，故第二类问题的串联管路系统有且仅有两个串联管子，其余均为三个管子串联或并联。

二.数学模型及算法1.算法首先，将已知参数的实际管路系统抽象简化为理想物理模型，并根据管路系统类型进行分类；然后，对其进行理论分析，计算出流动参数的计算方程；最后，通过编程实现对所求流动参数的计算。

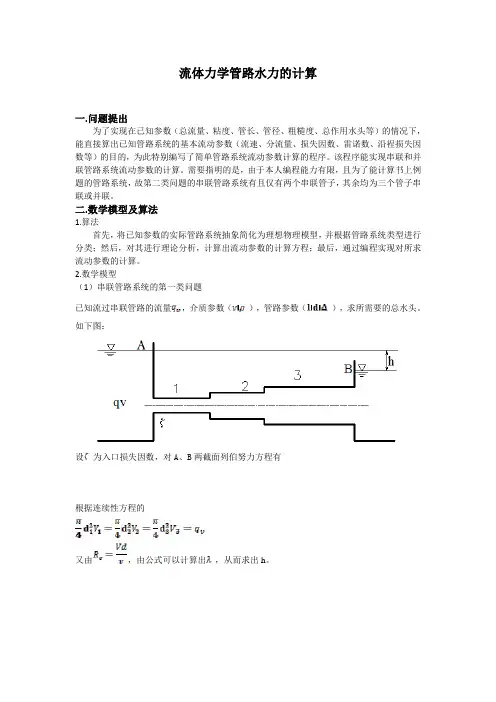
2.数学模型（1）串联管路系统的第一类问题已知流过串联管路的流量，介质参数（），管路参数（），求所需要的总水头。

如下图：设为入口损失因数，对A、B两截面列伯努力方程有根据连续性方程的又由，由公式可以计算出，从而求出h。

（2）串联管路系统的第二类问题已知总水头h，介质参数（），管路参数（），求通过的流量如下图：设为入口损失因数，对A、B两截面列伯努力方程有根据连续性方程的由此可得又，，由公式可以计算出。

将算出的与所取得对比，若二者之差均满足所取得精度，则计算结束，否则令作为新的重新计算为止。

最终可得流量（3）并联管路系统的第一类问题已知两点间的压力降（即能量损失）h，介质参数（），管路参数（），求总流量如下图：先取const，（i=1，2，3，下同）;由达西公式可求得所以由公式可以计算出，将算出的与所取得对比，若二者之差均满足所取得精度，则计算结束，否则令作为新的重新计算为止。

则（4）并联管路系统的第二类问题已知总流量，介质参数（），管路参数（），求各分支管路的流量及能量损失h如下图：根据经验，先取h=const;由此h值根据并联管路第一类问题计算出各分支管路的流量（i=1，2，3，下同）;则蒋总流量按如下分配用计算出的流量，结合公式、，可以计算出，从而求出；若中任两个之差满足给定精度，则h为所求值，否则令h=，从头重新计算，直到满足精度为止。

第5章 孔口管嘴出流与管路水力计算教学提示：孔口出流、管嘴出流是水利工程中常见的流动现象。

例如，大坝的泄水孔、电站引水隧洞的进水口、闸孔出流及某些流量量测设备中的流动均与孔口出流有关。

建筑施工用的水枪及消防水枪等则属于管嘴出流。

教学要求：要求学生了解孔口出流、管嘴出流、管路及管网的基本概念和公式，重点掌握串、并联管路的水力计算。

5.1 孔 口 出 流孔口出流是指流体从容器的孔口中流出。

当孔口内为锐缘尖，或者容器壁的厚度较小而不影响孔口出流，则称这种孔口为薄壁孔口。

本节将讨论常见的薄壁孔口出流。

根据孔口尺寸的大小，将孔口分成小孔口和大孔口。

作用于断面上各点的水头近似相等的孔口称为小孔口。

设作用于断面上的水头为H ，孔口直径为d ，则当H ≥d 时，孔口属于小孔口；当H ＜d 时，孔口属于大孔口。

5.1.1 小孔口出流1. 自由出流流体经孔口流入大气的出流称为自由出流。

薄壁孔口的自由出流如图5.1所示。

孔口出流经过容器壁的锐缘后，变成具有自由面周界的流股。

当孔口内的容器边缘不是锐缘状时，出流状态会与边缘形状有关。

图5.1 薄壁孔口自由出流由于质点惯性的作用，当水流绕过孔口边缘时，流线不能成直角地突然改变方向，只能以圆滑曲线逐渐弯曲，流出孔口后会继续弯曲并向中心收敛，直至离孔口约0.5d 处。

流流体力学·110··110·股在断面C ―C 处的断面面积最小，该断面称为收缩断面。

下面讨论作用水头H 恒定的孔口出流的规律。

探讨图5.1中断面A ―A 与C ―C 之间的流动。

从收缩断面的形心处引基准线0―0，并设断面A ―A 的总水头为g V H H A A 220α+=，断面C ―C 的压强为p C 、平均流速为V C ，两断面之间的能量损失为h w 。

则可写出两断面间的伯努利方程为：w C C C h gV g p H ++=220αρ由于沿程能量损失很小，则可认为两断面间的能量损失g V h h C j w 22ζ==，其中ζ为孔口的局部损失系数。

一、名词解释1.边界层:黏性流体流经固体壁面时，在固体壁面法线方向上存在一速度急剧变化的薄层，称为边界层。

2.管道进口段:边界层相交以前的管段称为管道进口段（或称起始段），其长度以L*表示。

3、粘性底层：紧贴壁面有一因壁面限制而脉动消失的层流薄层，其粘滞力使流速使流速急剧下降，速度梯度较大，这一薄层称为粘性底层。

二、简答题1：何谓普朗特混合长理论？根据这一理论紊流中的切应力应如何计算？答：沿流动方向和垂直于流动方向上的脉动速度都与时均速度的梯度有关。

2：什么是水力光滑管与水力粗糙管？与哪些因素有关？答：当粘性底层厚度大于管壁的粗糙突出部分时，粘性底层完全淹没了管壁的粗糙突出部分。

这时紊流完全感受不到管壁粗糙度的影响，流体好像在完全光滑的管子中流动一样。

这种情况的管内流动称作“水力光滑”，或简称“光滑管”。

当粘性底层厚度小于管壁的粗糙突出部分时，管壁的粗糙突出部分有一部分或大部分暴露在紊流区中，当流体流过突出部分时，将产生漩涡，造成新的能量损失，管壁粗糙度将对紊流产生影响。

这种情况的管内紊流称作“水力粗糙”，或简称“粗糙管”。

对于同样的管子，其流动处于水力光滑或水力粗糙取要看雷诺数的大小。

3、黏性流体总体的伯努利方程及适用条件？ 黏性流体总体的伯努利方程：g g g g v p z v p z a a 222222221111ααρρ++=++适用条件：⑴流动为定常流动；⑵流体为黏性不可压缩的重力流体；⑶列方程的两过流断面必须是缓变流截面，而不必顾及两截面间是否有急变流。

4、黏性流体在管内流动时产生的损失有哪几种？分别怎么计算？ 答：沿程损失是发生在缓变流整个流程中的能量损失，是由流体的粘滞力造成的损失。

单位重力作用下流体的沿程损失可用达西—魏斯巴赫公式计算。

g d l v h f 22λ=。

局部损失发生在流动状态急剧变化的急变流中，单位重力作用下流体流过某个局部件时，产生的能量损失:g v h j 22ζ=。

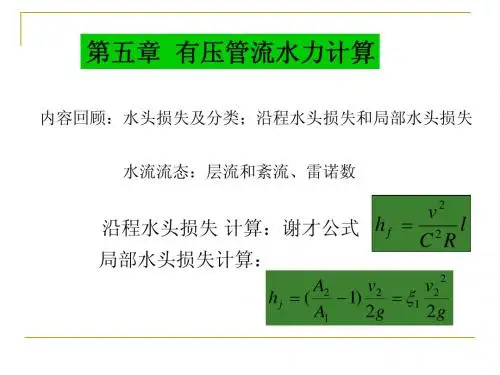
第五章压力管路的水力计算主要内容长管水力计算短管水力计算串并联管路和分支管路孔口和管嘴出流基本概念：1、压力管路：在一定压差下，液流充满全管的流动管路。

（管路中的压强可以大于大气压，也可以小于大气压）注：输送气体的管路都是压力管路。

2、分类：按管路的结构特点，分为简单管路：等径无分支复杂管路：串联、并联、分支按能量比例大小，分为长管：和沿程水头损失相比，流速水头和局部水头损失可以忽略的流动管路。

短管：流速水头和局部水头损失不能忽略的流动管路。

第一节管路的特性曲线一、定义：水头损失与流量的关系曲线称为管路的特性曲线。

二、特性曲线（1）把代入上式得：225222284212Q Q d g L d Q g d L g V d L h w απλπλλ==⎪⎭⎫ ⎝⎛== （2）把上式绘成曲线得图。

第二节 长管的水力计算一、简单长管1、 定义：由许多管径相同的管子组成的长输管路，且沿程损失较大、局部损失较小，计算时可忽略局部损失和流速水头。

2、计算公式：简单长管一般计算涉及公式2211A V A V = （3）fh p z p z +++γγ2211＝ （4）g V D L h f 22λ= （5）说明： 有时为了计算方便，h f 的计算采用如下形式：m m m f d L Q h --=52νβ（6）其中，β、m 值如下因为g V D L h f 22λ= 且所以（7）a. 层流时，Re 64=λ 代入（7）式得：15112415.415.4--==d LQ d L Q h f νν即：β＝ 4.15，m ＝1b. 水力光滑区，25.0Re 3164.0=λ代入（7）式得：25.0525.025.0175.425.075.10246.00246.0--==d LQ d L Q h f νν即：β＝ 0.0246，m ＝1c. 由大庆设计院推得经验公式，在混合区：877.4123.0877.10802.0d LQ Ah f ν=即：β＝ 0.0802A ，m ＝0.123其中，()0627.0lg 127.0,10r A ∆==-εεd. 粗糙区5225220826.082d L Q Q d g L g V d L h f λπλλ===即：β＝ 0.0826λ，m ＝03、简单长管的三类计算问题 （1）第一类：已知：输送流体的性质 μ，γ管道尺寸 d ，L ，Δ 地形 Δz流量 Q ， ， 求：h f ，Δp ，i解：Q →V确定流态 → β， m ，λ → h f → 伯努利方程求Δp（2） 第二类：已知：μ，γ，d ，L ，Δ，Δz ，Δp 求：Q解：Q 未知→流态也未知→ β， m ，λ 无法确定 → 试算法或绘图法A. 试算法a 、先假设一流态，取β， m 值，算出Q ’mm mf f L d h Q pz h --='∆+∆=25βνγb 、Q ’ →→ β’， m ’ ，校核流态如由 Q ’ →Re ’ 和假设一致， Q ’ 即为所求Q c 、如由 Q ’ →定出的流态和假设不一致，重复a 。