数学物理方法 第2章 复变函数的积分
- 格式:ppt
- 大小:767.00 KB
- 文档页数:17







数学物理方法总结第一章 复变函数复数的代数式:z=x+iy复数的三角式和指数式:(cos sin )z ρϕϕ=+和i z e ϕρ=欧拉公式:{1sin ()21cos ()2iz iz iz izz e e iz e e --=-=+柯西-黎曼方程(或称为柯西-黎曼条件):{u u x yv v x y∂∂=∂∂∂∂=-∂∂ (其中f(z)=u+iv)函数f(z)=u+iv 在点0z 及其领域上处处可导,则称f(z)在0z 点解析.在区域B 上每一点都解析,则称f(z)是在区域B 上的解析函数.解析函数的性质:1.若函数f(z)=u+iv 在区域B 上解析,则12(,),(,)u x y C v x y C ==(12,C C 为常数)是B 上的两组正交曲线族.2.若函数在区域B 上解析,则u,v 均为B 上的调和函数,即22220u vx y ∂∂+=∂∂ 例题: 已知某解析函数f(z)的实部22(,)u x y x y =-,求虚部和这个解析函数.解答: 由于22ux∂∂=2;22v y ∂∂=-2;则22220u v x y ∂∂+=∂∂曲线积分法u x ∂∂=2x;u y ∂∂=-2y.根据C-R 条件有:v x∂∂=2y;v y ∂∂=2x.于是 22dv ydx xdy =+;(,0)(,)(0,0)(,0)(,)(,)(,0)(22)(22)(22)22x x y x x y x y x v ydx xdy C ydx xdy ydx xdy Cxdy C xy C=++=++++=+=+⎰⎰⎰⎰凑全微分显式法由上式可知dv=2ydx+2xdy贝易得dv=d(2xy)则显然v=2xy+C不定积分法上面已有—=2y;丝=2xdx dy则第一式对y积分,x视为参数,有v=J2xy+(p(x)=2xy+(p(x)......................dv...上式对x求导有一=2y+^\x),而由C-R条件可知(p\x)=0,dx从而(p(x)=C.故v=2xy+C.f(z)=x2-y2+i(2x y+C)=z2+iC第二章复变函数的积分单连通区域柯西定理如果函数f(z)在闭单连通区域B上解析,则沿B上任意一分段光滑闭合闭合曲线1(也可以是B的边界),有血/⑵也=0.复连通区域柯西定理如果f(z)是闭复连通区域上的单值解析函数,则山任)也+£由/(z)也=0.式中1为区域外边界线,诸l为区域内边界线,积分均沿边界线的正方向进行.即血力>)也=力血/(z)d z.柯西公式f(a)=t^-也""dz2m z-an次求导后的柯西公式f(〃)(z)=£山声舄化2mi中(。


复变函数积分方法总结[键入文档副标题]acer[选取日期]复变函数积分方法总结数学本就灵活多变,各类函数的排列组合会衍生多式多样的函数新形势,同时也具有本来原函数的性质,也会有多类型的可积函数类型,也就会有相应的积分函数求解方法。
就复变函数:z=x+iy i²=-1 ,x,y分别称为z的实部和虚部,记作x=Re(z),y=Im(z)。
arg z=θ₁θ₁称为主值 -π<θ₁≤π,Arg=argz+2kπ。
利用直角坐标和极坐标的关系式x=rcosθ,y=rsinθ,故z= rcosθ+i rsinθ;利用欧拉公式e iθ=cosθ+isinθ。
z=re iθ。
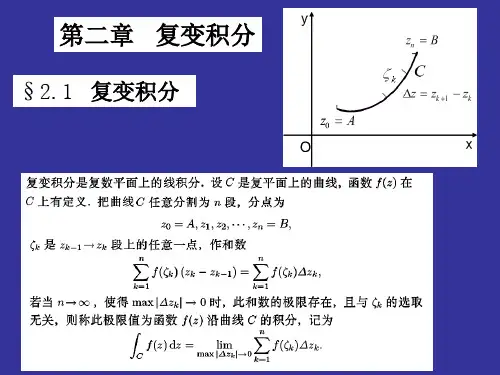
1.定义法求积分:定义:设函数w=f(z)定义在区域D内,C为区域D内起点为A终点为B的一条光滑的有向曲线,把曲线C任意分成n个弧段,设分点为A=z0,z1,…,z k-1,z k,…,z n=B,在每个弧段z k-1 z k(k=1,2…n)上任取一点ξk并作和式S n=ξ(z k-z k-1)=ξ∆z k记∆z k= z k- z k-1,弧段z k-1 z k的长度=,n),当0时,不论对c的分发即ξk的取法如何,S n有唯一的极限,则称该极限值为函数f(z)沿曲线C的积分为:=ξ∆z k设C负方向(即B到A的积分记作).当C为闭曲线时,f(z)的积分记作 (C圆周正方向为逆时针方向)例题:计算积分 ,其中C表示a到b的任一曲线。
(1)解:当C为闭合曲线时,=0.∵f(z)=1 S n=ξ(z k-z k-1)=b-a∴ =b-a,即 =b-a.(2)当C为闭曲线时,=0. f(z)=2z;沿C连续,则积分存在,设ξk=z k-1,则∑1= ( )(z k-z k-1)有可设ξk=z k,则∑2= ( )(z k-z k-1)因为S n的极限存在,且应与∑1及∑2极限相等。
所以S n= (∑1+∑2)==b2-a2∴=b2-a21.2 定义衍生1:参数法:f(z)=u(x,y)+iv(x,y), z=x+iy带入得:= - vdy + i + udy再设z(t)=x(t)+iy(t) (≤t≤)=参数方程书写:z=z0+(z1-z0)t(0≤t≤1);z=z0+re iθ,(0≤θ≤2π)例题1:积分路线是原点到3+i的直线段解:参数方程 z=(3+i)t=′=(3+i)3=6+i例题2:沿曲线y=x2计算( )解:参数方程或z=t+it2 (0≤t≤1)=( )=(1+i) + 2i]=-+i1.3定义衍生2 重要积分结果:z=z0+ re iθ,(0≤θ≤2π)由参数法可得:dθ=dθ=( )=例题1:例题2:解: =0 解 =2πi2.柯西积分定理法:2.1 柯西-古萨特定理:若f(z)dz在单连通区域B内解析,则对B内的任意一条封闭曲线有:=02.2定理2:当f为单连通B内的解析函数是积分与路线无关,仅由积分路线的起点z0与终点z1来确定。