重叠面积及动点问题

(1）求∠OＡB得度数,并求当点Ａ′在线段AB上时,S关于t得函数关系式;
(２)当纸片重叠部分得图形就就是四边形时,求t得取值范围;
（3)Ｓ存在最大值吗?若存在,求出这个最大值,并求此时ｔ得值;若不存在,请说明理由。
解:(1）∵A,B两点得坐标分别就就是Ａ(１0，０）与Ｂ(8，),
∴,
∴
当点A´在线段AB上时,∵,ＴＡ＝TＡ´,
(4)在(３)得条件下，抛物线与正方形一起平移，同时停止,求抛物线上两点间得抛物线弧所扫过得面积、
（14分)(1）；…………………………………………………2分
(2)设抛物线为,抛物线过,
解得…………………………………………………２分
∴、……………………………………………………………１分
（３)①当点A运动到点Ｆ时,
例1: 在梯形ABCD中,AＤ∥ＢC，AB=AＤ＝ＤC=２cm,BＣ=4ｃm,在等腰△PQR中,∠QPR=1２0°,底边QR＝６cm,点B、Ｃ、Q、Ｒ在同一直线l上,且C、Q两点重合,如果等腰△ＰQR以1cm/秒得速度沿直线l箭头所示方向匀速运动，t秒时梯形AＢCＤ与等腰△PQR重合部分得面积记为S平方厘米
∴S=(CE+ＯF)·EＦ
=(t－4+ｔ)×(8－t)
=－+4t－８ﻩﻩﻩﻩ………………9分
②当０<ｔ≤4时,S=，t=4时,S最大=2
当4<ｔ＜8时,S=-+４ｔ-8＝－(t－)+
ｔ＝时,S最大=
∵>2，∴当t=时,S最大＝ﻩ………………１２分
例４: 已知直角梯形纸片OABＣ在平面直角坐标系中得位置如图所示，四个顶点得坐标分别为Ｏ(0，0），A(10,0),B(8,),C(0,),点T在线段OA上(不与线段端点重合）,将纸片折叠，使点A落在射线AB上(记为点A′),折痕经过点Ｔ,折痕ＴＰ与射线AB交于点P,设点T得横坐标为ｔ,折叠后纸片重叠部分(图中得阴影部分）得面积为S;

与重叠部分面积有关的动点问题作业设计
资源镇初中侯仲球
1、如图，抛物线y =a (x -h )2+k 经过点A （0，1），且顶点坐标为B （1，2），它的对称轴与x 轴交于点C .
（1）求此抛物线的解析式.
（2）在第一象限内的抛物线上求点P ，使得⊿ACP 是以AC
为底的等腰三角形，请求出此时点P 的坐标.
（3）上述点是否是第一象限内此抛物线上与AC 距离最远的点，若是，请说明理由；若不是，请求出第一象限内此
抛物线上与AC 距离最远的点的坐标.
2、已知二次函数y=ax 2+bx+c （a ≠0）的图象经过点（1，0），（5，0），（3，﹣4）．
（1）求该二次函数的解析式；
（2）当y ＞﹣3，写出x 的取值范围；
（3）A 、B 为直线y=﹣2x ﹣6上两动点，且距离为2，点C 为二次函数图象上的动点，当点C 运动到何处时△ABC 的面积最小？求出此时点
C 的坐标及△ABC 面积的最小值．
3.如图，过A （8，0）、B （0
，x y 3=交于点C ．平行于y 轴的
直线l 从原点O 出发，以每秒1个单位长度的速度沿x 轴向右平移，到C 点时停止；l 分别交线段BC 、OC 于点D 、E ，以DE 为边向左侧作等边△DEF ，设△DEF 与△BCO 重叠部分的面积为S （平方单位），直线l 的运动时间为t （秒）．
（1）直接写出C 点坐标和t 的取值范围；
（2）求S 与t 的函数关系式；
（3）设直线l 与x 轴交于点P ，是否存在这样的点P ，使得以P 、O 、F 为顶点的三角形
为等腰三角形，若存在，请直接写出点P 的坐标；若不存在，请说明理由．
备用图1。

重叠法的经典例题一、例题在一个长方形中，长为8厘米，宽为6厘米，有两个半径为1厘米的圆重叠放在长方形内（圆与长方形的边相切），求阴影部分（两个圆重叠部分以外的区域）的面积。

二、题目解析1. 首先计算长方形的面积- 根据长方形面积公式S = a× b（其中a为长，b为宽），已知长方形长a = 8厘米，宽b = 6厘米，所以长方形面积S_长方形=8×6 = 48平方厘米。

2. 然后计算两个圆的面积- 根据圆的面积公式S=π r^2（其中r为半径），已知圆半径r = 1厘米，一个圆的面积S_圆=π×1^2=π平方厘米。

- 那么两个圆的面积S_两个圆=2π平方厘米，取π = 3.14，则S_两个圆=2×3.14 = 6.28平方厘米。

3. 接着计算两个圆重叠部分的面积- 两个半径为1厘米的圆重叠部分是一个类似橄榄形的图形。

我们可以先算出两个扇形（圆心角为90^∘，因为圆与长方形边相切）的面积之和，再减去中间正方形的面积。

- 一个扇形的面积是圆面积的(1)/(4)，所以一个扇形面积S_扇形=(1)/(4)×π×1^2=(π)/(4)平方厘米。

- 两个扇形面积S_两个扇形=(π)/(2)平方厘米，取π = 3.14，则S_两个扇形=1.57平方厘米。

- 中间正方形的面积S_正方形=1×1 = 1平方厘米。

- 所以两圆重叠部分面积S_重叠=1.57 - 1=0.57平方厘米。

4. 最后计算阴影部分面积- 阴影部分面积S_阴影=S_长方形-S_两个圆+S_重叠- 把S_长方形=48平方厘米，S_两个圆=6.28平方厘米，S_重叠=0.57平方厘米代入可得：- S_阴影=48 - 6.28+0.57 = 42.29平方厘米。

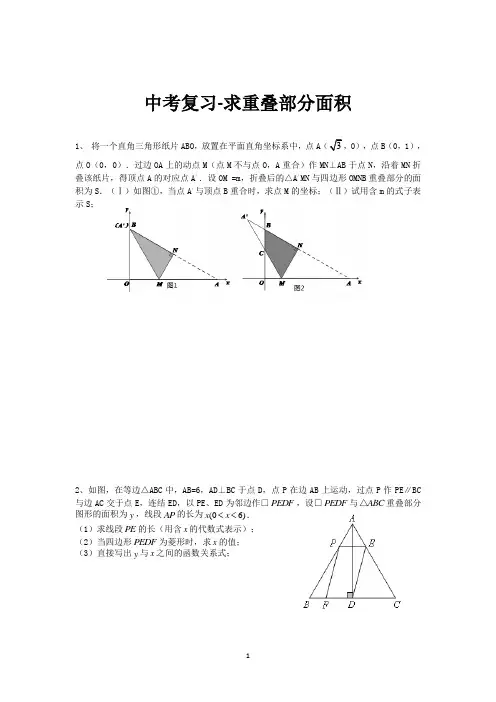
中考复习-求重叠部分面积1、将一个直角三角形纸片ABO，放置在平面直角坐标系中，点A30），点B（0，1），点O（0，0）．过边OA上的动点M（点M不与点O，A重合）作MN⊥AB于点N，沿着MN折叠该纸片，得顶点A的对应点A′．设OM =m，折叠后的△A′MN与四边形OMNB重叠部分的面积为S．（Ⅰ）如图①，当点A′与顶点B重合时，求点M的坐标；（Ⅱ）试用含m的式子表示S；2、如图，在等边△ABC中，AB=6，AD⊥BC于点D，点P在边AB上运动，过点P作PE∥BC△重叠部分与边AC交于点E，连结ED，以PE、ED为邻边作□PEDF，设□PEDF与ABC图形的面积为y，线段AP的长为(06)<<．x x（1）求线段PE的长（用含x的代数式表示）；（2）当四边形PEDF为菱形时，求x的值；（3）直接写出y与x之间的函数关系式；3、如图（1），在矩形ABCD中，AB=6，3，点O是AB的中点，点P在AB的延长线上，且BP=3．一动点E从O点出发，以每秒1个单位长度的速度沿OA匀速运动，到达A点后，立即以原速度沿AO返回；另一动点F从P点出发，以每秒1个单位长度的速度沿射线PA匀速运动，点E、F同时出发，当两点相遇时停止运动，在点E、F的运动过程中，如图（2）以EF为边作等边△EFG，使△EFG和矩形ABCD在射线PA的同侧．设运动的时间为t 秒（t＞0）．（1）如图（3），当等边△EFG的边FG恰好经过点C时，求运动时间t的值；（2）如图（4），当等边△EFG的顶点G恰好落在CD边上时，求运动时间t的值；（3）在整个运动过程中，设等边△EFG和矩形ABCD重叠部分的面积为S，请求出S与t之间的函数关系式，并写出相应的自变量的取值范围．4．如图1，在□ABCD中，AH⊥DC，垂足为H，AB=4，AD=7，AH=．现有两个动点E，F同时从点A出发，分别以每秒1个单位长度、每秒3个单位长度的速度沿射线AC方向匀速运动，在点E，F的运动过程中，以EF为边作等边△EFG，使△EFG与△ABC在射线AC的同侧，点G在射线AB上，当点E运动到点C时，E，F两点同时停止运动，设运动时间为t 秒．（1）试求出当点G与点B重合时t的值；（2）在整个运动过程中，设等边△EFG与△ABC重叠部分的面积为S，请求出S与t之间的函数表达式，并写出相应的自变量t的取值范围；（四边形解答4）5．如图，在矩形ABCD中，AB=3cm，BC=4cm，点O是对角线AC的中点，连结BO．动点P，Q 从点B同时出发，点P沿B→C→B以2cm/s的速度运动到终点B．点Q沿B→A以1cm/s的速度运动到终点A．以BP、BQ为边作矩形BPMQ（点M不与点A重合）．设矩形BPMQ与△OBC 重叠部分图形的面积为y（cm2），点P的运动时间为x（s）．（1）当点M在AC上时，求x的值；（2）直接写出点O在矩形BPMQ内部时x的取值范围；（3）当矩形BPMQ与△OBC重叠部分的图形是四边形时，求y与x之间的函数关系式．（4）直接写出直线AM将矩形ABCD的面积分成1：3的两部分时x的值．（四边形解答5）6、如图，在矩形ABCD中，AB＝8，BC＝6，点O为对角线BD的中点，点P从点A出发，沿折线AD－DO以每秒1个单位长度的速度向终点O运动，当点P与点A不重合时，过点P作PQ⊥AB于点Q，以PQ为边向右作正方形PQMN，设正方形PQMN与△ABD重叠部分图形的面积为S（平方单位），点P运动的时间为t（秒）．（1）求点N落在BD上时t的值；（2）直接写出点O在正方形PQMN内部时t的取值范围；（3）当点P在折线AD－DO上运动时，①求S与t之间的函数关系式；②直接写出DN平分△BCD面积时t的值．（四边形解答5）7、如图1，矩形ABCD中，AB=2，BC=6，点P、Q分别是线段AD和线段BC上的动点，满足∠PQB=60°．（1）填空：①∠ACB= 度；②PQ= ．（2）设线段BC的中点为N，PQ与线段AC相交于点M，若△CMN为直角三角形，请直接写出满足条件的AP的长度．（3）设AP=x，△PBQ与△ABC的重叠部分的面积为S，试求S与x的函数关系式和自变量x 的取值范围．8、已知，在矩形ABCD中，E为BC边上一点，AE⊥DE，AB=12，BE=16，F为线段BE上一点，EF=7，连接AF．如图①，现有一张硬质纸片△GMN，∠NGM=90°，NG=6，MG=8，斜边MN与边BC在同一直线上，点N与点E重合，点G在线段DE上．如图②，△GMN从图①的位置出发，以每秒1个单位的速度沿EB向点B匀速移动，同时，点P从A点出发，以每秒1个单位的速度沿AD向点D匀速移动，点Q为直线GN与线段AE的交点，连接PQ．当点N到达终点B时，△GMN和点P同时停止运动．设运动时间为t秒，解答下列问题：（1）在整个运动过程中，当点G在线段AE上时，求t的值．（2）在整个运动过程中，是否存在点P，使△APQ是等腰三角形．若存在，求出t的值；若不存在，说明理由．（3）在整个运动过程中，设△GMN与△AEF重叠部分的面积为S，请直接写出S与t之间的函数关系式以及自变量t的取值范围．（四边形解答5）。

BCPQ的面积最小？并求出最小值及此时PQ的长．
P
A O
x
Q
B
a
15
a
16
3、分类的原则：分类不重不漏；
4、分类的步骤：①确定讨论的对象及其范 围；②确定分类讨论的分类标准；③按所分类 别进行讨论； ④归纳小结、综合得出结论。
a
12
例、如图，正方形ABCD与正方形OEFG的边长均
为4cm，且点O是正方形ABCD的中心，当正方形
OEFG绕点O旋转时，
两个正方形的重叠部
A
D
改为“边长AD=6cm、CD=4cm的矩形ABCD，AA1=x
cm”，则它们的重叠部分的面积y=
cm 2 .
a
2
例2、如图，Rt⊿ABC的边BC与正方形的边CD都在直
线 上l，且AB=BC=CD=10cm.现将Rt⊿ABC以 1cm/s的速度沿直线 l向右移动，直到AB与DE重合.
设x秒时，三角形与正方形重叠部分面积为y cm 2. （1）请你指出重叠部分图形的形状；
分的面积是否相等？ 若相等，并求出重叠
O
Q
N
部分的面积；若不相 等，请说明理由.
B MP E
CG
A
D
O
B
C
特殊
F
一般
a
13
例、如图，在锐角△ABC中，BC=9，AH⊥BC于点H
，且AH=6，点D为AB边上的任意一点，过点D作
DE∥BC，交AC于点E.设△ADE的高AF为x(0<x<6),以
DE为折线将△ADE翻折，所得的△A′DE与梯形DBCE
运动中重叠部分的面积问题
a
1
例1、如图，将边长为3cm的正方形ABCD沿其对

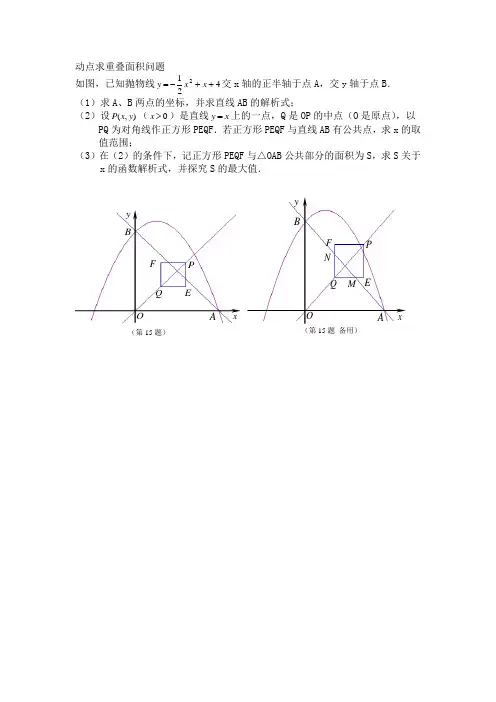
动点求重叠面积问题如图，已知抛物线4212++-=x x y 交x 轴的正半轴于点A ，交y 轴于点B ． （1）求A 、B 两点的坐标，并求直线AB 的解析式；（2）设),(y x P （0>x ）是直线x y =上的一点，Q 是OP 的中点（O 是原点），以PQ 为对角线作正方形PEQF ．若正方形PEQF 与直线AB 有公共点，求x 的取值范围；（3）在（2）的条件下，记正方形PEQF 与△OAB 公共部分的面积为S ，求S 关于x 的函数解析式，并探究S 的最大值．OABP EQFxy （第15题）OABxy（第15题 备用）PEQF M N解：（1）令0=y ，得04212=++-x x ，即0822=--x x ，解得21-=x ，42=x ，所以)0,4(A ．令0=x ，得4=y ，所以)4,0(B ．设AB 为b kx y +=，则⎩⎨⎧==+404b b k ，解得⎩⎨⎧=-=41b k ，所以直线AB 的解析式为4+-=x y ．（2）当点),(x x P 在直线AB 上时，4+-=x x ，解得2=x ，当点)2,2(x x Q 在直线AB 上时，422+-=xx ，解得4=x 所以，若正方形PEQF 与直线AB 有公共点，则42≤≤x ．（3）当点)2,(xx E 在直线AB 上时，（此时点F 也在直线AB 上）42+-=x x ，解得38=x ． ①当382<≤x 时，直线AB 分别与PE 、PF 有交点，设交点分别为C 、D ，此时，42)4(-=+--=x x x PC ，又PC PD =，所以22)2(221-==∆x PC S PCD ，从而，22)2(241--=x x S 88472-+-=x x78)716(472+--=x ．因为387162<≤，所以当716=x 时，78max =S ．②当438≤≤x 时，直线AB 分别与QE 、QF 有交点，设交点分别为M 、N ，此时，42)42(+-=-+-=x xx QN ，又QN QM =，所以22)4(2121-==∆x QN S QMN ，即2)4(21-=x S ．其中当38=x 时，98max =S ．综合①②得，当716=x 时，78max =S ．2、(2014浙江杭州)菱形A B C D的对角线A C，B D相交于点O，，B D＝4，动点P在线段B D上从点B向点D运动，P F⊥A B于点P F，四边形P F B G关于B D对称．四边形Q E D H与四边形P F B G关于A C对称，设菱形A BC D被这两个四边形盖住部分的面积为S1，未盖住部分的面积为S2，B P＝x．(1)用含x代数式分别表示S1，S2；(2)若S1＝S2，求x．解：（1）①当点P在BO上时，如图1所示．∵四边形ABCD是菱形，AC=4，BD=4，∴AC⊥BD，BO=BD=2，AO=AC=2，且S菱形ABCD=BD•AC=8．∴tan∠ABO==．∴∠ABO=60°．在Rt△BFP中，∵∠BFP=90°，∠FBP=60°，BP=x，∴sin∠FBP===sin60°=．∴FP=x．∴BF=．∵四边形PFBG关于BD对称，四边形QEDH与四边形PEBG关于AC对称，∴S△BFP=S△BGP=S△DEQ=S△DHQ．∴S1=4S△BFP=4××x•=．∴S2=8﹣．②当点P在OD上时，如图2所示．∵AB=4，BF=，∴AF=AB﹣BF=4﹣．在Rt△AFM中，∵∠AFM=90°，∠FAM=30°，AF=4﹣．∴tan∠FAM==tan30°=．∴FM=（4﹣）．∴S△AFM=AF•FM=（4﹣）•（4﹣）=（4﹣）2．∵四边形PFBG关于BD对称，四边形QEDH与四边形PEBG关于AC对称，∴S△AFM=S△AEM=S△CHN=S△CGN．∴S2=4S△AFM=4×（4﹣）2=（x﹣8）2．∴S1=8﹣S2=8﹣（x﹣8）2．综上所述：当点P在BO上时，S1=，S2=8﹣；当点P在OD上时，S1=8﹣（x﹣8）2，S2=（x﹣8）2．（2）①当点P在BO上时，0＜x≤2．∵S1=S2，S1+S2=8，∴S1=4．∴S1==4．解得：x1=2，x2=﹣2．∵2＞2，﹣2＜0，∴当点P在BO上时，S1=S2的情况不存在．②当点P在OD上时，2＜x≤4．∵S1=S2，S1+S2=8，∴S2=4．∴S2=（x﹣8）2=4．解得：x1=8+2，x2=8﹣2．∵8+2＞4，2＜8﹣2＜4，∴x=8﹣2．综上所述：若S1=S2，则x的值为8﹣2．3、如图，在Rt△ABC中，∠ACB=90°，AC=8cm，BC=4cm．D、E分别为边AB、BC的中点，连接DE．点P从点A出发，沿折线AD﹣DE﹣EB运动，到点B停止．点P在线段AD上以cm/s 的速度运动，在折线DE﹣EB上以1cm/s的速度运动．当点P与点A不重合时，过点P作PQ⊥AC于点Q，以PQ 为边作正方形PQMN，使点M在线段AQ上．设点P的运动时间为t（s）．（1）当点P在线段DE上运动时，线段DP的长为cm（用含t的代数式表示）．（2）当点N落在AB边上时，求t的值．（3）当正方形PQMN与△ABC重叠部分图形为五边形时，设五边形的面积为S （cm2），求S与t的函数关系式．（4）连接CD，当点N与点D重合时，有一点H从点M出发，在线段MN上以2.5cm/s的速度沿M﹣N﹣M连续做往返运动，直至点P与点E重合时，点H 停止往返运动；当点P在线段EB上运动时，点H始终在线段MN的中点处，直接写出在点P的整个运动过程中，点H落在线段CD上时t的取值范围．答案解：（1）t-2）∵在Rt△ABC中，AC=8cm，BC=4cm，∴AB=√（AC^2+BC^2)=√8^2+4^2=4√5，D为AB中点，∴AD=2√5，∴点P在AD段的运动时间为2√5/√5=2s．当点P在线段DE上运动时，DP段的运动时间为（t-2）s，∵DE段运动速度为1cm/s，∴DP=（t-2）cm．（2）当点N落在AB边上时，有两种情况，一是点N与点D重合时，此时DP=2=EC，即t-2=2，∴t=4，二是点P在线段EB上运动时，点N也能落在AB上，此时△BPN相似于△BCA AC=8cm，∵DE=1/2AC AC=8∴点P在DE段的运动时间为4s，∴PE=t-6，∴PB=BE-PE=8-t，PC=PE+CE=t-4．∵PN∥AC，∴PN：PB=AC：BC=2，∴PN=2PB=16-2t∴即，解得，∴当点N落在AB边上时，t=4或；（3）当正方形PQMN与△ABC重叠部分图形为五边形时，有两种情况，如下图所示：当2<t<4时，正方形PQMN与△ABC重叠分为五边形S=正方形面积-△NDF此时当时，正方形PQMN与△ABC重叠部分为五边形此时综上；（4）当或t=5或时，点D落在线段CD的中点。

（2）操作与求解： ）操作与求解： 正方形ODEF平行移动过程中，通过操作、观察，试 平行移动过程中， ①正方形 平行移动过程中 通过操作、观察， 判断S(S＞ 的变化情况是 判断 ＞0)的变化情况是 C ； A．逐渐增大 B．逐渐减少 ． ． C．先增大后减少 ． E D．先减少后增大 ． y A 4 B F 2 3 6 O 8 C x
D 3 A 6
C
3 3t
B 3t （M） ） 9 E
3 (1)0 < t ≤ 时 ， 3
F
D 3 A 6
C
3t − 3
9 E
B 3t （M） ）
3 3 3 (2) < t ≤ 2 ， S = 9t − 时 3 2
F
D 3 A 6
3C (3t − 6) −
B （M） ）
(3)求 PQR 梯 ABCD重 部 的 ∆ 与 形 叠 分 积 x 函 关 面 S与 的 数 系
A P
M D
O
Q R
B
C
N
A P O Q R PR:3,4,4.5,5
M D
14 20 PQ:4, , 3 3
N C 14 20 0~ 3 ~ 4 ~ 4.5~ ~ 5 ~ ~ 3 3 B
A P O Q R
M D
x
1 O Q R 2x B E xFC N 2 14 20 0~ 3 ~ 4 ~ 4.5~ ~ 5 ~ ~ 3 3 14 ， (4)4.5 < x ≤ 时 2 3 S = −8x + 72x −166
A P O Q R B E
M D
x
FC N 14 20 0~ 3 ~ 4 ~ 4.5~ ~ 5 ~ ~ 3 3 14 (5) < x ≤ 5 ， 时 13 2 400 3 S = − x + 60x − 2 3

与重叠部分面积有关的动点问题
如图，在Rt△ABC中，∠ACB=90°，AC=6cm，BC=8cm．点D、E、F分别 是边AB、BC、AC的中点，连接DE、DF，动点P，Q分别从点A、B同时出发， 运动速度均为1cm/s，点P沿A F D的方向运动到点D停止；点Q沿BC的方向 运动，当点P停止运动时，点Q也停止运动．在运动过程中，过点Q作BC的垂线 交AB于点M，以点P，M，Q为顶点作平行四边形PMQN．设平行四边形边形 2 PMQN与矩形FDEC重叠部分的面积为y（ cm ）（这里规定线段是面积为0有 几何图形），点P运动的时间为x（s） （1）当点P运动到点F时，CQ= cm； （2）在点P从点F运动到点D的过程中，某一时刻，点P落在MQ上，求此时BQ 的长度； （3）当点P在线段FD上运动时，求y与x之间的函数关系式．
二、由点的移动求重叠部分的面积
解题关键是要明确： 1、运动路线； 2、运动速度； 3、运动时间； 4、运动拐点（重叠部分的图形 发生变化的点位）
相等关系：路程=速度×时间 线段的长：用含字母的代数式表示线段的长
题例、如图，在Rt△ABC中，∠ACB=90°，AC=6cm， BC=8cm．点D、E、F分别是边AB、BC、AC的中点，连接DE、 DF，动点P，Q分别从点A、B同时出发，运动速度均为1cm/s，点 P沿A F D的方向运动到点D停止；点Q沿BC的方向运动，当点 P停止运动时，点Q也停止运动．在运动过程中，过点Q作BC的垂 线交AB于点M，以点P，M，Q为顶点作平行四边形PMQN．设平 行四边形边形PMQN与矩形FDEC重叠部分的面积为y（ cm2 ）（这 里规定线段是面积为0有几何图形），点P运动的时间为x（s） （3）当点P在线段FD上运动时，求y与x之间的函数关系式．

仰望天空，脚踏实地。
例2. 如图梯形ABCD 中，
AB//DC.绿色三角形的 面积是14平方厘米，红
看图：
色部分的面积是29.5平
方厘米。问：黄色三角
形的面积是多少平方厘
米？
答：黄色三角形的面 积是15.5平方厘米。
答：涂红色两块图形的面积大。
例3.右图所示为一个长方 形. AE:ED=9:5,
BF:FC=7:4. 问：涂红色的两块图形 的面积与涂蓝色的两块 图形的面积相比较，哪 个大? 请说明理由.
美丽花瓣中的数学问题
例4. 右图是一个对称的 图形（由分别与一个大 圆相切的四个共点的小 的等圆组成），问黑色 部分面积大还是阴影部 分面积大？
答：一样大。
理由：因为是对称图形，四个小圆半径相等， 且恰好是大圆半径的一半。这样，每个小圆 面积等于大圆面积的1/4，四个小圆面积之和 正好等于大圆面积。
答： △PAF与△PBG 面积之差是 2.16平方厘米
提示: 连接AG.易知正方形ABCD边长为
4厘米. △ADG面积为8平方厘米.
也就是矩形DEGF的面积为16平方厘米.
所以
DE 16 3.2 5
厘米.
可以求得AE=2.4厘米, CG=3厘米.
由重叠原理, 知S① + S③ = S② + S④.
（II）设k个小图形面积 之和为S，将这k个小图 形放入一个面积恰为S 的大图形内（这k个小 图形没有同时3个重叠 的部分），则在面积为 S的大图形内未被盖住 部分面积之和，等于k 个小图形重叠部分的面 积。
（II）的图示
例1. △ABC的面积为1,中线BM, CN 相交于G. 求△BGC的面积.
例15. P是长方形ABCD内一点，三角形 PAB的面积等于5，三角形PBC的面积等 于13.问三角形PBD的面积是多少？

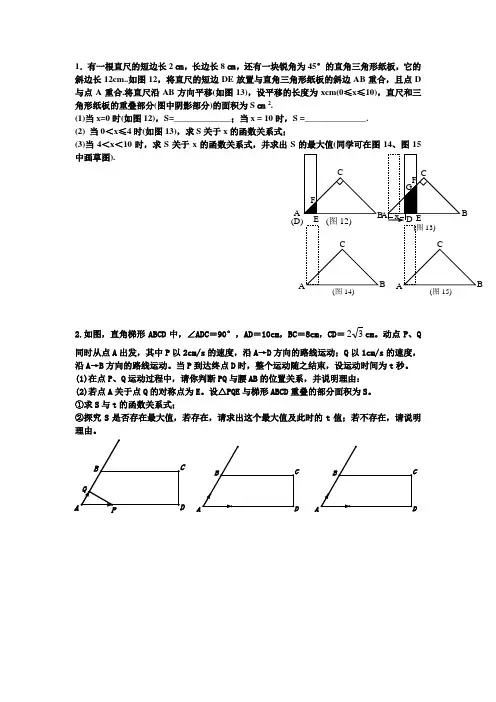
1．有一根直尺的短边长2㎝，长边长8㎝，还有一块锐角为45°的直角三角形纸板，它的斜边长12cm..如图12，将直尺的短边DE 放置与直角三角形纸板的斜边AB 重合，且点D 与点A 重合.将直尺沿AB 方向平移(如图13)，设平移的长度为xcm(0≤x ≤10)，直尺和三角形纸板的重叠部分(图中阴影部分)的面积为S ㎝2.(1)当x=0时(如图12)，S=_____________；当x = 10时，S =______________. (2) 当0＜x ≤4时(如图13)，求S 关于x 的函数关系式；(3)当4＜x ＜10时，求S 关于x 的函数关系式，并求出S 的最大值(同学可在图14、图15中画草图).2.如图，直角梯形ABCD 中，∠ADC ＝90°，AD ＝10cm ，BC ＝8cm ，CD ＝32cm 。

动点P 、Q 同时从点A 出发，其中P 以2cm/s 的速度，沿A →D 方向的路线运动；Q 以1cm/s 的速度，沿A →B 方向的路线运动。

当P 到达终点D 时，整个运动随之结束，设运动时间为t 秒。

(1)在点P 、Q 运动过程中，请你判断PQ 与腰AB 的位置关系，并说明理由： (2)若点A 关于点Q 的对称点为E 。

设△PQE 与梯形ABCD 重叠的部分面积为S 。

①求S 与t 的函数关系式；②探究S 是否存在最大值，若存在，请求出这个最大值及此时的t 值；若不存在，请说明理由。

A (图14)B(图15)A A A3.已知直角梯形纸片OABC 在平面直角坐标系中的位置如图所示，四个顶点的坐标分别为O(0，0)，A(10，0)，B(8，32)，C(0，32)，点T 在线段OA 上(不与线段端点重合)，将纸片折叠，使点A 落在射线AB 上(记为点A ′)，折痕经过点T ，折痕TP 与射线AB 交于点P ，设点T 的横坐标为t ，折叠后重叠部分(图中阴影部分)的面积为S ；（1）求∠OAB 的度数，并求当点A ′在线段AB 上时，S 关于t 的函数关系式； （2）当纸片重叠部分的图形是四边形时，求t 的取值范围；（3）S 存在最大值吗？若存在，求出这个最大值，并求此时t 的值；若不存在，说明理由。

后计算重叠部分的面积． 中所给 图形常常是动静 相映 ，这 里所 降低 了问题 的 难 度 ． 是 教 师 在 讲 解 此题 时 ，应 指 导 学 生 正确 画 题 但
说 的 动 指 的是 基 本 运 动 （ 移 类 、 旋转 类 、翻 折 类 ） 平 ．
出各种情况的 图形 ，以及相邻 情况的分界 图 ，从而使 图象语 言 的展现 能够为文字语 言、符号语 言的流畅表 达提供有 力的帮助 ，
收 稿 日期 ：２ １ － ２ ０ ０ １０ ～ ９
作者简介 ：赵渊 （９ ４ ） １ ７一 ，男，陕西汉 中人 ，中学高级教 师，主要从事数学教育与 中学教 学研 究
图 １
决 定 的 ，即 动 点 Ｐ与 定 点 Ｄ、Ａ 的相 对 位 置 关 系 ，以 及 动 点 Ｑ 、
与 定 点 、 Ｃ的相 对 位 置 关 系． 仅 仅 就 题 论 题 似 乎 有 一 种被 “ 牵着 鼻 子 走 ’ 感 觉 。 思 ，的
，
（） ｔ １ 当 ＝４时 ，求 Ｓ的值 ； （ ）当 ４≤ ｔ １ ，求 ．与 ｔ 间 的 函 数 关 系 式 ，并 求 出 ｓ ２ ≤ ０ ｓ 之
线 ｚ 头 所 示 方 向 匀 速 运 动 ，ｔ 时 梯 形 Ａ Ｃ 与 等 腰 ＡＰ Ｒ重 第 （ ） 题 所 述 ， 可 生 成 图 ２ １ ．继 续 运 动 可 生 成 图 ２ ２ 。接 箭 ｓ ＢＤ Ｑ １小 （） （）
合 部 分 的 面积 记 为 Ｓｃ ２ ｍ ．
Ａ Ｄ Ｐ
着动点 Ｐ到达定点 Ａ恰好是图 ２ １的对称 图形，可生成图 ｚ ３ 。 （） （ ）
接 着生成图 ２４ ．然后 动点 尺到达定点 处 ，接着动点 离开 （）
定 点 ，此 时 两 图 形无 重 叠．综 上 可得 ，分 类 产 生各 种 情 况 的 图 形 ，以 及 相 邻 情 况 的 分 界 图 的 生 成 ，是 由 若 干 点 的 相 对 位 置 所

重叠面积及动点问题1、已知△ABC中，∠B=90°，AB=8cm，BC=6cm，边长为2的正方形EFGH的EF边在直线AB上且点F与点A重合，当正方形EFGH沿AB方向以每秒1cm的速度运动，设运动时间为t秒，正方形EFGH与△ABC重叠面积为S，求S与t的函数关系式，并写出自变量的取值范围。

（F）2、如图，在Rt△ABC中，∠C=90°，AC=8，BC=6，点P在AB上，AP=2，点E、F同时从点P出发，分别沿PA、PB以每秒1个单位长度的速度向点A、B匀速运动，点E到达点A后立刻以原速度沿AB向点B运动，点F运动到点B时停止，点E也随之停止．在点E、F运动过程中，以EF为边作正方形EFGH，使它与△ABC在线段AB的同侧．设E、F运动的时间为t/秒（t＞0），正方形EFGH与△ABC重叠部分面积为S．（1）当时t=1时，正方形EFGH的边长是1．当t=3时，正方形EFGH的边长是4．（2）当0＜t≤2时，求S与t的函数关系式；3、如图，矩形ABCD中，AB=6，BC=2，点O是AB的中点，点P在AB的延长线上，且BP=3．一动点E从O点出发，以每秒1个单位长度的速度沿OA匀速运动，到达A点后，立即以原速度沿AO返回；另一动点F从P点发发，以每秒1个单位长度的速度沿射线PA 匀速运动，点E、F同时出发，当两点相遇时停止运动，在点E、F的运动过程中，以EF 为边作等边△EFG，使△EFG和矩形ABCD在射线PA的同侧．设运动的时间为t秒（t≥0）．（1）当等边△EFG的边FG恰好经过点C时，求运动时间t的值；（2）在整个运动过程中，设等边△EFG和矩形ABCD重叠部分的面积为S，请直接写出S 与t之间的函数关系式和相应的自变量t的取值范围；（3）设EG与矩形ABCD的对角线AC的交点为H，是否存在这样的t，使△AOH是等腰三角形？若存大，求出对应的t的值；若不存在，请说明理由．4、如图，Rt△ABC中，∠C=90°，BC=6，AC=8．点P，Q都是斜边AB上的动点，点P从B 向A运动（不与点B重合），点Q从A向B运动，BP=AQ．点D，E分别是点A，B 以Q，P为对称中心的对称点，HQ⊥AB于Q，交AC于点H．当点E到达顶点A时，P，Q同时停止运动．设BP的长为x，△HDE的面积为y．（1）求证：△DHQ∽△ABC；（2）求y关于x的函数解析式并求y的最大值；（3）当x为何值时，△HDE为等腰三角形？H（第4题）xx 5、如图，在梯形ABCD 中，AD ∥BC ，∠B ＝90°，BC ＝6，AD ＝3，∠DCB ＝30°.点E 、F 同时从B 点出发，沿射线BC 向右匀速移动.已知F 点移动速度是E 点移动速度的2倍，以EF 为一边在CB 的上方作等边△EFG ．设E 点移动距离为x （x ＞0）.⑴△EFG 的边长是____（用含有x 的代数式表示），当x ＝2时，点G 的位置在_______； ⑵若△EFG 与梯形ABCD 重叠部分面积是y ，求 ①当0＜x ≤2时，y 与x 之间的函数关系式； ②当2＜x ≤6时，y 与x 之间的函数关系式；⑶探求⑵中得到的函数y 在x 取含何值时，存在最大值，并求出最大值.6、如图9，在直角坐标系xoy 中，O 是坐标原点，点A 在x 正半轴上，OA=312cm ，点B 在y 轴的正半轴上，OB=12cm ，动点P 从点O 开始沿OA 以32cm/s 的速度向点A 移动，动点Q 从点A 开始沿AB 以4cm/s 的速度向点B 移动，动点R 从点B 开始沿BO 以2cm/s 的速度向点O 移动.如果P 、Q 、R 分别从O 、A、B 同时移动，移动时间为t （0＜t ＜6）s.（1）求∠OAB 的度数.（2）以OB 为直径的⊙O ‘与AB 交于点M ，当t 为何值时，PM 与⊙O ‘相切？ （3）写出△PQR 的面积S 随动点移动时间t 的函数关系式，并求s 的最小值及相应的t 值. （4）是否存在△APQ 为等腰三角形，若存在，求出相应的t 值，若不存在请说明理由.7、如图1，在平面直角坐标系中，已知点(0A ，点B 在x 正半轴上，且30ABO∠．动点P 在线段AB 上从点A 向点Bt 秒．在x 轴上取两点M N ，作等边PMN △． （1）求直线AB 的解析式；（2）求等边PMN △的边长（用t 的代数式表示），并求出当等边PMN △的顶点M 运动到与原点O 重合时t 的值； （3）如果取OB 的中点D ，以OD 为边在Rt AOB △内部作如图2所示的矩形ODCE ，点C 在线段AB 上．设等边PMN △和矩形ODCE 重叠部分的面积为S ，请求出当02t ≤≤秒时S 与t 的函数关系式，并求出S 的最大值．8、（2012重庆）已知：如图，在直角梯形ABCD 中，AD∥BC，∠B=90°，AD=2，BC=6，AB=3．E 为BC 边上一点，以BE 为边作正方形BEFG ，使正方形BEFG 和梯形ABCD 在BC 的同侧． （1）当正方形的顶点F 恰好落在对角线AC 上时，求BE 的长；（2）将（1）问中的正方形BEFG 沿BC 向右平移，记平移中的正方形BEFC 为正方形B′EFG，当点E 与点C 重合时停止平移．设平移的距离为t ，正方形B′EFG 的边EF 与AC 交于点M ，连接B′D，B′M，DM ，是否存在这样的t ，使△B′DM 是直角三角形？若存在，求出t 的值；若不存在，请说明理由；（3）在（2）问的平移过程中，设正方形B′EFG 与△ADC 重叠部分的面积为S ，请直接写出S 与t 之间的函数关系式以及自变量t 的取值范围．重叠面积及动点问题答案（图1） （图2）1、解：解：).108(162)5();8314(4)4();31438(6252783)3();382(233)2();20(83122≤<-=≤<=≤<-+-=≤<-=≤<=t t S t S t t t S t t S t t S ）（2、解：（1）当时t=1时，则PE=1，PF=1， ∴正方形EFGH 的边长是2； 当t=3时，PE=1，PF=3， ∴正方形EFGH 的边长是4； （2）：①当0＜t≤时，S 与t 的函数关系式是y=2t×2t=4t 2； ②当＜t≤时，S 与t 的函数关系式是： y=4t 2﹣[2t ﹣（2﹣t ）]×[2t ﹣（2﹣t ）]，=﹣t 2+11t ﹣3；③当＜t≤2时； S 与t 的函数关系式是：y=（t+2）×（t+2）﹣（2﹣t ）（2﹣t ）， =3t ；3、解：（1）当边FG 恰好经过点C 时，∠CFB=60°，BF=3﹣t ，在Rt △CBF 中，BC=2，tan ∠CFB=，即tan60=，解得BF=2，即3﹣t=2，t=1，∴当边FG 恰好经过点C 时，t=1；（2）当0≤t＜1时，S=2t+4；当1≤t＜3时，S=﹣t2+3t+；当3≤t＜4时，S=﹣4t+20；当4≤t＜6时，S=t2﹣12t+36；（3）存在．理由如下：在Rt△ABC中，tan∠CAB==，∴∠CAB=30°，又∵∠HEO=60°，∴∠HAE=∠AHE=30°，∴AE=HE=3﹣t或t﹣3，1）当AH=AO=3时，（如图②），过点E作EM⊥AH于M，则AM=AH=，在Rt△AME中，cos∠MAE═，即cos30°=，∴AE=，即3﹣t=或t﹣3=，∴t=3﹣或t=3+，2）当HA=HO 时，（如图③）则∠HOA=∠HAO=30°， 又∵∠HEO=60°，∴∠EHO=90°，EO=2HE=2AE ， 又∵AE+EO=3，∴AE+2AE=3，AE=1， 即3﹣t=1或t ﹣3=1，∴t=2或t=4；3）当OH=OA 时，（如图④），则∠OHA=∠OAH=30°， ∴∠HOB=60°=∠HEB ，∴点E 和点O 重合， ∴AE=3，即3﹣t=3或t ﹣3=3，t=6（舍去）或t=0；综上所述，存在5个这样的t 值，使△AOH 是等腰三角形，即t=3﹣或t=3+或t=2或t=2或t=0．4、解：（1）∵A 、D 关于点Q 成中心对称，HQ ⊥AB ，∴C HQD ∠=∠=90°，HD =HA ， ∴A HDQ ∠=∠，…………………………………………………………………………3分∴△DHQ ∽△ABC ． ……………………………………………………………………1分（2）①如图1，当5.20≤<x 时，ED =x 410-，QH =x A AQ 43tan =∠， 此时x x x x y 4152343)410(212+-=⨯-=． …………………………………………3分当45=x 时，最大值3275=y ．②如图2，当55.2≤<x 时，ED =104-x ，QH =x A AQ 43tan =∠， 此时x x x x y 4152343)104(212-=⨯-=． …………………………………………2分当5=x 时，最大值475=y ．∴y 与x 之间的函数解析式为⎪⎩⎪⎨⎧≤<-≤<+-=).55.2(41523),5.20(4152322x x x x x x yy 的最大值是475．……………………………………………………………………1分 （3）①如图1，当5.20≤<x 时，若DE =DH ，∵DH =AH =x A QA 45cos =∠， DE =x 410-，∴x 410-=x 45，2140=x ． 显然ED =EH ，HD =HE 不可能； ……………………………………………………1分②如图2，当55.2≤<x 时， 若DE =DH ，104-x =x 45，1140=x ； …………………………………………1分 若HD =HE ，此时点D ，E 分别与点B ，A 重合，5=x ； ………………………1分若ED =EH ，则△EDH ∽△HDA ，∴AD DH DH ED =，x x x x 24545104=-，103320=x ． ……………………………………1分 ∴当x 的值为103320,5,1140,2140时，△HDE 是等腰三角形. 5、解：⑴ x ，D 点；………………3分⑵ ①当0＜x ≤2时，△EFG 在梯形ABCD 内部，所以y ＝43x 2；………………6分②分两种情况：Ⅰ.当2＜x ＜3时，如图1，点E 、点F 在线段BC 上， △EFG 与梯形ABCD 重叠部分为四边形EFNM ，∵∠FNC ＝∠FCN ＝30°,∴FN ＝FC ＝6－2x.∴GN ＝3x －6. 由于在Rt △NMG 中，∠G ＝60°， 所以，此时 y ＝43x 2－83（3x －6）2＝2392398372-+-x x .………………9分 Ⅱ.当3≤x ≤6时，如图2，点E 在线段BC 上，点F 在射线CH 上， △EFG 与梯形ABCD 重叠部分为△ECP ， ∵EC ＝6－x, ∴y ＝83（6－x ）2＝239233832+-x x .………………11分 ⑶当0＜x ≤2时，∵y ＝43x 2在x ＞0时，y 随x 增大而增大， ∴x ＝2时，y 最大＝3； 当2＜x ＜3时，∵y ＝2392398372-+-x x 在x ＝718时，y 最大＝739； 当3≤x ≤6时，∵y ＝239233832+-x x 在x ＜6时，y 随x 增大而减小， ∴x ＝3时，y 最大＝839.………………12分 综上所述：当x ＝718时，y 最大＝739.6、解：（1）在Rt △AOB 中：tan ∠OAB=3331212==OA OB ∴∠OAB=30°（2）如图10，连接O ‘P ，O ‘M. 当PM 与⊙O ‘相切时，有∠PM O ‘=∠PO O ‘=90°，△PM O ‘≌△PO O ‘B E FC 图1图2xx由（1）知∠OBA=60°∵O ‘M= O ‘B∴△O ‘BM 是等边三角形∴∠B O ‘M=60°可得∠O O ‘P=∠M O ‘P=60°∴OP= O O ‘·tan ∠O O ‘P =6×tan60°=36 又∵OP=32t∴32t=36，t=3即：t=3时，PM 与⊙O ‘相切.（3）如图9，过点Q 作QE ⊥x 于点E ∵∠BAO=30°，AQ=4t ∴QE=21AQ=2t AE=AQ ·cos ∠OAB=4t ×t 3223= ∴OE=OA-AE=312-32t∴Q 点的坐标为（312-32t ，2t ） S △PQR = S △OAB -S △OPR -S △APQ -S △BRQ=)32312(2212)32312(21)212(32213121221t t t t t t -⋅-⋅---⋅⋅-⋅⋅ =372336362+-t t=318)3(362+-t （60＜＜t ） 当t=3时，S △PQR 最小=318 （4）分三种情况：如图11.○1当AP=AQ 1=4t 时， ∵OP+AP=312 ∴32t+4t=312∴t=2336+或化简为t=312-18 ○2当PQ 2=AQ 2=4t 时 过Q 2点作Q 2D ⊥x 轴于点D ， ∴PA=2AD=2A Q 2·cosA=34t 即32t+34t =312 ∴t=2○3当PA=PQ 3时，过点P 作PH ⊥AB 于点H AH=PA ·cos30°=（312-32t ）·23=18-3t AQ 3=2AH=36-6t 得36-6t=4t ， ∴t=3.6综上所述，当t=2，t=3.6，t=312-18时，△APQ 是等腰三角形.7、解：（1）直线AB的解析式为：y x =+ （2）方法一，90AOB ∠=，30ABO ∠=，2AB OA ∴==AP =，BP ∴=，PMN △是等边三角形，90MPB ∴∠= ，tan PM PBM PB ∠=，)83PM t ∴=⨯=-． 方法二，如图1，过P 分别作PQ y ⊥轴于Q ，PS x ⊥轴于S ，可求得122AQ AP ==，2PS QO ==，822PM t ⎛⎫∴=÷=- ⎪ ⎪⎝⎭， （图1）当点M 与点O 重合时，60BAO ∠= ， 2AO AP ∴=．∴=，2t ∴=．（3）①当01t ≤≤时，见图2． 设PN 交EC 于点H ，重叠部分为直角梯形EONG ， 作GH OB ⊥于H ．60GNH ∠=，GH = 2HN ∴=， 8PM t =- ， 162BM t ∴=-， 12OB = ，(8)(16212)4ON t t t ∴=----=+， 422OH ON HN t t EG ∴=-=+-=+=，1(24)2S t t ∴=+++⨯=+S 随t 的增大而增大，∴当1t =时，S =最大②当12t <<时，见图3． 设PM 交EC 于点I ，交EO 于点F ，PN 交EC 于点G ， 重叠部分为五边形OFIGN ．方法一，作GH OB ⊥于H，FO = ，)EF ∴==-，22EI t ∴=-，21(22FEI ONGE S S S t ∴=-=+--=-++△梯形方法二，由题意可得42MO t =-，(42)OF t =-PC =，4PI t =-，再计算21(42)2FMO S t =-△2(8)4PMN S t =-△，2)4PIG S t =-△ （图3）2221(8))(42)442PMN PIG FMO S S S S t t t ∴=--=-----△△△2=-++0-< ，∴当32t =时，S有最大值，2S =最大． ③当2t =时，6MP MN ==，即N 与D 重合，设PM 交EC 于点I ，PD 交EC 于点G ，重叠部 分为等腰梯形IMNG ，见图4．2262S ==综上所述：当01t ≤≤时，S =+；当12t <<时，2S =-++当2t =时，S =2>S ∴的最大值是2．考点：相似三角形的判定与性质；勾股定理；正方形的性质；直角梯形。

初中数学动点难题：数轴上两长方形面积重叠问题（变型题）数轴上的动点问题难不难？难！！“书上有路勤为径，学海无涯苦作舟”，再难的题目都有解题方法。

笔者继续就浙教版七年级数学---数轴上的动点问题变型题进行探究，同样分别用几何图形和代数方法解数轴上的动点问题。

如图，长方形OABC的边OA在数轴上，O为原点，长方形OABC 面积为12. OC边长为3⑴数轴上点A表示的数是----------------------。

⑵将长方形OABC沿OA所在直线水平移动，移动后的长方形记为O'A'B'C'.若移动后的长方形O'A'B'C'与原长方形OABC重叠部分的面积恰好等于原长方形OABC的面积的一半时，则数轴上点A'表示的数是多少？解：⑴.由题意得：A表示的数为：4⑵问移动到A'在数轴上是什么位置的时候，长方形O'A'B'C'与原长方形OABC重叠部分的面积恰好等于原长方形OABC的面积的一半一、利用几何画板来演示，长方形的移动变化（如图重合时的情形）：下面我们来移动长方形，使得重叠部分C'O'AB的面积恰好等于原长方形OABC的面积的一半（如图3）：对比移动前后图，我们发现面积：C'O'AB=1/2OABC 时，OA'由4移动到6的位置，这样我们利用图形就解得A'表示的数为6.二、下面笔者用代数的方法解题：解：设A'表示的数为x,由题意得：∵0A=4，OC=3∴[4-（x-4）]*OC=6解之得：x=6答：略此题用方程代数解题，主要考察学生空间想象能力，第一步：OA'-OA，第二步：OA-(OA'-OA)第三步：【OA-(OA'-OA)】*OC最后：解方程。

探究变型题二（供读者自行解答）：长方形OABC的边OA在数轴上，O为原点，长方形OABC面积为12. OC边长为3。

怎样求重叠部分的面积例1. 如图1，将边长为1的正方形ABCD绕点A按逆时针方向旋转30度，至正方形，求旋转前后两个正方形重叠部分的面积？图1解：由正方形ABCD绕点A按逆时针方向旋转30度，至正方形设，则，根据勾股定理，变题：如图2，将边长为1的正方形ABCD绕点A按逆时针方向旋转60度，至正方形，求旋转前后两个正方形重叠部分的面积？图2分析：将原题中的30°变成60°后，原来的解题方法已经不能再用了，那就要另外想办法了。

仍然要连结AE，，只要求出，问题就解决了。

所以，本题的关键就是求出的长。

解：连结AE，作EF∥AD∵正方形ABCD绕点A按逆时针方向旋转60度，至正方形∵EF∥AD∴∠1＝∠4∴∠1＝∠2∴EF＝AF设，则根据勾股定理，即例2. 如图3，正方形ABCD的面积为S，对角线相交于点O，点O是正方形的一个顶点，如果两个正方形的边长相等，那么正方形绕点O转动时，图3（1）求两个正方形重叠部分的面积。

（2）如果正方形的边长大于正方形ABCD的边长，则重叠部分的面积等于多少？与上述结论是否一致？（3）将正方形改为，只要满足什么条件，重叠部分的面积不变？（4）如果把正方形ABCD改为等边△ABC，O为等边△ABC的中心，以O为顶点的扇形绕点O无论怎样转动，要使它与等边△ABC的重叠部分的面积总保持不变，问扇形应满足什么条件？并且说明你的理由。

（1）解：∵ABCD为正方形∴OA＝OB，AC⊥BD∠1＝∠2＝45°∠3＋∠BOE＝90°∵是正方形∴∠BOE＋∠4＝90°∴∠3＝∠4∴△AOE≌△BOF∴两个正方形重叠部分的面积（2）如果正方形的边长大于正方形ABCD的边长，则重叠部分的面积仍然等于与上述结论一致。

因为求解的过程没有任何改变。

（3）将正方形变为，只要满足，并且与正方形ABCD没有交点，那么求重叠部分的面积的方法与上面的方法一样，所以重叠部分的面积不改变。

初中数学动点难题：数轴上两长方形面积重叠问题再探究数轴上的动点问题难不难？动点变式题确实特别难？对，特别难，难在要求学生具有超丰富的空间想象力和严谨的思维逻辑力，笔者就在数轴上的动点问题探究变式题二（数据有所修改）继续进行分享，还是用几何图形和代数方法来解题。

如图，长方形OABC的边OA在数轴上，O为原点，长方形OABC 的面积为14cm2. OC边长为4cm.将长方形OABC沿OA所在直线水平移动，移动后的长方形记为O'A'B'C'.若D为线段AA' 的中点，点E在线段OO'上，且OE=1/3OO',求当长方形OABC移动的距离为多少时，D、E两点到原点O的距离相等？解：由题意可知：OA=14=3.5cm题目要求：若D为线段AA' 的中点，点E在线段OO'上，且OE=OO',求当长方形OABC移动的距离为多少时，D、E两点到原点O的距离相等？一、首先用几何画板进行图形轨迹分析，解决问题：⑴首先，让长方形OABC向数轴的正方向移动，如图2：∵ 发现越往右移动，始终OD>OE，∴移动长方形OABC向右移动，得不到OD=OE⑵要使D、E两点到原点O的距离相等，我们只有向左移动长方形，得到如下图形：从图表中，我们发现OE=OD时，长方形向左移动3个单位，重叠距离为0.5个单位，相等的距离为2个单位。

∴当长方形OABC移动的距离为3个单位时，D、E两点到原点O 的距离相等。

二、使用完几何画板解题，我们用代数形式验证答案的正确性？解：设移动的距离为x，由题意得x*2/3=3.5-x+x/2化简整理得：7/6*x=3.5解之得：x=3答：略总结：用代数解题，需要使用分类讨论，分析得到只有长方形OABC向数轴左边移动，才能得到我们需要的结果。

三、探究数轴动点问题三(供读者自行解答)：如图，已知数轴上A、B两点所表示的数分别为-2和8．（1）求线段AB的长；（2）若P为射线BA上的一点（点P不与A、B两点重合），M 为PA的中点，N为PB的中点，当点P在射线BA上运动时，线段MN的长度是否发生改变？若不变，请你画出图形，并求出线段MN 的长；若改变，请说明理由．（3）若有理数a、b、c在数轴上的位置如图所示：且d=|a+b|-|-2-b|-|a-2c|-5，试求7（d+2c）2+2（d+2c）-5（d+2c）2-3（d+2c）的值．PS:。

动点重叠面积专题模型1 点移动问题例1．如图1，△ABC中，∠C=90°，线段DE在射线BC上，且DE=AC，线段DE沿射线BC运动，开始时，点D与点B重合，点D到达点C时运动停止，过点D作DF=DB，与射线BA相交于点F，过点E作BC的垂线，与射线BA相交于点G．设BD=x，四边形DEGF与△ABC重叠部分的面积为S，S关于x的函数图象如图2所示（其中0＜x≤1，1＜x≤m，m＜x≤3时，函数的解析式不同）（1）填空：BC的长是_______；（2）求S关于x的函数关系式，并写出x的取值范围．随堂练习练习1.如图1，在四边形ABCD中，∠BAD=∠ABC=90°，点E从点C出发，以每秒1个单位长度的速度沿射线CB运动，在射线CD上取点F，且CF=CE，连接EF，当EF经过点A时，点E停止运动，△CEF与四边形ABCD重叠部分的面积为S，点E的运动时间为t秒，且知当0＜t≤2时，S=34t2，S关于t的函数图象如图2所示，（其中0＜t≤2，2＜t≤m，m＜t≤4时，函数的解析式不同）．（1）∠BAC=________；（2）求m的值；（3）当2＜t≤4时，求S与t之间的函数关系式．练习2.如图，△ABC中，∠C=90°，AC=8cm，BC=6cm，点P、Q同时从点C出发，以1cm/s的速度分别沿CA、CB匀速运动．当点Q到达点B时，点P、Q同时停止运动．过点P作AC的垂线l交AB于点R，连接PQ、RQ，并作△PQR关于直线l对称的图形，得到△PQ′R．设点Q的运动时间为t（s），△PQ′R与△PAR重叠部分的面积为S（cm2）．（1）t为何值时，点Q′恰好落在AB上？（2）求S与t的函数关系式，并写出t的取值范围；（3）S能否为98cm2？若能，求出此时的t值；若不能，说明理由．练习3.如图，一次函数y=﹣43x+4的图象与x轴、y轴分别相交于点A、B．P是射线BO上的一个动点（点P不与点B重合），过点P作PC⊥AB，垂足为C，在射线CA上截取CD=CP，连接PD．设BP=t．（1）t为何值时，点D恰好与点A重合？（2）设△PCD与△AOB重叠部分的面积为S，求S与t的函数关系式，并直接写出t的取值范围．练习4.如图，直线y=34x﹣3与x轴、y轴分别相交于点A、B，P是从点A出发，沿射线AO运动的一点（点P不与点A重合），过点P作PC⊥AB，垂足为C，当点C与点B重合时，点P停止运动，设AP=t．（1）在图中画出△PCA关于直线PC对称的图形△PCD；（2）t为何值时，点D恰好与点B重合？（3）设△PCD与△AOB重叠部分的面积为S，求S与t的函数关系式，并直接写出t的取值范围．练习5.如图，在矩形ABCD中，AB=1，BC=3，点E为BC边上的动点（点E与点B、C不重合），设BE=x．操作：在射线BC上取一点F，使得EF=BE，以点F为直角顶点、EF为边作等腰直角三角形EFG，设△EFG与矩形ABCD重叠部分的面积为S．（1）求S与x的函数关系式，并写出自变量x的取值范围．（2）S是否有最大值？若存在，请直接写出最大值，若不存在，请说明理由．练习6.如图所示，矩形ABCD中，AB=6，AD=3，点O在边DC上，且DO=4，点P，Q同时从点O出发，点P沿OA以1cm/s的速度移动，点Q沿O→C→B→A的路线以2cm/s的速度移动，当点P移动到点A时，点Q也停止移动．（1）求sin∠AOD的值；（2）设点P移动时间为t（s），P，Q两点运动路线与线段PQ围成的图形面积为S．①当t=s时，点Q到达C点．②求S与t的函数关系式．模型图形移动问题例1.如图1，两个全等的△ABC和△DEF中，∠ACB=∠DFE=90°，AB=DE，其中点B和点D重合，点F在BC上，将△DEF沿射线BC平移，设平移的距离为x，平移后的图形与△ABC重合部分的面积为y，y关于x的函数图象如图2所示（其中0≤x≤m，m＜x≤3，3＜x≤4时，函数的解析式不同＝（1）填空：BC的长为；（2）求y关于x的函数关系式，并写出x的取值范围．随堂练习练习1.如图1，在△ABC中．∠C=90°，AC＞BC，正方形CDEF的顶点D在边AC上，点F 在射线CB上设CD=x，正方形CDEF与△ABC重叠部分的面积为S，S关于x的函数图象如图2所示（其中0＜x≤m，m＜x≤2，2＜x≤n时，函数的解析式不同）．（1）填空：m的值为；（2）求S关于x的函数解析式，并写出x的取值范围；（3）S的值能否为132？若能，直接写出此时x的值；若不能，说明理由．练习2.如图，矩形ABCD中，AB=2，BC=23，将矩形沿对角线AC剪开，请解决以下问题：（1）将△ACD绕点C顺时针旋转90°得到△A′CD′，请在备用图中画出旋转后的△A′CD′，连接AA′，并求线段AA′的长度；（2）在（1）的情况下，将△A′CD′沿CB向左平移t（0＜t＜23），设平移后的图形与△ABC重叠部分的面积为S，求S与t的函数关系式，并直接写出t的取值范围．练习3.如图,正方形ABCD中,AB=45，P是BC的中点，DE⊥AP，垂足为点E.(1)求AP的长。