6、因动点问题产生的面积问题
- 格式:doc
- 大小:2.97 MB
- 文档页数:14


中考数学压轴题:由动点引出的几种面积问题动点题是近年来中考的一个热点问题也是难点问题,而因动点产生的面积问题是这类题目考查的重点。
解这类题目要掌握几个基本图形及思路,而后“以静制动”、“转化求解”。
即把动态问题变为静态问题,变为我们所熟知的模型来解。
基本方法:铅锤法!即利用“铅垂高、水平宽”求三角形面积.类型一、一次函数由动点问题引出的面积问题【分析】(1)Rt△AOH中利用勾股定理即可求得菱形的边长;(2)根据(1)即可求得OC的长,则C的坐标即可求得,利用待定系数法即可求得直线AC的解析式;(3)根据S△ABC=S△AMB+SBMC求得M到直线BC的距离为h,然后分成P在AM上和在MC上两种情况讨论,利用三角形的面积公式求解.【点评】本题考查了待定系数法求一次函数的解析式以及菱形的性质,根据三角形的面积关系求得M到直线BC的距离h是关键.类型二、二次函数由动点问题引出的面积问题【分析】(2)过点P作PE∥y轴交x轴于点E,交直线AC于点F,过点C作CQ∥y轴交x轴于点Q,设点P的坐标为(x,﹣x^2﹣2x+3)(﹣2<x<1),则点E的坐标为(x,0),点F的坐标为(x,﹣x+1),进而可得出PF的值,由点C的坐标可得出点Q 的坐标,进而可得出AQ的值,利用三角形的面积公式可得出S△APC=﹣1.5x^2﹣1.5x+3,再利用二次函数的性质,即可解决最值问题;【点评】本题考查了待定系数法求一次函数解析式、待定系数法求二次函数解析式、二次函数图像上点的坐标特征、一次函数图像上点的坐标特征、二次函数的性质、三角形的面积以及周长,解题的关键是:(1)根据点的坐标,利用待定系数法求出抛物线及直线AC的函数关系式;(2)利用三角形的面积公式找出S△APC=﹣1.5x^2﹣1.5x+3;(3)利用二次函数图像的对称性结合两点之间线段最短找出点M的位置.类型三、利用相似三角形求解由动点问题引出的面积问题【分析】(1)利用待定系数法即可;(2)①分别用t表示PE、PQ、EQ,用△PQE∽△QNC表示NC及QN,列出矩形PQNM面积与t的函数关系式问题可解;②由①利用线段中点坐标分别等于两个端点横纵坐标平均分的数量关系,表示点M坐标,分别讨论M、N、Q在抛物线上时的情况,并分别求出t值.【点评】本题是代数几何综合题,考查了二次函数、一次函数、三角形相似和矩形的有关性质,解答时应注意数形结合和分类讨论的数学思想.类型四、利用转化思想解决由动点问题引出的面积问题【分析】(1)根据待定系数法,可得函数解析式,根据自变量与函数值的对应关系,可得答案;(2)根据勾股定理,可得BC的长,根据等角的正切值相等,可得HO的长,根据待定系数法,可得BE的解析式,根据解方程组,可得E点坐标;(3)由题意△PMN是等腰直角三角形,得PM=PN=1,设M(a,a^2+3a﹣4)则N(a+1,a^2+3a+1)或(a+1,a^2+3a﹣5),代入抛物线的解析式即可求解.【点评】本题考查二次函数的有关知识、一次函数、直角三角形等知识,掌握两个函数的交点问题转化为方程组的解的问题是解题的关键,还要记住一个结论斜边为定值时直角边相等时面积最大.。

例21:2011年四川省南充市中考第22题抛物线y=ax2+bx+c与x轴的交点为A(m﹣4,0)和B(m,0),与直线y=﹣x+p相交于点A和点C(2m﹣4,m﹣6).(1)求抛物线的解析式;(2)若点P在抛物线上,且以点P和A,C以及另一点Q为顶点的平行四边形ACQP面积为12,求点P,Q 的坐标;(3)在(2)条件下,若点M是x轴下方抛物线上的动点,当△PQM的面积最大时,请求出△PQM的最大面积及点M的坐标.解答:解:(1)∵点A(m﹣4,0)和C(2m﹣4,m﹣6)在直线y=﹣x+p上∴,解得:,∴A(﹣1,0),B(3,0),C(2,﹣3),设抛物线y=ax2+bx+c=a(x﹣3)(x+1),∵C(2,﹣3),代入得:﹣3=a(2﹣3)(2+1),∴a=1∴抛物线解析式为:y=x2﹣2x﹣3,答:抛物线解析式为y=x2﹣2x﹣3.(2)解:AC=3,AC所在直线的解析式为:y=﹣x﹣1,∠BAC=45°,∵平行四边形ACQP的面积为12,∴平行四边形ACQP中AC边上的高为=2,过点D作DK⊥AC与PQ所在直线相交于点K,DK=2,∴DN=4,∵ACPQ,PQ所在直线在直线ACD的两侧,可能各有一条,∴PQ的解析式或为y=﹣x+3或y=﹣x﹣5,∴,解得:或,,方程无解,即P1(3,0),P2(﹣2,5),∵ACPQ是平行四边形,A(﹣1,0),C(2,﹣3),∴当P(3,0)时,Q(6,﹣3),当P(﹣2,5)时,Q(1,2),∴满足条件的P,Q点是P1(3,0),Q1(6,﹣3)或P2(﹣2,5),Q2(1,2)答:点P,Q的坐标是P1(3,0),Q1(6,﹣3)或P2(﹣2,5),Q2(1,2).(3)解:设M(t,t2﹣2t﹣3),(﹣1<t<3),过点M作y轴的平行线,交PQ所在直线雨点T,则T(t,﹣t+3),MT=(﹣t+3)﹣(t2﹣2t﹣3)=﹣t2+t+6,过点M作MS⊥PQ所在直线于点S,MS=MT=(﹣t2+t+6)=﹣(t﹣)2+,∴当t=时,M(,﹣),△PQM中PQ边上高的最大值为,答:△PQM 的最大面积是,,点M 的坐标是(,﹣).点评:本题主要考查对用待定系数法求二次函数的解析式,二次函数的最值,平行四边形的性质,解二元一次方程组等知识点的理解和掌握,综合运用这些性质进行计算是解此题的关键,此题是一个综合性比较强的题目,有一定的难度.例22:2010年广东省湛江市中考第28题如图,在平面直角坐标系中,点B 的坐标为(-3,-4),线段OB 绕原点逆时针旋转后与x 轴的正半轴重合,点B 的对应点为点A .(1)直接写出点A 的坐标,并求出经过A 、O 、B 三点的抛物线的解析式;(2)在抛物线的对称轴上是否存在点C ,使BC +OC 的值最小?若存在,求出点C 的坐标;若不存在,请说明理由;(3)点P 是抛物线上的一个动点,且在x 轴的上方,当点P 运动到什么位置时,△PAB 的面积最大?求出此时点P 的坐标和△PAB 的最大面积.解:(1)A(5,0) ………1分由抛物线经过点O ,可设抛物线的解析式为bx ax y +=2…2分⎩⎨⎧=-=+4390525b a b a 解得⎪⎪⎩⎪⎪⎨⎧=-=6561b a …………………………4分 ∴抛物线的解析式为x x y 65612+-=…………………………5分 (2)如图,由(1)得抛物线的对称轴是直线25=x ,点O 、A 关于直线25=x 对称,连接AB 交直线25=x 于点C ,则点C 使BC+OC 的值最小………………………6分设直线AB 的解析式为b kx y +=,得⎩⎨⎧-=+-=+4305b k b k ,解得⎪⎪⎩⎪⎪⎨⎧-==2521b k∴直线的解析式为2521-=x y ………………………8分把25=x 代入2521-=x y ,得45-=y ,∴点C 的坐标为)45,25(-………………9分(3)如图,过点P 作y 轴的平行线交AB 于点D ,设点P 的横坐标为x ,得)6561,(2x x x P +-, )2521,(-x x D ………………10分∴PAD PBD PAB S S S ∆∆∆+==)(21B A x x PD -∙=))((21B A D p x x y y --=[])3(5)2521()6561(212--⨯⎥⎦⎤⎢⎣⎡--+-x x x =1034322++-x x =332)1(322+--x ∴当1=x 时,PAB S ∆的最大值为332………………12分 把1=x 代入x x y 65612+-=,得32=y ,∴此时点P 的坐标为)32,1(………………13分例23:2012年广东省广州市中考数学模拟第25题平面直角坐标系中,平行四边形ABOC 如图放置,点A 、C 的坐标分别为(0,3)、(1-,0),将此平行四边形绕点0顺时针旋转90°,得到平行四边形'''A B OC 。
第6讲 因动点产生的面积问题【例1】如图,在直角坐标系中,抛物线c bx x y ++=2经过点上(0,10)和(4,2). (1) 求这条抛物线的解析式。
(2) 如图,在边长一定的矩形ABCD 中,CD =1,点C 在y 轴右侧沿抛物线c bx x y ++=2滑动,在滑动过程中C D ∥x 轴,AB 在CD 的下方。
当点D 在y 轴上时,AB 落在x 轴上。
1) 求边BC 的长;2) 当矩形ABCD 在滑动过程中被x 轴分成两部分的面积比为1:4时,求点C 的坐标。
【例2】如图15,在Rt ABC △中,90C ∠=,50AB =,30AC =,D E F,,分别是AC AB BC ,,的中点.点P 从点D 出发沿折线DE EF FC CD ---以每秒7个单位长的速度匀速运动;点Q 从点B 出发沿BA 方向以每秒4个单位长的速度匀速运动,过点Q 作射线QK AB ⊥,交折线BC CA -于点G .点P Q ,同时出发,当点P 绕行一周回到点D 时停止运动,点Q 也随之停止.设点P Q ,运动的时间是t 秒(0t >).(1)D F ,两点间的距离是 ;(2)射线QK 能否把四边形CDEF 分成面积相等的两部分?若能,求出t 的值.若不能,说明理由;(3)当点P 运动到折线EF FC -上,且点P 又恰好落在射线QK 上时,求t 的值; (4)连结PG ,当PG AB ∥时,请直接..写出t 的值.【例3】如图1,抛物线23y ax ax b =-+经过A (-1,0),C (3,2)两点,与y 轴交于点D ,与x 轴交于另一点B 。
⑴求此抛物线的解析式;⑵若直线1(0)y kx k =-≠将四边形ABCD 面积二等分,求k 的值;⑶如图2,过点E (1,-1)作EF ⊥x 轴于点F ,将△AEF 绕平面内某点旋转180°后得△MNQ (点M ,N ,Q 分别与点A ,E ,F 对应),使点M ,N 在抛物线上,求点M ,N 的坐标.图15【例4】如图,在平面直角坐标系中,矩形ABOC 的边BO 在x 轴正半轴上,边CO在y 轴的正半轴上,且322==OB AB ,,矩形ABOC 绕点O 逆时针旋转后得到矩形EFOD ,且点A 落在y 轴上的E 点,点B 的对应点为点F ,点C 的对应点为点D .(1)求F 、E 、D 三点的坐标;(2)若抛物线c bx ax y ++=2经过点F 、E 、D ,求此抛物线的解析式; (3)在x 轴上方的抛物线上求点Q 的坐标,使得三角形QOB 的面积等于矩形ABOC 的面积?【例5】如图①,正方形 ABCD 中,点A 、B 的坐标分别为(0,10),(8,4), 点C 在第一象限.动点P 在正方形 ABCD 的边上,从点A 出发沿A →B →C →D 匀速运动,同时动点Q 以相同速度在x 轴正半轴上运动,当P 点到达D 点时,两点同时停止运动,设运动的时间为t 秒.(1)当P 点在边AB 上运动时,点Q 的横坐标x (长度单位)关于运动时间t (秒)的函数图象如图②所示,请写出点Q 开始运动时的坐标及点P 运动速度;(2)求正方形边长及顶点C 的坐标;(3)在(1)中当t 为何值时,△OPQ 的面积最大,并求此时P 点的坐标;(4)如果点P 、Q 保持原速度不变,当点P 沿A →B →C →D 匀速运动时,OP 与PQ 能否相等,若能,写出所有符合条件的t 的值;若不能,请说明理由.参考答案【例2】解:(1)25. (2)能.如图5,连结DF ,过点F 作FH AB ⊥于点H , 由四边形CDEF 为矩形,可知QK 过DF 的中点O 时,QK 把矩形CDEF 分为面积相等的两部分(注:可利用全等三角形借助割补法或用中心对称等方法说明), 此时12.5QH OF ==.由20BF =,HBF CBA △∽△,得16HB =.故12.5161748t +==. (3)①当点P 在EF 上6(25)7t ≤≤时,如图6.4QB t =,7DE EP t +=,由PQE BCA △∽△,得7202545030t t--=. 21441t ∴=. ②当点P 在FC 上6(57)7t ≤≤时,如图7. 已知4QB t =,从而5PB t =,由735PF t =-,20BF =,得573520t t =-+.解得172t =. (4)如图8,213t =;如图9,39743t =. (注:判断PG AB ∥可分为以下几种情形:当6027t <≤时,点P 下行,点G 上行,可知其中存在PG AB ∥的时刻,如图8;此后,点G 继续上行到点F 时,4t =,而点P 却在下行到点E 再沿EF 上行,发现点P 在EF 上运动时不存在PG AB ∥;当6577t ≤≤时,点P G ,均在FC 上,也不存在PG AB ∥;由于点P 比点G 先到达点C 并继续CD 下行,所以在6787t <<中存在PG AB ∥的时刻,如图9;当810t ≤≤时,P G ,均在CD 上,不存在PG AB ∥)【例3】(1)如图1, ∵抛物线.⎩⎨⎧+-=++=.992,30b a a b a a 解得,.221⎪⎩⎪⎨⎧=-=b a∴抛物线的解析式y=-223212++x x . (2)方法1:如图1,由y=-223212++x x 得B (B图6 B 图7B图9(0,2).∴CD ∥AB ∴S ABCD 梯形=21(5+3)×2=8 设直线y=kx-1分别交AB 、CD 于点H 、T ,则H (k 1,0)、T (k 3,2). ∵直线y=kx-1平分四边形ABCD 面积, ∴S AHTD 梯形=21S ABCD 梯形=4.∴21(k 1+1+k 3)×2=4 ∴k=34,∴k=34时,直线y=34x-1将四边形ABCD 面积二等分.方法2:过点C 作CG ⊥AB 与点G . 由y=-223212++x x 得B (4,0)、D (0,2). ∴CD ∥AB 由抛物线的对称性得四边形ABCD 是等腰梯形, ∴BCG AOD S S ∆∆= 设矩形ODCH 的对称中心为R ,则R (23,1).由矩形的中心对称性知:过R 点任一直线将它的面积平分,∴过R 点且与CD 相交的任一直线将梯形ABCD 面积平分.当直线y=kx-1经过点R 时,得1=23k-1 ∴k=34,(3)方法1:如图2,由题意知,四边形AEMN 是平行四边形, ∴AN ∥EM 且AN=EM. ∵E (1,-1)、A (-1,0) ∴设M (m ,n ),则N (m-2,n+1).∵M 、N 在抛物线上,∴⎪⎪⎩⎪⎪⎨⎧+-+--=+++-=2)2(23)2(2112232122m m n m m n 解得⎩⎨⎧==.1,3n m∴M (3,2),N (1,3).方法2:如图2,由题意知△AEF ≌△MNQ .∴MQ=AF=2,NQ=EF=1,∠MQN=∠AFE=90设M (m ,223212++-m m ),N (n ,223212++-n n ), ∴⎪⎩⎪⎨⎧=++--++-=-;1)22321(22321,222m m n n n m 解得⎩⎨⎧==.1,3n m ∴M (3,2),N (1,3).注:中对学生的解法提炼出来的.方法3:如图2,设旋转中心P (m ,n ), ∵A (-1,0) E (1,-1) , 根据中点坐标公式得M (2m+1,2n ) N (2m-1,2n+1).∵M 、N 在抛物线上,∴⎪⎪⎩⎪⎪⎨⎧+-+--=+++++-=2)12(23)12(21122)12(23)12(21222m m n m m n 解得⎩⎨⎧==.1,1n m∴M (3,2),N (1,3).方法4:如图2,由题意知,四边形AEMN 是平行四边形,∴NM ∥AE 且MN=AE=5,∵直线AE 的解析式为y=2121--x , ∴可设MN 的解析式为y=x 21-+b ,联立方程组⎪⎪⎩⎪⎪⎨⎧++-=+=.22321,21- 2x x y b x y 消去y ,整理得 2x -4x-4+2b=0设M (),11y x 、N (22,y x ),由根与系数关系得421=+x x , 21x x =2b-4∴(221)x x -=(221)x x +-421x x =32-8b而MN 2=(221)x x -+(21y y -)2=(221)x x -+[(-211x +b )-(-212x +b )]2 =45(221)x x - ∴45(221)x x -=5 ∴32-8b=4 解得b=27 将b=27代入方程组解得⎩⎨⎧==.1,311y x ,⎩⎨⎧==.3,122y x∴M (3,2),N (1,3).【例4】解:(1)联结AO , 矩形ABOC 322==OB AB ,40=∴A ----(1分)矩形ABOC 绕点O 逆时针旋转后得到矩形EFOD ,A 落在y 轴上的点E4==∴EO AO )4,0(E ∴ --------------------------------------------(1分) 过D 点作D H ⊥X 轴于H ,AOB DOH ABO DHO ∠=∠∠=∠, ,DHO ∆∴∽ABO ∆AODOOB HO AB DH ==∴4,2,32,2====AO DO OB AB 3,1==∴OH DH)1,3(-∴D ------------------------------------------------------------(1分)同理求得)3,3(F ∴-----------------------------------------------------------------------(1分) (2)因为抛物线c bx ax y ++=2经过点F 、E 、D⎪⎩⎪⎨⎧+-=++=∴43314333b a b a 求得:4,33,32==-=c b a ---------------------------------------------------------(3分) 所求抛物线为:433322++-=x x y ---------------------------------------------(1分) (3)因为在x 轴上方的抛物线上有点Q ,使得三角形QOB 的面积等于矩形ABOC 的面积设三角形Q O B 的OB 边上的高为h ,则3223221⨯=⨯⨯h ,所以4=h --------------------(1分)因为点Q 在x 轴上方的抛物线上, )4,(x Q ∴23.0,433324212==++-=∴x x x x ----------------------------------(1分) 所以Q 的坐标是)4,0(或)4,23(--------------------------------------------------------(2分) 【例5】解:(1)Q (1,0) ·············································································································· 1分 点P 运动速度每秒钟1个单位长度. ················································································· 2分 (2) 过点B 作BF ⊥y 轴于点F ,BE ⊥x 轴于点E ,则BF =8,4OF BE ==. ∴1046AF =-=. 在Rt △AFB中,10AB 3分过点C 作CG ⊥x 轴于点G ,与FB 的延长线交于点H . ∵90,ABC AB BC ∠=︒= ∴△ABF ≌△BCH . ∴6,8BH AF CH BF ====. ∴8614,8412OG FH CG ==+==+=.∴所求C 点的坐标为(14,12). 4分(3) 过点P 作PM ⊥y 轴于点M ,PN ⊥x 轴于点N , 则△APM ∽△ABF . ∴AP AM MP AB AF BF ==. 1068t A M M P∴==. ∴3455AM t PM t ==,. ∴3410,55PN OM t ON PM t ==-==.设△OPQ 的面积为S (平方单位)∴213473(10)(1)5251010S t t t t =⨯-+=+-(0≤t ≤10) ····························································· 5分说明:未注明自变量的取值范围不扣分.∵310a =-<0 ∴当474710362()10t =-=⨯-时, △OPQ 的面积最大. ································ 6分 此时P 的坐标为(9415,5310) . ······················································································· 7分(4) 当 53t =或29513t =时, OP 与PQ 相等. ····························································· 9分对一个加1分,不需写求解过程.。


「初中数学」动点产生的面积问题
【预备知识】三角形面积计算的常用策略
一、割补法
(1)若三角形至少有一边和坐标轴平行时,我们将其称为规则三角形
(2)若三角形三边都不和坐标轴平行时,我们将其称为不规则三角形
二、面积转化法
(1)借助平行线转化
(2)借助同底或同高,转化面积比
(3)借助相似三角形
【附】常见相似结构
【热身训练】
1、请在直角坐标系中画出以A、B、C为顶点的三角形,并求出其面积
(1)A(-1,0),B(3,0),C(0,3)
(2)A(-1,0),B(3,3),C(2,4)
【解析】
【注】
①割补法就是把不规则三角形,转化为规则三角形来解决;
②【方法1】中,我们也可以补成一个正方形;
③观察发现,AB=AC=5,可先求出BC,然后解等腰
△ABC,也可解,因不属于通法,在此省略
2、如图,在平面直角坐标系中,直线y=-x+8与x轴、y轴分别交于点A、B,
点P(x,y)是直线AB上一动点(点P不与点A重合),点C(6,0),O是坐标原点,
设△PCO的面积为S.
(1)求S与x的函数关系式
(2)当点P运动到什么位置时,△PCO的面积为15?
【解析】
【注】
①本题第(1)问也可以去绝对值,分x8和x8两种情况进行讨论,加上绝对值在第(2)问求解P点坐标时会省去讨论,并简化计算,但此时不要忽略x≠8(P不与A重合;
②【扩展】其他条件不变,若C坐标为(6,1),试求上面两问
【经典例题】
【解析】
【注】【总结与反思】
【切记】
我们推出的结论,只适合验证结论或秒杀小题,切不可
在做大题时直接使用!。

运动变化题是随着图形的某一元素的运动变化,导致问题的结论改变或者保持不变的几何题,它揭示了“运动”与“静止”、“一般”与“特殊”的内在联系.解题的关键是分清几何元素运动的方向和捷径,注意在运动过程中哪些是变量,哪些不是变量,通常要根据几何元素所处的不同位置加以分类讨论,同时,综合运用勾股定理、方程和函数等知识,本节课的内容涉及三角形、特殊的四边形的面积问题.本节主要是在函数背景下求三角形或四边形的面积问题,较复杂的题目可以采取“割补”的思想构造较简单的图形进行求解.动点产生的面积问题内容分析知识结构模块一:面积计算的问题知识精讲【例1】 如图,已知直线l :22y x =-+与x 轴、y 轴分别交于点B 、C ,将直线y=x向上平移1个单位长度得到直线P A ,点Q 是直线P A 与y 轴的交点,求四边形PQOB 的面积. 【难度】★★ 【答案】 【解析】【例2】 如图,已知直线AB :2y x =+与直线OA :13y x =交于点A ,与直线OB :3y x =交于点B 两点.求△AOB 的面积. 【难度】★★ 【答案】 【解析】例题解析【例3】 如图,已知直线3y x =+的图像与x 轴、y 轴分别交于A 、B 两点,直线l 经过原点,与线段AB 交于点C ,把△AOB 的面积分为2:1两部分,求直线l 的解析式. 【难度】★★ 【答案】 【解析】【例4】 如图,已知,在矩形ABCD 中,AB =10,BC =12,四边形EFGH 的三个顶点E 、F 、H 分别在矩形ABCD 边AB 、BC 、DA 上,AE =2.(1)如图1,当四边形EFGH 为正方形时,求△GFC 的面积;(2)如图2,当四边形EFGH 为菱形,且BF =a 时,求△GFC 的面积.(用含a 的代数式表示)【难度】★★★ 【答案】 【解析】A B CDE F 图1GHABCDE F 图2GH【例5】 如图1,正方形ABCD 的边长为2,点A (0, 1)和点D 在y 轴正半轴上,点B 、C 在第一象限,一次函数y =kx +2的图像l 交AD 、CD 分别于E 、F . (1)若△DEF 与△BCF 的面积比为1∶2,求k 的值; (2)联结BE ,当BE 平分∠FBA 时,求k 的值. 【难度】★★★ 【答案】 【解析】【例6】 如图,在平面直角坐标系中,函数y =2x +12的图像分别交x 轴、y 轴于A 、B 两点,过点A 的直线交y 轴正半轴于点M ,且点M 为线段OB 的中点. (1)求直线AM 的表达式;(2)试在直线AM 上找一点P ,使得S △ABP =S △AOB ,请求出点P 的坐标; (3)若点H 为坐标平面内任意一点,是否存在点H ,使以A 、B 、M 、H 为顶点的四边形是等腰梯形?若存在,请直接写出点H 的坐标;若不存在,请说明理由. 【难度】★★★ 【答案】 【解析】【例7】 如图1,已知直角坐标平面内点A (2, 0),P 是函数y =x (x >0)图像上一点,PQ ⊥AP 交y 轴正半轴于点Q . (1)试证明:AP =PQ ;(2)设点P 的横坐标为a ,点Q 的纵坐标为b ,那么b 关于a 的函数关系式是_______;(3)当S △AOQ =23S △APQ 时,求点P 的坐标.【难度】★★★ 【答案】 【解析】本节主要研究点在运动的背景下,产生的面积与动点之间的关系,关键点是找出决定这个面积变化的几个量是怎样变化的,重点在于思维能力的培养,难度较大.模块二:与面积相关的函数解析式知识精讲【例8】 如图,矩形ABCD 中,AB =1,AD =2,M 是CD 的中点,点P 在矩形的边上沿A B C M →→→运动,试写出△APM 的面积y 与点P 经过的路程x 之间的函数关系,写出定义域,并画出函数图像. 【难度】★★ 【答案】 【解析】【例9】 如图,在梯形ABCD 中,AD //BC ,AB =CD =AD =5cm ,BC =11cm ,点P 从点D 出发沿DA 边以每秒1cm 的速度移动,点Q 从点B 出发沿BC 边以每秒2cm 的速度移动(当点P 到达点A 时,点P 与点Q 同时停止移动),假设点P 移动的时间为x (秒),四边形ABQP 的面积为y (cm 2). (1)求y 关于x 的函数解析式,并写出它的定义域;(2)在移动的过程中,求四边形ABQP 的面积与四边形QCDP 的面积相等时x 的值;(3)在移动过程中,是否存在x 使得PQ =AB ,若存在,求出所有的x 的值;若不存在,请说明理由. 【难度】★★ 【答案】 【解析】例题解析BAB CDMP【例10】已知:如图1,在线段AE的同侧作正方形ABCD和正方形BEFG(BE<AB),连结EG并延长交DC于点M,作MN⊥AB,垂足为N,MN交BD于P.设正方形ABCD的边长为1.(1)证明:△CMG≌△NBP;(2)设BE=x,四边形MGBN的面积为y,求y关于x的函数解析式,并写出定义域;(3)如果按照题设方法作出的四边形BGMP是菱形,求BE的长.【难度】★★★【答案】【解析】【例11】已知:在梯形ABCD中,AD//BC,∠B=90°,AB=BC=4,点E在边AB 上,CE=CD.(1)如图1,当∠BCD为锐角时,设AD=x,△CDE的面积为y,求y与x之间的函数解析式,并写出函数的定义域;(2)当CD=5时,求△CDE的面积.【难度】★★★【答案】【解析】AB CDEA BCDEFGPMN【例12】 如图1,四边形OABC 是矩形,点A 、C 的坐标分别为(3,0),(0,1),点D是线段BC 上的动点(与端点B 、C 不重合),过点D 作直线12y x m =-+交折线OAB 于点E .(1)当点E 恰为AB 中点时,求m 的值;(2)当点E 在线段OA 上,记△ODE 的面积为y ,求y 与m 的函数关系式并写出定义域;(3)当点E 在线段OA 上时,若矩形OABC 关于直线DE 的对称图形为四边形O 1A 1B 1C 1,试判断四边形O 1A 1B 1C 1与矩形OABC 的重叠部分的面积是否发生变化,若不变,写出该重叠部分的面积;若改变,写出重叠部分面积S 关于m 的函数关系式. 【难度】★★★ 【答案】 【解析】【例13】 如图1,在正方形ABCD 中,点E 在边AB 上(点E 与点A 、B 不重合),过点E 作FG ⊥DE ,FG 与边BC 相交于点F ,与边DA 的延长线相交于点G . (1)当E 是AB 中点时,求证AG =BF ;(2)当E 在边AB 上移动时,观察BF 、AG 、AE 之间具有怎样的数量关系?并证明你所得到的结论;(3)联结DF ,如果正方形的边长为2,设AE =x ,△DFG 的面积为y ,求y 与x 之间的函数解析式,并写出函数的定义域.【难度】★★★ 【答案】 【解析】xA BCD EFG【例14】 如图1,梯形ABCD 中,AD //BC ,∠B =90°,AD =18,BC =21.点P 从点A 出发沿AD 以每秒1个单位的速度向点D 匀速运动,点Q 从点C 沿CB 以每秒2个单位的速度向点B 匀速运动.点P 、Q 同时出发,其中一个点到达终点时两点停止运动,设运动的时间为t 秒.(1)当AB =10时,设A 、B 、Q 、P 四点构成的图形的面积为S ,求S 关于t 的函数关系式,并写出定义域;(2)设E 、F 为AB 、CD 的中点,求四边形PEQF 是平行四边形时t 的值.【难度】★★★ 【答案】【解析】【例15】 如图1,在菱形ABCD 中,∠B =45°,AB =4.左右作平行移动的正方形EFGH 的两个顶点F 、G 始终在边BC 上.当点G 到边BC 中点时,点E 恰好在边AB 上.(1)如图1,求正方形EFGH 的边长;(2)设点B 与点F 的距离为x ,在正方形EFGH 作平行移动的过程中,正方形EFGH 与菱形ABCD 重叠部分的面积为y ,求y 与x 的函数解析式,并写出它的定义域;(3)联结FH 、HC ,当△FHC 是等腰三角形时,求BF 的长. 【难度】★★★ 【答案】 【解析】ABCDE PAQ 图1备用图HAB C DEF G【例16】 如图1,在平面直角坐标系中,O 为坐标原点,四边形OABC 是矩形.A (0,4),C (5, 0),点D 是y 轴正半轴上一点,将四边形OABC 沿着过点D 的直线翻折,使得点O 落在线段AB 上的点E 处.过点E 作y 轴的平行线与x 轴交于点N .折痕与直线EN 交于点M ,联结DE 、OM . 设OD =t ,MN =s . (1)试判断四边形EDOM 的形状,并证明;(2)当点D 在线段OA 上时,求s 关于t 的函数解析式,并写出函数的定义域; (3)用含t 的代数式表示四边形EDOM 与矩形OABC 重叠部分的面积.【难度】★★★ 【答案】 【解析】【例17】 已知:如图1,梯形ABCD 中,AD //BC ,∠A =90°,∠C =45°,AB =AD =4.E 是直线AD 上一点,联结BE ,过点E 作EF ⊥BE 交直线CD 于点F .联结BF .(1)若点E 是线段AD 上一点(与点A 、D 不重合),(如图1所示) ①求证:BE =EF ;②设DE =x ,△BEF 的面积为y ,求y 关于x 的函数解析式,并写出此函数的定义域;(2)直线AD 上是否存在一点E ,使△BEF 是△ABE 面积的3倍,若存在,直接写出DE 的长,若不存在,请说明理由.【难度】★★★ 【答案】 【解析】AB DEFABCD图1备用图备用图ABCD【例18】如图,已知正方形ABCD的边长为3,菱形EFGH的三个顶点E、G、H分别在正方形的边AB、CD、DA上,AH=1,联结CF.(1)当DG=1时,求证菱形EFGH为正方形;(2)设DG=x,△FCG的面积为y,写出y关于x的函数解析式,并指出x的取值范围;(3)当DGGHE的度数.【难度】★★★【答案】【解析】A BCDEFGH【例19】已知:如图,四边形OABC的四个顶点坐标分别为O(0,0),A(8,0),B(4,4),C(0,4),直线l:y=x+m保持与四边形OABC的边交于点M、N(M 在折线AOC上,N在折线ABC上).设四边形OABC在l右下方部分的面积为S1,在l左上方部分的面积为S2,记S=S1-S2(S≥0).(1)求∠OAB的大小;(2)当M、N重合时,求l的解析式;(3)当m≤0时,线段AB上是否存在点N,使得S=0?若存在,求m的值;若不存在,请说明理由;(4)求S与m的函数关系式.【难度】★★★【答案】【解析】x【例20】 在边长为4的正方形ABCD 中,点O 是对角线AC 的中点,P 是对角线AC上一动点,过点P 作PF ⊥CD 于点F ,作PE ⊥PB 交直线CD 于点E ,设P A =x ,PCE S y =△.(1)求证:DF =EF ;(2)当点P 在线段AO 上时,求y 关于x 的函数关系式及自变量x 的取值范围;(3)点P 在运动过程中能否使△PEC 为等腰三角形?如果能,请直接写出P A 的长;如果不能,请简单说明理由. 【难度】★★★ 【答案】 【解析】【习题1】 如图,直线443y x =-+与y 轴交于点A ,与直线4455y x =+交于点B ,且直线4455y x =+与x 轴交于点C ,求△ABC 【难度】★★ 【答案】 【解析】随堂检测ABCD E F P O【习题2】已知直线2y x=-+与x轴、y轴分别交于A点和B点,另一条直线(0)y kx b k=+≠经过点C(1,0),且把△AOB分成两部分.若△AOB被分成的两部分面积比为1:5,求k和b的值.【难度】★★★【答案】【解析】【习题3】直线364y x=-+与坐标轴分别交与点A、B两点,点P、Q同时从O点出发,同时到达A点,运动停止.点Q沿线段OA运动,速度为每秒1个单位长度,点P沿O B A→→运动.(1)直接写出A、B两点的坐标;(2)设点Q的运动时间为t秒,△OPQ的面积为S,求出S与t之间的函数关系;(3)当485S=时,求出点P的坐标,并直接写出以点O、P、Q为顶点的平行四边形的第四个顶点M的坐标.【难度】★★★【答案】【解析】【习题4】 如图,已知:过点A (8,0)、B (0,y =交于点C ,平行于y 轴的直线l 从原点O 出发,以每秒1个单位长度的速度沿x 轴向右平移,到C 点时停止;l 分别交线段BC 、OC 于点D 、E ,以DE 为边向左侧作等边△DEF ,设△DEF 与△BCO 重叠部分的面积为S (平方单位),直线l 的运动时间为t (秒).(1) 写出点C 的坐标和t 的取值范围; (2) 求s 与t 的函数关系式. 【难度】★★★ 【答案】 【解析】【作业1】 如图,已知直线P A :(0)y x n n =+>与直线PB :2()y x m m n =-+>交于点P .(1)用m 、n 表示出A 、B 、P 点的坐标;(2)若点Q 是直线P A 与y 轴的交点,且四边形PQOB 的面积56,AB=2,试求点P 的坐标,并写出直线P A 与PB 的解析式. 【难度】★★ 【答案】 【解析】课后作业【作业2】 如图所示,直线y kx b =+的截距为6,该直线分别交x 轴、y 轴于E 、F ,点E 的坐标为(-4,0). (1)求直线y kx b =+的表达式;(2)若点P (x ,y )是该直线第二象限上的一个动点,P A ⊥x 轴,PB ⊥y 轴,垂足分别为点A 、B ,试求四边形OAPB 的面积S 与x 的函数关系式,并写出自变量x 的取值范围. 【难度】★★★ 【答案】 【解析】【作业3】 如图,已知:直角梯形ABCD 中,AB ∥CD ,∠A =90°,AB =6,AD =4,DC =3,点P 从点A 出发,沿ADCB 方向移动,动点Q 从点A 出发,在AB 边上移动,设点P 移动的路程为x ,点Q 移动的路程为y ,线段PQ 平分梯形ABCD 的周长. (1) 求y 关于x 的函数解析式,并写出x 和y 的取值范围;(2) 当P 不在BC 边上时,线段PQ 能否平分ABCD 的面积?若能,求出此时x 的值;若不能,说明理由. 【难度】★★★ 【答案】 【解析】ABCDP Q【作业4】如图,在平面直角坐标系中,两个函数162y x y x==-+,的图像交于点A,动点P从点O开始在线段O向点A方向以每秒1个单位的速度运动,作PQ∥x 轴交直线BC于点Q,以PQ为一边向下作正方形PAMN,设它与△ABO重叠部分的面积为S.(1)求点A的坐标;(2)试求出点P在线段OA上运动时,S与运动的时间t(秒)的关系式.【难度】★★★【答案】【解析】。

因动点产生的面积问题解题策略一.解题策略解读:面积的存在性问题常见的题型和解题策略有两类:图1 图2 图3 计算面积常用到的策略还有:图4 图5 图6例1.已知抛物线y=mx2+(1-2m)x+1-3m与x轴交于不同的两点A、 B.(1) 求m的取值范围;(2) 证明该抛物线一定经过非坐标轴上的一点P,并求出点P的坐标;(3) 当<m≤8时,由(2)求出的点P和点A、 B构成的△ABP的面积是否有最值,若有,求出最值及相应的m的值;若没有,请说明理由.思路:1. 已知的抛物线的解析式可以因式分解的,抛物线过x轴上的定点(-1, 0).2. 第(2)题分两步,先对m赋予两个不同的值,联立求方程组的解,再验证这个点是确定的.3. 第(3)题中△ABP的高为定值,点A为定点,求△ABP的最大面积,其实就是求点B的横坐标的最大值.例2.问题提出(1) 如图1,已知△ABC,请画出△ABC关于直线AC对称的三角形.问题探究(2) 如图2,在矩形ABCD中,AB=4, AD=6, AE=4, AF=2.是否在边BC、CD上分别存在点G、 H,使得四边形EFGH的周长最小?若存在,求出它周长的最小值;若不存在,请说明理由.问题解决(3) 如图3,有一块矩形板材ABCD, AB=3米, AD=6米,现想从此板材中截出一个面积尽可能大的四边形EFGH部件,使∠EFG=90°,米,∠EHG=45°.经研究,只有当点E、 F、 G分别在边AD、 AB、 BC上时,且AF<BF,并满足点H在矩形ABCD内部或边上时,才有可能截出符合要求的部件.试问能否截得符合要求的面积尽可能大的四边形EFGH部件?若能,求出截得的四边形EFGH 部件的面积;若不能,请说明理由.图1 图2 图3思路:1. 第(2)题的模型是“打台球”两次碰壁问题,依据光的反射原理.2. 第(3)题需先设AF的长并求解,再验证点H在矩形内部,然后计算面积.例3.如图1,在平面直角坐标系中,矩形OCDE的顶点C和E分别在y轴的正半轴和x轴的正半轴上,OC=8, OE=17.抛物线y=x2-3x+m与y轴交于点A,抛物线的对称轴与x轴交于点B,与CD交于点K.(1) 将矩形OCDE沿AB折叠,点O恰好落在边CD上的点F处.①求点F的坐标;②请直接写出抛物线的函数表达式;(2) 将矩形OCDE沿着经过点E的直线折叠,点O恰好落在边CD上的点G处,连结OG,折痕与OG交于点H,点M是线段EH上的一个动点(不与点H重合),连结MG, MO,过点G作GP⊥OM于点P,交EH于点N,连结ON.点M从点E开始沿线段EH向点H运动,至与点N重合时停止,△MOG和△NOG的面积分别表示为S1和S2,在点M的运动过程中,S1·S2(即S1与S2的积)的值是否发生变化?若变化,请直接写出变化的范围;若不变,请直接写出这个值.温馨提示: 考生可以根据题意,在备用图中补充图形,以便作答.图1 备用图思路:1. 第(1)题中点F的位置是由A、 B两点确定的,A、 B两点的坐标都隐含在抛物线的解析式中.2. 第(2)题思路在画示意图过程中,点G是关键点.以E为圆心,EO为半径画弧,交CD于点G.例 4.如图,已知平行四边形ABCD的三个顶点A(n, 0)、 B(m, 0)、 D(0,2n)(m>n>0),作平行四边形ABCD关于直线AD的对称图形AB1C1 D.(1) 若m=3,试求四边形CC1B1B面积S的最大值;(2) 若点B1恰好落在y轴上,试求的值.思路:1. 第(1)题先说理再计算,说理四边形CC1B1B是矩形.2. 第(2)题根据AB1=AB列关于m、 n的方程,整理就可以得到m与n的关系.例5.如图,在平面直角坐标系中,抛物线y=-x2+bx+c经过点A(3, 0)和点B(2, 3),过点A的直线与y轴的负半轴相交于点C,且tan∠CAO=.(1) 求这条抛物线的表达式及对称轴;(2) 连结AB、 BC,求∠ABC的正切值;(3) 若点D在x轴下方抛物线的对称轴上,当S△ABC =S△ADC时,求点D的坐标.解析:1. 直觉告诉我们,△ABC是直角三角形.2. 第(3)题的意思可以表达为: B、 D在直线AC的两侧,到直线AC的距离相等.于是我们容易想到,平行线间的距离处处相等.例6.如图,半圆O的直径AB=10,有一条定长为6的动弦CD在弧AB上滑动(点C、D分别不与点A、 B重合),点E、 F在AB上,EC⊥CD, FD⊥CD.(1) 求证:EO=FO;(2) 连结OC,如果△ECO中有一个内角等于45°,求线段EF的长;(3) 当动弦CD在弧AB上滑动时,设变量CE=x,四边形CDFE的面积为S,周长为l,问:S与l是否分别随着x变化而变化?试用所学过的函数知识直接写出它们的函数解析式及函数定义域,以说明你的结论.思路:1. 用垂径定理和平行线等分线段定理证明点O是EF的中点.2. 第(2)题的△ECO中,∠ECO是定值,45°的角分两种情况.3. 第(3)题用x表示OE的长,在△ECO中,∠ECO是定值.例7.直线y=2x+m与抛物线y=ax2+ax+b都过点M(1, 0),且a<b.(1) 求抛物线顶点Q的坐标(用含a的式子表示);(2) 试说明抛物线与直线有两个交点;(3) 设抛物线与直线的另一个交点为N.①若-1≤a≤-时,求MN的取值范围;②求△QMN的面积最小值.思路:1. 将M(1, 0)分别代入直线和抛物线的解析式,可以确定m的值,用a表示b.2. 联立直线与抛物线的解析式,消去y,得到关于a的一元二次方程,判断Δ>0.3. 第(3)题①,分别求a=-1和a=-时直线与抛物线的交点M、 N的坐标,再求MN的长,两个MN的长,就是MN的取值范围的两端值.例8.已知Rt△EFP和矩形ABCD如图1摆放(点P与点B重合),点F、 B(P)、 C 在同一直线上,AB=EF=6cm, BC=FP=8cm, ∠EFP=90°.如图2, △EFP从图1位置出发,沿BC方向匀速运动,速度为1cm/s, EP与AB交于点G;同时,点Q从点C出发,沿CD方向匀速运动,速度为1cm/s.过点Q作QM⊥BD,垂足为H,交AD于点M,连结AF、 PQ.当点Q停止运动时,△EFP也停止运动.设运动时间为t(s)(0<t<6).解答下列问题:(1) 当t为何值时,PQ∥BD?(2) 设五边形AFPQM的面积为y(cm2),求y与t之间的函数关系式;(3) 在运动过程中,是否存在某一时刻t,使S五边形AFPQM ∶S矩形ABCD=9∶8?若存在,求出t的值;若不存在,请说明理由;(4) 在运动过程中,是否存在某一时刻t,使点M在线段PG的垂直平分线上?若存在,求出t的值;若不存在,请说明理由.图1 图2思路:1. 把线段BP、 PC、 CQ、 DQ的长用t表示出来.再把线段BG、 DM的长用t表示出来.2. 用割补法求五边形AFPQM的面积,等于直角梯形减去两个直角三角形的面积.3. 第(3)题用第(2)题的结果,直接解方程就可以了.4. 第(4)题是根据MP2=MG2列方程,需要构造以MP为斜边的直角三角形.例9.如图1,在平面直角坐标系中,过原点O及点A(8, 0)、 C(0, 6)作矩形OABC,连结OB,点D为OB的中点,点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF.已知点E从点A出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒.(1) 如图1,当t=3时,求DF的长;(2) 如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值;(3) 连结AD,当AD将△DEF分成的两部分的面积比为1∶2时,求相应的t的值.图1 图2思路;1. 作DM⊥AB于M, DN⊥OA于N,那么△NDF与△MDE的相似比为3∶4.2. 面积比为1∶2要分两种情况讨论.把面积比转化为两个同高三角形底边的比.3. 过点E作OA的平行线,构造“8字型”相似,这样就把底边的比利用起来了.例10.如图1,二次函数y=x2+bx+c的图象与x轴交于A、 B两点,与y轴交于点C, OB=OC.点D在函数图象上,CD∥x轴,且CD=2,直线l是抛物线的对称轴,E是抛物线的顶点.(1) 求b、 c的值;(2) 如图1,连结BE,线段OC上点F关于直线l的对称点F'恰好在线段BE上,求点F的坐标;(3) 如图2,动点P在线段OB上,过点P作x轴的垂线分别与BC交于点M,与抛物线交于点N.试问:抛物线上是否存在点Q,使得△PQN与△APM的面积相等,且线段NQ的长度最小?如果存在,求出点Q的坐标;如果不存在,说明理由.图1 图2思路:1. 由已知抛物线的解析式可得C(0, c),再用c表示B、 D两点的坐标,然后将B、 D代入抛物线的解析式列关于b、 c的方程组.2. 第(2)题: 通过点C、 F分别与点D、 F'关于直线l对称,得到点F'是BE的中点,从而求得点F的坐标.3. 第(3)题: 设点P的横坐标为m,用m表示点M、 N的坐标,进而用m表示线段PM、 PN、 PA的长,根据两个三角形的面积相等,求出PN边上的高QH.最后讨论NQ与QH的关系.例11.如图,在平面直角坐标系中,直线y=12x+2与x 轴交于点A,与y 轴交于点C.抛物线y=-x 2+bx+c 经过A 、 C 两点,与x 轴的另一个交点为点B.(1) 求抛物线的函数表达式;(2) 点D 为直线AC 上方抛物线上一动点.① 连结BC 、 CD.设直线BD 交线段AC 于点E, △CDE 的面积为S 1, △BCE 的面积为S 2,求 12S S 的最大值; ② 过点D 作DF ⊥AC,垂足为F,连结CD.是否存在点D,使得△CDF 中的某个角恰好等于∠BAC 的2倍?若存在,求出点D 的坐标;若不存在,请说明理由.图1 备用图思路: 1. △CDE 与△BCE 是同高三角形,面积比等于底边的比.构造“8字型”,把底边的比转化为竖直线段的比.2. 第(3)题的第一种情况∠DCF=2∠BAC,过点C 作x 轴的平行线,通过内错角相等,再作轴对称的角,很容易找到点D 的位置.3. 第(3)题的第二种情况∠CDF=2∠BAC,先要探求2∠BAC的大小(正切值),如果这一步探究不出来,基本上进行不下去.例12.已知Rt△OAB,∠OAB=90°,∠ABO=30°,斜边OB=4,将Rt△OAB绕点O 顺时针旋转60°,如题图1,连接BC.(1)填空:∠OBC= ;(2)如图1,连接AC,作OP⊥AC,垂足为P,求OP的长度;(3)如图2,点M,N同时从点O出发,在△OCB边上运动,M沿O→C→B路径匀速运动,N沿O→B→C路径匀速运动,当两点相遇时运动停止,已知点M的运动速度为1.5单位/秒,点N的运动速度为1单位/秒,设运动时间为x秒,△OMN 的面积为y,求当x为何值时y取得最大值?最大值为多少?思路:(1)由旋转的性质可以证明△OBC是等边三角形,从而可得∠OBC的度数;(2)求出△AOC的面积,利用三角形的面积公式计算即可;(3)分三种情形讨论求解即可解决问题:①当0<x≤83时,M在OC上运动,N在OB上运动,此时过点N作NE⊥OC且交OC于点E,利用面积公式表示出△OMN的面积(y值);②当8 3<x≤4时,M在BC上运动,N在OB上运动.作MH⊥OB于H,利用∠CBO=60°表示出MH,再利用面积公式表示出△OMN的面积(y值);③当4<x≤4.8时,M、N都在BC上运动,作OG⊥BC于G,易求OG,再利用面积公式表示出△OMN的面积(y值),最后分别求出三种情况下面积最大值,从而求出整个运动过程中y的最大值.例13. 在平面直角坐标系中,抛物线2y ax bx c=++交x轴于A、B两点,交y轴于点C(0,43-),OA=1,OB=4,直线l过点A,交y轴于点D,交抛物线于点E,且满足tan∠OAD=34.(1)求抛物线的解析式;(2)动点P从点B出发,沿x轴正方向以每秒2个单位长度的速度向点A运动,动点Q从点A出发,沿射线AE以每秒1个单位长度的速度向点E运动,当点P运动到点A时,点Q也停止运动,设运动为t秒.①在P、Q的运动过程中,是否存在某一时刻t,使得△ADC与△PQA相似,若存在,求出t的值;若不存在,请说明理由;②在P、Q的运动过程中,是否存在某一时刻t,使得△APQ与△CAQ的面积之和最大?若存在,求出t的值;若不存在,请说明理由.思路:本题是代数几何综合题,以平面直角坐标系为背景,考查了求二次函数解析式,二次函数的性质,,方程组的解法,几何图形面积的表示,相似三角形的判定与性质,分类讨论思想,三角形的面积的最值问题,综合性强,难度大,解题的关键是需要学生有良好的运算能力及分析问题和解决问题的能力,还得富有耐心.(1)利用A、B、C三点的坐标确定二次函数的解析式.(2)利用题目的已知条件表示出相关线段的长,①中利用三角函数值探索出∠PAQ=∠ACD,再根据题目中的要求使得△ADC与△PQA相似,进行分类讨论得到对应线段成比例,列出关于t的方程求解即可;②直接利用三角形的面积公式列出△APQ与△CAQ 的面积之和与时间t之间的函数关系式,再将所得的二次函数的解析式配方确定最值即可得到答案.。

二次函数-因动点产生的面积问题例1、如图1,已知抛物线212y x bx c =++(b 、c 是常数,且c <0)与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴的负半轴交于点C ,点A 的坐标为(-1,0).(1)b =______,点B 的横坐标为_______(上述结果均用含c 的代数式表示);(2)连结BC ,过点A 作直线AE //BC ,与抛物线交于点E .点D 是x 轴上一点,坐标为(2,0),当C 、D 、E 三点在同一直线上时,求抛物线的解析式;(3)在(2)的条件下,点P 是x 轴下方的抛物线上的一动点,连结PB 、PC .设△PBC 的面积为S . ①求S 的取值范围;②若△PBC 的面积S 为正整数,则这样的△PBC 共有_____个.图1思路点拨1.用c 表示b 以后,把抛物线的一般式改写为两点式,会发现OB =2OC . 2.当C 、D 、E 三点共线时,△EHA ∽△COB ,△EHD ∽△COD .3.求△PBC 面积的取值范围,要分两种情况计算,P 在BC 上方或下方.4.求得了S 的取值范围,然后罗列P 从A 经过C 运动到B 的过程中,面积的正整数值,再数一数个数.注意排除点A 、C 、B 三个时刻的值. 满分解答(1)b =12c +,点B 的横坐标为-2c . (2)由2111()(1)(2)222y x c x c x x c =+++=++,设E 1(,(1)(2))2x x x c ++.过点E 作EH ⊥x 轴于H .由于OB =2OC ,当AE //BC 时,AH =2EH .所以1(1)(2)x x x c +=++.因此12x c =-.所以(12,1)E c c --. 当C 、D 、E 三点在同一直线上时,EH CO DH DO =.所以1212c cc --=--.整理,得2c 2+3c -2=0.解得c =-2或12c =(舍去). 所以抛物线的解析式为213222y x x =--.(3)①当P 在BC 下方时,过点P 作x 轴的垂线交BC 于F . 直线BC 的解析式为122y x =-. 设213(,2)22P m m m --,那么1(,2)2F m m -,2122FP m m =-+. 所以S △PBC =S △PBF +S △PCF =221()24(2)42B C FP x x FP m m m -==-+=--+.因此当P 在BC 下方时,△PBC 的最大值为4. 当P 在BC 上方时,因为S △ABC =5,所以S △PBC <5. 综上所述,0<S <5.②若△PBC 的面积S 为正整数,则这样的△PBC 共有11个. 考点伸展点P 沿抛物线从A 经过C 到达B 的过程中,△PBC 的面积为整数,依次为(5),4,3,2,1,(0),1,2,3,4,3,2,1,(0).当P 在BC 下方,S =4时,点P 在BC 的中点的正下方,F 是BC 的中点.例 2、如图1,在平面直角坐标系中放置一直角三角板,其顶点为A (0, 1)、B (2, 0)、O (0, 0),将此三角板绕原点O 逆时针旋转90°,得到三角形A ′B ′O .(1)一抛物线经过点A ′、B ′、B ,求该抛物线的解析式;(2)设点P 是第一象限内抛物线上的一个动点,是否存在点P ,使四边形PB ′A ′B 的面积是△A ′B ′O 面积的4倍?若存在,请求出点P 的坐标;若不存在,请说明理由;(3)在(2)的条件下,试指出四边形PB ′A ′B 是哪种形状的四边形?并写出它的两条性质.图1思路点拨1.四边形PB ′A ′B 的面积是△A ′B ′O 面积的4倍,可以转化为四边形PB ′OB 的面积是 △A ′B ′O 面积的3倍.2.联结PO ,四边形PB ′OB 可以分割为两个三角形.3.过点向x 轴作垂线,四边形PB ′OB 也可以分割为一个直角梯形和一个直角三角形. 满分解答(1)△AOB 绕着原点O 逆时针旋转90°,点A ′、B ′的坐标分别为(-1, 0) 、(0, 2). 因为抛物线与x 轴交于A ′(-1, 0)、B (2, 0),设解析式为y =a (x +1)(x -2), 代入B ′(0, 2),得a =1.所以该抛物线的解析式为y =-(x +1)(x -2) =-x 2+x +2. (2)S △A ′B ′O =1.如果S 四边形PB ′A ′B =4 S △A ′B ′O =4,那么S 四边形PB ′OB =3 S △A ′B ′O =3. 如图2,作PD ⊥OB ,垂足为D . 设点P 的坐标为 (x ,-x 2+x +2).232'1111(')(22)22222PB OD S DO B O PD x x x x x x =+=-++=-++梯形. 2321113(2)(2)22222PDBS DB PD x x x x x ∆=⨯=--++=-+. 所以2'''2+2PDB PB A D PB OD S S S x x ∆=+=-+四边形梯形. 解方程-x 2+2x +2=3,得x 1=x 2=1. 所以点P 的坐标为(1,2).图2 图3 图4(3)如图3,四边形PB ′A ′B 是等腰梯形,它的性质有:等腰梯形的对角线相等;等腰梯形同以底上的两个内角相等;等腰梯形是轴对称图形,对称轴是经过两底中点的直线. 考点伸展第(2)题求四边形PB ′OB 的面积,也可以如图4那样分割图形,这样运算过程更简单.'11'222PB O P S B O x x x ∆=⋅=⨯=. 22112(2)222PBOP S BO y x x x x ∆=⋅=⨯-++=-++. 所以2'''2+2PB O PBO PB A D S S S x x ∆∆=+=-+四边形.甚至我们可以更大胆地根据抛物线的对称性直接得到点P :作△A ′OB ′关于抛物线的对称轴对称的△BOE ,那么点E 的坐标为(1,2).而矩形EB ′OD 与△A ′OB ′、△BOP 是等底等高的,所以四边形EB ′A ′B 的面积是△A ′B ′O 面积的4倍.因此点E 就是要探求的点P .例 3、如图1,在平面直角坐标系中,直线112y x =+与抛物线y =ax 2+bx -3交于A 、B 两点,点A 在x 轴上,点B 的纵坐标为3.点P 是直线AB 下方的抛物线上的一动点(不与点A 、B 重合),过点P 作x 轴的垂线交直线AB 于点C ,作PD ⊥AB 于点D .(1)求a 、b 及sin ∠ACP 的值;(2)设点P 的横坐标为m .①用含m 的代数式表示线段PD 的长,并求出线段PD 长的最大值;②连结PB ,线段PC 把△PDB 分成两个三角形,是否存在适合的m 的值,使这两个三角形的面积比为9∶10?若存在,直接写出m 的值;若不存在,请说明理由.图1思路点拨1.第(1)题由于CP //y 轴,把∠ACP 转化为它的同位角. 2.第(2)题中,PD =PC sin ∠ACP ,第(1)题已经做好了铺垫.3.△PCD 与△PCB 是同底边PC 的两个三角形,面积比等于对应高DN 与BM 的比. 4.两个三角形的面积比为9∶10,要分两种情况讨论. 满分解答(1)设直线112y x =+与y 轴交于点E ,那么A (-2,0),B (4,3),E (0,1). 在Rt △AEO 中,OA =2,OE =1,所以5AE =.所以25sin AEO ∠=. 因为PC //EO ,所以∠ACP =∠AEO .因此25sin ACP ∠=将A (-2,0)、B (4,3)分别代入y =ax 2+bx -3,得4230,1643 3.a b a b --=⎧⎨+-=⎩解得12a =,12b =-. (2)由211(,3)22P m m m --,1(,1)2C m m +,得221111(1)(3)42222PC m m m m m =+---=-++.所以2225251595sin 4)1)2PD PC ACP m m m =∠==-++=-+. 所以PD 95. (3)当S △PCD ∶S △PCB =9∶10时,52m =; 当S △PCD ∶S △PCB =10∶9时,329m =.图2考点伸展第(3)题的思路是:△PCD 与△PCB 是同底边PC 的两个三角形,面积比等于对应高DN 与BM 的比. 而252511cos cos 4)(2)(4)25DN PD PDN PD ACP m m m m =∠=∠=-++=-+-, BM =4-m .①当S △PCD ∶S △PCB =9∶10时,19(2)(4)(4)510m m m -+-=-.解得52m =.②当S △PCD ∶S △PCB =10∶9时,110(2)(4)(4)59m m m -+-=-.解得329m =.例 4、如图1,直线l 经过点A (1,0),且与双曲线my x=(x >0)交于点B (2,1).过点(,1)P p p -(p >1)作x 轴的平行线分别交曲线m y x =(x >0)和my x=-(x <0)于M 、N 两点. (1)求m 的值及直线l 的解析式;(2)若点P 在直线y =2上,求证:△PMB ∽△PNA ;(3)是否存在实数p ,使得S △AMN =4S △AMP ?若存在,请求出所有满足条件的p 的值;若不存在,请说明理由.图1思路点拨1.第(2)题准确画图,点的位置关系尽在图形中.2.第(3)题把S △AMN =4S △AMP 转化为MN =4MP ,按照点M 与线段NP 的位置关系分两种情况讨论. 满分解答(1)因为点B (2,1)在双曲线my x=上,所以m =2.设直线l 的解析式为y kx b =+,代入点A (1,0)和点B (2,1),得0,2 1.k b k b +=⎧⎨+=⎩ 解得1,1.k b =⎧⎨=-⎩ 所以直线l 的解析式为1y x =-. (2)由点(,1)P p p -(p >1)的坐标可知,点P 在直线1y x =-上x 轴的上方.如图2,当y =2时,点P 的坐标为(3,2).此时点M 的坐标为(1,2),点N 的坐标为(-1,2).由P (3,2)、M (1,2)、B (2,1)三点的位置关系,可知△PMB 为等腰直角三角形. 由P (3,2)、N (-1,2)、A (1,0)三点的位置关系,可知△PNA 为等腰直角三角形. 所以△PMB ∽△PNA .图2 图3 图4(3)△AMN 和△AMP 是两个同高的三角形,底边MN 和MP 在同一条直线上. 当S △AMN =4S △AMP 时,MN =4MP .①如图3,当M 在NP 上时,x M -x N =4(x P -x M ).因此222()4(1)x x x x ⎛⎫⎛⎫--=-- ⎪ ⎪⎝⎭⎝⎭.解得113x +=或1132x -=(此时点P 在x 轴下方,舍去).此时1132p +=. ②如图4,当M 在NP 的延长线上时,x M -x N =4(x M -x P ).因此222()4(1)x x x x ⎛⎫⎛⎫--=-- ⎪ ⎪⎝⎭⎝⎭.解得152x +=或152x -=(此时点P 在x 轴下方,舍去).此时152p +=.考点伸展在本题情景下,△AMN 能否成为直角三角形?情形一,如图5,∠AMN =90°,此时点M 的坐标为(1,2),点P 的坐标为(3,2). 情形二,如图6,∠MAN =90°,此时斜边MN 上的中线等于斜边的一半. 不存在∠ANM =90°的情况.图5 图6例5、如图1,四边形OABC 是矩形,点A 、C 的坐标分别为(3,0),(0,1).点D 是线段BC 上的动点(与端点B 、C 不重合),过点D 作直线12y x b =-+交折线OAB 于点E . (1)记△ODE 的面积为S ,求S 与b 的函数关系式;(2)当点E 在线段OA 上时,若矩形OABC 关于直线DE 的对称图形为四边形O 1A 1B 1C 1,试探究四边形O 1A 1B 1C 1与矩形OABC 的重叠部分的面积是否发生变化?若不变,求出重叠部分的面积;若改变,请说明理由.图1思路点拨1.数形结合,用b表示线段OE、CD、AE、BE的长.2.求△ODE的面积,要分两种情况.当E在OA上时,OE边对应的高等于OC;当E在AB边上时,要利用割补法求△ODE的面积.3.第(3)题中的重叠部分是邻边相等的平行四边形.4.图形翻着、旋转等运动中,计算菱形的边长一般用勾股定理.满分解答(1)①如图2,当E在OA上时,由12y x b=-+可知,点E的坐标为(2b,0),OE=2b.此时S=S△ODE=112122OE OC b b⋅=⨯⨯=.②如图3,当E在AB上时,把y=1代入12y x b=-+可知,点D的坐标为(2b-2,1),CD=2b-2,BD=5-2b.把x=3代入12y x b=-+可知,点E的坐标为3(3,)2b-,AE=32b-,BE=52b-.此时S=S矩形OABC-S△OAE-S△BDE-S△OCD=1315133()()(52)1(22) 22222b b b b-⨯-----⨯⨯-252b b=-+.(2)如图4,因为四边形O1A1B1C1与矩形OABC关于直线DE对称,因此DM=DN,那么重叠部分是邻边相等的平行四边形,即四边形DMEN是菱形.作DH⊥OA,垂足为H.由于CD=2b-2,OE=2b,所以EH=2.设菱形DMEN的边长为m.在Rt△DEH中,DH=1,NH=2-m,DN=m,所以12+(2-m)2=m2.解得54m=.所以重叠部分菱形DMEN的面积为54.图2 图3 图4考点伸展把本题中的矩形OABC绕着它的对称中心旋转,如果重叠部分的形状是菱形(如图5),那么这个菱形的最小面积为1,如图6所示;最大面积为53,如图7所示.图5 图6 图7例 6、如图1,在△ABC中,∠C=90°,A C=3,BC=4,CD是斜边AB上的高,点E在斜边AB上,过点E作直线与△ABC的直角边相交于点F,设AE=x,△AEF的面积为y.(1)求线段AD的长;(2)若EF⊥AB,当点E在斜边AB上移动时,①求y与x的函数关系式(写出自变量x的取值范围);②当x取何值时,y有最大值?并求出最大值.(3)若点F在直角边AC上(点F与A、C不重合),点E在斜边AB上移动,试问,是否存在直线EF将△ABC的周长和面积同时平分?若存在直线EF,求出x的值;若不存在直线EF,请说明理由.图1 备用图思路点拨1.第(1)题求得的AD 的长,就是第(2)题分类讨论x 的临界点. 2.第(2)题要按照点F 的位置分两种情况讨论.3.第(3)题的一般策略是:先假定平分周长,再列关于面积的方程,根据方程的解的情况作出判断.满分解答(1) 在Rt △ABC 中, AC =3,BC =4,所以AB =5.在Rt △ACD 中,39cos 355AD AC A ==⨯=. (2) ①如图2,当F 在AC 上时,905x <<.在Rt △AEF 中,4tan 3EF AE A x ==.所以21223y AE EF x =⋅=. 如图3,当F 在BC 上时,955x <≤.在Rt △BEF 中,3tan (5)4EF BE B x ==-.所以21315288y AE EF x x =⋅=-+. ②当905x <<时,223y x =的最大值为5425;当955x <≤时,231588y x x =-+23575)8232x =--+(的最大值为7532. 因此,当52x =时,y 的最大值为7532.图2 图3 图4(3)△ABC 的周长等于12,面积等于6.先假设EF 平分△ABC 的周长,那么AE =x ,AF =6-x ,x 的变化范围为3<x ≤5.因此1142sin (6)(6)2255AEF S AE AF A x x x x ∆=⋅⋅=-⨯=--.解方程2(6)35x x --=,得1362x =因为1362x =+3≤x ≤5范围内(如图4),因此存在直线EF 将△ABC 的周长和面积同时平分. 考点伸展如果把第(3)题的条件“点F 在直角边AC 上”改为“点F 在直角边BC 上”,那么就不存在直线EF将△ABC 的周长和面积同时平分.先假设EF 平分△ABC 的周长,那么AE =x ,BE =5-x ,BF =x +1. 因此21133sin (5)(1)(45)22510BEF S BE BF B x x x x ∆=⋅⋅=-+⨯=---. 解方程23(45)310x x ---=.整理,得2450x x -+=.此方程无实数根.例7、如图1,正方形 ABCD 中,点A 、B 的坐标分别为(0,10),(8,4),点C 在第一象限.动点P 在正方形ABCD 的边上,从点A 出发沿A →B →C →D 匀速运动,同时动点Q 以相同速度在x 轴上运动,当P 点到D 点时,两点同时停止运动,设运动的时间为t 秒.(1)当P 点在边AB 上运动时,点Q 的横坐标x (长度单位)关于运动时间t (秒)的函数图象如图2所示,请写出点Q 开始运动时的坐标及点P 运动速度;(2)求正方形边长及顶点C 的坐标;(3)在(1)中当t 为何值时,△OPQ 的面积最大,并求此时P 点的坐标.(4)如果点P 、Q 保持原速度速度不变,当点P 沿A →B →C →D 匀速运动时,OP 与PQ 能否相等,若能,写出所有符合条件的t 的值;若不能,请说明理由.图1 图2思路点拨1.过点B 、C 、P 向x 轴、y 轴作垂线段,就会构造出全等的、相似的直角三角形,出现相等、成比例的线段,用含有t的式子表示这些线段是解题的基础.2.求点C的坐标,为求直线BC、CD的解析式作铺垫,进而为附加题用两点间的距离公式作准备.3.不论点P在AB、BC还是CD上,点P所在的直角三角形的三边比总是3∶4∶5,灵活运用方便解题.4.根据二次函数的解析式求函数的最值时,要注意定义域与对称轴的位置关系.满分解答(1)Q(1,0),点P每秒钟运动1个单位长度.(2)过点B作BE⊥y轴于点E,过点C作x轴的垂线交直线BE于F,交x轴于H.在Rt△ABE中,BE=8,AE=10-4=6,所以AB=10.由△ABE≌△BCF,知BF=AE=4,CF=BE=6.所以EF=8+6=14,CH=8+4=12.因此点C的坐标为(14,12).(3)过点P作PM⊥y轴于M,PN⊥x轴于N.因为PM//BE,所以AP AM MPAB AF BF==,即1068t AM MP==.因此34,55AM t PM t==.于是3410,55PN OM t ON PM t==-==.设△OPQ的面积为S(平方单位),那么2113347(1)(10)52251010S OQ PN t t t t=⋅⋅=+-=-++,定义域为0≤t≤10.因为抛物线开口向下,对称轴为直线476t=,所以当476t=时,△OPQ的面积最大.此时P的坐标为(9415,5310).(4)当53t=或29513t=时, OP与PQ相等.图3 图4考点伸展附加题的一般思路是:点Q的横坐标是点P的横坐标的2倍.先求直线AB、BC、CD的解析式,根据直线的解析式设点P 的坐标,再根据两点间的距离公式列方程PO =PQ .附加题也可以这样解:①如图4,在Rt △AMP 中,设AM =3m ,MP =4 m ,AP =5m ,那么OQ =8m .根据AP 、OQ 的长列方程组5,81,m t m t =⎧⎨=+⎩解得53t =. ②如图5,在Rt △GMP 中,设GM =3m ,MP =4 m ,GP =5m ,那么OQ =8m .在Rt △GAD 中,GD =7.5.根据GP 、OQ 的长列方程组537.5,81,m t m t =-⎧⎨=+⎩解得29513t =.③如图6,设MP =4m ,那么OQ =8m .根据BP 、OQ 的长列方程组51010,81,m t m t -=-⎧⎨=+⎩解得53t =,但这时点P 不在BC 上.图5 图6。
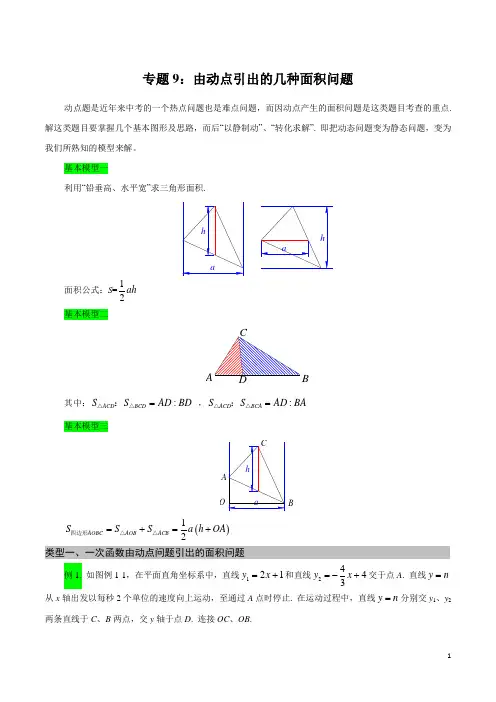
专题9:由动点引出的几种面积问题动点题是近年来中考的一个热点问题也是难点问题,而因动点产生的面积问题是这类题目考查的重点. 解这类题目要掌握几个基本图形及思路,而后“以静制动”、“转化求解”. 即把动态问题变为静态问题,变为我们所熟知的模型来解。
基本模型一利用“铅垂高、水平宽”求三角形面积.面积公式:S =12ah 基本模型二CABD其中::ACD BCD S S AD BD =△△: ,:ACD BCA S S AD BA =△△: 基本模型三OB()12AOB ACB AOBC S S S a h OA =+=+△△四边形 类型一、一次函数由动点问题引出的面积问题例1. 如图例1-1,在平面直角坐标系中,直线121y x =+和直线2443y x =-+交于点A . 直线y n =从x 轴出发以每秒2个单位的速度向上运动,至通过A 点时停止. 在运动过程中,直线y n =分别交y 1、y 2两条直线于C 、B 两点,交y 轴于点D . 连接OC 、OB .(1)设运动时间为t (s ),求t 的取值范围.(2)求出△OBC 的面积S 与t 的函数关系式,并求出S 的最大值及此时n 的值.y=n类型二、二次函数由动点问题引出的面积问题例2. 如图例2-1,二次函数y =ax 2+bx +c 的图像与x 轴的交点为A 、D (A 在D 的右侧),与y 轴的交点为C ,且A (4,0),C (0,-3),对称轴是直线x =1. (1)求二次函数的解析式;(2)若M 是第四象限抛物线上一动点,且横坐标为m ,设四边形OCMA 的面积为S .请写出S 与m 之间的函数关系式,并求出当m 为何值时,四边形OCMA 的面积最大.图例2-1图例2-2类型三、反比例函数由动点问题引出的面积问题例3. 如图例3-1,直线y=2x+6与反比例函数kyx(k>0)的图象交于点A(1,m),与x轴交于点B,平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M,交AB于点N,连接BM.(1)求m的值和反比例函数的表达式;(2)直线y=n沿y轴方向平移,当n为何值时,△BMN的面积最大?图例3-1类型四、利用三角函数求解由动点问题引出的面积问题例4. 如图例4-1,在矩形OABC中,点O为原点,边OA的长度为8,对角线AC=10,抛物线y =-49x 2+bx +c 经过点A 、C ,与AB 交于点D .(1)求抛物线的解析式;(2)点P 为线段BC 上一个动点(不与点C 重合),点Q 为线段AC 上一个动点,AQ =CP ,连接PQ ,设CP =m ,△CPQ 的面积为S . 求S 关于m 的函数表达式并求出S 最大时的m 值.图例4-1.类型五、由动点问题引出的面积存在性问题例5. 如图例5-1,在平面直角坐标系中,△ABC 是等腰直角三角形,∠BAC =90°,A (1,0),B (0,2),C (3,1)抛物线2122y x bx =+-的图象过C 点,交y 轴于点D . (1)在后面的横线上直接写出点D 的坐标及b 的值: ,b = ;(2)平移该抛物线的对称轴所在直线l ,设l 与x 轴交于点G (x ,0),当OG 等于多少时,恰好将△ABC的面积分为相等的两部分?AOxyBCGF H E图例5-1 图例5-2类型六、利用转化思想解决由动点问题引出的面积问题如图例6-1,在平面直角坐标系中,抛物线24 5y ax x c=++与直线2255y x=--交于A、B两点,已知点B的横坐标是4,直线2255y x=--与x、y轴的交点分别为A、C,点P是抛物线上一个动点.(1)求抛物线的解析式;(2)若点P在直线2255y x=--上方,求△P AC的最大面积.OxyPACBGEH 图例6-1专题9:由动点引出的几种面积问题动点题是近年来中考的一个热点问题也是难点问题,而因动点产生的面积问题是这类题目考查的重点. 解这类题目要掌握几个基本图形及思路,而后“以静制动”、“转化求解”. 即把动态问题变为静态问题,变为我们所熟知的模型来解。

初中数学动点问题大全动点问题一直是中考热点题型,近几年考察探究运动中的特殊性:等腰三角形、直角三角形、相似三角形、平行四边形、梯形、特殊角或其三角函数值、线段或面积的最值问题等,下面就此问题的常见题型作简单介绍。
题型一动点形成的面积问题1.面积公式:三角形面积用12S ah =来表示,利用未知数的代数式来表示底和高。
2.面积比等于相似比的平方:面积无法用底和高表示时,利用相似三角形的面积比等于相似比的平方来求解,只需要知道相似比和另一个三角形面积即可表示。
3.相似三角形:当面积公式和面积比等于相似比的平方不能有效解题时,利用相似三角形的比例关系求解。
角度1:利用公式法解决动点面积问题例题1:在平面直角坐标系xOy 中,抛物线2y x bx c =-++经过点30A (,)和23B (,).过点A 的直线与y 轴的负半轴相交于点C ,且1tan 3CAO ∠=.(1)求这条抛物线的表达式及对称轴;(2)连接AB 、BC ,求ABC ∠的正切值;(3)若点D 在x 轴下方的对称轴上,当ABC ADC S S ∆∆=时,求点D 的坐标.变式1:如图,在平面直角坐标系xOy 中,已知点A 的坐标为(,3)a (其中4a >),射线O 与反比例函数12y x =的图像交于点P ,点B 、C 分别在函数12y x=的图像上,且//AB x 轴,//AC y 轴.(1)当点P 横坐标为6,求直线AO 的表达式;(2)联结BO ,当AB BO =时,求点A 坐标;(3)联结BP 、CP ,试猜想:ABP ACP S S ∆∆的值是否随a 的变化而变化?如果不变,求出ABP ACP S S ∆∆的值;如果变化,请说明理由.O x y (备用图)O xy解析:(1)∵反比例函数12y x=的图像经过横坐标为6的点P ,∴点P 的坐标为(6,2).设直线AO 的表达式为y kx =(0k ≠).将点P (6,2)代入y kx =,解得13k =.∴所求反比例函数的解析式为13y x =.(2)∵AB //x 轴,∴点B 纵坐标为3,将3y =代入12y x=,得4x =.∴B 坐标为(4,3).∵AB =BO ,∴224(40)(30)a -=-+-9a =.∴点A 坐标为(9,3).(3)不变.延长AB 交y 轴于点D ,延长AC 交x 轴于点E ,∴32ADO AEO S S a ∆∆==.∵点C 坐标为(a ,12a ).∴6CEO S ∆=,同理6BDO S ∆=,∴ADO BDO AEO CEO S S S S ∆∆∆∆-=-,即ABO ACO S S ∆∆=.∵△ABP 与△ABO 同高,∴ABP ABO S AP S AO ∆∆=.同理ACP ACO S AP S AO ∆∆=.∴1ABP ACP S S ∆∆=.即当a 变化时,ABP ACPS S ∆∆的值不变,且恒为1变式2:如图,在直角坐标系中,一条抛物线与x 轴交于A 、B 两点,与y 轴交于C 点,其中(3,0)B ,(0,4)C ,点A 在x 轴的负半轴上,4OC OA =;(1)求这条抛物线的解析式,并求出它的顶点坐标;(2)联结AC 、BC ,点P 是x 轴正半轴上一个动点,过点P 作//PM BC 交射线AC 于点M ,联结CP ,若CPM ∆的面积为2,则请求出点P 的坐标;解析:(1)设这条抛物线的解析式为2(0)y ax bx c a =++≠它的顶点坐标为16(1,)3(2)过点P 作PH AC ⊥,垂足为H .∵P 点在x 轴的正半轴上,∴设0P x (,).∵A )0,1(-,∴1PA x =+.∵在Rt AOC ∆中,222OA OC AC +=;又∵14OA OC ==,∴17AC =90sin 117PH PH PHA CAO AP x ∠=︒∴∠===+ 17PH =//BP CM PM BC AB AC ∴= ;300B P x (,),(,)1点P 在点B 的左侧时,3BP x =-,∴3417x -=17(3)4x CM -=∵2PCM S =△∴122CM PH ⋅⋅=,∴17(3)12217x -=解得110x .P =∴(,)2点P 在点B 的右侧时,3BP x =-,∴3417x -=17(3)x CM -=∵2PCM S =△∴122CM PH ⋅⋅=,∴17(3)122417x -=解得11x =+,21x =-(不合题意,舍去)∴P(1+0).综上所述,P 的坐标为(1,0)或(1+0)角度2:利用面积比等于相似比的平方解决动点面积问题例题2:如图,已知在梯形ABCD 中,//AD BC ,5AB DC ==,4AD =.M 、N 分别是边AD 、BC 上的任意一点,联结AN 、DN .点E 、F 分别在线段AN 、DN 上,且//ME DN ,//MF AN ,联结EF .(1)如图1,如果//EF BC ,求EF 的长;(2)如果四边形MENF 的面积是ADN ∆的面积的38,求AM 的长;解析:(1)∵AD //BC ,EF //BC ,∴EF //A D .又∵ME //DN ,∴四边形EF DM 是平行四边形.∴EF =DM .同理可证,EF =AM .∴AM =DM .∵AD =4,∴122EF AM AD ===.(2)∵38ADN MENF S S ∆=四边形,∴58AME DMF ADN S S S ∆∆∆+=.即得58AME DMF ADN ADN S S S S ∆∆∆∆+=.∵ME //DN ,∴△AME ∽△AN D .∴22AME ADN S AM S AD∆∆=.同理可证,△DM F ∽△DN A .即得22DMF ADN S DM S AD ∆∆=.设AM =x ,则4DM AD AM x =-=-.∴22(4)516168x x -+=.即得2430x x -+=.解得11x =,23x =.∴AM 的长为1或3.A B CD M N EF (图1)AB C D M N E F变式3:已知直线1l 、2l ,12//l l ,点A 是1l 上的点,B 、C 是2l 上的点,AC BC ⊥,60ABC ∠=︒,4AB =,O 是AB 的中点,D 是CB 延长线上的点,将DOC ∆沿直线CO 翻折,点D 与'D 重合.(1)如图1,当点'D 落在直线1l 上时,求DB 的长;(2)延长DO 交1l 于点E ,直线'OD 分别交1l 、2l 于点M 、N .①如图2,当点E 在线段AM 上时,设x AE =,y DN =,求y 关于x 的函数解析式及其定义域;②若DON ∆的面积为323时,求AE 的长.解析:变式4:如图1,在梯形ABCD 中,//AD BC ,对角线BC AC ⊥,4AD =cm ,︒=∠45D ,3=BC cm .(1)求B ∠cos 的值;(2)点E 为BC 延长线上的动点,点F 在线段CD 上(点F 与点C 不重合),且满足ADE AFC ∠=∠,如图2,设x BE =,y DF =,求y 关于x 的函数解析式,并写出函数的定义域;(3)点E 为射线BC 上的动点,点F 在射线CD 上,仍然满足ADE AFC ∠=∠,当AFD ∆的面积为2cm 2时,求BE 的长.解析:(1)∵//AD BC ,∴ACB DAC ∠=∠.∵AC BC ⊥,∴90ACB ∠=︒.∴90DAC ∠=︒.∵45D ∠=︒,∴45ACD ∠=︒.∴AD AC =.∵4AD =,∴4AC =.∵3=BC ,∴5AB ==.∴3cos 5BC B AB ∠==.(2)∵//AD BC ,∴ADF DCE ∠=∠.∵AFC FDA FAD ∠=∠+∠,ADE FDA EDC ∠=∠+∠,又AFC ADE ∠=∠,∴FAD EDC ∠=∠.∴ADF DCE ∆~∆.∴AD DF DC CE =.在Rt ADC ∆中,222AC AD DC +=,又4==AC AD ,∴24=DC .∵x BE =,∴3-=x CE .y DF =,∴3244-=x y .22322-=x y .定义域为113<<x .(3)当点E 在BC 的延长线上,由(2)可得:ADF DCE ∆~∆,∴2(DC AD S S DCE ADF =∆∆.∵2AFD S ∆=,4=AD ,24=DC ,∴4=∆DCE S .∵AC CE S DCE ⨯⨯=∆21,∴44)3(21=⨯-⨯BE ,∴5BE =.当点E 在线段BC 上,同理可得:44)3(21=⨯-⨯BE .∴1BE =.所以BE 的长为5或1.角度3:利用锐角三角比法解决动点面积问题例题3:已知在平面直角坐标系xoy (如图)中,抛物线212y x bx c =++经过点(4,0)A 、点(0,4)C -,点B 与点A 关于这条抛物线的对称轴对称;(1)用配方法求这条抛物线的顶点坐标;(2)联结AC 、BC ,求ACB ∠的正弦值;(3)点P 是这条抛物线上的一个动点,设点P 的横坐标为(0)m m >,过点P 作y 轴的垂线PQ ,垂足为Q ,如果QPO BCO ∠=∠,求m 的值;解析:变式5:已知在平面直角坐标系xoy 中,抛物线2(0)y ax bx c a =++>与x 轴相交于(1,0),(3,0)A B -两点,对称轴l 与x 轴相交于点C ,顶点为点D ,且ADC ∠的正切值为12.(1)求顶点D 的坐标;(2)求抛物线的表达式;(3)F 点是抛物线上的一点,且位于第一象限,联结AF ,若FAC ADC ∠=∠,求F 点的坐标.解析:(1)∵抛物线与x 轴相交于()1,0A -,()3,0B 两点,∴对称轴l :直线1x =,2AC =∵90ACD ∠=︒,1tan 2ADC ∠=,∴4CD =,∵0a >,∴()1,4D -(2)设()214y a x =--将1,0x y =-=代入上式,得,1a =所以,这条抛物线的表达为223y x x =--(3)过点F 作FH x ⊥轴,垂足为点H设()2,23F x x x --,∵FAC ADC ∠=∠,∴tan tan FAC ADC ∠=∠,∵1tan 2ADC ∠=,∴1tan 2FH FAC AH ∠==∵223FH x x =--,1AH x =+,∴223112x x x --=+解得172x =,21x =-(舍),∴79,24F ⎛⎫ ⎪⎝⎭巩固1:如图,在直角坐标系xOy 中,抛物线c ax ax y +-=22与x 轴的正半轴相交于点A 、与y 轴的正半轴相交于点B ,它的对称轴与x 轴相交于点C ,且OBC OAB ∠=∠,3AC =.(1)求此抛物线的表达式;(2)如果点D 在此抛物线上,DF OA ⊥,垂足为F ,DF 与线段AB 相交于点G ,且2:3:=∆∆AFG ADG S S ,求点D 的坐标.解析:(1)∵抛物线c ax ax y +-=22的对称轴为直线12=--=a a x ,∴OC =1,OA =OC +AC =4,∴点A (4,0).∵∠OBC =∠OAB ,∴tan ∠OAB =tan ∠OBC ,∴OBOC OA OB =,∴OB OB 14=,∴OB =2,∴点B (0,2),∴⎩⎨⎧+-==,8160,2c a a c ∴⎪⎩⎪⎨⎧=-=.2,41c a ∴此抛物线的表达式为221412++-=x x y .(2)由2:3:=∆∆AFG ADG S S 得DG :FG =3:2,DF :FG =5:2,设m OF =,得m AF -=4,221412++-=m m DF ,由FG //OB ,得OA AF OB FG =,∴24m FG -=,∴2:524:)22141(2=-++-m m m ,∴01272=+-m m ,∴4,321==m m (不符合题意,舍去),∴点D 的坐标是(3,45)巩固2:如图,已知ABC ∆与BDE ∆都是等边三角形,点D 在边AC 上(不与A 、C 重合),DE 与AB 相交于点F .(1)求证:BCD DAF ∆∆∽;(2)若1BC =,设CD x =,AF y =;①求y 关于x 的函数解析式及定义域;②当x 为何值时,79BEF BCD S S ∆∆=?(1)证明:∵ABC ∆与BDE ∆都是等边三角形,∴60A C BDE ∠=∠=∠=︒A C BO yx∵ADF BDE C DBC ∠+∠=∠+∠,∴ADF DBC ∠=∠,∴BCD ∆∽DAF∆(2)∵BCD ∆∽DAF ∆,∴BC CD AD AF=∵1BC =,设CD x =,AF y =,∴11x x y=-,∴()201y x x x =-<<(3)解法一:∵ABC ∆与BDE ∆都是等边三角形,∴60E C ∠=∠=︒,60EBD CBA ∠=∠=︒,∴EBF CBD∠=∠∴EBF ∆∽CBD ∆,∴BE BF BC BD=,∵BE BD =,1BC =,∴2BE BF =∵EBF ∆∽CBD ∆,79BEF BCD S S ∆∆=,∴2279BEF BCD S BE S BC ∆∆==,∴279BE BF ==,∴29AF =∴229x x -=,解得1221,33x x ==,∴当13x =或23时,79BEF BCD S S ∆∆=解法二:∵△ABC 与BDE ∆都是等边三角形,∴60E C ∠=∠=︒,60EBD CBA ∠=∠=︒,∴EBF CBD∠=∠∴EBF ∆∽CBD ∆,∵79BEF BCD S S ∆∆=,∴2279BEF BCDS BE S BC ∆∆==∵1BC =,BE BD =,∴279BD =过点B 作BH AC ⊥于点H ,∵60C ∠=︒,∴BH =16DH =,12CH =当点D 在线段CH 上时,111263CD CH DH =-=-=当点D 在线段CH 的延长线上时,112263CD CH DH =+=+=综上所述,当13x =或23时,79BEF BCD S S ∆∆=.巩固3:在矩形ABCD 中,4AB =,6AD =,点P 是射线DA 上一动点,将三角板直角顶点重合于点P ,三角板两直角边中的一边始终经过点C ,另一直角边交射线BA 于点E .(1)判断EAP ∆与PDC ∆一定相似吗?请证明你的结论;(2)设PD x =,AE y =,求y 与x 的函数关系式,并写出它的定义域;(3)是否存在这样的点P ,是EAP ∆周长等于PDC ∆周长的2倍?若存在,请求出PD 的长度;若不存在,请简要说明理由.解析:(1)△EAP ∽△PDC①当P 在AD 边上时,如图(1):∵矩形ABCD ,==90D A ∠∠ ,∴1+2=90∠∠据题意=90CPE ∠ ∴3+2=90∠∠ ,∴1=3∠∠,∴△EAP ∽△PDC②当P 在AD 边上时,如图(2):同理可得△EAP ∽△PDC(2)若点P 在边AD 上,据题意:PD x =6PA x =-4DC =AE y =又∵△EAP ∽△PDC ,∴AE PA PD DC =,∴64y x x -=,∴22613442x x y x x -==-+()06x <<若点P 在边DA 延长线上时,据题意PD x =,则6PA x =-,4DC =,AE y =,∵△EAP ∽△PDC ,∴AE PA PD DC =,∴64y x x -=,∴()2664x x y x -=>(3)假如存在这样的点P ,使△EAP 周长等于PDC ∆的2倍①若点P 在边AD 上∵△EAP ∽△PDC ∴():6:4EAP PDC C C x =- ,∴()6:42x -=,∴2x =-不合题意舍去;②若点P 在边DA 延长线上,同理得()6:42x -=,∴14x =综上所述:存在这样的点P 满足题意,此时14PD =巩固4:如图,已知抛物线2y ax bx c =++经过点(0,4)A -,点(2,0)B -,点(4,0)C .(1)求这个抛物线的解析式,并写出顶点坐标;(2)已知点M 在y 轴上,OMB OAB ACB ∠+∠=∠,求点M 的坐标.解析:(1)∵抛物线2y ax bx c =++经过点(0,4)A -,点(2,0)B -,点(4,0)C ∴44201640c a b c a b c =-⎧⎪-+=⎨⎪++=⎩解得方程组的解为1214a b c ⎧=⎪⎪=-⎨⎪=-⎪⎩∴这个抛物线的解析式为:2142y x x =--顶点为9(1,)2-(2)如图:取OA 的中点,记为点N ∵OA =OC =4,∠AOC =90°∴∠ACB =45°∵点N 是OA 的中点∴ON =2又∵OB =2∴OB =ON又∵∠BON =90°∴∠ONB =45°∴∠ACB =∠ONB∵∠OMB +∠OAB =∠ACB ∠NBA +∠OAB =∠ONB ∴∠OMB =∠NBA1°当点M 在点N 的上方时,记为M 1∵∠BAN =∠M 1AB ,∠NBA =∠OM 1B ,∴△ABN ∽△AM 1B ∴1AN AB AB AM =又∵AN =2,AB =∴110AM =又∵A (0,—4)∴1(0,6)M 2°当点M 在点N 的下方时,记为M 2,点M 1与点M 2关于x 轴对称,∴2(0,6)M -综上所述,点M 的坐标为(0,6)或(0,6)-题型二动点形成的相切问题1.直线和圆相切:圆心到直线距离等于半径构造直角三角形,利用三角比、勾股定理等来表示圆心到直线距离及半径,建立等量关系2.圆和圆相切:两圆半径和等于圆心距.利用平行线分线段成比例、勾股定理、三角比、相似等表示相关线段,建立等量关系角度4:直线与圆相切问题例题4:如图,在ABC ∆中,10,12,AB AC BC ===点E F 、分别在边BC AC 、上(点F 不与点A 、C 重合)//EF AB .把ABC ∆沿直线EF 翻折,点C 与点D 重合,设FC x =.(1)求B ∠的余切值;(2)当点D 在ABC ∆的外部时,DE DF 、分别交AB 于M 、N ,若MN y =,求y 关于x 的函数关系式并写出定义域;(3)(下列所有问题只要直接写出结果即可)以E 为圆心、BE 长为半径的E 与边AC 1没有公共点时,求x 的取值范围.2一个公共点时,求x 的取值范围.3两个公共点时,求x 的取值范围.AE CB FA B D GC EF变式6:已知:矩形ABCD 中,过点B 作BG ⊥AC 交AC 于点E ,分别交射线AD 于F 点、交射线CD 于G 点,BC =6.(1)当点F 为AD 中点时,求AB 的长;(2)联结AG ,设AFG AB x S y ∆==,,求y 关于x 的函数关系式及自变量x 的取值范围;(3)是否存在x 的值,使以D 为圆心的圆与BC 、BG 都相切?若存在,求出x 的值;若不存在,请说明理由.解析:(1)∵点F 为AD 中点,且AD =BC =6,∴AF =3∵矩形ABCD 中,∠ABC =90°,BG ⊥AC 于点E ,∴∠ABE +∠EBC =90°,∠AC ∠EBC =90°∴∠ABE =∠ACB ,∴△ABF ∽△BCF ,∴AB AF BC AB =∴AB =23(2)由(1)可得△ABF ∽△BCF ∴AB AF BC AB =∵AB =x ,BC =6∴AF =62x ;同理可得:CG =x36①当F 点在线段AD 上时DG =CG -CD =x x x x 23636-=-∴S ⊿AFG =1236213x x CG AF -=⋅。
教育学科教师辅导讲义,已知P (m ,0),Q (0,n )(m >0,n >0),反比例函数xmy =的图象与线段PQ 交于DOQ S ∆=,求n 的值,把三角形分成面积比是2:1的两部分,没有规定谁是2份,谁是1份,所以要分两种情况进行.用字母代替数,给理解带来了困难,要仔细审题;也给计算带来了麻烦,要谨慎计算..理清思路,从一个小三角形的面积是整个三角形面积的三分之一人手,写出点C 的含有字母的坐标,例1告诉我们两个三角形同高时,面积的比等于底的比,还告诉我们当右边求得了结果,还要思考左边是否还存在另一个解,要左思右想,不要丢解.例2告诉我们当面积的比是1比2,没有规定谁是比例前项,谁是比例后项,要面面俱到.另外第(2)小题还告诉我们两个小三角形面积的比,不如化为一个小三角形与整4.点P 在点A 的左侧存在,再考虑点法求之.解(1)因为点A 的横坐标为4,当是直线x y 21=与双曲线=xky (2)如图(2),因为点C 在双曲线上,当A 、C 分别作x 轴、y 轴的垂线,垂足为,4,32==∆ONC ONDM S s 矩形.4,9==s S s ,所以如图(4),当m >4时,因为POE AOp AFEP AOF s s s s ∆∆∆+=+梯形,所以,6==∆POA PEFA s s 梯形 所以,6)4()82(21=-⋅+m m解得m =8或m =-2(舍去),所以点P 的坐标为(8,1).综上所述,四边形的面积为24时,点P 的坐标为(2,4),(8,1).4、以上面积问题存在于正、反比例函数和一次函数中,那么在二次函数中是否也有这样 的规律呢?回答是肯定的,如图(3),因为12=∆∆BEF CEF S s ,所以,31CBCFs s BEC CEF ==∆∆ 因为EF ∥AC ,所以,31==CB CF AB AE ,37,35531==⨯=OE AE 即⋅-)0,37(E 综上所述,当△CEF 与△BEF 的面积之比为1:2时,E 点的坐标为)0,32(-或-37(分析1.由点C (0,m )和OB =OC 2.点E 在直线BC 上运动,所以要求出直线 3.因为点P 在x 轴上,PD 4.直线BC 把△PDB 分成面积之比为 5.因为点E 、点D 在x 轴的下方,要把它们的纵坐标改写成线段的长度,注意正、负号的问题.解(1)因为抛物线x y -=2所以点C 的坐标为(0,m )所以点B 的坐标为(-m ,0)33综上所述,直线BC 能把△PDB 分成面积之比为2:3的两部分,此时P 的坐标为)0,23(分析1.由顶点式求出抛物线的解析式,化成一般式,得到与 2.点P 在抛物线上,设出点P 的坐标.但是点P 的纵坐标要套上绝对值,以保证恒为正,这样的结果有四个.解(1)因为c bx ax y ++=2的顶点为又因为图象经过点A (-1,0),所以所以,4)1(2+--=x y 即-=x y (2)存在.点C (0,3)在直线y =kx +②如图(4),当点P 在x 轴下方的抛物线上时,解得,2222±=x 所以,2222(--p (如图(5).二、专题过关2、如图,在直角坐标系xOy 中,二次函数于0、A 两点.(1)求这个二次函数的解析式;(2)在这条抛物线的对称轴右边的图像上有一点(3)对于(2)中的点B ,在此抛物线上是否存在点1、因为点B (2,1)在双曲线x m y =上,所以1设直线l 的解析式y =kx +b ,因为直线l 经过A (1图1以后,把抛物线的一般式改写为两点式,会发现OB=EHA∽△COB,△EHD∽△COD.面积的取值范围,要分两种情况计算,P在BC上方或下方.P从A经过C运动到B的过程中,2、如图,一次函数33-=x y CD =CA .(1)求A 、B 两点的坐标; (2)求∠OCD 的度数;(3)如果△CDO 的面积是△ABO3、如图,一次函数图象交反比例函数分别交x 轴、y 轴于点C 、D .过点行于MN 的直线,分别交y 轴于点(1)如果线段OE 、OF 的长是方程 (2)设点M 、N 的横坐标分别为5、如图,已知:抛物线2+=bx x y 且OA =OC .(1)求这条抛物线的解析式;(2)过点C 作CE ∥x 轴,交抛物线于点 (3)设点M 在抛物线的对称轴l参考答案1、21;1)1(x y x y -=--=(2)因为点P 在1--=x y 上,所以设1521,15=⋅⋅=∆yp BC s PBC 解得x =-7或x =5,所以P (-∠CDH =30°,所以),3(21DH x CH -=又因为041AB CDO S S ∆∆=所以⨯⨯x 2103622=+-x x ,解得233±=x ⋅+)0,233(C均为平行四边形.所以OE ME A n DGEM ∙==∙;666=所以DMKH DGEM DMKH DNFH S S S S -=-即HKEG MNFK S S =4、(1)因为抛物线的对称轴l 与x 轴交于点解析式可以为,)5(2k x a y +-= 又它经过O (0,0)、A (7,4),所以有方程组5、(1)因为抛物线3b 2-+=x x y与y 轴交于点C (0,-3),并且OA =OC ,所以点A 的坐标为A (-3,0).将A (-3,0)代入b =2.所以抛物线的解析式为.322-+=x x y(2)如图1,由,4)1(3222-+=-+=x x x y得顶点D 的坐标为(-1,-4).又因为CE ∥轴,所以点C 与点E 关于抛物线的对称轴对称.因此6、(1)因为BC ∥OA ,所以BC ⊥CD .因为CD =CB =3,所以△BCD 是等腰直角三角形,所以∠BDC =45°,又因为BD ⊥ED ,所以∠ODE =45。
由动点形生成的面积问题面积是平面几何中一个重要的概念,关联着平面图形中的重要元素边与角,由动点而生成的面积问题,是抛物线与直线形结合的觉形式,解决这类问题常用到以下与面积相关的知识(1)图形的割补(2)等积变形(3)等比转化例题1(2010四川宜宾)将直角边长为6的等腰Rt△AOC放在如图所示的平面直角坐标系中,点O为坐标原点,点C、A分别在x、y轴的正半轴上,一条抛物线经过点A、C及点B(–3,0).(1)求该抛物线的解析式;(2)若点P是线段BC上一动点,过点P作AB的平行线交AC于点E,连接AP,当△APE的面积最大时,求点P的坐标;(3)在第一象限内的该抛物线上是否存在点G,使△AGC的面积与(2)中△APE的最大面积相等?若存在,请求出点G的坐标;若不存在,请说明理由例题2(2010 湖北孝感) 如图,已知二次函数图像的顶点坐标为(2,0),直线1+=x y 与二次函数的图像交于A 、B 两点,其中点A 在y 轴上。
(1)二次函数的解析式为y= ;(3分)(2)证明点)12,(--m m 不在(1)中所求的二次函数的图像上;(3分)(3)若C 为线段AB 的中点,过C 点作x CE ⊥轴于E 点,CE 与二次函数的图像交于D点。
①y 轴上存在点K ,使以K 、A 、D 、C 为顶点的四边形是平行四边形,则K 点的坐标是 ;(2分)②二次函数的图像上是否存在点P ,使得ABD PO E S S ∆∆=2?若存在,求出P 点坐标;若不存在,请说明理由。
(4分)例题3(2010 四川自贡)如图,在直角坐标平面内,O为坐标原点,A点的坐标为(1,0),B点在x轴上且在点A的右侧,AB=OA,过点A和B作x轴的垂线分别交二次函数y=x2的图象于点C和D,直线OC交BD于M,直线CD交y轴于点H。
记C、D的横坐标分别为x C,x D,点H的纵坐标y H。
(1)证明:①S△CMD∶S梯形ABMC=2∶3 ②x C·x D=-y H(2)若将上述A点坐标(1,0)改为A点坐标(t,0),t>0,其他条件不变,结论S△CMD:S梯形ABMC=2∶3是否仍成立?请说明理由。
因动点产生的面积问题解题策略一.解题策略解读:面积的存在性问题常见的题型和解题策略有两类:图1 图2 图3 计算面积常用到的策略还有:图4 图5 图6例1.已知抛物线y=mx2+(1-2m)x+1-3m与x轴交于不同的两点A、 B.(1) 求m的取值范围;(2) 证明该抛物线一定经过非坐标轴上的一点P,并求出点P的坐标;(3) 当<m≤8时,由(2)求出的点P和点A、 B构成的△ABP的面积是否有最值,若有,求出最值及相应的m的值;若没有,请说明理由.思路:1. 已知的抛物线的解析式可以因式分解的,抛物线过x轴上的定点(-1, 0).2. 第(2)题分两步,先对m赋予两个不同的值,联立求方程组的解,再验证这个点是确定的.3. 第(3)题中△ABP的高为定值,点A为定点,求△ABP的最大面积,其实就是求点B的横坐标的最大值.例2.问题提出(1) 如图1,已知△ABC,请画出△ABC关于直线AC对称的三角形.问题探究(2) 如图2,在矩形ABCD中,AB=4, AD=6, AE=4, AF=2.是否在边BC、CD上分别存在点G、 H,使得四边形EFGH的周长最小?若存在,求出它周长的最小值;若不存在,请说明理由.问题解决(3) 如图3,有一块矩形板材ABCD, AB=3米, AD=6米,现想从此板材中截出一个面积尽可能大的四边形EFGH部件,使∠EFG=90°,米,∠EHG=45°.经研究,只有当点E、 F、 G分别在边AD、 AB、 BC上时,且AF<BF,并满足点H在矩形ABCD内部或边上时,才有可能截出符合要求的部件.试问能否截得符合要求的面积尽可能大的四边形EFGH部件?若能,求出截得的四边形EFGH 部件的面积;若不能,请说明理由.图1 图2 图3思路:1. 第(2)题的模型是“打台球”两次碰壁问题,依据光的反射原理.2. 第(3)题需先设AF的长并求解,再验证点H在矩形内部,然后计算面积.例3.如图1,在平面直角坐标系中,矩形OCDE的顶点C和E分别在y轴的正半轴和x轴的正半轴上,OC=8, OE=17.抛物线y=x2-3x+m与y轴交于点A,抛物线的对称轴与x轴交于点B,与CD交于点K.(1) 将矩形OCDE沿AB折叠,点O恰好落在边CD上的点F处.①求点F的坐标;②请直接写出抛物线的函数表达式;(2) 将矩形OCDE沿着经过点E的直线折叠,点O恰好落在边CD上的点G处,连结OG,折痕与OG交于点H,点M是线段EH上的一个动点(不与点H重合),连结MG, MO,过点G作GP⊥OM于点P,交EH于点N,连结ON.点M从点E开始沿线段EH向点H运动,至与点N重合时停止,△MOG和△NOG的面积分别表示为S1和S2,在点M的运动过程中,S1·S2(即S1与S2的积)的值是否发生变化?若变化,请直接写出变化的范围;若不变,请直接写出这个值.温馨提示: 考生可以根据题意,在备用图中补充图形,以便作答.图1 备用图思路:1. 第(1)题中点F的位置是由A、 B两点确定的,A、 B两点的坐标都隐含在抛物线的解析式中.2. 第(2)题思路在画示意图过程中,点G是关键点.以E为圆心,EO为半径画弧,交CD于点G.例 4.如图,已知平行四边形ABCD的三个顶点A(n, 0)、 B(m, 0)、 D(0,2n)(m>n>0),作平行四边形ABCD关于直线AD的对称图形AB1C1 D.(1) 若m=3,试求四边形CC1B1B面积S的最大值;(2) 若点B1恰好落在y轴上,试求的值.思路:1. 第(1)题先说理再计算,说理四边形CC1B1B是矩形.2. 第(2)题根据AB1=AB列关于m、 n的方程,整理就可以得到m与n的关系.例5.如图,在平面直角坐标系中,抛物线y=-x2+bx+c经过点A(3, 0)和点B(2, 3),过点A的直线与y轴的负半轴相交于点C,且tan∠CAO=.(1) 求这条抛物线的表达式及对称轴;(2) 连结AB、 BC,求∠ABC的正切值;(3) 若点D在x轴下方抛物线的对称轴上,当S△ABC =S△ADC时,求点D的坐标.解析:1. 直觉告诉我们,△ABC是直角三角形.2. 第(3)题的意思可以表达为: B、 D在直线AC的两侧,到直线AC的距离相等.于是我们容易想到,平行线间的距离处处相等.例6.如图,半圆O的直径AB=10,有一条定长为6的动弦CD在弧AB上滑动(点C、D分别不与点A、 B重合),点E、 F在AB上,EC⊥CD, FD⊥CD.(1) 求证:EO=FO;(2) 连结OC,如果△ECO中有一个内角等于45°,求线段EF的长;(3) 当动弦CD在弧AB上滑动时,设变量CE=x,四边形CDFE的面积为S,周长为l,问:S与l是否分别随着x变化而变化?试用所学过的函数知识直接写出它们的函数解析式及函数定义域,以说明你的结论.思路:1. 用垂径定理和平行线等分线段定理证明点O是EF的中点.2. 第(2)题的△ECO中,∠ECO是定值,45°的角分两种情况.3. 第(3)题用x表示OE的长,在△ECO中,∠ECO是定值.例7.直线y=2x+m与抛物线y=ax2+ax+b都过点M(1, 0),且a<b.(1) 求抛物线顶点Q的坐标(用含a的式子表示);(2) 试说明抛物线与直线有两个交点;(3) 设抛物线与直线的另一个交点为N.①若-1≤a≤-时,求MN的取值范围;②求△QMN的面积最小值.思路:1. 将M(1, 0)分别代入直线和抛物线的解析式,可以确定m的值,用a表示b.2. 联立直线与抛物线的解析式,消去y,得到关于a的一元二次方程,判断Δ>0.3. 第(3)题①,分别求a=-1和a=-时直线与抛物线的交点M、 N的坐标,再求MN的长,两个MN的长,就是MN的取值范围的两端值.例8.已知Rt△EFP和矩形ABCD如图1摆放(点P与点B重合),点F、 B(P)、 C 在同一直线上,AB=EF=6cm, BC=FP=8cm, ∠EFP=90°.如图2, △EFP从图1位置出发,沿BC方向匀速运动,速度为1cm/s, EP与AB交于点G;同时,点Q从点C出发,沿CD方向匀速运动,速度为1cm/s.过点Q作QM⊥BD,垂足为H,交AD于点M,连结AF、 PQ.当点Q停止运动时,△EFP也停止运动.设运动时间为t(s)(0<t<6).解答下列问题:(1) 当t为何值时,PQ∥BD?(2) 设五边形AFPQM的面积为y(cm2),求y与t之间的函数关系式;(3) 在运动过程中,是否存在某一时刻t,使S五边形AFPQM ∶S矩形ABCD=9∶8?若存在,求出t的值;若不存在,请说明理由;(4) 在运动过程中,是否存在某一时刻t,使点M在线段PG的垂直平分线上?若存在,求出t的值;若不存在,请说明理由.图1 图2思路:1. 把线段BP、 PC、 CQ、 DQ的长用t表示出来.再把线段BG、 DM的长用t表示出来.2. 用割补法求五边形AFPQM的面积,等于直角梯形减去两个直角三角形的面积.3. 第(3)题用第(2)题的结果,直接解方程就可以了.4. 第(4)题是根据MP2=MG2列方程,需要构造以MP为斜边的直角三角形.例9.如图1,在平面直角坐标系中,过原点O及点A(8, 0)、 C(0, 6)作矩形OABC,连结OB,点D为OB的中点,点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF.已知点E从点A出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒.(1) 如图1,当t=3时,求DF的长;(2) 如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值;(3) 连结AD,当AD将△DEF分成的两部分的面积比为1∶2时,求相应的t的值.图1 图2思路;1. 作DM⊥AB于M, DN⊥OA于N,那么△NDF与△MDE的相似比为3∶4.2. 面积比为1∶2要分两种情况讨论.把面积比转化为两个同高三角形底边的比.3. 过点E作OA的平行线,构造“8字型”相似,这样就把底边的比利用起来了.例10.如图1,二次函数y=x2+bx+c的图象与x轴交于A、 B两点,与y轴交于点C, OB=OC.点D在函数图象上,CD∥x轴,且CD=2,直线l是抛物线的对称轴,E是抛物线的顶点.(1) 求b、 c的值;(2) 如图1,连结BE,线段OC上点F关于直线l的对称点F'恰好在线段BE上,求点F的坐标;(3) 如图2,动点P在线段OB上,过点P作x轴的垂线分别与BC交于点M,与抛物线交于点N.试问:抛物线上是否存在点Q,使得△PQN与△APM的面积相等,且线段NQ的长度最小?如果存在,求出点Q的坐标;如果不存在,说明理由.图1 图2思路:1. 由已知抛物线的解析式可得C(0, c),再用c表示B、 D两点的坐标,然后将B、 D代入抛物线的解析式列关于b、 c的方程组.2. 第(2)题: 通过点C、 F分别与点D、 F'关于直线l对称,得到点F'是BE的中点,从而求得点F的坐标.3. 第(3)题: 设点P的横坐标为m,用m表示点M、 N的坐标,进而用m表示线段PM、 PN、 PA的长,根据两个三角形的面积相等,求出PN边上的高QH.最后讨论NQ与QH的关系.例11.如图,在平面直角坐标系中,直线y=12x+2与x 轴交于点A,与y 轴交于点C.抛物线y=-x 2+bx+c 经过A 、 C 两点,与x 轴的另一个交点为点B.(1) 求抛物线的函数表达式;(2) 点D 为直线AC 上方抛物线上一动点.① 连结BC 、 CD.设直线BD 交线段AC 于点E, △CDE 的面积为S 1, △BCE 的面积为S 2,求 12S S 的最大值; ② 过点D 作DF ⊥AC,垂足为F,连结CD.是否存在点D,使得△CDF 中的某个角恰好等于∠BAC 的2倍?若存在,求出点D 的坐标;若不存在,请说明理由.图1 备用图思路: 1. △CDE 与△BCE 是同高三角形,面积比等于底边的比.构造“8字型”,把底边的比转化为竖直线段的比.2. 第(3)题的第一种情况∠DCF=2∠BAC,过点C 作x 轴的平行线,通过内错角相等,再作轴对称的角,很容易找到点D 的位置.3. 第(3)题的第二种情况∠CDF=2∠BAC,先要探求2∠BAC的大小(正切值),如果这一步探究不出来,基本上进行不下去.例12.已知Rt△OAB,∠OAB=90°,∠ABO=30°,斜边OB=4,将Rt△OAB绕点O 顺时针旋转60°,如题图1,连接BC.(1)填空:∠OBC= ;(2)如图1,连接AC,作OP⊥AC,垂足为P,求OP的长度;(3)如图2,点M,N同时从点O出发,在△OCB边上运动,M沿O→C→B路径匀速运动,N沿O→B→C路径匀速运动,当两点相遇时运动停止,已知点M的运动速度为1.5单位/秒,点N的运动速度为1单位/秒,设运动时间为x秒,△OMN 的面积为y,求当x为何值时y取得最大值?最大值为多少?思路:(1)由旋转的性质可以证明△OBC是等边三角形,从而可得∠OBC的度数;(2)求出△AOC的面积,利用三角形的面积公式计算即可;(3)分三种情形讨论求解即可解决问题:①当0<x≤83时,M在OC上运动,N在OB上运动,此时过点N作NE⊥OC且交OC于点E,利用面积公式表示出△OMN的面积(y值);②当8 3<x≤4时,M在BC上运动,N在OB上运动.作MH⊥OB于H,利用∠CBO=60°表示出MH,再利用面积公式表示出△OMN的面积(y值);③当4<x≤4.8时,M、N都在BC上运动,作OG⊥BC于G,易求OG,再利用面积公式表示出△OMN的面积(y值),最后分别求出三种情况下面积最大值,从而求出整个运动过程中y的最大值.例13. 在平面直角坐标系中,抛物线2y ax bx c=++交x轴于A、B两点,交y轴于点C(0,43-),OA=1,OB=4,直线l过点A,交y轴于点D,交抛物线于点E,且满足tan∠OAD=34.(1)求抛物线的解析式;(2)动点P从点B出发,沿x轴正方向以每秒2个单位长度的速度向点A运动,动点Q从点A出发,沿射线AE以每秒1个单位长度的速度向点E运动,当点P运动到点A时,点Q也停止运动,设运动为t秒.①在P、Q的运动过程中,是否存在某一时刻t,使得△ADC与△PQA相似,若存在,求出t的值;若不存在,请说明理由;②在P、Q的运动过程中,是否存在某一时刻t,使得△APQ与△CAQ的面积之和最大?若存在,求出t的值;若不存在,请说明理由.思路:本题是代数几何综合题,以平面直角坐标系为背景,考查了求二次函数解析式,二次函数的性质,,方程组的解法,几何图形面积的表示,相似三角形的判定与性质,分类讨论思想,三角形的面积的最值问题,综合性强,难度大,解题的关键是需要学生有良好的运算能力及分析问题和解决问题的能力,还得富有耐心.(1)利用A、B、C三点的坐标确定二次函数的解析式.(2)利用题目的已知条件表示出相关线段的长,①中利用三角函数值探索出∠PAQ=∠ACD,再根据题目中的要求使得△ADC与△PQA相似,进行分类讨论得到对应线段成比例,列出关于t的方程求解即可;②直接利用三角形的面积公式列出△APQ与△CAQ 的面积之和与时间t之间的函数关系式,再将所得的二次函数的解析式配方确定最值即可得到答案.。
二次函数-因动点产生的面积问题例1、如图1,已知抛物线212y x bx c =++(b 、c 是常数,且c <0)与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴的负半轴交于点C ,点A 的坐标为(-1,0).(1)b =______,点B 的横坐标为_______(上述结果均用含c 的代数式表示);(2)连结BC ,过点A 作直线AE //BC ,与抛物线交于点E .点D 是x 轴上一点,坐标为(2,0),当C 、D 、E 三点在同一直线上时,求抛物线的解析式;(3)在(2)的条件下,点P 是x 轴下方的抛物线上的一动点,连结PB 、PC .设△PBC 的面积为S . ①求S 的取值范围;②若△PBC 的面积S 为正整数,则这样的△PBC 共有_____个.图1思路点拨1.用c 表示b 以后,把抛物线的一般式改写为两点式,会发现OB =2OC . 2.当C 、D 、E 三点共线时,△EHA ∽△COB ,△EHD ∽△COD .3.求△PBC 面积的取值范围,要分两种情况计算,P 在BC 上方或下方.4.求得了S 的取值范围,然后罗列P 从A 经过C 运动到B 的过程中,面积的正整数值,再数一数个数.注意排除点A 、C 、B 三个时刻的值. 满分解答(1)b =12c +,点B 的横坐标为-2c . (2)由2111()(1)(2)222y x c x c x x c =+++=++,设E 1(,(1)(2))2x x x c ++.过点E 作EH ⊥x 轴于H .由于OB =2OC ,当AE //BC 时,AH =2EH .所以1(1)(2)x x x c +=++.因此12x c =-.所以(12,1)E c c --. 当C 、D 、E 三点在同一直线上时,EH CO DH DO =.所以1212c cc --=--.整理,得2c 2+3c -2=0.解得c =-2或12c =(舍去). 所以抛物线的解析式为213222y x x =--.(3)①当P 在BC 下方时,过点P 作x 轴的垂线交BC 于F . 直线BC 的解析式为122y x =-. 设213(,2)22P m m m --,那么1(,2)2F m m -,2122FP m m =-+. 所以S △PBC =S △PBF +S △PCF =221()24(2)42B C FP x x FP m m m -==-+=--+.因此当P 在BC 下方时,△PBC 的最大值为4. 当P 在BC 上方时,因为S △ABC =5,所以S △PBC <5. 综上所述,0<S <5.②若△PBC 的面积S 为正整数,则这样的△PBC 共有11个. 考点伸展点P 沿抛物线从A 经过C 到达B 的过程中,△PBC 的面积为整数,依次为(5),4,3,2,1,(0),1,2,3,4,3,2,1,(0).当P 在BC 下方,S =4时,点P 在BC 的中点的正下方,F 是BC 的中点.例 2、如图1,在平面直角坐标系中放置一直角三角板,其顶点为A (0, 1)、B (2, 0)、O (0, 0),将此三角板绕原点O 逆时针旋转90°,得到三角形A ′B ′O .(1)一抛物线经过点A ′、B ′、B ,求该抛物线的解析式;(2)设点P 是第一象限内抛物线上的一个动点,是否存在点P ,使四边形PB ′A ′B 的面积是△A ′B ′O 面积的4倍?若存在,请求出点P 的坐标;若不存在,请说明理由;(3)在(2)的条件下,试指出四边形PB ′A ′B 是哪种形状的四边形?并写出它的两条性质.图1思路点拨1.四边形PB ′A ′B 的面积是△A ′B ′O 面积的4倍,可以转化为四边形PB ′OB 的面积是 △A ′B ′O 面积的3倍.2.联结PO ,四边形PB ′OB 可以分割为两个三角形.3.过点向x 轴作垂线,四边形PB ′OB 也可以分割为一个直角梯形和一个直角三角形. 满分解答(1)△AOB 绕着原点O 逆时针旋转90°,点A ′、B ′的坐标分别为(-1, 0) 、(0, 2). 因为抛物线与x 轴交于A ′(-1, 0)、B (2, 0),设解析式为y =a (x +1)(x -2), 代入B ′(0, 2),得a =1.所以该抛物线的解析式为y =-(x +1)(x -2) =-x 2+x +2. (2)S △A ′B ′O =1.如果S 四边形PB ′A ′B =4 S △A ′B ′O =4,那么S 四边形PB ′OB =3 S △A ′B ′O =3. 如图2,作PD ⊥OB ,垂足为D . 设点P 的坐标为 (x ,-x 2+x +2).232'1111(')(22)22222PB OD S DO B O PD x x x x x x =+=-++=-++梯形. 2321113(2)(2)22222PDBS DB PD x x x x x ∆=⨯=--++=-+. 所以2'''2+2PDB PB A D PB OD S S S x x ∆=+=-+四边形梯形. 解方程-x 2+2x +2=3,得x 1=x 2=1. 所以点P 的坐标为(1,2).图2 图3 图4(3)如图3,四边形PB ′A ′B 是等腰梯形,它的性质有:等腰梯形的对角线相等;等腰梯形同以底上的两个内角相等;等腰梯形是轴对称图形,对称轴是经过两底中点的直线. 考点伸展第(2)题求四边形PB ′OB 的面积,也可以如图4那样分割图形,这样运算过程更简单.'11'222PB O P S B O x x x ∆=⋅=⨯=. 22112(2)222PBOP S BO y x x x x ∆=⋅=⨯-++=-++. 所以2'''2+2PB O PBO PB A D S S S x x ∆∆=+=-+四边形.甚至我们可以更大胆地根据抛物线的对称性直接得到点P :作△A ′OB ′关于抛物线的对称轴对称的△BOE ,那么点E 的坐标为(1,2).而矩形EB ′OD 与△A ′OB ′、△BOP 是等底等高的,所以四边形EB ′A ′B 的面积是△A ′B ′O 面积的4倍.因此点E 就是要探求的点P .例 3、如图1,在平面直角坐标系中,直线112y x =+与抛物线y =ax 2+bx -3交于A 、B 两点,点A 在x 轴上,点B 的纵坐标为3.点P 是直线AB 下方的抛物线上的一动点(不与点A 、B 重合),过点P 作x 轴的垂线交直线AB 于点C ,作PD ⊥AB 于点D .(1)求a 、b 及sin ∠ACP 的值;(2)设点P 的横坐标为m .①用含m 的代数式表示线段PD 的长,并求出线段PD 长的最大值;②连结PB ,线段PC 把△PDB 分成两个三角形,是否存在适合的m 的值,使这两个三角形的面积比为9∶10?若存在,直接写出m 的值;若不存在,请说明理由.图1思路点拨1.第(1)题由于CP //y 轴,把∠ACP 转化为它的同位角. 2.第(2)题中,PD =PC sin ∠ACP ,第(1)题已经做好了铺垫.3.△PCD 与△PCB 是同底边PC 的两个三角形,面积比等于对应高DN 与BM 的比. 4.两个三角形的面积比为9∶10,要分两种情况讨论. 满分解答(1)设直线112y x =+与y 轴交于点E ,那么A (-2,0),B (4,3),E (0,1). 在Rt △AEO 中,OA =2,OE =1,所以5AE =.所以25sin AEO ∠=. 因为PC //EO ,所以∠ACP =∠AEO .因此25sin ACP ∠=将A (-2,0)、B (4,3)分别代入y =ax 2+bx -3,得4230,1643 3.a b a b --=⎧⎨+-=⎩解得12a =,12b =-. (2)由211(,3)22P m m m --,1(,1)2C m m +,得221111(1)(3)42222PC m m m m m =+---=-++.所以2225251595sin 4)1)2PD PC ACP m m m =∠==-++=-+. 所以PD 95. (3)当S △PCD ∶S △PCB =9∶10时,52m =; 当S △PCD ∶S △PCB =10∶9时,329m =.图2考点伸展第(3)题的思路是:△PCD 与△PCB 是同底边PC 的两个三角形,面积比等于对应高DN 与BM 的比. 而252511cos cos 4)(2)(4)25DN PD PDN PD ACP m m m m =∠=∠=-++=-+-, BM =4-m .①当S △PCD ∶S △PCB =9∶10时,19(2)(4)(4)510m m m -+-=-.解得52m =.②当S △PCD ∶S △PCB =10∶9时,110(2)(4)(4)59m m m -+-=-.解得329m =.例 4、如图1,直线l 经过点A (1,0),且与双曲线my x=(x >0)交于点B (2,1).过点(,1)P p p -(p >1)作x 轴的平行线分别交曲线m y x =(x >0)和my x=-(x <0)于M 、N 两点. (1)求m 的值及直线l 的解析式;(2)若点P 在直线y =2上,求证:△PMB ∽△PNA ;(3)是否存在实数p ,使得S △AMN =4S △AMP ?若存在,请求出所有满足条件的p 的值;若不存在,请说明理由.图1思路点拨1.第(2)题准确画图,点的位置关系尽在图形中.2.第(3)题把S △AMN =4S △AMP 转化为MN =4MP ,按照点M 与线段NP 的位置关系分两种情况讨论. 满分解答(1)因为点B (2,1)在双曲线my x=上,所以m =2.设直线l 的解析式为y kx b =+,代入点A (1,0)和点B (2,1),得0,2 1.k b k b +=⎧⎨+=⎩ 解得1,1.k b =⎧⎨=-⎩ 所以直线l 的解析式为1y x =-. (2)由点(,1)P p p -(p >1)的坐标可知,点P 在直线1y x =-上x 轴的上方.如图2,当y =2时,点P 的坐标为(3,2).此时点M 的坐标为(1,2),点N 的坐标为(-1,2).由P (3,2)、M (1,2)、B (2,1)三点的位置关系,可知△PMB 为等腰直角三角形. 由P (3,2)、N (-1,2)、A (1,0)三点的位置关系,可知△PNA 为等腰直角三角形. 所以△PMB ∽△PNA .图2 图3 图4(3)△AMN 和△AMP 是两个同高的三角形,底边MN 和MP 在同一条直线上. 当S △AMN =4S △AMP 时,MN =4MP .①如图3,当M 在NP 上时,x M -x N =4(x P -x M ).因此222()4(1)x x x x ⎛⎫⎛⎫--=-- ⎪ ⎪⎝⎭⎝⎭.解得113x +=或1132x -=(此时点P 在x 轴下方,舍去).此时1132p +=. ②如图4,当M 在NP 的延长线上时,x M -x N =4(x M -x P ).因此222()4(1)x x x x ⎛⎫⎛⎫--=-- ⎪ ⎪⎝⎭⎝⎭.解得152x +=或152x -=(此时点P 在x 轴下方,舍去).此时152p +=.考点伸展在本题情景下,△AMN 能否成为直角三角形?情形一,如图5,∠AMN =90°,此时点M 的坐标为(1,2),点P 的坐标为(3,2). 情形二,如图6,∠MAN =90°,此时斜边MN 上的中线等于斜边的一半. 不存在∠ANM =90°的情况.图5 图6例5、如图1,四边形OABC 是矩形,点A 、C 的坐标分别为(3,0),(0,1).点D 是线段BC 上的动点(与端点B 、C 不重合),过点D 作直线12y x b =-+交折线OAB 于点E . (1)记△ODE 的面积为S ,求S 与b 的函数关系式;(2)当点E 在线段OA 上时,若矩形OABC 关于直线DE 的对称图形为四边形O 1A 1B 1C 1,试探究四边形O 1A 1B 1C 1与矩形OABC 的重叠部分的面积是否发生变化?若不变,求出重叠部分的面积;若改变,请说明理由.图1思路点拨1.数形结合,用b表示线段OE、CD、AE、BE的长.2.求△ODE的面积,要分两种情况.当E在OA上时,OE边对应的高等于OC;当E在AB边上时,要利用割补法求△ODE的面积.3.第(3)题中的重叠部分是邻边相等的平行四边形.4.图形翻着、旋转等运动中,计算菱形的边长一般用勾股定理.满分解答(1)①如图2,当E在OA上时,由12y x b=-+可知,点E的坐标为(2b,0),OE=2b.此时S=S△ODE=112122OE OC b b⋅=⨯⨯=.②如图3,当E在AB上时,把y=1代入12y x b=-+可知,点D的坐标为(2b-2,1),CD=2b-2,BD=5-2b.把x=3代入12y x b=-+可知,点E的坐标为3(3,)2b-,AE=32b-,BE=52b-.此时S=S矩形OABC-S△OAE-S△BDE-S△OCD=1315133()()(52)1(22) 22222b b b b-⨯-----⨯⨯-252b b=-+.(2)如图4,因为四边形O1A1B1C1与矩形OABC关于直线DE对称,因此DM=DN,那么重叠部分是邻边相等的平行四边形,即四边形DMEN是菱形.作DH⊥OA,垂足为H.由于CD=2b-2,OE=2b,所以EH=2.设菱形DMEN的边长为m.在Rt△DEH中,DH=1,NH=2-m,DN=m,所以12+(2-m)2=m2.解得54m=.所以重叠部分菱形DMEN的面积为54.图2 图3 图4考点伸展把本题中的矩形OABC绕着它的对称中心旋转,如果重叠部分的形状是菱形(如图5),那么这个菱形的最小面积为1,如图6所示;最大面积为53,如图7所示.图5 图6 图7例 6、如图1,在△ABC中,∠C=90°,A C=3,BC=4,CD是斜边AB上的高,点E在斜边AB上,过点E作直线与△ABC的直角边相交于点F,设AE=x,△AEF的面积为y.(1)求线段AD的长;(2)若EF⊥AB,当点E在斜边AB上移动时,①求y与x的函数关系式(写出自变量x的取值范围);②当x取何值时,y有最大值?并求出最大值.(3)若点F在直角边AC上(点F与A、C不重合),点E在斜边AB上移动,试问,是否存在直线EF将△ABC的周长和面积同时平分?若存在直线EF,求出x的值;若不存在直线EF,请说明理由.图1 备用图思路点拨1.第(1)题求得的AD 的长,就是第(2)题分类讨论x 的临界点. 2.第(2)题要按照点F 的位置分两种情况讨论.3.第(3)题的一般策略是:先假定平分周长,再列关于面积的方程,根据方程的解的情况作出判断.满分解答(1) 在Rt △ABC 中, AC =3,BC =4,所以AB =5.在Rt △ACD 中,39cos 355AD AC A ==⨯=. (2) ①如图2,当F 在AC 上时,905x <<.在Rt △AEF 中,4tan 3EF AE A x ==.所以21223y AE EF x =⋅=. 如图3,当F 在BC 上时,955x <≤.在Rt △BEF 中,3tan (5)4EF BE B x ==-.所以21315288y AE EF x x =⋅=-+. ②当905x <<时,223y x =的最大值为5425;当955x <≤时,231588y x x =-+23575)8232x =--+(的最大值为7532. 因此,当52x =时,y 的最大值为7532.图2 图3 图4(3)△ABC 的周长等于12,面积等于6.先假设EF 平分△ABC 的周长,那么AE =x ,AF =6-x ,x 的变化范围为3<x ≤5.因此1142sin (6)(6)2255AEF S AE AF A x x x x ∆=⋅⋅=-⨯=--.解方程2(6)35x x --=,得1362x =因为1362x =+3≤x ≤5范围内(如图4),因此存在直线EF 将△ABC 的周长和面积同时平分. 考点伸展如果把第(3)题的条件“点F 在直角边AC 上”改为“点F 在直角边BC 上”,那么就不存在直线EF将△ABC 的周长和面积同时平分.先假设EF 平分△ABC 的周长,那么AE =x ,BE =5-x ,BF =x +1. 因此21133sin (5)(1)(45)22510BEF S BE BF B x x x x ∆=⋅⋅=-+⨯=---. 解方程23(45)310x x ---=.整理,得2450x x -+=.此方程无实数根.例7、如图1,正方形 ABCD 中,点A 、B 的坐标分别为(0,10),(8,4),点C 在第一象限.动点P 在正方形ABCD 的边上,从点A 出发沿A →B →C →D 匀速运动,同时动点Q 以相同速度在x 轴上运动,当P 点到D 点时,两点同时停止运动,设运动的时间为t 秒.(1)当P 点在边AB 上运动时,点Q 的横坐标x (长度单位)关于运动时间t (秒)的函数图象如图2所示,请写出点Q 开始运动时的坐标及点P 运动速度;(2)求正方形边长及顶点C 的坐标;(3)在(1)中当t 为何值时,△OPQ 的面积最大,并求此时P 点的坐标.(4)如果点P 、Q 保持原速度速度不变,当点P 沿A →B →C →D 匀速运动时,OP 与PQ 能否相等,若能,写出所有符合条件的t 的值;若不能,请说明理由.图1 图2思路点拨1.过点B 、C 、P 向x 轴、y 轴作垂线段,就会构造出全等的、相似的直角三角形,出现相等、成比例的线段,用含有t的式子表示这些线段是解题的基础.2.求点C的坐标,为求直线BC、CD的解析式作铺垫,进而为附加题用两点间的距离公式作准备.3.不论点P在AB、BC还是CD上,点P所在的直角三角形的三边比总是3∶4∶5,灵活运用方便解题.4.根据二次函数的解析式求函数的最值时,要注意定义域与对称轴的位置关系.满分解答(1)Q(1,0),点P每秒钟运动1个单位长度.(2)过点B作BE⊥y轴于点E,过点C作x轴的垂线交直线BE于F,交x轴于H.在Rt△ABE中,BE=8,AE=10-4=6,所以AB=10.由△ABE≌△BCF,知BF=AE=4,CF=BE=6.所以EF=8+6=14,CH=8+4=12.因此点C的坐标为(14,12).(3)过点P作PM⊥y轴于M,PN⊥x轴于N.因为PM//BE,所以AP AM MPAB AF BF==,即1068t AM MP==.因此34,55AM t PM t==.于是3410,55PN OM t ON PM t==-==.设△OPQ的面积为S(平方单位),那么2113347(1)(10)52251010S OQ PN t t t t=⋅⋅=+-=-++,定义域为0≤t≤10.因为抛物线开口向下,对称轴为直线476t=,所以当476t=时,△OPQ的面积最大.此时P的坐标为(9415,5310).(4)当53t=或29513t=时, OP与PQ相等.图3 图4考点伸展附加题的一般思路是:点Q的横坐标是点P的横坐标的2倍.先求直线AB、BC、CD的解析式,根据直线的解析式设点P 的坐标,再根据两点间的距离公式列方程PO =PQ .附加题也可以这样解:①如图4,在Rt △AMP 中,设AM =3m ,MP =4 m ,AP =5m ,那么OQ =8m .根据AP 、OQ 的长列方程组5,81,m t m t =⎧⎨=+⎩解得53t =. ②如图5,在Rt △GMP 中,设GM =3m ,MP =4 m ,GP =5m ,那么OQ =8m .在Rt △GAD 中,GD =7.5.根据GP 、OQ 的长列方程组537.5,81,m t m t =-⎧⎨=+⎩解得29513t =.③如图6,设MP =4m ,那么OQ =8m .根据BP 、OQ 的长列方程组51010,81,m t m t -=-⎧⎨=+⎩解得53t =,但这时点P 不在BC 上.图5 图6。
1.6 因动点产生的面积问题例1 2013年苏州市中考第29题如图1,已知抛物线212y x bx c =++(b 、c 是常数,且c <0)与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴的负半轴交于点C ,点A 的坐标为(-1,0).(1)b =______,点B 的横坐标为_______(上述结果均用含c 的代数式表示);(2)连结BC ,过点A 作直线AE //BC ,与抛物线交于点E .点D 是x 轴上一点,坐标为(2,0),当C 、D 、E 三点在同一直线上时,求抛物线的解析式;(3)在(2)的条件下,点P 是x 轴下方的抛物线上的一动点,连结PB 、PC .设△PBC 的面积为S .①求S 的取值范围;②若△PBC 的面积S 为正整数,则这样的△PBC 共有_____个.图1满分解答(1)b =12c +,点B 的横坐标为-2c . (2)由2111()(1)(2)222y x c x c x x c =+++=++,设E 1(,(1)(2))2x x x c ++.过点E 作EH ⊥x 轴于H .由于OB =2OC ,当AE //BC 时,AH =2EH .所以1(1)(2)x x x c +=++.因此12x c =-.所以(12,1)E c c --.当C 、D 、E 三点在同一直线上时,EH CO DH DO =.所以1212c cc --=--. 整理,得2c 2+3c -2=0.解得c =-2或12c =(舍去).所以抛物线的解析式为213222y x x =--.(3)①当P 在BC 下方时,过点P 作x 轴的垂线交BC 于F . 直线BC 的解析式为122y x =-. 设213(,2)22P m m m --,那么1(,2)2F m m -,2122FP m m =-+. 所以S △PBC =S △PBF +S △PCF =221()24(2)42B C FP x x FP m m m -==-+=--+.因此当P 在BC 下方时,△PBC 的最大值为4.当P 在BC 上方时,因为S △ABC =5,所以S △PBC <5. 综上所述,0<S <5.②若△PBC 的面积S 为正整数,则这样的△PBC 共有11个.考点伸展点P 沿抛物线从A 经过C 到达B 的过程中,△PBC 的面积为整数,依次为(5),4,3,2,1,(0),1,2,3,4,3,2,1,(0).当P 在BC 下方,S =4时,点P 在BC 的中点的正下方,F 是BC 的中点.例 2 2012年菏泽市中考第21题如图1,在平面直角坐标系中放置一直角三角板,其顶点为A (0, 1)、B (2, 0)、O (0, 0),将此三角板绕原点O 逆时针旋转90°,得到三角形A ′B ′O .(1)一抛物线经过点A ′、B ′、B ,求该抛物线的解析式;(2)设点P 是第一象限内抛物线上的一个动点,是否存在点P ,使四边形PB ′A ′B 的面积是△A ′B ′O 面积的4倍?若存在,请求出点P 的坐标;若不存在,请说明理由;(3)在(2)的条件下,试指出四边形PB ′A ′B 是哪种形状的四边形?并写出它的两条性质.图1满分解答(1)△AOB 绕着原点O 逆时针旋转90°,点A ′、B ′的坐标分别为(-1, 0) 、(0, 2). 因为抛物线与x 轴交于A ′(-1, 0)、B (2, 0),设解析式为y =a (x +1)(x -2), 代入B ′(0, 2),得a =1.所以该抛物线的解析式为y =-(x +1)(x -2) =-x 2+x +2. (2)S △A ′B ′O =1.如果S 四边形PB ′A ′B =4 S △A ′B ′O =4,那么S 四边形PB ′OB =3 S △A ′B ′O =3. 如图2,作PD ⊥OB ,垂足为D . 设点P 的坐标为 (x ,-x 2+x +2).232'1111(')(22)22222PB OD S DO B O PD x x x x x x =+=-++=-++梯形. 2321113(2)(2)22222PDBS DB PD x x x x x ∆=⨯=--++=-+. 所以2'''2+2PDB PB A D PB OD S S S x x ∆=+=-+四边形梯形. 解方程-x 2+2x +2=3,得x 1=x 2=1.所以点P 的坐标为(1,2).图2 图3 图4(3)如图3,四边形PB ′A ′B 是等腰梯形,它的性质有:等腰梯形的对角线相等;等腰梯形同以底上的两个内角相等;等腰梯形是轴对称图形,对称轴是经过两底中点的直线.考点伸展第(2)题求四边形PB ′OB 的面积,也可以如图4那样分割图形,这样运算过程更简单.'11'222PB O P S B O x x x ∆=⋅=⨯=. 22112(2)222PBOP S BO y x x x x ∆=⋅=⨯-++=-++. 所以2'''2+2PB O PBO PB A D S S S x x ∆∆=+=-+四边形.甚至我们可以更大胆地根据抛物线的对称性直接得到点P :作△A ′OB ′关于抛物线的对称轴对称的△BOE ,那么点E 的坐标为(1,2).而矩形EB ′OD 与△A ′OB ′、△BOP 是等底等高的,所以四边形EB ′A ′B 的面积是△A ′B ′O 面积的4倍.因此点E 就是要探求的点P .例 3 2012年河南省中考第23题如图1,在平面直角坐标系中,直线112y x =+与抛物线y =ax 2+bx -3交于A 、B 两点,点A 在x 轴上,点B 的纵坐标为3.点P 是直线AB 下方的抛物线上的一动点(不与点A 、B 重合),过点P 作x 轴的垂线交直线AB 于点C ,作PD ⊥AB 于点D .(1)求a 、b 及sin ∠ACP 的值; (2)设点P 的横坐标为m .①用含m 的代数式表示线段PD 的长,并求出线段PD 长的最大值;②连结PB ,线段PC 把△PDB 分成两个三角形,是否存在适合的m 的值,使这两个三角形的面积比为9∶10?若存在,直接写出m 的值;若不存在,请说明理由.图1满分解答(1)设直线112y x =+与y 轴交于点E ,那么A (-2,0),B (4,3),E (0,1). 在Rt △AEO 中,OA =2,OE =1,所以5AE =.所以25sin 5AEO ∠=. 因为PC //EO ,所以∠ACP =∠AEO .因此25sin 5ACP ∠=. 将A (-2,0)、B (4,3)分别代入y =ax 2+bx -3,得4230,1643 3.a b a b --=⎧⎨+-=⎩解得12a =,12b =-. (2)由211(,3)22P m m m --,1(,1)2C m m +,得221111(1)(3)42222PC m m m m m =+---=-++.所以2225251595sin (4)(1)55255PD PC ACP PC m m m =∠==-++=--+. 所以PD 的最大值为955. (3)当S △PCD ∶S △PCB =9∶10时,52m =; 当S △PCD ∶S △PCB =10∶9时,329m =.图2考点伸展第(3)题的思路是:△PCD 与△PCB 是同底边PC 的两个三角形,面积比等于对应高DN 与BM 的比.而252511cos cos (4)(2)(4)5525DN PD PDN PD ACP m m m m =∠=∠=⨯-++=-+-,BM =4-m .①当S △PCD ∶S △PCB =9∶10时,19(2)(4)(4)510m m m -+-=-.解得52m =.②当S △PCD ∶S △PCB =10∶9时,110(2)(4)(4)59m m m -+-=-.解得329m =.例 4 2011年南通市中考第28题如图1,直线l 经过点A (1,0),且与双曲线my x=(x >0)交于点B (2,1).过点(,1)P p p -(p >1)作x 轴的平行线分别交曲线m y x =(x >0)和my x=-(x <0)于M 、N 两点.(1)求m 的值及直线l 的解析式;(2)若点P 在直线y =2上,求证:△PMB ∽△PNA ;(3)是否存在实数p ,使得S △AMN =4S △AMP ?若存在,请求出所有满足条件的p 的值;若不存在,请说明理由.图1满分解答(1)因为点B (2,1)在双曲线my x=上,所以m =2.设直线l 的解析式为y kx b =+,代入点A (1,0)和点B (2,1),得0,2 1.k b k b +=⎧⎨+=⎩ 解得1,1.k b =⎧⎨=-⎩ 所以直线l 的解析式为1y x =-. (2)由点(,1)P p p -(p >1)的坐标可知,点P 在直线1y x =-上x 轴的上方.如图2,当y =2时,点P 的坐标为(3,2).此时点M 的坐标为(1,2),点N 的坐标为(-1,2).由P (3,2)、M (1,2)、B (2,1)三点的位置关系,可知△PMB 为等腰直角三角形. 由P (3,2)、N (-1,2)、A (1,0)三点的位置关系,可知△PNA 为等腰直角三角形. 所以△PMB ∽△PNA .图2 图3 图4(3)△AMN 和△AMP 是两个同高的三角形,底边MN 和MP 在同一条直线上. 当S △AMN =4S △AMP 时,MN =4MP .①如图3,当M 在NP 上时,x M -x N =4(x P -x M ).因此222()4(1)x x x x ⎛⎫⎛⎫--=-- ⎪ ⎪⎝⎭⎝⎭.解得1132x +=或1132x -=(此时点P 在x 轴下方,舍去).此时1132p +=. ②如图4,当M 在NP 的延长线上时,x M -x N =4(x M -x P ).因此222()4(1)x x x x ⎛⎫⎛⎫--=-- ⎪ ⎪⎝⎭⎝⎭.解得152x +=或152x -=(此时点P 在x 轴下方,舍去).此时152p +=.考点伸展在本题情景下,△AMN 能否成为直角三角形?情形一,如图5,∠AMN =90°,此时点M 的坐标为(1,2),点P 的坐标为(3,2). 情形二,如图6,∠MAN =90°,此时斜边MN 上的中线等于斜边的一半. 不存在∠ANM =90°的情况.图5 图6例5 2010年广州市中考第25题如图1,四边形OABC 是矩形,点A 、C 的坐标分别为(3,0),(0,1).点D 是线段BC 上的动点(与端点B 、C 不重合),过点D 作直线12y x b =-+交折线OAB 于点E . (1)记△ODE 的面积为S ,求S 与b 的函数关系式; (2)当点E 在线段OA 上时,若矩形OABC 关于直线DE 的对称图形为四边形O 1A 1B 1C 1,试探究四边形O 1A 1B 1C 1与矩形OABC 的重叠部分的面积是否发生变化?若不变,求出重叠部分的面积;若改变,请说明理由.图满分解答(1)①如图2,当E 在OA 上时,由12y x b =-+可知,点E 的坐标为(2b ,0),OE =2b .此时S =S △ODE =112122OE OC b b ⋅=⨯⨯=. ②如图3,当E 在AB 上时,把y =1代入12y x b =-+可知,点D 的坐标为(2b -2,1),CD =2b -2,BD =5-2b .把x =3代入12y x b =-+可知,点E 的坐标为3(3,)2b -,AE=32b -,BE =52b -.此时S =S 矩形OABC -S △OAE - S △BDE -S △OCD=1315133()()(52)1(22)22222b b b b -⨯-----⨯⨯- 252b b =-+.(2)如图4,因为四边形O 1A 1B 1C 1与矩形OABC 关于直线DE 对称,因此DM =DN ,那么重叠部分是邻边相等的平行四边形,即四边形DMEN 是菱形.作DH ⊥OA ,垂足为H .由于CD =2b -2,OE =2b ,所以EH =2.设菱形DMEN 的边长为m .在Rt △DEH 中,DH =1,NH =2-m ,DN =m ,所以12+(2-m )2=m 2.解得54m =.所以重叠部分菱形DMEN 的面积为54.图2 图3 图4考点伸展把本题中的矩形OABC 绕着它的对称中心旋转,如果重叠部分的形状是菱形(如图5),那么这个菱形的最小面积为1,如图6所示;最大面积为53,如图7所示.图5 图6 图7例 6 2010年扬州市中考第28题如图1,在△ABC 中,∠C =90°,A C =3,BC =4,CD 是斜边AB 上的高,点E 在斜边AB 上,过点E 作直线与△ABC 的直角边相交于点F ,设AE =x ,△AEF 的面积为y .(1)求线段AD 的长;(2)若EF ⊥AB ,当点E 在斜边AB 上移动时,①求y 与x 的函数关系式(写出自变量x 的取值范围); ②当x 取何值时,y 有最大值?并求出最大值.(3)若点F 在直角边AC 上(点F 与A 、C 不重合),点E 在斜边AB 上移动,试问,是否存在直线EF 将△ABC 的周长和面积同时平分?若存在直线EF ,求出x 的值;若不存在直线EF ,请说明理由.图1 备用图满分解答(1) 在Rt △ABC 中, AC =3,BC =4,所以AB =5.在Rt △ACD 中,39cos 355AD AC A ==⨯=.(2) ①如图2,当F 在AC 上时,905x <<.在Rt △AEF 中,4tan 3EF AE A x ==.所以21223y AE EF x =⋅=. 如图3,当F 在BC 上时,955x <≤.在Rt △BEF 中,3tan (5)4EF BE B x ==-.所以21315288y AE EF x x =⋅=-+. ②当905x <<时,223y x =的最大值为5425;当955x <≤时,231588y x x =-+23575)8232x =--+(的最大值为7532. 因此,当52x =时,y 的最大值为7532.图2 图3 图4(3)△ABC 的周长等于12,面积等于6.先假设EF 平分△ABC 的周长,那么AE =x ,AF =6-x ,x 的变化范围为3<x ≤5.因此1142sin (6)(6)2255AEF S AE AF A x x x x ∆=⋅⋅=-⨯=--.解方程2(6)35x x --=,得1362x =±. 因为1362x =+在3≤x ≤5范围内(如图4),因此存在直线EF 将△ABC 的周长和面积同时平分.考点伸展如果把第(3)题的条件“点F 在直角边AC 上”改为“点F 在直角边BC 上”,那么就不存在直线EF 将△ABC 的周长和面积同时平分.先假设EF 平分△ABC 的周长,那么AE =x ,BE =5-x ,BF =x +1.因此21133sin (5)(1)(45)22510BEF S BE BF B x x x x ∆=⋅⋅=-+⨯=---. 解方程23(45)310x x ---=.整理,得2450x x -+=.此方程无实数根.例7 2009年兰州市中考第29题如图1,正方形 ABCD 中,点A 、B 的坐标分别为(0,10),(8,4),点C 在第一象限.动点P 在正方形ABCD 的边上,从点A 出发沿A →B →C →D 匀速运动,同时动点Q 以相同速度在x 轴上运动,当P 点到D 点时,两点同时停止运动,设运动的时间为t 秒.(1)当P 点在边AB 上运动时,点Q 的横坐标x (长度单位)关于运动时间t (秒)的函数图象如图2所示,请写出点Q 开始运动时的坐标及点P 运动速度;(2)求正方形边长及顶点C 的坐标;(3)在(1)中当t 为何值时,△OPQ 的面积最大,并求此时P 点的坐标.(4)如果点P 、Q 保持原速度速度不变,当点P 沿A →B →C →D 匀速运动时,OP 与PQ 能否相等,若能,写出所有符合条件的t 的值;若不能,请说明理由.图1 图2满分解答(1)Q (1,0),点P 每秒钟运动1个单位长度.(2)过点B 作BE ⊥y 轴于点E ,过点C 作x 轴的垂线交直线BE 于F ,交x 轴于H . 在Rt △ABE 中,BE =8,AE =10-4=6,所以AB =10.由△ABE ≌△BCF ,知BF =AE =4,CF =BE =6.所以EF =8+6=14,CH =8+4=12.因此点C 的坐标为(14,12).(3)过点P 作PM ⊥y 轴于M ,PN ⊥x 轴于N .因为PM //BE ,所以AP AM MPAB AF BF==,即1068t AM MP ==.因此34,55AM t PM t ==.于是3410,55PN OM t ON PM t ==-==. 设△OPQ 的面积为S (平方单位),那么2113347(1)(10)52251010S OQ PN t t t t =⋅⋅=+-=-++,定义域为0≤t ≤10.因为抛物线开口向下,对称轴为直线476t =,所以当476t =时,△OPQ 的面积最大.此时P 的坐标为(9415,5310). (4)当53t =或29513t =时, OP 与PQ 相等.图3 图4考点伸展附加题的一般思路是:点Q 的横坐标是点P 的横坐标的2倍.先求直线AB 、BC 、CD 的解析式,根据直线的解析式设点P 的坐标,再根据两点间的距离公式列方程PO =PQ .附加题也可以这样解:①如图4,在Rt △AMP 中,设AM =3m ,MP =4 m ,AP =5m ,那么OQ =8m .根据AP 、OQ 的长列方程组5,81,m t m t =⎧⎨=+⎩解得53t =.②如图5,在Rt △GMP 中,设GM =3m ,MP =4 m ,GP =5m ,那么OQ =8m .在Rt △GAD 中,GD =7.5.根据GP 、OQ 的长列方程组537.5,81,m t m t =-⎧⎨=+⎩解得29513t =.③如图6,设MP =4m ,那么OQ =8m .根据BP 、OQ 的长列方程组51010,81,m t m t -=-⎧⎨=+⎩解得53t ,但这时点P不在BC上.例9 2011年上海市松江区中考模拟第24题如图1,在平面直角坐标系xOy中,直角梯形OABC的顶点O为坐标原点,顶点A、C 分别在x轴、y轴的正半轴上,CB∥OA,OC=4,BC=3,OA=5,点D在边OC上,CD =3,过点D作DB的垂线DE,交x轴于点E.(1)求点E的坐标;(2)二次函数y=-x2+bx+c的图象经过点B和点E.①求二次函数的解析式和它的对称轴;②如果点M在它的对称轴上且位于x轴上方,满足S△CEM=2S△ABM,求点M的坐标.图1动感体验请打开几何画板文件名“11松江24”,拖动点M在抛物线的对称轴上运动,观察面积比的度量值,可以体验到,有两个时刻,面积的比值等于2.思路点拨1.这三道题目步步为赢,错一道题目,就要影响下一道的计算.2.点M 在抛物线的对称轴上且位于x 轴上方,要分两种情况讨论,分别为点M 在线段FB 和FB 的延长线上.因为用点M 的纵坐标表示△ABM 的底边长,因点M 的位置不同而不同.满分解答(1)因为BC ∥OA ,所以BC ⊥CD .因为CD =CB =3,所以△BCD 是等腰直角三角形.因此∠BCD =45°.又因为BC ⊥CD ,所以∠ODE =45°.所以△ODE 是等腰直角三角形,OE =OD =1.所以点E 的坐标是(1,0).(2)①因为抛物线y =-x 2+bx +c 经过点B (3,4)和点E (1,0),所以934,10.b c b c -++=⎧⎨-++=⎩解得6,5.b c =⎧⎨=-⎩所以二次函数的解析式为y =-x 2+6x -5,抛物线的对称轴为直线x =3.②如图2,如图3,设抛物线的对称轴与x 轴交于点F ,点M 的坐标为(3,t ).CEM MEF COE OFMC S S S S ∆∆∆=--梯形111(4)321442222tt t =+⨯-⨯⨯-⨯⨯=+. (ⅰ)如图2,当点M 位于线段BF 上时,t t S ABM -=⨯-=∆42)4(21.解方程)4(242t t -=+,得58=t .此时点M 的坐标为(3,58). (ⅱ)如图3,当点M 位于线段FB 延长线上时,42)4(21-=⨯-=∆t t S ABM .解方程)4(242-=+t t,得8=t .此时点M 的坐标为(3,8).图2 图3考点伸展对于图2,还有几个典型结论:此时,C 、M 、A 三点在同一条直线上;△CEM 的周长最小.可以求得直线AC 的解析式为445y x =-+,当x =3时,85y =.因此点M (3,58)在直线AC 上. 因为点A 、E 关于抛物线的对称轴对称,所以ME +MC =MA +MC . 当A 、M 、C 三点共线时,ME +MC 最小,△CEM 的周长最小.在△ABC 中,∠C =90°,AC =3,BC =4,CD 是斜边AB 上的高,点E 在斜边AB 上,过点E 作直线与△ABC 的直角边相交于点F ,设AE =x ,△AEF 的面积为y . (1)求线段AD 的长;(2)若EF ⊥AB ,当点E 在线段AB 上移动时,①求y 与x 的函数关系式(写出自变量x 的取值范围) ②当x 取何值时,y 有最大值?并求其最大值;(3)若F 在直角边AC 上(点F 与A 、C 两点均不重合),点E 在斜边AB 上移动,试问:是否存在直线EF 将△ABC 的周长和面积同时平分?若存在直线EF ,求出x 的值;若不存在直线EF ,请说明理由.。