波动之波的叠加原理动画

波动学中的波的衍射与波的叠加知识点总结波动学是物理学的一个重要分支，在其中，波的衍射与波的叠加是两个基本概念。

波的衍射是指波在遇到障碍物或开口时发生弯曲、扩散的现象，而波的叠加则是指两个或多个波在空间中相遇并叠加形成新的波的现象。

本文将对这两个知识点进行总结。

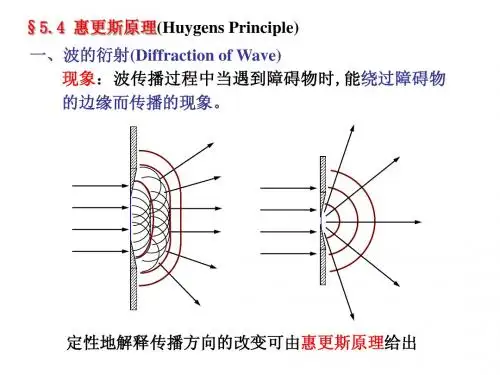
一、波的衍射1. 衍射现象波的衍射是互相干涉的结果，在遇到障碍物或开口时，波将弯曲、扩散并在障碍物后方形成特定的衍射图案。

衍射现象证明了波动的传播特性。

2. 衍射的条件波的衍射需要满足以下条件：a) 波长与障碍物（或开口）的大小相当，即波的大小与障碍物（或开口）的大小相比非常小。

b) 波遇到的障碍物（或开口）的边缘不光滑。

c) 波在障碍物（或开口）附近经过衍射后会扩散到整个区域。

3. 衍射公式衍射的数学描述可以通过衍射公式来完成，常见的衍射公式有菲涅尔衍射公式、夫琅禾费衍射公式等。

这些公式能够准确计算出衍射现象的衍射角、衍射图案等。

二、波的叠加1. 叠加原理波的叠加原理是指当两个或多个波在同一空间相遇时，它们会按照各自的振幅和相位相加形成一个新的波。

叠加可以是构造干涉现象和衍射现象的基础。

2. 干涉现象干涉是指两个或多个波在空间中相遇并干涉形成干涉图案的现象。

常见的干涉现象包括干涉条纹和干涉环。

干涉的结果可以是增强波的振幅，也可以是减弱甚至相互抵消。

3. 叠加的数学表达波的叠加可以通过波函数的相加来描述，根据波函数的性质，可以使用复数或矢量形式进行叠加计算。

叠加计算可以考虑波的振幅、相位和频率等因素。

三、波的衍射与波的叠加的关系波的衍射与波的叠加密切相关，二者相互影响。

1. 波的衍射可以看作波的叠加的结果，当波遇到障碍物或开口时，波的各个部分会发生干涉叠加形成特定的衍射图案。

2. 波的叠加可以导致干涉现象，当波的振幅和相位相加时，产生干涉效应，形成明暗相间的条纹或环。

综上所述，波动学中的波的衍射与波的叠加是两个重要的概念。

波的衍射是波遇到障碍物或开口时发生的弯曲、扩散现象，而波的叠加是两个或多个波在空间中相遇并按照振幅和相位相加形成新的波的现象。

波的干涉为什么两个波会相互叠加或相消波的干涉现象是波动学中一个重要的现象，它指的是当两个或多个波传播至同一空间时，它们会相互影响并产生叠加或相消的现象。

为了解释为什么会出现这种现象，我们首先需要了解波的性质和波的干涉原理。

一、波的性质波是物质或能量在空间中传递的一种震动或摆动，常见的波有机械波和电磁波。

波具有以下性质：1. 波动性：波传播时会出现周期性的振动或摆动；2. 传播性：波能够在空间中传递；3. 叠加性：两个或多个波在同一空间相遇时，能够相互叠加或相消。

二、波的干涉现象波的干涉可以分为构造干涉和破坏干涉两种情况。

1. 构造干涉构造干涉是指两个波叠加形成干涉条纹的现象。

当两个波处于相位差为整数倍的状态时，它们会相互叠加，使得波的振幅增强，形成明亮的干涉条纹。

这被称为构造干涉。

构造干涉遵循叠加原理，即两个波的振幅代数和等于两个波的单独振幅之和。

2. 破坏干涉破坏干涉是指两个波叠加导致波的振幅减弱、消失或相消的现象。

当两个波处于相位差为半整数倍的状态时，它们会相互抵消，使得波的振幅减弱甚至消失，形成暗淡或消失的干涉条纹。

这被称为破坏干涉。

三、波的干涉原理波的干涉现象可以通过波的叠加原理和相位差来解释。

1. 波的叠加原理波的叠加原理是指两个或多个波在同一空间中相遇时，它们会按照叠加原理进行相互叠加或相消。

叠加原理表明，波的振幅代数和等于两个波的单独振幅之和。

在干涉现象中，当两个波的振幅相加时，形成明亮的干涉条纹；当两个波的振幅相消时，形成暗淡或消失的干涉条纹。

2. 相位差相位差是波的两个波峰或两个波谷之间的相位角的差值。

相位差的大小决定了两个波的干涉结果。

当两个波的相位差是整数倍时，它们会相互叠加，形成明亮的干涉条纹；当两个波的相位差是半整数倍时，它们会相互抵消，形成暗淡或消失的干涉条纹。

通过控制波的振幅、频率和相位差，我们可以实现对干涉现象的调控和利用。

波的干涉现象在实际应用中有许多重要的应用，如光的干涉在干涉仪、激光干涉测量等领域的应用。

§6-4 关于波动的基本概念一、波的产生和传播弹性介质和波源——机械波产生的条件弹性介质是指由弹性力组合的连续介质。

波源处质点的振动通过弹性介质中的弹性力将振动传播开去，从而形成机械波。

波动(wave) (或行波)是振动状态的传播，是能量的传播，而不是质点的传播。

二、横波(transverse wave)和纵波(longitudinal wave)横波——参与波动的质点的振动方向与波的传播方向相垂直的波，如电磁波。

纵波——参与波动的质点的振动方向与波的传播方向相平行的波，如声波。

任一波，例如：水波、地表波，都能分解为横波与纵波来进行研究。

三、波线和波面波线(wave ray)（或波射线）——从波源沿各传播方向所画的带箭头的线。

波面(wave surface)（或相面、波阵面）——波在传播过程中，所有振动相位相同的点球面波，平面波在各向同性的均匀介质中，波线与波面垂直。

四、波速、波长以及波的周期和频率波速u ：单位时间内振动传播的距离，也就是波面 向前推进的速率。

固体中横波的波速 ρG u =(G 为切变模量，ρ为密度) 固体中纵波的波速 ρY u =(Y 为杨氏模量)流体中纵波的波速 ρBu =B 为体变模 量，定义为 V p B ∆∆-=波长λ：沿同一波线上相位差为2p 的两个相邻质 点间的距离。

横波：波长等于两相邻波峰之间或相邻波谷之间的距离。

纵波：波长等于两相邻密部之间或相邻疏部之间的距离。

周期T ：一个完整的波(即一个波长的波)通过波线 上某点所需要的时间。

频率ν：单位时间内通过波线上某点完整波的数目。

关系： T 1=νTu λνλ==五、波动所遵从的基本原理1. 波的叠加原理两列或两列以上的波可以互不影响地同时通过某一区域；在相遇区域内共同在某质点引起的振动，是各列波单独在该质点所引起的振动的合成。

2. 惠更斯原理波所到之处各点，都可以看作是发射子波的波源，在以后任一时刻，这些子波的包络就是波在该时刻的波面。

波的叠加两个或多个波在空间中相遇时会叠加形成新的波动形态波的叠加：两个或多个波在空间中相遇时会叠加形成新的波动形态波动现象是物理学中的重要研究领域，而波的叠加则是其中一个重要的现象。

当两个或多个波在空间中相遇时，它们会进行叠加运算，形成新的波动形态。

本文将探讨波的叠加现象及其基本原理，并举例说明其在实际生活和科学研究中的应用。

波的基本概念在介绍波的叠加前，我们先来了解一下波的基本概念。

波是指能量、信息等沿着介质传播的过程，常见的波包括水波、声波、光波等。

波具有振幅、频率、波长等特性，可以通过数学函数来描述其形态和运动规律。

波的叠加原理波的叠加原理是指当两个或多个波在空间中相遇时，它们会进行叠加运算，形成新的波动形态。

具体而言，如果两个波在同一位置的振动方向相同且振幅相等，那么它们将进行叠加，形成更大的振幅；如果两个波在同一位置的振动方向相反且振幅相等，那么它们将进行叠加，形成完全相消的状态。

叠加的结果可以通过波的干涉和波的衍射等现象进行观察。

当两个波的叠加使得振幅增大时，称为构成干涉；当两个波的叠加使得振幅减小或完全消失时，称为构成衍射。

干涉和衍射是波动现象的重要现象，它们广泛应用于各个领域，如光学、声学等。

波的叠加应用举例波的叠加现象在科学研究和实际生活中具有广泛的应用。

以下是两个例子：1. 光干涉光干涉是波的叠加原理在光学中的应用。

当两束光线同时照射到一个光学元件上时，它们会进行叠加运算。

如果两束光线的相位差满足一定条件，就会形成明暗相间的干涉条纹，这就是干涉现象。

干涉条纹的形态和光学元件的性质有关，通过观察干涉条纹的变化，可以研究和测量光学元件的特性。

2. 声音叠加在音乐演奏或者声学研究中，听众经常会听到许多乐器或者声源同时发出的声音。

这些声音在空间中相遇时会进行叠加运算，形成新的声音效果。

如果声波的频率和幅度相同，它们将会增强彼此的音量；如果声波的频率相同但振幅相反，它们将会相互抵消，产生沉寂的效果。