变径圆弧螺旋线

每一页得曲线类型如下:ﻫ第1页：碟形弹簧、葉形线、螺旋线（Hｅｌicaｌ curve）、蝴蝶曲线与渐开线;ﻫ第２页：螺旋线、对数曲线、球面螺旋线、双弧外摆线与星行线;ﻫ第3页：心脏线、圆内螺旋线、正弦曲线、太阳线与费马曲线（有点像螺纹线）；第4页：Taｌbot 曲线、４叶线、Ｒhodoneａ曲线、抛物线与螺旋线；第5页:三叶线、外摆线、Lisｓａｊoｕs 曲线、长短幅圆内旋轮线与长短幅圆外旋轮线;第6页：三尖瓣线、概率曲线、箕舌线、阿基米德螺线与对数螺线；ﻫ第7页：蔓叶线、taｎ曲线、双曲余弦、双曲正弦与双曲正切；第8页:一峰三驻点曲线、八字曲线、螺旋曲线、圆与封闭球形环绕曲线；第9页：柱坐标螺旋曲线、蛇形曲线、８字形曲线、椭圆曲线与梅花曲线;ﻫ第10页：花曲线、空间感更强得花曲线、螺旋上升得椭圆线、螺旋花曲线与鼓形线;第11页：长命锁曲线、簪形线、螺旋上升曲线、蘑菇曲线与8字曲线;第１2页：梅花曲线、桃形曲线、碟形弹簧、环形二次曲线与蝶线；ﻫ第１3页：正弦周弹簧、环形螺旋线、内接弹簧、多变内接式弹簧与柱面正弦波线；ﻫ第1４页：ufo(漩涡线)手把曲线、篮子、圆柱齿轮齿廓得渐开线方程与对数螺旋曲线;ﻫ第１5页：罩形线、向日葵线、太阳线、塔形螺旋线与花瓣线;ﻫ第1６页:双元宝线、阿基米德螺线得变形、渐开线方程、双鱼曲线与蝴蝶结曲线;ﻫ第1７页：“两相望”曲线、小蜜蜂、弯月、热带鱼与燕尾剪；第18页：天蚕丝、心电图、变化后得星形线、小白兔与大家好；ﻫ第１9页:蛇形线、五环、蜘蛛网、次声波与十字渐开线；ﻫ第２0页：内五环与蜗轨线;1、碟形弹簧圓柱坐标方程：r = 5ｔheｔａ＝ t*3600 ﻫz =（ｓｉn(３、5＊thetａ-９０））+24*ｔ2、葉形线、ﻫ笛卡儿坐標标方程:a=10x=3＊ａ*ｔ/(1+（t^3）) ﻫy=3*a＊(t^２）/(1+(t^３）)３、螺旋线(Heｌicａl ｃurvｅ)圆柱坐标（cylindｒｉcal）ﻫ方程: r=t ﻫｔhｅta＝10+t*(20＊3６０）ﻫｚ=t＊３4、蝴蝶曲线球坐标ﻫ方程：rho = 8 * ｔﻫtheta ＝３60 ＊ t ＊ 4pｈｉ = —３60 ＊ t * 8５、渐开线ﻫ采用笛卡尔坐标系方程：r=1 ﻫａng=３６0＊t ﻫs=2＊pi*r＊tx0=s*cos（aｎｇ）ﻫy0=s*sin（ang) ﻫｘ=x0＋s＊sｉn（ang) ﻫｙ=y0-s＊coｓ（ａnｇ) z＝06、螺旋线、笛卡儿坐标方程：x = 4 * ｃos （ t *（5＊360））ﻫｙ = 4 * sin （ t *(５＊360））z = 10*ｔ7、对数曲线笛卡尔坐标系方程：z=０ｘ = 10＊ｔﻫｙ = lｏg（10*t＋0、０001）8、球面螺旋线ﻫ采用球坐标系ﻫ方程:rｈｏ＝4thｅta＝t＊180phｉ=t*36０＊2０9、双弧外摆线卡迪尔坐标ﻫ方程： l=２、5 ﻫb=２、5 ﻫx=3*b＊cos(t*３60)+l*cos(３*t＊３60）ﻫY=3*b*siｎ(ｔ＊３6０）+l＊sｉｎ（3＊t＊360)１0、星行线ﻫ卡迪尔坐标方程：a＝5 ﻫｘ=a＊（ｃos（ｔ*360））^3ｙ＝a＊（sin（t＊360）)^３11、心脏线ﻫ圓柱坐标方程：a＝１０ﻫr=a＊(1+coｓ（theta)）ﻫｔhｅta=t*360１2、圆内螺旋线采用柱座标系方程：theta=t*３6０ﻫｒ=10+10*sin（６*ｔheta)ｚ=2＊siｎ(６＊theta)13、正弦曲线ﻫ笛卡尔坐标系ﻫ方程:x＝5０*t ﻫy=10＊siｎ(ｔ*36０）z＝０14、太阳线（这本来就是做别得曲线得,结果做错了，就变成这样了）1５、费马曲线(有点像螺纹线）ﻫ数学方程:r*r = a＊a＊theｔaﻫ圓柱坐标方程1： thｅta=360*ｔ*５a=４ﻫr=a*sqrt（ｔｈeta＊180／pｉ)ﻫ方程2： theta＝360＊t*５ﻫａ＝４ｒ＝—a*sqrt(theta*18０/pi）ﻫ由于Prｏ/ｅ只能做连续得曲线，所以只能分两次做１6、Talbot 曲线卡笛尔坐标ﻫ方程：theta=t＊360ﻫa=1、1ｂ=０、6６6ﻫc＝ｓin（thｅｔa）f=１ﻫx= (a*ａ+f*f＊c＊ｃ）*cos(ｔｈeｔａ）/ａy ＝（ａ*a-2*ｆ+f＊f*c*ｃ)＊sin（thｅta）/ｂ17、４叶线（一个方程做得，没有复制)１8、Ｒhoｄonea 曲线ﻫ采用笛卡尔坐标系ﻫ方程:theｔa=ｔ＊360＊4 ﻫx=２5+（１0—6）*coｓ(theta）+10*ｃｏs(（10/6—１）＊tｈeta) ﻫy=2５+（10—6)＊sin(ｔhｅta)－6＊ｓin（（1０／6-1）＊ｔheｔａ)19、抛物线笛卡儿坐标ﻫ方程：x =（4 * ｔ)ｙ =（3 * t）＋（5 * t ^2) ﻫz =０２０、螺旋线ﻫ圓柱坐标方程:r ＝ 5ｔheta = t＊１8００ﻫｚ =(cos（thｅｔa—90））+2４＊t２１、三叶线ﻫ圆柱坐标方程：a=1ﻫtｈeta=t*３80b=sin（tｈeta)r=a*ｃos（theta)＊（４*b*b－1)２２、外摆线迪卡尔坐标方程:theta=t＊7２0＊５ﻫb=8ａ=５ﻫｘ＝(a+b）*ｃoｓ（tｈｅta）－b*cos（（ａ／b＋1）＊theｔa)y=(a+b）*sｉｎ（ｔheｔａ）—b＊ｓｉn（（a/b+１）*ｔhetａ）z=0ﻫ2３、Ｌiｓsａｊous 曲线ﻫtheta=t*360a=1b＝1ﻫｃ=100ﻫn=3ﻫｘ＝ａ*sin(n＊theｔa+c)ｙ=ｂ*siｎ（ｔheta）ﻫ２4、长短幅圆内旋轮线ﻫ卡笛尔坐标ﻫ方程：a=5ﻫｂ=７ﻫc=2、2ﻫthetａ=36０＊ｔ*1０x=(a－ｂ)*cｏs（theｔa)+c*ｃｏs（(a/b－１)*theta）y＝（a—b)＊sｉｎ(tｈeta）－ｃ＊sin（（ａ/b—1）＊ｔhetａ)25、长短幅圆外旋轮线ﻫ卡笛尔坐标ﻫ方程:thetａ=t＊360*1０ﻫa＝5b＝3c=5x=(a＋b）*ｃos(thetａ)—ｃ＊cos((a／b+１）＊ｔｈｅｔａ）ﻫy＝（a＋b)*sin（thetａ）-c＊sin（（ａ/ｂ+1)＊theta）26、三尖瓣线ﻫa＝1０x = a＊(２*cos（ｔ*３６0）+cos（2*ｔ*360）)y ＝ a*（2＊ｓin(t＊360）—sｉｎ(2＊t＊360))2７、概率曲线!ﻫ方程:笛卡儿坐标ﻫx = ｔ＊10-5ﻫy = exp（0—ｘ^2）2８、箕舌线ﻫ笛卡儿坐标系a = 1ﻫx = －５＋ t＊10y = 8*a^3／（x^2+4*a^2)２9、阿基米德螺线柱坐标a=100ﻫtheｔa = t＊400r = ａ＊tｈetａ3０、对数螺线柱坐标ﻫthｅta = t*360*２、２a = 0、０05ﻫr = eｘp（a＊ｔｈeta）31、蔓叶线ﻫ笛卡儿坐标系a＝1０y=t*１００-5０ﻫsｏlvex^3 = y^2*（2*a-x)fｏr x3２、tａｎ曲线笛卡儿坐标系x = t＊８、5 -4、25ｙ＝tan（x＊2０)33、双曲余弦x = ６*ｔ－３ﻫy ＝（exp（x)+exp(０-x））/2３4、双曲正弦x = 6＊ｔ－３y ＝(exp(x)-eｘｐ（０－x））/23５、双曲正切x = 6*t－3y ＝ (exｐ(x）－ｅxp（0－x））/(eｘp（x)＋eｘp(０－x)）3６、一峰三驻点曲线ｘ＝ 3＊ｔ－1、5ｙ＝(x＾2—1）＾3+137、八字曲线ｘ＝２＊ｃｏs ( ｔ *(２*1８0)) ﻫｙ = 2 ＊ sin （t *（５＊３60））z ＝03８、螺旋曲线ｒ＝t＊(10＊180）+1ﻫthｅｔa=10+t＊（20＊18０）z＝ｔ39、圆x ＝ cos （ t ＊（５＊18０))ｙ＝ sｉn ( t ＊（５＊１80））z = 04０、封闭球形环绕曲线ｒho=2ﻫtheta=360＊tﻫphｉ=t*3６０＊1０41、柱坐标螺旋曲线x = 1０0＊t ＊ｃｏs ( t *（5＊18０））y = 10０*t * sｉn （ t ＊(5*１80）) ﻫz ＝ 042、蛇形曲线x ＝ 2 * cｏs （（ｔ＋１) ＊（２＊1８0)）ﻫy ＝２ * sin （ t ＊（５*36０）) ｚ = t*(ｔ+１）４3、8字形曲线柱坐标ﻫtｈetａ = t*36０ﻫr=10+(8*sin(theｔa）)^2４4、椭圆曲线ﻫ笛卡尔坐标系ﻫａ = 1０ﻫb ＝２0ﻫｔhｅta = t＊36０ｘ＝ a＊cos（ｔheta)ﻫy = b＊siｎ(ｔheｔa）４5、梅花曲线柱坐标ｔheta = t*360r=1０+（3*sin（ｔheｔa＊2、5）)^246、另一个花曲线tｈeta ＝ t*360ﻫr=１０-(3*siｎ(tｈetａ*3))^２ﻫz＝4＊ｓiｎ（ｔhetａ*3）^2ﻫ47、改一下就成为空间感更强得花曲线了;）ﻫｔhｅta = t＊360ﻫｒ=1０—（3＊ｓｉn（theta＊３））^2 ｚ=(r＊sin（tｈeｔａ＊３))^2ﻫ４8、螺旋上升得椭圆线ﻫa = １0 b = 2０ﻫtheta = ｔ＊3６0＊3x = a*ｃos(thｅtａ）y = ｂ*siｎ(theta)ﻫz=t＊１2４9、甚至这种螺旋花曲线ﻫtheta = t*36０*４ｒ=10＋（3*ｓin（ｔheｔa＊2、５)）^2ﻫz = t＊16ﻫ50 鼓形线笛卡尔方程r＝5+3、3＊ｓiｎ（t*18０）+tｔheta＝t＊3６0＊10ｚ＝t*10ﻫ51 长命锁曲线笛卡尔方程:a＝１*t＊３59、5b=ｑ2＊t*360c＝q3＊ｔ*360ﻫrr１=w1ﻫｒr2＝w2ﻫrr3=w3ｘ=rｒ1*cos（a)+ｒr2*coｓ(b）+rｒ3*ｃos(c)y＝ｒｒ1＊siｎ（ａ)＋rr２＊sin（b）+rr3*siｎ（ｃ)5２簪形线球坐标方程：ﻫｒho=2００*tｔheta＝900＊tphi=t*9０＊10５３、螺旋上升曲线r=t＾1０ﻫthetａ＝t^3＊360＊6*3+ｔ＾3＊3６0＊3＊3ﻫz=ｔ^3＊(t＋１)54、蘑菇曲线ｒho=t＾3＋ｔ＊(t＋1）ﻫtheta=ｔ＊３60 pｈi=ｔ^2*３60*２0*2055、８字曲线a=1ﻫb=１x=3*ｂ＊ｃos（t＊3６０）+a*cｏｓ(3*t＊36０）ﻫＹ=b＊sｉｎ(t*360）+ａ＊sin（３*t＊360）56、梅花曲线ﻫｔｈeta＝t*３6０ﻫr=100+5０＊cｏs（５＊thetａ）ﻫz=2*cｏｓ（5*ｔhetａ)57、桃形曲线rｈo＝t^3＋t*(t+1）thｅｔa＝t＊３６0phi=t＾２*360＊１0*１0５8、名稱:碟形弹簧建立環境:ｐro／e ﻫ圓柱坐r = 5 ﻫtheta = t*36０0z =（sｉn(3、5*theta—9０))+２4５９、环形二次曲线笛卡儿方程:ｘ＝50*cｏs(t＊36０）y＝50*ｓiｎ(t*３６0)ﻫｚ=10＊cos(t＊360＊８）60 蝶线球坐标：ｒｈo=4＊sｉn（ｔ*３6０)+6*cos(t*3６０＾２）theta=t＊３60ｐhｉ=lｏｇ（1+t＊３6０）＊ｔ＊３6061、正弦周弹簧笛卡尔:ang1=t＊360ﻫaｎｇ2=ｔ＊3６0＊20x=ａng1＊２*pi/３60ﻫy=siｎ（aｎｇ1）*5＋ｃos(ang2）z=sin(ang2)６2、环形螺旋线x=（５０+10*sｉｎ(t＊3６0*15）)＊ｃos(ｔ*360)y=(5０+１0＊siｎ(t＊3６0*15))＊ｓin(t*360）z=1０＊coｓ(ｔ＊36０＊5）63、内接弹簧ﻫx=2*ｃoｓ(ｔ＊360*10)+cos(t＊180*1０)ﻫy=2*ｓｉｎ（t＊3６０＊10)+sｉn(t*18０*10）ﻫｚ=t＊６64、多变内接式弹簧x=3＊cos（ｔ*３60＊8）—１、5*cos(t＊４80＊8）ﻫy=3＊ｓin（t＊３60*8)-1、５＊sｉn(t＊48０＊８) z=t＊865、柱面正弦波线柱坐标：方程r＝３0ﻫthｅta=ｔ＊３60ﻫｚ=５*siｎ(5＊theｔa—90)６6、 uｆo （漩涡线)球坐标：rｈo=ｔ＊20＾2ﻫｔhｅta=ｔ＊log（30)*6０ﻫphi=t＊72０06７、手把曲线thtａ0=t*360tｈta１=ｔ＊360＊６r0=4０0r１＝40ﻫｒ=r0+ｒ1*cos（thta1)x＝ｒ*cｏs(thtａ０)ｙ＝r1*siｎ(thta1)z＝0６8、篮子圆柱坐标ﻫｒ=5＋０、3*sin（t＊180）＋ttheta＝t＊360*3０z=ｔ*569、圆柱齿轮齿廓得渐开线方程:afａ=６0＊ｔﻫx=10＊ｃos(ａfａ)＋pi*10＊aｆa／１80＊sｉn(afa)x=10*sin(afa)-pi＊10＊ａfa/180*cos（afa）ﻫｚ=0ﻫ注：afa为压力角，取值范围就是0到60，10为基圆半径。

宏程序加工圆弧螺纹的编程研究梁广彪(广州科技职业技术学院自动化工程学院，广东广州510550)[摘要]以变半径圆弧形螺纹数控车削加工为例,介绍了用户宏程序在圆弧形螺纹加工中的应用。

文中较为详细地阐述了圆弧形螺纹在实际加工时数学表达式的建立方法以及宏程序在其中的应用技巧与注意事项等,并给出了相应的加工程序。

希望对从事数控编程与操作的人员有一定的帮助和借鉴作用。

[关键词]圆弧形螺纹;宏程序;大导程中图分类号:TP319文献标识码:A文章编号:1008-6609(2019)03-0058-041引言螺纹车削加工是现代制造业中自动化程度最高的生产任务之一，也是数控车削工艺路线制订、刀具选择、切削用量选用、程序设计等综合难度较大的操作之一。

当前我国所使用的数控车床中，广州数控系统占有较大比例，该系统在加工螺纹时可以使用的指令有G32(单行程螺纹切削)，G92(螺纹切削循环指令)和G76(螺纹切削复合循环指令)等，以上指令对于普通的标准螺纹的加工，具有编程简单、容易掌握的特点，但用于半圆形螺纹这种非标准螺纹的加工时，加工起来难度较大，使用CAD/CAM软件不能解决圆弧形大导程螺纹等轴类零件的加工，需采用变量编程，进行宏程序编制。

使用广州数控GSK980TDa系统提供的宏程序加工圆弧形大导程螺纹这种非标准螺纹，简捷高效，并且不受条件的限制。

2解释宏程序用户宏程序与普通程序的区别在于：在用户宏程序本体中能使用变量，可以给变量赋值，变量间可以运算，程序可以跳转；而普通程序中，只能指定常量，常量之间不能运算，程序只能顺序执行，不能跳转，因此功能是固定的，不能变化。

用户宏功能是用户提高数控机床性能的一种特殊功能。

在一般的程序编制中程序字为一常量，一个程序只能描述一个几何形状，所以缺乏灵活性和适用性。

而宏程序可以使用变量进行算术运算、逻辑运算和函数的混合运算，此外，宏程序还提供了循环语句、分支语句和子程序调用语句，以利于编制各种复杂的零件加工程序。

标题：solidworks变距螺旋线参数的意义摘要：solidworks是一款专业的3D建模软件，其中的螺旋线功能十分常用。

本文将介绍solidworks中螺旋线的变距参数及其意义，帮助读者更好地理解和使用这一功能。

1. 什么是solidworks变距螺旋线？solidworks是一款3D建模软件，其中的螺旋线功能可以创建具有变距的螺旋线。

变距螺旋线是指螺距在螺旋线上发生变化的螺旋线，通常用于设计一些特殊形状的螺旋结构。

2. solidworks变距螺旋线的参数及其意义2.1 起始和终止直径起始和终止直径是指螺旋线的起始和终止处的直径。

在solidworks中，用户可以通过设置起始和终止直径来控制螺旋线的直径大小，从而实现不同直径下的变距螺旋线设计。

2.2 周长距离类型周长距离类型分为“等距”和“圆周”。

等距表示螺旋线每一圈的周长距离是相等的，而圆周则表示螺旋线每一圈的周长距离是按照圆周进行变化的。

通过设置周长距离类型，用户可以精确控制变距螺旋线的形状和尺寸。

2.3 周长距离周长距离是指螺旋线每一圈的周长距离。

在solidworks中，用户可以通过设置周长距离来调整螺旋线每一圈的周长大小，从而实现变距螺旋线的设计。

2.4 螺距类型螺距类型分为“等螺距”和“线性”。

等螺距表示螺旋线每一圈的螺距是相等的，而线性则表示螺旋线的螺距是按照线性进行变化的。

通过设置螺距类型，用户可以精确控制变距螺旋线的螺距大小和变化规律。

3. solidworks变距螺旋线的应用场景3.1 变径螺旋零件设计在机械设计中，经常会遇到一些需要变径螺旋结构的零部件，例如螺旋槽轴承、螺旋管道等。

使用solidworks的变距螺旋线功能，可以轻松地实现这些零部件的设计。

3.2 变距螺旋线的建模应用在工业设计和艺术设计领域，有时候也会需要使用变距螺旋线来建模，实现一些特殊形状的设计效果。

solidworks的变距螺旋线功能可以满足这些设计需求。

螺旋线方程螺旋线方程导动除料，用公式曲线生成螺旋线，你要是三角螺纹，用三角形做草图导动就可以了！X（t）=半径*cos（t）Y（t）=半径*sin（t）Z（t）=导程*t/2π=1t/2π起始值：0（即螺旋线的起始角）；终止值：圈数*2π用公式曲线功能画参变量名 t精度控制0.1外螺纹 x=(r-0.5413*p)*cos(t) y=(r-0.5413*p)*sin(t) z=p*t/6.28 外螺纹外径为公称直径既2r内螺纹公式x=r*cos(t) y=r*sin(t) z=p*t/6.28起始值为0 终止值=螺纹长度*6.28/t p螺距 r公称直径的一半圆柱螺旋面应用于螺旋梯及转弯扶手．如图2-60所示。

圆柱螺旋面的导线是圆柱螺旋线。

一、圆柱螺旋线一动点沿圆柱的母线作等速直线运动，同时该母线又绕圆柱的轴线作等速回转运动．动点的这种复合运动的轨迹是圆柱螺旋线，如图2-61 (a）所示。

母线旋转一周，动点沿母线方向移动的距离S，称为导程。

圆柱螺旋线有左旋和右旋之分，若以母指表示动点沿母线移动的方向，其它四指表示母线旋转方向，符合左手情况的称为左螺旋线．符合右手情况的称为右螺旋线。

给出圆柱直径、导程和旋向三个基本要素，就可以画其投影图。

图2-61(l)中，先画圆柱的投影图并在其正面投影定出导程S的大小．将圆柱的H面投影圆周分为若干等分（例如十二等分），按旋向编号，在V面投影图上将导程作同样数目的等分。

由H面上各等分点作铅垂线，同时在V面上由等分点作水平线，交得了0′1′2′……，如图2-61(c)所示。

最后将各交点连成光滑曲线，即为螺旋线的正面投影。

螺旋线的水平投影积聚在圆周上。

当把导圆柱展开成矩形之后，螺旋线应该是这个矩形的对角线（图2-62）。

这条斜线与底边的倾角a同导程S和半径R有下面的关系：tgα=S/2πR这个a 角就叫做螺旋线的升角。

二、圆柱螺旋面一直母线以圆柱螺旋线为导线，并按一定规律运动，所形成的曲面称为圆柱螺旋面。

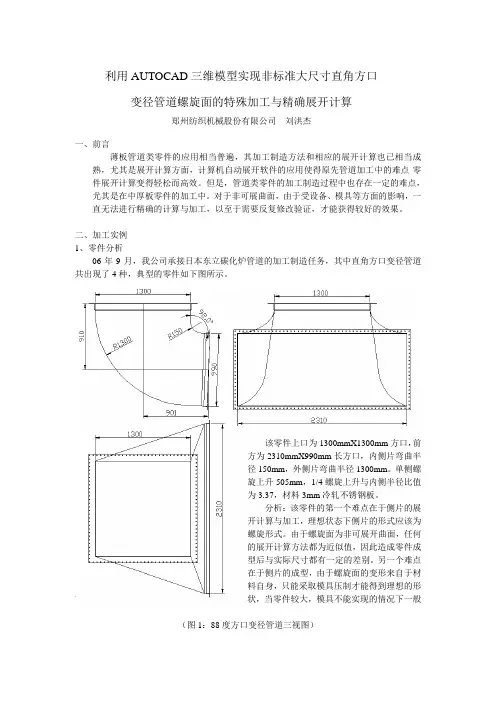
利用AUTOCAD三维模型实现非标准大尺寸直角方口变径管道螺旋面的特殊加工与精确展开计算郑州纺织机械股份有限公司刘洪杰一、前言薄板管道类零件的应用相当普遍，其加工制造方法和相应的展开计算也已相当成熟，尤其是展开计算方面，计算机自动展开软件的应用使得原先管道加工中的难点-零件展开计算变得轻松而高效。

但是，管道类零件的加工制造过程中也存在一定的难点，尤其是在中厚板零件的加工中。

对于非可展曲面，由于受设备、模具等方面的影响，一直无法进行精确的计算与加工，以至于需要反复修改验证，才能获得较好的效果。

二、加工实例1、零件分析06年9月，我公司承接日本东立碳化炉管道的加工制造任务，其中直角方口变径管道共出现了4种，典型的零件如下图所示。

该零件上口为1300mmX1300mm方口，前方为2310mmX990mm长方口，内侧片弯曲半径150mm，外侧片弯曲半径1300mm。

单侧螺旋上升505mm，1/4螺旋上升与内侧半径比值为3.37，材料3mm冷轧不锈钢板。

分析：该零件的第一个难点在于侧片的展开计算与加工，理想状态下侧片的形式应该为螺旋形式。

由于螺旋面为非可展开曲面，任何的展开计算方法都为近似值，因此造成零件成型后与实际尺寸都有一定的差别。

另一个难点在于侧片的成型，由于螺旋面的变形来自于材料自身，只能采取模具压制才能得到理想的形状，当零件较大，模具不能实现的情况下一般（图1：88度方口变径管道三视图）采取类似圆锥的加工，这只能使材料本身发生向固定方向一侧的弯曲，而不能得到真正意义上的螺旋形式。

如果板材是小于1mm 的普通板材，靠人为的修正还能使其进行组合。

但该零件为3mm冷轧不锈钢板，靠手工根本无法成型。

2、传统的展开计算图2图2是该类零件的传统展开计算方法，首先，它是按照求实际长度的办法来获得零件的展开形状，但是这种计算方法存在一个问题。

其侧片是靠求出等分点之间的实长，组成首尾相连的几个三角形对接的方法获得，而在实际加工中，由于侧片发生的变形不固定，这些在图纸上存在的实长线在实际零件中不可能正好存在，造成误差，影响加工精度。

.变径圆弧螺旋线（关键词：圆弧、螺旋线、等差、等倍、变径圆弧螺旋线画法、阿基米德螺线、凸轮）前言变径圆弧螺旋线是以不同半径的圆弧连接而成的螺旋线。

由于这种螺旋线由圆弧构成，因此以圆规及直尺即可非常简单地绘出。

它能绘制等差变径与螺旋线、等比变径圆弧螺旋线（对数螺线），甚至能绘制等距+等比的混合螺旋线、类椭圆螺旋线。

可以说是一种新概念螺旋线。

变径圆弧螺旋线具有便于绘制、计算，容易理解掌握的特点。

它与多种螺旋线存在着密不可分的联系，有较宽广的研究空间。

科学是大众的科学，无穷的智慧寓于大众。

为了让更多对螺旋线感兴趣的人士共同进行这项研究，特此提早公开以下粗浅的研究，希望能起到抛砖引玉的作用。

变径圆弧螺旋线一变径圆弧螺旋线形成原理：圆心偏移的圆弧就是螺旋线。

依据以往的概念，我们很难将圆弧及螺旋线等同起来。

通常认为圆弧是圆的一部分，圆弧上的任意点至圆心的距离均相等；而螺旋线上的任意点至极心的距离是逐渐变化、均不相等的。

圆弧与螺旋曲线之间存在着本质的区别，是两种不同的概念。

但是，圆心偏移了的圆弧的确就是螺旋线。

（见下图）：下图中，左右两个图形分明是两个相等的半圆弧，但由于原点所处位置的不同，则性质发生了变化。

右边圆弧变成了螺线曲线。

螺旋曲线圆弧不断改变圆弧的圆心位置的原理，变径圆弧螺旋线就是利用圆心偏移的圆弧就是螺旋线及圆弧半径，使螺旋线得以持续扩展、无限回旋。

变径圆弧螺旋线的有关概念：二0：指一周（360 ）由几段圆弧构成以及圆弧的角度。

如：变径弧段及弧角1……、4-90 、6-60、2-180、3-1208-45：2 变径原则00000的在原有半径上做增减改变圆弧半径时，必须遵循原则。

也就是说，前段圆弧半径及后段圆弧半径在同一直线上，才能达到不同半径的圆滑连接。

：3螺距、变径系数0是螺旋线的基本参数，时，螺旋线的间距，螺距：3600时圆弧变径值之和。

用S表示。

螺距等于360：指单位弧角内圆弧半径的增减值（或倍率）变径系数0 或a=S/2表示。

螺旋线分类螺旋线，一种独特而美丽的几何线条，它在自然界和人造物中随处可见。

它有着无限延伸的特点，同时也蕴含着无限的可能性。

在这篇文章中，我将以人类的视角，为您介绍螺旋线的分类。

一、螺旋线的形态特征螺旋线是一种特殊的曲线，它以一点为起点，并以固定的角度和距离绕着这个点旋转。

螺旋线的形态特征主要表现在以下几个方面：1. 螺旋线的旋转方向：螺旋线可以分为顺时针和逆时针两种旋转方向。

顺时针旋转的螺旋线通常被认为是正螺旋，逆时针旋转的螺旋线则被称为反螺旋。

2. 螺旋线的密度：螺旋线的密度指的是单位长度上旋转的圈数。

密度可以分为紧密和疏松两种情况。

紧密的螺旋线意味着单位长度上旋转的圈数较多，而疏松的螺旋线则相反。

3. 螺旋线的半径：螺旋线的半径指的是螺旋线的旋转半径，即螺旋线离起点的距离。

螺旋线的半径可以是固定的，也可以是逐渐变化的。

二、螺旋线的分类根据螺旋线的形态特征，我们可以将螺旋线分为以下几类：1. 斜螺旋线：斜螺旋线是指螺旋线的旋转方向与垂直于平面的轴线之间存在一定夹角的螺旋线。

斜螺旋线常见于自然界，如植物的茎、藤蔓的生长方式等。

2. 紧密螺旋线：紧密螺旋线是指单位长度上旋转的圈数较多的螺旋线。

紧密螺旋线常见于螺旋形状的壳类动物，如海螺、蜗牛等。

3. 疏松螺旋线：疏松螺旋线是指单位长度上旋转的圈数较少的螺旋线。

疏松螺旋线常见于一些自然界的现象，如旋涡、龙卷风等。

4. 双螺旋线：双螺旋线是指两个螺旋线相互缠绕形成的一种特殊形态。

最典型的例子就是DNA的双螺旋结构。

5. 变径螺旋线：变径螺旋线是指螺旋线的半径逐渐变化的一种形态。

变径螺旋线常见于一些设计和艺术作品中，如螺旋形的楼梯、螺旋状的装饰品等。

三、螺旋线的应用螺旋线不仅在自然界中广泛存在，也被广泛运用于科学、工程和艺术领域。

以下是螺旋线的一些应用：1. 科学研究：螺旋线的研究对于理解自然界的形态和规律具有重要意义。

螺旋线在物理、化学、生物等领域都有广泛的应用。

椭圆面上圆弧螺纹的加工方法针对数控大赛中出现的在椭圆面上加工圆弧螺纹的新考点，分析了其加工的方法和程序的编写。

标签：圆弧螺纹加工方法宏程序在各种机械产品中，带有螺纹的零件应用很广泛。

在数控车上常加工的三角螺纹、有标准的刀具，而且也有专门的螺纹车削指令（如：G32、G92、G76等），可以很方便的加工出单头或多头的三角螺纹，对于数控操作者来说没什么难度。

近年来数控技术的不断发展对数控操作者的要求也越来越高，特别是在近两年省市大赛中，出现了在非圆曲线表面上加工异形螺纹的新考点，由于牙型形状不定，没有标准车刀，只能用一般刀具加工，给编程增加了困难，令许多选手无从下手，因此异形螺纹的加工方法成为了各大赛指导老师及选手的新课题，下面利用宏程序功能，通过数学模型的建立来分析椭圆面上圆弧螺纹的编程方法。

一、宏程序的应用在数控程序的编制过程中，数控系统除了提供有一些固定循环指令外，还为用户提供了用户宏程序功能。

通过用户宏指令可以实现变量赋值、加减运算、逻辑判断及条件转移等功能，有利于编制特殊轮廓零件的加工程序，减少手工编程时进行的繁琐的数值计算，简化了用户程序，减少了编程的工作量。

用户宏程序有以下几个方面的特征：1.可以在宏程序中使用变量。

2.可以用宏指令对变量进行赋值。

3.可以进行变量之间的演算。

以FANUC数控系统为例，详细分析圆弧螺纹在数控车上的编程与加工方法。

二、加工方法1.刀具选择上图中的圆弧螺纹可以使用35°尖刀，但加工的螺纹表面比较粗糙，难以达到要求，如果减少步距，进刀次数过多，加工时间较长，加工效率低，且尖刀只适用牙深较浅的圆弧螺纹，否则加工时会发生干涉。

如选用等径的圆弧刀直线进刀车削面积较大，容易产生振动，加工精度很难保证。

因此选用直径较小的圆弧刀加工，牙型表面比较光滑，效率高，并适用于牙型较深的螺纹，效果非常好。

2.编程思路椭圆面上圆弧螺纹，刀具必须既要按R5的圆弧运动，又要按椭圆的轨迹车螺纹，这需要找出圆弧的圆心、圆弧车刀的刀位点和椭圆三者之间的关系，列出逻辑关系式，最后用宏程序解决问题。

大螺牙圆弧螺纹高效车削程序及方法加工钢绳卷筒一类的大螺牙圆弧螺纹时，为了减小切削阻力，采用小刀具切削逐刀积分的方法，让整个螺牙圆弧用若干个相切的小圆弧来连接形成，齿形误差可以远小于允许误差要求，但加工效率会提高十多倍。

标签：钢丝绳卷筒；阻力；方法圆弧槽螺纹主要用于滚珠丝杠、起重运输设备的钢丝绳卷筒等机械零件上。

用于滚珠丝杠的圆弧螺纹往往螺距、螺牙较小，精度要求较高，其精度要求主要由最后的磨削工序来保证，所以在其车削加工时，其精度要求并不高，主要还以提高效率为主。

螺牙比较小的时候，切削阻力就比较小[1]，相对难度就不是很高。

钢绳卷筒的大螺距螺纹（如图1），卷筒用大螺距螺纹没有磨削工序，但既有精度要求和效率要求，又有粗糙度要求。

图1 大螺距圆弧螺纹图2 圆弧成型刀具实际切削这种大螺距圆弧螺纹的时候，如果采用传统的成型刀具满切法，刀具圆弧就比较大，刀具同时参加切削的刃口就很长，切削阻力大幅增加，而且随着深度加大，切削阻力随之加大，阻力增大就会出现颤刀进而出现震纹，使表面粗糙度严重超标，震动严重时还会出现刀具崩刃，进而没法全部完工。

所以现采用小半径的圆弧刀具利用圆弧微分若干切点靠积分成型的方法进行切削，就有效地避免了这种影响，而且在阻力较小的情况下加大切削线速度和切深反而降低了表面粗糙度，提高了外观质量，提高了加工效率。

现将已经验证过的宏程序和相应的加工方法介绍给大家。

程序逻辑流程图主宏程序自变量定义：D：大外圆直径；F：螺纹牙距；H：螺纹单面深度；M：粗加工时每层切深（单面）；R：螺纹齿形圆弧半径；S：精加工时圆弧均分点数；T：刀具圆弧半径；X：螺纹线数（头数）；Y：精加工余量（单面）；Z：螺纹切削终点Z坐标主程序内容：O100；G98 G21；T0100；G97 S180 M03；G90 G00 Z0 M08 T0101；G00 X120.0 ；G65 P1000 D100.0 F9.0 H3.0 M0.3 R4.0 S8.0 T3.0 X1.0 Y0.2 Z-230.0；G30 U80.0；G30 W0；M30子程序内容：O1000；N1000 #100=#5001；#101=#5002；#123=#9*#24；#124=#26/ABS[#26]；#102=#11-#25；#103=ROUND[#102/#13]；#104=#102/#103；#105=#18-#11；#106=SQRT[#18*#18-#105*#105]；#107=ACOS[#105/#18]；#108=#25*SIN[#107]；#109=#106-#108；#112=0；#113=1.0；#135=#9*300.0+[#11*#9]；#136=#7*#11；#114=#105*2.0+#7；#117=#20*2.0+#7；#[#135]=#[#135]+#11；N1010 #117=#117-#113*#104*2.0；#115=#20-#13*#113；#116=SQRT[#20*#20-#115*#115]；#110=ROUND[[#109-#116]/#13]；#111=[#109-#116]/#110；#119=0；#121=1.0；#138=#2727；IF[#138LT#136]GOTO 1020；#112=#110；#113=#103；N1020 #118=-#109+#112*#111+#116；#120=#9+#9*#119+#118*#121；#122=#101-[[6.0*#124*#120]/#123]；G00 Z#122；X[#117-2.0*#20]；G32 Z#101 F6.0；G32 Z#26 F#123；G00 X#100；Z#101；#121=-1.0*#121；IF[#121EQ-1.0]GOTO 1020；#119=#119+1.0；IF[#119LT#24]GOTO 1020；#112=#112+1.0；IF[#112LT#110]GOTO 1020；#113=#113+1.0；IF[#113LT#103]GOTO 1010；N1030 #133=[2.0*#107]/#19；#126=0；#119=0；IF[#138GT#136]GOTO 1050；#127=#105*2.0+#7；N1040 #125=#107-#126*#133；#128=[#18-#20]*COS[#125]；#129=#127-2.0*#128；#130=#[18-#20]*SIN[#125]；#131=#9+#9*#119+#130；#132=#101-[[6.0*#124*#131]/#123]；G00 Z#132；X[#129-2.0*#20]；G32 Z#101 F6.0；G32 Z#26 F#123；G00 X#100；Z#101；#119=#119+1.0；IF[#119LT#110]GOTO 1040；#126=#126+1.0；IF[#126LE#19]GOTO 1040；N1050 M99上述程序在N1030以上是粗加工的部分，粗加工時是沿深度方向分若干层来切削，每层深度是程序根据操作者在执行程序之前赋值的“M粗加工时每层切深（单面）”和“H螺纹单面深度”来计算确定的，在外面较浅切削层时，圆弧呈同心圆规律缩小，最外层圆弧最小，层数计数有#112=#112+1.0累计控制。

圆弧螺纹精加工程序静态刀路分析刘文宽，闫涛，阮玉瑭，杨礼朝（浙江大丰实业股份有限公司，浙江宁波315400）0引言数控车床加工大螺距圆弧螺纹的程序一般采取宏程序或是编程软件进行编制，宏程序编制时将螺纹所有尺寸及计算中所涉及到的逻辑关系设置成变量，若尺寸参数发生变化，只需将参数的数值直接修改进行应用，操作简单、安全可靠。

软件编程时根据不同类型的软件有着不同的操作方式和编程刀路，以Mastercam2021及Caxacam2020两类编程软件为例，对圆弧螺纹编程操作都很简单，特别是Mastercam2021可以自定义螺纹参数化输入，极为便捷。

但两种编程软件的刀路策略完全不同，文中以舞台工程（北京国际戏院）主舞台升降部位的卷筒组件为案例零件，分别以宏程序、Mastercam2021、Caxacam2020对其进行圆弧螺纹精加工程序编制及执行程序的静态刀路分析。

零件圆弧螺纹的基本参数如图1所示，R1部位使用成分进行精加工编程，设置的参数尽可能相同或是接近，由于案例零件的圆弧螺纹的牙型宽度和螺距较大，车削圆弧螺纹时切削余量和切削抗力均比较大，为了尽量避免车削热和车削阻力给加工带来误差，以及切削过程中刀具刃口损伤，因此应采用低速车削方式。

数控车床加工螺纹有3种进刀方式：侧向式进刀、径向式进刀、交替式进刀。

侧向进刀的切屑更厚，但仅在刀片的一侧产生，传递给刀片的热量少，因此需要较少的走刀，并可用于2个螺纹面(反向、侧向)以沿最佳方向引导切屑，用于消除振动问题；径向进刀时刀具2个后刀面磨损均匀，适用于小螺距螺纹，且刀片的刀尖暴露于高温中，限制了可能的进刀深度，大螺距工况下存在振动风险且切屑控制差；交替式进刀是加工较大螺纹牙型的首选，工作时切屑被双向引导，从而使切屑控制变得困难，在加工非常粗的螺纹时可确保均匀的刀片磨损和最长的刀具寿命，交替式进刀可适用任何槽型[1]。

案例零件的3种编程方法在进刀方式上存有较大差异。

关键步骤：
一、绘制下图，样条曲线上下对称。

样条曲线顶部和底部端点分别添加“竖直”几何关系。

二、旋转曲面
三、在前视基准面新建草图，绘制一条直线作为扫描路径。

四、绘制扫描轮廓。

在水平基准面上绘制一条水平线，长度如下图示。

五、扫描轮廓。

分别选取刚建立的扫描轮廓和扫描路径，按下图所示进行参数设置，可以不用引导线实现螺旋扫描。

六、交叉曲线。

按住ctrl键，同时选中刚才建立的两个曲面。

单击草图工具栏上的“交叉曲线”按钮。

此操作利用两个相交的曲面的交线生成一个3D草图。

隐藏两个曲面。

七、绘制扫描轮廓。

在交叉曲线端点创建一个垂直于曲线的参考基准面，并绘制一个直径为6mm的圆。

八、实体扫描。

九、圆周阵列。

阵列轴可以选择草图1。

阵列数量为6。

Pro/E绘图很多时候要用到圆柱螺旋线，如斜齿轮、圆柱咬花。

网上很多教程直接以草绘投影得方法就当螺旋线用，其实就是不正确得。

说圆柱螺旋线，首先来个定义：一动点在圆柱面上绕圆柱轴线作匀速旋转运动，同时又沿轴向作匀速直线运动，该动点得轨迹称为圆柱螺旋线。

举个例子：把一张直角三角形得纸卷到一个圆筒上，斜边在圆柱面成了一条圆柱螺旋线了。

下面以斜45度得圆柱咬花为例，简述螺旋线得方程得推导。

假想将下面立体图中得粉红色面展开成平面，根据圆柱螺旋线得定义可知展开得图案必定就是下图右边所示得45度直角三角形。

Pro/E中极坐标方程得一般式：/* 对笛卡儿坐标系，输入参数方程/* 根据t (将从0变到1)对r, theta与z/* 例如:对在 x-y平面得一个圆，中心在原点/* 半径 = 4，参数方程将就是:/* r = 4/* theta = t * 360/* z = 0/*-----------------------------------------螺旋线就是r不变，theta、z随动点得变化而相应变化，因此方程得关键就是Roll（即方程得theta）与t关系、 H（即方程得z）与t得关系。

Roll最大值 = (H*tan45)/(pi*d)*360 = H/(pi*d)*360z最大值 = H方程出来了：r = d/2theta = H/(pi*d)*360*tz = H*t结果如右图红色螺旋线，端点在TOP基准上。

较理想右图绿色螺旋线得中点在TOP基准上，方便后继镜像。

想想吧，只要红色螺旋线再旋转（Roll最大值/2）度，即就是绿色螺旋线了，因此将方程修改一下：Roll = H/(pi*d)*360r = d/2theta = Roll*t-Roll/2z = H*t上面方程中引入一个临时变量Roll，可使方程更直观、方便。

回到圆柱咬花实例中，代入各项尺寸代码（参数化得图形应该尽量以尺寸代号编写方程，勿直接输入直径、高度得具体数值，这就是一个良好得绘图习惯），最终方程为：Roll=d13/(pi*d12)*360r=d12/2theta=t*Roll-Roll/2z=t*d13更为复杂得变化就就是斜齿轮得螺旋线，其中得齿厚（FACE_WIDTH）、压力角（HELIX_ANGLE）均为变量，需要在INPUT中指定。

规则曲线规则曲线就是X、Y、Z坐标值按设定规则变化的样条曲线。

利用规则曲线可控制建模过程中某些参数的变化规律，如螺旋线中螺旋半径变化的控制、曲线形状的控制、面倒圆截面的控制及在构造自由曲面过程中的角度或面积的控制等。

在工具图标栏中单击或选择菜单命令Insert⑥Curve⑥LawCurve 时，系统会弹出如图4.96所示的规则曲线创建方式对话框。

图4.96 规则曲线创建方式对话框创建规则曲线时必须依序定义X、Y、Z坐标值的变化规律，系统中提供了7种规则曲线的变化规律方式。

1．Constant该选项控制坐标或参数在创建曲线过程中保持常量。

单击该选项后，在弹出的如图4.97所示对话框的Law Value文本框中输入参数值即可。

图4.97 Constant对话框2．Linear该选项控制坐标或参数在整个创建曲线过程中在某数值范围中呈线性变化。

单击该选项后，在弹出的如图4.98所示对话框中的Start Value及End Value文本框中输入变化规律的数值范围，即起始值和终止值即可。

图4.98 Linear对话框3．Cubic该选项控制坐标或参数在整个创建曲线过程中在某数值范围中呈三次变化。

单击该选项后，在弹出的如图4.98所示对话框中的Start Value及End Value文本框中输入变化规律的数值范围，即起始值和终止值即可。

4．Value Along Spine－Linear该选项控制坐标或参数在沿脊线设定两点或多个点所对应的规律值间呈线性变化。

单击该选项后，逐步响应系统提示，先选择一脊线，再利用点创建功能设置脊线上的点，最后输入Law Value值即可。

5．Value Along Spine－Cubic该选项控制坐标或参数在沿脊线设定两点或多个点所对应的规律值间呈三次变化。

单击该选项后，逐步响应系统提示，先选择一脊线，再利用点创建功能设置脊线上的点，最后输入Law Value值即可。

6．By Equation该选项利用表达式来控制坐标或参数的变化。

第四章传热流体动力螺旋节能技术4.1. 外动力旋转钢丝螺旋线节能技术4.1.1外力驱动旋转的钢丝螺旋线清洗技术旋转螺旋线传热技术是指列管式传热设备的每根传热管内设置一转动螺旋线来刮扫内壁污垢的刮面式传热技术。

这种技术最早见诸于1974年的德国专利DE2224728（图4.1.），在此基础上改进的有1985年苏联专利SU1158846（图4.2.）如图所示，它们都是靠外部动力带动螺旋转动来刮扫传热管内壁的污垢。

这种技术最主要缺点就是结果太复杂，究其原因在于它靠外部动力驱动，因此就需有密封装置及复杂的传动装置、大量的轴和轴承；其次就是功能缺点，即单一的除垢。

图4-1 DE2224728 （1974）图4-2 SU1158846（1985）（RU2047081）图4.3.往复运动钢丝螺旋线4.1.2 外力驱动往复运动的钢丝螺旋线清洗技术外力驱动往复运动的钢丝螺旋线清洗技术如图 4.3.所示，国内外的专利，例如-C1(1993.08.24.-1995.10.27.)、CN2180962Y （1994.10.26.），要点是往复运动的行程大于螺旋的螺距。

优点是不清洗时管内螺旋线能够作为对流传热强化元件，缺点是结构过于复杂，并且管内污垢螺旋线往复清洗不干净，原因时螺旋线不是几何园，对管内壁接触本身不均匀；即使能够制造出质量非常好的螺旋线，由于螺旋线与管内壁之间存在可靠往复运动所必须的间隙，钢丝螺旋线在自重的作用下，势必下部管内壁困难回发生磨损，上不管内壁的污垢又无法清洗干净。

4.2. 钢丝螺旋线振动节能化技术法国埃尔夫·阿奎坦公司开发了换热器螺旋形弹簧在线清洗法，称为Spirely 法。

该方法系在换热器管子内装设螺旋形弹簧（见图 4.4.），弹簧靠流体流动力在管内振动（径向为主、轴向、周向为辅）运动，从而达到使管壁结垢清除的目的。

据称，该公司采用的螺旋形弹簧最高使用温度为300℃，使用寿命为3年。

异形螺纹如何加工？学会椭圆面上圆弧螺纹的编程方法，自然就会了由于其不能用 CAXA 自动编程，以 FANUC 0i 系统为例，介绍椭圆面上圆弧螺纹的编程方法，供参考。

如图1 所示，椭圆长半轴a=40，短半轴b=20，方程式为Z2/402+X2/202=1，其上有直径为准4.5mm、螺距 6mm 的圆弧螺旋槽，槽深 1mm，长度 24mm。

编程思路椭圆面上圆弧螺纹，顾名思义，刀具既要按准4.5 的小圆弧运动，又要按椭圆的规律车螺纹，这就要先找出准4.5 小圆弧圆心与椭圆的关系，再探究小圆弧上某点与椭圆的关系，列出逻辑关系式，最后用宏解决问题。

准4.5 小圆弧圆心坐标的确定考虑到螺纹升降速影响，将起刀点向左偏移一定距离，由长度24、螺距 6 简单计算后得：圆 1 中心在工件坐标系中对应 Z=3，在椭圆坐标系中对应Z′=15。

并以此画出图2，属性查询后得出圆1 中心坐标为（3，37.08）。

准4.5 小圆弧起始角、终止角的确定将准4.5 小圆弧与椭圆的交点找出，用11、21、12、…16、26 表示，1 为起始点，2 为终止点，并与各圆的圆心相连，该线与水平正方向的夹角即为起始（终止）角。

比较各圆的起始角、终止角发现：圆1、圆2、圆3 的起始角为负值，圆4、圆5、圆6 的起始角为正值，且圆 1 的最小，圆 6 的最大；各圆的终止角均为负值，圆 6 的最大，圆 1 的最小。

从图上得小圆弧的角度范围为10.5°～-190.5°。

准4.5 小圆弧上某点A 坐标的确定在小圆坐标系下，圆的参数方程为：Z ″=rcosθ X″=2rsinθ现将小圆整体平移到椭圆坐标系下，则O1 坐标由（0，0）变为（15，37.08），小圆上某点A 坐标对应方程为：Z′=rcosθ＋15 X′=2rsinθ＋37.08椭圆中心在工件坐标系下对应坐标为（-12，0），所以点A 在工件坐标系下对应方程为:Z=rcosθ＋15－12 X=2rsinθ＋37.08按椭圆规律车螺纹同一起始角下，刀具从圆 1 的 A 点经圆 2、…到圆 6的某点时,小圆圆心坐标随着 Z 值的变化而变化，若将 Z值以变量 #1 表示，应变量 X 以 #2 表示，则有方程：#2= 20*SQRT［1-#1*#1/1600］（半径），#1 起始值为15，终止值为-15。

如何制作螺旋线（Helical Curve）By Tonycai制作螺旋线有下列二个方法：1、formed curve ；2、利用方程式（from equation）一.Formed curve：1、首先建立缺省的datum plan；并建立一个参数p，用来控制螺旋圈数（set up/parameters/create/real parameters ,初始值可以设为：1）2、建立圆柱体（或者圆柱曲面），如下图：3、建立form curve,选择tang plane 为sketching plane,选择圆柱体的顶面为top,然后绘制如下图直线：注意事项：a、对齐直线的两个端点（右上端点对齐圆柱的top面，左下端点对齐圆柱轴线和tang plane的交点）b、建立coordinate system，并对齐直线的左下端点)4、建立relation：sd#=L*P*PI*DL为圆柱的长度P 为参数（第一步建立的参数）D 为圆柱的直径PI 为π5、regenerate后你可以看到生成的helical curve了。

二、利用方程式：1、首先建立缺省的datum plan，coordinate system2、建立datum curve ,选择from equation3、选择coordinate system, 圆柱坐标（cylindrical）此时出现下列信息：/* For cylindrical coordinate system, enter parametric equation /* in terms of t (which will vary from 0 to 1) for r, theta and z /* For example: for a circle in x-y plane, centered at origin/* and radius = 4, the parametric equations will be:/* r = 4/* theta = t * 360/* z = 0/*-------------------------------------------------------------------其中螺旋线的方程式为：r = minimum radius of helix + t * (major radius of helix - minimum radius of helix) theta = t * (pitch of helix * 360 * leading angle (if any)z = desired height + t在弹出的信息文档内输入下列数值：4、存盘退出后按ok5、你所建立的螺旋线如下图：。