华科数理统计作业答案

数理统计课后习题解答应用数理统计第一章1.1 解：已知总体2(,)X N μσ ，则2(,)X N nσμ ，2(0,)X N nσμ-{1}0.95P X P μ-<=<=(0,1)N ,从而上式P=()σΦ查标准正态分布表得(1.96)0.975Φ=， n 最小要取221.96σ1.2 解：(1) 单个元件寿命长于800小时的概率为{800}1{800}i i P X P X >=-≤=0.001580010.0015e -⨯-⨯=0.9995∴ 该事件的概率为60.9995(2) 单个元件寿命短于3000小时的概率为{3000}i P X ≤=0.001530000.0015e -⨯⨯=40.166610-⨯∴ 该事件的概率为100.166610-⨯1.3 解：(1) X 1,X 2,X 3的联合概率函数为123331231123(,,)()!!!x x xs i i p x x x p x e x x x λλ++-===∏(2) X 1,X 2,X 3的联合概率密度为1233()1231(,,)()x x x s i i f x x x f x e λλ-++===∏(3) X 1,X 2,X 3的联合概率密度为 当i a x b ≤≤时，3123311(,,)()()s i i f x x x f x b a ===-∏当i x 取其他值时，31231(,,)()0s ii f x x x f x ===∏(4) X 1,X 2,X 3的联合概率密度为222123313[()()()]221231(,,)()(2)x x x s i i f x x x f x eμμμπ---+-+-===∏1.4 解：1,...,n X X 的联合概率密度为当0x <<∞时，2211(ln )2221111(,...,)()(2)ni i n nx s n ini ii f x x f x exμσπσ=---==∑==∏∏当x 为其他值时，1(,...,)0s n f x x =1.5 证明：原式＝21[()()]nii XX X a =-+-∑＝22111()2()()()nnnii i i i XX X a X X X a ===-+--+-∑∑∑∵1()nii XX =-∑＝0∴ 原式＝2211()()nnii i XX X a ==-+-∑∑＝221()ni nS X a =+-∑ ∴ 当a ＝X 时，21()nii Xa =-∑有最小值且其值等于2nS 。

学院：机械工程学院1、收集到 26 家保险公司人员构成的数据，现希望对目前保险公司从业人员受高等教育的 程度和年轻化的程度进行推断，具体来说就是推断具有高等教育水平的员工平均比例是否 低于 80%，35 岁以下的年轻人的平均比例是否为 0.5。

（数据见 练习 2 数据.xls—练习 2.1） 解：希望通过分析这26家保险公司人员构成的数据，研究目前保险公司从业人员受高等教 育的程度和年轻化的程度。

（1）推断高等教育水平的员工平均比例是否低于80%设原假设：保险公司具有高等教育水平的员工比例平均值不低于0.8，即H 0: μ=μ0≥0.8 备择假设：H 1：μ<0.8n=26，属于小样本，由于σ2未知，选用t 检验，检验统计量 T =计算的 x =0.729273 ，s 2=0.039274 X -μ0S/，取α=0.05拒绝域： x -μ0 S / ≤ -t ∂ (n -1), t == -1.784查t 检验分布表知临界值t α(26-1)=-1.7081显然，t=-1.784<- t α(25) =-1.7081,因此在α=0.05 的水平上拒绝原假设，选择备择假设 结论：保险公司具有高等教育水平的员工比例平均值低于0.8 （2）推断35 岁以下的年轻人的平均比例是否为0.5设原假设：年轻人比例的平均值与0.5 无显著性差异，即H 0: μ=μ0=0.5 备择假设H 1： μ≠0.5.n=26，属于小样本，由于σ2未知，选用t 检验，检验统计量 T =计算的 x =0.713875 ，s 2=0.022705X -μ0 S /，取α=0.05拒绝域： | x - μ0 | S / ≥ t ∂/2 (n -1), t == 7.097查表知α=0.05 的双尾t 检验临界值t α/2（25）=2.0595。

故超出[-2.0595,2.0595]的值均在拒 绝域内由于t=7.097不在拒绝域[-2.0595,2.0595]范围内，因此在α=0.05 的水平上拒绝原假设，选 择备择假设结论：保险公司 35 岁以下年轻人比例平均值不等于 0.52、练习 1 中保险公司的类别分为：1. 全国性公司；2. 区域性公司；3. 外资和中外合资公 司。

数理统计一、填空题1、设n X X X ,,21为母体X 的一个子样，如果),,(21n X X X g ， 则称),,(21n X X X g 为统计量。

不含任何未知参数2、设母体σσμ),,(~2N X 已知，则在求均值μ的区间估计时，使用的随机变量为nX σμ-3、设母体X 服从修正方差为1的正态分布，根据来自母体的容量为100的子样，测得子样均值为5，则X 的数学期望的置信水平为95%的置信区间为 。

025.01015u ⨯±4、假设检验的统计思想是 。

小概率事件在一次试验中不会发生5、某产品以往废品率不高于5%，今抽取一个子样检验这批产品废品率是否高于5%， 此问题的原假设为 。

0H ：05.0≤p6、某地区的年降雨量),(~2σμN X ，现对其年降雨量连续进行5次观察，得数据为： (单位：mm) 587 672 701 640 650 ，则2σ的矩估计值为 。

1430.87、设两个相互独立的子样2121,,,X X X 与51,,Y Y 分别取自正态母体)2,1(2N 与)1,2(N ，2*22*1,S S 分别是两个子样的方差，令2*2222*121)(,S b a aS +==χχ，已知)4(~),20(~222221χχχχ，则__________,==b a 。

用)1(~)1(222*--n S n χσ，1,5-==b a8、假设随机变量)(~n t X ，则21X 服从分布 。

)1,(n F 9、假设随机变量),10(~t X 已知05.0)(2=≤λX P ，则____=λ 。

用),1(~2n F X 得),1(95.0n F =λ10、设子样1621,,,X X X 来自标准正态分布母体)1,0(N ，X 为子样均值，而01.0)(=>λX P ， 则____=λ01.04)1,0(~1z N nX=⇒λ 11、假设子样1621,,,X X X 来自正态母体),(2σμN ，令∑∑==-=161110143i i i iX XY ，则Y 的分布)170,10(2σμN12、设子样1021,,,X X X 来自标准正态分布母体)1,0(N ，X 与2S 分别是子样均值和子样方差，令2*210SX Y =，若已知01.0)(=≥λY P ，则____=λ 。

数理统计习题答案习题5.1解答1. 设总体服从()λP 分布，试写出样本的联合分布律. n X X X ,,,12 解:()的分布律为：即X P X ~,λ ()!k e P X k k λλ-==, 0,1,2,,,n k =n X X X ,,,12 的联合分布律为：()n n P X x X x X x ===,,,1122 = ()()()n n P X x P X x P X x === 1122=nx x x x e x e x e nλλλλλλ---⋅2121=λλn n x x xe x x x n-+++!!!1212, n i n x i 0,1,2,,,1,2,, ==2. 设总体X 服从()0,1N 分布，试写出样本的联合分布密度. n X X X ,,,12 解：，即()~0,1X N X 分布密度为：()2221x p x e -=π，+∞<<-∞xn X X X ,,,12 的联合分布密度为：()∏==ni i n x x x p x p112*(),,...=22222221212121n x x x eee --⋅-πππ=()}212exp{122∑=--n i i x n π x i n i ,1,2,, =+∞<<∞-. 3. 设总体X 服从()2,μσN 分布,试写出样本的联合分布密度. n X X X ,,,12 解：()2~,μσX N ，即X 分布密度为：()p x =()}2exp{2122σμπσ--x ，∞<<∞-xn X X X ,,,12 的联合分布密度为：()∏==ni i n x xx p x p 112*,,...)(=)()}21exp{121222∑-⋅⋅-=-ni i n n x μσπσ, x i n i ,1,2,, =+∞<<∞-.4. 根据样本观测值的频率分布直方图可以对总体作什么估计与推断? 解：频率分布直方图反映了样本观测值落在各个区间长度相同的区间的频率大小，可以估计X 取值的位置与集中程度，由于每个小区间的面积就是频率，所以可以估计或推断X 的分布密度. 5. 略. 6. 略.习题5.2解答1. 观测5头基础母羊的体重(单位：kg)分别为53.2,51.3,54.5,47.8,50.9，试计算这个样本观测值的数字特征：(1)样本总和，(2)样本均值，(3)离均差平方和，(4)样本方差，(5)样本标准差，(6)样本修正方差，(7)样本修正标准差，(8)样本变异系数，(9)众数，(10)中位数，(11)极差，(12)75%分位数.解：设53.2,51.3,54.5,47.8,50.954321=====x x x x x()257.7151=∑=i ix，()51.54251==∑=i ix x(3) ss =()2512512xx xnx i ii i-=-∑∑===13307.84－5×51.542=25.982(4)=2s ()∑=-51251i i x x =51ss =5.1964, (5)s =2.28; (6) =s s *ss n 11-=6.4955(7)=2.5486; (8)*s cv =100⨯*xs =4.945;(9)每个数都是一个,故没有众数.(10)中位数为=51.3; (11)极差为54.5－47.8=6.7;(12)0.75分位数为53.2. 3x2. 观测100支金冠苹果枝条的生长量(单位：cm)得到频数表如下：组下限 19.5 24.5 29.5 34.5 39.5 44.5 49.5 54.5 59.5 组上限 24.5 29.5 34.5 39.5 44.5 49.5 54.5 59.5 64.5 组中值 22 27 32 37 42 47 52 57 62频数 8 11 13 18 18 15 10 4 3试计算这个样本观测值的数字特征：(1)样本总和，(2)样本均值，(3)离均差平方和，(4)样本方差，(5)样本标准差，(6)样本修正方差，(7)样本修正标准差，(8)样本变异系数，(9)众数，(10)中位数，(11)极差，(12)75%分位数.解：设组中值依次为,频数依次为,129,,,x x x 129,,,n n n +=++=912n n n n 100,()=∑=911i i in x 3950;()=+=∑=911912i i in xn n x 39.5;()()-=-==∑∑==29129123ss n x x n xnx i i ii i i 210039.5166300-⨯=10275;()==s ss 100142102.75; ()=s 510.137;()=-=*ss n s 1162103.788 ()=*s 710.188;()=⨯=*1008xs cv 25.79;()93742或众数是()50,210=n ;中位数为39.523742=+;()11极差为:62-22=40;()4783,0.7568,12612512分位数为+++=+++=∴n n n n n n .3.略.4. 设是一组实数，a 和是任意非零实数，n x x x ,,,12 b bx ay i i -=(i n 1,, =)，x 、y 分别为、的均值， =i x i y 2xs ∑-iixn(x 2)1，=2ys 1n(y y i i-)∑2，试证明：① b x a y -=；② 222b s s x y =. 解①：∑∑==-==ni i ni i b x a ny ny 1111= ()∑=-ni i x a bn11= ⎪⎪⎭⎫ ⎝⎛-∑=n i i x na nb 11= b x a -;②=2y s 1n∑-ii y y 2()=∑=⎪⎪⎭⎫⎝⎛---ni i b x a b x a n121=∑=⎪⎪⎭⎫⎝⎛-ni i b x x n 121=221x s b .1.求分位数（1），（2）()820.05x ()1220.95x 。

第一章:统计量及其分布19.设母体ξ服从正态分布N(),,2σμξ和2n S 分别为子样均值和子样方差,又设()21,~σμξN n +且与n ξξξ,,,21 独立, 试求统计量111+--+n n S nn ξξ的抽样分布. 解: 因为ξξ-+1n 服从⎪⎭⎫⎝⎛+21,0σn n N 分布. 所以()1,0~121N nn n σξξ+-+ 而()1~222-n nS nχσ且2n S 与ξξ-+1n 独立,, 所以()1~1111--÷+--+n t S n n n n S nnn σξξ分布. 即111+--+n n S nn εε服从()1-n t 分布. 20.(),,,1,,n i i i =ηξ是取自二元正态分布N()ρσσμμ222121,,,的子样,设()∑∑∑===-===n i i i ni n i i n S n n 12111,1,1ξξηηξξξ2,()2121∑=-=n i i n S ηηη和 ()()()()∑∑∑===----=ni i ni ii ni ir 12211ηηξξηηξξ试求统计量()122221--+---n S rS S S ηξηξμμηξ的分布.解: 由于().21μμηξ-=-E ()()=-+=-ηξηξηξ,c o v 2D D D nn nn2122212σσρσσ-+.所以()()n 212221212σρσσσμμηξ-+---服从()1,0N 分布 .()()()()()()()[]211212121222122ηξηξηηξξηηξξ---=----+-=-+∑∑∑∑====i ini i i ni i ni i ni S rS S S ni i ηξ-是正态变量,类似于一维正态变量的情况,可证ηξηξS rS S S 222-+与ηξ-相互独立.()()1~22221222122--+-+n S rS S S n χσρσσσηξηξ, 所以 统计量()122221--+---n S rS S S ηξηξμμηξ()()()()1)2(222122212221222121--+-+-+---=n S rS S S n nσρσσσσρσσσμμηξηξηξ服从()1-n t 分布.第二章：估计量1. 设n ξξ,,1 是来自二点分布的一个子样,试求成功概率p 的矩法估计量.解: p E =ξ ξ=∴pˆ 3. 对容量为n 的子样,求密度函数()()⎪⎩⎪⎨⎧<<-=其它,00,2;2ax x a a a x f 中参数a 的矩法估计3. 对容量为n 的子样,求密度函数 ()()⎪⎩⎪⎨⎧<<-=其它,00,2;2ax x a a a x f 中参数a 的矩法估计量. 解: ()322adx x a ax E a=-=⎰ξ 令ξ=3a 得ξ3ˆ=a . 4. 在密度函数 ()()10,1<<+=x x a x f a中参数a 的极大似然估计量是什么? 矩法估计量是什么? 解: (1) ()()()∏∏==+=+=ni i ni nni x x L 111ααααα ()i i x ∀<<1∴()().ln 1ln ln 1⎪⎪⎭⎫⎝⎛⋅++=∏=n i i x n L ααα令()0ln 1ln 1=++=∂∂∑=i ni x nL ααα， 得 ∑=--=ni iL xn1ln 1ˆα。

第一章3. 解：因为i i x ay c-=所以 i i x a cy =+11nii x x n ==∑()1111ni i ni i a cy n na cy n ===+⎛⎫=+ ⎪⎝⎭∑∑1nii c a y n a c y==+=+∑所以 x a c y =+ 成立因为 ()2211n x i i s x xn ==-∑()()()22122111ni i ini i nii a cy a c y n cy c y n c y y n====+--=-=-∑∑∑又因为 ()2211n y i i s y yn ==-∑所以 222xys c s = 成立 6. 解：变换()1027i i y x =-11li i i y m y n ==∑()13529312434101.5=-⨯-⨯+⨯+=- 2710yx=+= ()2211lyi i i s m y yn ==-∑()()()()22221235 1.539 1.5412 1.534 1.510440.25⎤=⨯-++⨯-++⨯+++⎡⎣⎦= 221 4.4025100x y s s == 7解：*11li i i x m x n ==∑()1156101601416426172121682817681802100166=⨯+⨯+⨯+⨯+⨯+⨯+⨯=()22*11li i i s m x xn ==-∑()()()()()()()2222222110156166141601662616416628168166100121721668176166218016633.44=⨯-+⨯-+⨯-+⨯-⎡⎣⎤+⨯-+⨯-+⨯-⎦=8解：将子样值重新排列（由小到大） -4，，，，，0，0，，，，，，()()()()()172181203.2147.211.2e n n e nM X X R X X M X X +⎛⎫ ⎪⎝⎭⎛⎫+ ⎪⎝⎭====-=--==== 9解：121211121211n n i j i j n x n x n n x n n ==+=+∑∑112212n x n x n n +=+()12221121n n ii s x x n n +==-+∑()()()1212221122111122121222222111222112212122222211221122112212121222211211122121n n i i n n i ji j x xn n x x n x n x n n n n n s x n sx n x n xn n n n n s n s n x n x n x n x n n n n n n n n n x n n s n sn n +====-++⎛⎫+=- ⎪++⎝⎭+++⎛⎫+=-⎪++⎝⎭⎛⎫+++=+- ⎪+++⎝⎭+++=++∑∑∑()()()()()()22212211222122222112212112212122121222212121122212122n n x n x n x n n n s n s n n x n n x n n x x n n n n n n x x n s n sn n n n +-++++-=+++-+=+++12. 解：()ix P λ i Ex λ= i Dx λ= 1,2,,i n =⋅⋅⋅1122111111n n i i i i nni i i i n E X E x Ex n n n n DX D x Dx n nn n λλλλ============∑∑∑∑13.解：(),ix U a b 2i a b Ex += ()212i b a Dx -= 1,2,,i n =⋅⋅⋅ 在此题中()1,1i x U - 0i Ex = 13i Dx = 1,2,,i n =⋅⋅⋅112111101113n ni i i i nni ii i E X E x Ex n n DX D x Dx n nn ==========∑∑∑∑14.解：因为()2,iXN μσ 0i X Eμσ-= 1i X Dμσ-=所以 ()0,1i X N μσ- 1,2,,in =⋅⋅⋅由2χ分布定义可知()222111nniii i X Y Xμμσσ==-⎛⎫=-= ⎪⎝⎭∑∑服从2χ分布所以 ()2Yn χ15. 解：因为()0,1iX N1,2,,i n =⋅⋅⋅()1230,3X X X N ++0=1=所以()0,1N()221χ同理()221χ由于2χ分布的可加性，故()222123Y χ=+可知 13C =16. 解：（1）因为 ()20,i X N σ 1,2,,i n =⋅⋅⋅()0,1iX N σ所以 ()22121ni i X Y n χσσ=⎛⎫= ⎪⎝⎭∑(){}11122Y Yy F y P Y y P σσ⎧⎫=≤=≤⎨⎬⎩⎭()220yf x dx σχ=⎰()()211'221Y Y y f y F y f χσσ⎛⎫==⨯ ⎪⎝⎭因为 ()2122202200n x n x e x n f x x χ--⎧⎪>⎪⎛⎫=⎨Γ⎪⎪⎝⎭⎪≥⎩所以 ()21122202200ny n nY y e y n f y y σσ--⎧⎪>⎪⎛⎫=⎨Γ⎪⎪⎝⎭⎪≤⎩（2） 因为 ()20,i X N σ 1,2,,i n =⋅⋅⋅()0,1iX N σ所以()22221ni i X nY n χσσ=⎛⎫= ⎪⎝⎭∑(){}()22222220nyY nYny F y P Y y P f x dx σχσσ⎧⎫=≤=≤=⎨⎬⎩⎭⎰()()222'22Y Y ny nf y F y f χσσ⎛⎫== ⎪⎝⎭故 ()221222202200n nny n n Y n y e y n f y y σσ--⎧⎪>⎪⎛⎫=⎨Γ⎪⎪⎝⎭⎪≤⎩（3）因为 ()20,iX N σ 1,2,,i n =⋅⋅⋅()10,1ni N =所以()22311n i Y n χσ=⎛= ⎝(){}()()22333210yn Y Y F y P Y y P y f x dx n σχσ⎧⎫=≤=≤=⎨⎬⎩⎭⎰()()()233'2211Y Y y f y F y f n n χσσ⎛⎫== ⎪⎝⎭()()221000x x f x x χ-⎧>=≤⎩故 ()232000y n Y y f y y σ-⎧>=≤⎩ （4）因为()20,iX N σ 1,2,,i n =⋅⋅⋅所以()()1224210,11ni ni N Y χσ==⎛= ⎝(){}()()()()()224224442210'2211yY Y Y y F y P Y y P f x dxy f y F y f σχχχσσσσ⎧⎫=≤=≤=⎨⎬⎩⎭⎛⎫== ⎪⎝⎭⎰ 故()242000yY y f y y σ-⎧>=≤⎩17.解：因为 ()Xt n存在相互独立的U ，V()0,1UN ()2Vn χ 使X = ()221Uχ则 221U X V n=由定义可知 ()21,F n χ18解：因为 ()20,iX N σ 1,2,,i n =⋅⋅⋅()10,1ni N =()221n mi i n X m χσ+=+⎛⎫ ⎪⎝⎭∑所以()1nniX Yt m ==（2）因为()0,1iX N σ1,2,,i n m =⋅⋅⋅+()()221221ni i n mi i n X n X m χσχσ=+=+⎛⎫ ⎪⎝⎭⎛⎫ ⎪⎝⎭∑∑所以 ()221122211,ni n i ii n mn mi ii n i n X m X n Y F n m X n X mσσ==++=+=+⎛⎫⎪⎝⎭==⎛⎫ ⎪⎝⎭∑∑∑∑19.解：用公式计算()20.010.019090χ=查表得 0.01 2.33U =代入上式计算可得()20.01909031.26121.26χ=+=20.解：因为()2Xn χ 2E n χ= 22D n χ=由2χ分布的性质3可知()0,1N{}P X c P ≤=≤22lim t n P dt -→∞-∞≤==Φ 故 {}PX c ≤≈Φ第 二 章 1.,0()0,0()()1()111x x x x xe xf x x E x f x xdx xe dxxe e d x e xλλλλλλλλλλλλ-+∞+∞--∞+∞+∞--+∞-⎧≥=⎨<⎩=⋅==-+=-==⎰⎰⎰令从而有1x λ∧= 2.()111121).()(1)(1)1111k k x x E x k p p p k p ppp ∞∞--===-=-==⎡⎤--⎣⎦∑∑令1p ＝X所以有1p X ∧=２）．其似然函数为1`11()(1)(1)ni x i i nX nni L P P p p p -=-=∑=-=-∏1ln ()ln ()ln(1)ni i L P n p X n p ==+--∑1ln 1()01ni i d L n X n dp p p ==--=-∑解之得11nii np X X∧===∑３． 解：因为总体Ｘ服从Ｕ（a ，b ）所以()2122!2!!()12ni i a b n E X r n r X X X X a b S X b X =∧∧+=--⎧=⎪⎪⎨-⎪=⎪⎩⎧=⎪⎨⎪=⎩∑222（a-b ）（） D （X ）=12令E （X ）= D （X ）=S ，1S =n a+b 2（）a 4. 解：（1）设12,,n x x x 为样本观察值则似然函数为：111()(),01,1,2,,ln ()ln ln ln ln 0nni i i nii in i i L x x i nL n x d L nx d θθθθθθθθ-====<<==+=+=∏∑∑（-1）解之得：11ln ln nii nii nxnxθθ=∧==-==∑∑（2）母体X 的期望1()()1E x xf x dx x dx θθθθ+∞-∞===+⎰⎰而样本均值为：11()1nii X x n E x X X Xθ=∧===-∑令得5.。

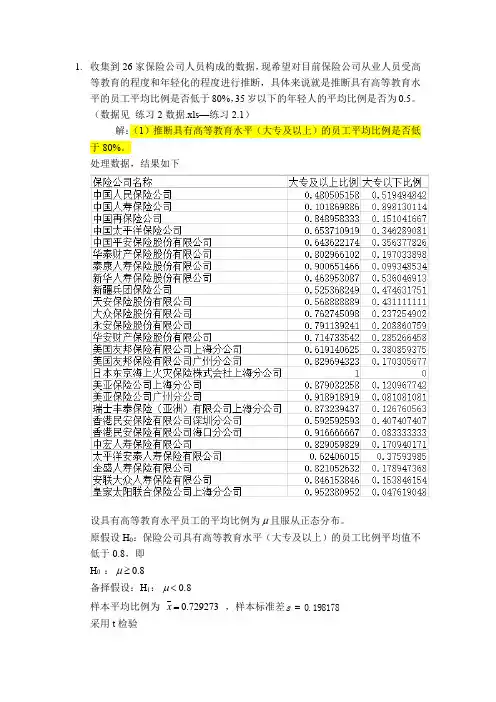
1. 收集到26家保险公司人员构成的数据，现希望对目前保险公司从业人员受高等教育的程度和年轻化的程度进行推断，具体来说就是推断具有高等教育水平的员工平均比例是否低于80%，35岁以下的年轻人的平均比例是否为0.5。

（数据见 练习2数据.xls—练习2.1）解：（1）推断具有高等教育水平（大专及以上）的员工平均比例是否低于80%。

处理数据，结果如下设具有高等教育水平员工的平均比例为μ且服从正态分布。

原假设H 0：保险公司具有高等教育水平（大专及以上）的员工比例平均值不低于0.8，即 H 0 ：8.0≥μ备择假设：H 1：8.0<μ样本平均比例为 0.729273x = ，样本标准差198178.0=s 采用t 检验()()0.050.952525 1.7081t t =-=--1.8198=26/198178.08.0729273.0/s -x T =-==n μ，落在拒绝域内，拒绝原假设。

结论：没有足够的证据表明具有高等教育水平（大专及以上）的员工平均比例高于80%。

（2）35岁以下的年轻人的平均比例是否为0.5 处理数据，结果如下：设35岁以下的年轻人的平均比例μ服从正态分布。

原假设H 0：年轻人比例的平均值与0.5无显著性差异，即H 0：5.0=μ 备择假设H 1： 5.0≠μ样本平均比例为 0.713875x = ，标准差s =0.150683 采用双尾t 检验：t 0.25=2.0595T =x̅−μs √n =0.713875−0.50.150683√26=7.2374落在拒绝域内，拒绝原假设。

结论：没有足够的证据表明35岁以下的年轻人的平均比例为0.5。

2. 练习1中保险公司的类别分为：1. 全国性公司；2. 区域性公司；3. 外资和中外合资公司。

试分析公司类别1与3的人员构成中，具有高等教育水平的员工比例的均值是否存在显著性的差异。

（数据见 练习2数据.xls—练习2.1） 解：分别设1类、3类公司具有高等教育水平员工比例为12,μμ 处理数据，结果如下设具有高等教育水平员工比例12μμ、服从正态分布。

第一章 基本概念习题一1、 设总体X 的样本容量5n =,写出在下列4种情况下样本的联合概率分布.1)、 ~(1,)X B p ; 2)、 ~()X p λ; 3)、 ~[,]X U a b ; 4)、 ~(,1)X N μ; 解 1）、所求的联合概率分布为555551234511(,,,,)()(1)(1)i i x x i i i f x x x x x f x p p p p -====-=-∏∏这里5115i i x x ==∑.2）、所求的联合概率分布为5555123455111(,,,,)()!!ixxi i i i i i f x x x x x f x ee x x λλλλ--======∏∏∑这里5110, 5i i x x λ=>=∑.3）、所求的联合概率分布为551234551111(,,,,)()()i i i f x x x x x f x b a b a =====--∏∏这里[,], 1,2,3,4,5.i x a b i ∈=4）、所求的联合概率分布为5221()()55221234551121(,,,,)()(2)i ii x x i i i f x x x x x f x eμμπ=----==∑===∏.2、 为了研究玻璃产品在集装箱托运过程中的损坏情况，现随机抽取20个集装箱检查其产品损坏的件数，记录结果为：1,1,1,1,2,0,0,1,3,1,0,0,2,4,0,3,1,4,0,2.写出样本的频率分布、经验分布函数并画出其图形. 解 1）、所求样本经验分布函数：0, 00.3, 010.65, 12()0.8, 230.9, 341, 4n x x x F x x x x <⎧⎪≤<⎪⎪≤<=⎨≤<⎪⎪≤<⎪≥⎩.试画出身高直方图，它是否近似服从某个正态分布密度函数的图形.解 根据作直方图的步骤，计算结果如下，其图形如图所示.直方图计算表区间分组 组中值 频数i v 频率i f 纵坐标值i y [165,167） 166 3 0.03 0.015 [167,169） 168 10 0.10 0.05 [169,171） 170 21 0.21 0.105 [171,173） 172 23 0.23 0.115 [173,175） 174 22 0.22 0.11 [175,177） 176110.11 0.055 [177,179] 178 5 0.05 0.0254、 设总体X 的方差为4,均值为μ，现抽取容量为100的样本，试确定常数k ，使得满足(||)0.9P X k μ-<=.解 由题意知10011100ii X x ==∑的方差为4100,有： (||)()(P X k P k X k P μμ-<=-<-<=<< (55)(5)(5)2(5)115X P k k k k k μ-=-<<=Φ-Φ-=Φ-. 由(||)0.9P X k μ-<=，得到2(5)10.9k Φ-=即(5)0.95k Φ=.查表得5 1.65k =，因此所求的0.33k =.5、 从总体2(52,6.3)X N 中抽取容量为36的样本，求样本均值落在50.8到53.8之间的概率.解 由总体2(52,6.3)X N ，设361136i i X x ==∑，知：(52,36XN . 所求的概率为50.8525253.852(50.853.8)()X P X P ---≤≤=≤≤(1.71)( 1.14)(1.71)(1.14)1=Φ-Φ-=Φ+Φ-查表得(1.71)0.9567Φ=，(1.14)0.8729Φ=.因此所求的概率(50.853.8)0.8293P X ≤≤=.6、 从总体(20,3)XN 中分别抽取容量为10与15的两个独立的样本，求它们的均值之差的绝对值大于0.3的概率.解 由总体(20,3)XN ，设110n =，215n =，1011110i i X x ==∑，1521115i i X x ==∑，知：1(20,10X N ，2(20,15X N ，121(0,)2X X N -.所求的概率为212121(||0.3)1(||0.3)1(0.30.3)P X X P X X P X X ->=--≤=--≤-≤11[21]P =-≤≤=-Φ- 22(0.4242)≈-Φ查表得(0.4242)0.6628Φ=.因此所求的概率21(||0.3)0.6744P X X ->=.7、 设1210,,,X X X 是来自总体(0,4)XN 的样本，试确定c ，使得1021()0.05i i P X c =>=∑.解 由题意1210,,,X X X 均服从(0,4)XN ，知102210()(10)2i i X χ=-∑即21021(10)4i i x χ=∑.于是有：210102220.0511()()((10))44i ii i X c P X c P P χχ==>=>=>∑∑.查表得20.05(10)18.307χ=.有18.3074c=，得73.24c =. 8、 设总体X 具有连续的分布函数()F x ，12,,,n X X X 是来自总体X 的样本，且i EX μ=，定义随机变量1, , (1,2,,)0, i i i X Y i n X μμ>⎧==⎨≤⎩试确定统计量1ni i Y =∑的分布.解 由题意知(1,)iY B p ，()1()1i i p P X P X μμμ=>=-≤=-， 1,2,,i n =.从而由二项分布定义知1(,)nii YB n p =∑.9、设12,,,n X X X 是来自总体X 的样本，试求2,,EX DX ES .假设总体的分布为：1)、 ~(,)X B N p ; 2)、 ~()X p λ; 3)、 ~[,]X U a b ; 4)、 ~(,1)X N μ.解 1）、由~(,)X B N p ，知, (1)EX Np DX Np p ==-，11ni i X X n ==∑，故有：11111()()n n i i i E X E X Np nNp Np n n n=====⋅=∑∑；22211111(1)()()(1)(1)n n i i i Np p D X D X Np p nNp p n n n n==-==-=⋅-=∑∑； 2()(1)ES D X Np p ==-.2）、由~()X p λ，知, EX DX λλ==，11ni i X X n ==∑，故有：11111()()n n i i i E X E X n n n nλλλ=====⋅=∑∑；22211111()()n n i i i D X D X n n n n nλλλ=====⋅=∑∑；2()ES D X λ==.3）、由~[,]X U a b ，知2(), 22b a b a EX DX --==，11ni i X X n ==∑，故有： 11111()()222n n i i i b a b a b aE X E X n n n n ==---===⋅=∑∑； 2222221111()1()()()()222n n i i i b a b a b a D X D X n n n n n==---===⋅=∑∑； 22()()2b a ES D X -==.4）、由~(,1)X N μ，知, 1EX DX μ==，11ni i X X n ==∑，故有：11111()()n n i i i E X E X n n n n μμμ=====⋅=∑∑；222111111()()1n n i i i D X D X n n n n nλ=====⋅⨯=∑∑；2()1ES D X ==.10、设12,,,n X X X 是来自总体2(,)XN μσ的样本，求：21[()]ni i E X X =-∑与21[()]ni i D X X =-∑.解 已知2211()1n i i S X X n ==--∑，故221()(1)ni i X X n S =-=-∑.有： 22221[()](1)(1)(1)(1)ni i E X X E n S n ES n DX n σ=-=-=-=-=-∑；222421(1)[()](1)[]ni i n S D X X D n S D σσ=--=-=∑.易知222(1)(1)n S n χσ--，于是241[()]2(1)ni i D X X n σ=-=-∑.11、设12,,,n X X X 是来自正态总体(0,1)N ，定义1||Y X =，211||ni i Y X n ==∑，计算1EY ，2EY .解 由(0,1), 1,2,,iX N i n =，则111(0,)nii X X N nn==∑.于是所求的2||211||||||1X nEY E X X e d X -⋅+∞-∞==⋅⎰2||20||||X nX ed X -+∞=⋅⎰2||22||2X nX ed -+∞=⎰2|2201||()2nX ed n n-+∞=--⎰2||20X n+∞-==. 2111111||||||n n ni i i i i i EY E X E X E X n n n ======∑∑∑2||211||||i X nii i X e d X n +∞--∞==∑⎰2||2012i X i i n X edX n +∞-=⋅⋅⎰12n n ==. 12、设12,,,n X X X 是来自总体(,4)XN μ的样本，X 为样本均值，试问样本容量n 应分别取多大，才能使以下各式成立：1)、2||0.1E X μ-≤; 2)、||0.1E X μ-≤; 3)、(||1)0.95P X μ-≤≥.解 由(,4), 1,2,,iX N i n μ=，则114(,)nii X X N n nμ==∑.1）、222||(2)E X E X X μμμ-=-+222E XE X μμ=-+2222()2DX E X μμμ=+-⋅+22442n n μμμμ=+-⋅+=. 由2||0.1E X μ-≤，得40.1n≤即40n≥.2）、2||421||||||2X nE X X ed X μμμμ--⋅+∞-∞-=-⋅-⎰2||42||||X nX ed X μμμ--⋅+∞-∞=-⋅-2||42204||()42nX ed n nμμ--⋅+∞-=--⋅⎰=由||0.1E X μ-≤0.1≤即800255n π≥≈. 3）、(||1)(11)P X PX μμ-≤=-≤-≤11()222X Pμ-=-≤≤ 21=Φ-. 由(||1)0.95P X μ-≤≥，得210.95Φ-≥即0.975Φ≥.由查表可列：1.962≥，得15.3664n ≥，故n 应为16.13、设12,,,n X X X 和12,,,n Y Y Y 是两样本均值X 和Y 之间的关系式1()i i Y X a b=-（,a b 均为常数，0b ≠），试求两样本均值X 和Y 之间的关系，两样本方差2X S 和2Y S 之间的关系.解 由1()i i Y X a b=-，有： 11111111111()()n n n i i i i i i Y Y X a X na X a n n b b n b n b=====-=⋅-⋅⋅=-∑∑∑.又222111111()[()()]11n n Yi ii i S Y Y X a X a n n b b===-=-----∑∑ 22111()1ni i X X b n ==⋅--∑ 221X S b =. 综上有1()Y X a b =-，2221Y X S S b=.14、设125,,,X X X 是来自总体(0,1)XN 的样本.1)、试确定常数11,c d ，使得2221121345()()()c X X d X X X n χ++++，并求出n ;2)、试确定常数2c ，使得222212345()/()(,)c X X X X X F m n +++，并求出m 和n .解 1)、由题意知：12(0,2)X X N +，345(0,3)X X X N ++(0,1)N，(0,1)N .故有：222(2)χ+.即2221234511()()(2)23X X X X X χ++++.由上得：1111,,223c d n ===. 1)、由题意知：22212(2)X X χ+，345(0,3)X X X N ++22(1)χ.故有：221222(2,1)X X F +，即221223453()2(2,1)()X X F X X X +++.由上得：23,2,12c m n ===. 15、设(),(,)p p t n F m n 分别是t 分布和F 分布的p 分位数，求证21/21[()](1,)p p t n F n --=.证明 设(1,)FF n ，则1(,1)F n F.于是111((1,))()((,1))(,1)p p p P F F n P F P F n F n F-≤=≤=≥11((,1))p P F n F=-≤ 1p =-.又221/21/21/2([()])(()())p p p P T t n P t n T t n ---≤=-≤≤ 1/22(())1p P T t n -=≤- 2(1/2)1p =-- 1p =-. 已知当()Tt n 时，2(1,)T F n .由上即可得证：21/21[()](1,)p p t n F n --=.16、设12,X X 是来自总体(0,1)XN 的一个样本，求常数c ，使212221212()0.1()()X X P c X X X X ⎛⎫+>= ⎪++-⎝⎭. 解 由题意知22221(2)X X χ+，12(0,2)X X N +，12(0,2)X X N -，(0,1)N(0,1)N .于是有：221212222212121212()()22()()()()X X X X P c P c X X X X X X X X ⎛⎫⎛⎫++>=> ⎪ ⎪++-++-⎝⎭⎝⎭2P c ⎛⎫⎪⎪⎪=>⎪⎪⎪⎭12P c ⎛⎫ ⎪⎪⎪=-⎪⎪⎪⎭0.1=.(1,2)F ，故有：21(1,2)0.1c F -=.查表得0.92(1,2)8.53c F ==，即 4.265c =.17、设121,,,,n n X X X X +是来自总体2(,)XN μσ的容量1n +的样本，2,X S 为样本121,,,,n n X X X X +的样本均值和样本方差，求证： 1)、(1)T t n =-;2)、211(0,)n n X X N n σ++-; 3)、211(0,)n X XN nσ--.证明 1）、由题意知：211(,)nii X X N n nσμ==∑，21(,)nX N μσ+，(0,1)N .又知2221(1)nS n χσ--，故所求的(1)T t n =-.2)、由211(,)nii X X N n nσμ==∑，21(,)n X N μσ+，有：11()()()0n n E X X E X E X μμ++-=-=-=;222111()()()n n n D X X D X D X nnσσσ+++-=+=+=.故有211(0,)n n X X N nσ++-. 3)、由21(,)X N μσ，211(,)nii X X N n nσμ==∑，有：111211111n i n i n X X X X X X X n n n n=--=-=---∑； 112111()()n n E X X E X X X n n n --=--- 12111n n EX EX EX n n n -=--- 11n n n nμμ--=- 0=；112111()()n n D X X D X X X n n n--=---212222(1)11n n DX DX DX n n n-=+++22222(1)1n n n nσσ--=+ 21n nσ-= 故有211(0,)n X XN nσ--.18、设12,,,n X X X 是来自总体2(,)XN μσ的一个样本，X 为样本均值，求n ，使得(||0.25)0.95P X μσ-≤≥.解 由题意易知211(,)nii X X N n nσμ==∑，所求的(||0.25)(0.250.25)P X PX μσσμσ-≤=-≤-≤0.250.25()P X σσμσσ=-≤-≤21=Φ-.由题意210.95Φ-≥，解得0.975Φ≥.查表得1.964≥，故62n ≥. 19、设12,,,n X X X 是来自总体[,]XU a b 的样本，试求：1)、(1)X 的密度函数; 2)、()n X 的密度函数. 解 因为[,]XU a b ，所以X 的密度函数与分布函数分别为1, [,],()0, [,],x a b f x b a x a b ⎧∈⎪=-⎨⎪∉⎩0, ,(), ,1, .x a x a F x a x b b a x b ≤⎧⎪-⎪=<≤⎨-⎪>⎪⎩因此所求的(1)1()(1())()n f x n F x f x -=-11(1), [,],0, [,],n x a n x a b b a b ax a b --⎧-∈⎪=--⎨⎪∉⎩1(), [,],()0, [,],n n n b x x a b b a x a b -⎧-∈⎪=-⎨⎪∉⎩()1()(())()n n f x n F x f x -=11(), [,],0, [,],n x a n x a b b a b ax a b --⎧∈⎪=--⎨⎪∉⎩1(), [,],()0, [,].n nn x a x a b b a x a b -⎧-∈⎪=-⎨⎪∉⎩20、设125,,,X X X 是来自总体(12,4)XN 的样本，试求：1)、(1)(10)P X <; 2)、(5)(15)P X <. 解 由题意知：(12,4)iX N ，易得12(0,1)2i X N -.所求的55(1)(1)11(10)1(10)1(10)1(1(10))i i i i P X P X P X P X ==<=-≥=-≥=--<∏∏5551121(1(1))1(1(1))1(11(1))2i i X P =-=--<-=--Φ-=--+Φ∏ 51(1)0.5785=-Φ=；5(5)1(15)(15)i i P X P X =<=<∏5112(1.5)2i i X P =-=<∏ 55(1.5)0.93320.7077=Φ=≈. 21、设121,,,,,,m m m n X X X X X++为来自总体2(0,)XN σ的一个样本，试确定下列统计量的分布：1)、1miX Y =; 2)、21221mi i m ni i m n X Y m X =+=+=∑∑;3)、223221111()()mm n i i i i m Y X X m n σσ+==+=+∑∑. 解 1）、由2(0,) 1,2,,,1,,iX N i m m m n σ=++，知：21(0,)mii XN m σ=∑，21(0,)m nii m XN n σ+=+∑(0,1)miXN ∑，221()m ni i m X n χσ+=+⎛⎫⎪⎝⎭∑.1)、1()mmiimiXXX Y t n ===∑∑;2)、22122121222211122(,)mmii mii i i m nm nm ni i ii m i m i m XXn X n mY F m n mm X XXnσσσσ===+++=+=+=+===∑∑∑∑∑∑;3)、222223221111()()(2)m m ni i m m ni ii i m X X Y X X m n χσσ++==+=+=+∑∑∑∑.22、设总体X 服从正态分布2(,)N μσ，12,,,n X X X 是来自总体X ，2S 为样本方差，问样本容量n 取多大能满足22(1)32.670.95n S P σ⎛⎫-≤= ⎪⎝⎭？ 解 已知：222(1)(1)n S n χσ--，由所求的22(1)32.670.95n S P σ⎛⎫-≤= ⎪⎝⎭有： 0.95(1)32.67n χ-=.查表得0.95(21)32.67χ=.故有121n -=即22n =.23、从两个正态总体中分别抽取容量为20和15的两独立的样本，设总体方差相等，2212,S S 分别为两样本方差，求2122 2.39S P S ⎛⎫> ⎪⎝⎭.解 由题意可得2122(19,14)S F S ，易得221122222.391 2.39S S P P S S ⎛⎫⎛⎫>=-≤ ⎪ ⎪⎝⎭⎝⎭. 由上知2.39为(19,14)F 的分位数，即(19,14) 2.39p F =.查表得0.95(19,14) 2.39F =.于是2122 2.390.95S P S ⎛⎫≤= ⎪⎝⎭.故所求的221122222.391 2.3910.950.05S S P P S S ⎛⎫⎛⎫>=-≤=-= ⎪ ⎪⎝⎭⎝⎭. 24、设总体2(,)XN μσ，抽取容量为20的样本1220,,,X X X ，求概率：1)、20212()10.8537.57i i X P μσ=⎛⎫- ⎪ ⎪≤≤ ⎪⎪⎝⎭∑;2)、20212()11.6538.58ii XX P σ=⎛⎫-⎪⎪≤≤ ⎪ ⎪⎝⎭∑.解 1）、由题意知2022022121()()(20)ii i i XX μμχσσ==--=∑∑.于是有：()202212()10.8537.5710.85(20)37.57i i X P P μχσ=⎛⎫- ⎪ ⎪≤≤=≤≤ ⎪⎪⎝⎭∑ ()()22(20)37.57(20)10.85P P χχ=≤-≤查表得20.99(20)37.57χ=，20.05(20)10.85χ=.故所求的20212()10.8537.57i i X P μσ=⎛⎫- ⎪ ⎪≤≤ ⎪⎪⎝⎭∑()()22(20)37.57(20)10.85P P χχ=≤-≤ 1.99 1.050.94=-=. 2）、由题意知220222119()(19)i i X XS χσσ=-=∑.于是有：()202212()11.6538.5811.65(19)38.58i i X X P P χσ=⎛⎫- ⎪⎪≤≤=≤≤ ⎪⎪⎝⎭∑ ()()22(19)38.58(19)11.65P P χχ=≤-≤查表得20.995(19)38.58χ=，20.1(19)11.65χ=.故所求的 20212()11.6538.58i i X X P σ=⎛⎫-⎪⎪≤≤ ⎪ ⎪⎝⎭∑()()22(19)38.58(19)11.65P P χχ=≤-≤0.9950.10.895=-=. 25、设总体2(80,)XN σ，从中抽取容量为25的样本，试在下列两种情况下求(|80|3)P X ->的值：1)、已知20σ=; 2)、σ未知，但已知样本标准差7.2674s =. 解 1）、由2(80,)XN σ，20σ=知(80,4)XN .所求的(|80|3)1(|80|3)1(3803)P X P X P X ->=--≤=--≤-≤380331()1[2()1]4444X P -=--≤≤=-Φ- 322()220.77340.45324=-Φ=-⨯=. 2）、已知(1)T t n =-，可得80(24)7.26745X t -.所求的(|80|3)1(|80|3)1(3803)P X P X P X ->=--≤=--≤-≤37.2674538031()1[2(24)1]7.26747.26747.2674555X P t -=--≤≤=--37.2674522(24)220.9750.05t=-=-⨯=.26、设12,,,n X X X 为来自总体2(,)XN μσ的样本，X ，2S 为 样本均值和样本方差，当20n =时，求1)、 4.472P X σμ⎛⎫<+ ⎪⎝⎭; 2)、222||2P S σσ⎛⎫-<⎪⎝⎭; 3)、确定(0)C C >，使0.90SP C X μ⎛⎫>=⎪-⎝⎭.解 1）(0,1)N .所求的14.472 4.472 4.472X P X P X P σσμμμσ⎛⎫-⎛⎫⎛⎫<+=-<=< ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭0.8413P⎛⎫=<=Φ=.2)、已知222(1)(1)n S n χσ--，则22219(19)S χσ.所求的22222222223||22222P S P S P S σσσσσσσ⎛⎫⎛⎫⎛⎫-<=-<-<=<< ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭22222223131919319222222S S P S P P σσσσ⎛⎫⎛⎫⎛⎫⨯=<<=<<=<< ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭223191922(19)(19)0.900.250.875χχ⨯=-=-=.3)(1)t n -，于是1(19)S X P C P P t S C X μμ⎛⎫⎛⎫⎛⎫->=<=<= ⎪ ⎪-⎝⎭⎝⎭.由题意知：(19)0.90t=.查表得 1.328(19)0.90t =即1.328=.因此所求的3.3676C ≈.27、设总体X 的均值μ与方差2σ存在，若12,,,n X X X 为它的一个样本，X 是样本均值，试证明对i j ≠，相关系数1(,)1i j r X X X X n --=--. 解 由题意知 ()()2,E X D X μσ==，由12,,,n X X X 为总体的一个样本，故()()()2,1,2,,i i E X D X i n μσ===，()()()i j i j E X X E X E X =.由X 是样本均值，故()()2,E X D X nσμ==.令()()12111i i i n i i n X X X X X X Y X X n-+--++++++=-=，()()()12111j j j nj j n X X X XXXY X X i j n-+--++++++=-=≠，则()()()()()()11110,0i jn n n n E Y EY nnμμμμ------====，()()()()2121111i i i n i n X X X X X X n D Y D n n σ-+--++++++-⎛⎫==⎪⎝⎭，()()()()2121111j j j n j n X X X X X X n D Y D n n σ-+⎛⎫--++++++-⎪== ⎪⎝⎭， ()()()()()()cov ,cov ,i j i j i j i j i j X X X X Y Y E YY E Y E Y E YY --==-=()()()()1211121111j j j n i i i n n X X X X X X n X X X X X X E n n-+-+⎡⎤--++++++--++++++=⋅⎢⎥⎢⎥⎣⎦()()()()()()()()()()()22222211-1-1-1i j i i j j n E X E X n D X n E X n D X n E X n ------=+()()()()22211212n E X n D X n nσ-+-=- ()cov ,1,1i j X X X X r X X X X n ----==--. 28、设总体2(,)XN μσ，从该总体中抽取简单随机样本122,,,(1)n X X X n ≥，X是它的样本均值，求统计量21(2)nin i i T XX X +==+-∑的数学期望.解 令2(2,2)i i n iY X X N u σ+=+，12ni i Y Y X ===∑.于是有22211(2)(2)(1)nni n i i Yi i T X X X Y Y n S +===+-=-=-∑∑. 因此所求的统计量21(2)nin i i T XX X +==+-∑的数学期望222(1)(1)2(1)Y Y ET E n S n ES n σ=-=-=-.。