下载文档原格式
转动惯量公式是什么怎么计算
在经典力学中，转动惯量通常以I或J表示，SI单位为kg·m²。
对于一个质点，I=mr²，其中m是其质量，r是质点和转轴的垂直距离。
转动惯量是什么
转动惯量是刚体绕轴转动时惯性（回转物体保持其匀速圆周运动或静止的特性）的量度，用字母I或J表示。
在经典力学中，转动惯量（又称质量惯性矩，简称惯矩）通常以I或J表示，SI 单位为kg·m²。
对于一个质点，I=mr²，其中m 是其质量，r是质点和转轴的垂直距离。
转动惯量在旋转动力学中的角色相当于线性动力学中的质量，可形式地理解为一个物体对于旋转运动的惯性，用于建立角动量、角速度、力矩和角加速度等数个量之间的关系。
质量转动惯量
其量值取决于物体的外形、质量分布及转轴的位置。
刚体的转动惯量有着重要的物理意义，在科学试验、工程技术、航天、电力、机械、仪表等工业领域也是一个重要参量。
电磁系仪表的指示系统，因线圈的转动惯量不同，可分别用于测量微小电流（检流计）或电量（冲击电流计）。
在发动机叶片、飞轮、陀螺以及人造卫星的形状设计上，精确地测定转动惯量，都是非常必要的。
转动惯量只打算于刚体的外形、质量分布和转轴的位置，而同刚体绕轴的转动状态（如角速度的大小）无关。
外形规章的匀质刚体，其转动惯量可直接用公式计算得到。
而对于不规章刚体或非均质刚体的转动惯量，一般通过试验的方法来进行测定，因而试验方法就显得非常重要。
转动惯量应用于刚体各种运动的动力学计算中。
常见转动惯量计算公式转动惯量是描述物体转动惯性的物理量，在物理学中有着重要的地位。
那咱就来聊聊常见的转动惯量计算公式。
先来说说转动惯量的定义哈。
它可以理解为物体对于旋转运动的“抗拒程度”。
想象一下，一个巨大的飞轮和一个小小的陀螺，让它们转起来，明显能感觉到飞轮更难转动起来，也更难停下，这就是因为飞轮的转动惯量大。
常见的转动惯量计算公式里，对于一个质点，其转动惯量等于质点的质量乘以质点到转轴距离的平方。
这就好比我们去推一个离转轴远的球比推一个离转轴近的球更费劲。
再来说说均匀细棒绕垂直于棒的中心轴转动的情况。
假设细棒长度为 L ，质量为 m ，那转动惯量就等于 1/12 * m * L²。
我记得之前给学生们讲这个的时候，有个调皮的孩子就问我：“老师，这细棒要是变成金箍棒，是不是转动惯量就大得吓人啦？”全班都被他逗乐了。
还有圆盘绕中心轴转动的情况。
假如圆盘半径为 R ，质量为 M ，其转动惯量就是 1/2 * M * R²。
这就好像我们转一个大圆盘和转一个小圆盘，大圆盘明显更“稳重”，不容易被转动。
另外，对于圆环绕中心轴转动，转动惯量是 M * R²，这里的 M 是圆环的质量，R 是圆环的半径。
在实际生活中，转动惯量的概念也无处不在。
就像骑自行车，车轮的转动惯量会影响骑行的感受。
车轮大而且重的自行车，起步的时候会感觉比较吃力，但一旦速度起来了，保持稳定就相对容易些，这就是因为大而重的车轮转动惯量大。
在工程领域，转动惯量的计算更是至关重要。
比如设计汽车的发动机曲轴，就得精确计算转动惯量，以确保发动机运转的平稳性和可靠性。
总之，转动惯量的计算公式虽然看起来有些复杂，但只要我们多结合实际去理解，就会发现它们其实也没那么难。
希望大家都能掌握这些常见的转动惯量计算公式，更好地理解我们周围的物理世界。
转动惯量计算方法转动惯量是描述物体对转动运动的惯性大小的物理量，它在物理学中有着重要的应用。
在工程和科学领域中，我们经常需要计算各种物体的转动惯量，以便更好地理解它们的转动特性。
本文将介绍一些常见的转动惯量计算方法，希望能够帮助读者更好地理解和运用这一概念。
首先，我们来介绍一下关于点质点的转动惯量计算方法。
对于一个质点，其转动惯量可以通过以下公式计算：\[ I = mr^2 \]其中，m为质点的质量，r为质点到转轴的距离。
这个公式表明，转动惯量与质点的质量成正比，与质点到转轴的距离的平方成正比。
这是一个非常基础的转动惯量计算方法，适用于质点的简单情况。
接下来，我们来介绍一下关于刚体的转动惯量计算方法。
对于一个刚体，其转动惯量可以通过积分的方法计算：\[ I = \int r^2 dm \]其中，r为刚体上各个质点到转轴的距离，dm为刚体上各个质点的质量微元。
通过对整个刚体进行积分，我们可以得到刚体的转动惯量。
这个方法适用于各种形状的刚体，可以比较准确地计算出其转动惯量。
此外，对于一些特殊形状的物体，我们也可以利用一些特殊的公式来计算其转动惯量。
比如对于绕轴旋转的圆环，其转动惯量可以通过以下公式计算：\[ I = mr^2 \]其中，m为圆环的质量，r为圆环的半径。
这个公式适用于绕轴旋转的圆环，可以方便地计算出其转动惯量。
总结一下，转动惯量的计算方法有很多种，我们可以根据具体的情况选择合适的方法来计算。
对于质点，可以利用简单的公式进行计算；对于刚体，则可以通过积分的方法得到转动惯量；对于一些特殊形状的物体，也可以利用特殊的公式来计算。
希望本文介绍的内容能够对大家有所帮助，让大家对转动惯量的计算有更深入的理解。
说明：本文《转动惯量的计算》特地收集贡献出来供各位工程技术人员在参阅本人劣作《风机动平衡调试方法》时参考。
深圳华晶玻璃瓶有限公司工程部（动力车间）李宜斌编辑2010-10-21转动惯量的计算转动惯量应用于刚体各种运动的动力学计算中。
单个质点的转动惯量：I = m× r2.质点系的转动惯量：I = Σ m i×r i2.质量连续分布的刚体的转动惯量：I = ∫m r2dm。
以上各式中的r理解为质点到转轴的距离。
刚体绕轴转动惯性的度量。
其数值为J=∑ mi*ri^2，式中mi表示刚体的某个质点的质量，ri表示该质点到转轴的垂直距离。
求和号（或积分号）遍及整个刚体。
转动惯量只决定于刚体的形状、质量分布和转轴的位置，而同刚体绕轴的转动状态（如角速度的大小）无关。
规则形状的均质刚体，其转动惯量可直接计得。
不规则刚体或非均质刚体的转动惯量，一般用实验法测定。
描述刚体绕互相平行诸转轴的转动惯量之间的关系，有如下的平行轴定理：刚体对一轴的转动惯量，等于该刚体对同此轴平行并通过质心之轴的转动惯量加上该刚体的质量同两轴间距离平方的乘积。
由于和式的第二项恒大于零，因此刚体绕过质量中心之轴的转动惯量是绕该束平行轴诸转动惯量中的最小者。
垂直轴定理：一个平面刚体薄板对于垂直它的平面轴的转动惯量，等于绕平面内与垂直轴相交的任意两正交轴的转动惯量之和。
表达式:Iz=Ix+Iy刚体对一轴的转动惯量，可折算成质量等于刚体质量的单个质点对该轴所形成的转动惯量。
由此折算所得的质点到转轴的距离，称为刚体绕该轴的回转半径κ，转动惯量的量纲为L^2M，在SI单位制中，它的单位是kg·m^2。
刚体绕某一点转动的惯性由更普遍的惯量张量描述。
惯量张量是二阶对称张量，它完整地刻画出刚体绕通过该点任一轴的转动惯量的大小。
补充对转动惯量的详细解释及其物理意义：先说转动惯量的由来，先从动能说起大家都知道动能E=(1/2)mv^2，而且动能的实际物理意义是：物体相对某个系统（选定一个参考系）运动的实际能量，（P势能实际意义则是物体相对某个系统运动的可能转化为运动的实际能量的大小）。
1.圆柱体转动惯量(齿轮、联轴节、丝杠、轴的转动惯量)之欧侯瑞魂创作82MD J =对于钢材：341032-⨯⨯=gLrD J π)(1078.0264s cm kgf L D ⋅⋅⨯-M-圆柱体质量(kg)；D-圆柱体直径(cm)； L-圆柱体长度或厚度(cm)； r-资料比重(gf /cm 3)。
2.丝杠折算到马达轴上的转动惯量：2iJsJ =(kgf·cm·s 2)J s –丝杠转动惯量(kgf·cm·s 2)； i-降速比，12z z i =3. 工作台折算到丝杠上的转动惯量g w22⎪⎭⎫ ⎝⎛⋅=n v J π g w2s 2⎪⎭⎫ ⎝⎛=π(kgf·cm·s 2) v -工作台移动速度(cm/min)； n-丝杠转速(r/min)； w-工作台重量(kgf)； g-重力加速度，g=980cm/s 2； s-丝杠螺距(cm)2. 丝杠传动时传动系统折算到驱轴上的总转动惯量：())s cm (kgf 2g w 122221⋅⋅⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+++=πs J J iJ J S tJ 1-齿轮z 1及其轴的转动惯量； J 2-齿轮z 2的转动惯量(kgf·cm·s 2)； J s -丝杠转动惯量(kgf·cm·s 2)； s-丝杠螺距，(cm)； w-工件及工作台重量(kfg).5. 齿轮齿条传动时折算到小齿轮轴上的转动惯量2gw R J =(kgf·cm·s 2)R-齿轮分度圆半径(cm); w-工件及工作台重量(kgf)6. 齿轮齿条传动时传动系统折算到马达轴上的总转动惯量⎪⎪⎭⎫⎝⎛++=2221g w 1R J i J J tJ 1，J 2-分别为Ⅰ轴，Ⅱ轴上齿轮的转动惯量(kgf·cm·s 2)；R-齿轮z 分度圆半径(cm)；w-工件及工作台重量(kgf)。
转动惯量公式是什么怎么计算
在经典力学中，转动惯量通常以I或J表示，SI单位为kg·m ²。
对于一个质点，I=mr²，其中m是其质量，r是质点和转轴的垂直距离。
转动惯量公式是什么怎么计算
1转动惯量是什么
转动惯量是刚体绕轴转动时惯性（回转物体保持其匀速圆周运动或静止的特性）的量度，用字母I或J表示。
在经典力学中，转动惯量（又称质量惯性矩，简称惯矩）通常以I或J表示，SI 单位为kg·m²。
对于一个质点，I=mr²，其中m 是其质量，r是质点和转轴的垂直距离。
转动惯量在旋转动力学中的角色相当于线性动力学中的质量，可形式地理解为一个物体对于旋转运动的惯性，用于建立角动量、角速度、力矩和角加速度等数个量之间的关系。
2质量转动惯量
其量值取决于物体的形状、质量分布及转轴的位置。
刚体的转动惯量有着重要的物理意义，在科学实验、工程技术、航
天、电力、机械、仪表等工业领域也是一个重要参量。
电磁系仪表的指示系统，因线圈的转动惯量不同，可分别用于测量微小电流（检流计）或电量（冲击电流计）。
在发动机叶片、飞轮、陀螺以及人造卫星的外形设计上，精确地测定转动惯量，都是十分必要的。
转动惯量只决定于刚体的形状、质量分布和转轴的位置，而同刚体绕轴的转动状态（如角速度的大小）无关。
形状规则的匀质刚体，其转动惯量可直接用公式计算得到。
而对于不规则刚体或非均质刚体的转动惯量，一般通过实验的方法来进行测定，因而实验方法就显得十分重要。
转动惯量应用于刚体各种运动的动力学计算中。
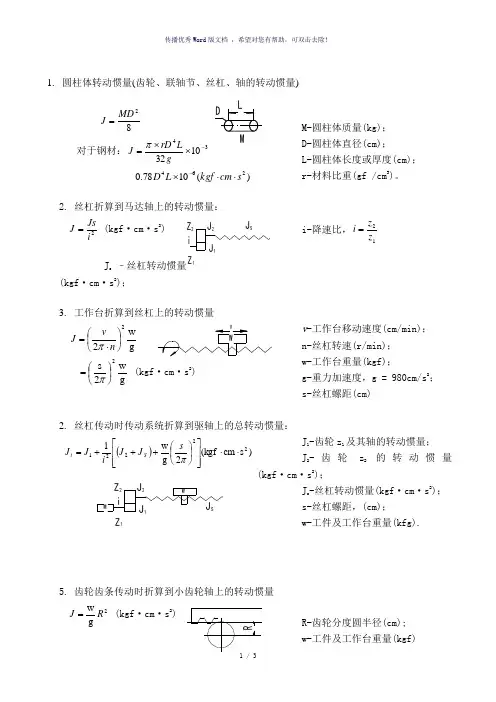
1. 圆柱体转动惯量(齿轮、联轴节、丝杠、轴的转动惯量)82MD J =对于钢材：341032-⨯⨯=gLrD J π)(1078.0264s cm kgf L D ⋅⋅⨯-M-圆柱体质量(kg)； D-圆柱体直径(cm)； L-圆柱体长度或厚度(cm)； r-材料比重(gf /cm 3)。
2. 丝杠折算到马达轴上的转动惯量：2i Js J =(kgf·c m·s 2) J s (kgf·c m·s 2)； i-降速比，12z z i =3. 工作台折算到丝杠上的转动惯量gw22⎪⎭⎫ ⎝⎛⋅=n v J π g w 2s 2⎪⎭⎫ ⎝⎛=π (kgf·c m·s 2) v -工作台移动速度(cm/min)； n-丝杠转速(r/min)； w-工作台重量(kgf)；g-重力加速度，g = 980cm/s 2； s-丝杠螺距(cm)2. 丝杠传动时传动系统折算到驱轴上的总转动惯量：())s cm (kgf 2g w 122221⋅⋅⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+++=πs J J iJ J S tJ 1-齿轮z 1及其轴的转动惯量； J 2-齿轮z 2的转动惯量(kgf ·cm ·s 2)；J s -丝杠转动惯量(kgf ·cm ·s 2)； s-丝杠螺距，(cm)； w-工件及工作台重量(kfg).5. 齿轮齿条传动时折算到小齿轮轴上的转动惯量2gw R J =(kgf ·c m·s 2)R-齿轮分度圆半径(cm); w-工件及工作台重量(kgf)6. 齿轮齿条传动时传动系统折算到马达轴上的总转动惯量⎪⎪⎭⎫⎝⎛++=2221g w 1R J i J J tJ 1，J 2-分别为Ⅰ轴，Ⅱ轴上齿轮的转动惯量(kgf ·c m·s 2)；R-齿轮z 分度圆半径(cm)； w-工件及工作台重量(kgf)。
nema标准中的计算是如下（转化公式）：J=A×0.055613×（Pn^0.95）÷（n/1000）^2.4-0.004474×（Pn^1.5）÷（n/1000）^1.8A小于等于1800rpm时取24，A大于1800rpm时取27 Pn为功率（kw） n 为同步转速高压电动机在设计时，要求计算出转子的转动惯量。
下面对计算方法做一分析。
转动惯量是物体在转动时惯性的度量，它不仅与物体质量的大小有关，还与物体质量分体情况有关。
机械工程师手册给出了一些简单形状物体的转动惯量。
1、圆柱体沿轴线转动惯量：Kg•m2 (1)式中：M —圆柱体质量KgR —圆柱体外径半径 m2、空心圆柱体沿轴线转动惯量：Kg•m2 (2)式中： M —空心圆柱体质量KgR —空心圆柱体外半径 mr —空心圆柱体内半径m3、薄板沿对称线转动惯量：Kg•m2 (3)式中：M —薄板质量Kga —薄板垂直于轴线方向的宽度m物体的转动惯量除了用J表示外，在工程上有的用物体的重量G和物体的回转直径D的平方的乘积GD2来表示，也称为物体的飞轮力矩或惯量矩，单位N•m2或Kg f m2。
物体的飞轮力矩GD2和转动惯量J之间的关系，用下式表示：N•m2 (4)式中：g —重力加速度 g=9.81 m/s2将重力单位N化为习惯上的重力单位Kgf ，则（4）变为：Kg f m2 (5)由以上公式，可以对鼠笼型高压电机的转动惯量进行计算。
计算时，将高压电机转子分解为转子铁心（包括导条和端环）、幅铁、转轴三部分，分别算出各部分的Jn，各部分的转动惯量相加即得电机的转动惯量J。
如需要，按（5）式换算成飞轮力矩GD2。
一般产品样本中要求给定的是转动惯量J，兰州引进的电磁设计程序计算出的是飞轮力矩GD2。
计算程序如下：1、转子铁心的转动惯量，按空心圆柱公式（2）进行计算，考虑导条端环度大小的因素，以系数c进行修正。
转动惯量计算方法转动惯量是描述物体对转动的惯性大小的物理量，它在物理学和工程学中有着广泛的应用。
在实际工程问题中，我们经常需要计算物体的转动惯量，以便对物体的旋转运动进行分析和设计。
本文将介绍几种常见的转动惯量计算方法，希望对大家有所帮助。
首先，我们来介绍一种简单的转动惯量计算方法——几何法。
几何法是一种通过物体的几何形状来计算其转动惯量的方法。
对于简单的几何形状，比如长方形、圆柱体等，我们可以通过几何公式直接计算出其转动惯量。
以长方形为例，其转动惯量可以通过公式I=1/12m(a^2+b^2)来计算，其中m为物体的质量，a和b分别为长方形的两个边长。
这种方法简单直观，适用于一些简单的几何形状，但对于复杂的形状，几何法并不适用。
其次，我们介绍一种更加通用的转动惯量计算方法——积分法。
积分法是一种通过对物体的质量分布进行积分来计算其转动惯量的方法。
对于一个质量分布不均匀的物体，我们可以将其分解为无穷小的质量元，然后对每一个质量元的转动惯量进行积分求和，即可得到整个物体的转动惯量。
这种方法适用于各种形状的物体，可以较为准确地计算出其转动惯量。
除了几何法和积分法，还有一种常用的转动惯量计算方法——平行轴定理。
平行轴定理是指物体对于某一轴的转动惯量等于其对于平行于该轴且通过质心的轴的转动惯量之和，即I=Icm+md^2，其中Icm为物体对质心的转动惯量，m为物体的质量，d为质心到所选轴的距离。
利用平行轴定理，我们可以将复杂形状的物体的转动惯量计算简化为对质心的转动惯量的计算，大大提高了计算的效率。
综上所述，转动惯量的计算方法有多种，每种方法都有其适用的范围和特点。
在实际应用中，我们可以根据物体的形状和质量分布来选择合适的计算方法，以便准确地计算出物体的转动惯量。
希望本文介绍的几种方法能够对大家有所帮助，谢谢阅读！。
1.圆柱体转动惯量(齿轮、联轴节、丝杠、轴的转动惯量)之吉白夕凡创作82MD J =对于钢材：341032-⨯⨯=gLrD J π)(1078.0264s cm kgf L D ⋅⋅⨯-M-圆柱体质量(kg)；D-圆柱体直径(cm)； L-圆柱体长度或厚度(cm)； r-资料比重(gf /cm 3)。
2.丝杠折算到马达轴上的转动惯量：2iJsJ =(kgf·cm·s 2)J s –丝杠转动惯量(kgf·cm·s 2)； i-降速比，12z z i =3. 工作台折算到丝杠上的转动惯量g w22⎪⎭⎫ ⎝⎛⋅=n v J π g w2s 2⎪⎭⎫ ⎝⎛=π(kgf·cm·s 2) v -工作台移动速度(cm/min)； n-丝杠转速(r/min)； w-工作台重量(kgf)； g-重力加速度，g=980cm/s 2； s-丝杠螺距(cm)2. 丝杠传动时传动系统折算到驱轴上的总转动惯量：())s cm (kgf 2g w 122221⋅⋅⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+++=πs J J iJ J S tJ 1-齿轮z 1及其轴的转动惯量； J 2-齿轮z 2的转动惯量(kgf·cm·s 2)； J s -丝杠转动惯量(kgf·cm·s 2)； s-丝杠螺距，(cm)； w-工件及工作台重量(kfg).5. 齿轮齿条传动时折算到小齿轮轴上的转动惯量2gw R J =(kgf·cm·s 2)R-齿轮分度圆半径(cm); w-工件及工作台重量(kgf)6. 齿轮齿条传动时传动系统折算到马达轴上的总转动惯量⎪⎪⎭⎫ ⎝⎛++=2221g w 1R J i J J tJ 1，J 2-分别为Ⅰ轴，Ⅱ轴上齿轮的转动惯量(kgf·cm·s 2)；R-齿轮z 分度圆半径(cm)；w-工件及工作台重量(kgf)。
实验三刚体转动惯量的测定转动惯量是刚体转动中惯性大小的量度。
它与刚体的质量、形状大小和转轴的位置有关。
形状简单的刚体，可以通过数学计算求得其绕定轴的转动惯量；而形状复杂的刚体的转动惯量，则大都采用实验方法测定。
下面介绍一种用刚体转动实验仪测定刚体的转动惯量的方法。
实验目的：1、理解并掌握根据转动定律测转动惯量的方法；2、熟悉电子毫秒计的使用。
实验仪器：刚体转动惯量实验仪、通用电脑式毫秒计。
仪器描述：刚体转动惯量实验仪如图一，转动体系由十字型承物台、绕线塔轮、遮光细棒等（含小滑轮）组成。
遮光棒随体系转动，依次通过光电门，每π弧度（半圈）遮光电门一次的光以计数、计时。
塔轮上有五个不同半径（r）的绕线轮。
砝码钩上可以放置不同数量的砝码，以获得不同的外力矩。
实验原理：空实验台（仅有承物台）对于中垂轴OO’的转动惯量用J o表示，加上试样（被测物体）后的总转动惯量用J表示，则试样的转动惯量J1：J1 = J –J o (1)由刚体的转动定律可知：T r – M r = J α (2) 其中M r 为摩擦力矩。
而 T = m(g -r α) (3) 其中 m —— 砝码质量 g —— 重力加速度 α —— 角加速度 T —— 张力1． 测量承物台的转动惯量J o未加试件，未加外力（m=0 , T=0）令其转动后，在M r 的作用下，体系将作匀减速转动，α=α1，有 -M r1 = J o α1 (4) 加外力后，令α =α2m(g –r α2)r –M r1 = J o α2 (5) （4）（5）式联立得J o =212212mr mgrααααα--- (6)测出α1 , α2，由（6）式即可得J o 。
2． 测量承物台放上试样后的总转动惯量J ，原理与1.相似。
加试样后，有 -M r2=J α3 (7) m(g –r α4)r –Mr 2= J α4 (8)∴ J =234434mr mgr ααααα---(9)注意：α1 , α3值实为负，因此（6）、（9）式中的分母实为相加。
3． 测量的原理设转动体系的初角速度为ωo ，t = 0 时θ= 0 ∵ θ=ωo t + 221t α (10)测得与θ1 , θ2相应的时间t 1 , t 2由 θ1=ωo t 1 + 2121t α (11)θ2=ωo t 2 + 2221t α (12)得 2211222112)(2t t t t t t --=θθα (13) ∵ t = 0时，计时次数k=1（θ=л时，k = 2） ∴ []2211222112)1()1(2t t t t t k t k ----=πα (14) k 的取值不局限于固定的k 1 , k 2两个，一般取k =1 , 2 , 3 , …,30,…实验方法：本实验采用HMS-2型“通用电脑式毫秒计”来测量k 及其相应的t 值，毫秒计的使用方法见本实验附录。
先完成砝码的挂接和绕线，然后复位毫秒计，放开砝码。
砝码在重力作用下带动体系加速转动。
“毫秒计”将自动记下k 及其相应的t 值。
由式（14）即得α2。
待砝码挂线自动脱离后，即可接着测α1。
所以,实验一次即可完成对体系的转动惯量J 的测量。
此时应注意两点：①、从测α2到测α1的计时分界处要记清，处理数据时不能混杂；②、测α1的开始时间虽然可以选为较远地离开分界处，但以后的每个时间的数据都必须减去开始的时间数值。
α3 , α 4 的测量方法与α1 , α 2相同。
实验步骤：1、 按（图一）安装调试好仪器，细线的一端连结钩挂砝码6，另一端打一适当大小的结塞入塔轮3的缝中，绕线于塔轮时应单层逐次排列。
线的长度应使砝码触地前一点点脱离塔轮。
选取塔轮半径r = 2.5×10-2m ，砝码质量m = 6.0×10-2kg 当实验台离地面高度为h 时，有h =r k π22'⨯，式中k ，为每半圈记一次时间的数目，k’ = k –1 . 通过该式适当选取h ，使k ’≤10为加速；k ’>10为减速。
一般选k ’ > 13进行计算。
2、测量承物台的转动惯量J 0 o参阅[实验方法]中的说明及后面附录“HMS-2型通用电脑式毫秒计”使用说明。
记录每一值对应时间于下表。
选取不同的12及对应的12值代入（14）即可求得α1和α2，将α1α2再代入（6）即可计算出此承物台的转动惯量J o 。
注意：（1） 计算α2时，将数据分成四组，按等权原则，取k 1= 2, 3, 4, 5时对应的k 2分别为 k 2 = 6, 7, 8, 9（即Δk = k 2 – k 1 = 4）, 按公式（14）进行计算。
即由 []2211222112)1()1(2t t t t t k t k ----=πα 求出α21, α22, α23 ,α24 , 再求得2α。
（2） 同理计算α1时，也将数据分成四组，按等权原则，取k’1 = 2, 3, 4, 5时对应的k ,2分别为 k’2 = 6, 7, 8, 9 按公式（14）进行计算，得出α11, α12, α13 ,α14 ,再求得1α（此时k’ = k –15即取k=15时 t’= 0）1． 测量试样的转动惯量J 1将待测试样放至承物台上，按上面2中测量方法，可测得系统（承物台加待测试样）的转动惯量J 。
由式（1）J 1 = J - J o 可求出待测试样的转动惯量。
待测试样（1） 铝环 （2） 铝圆盘*（3）移轴砝码（两个）：对称地倒插于承物台十字架的小孔内，两砝码距离2X ,取值分别为a. 2X 1= 10cmb. 2X 2= 20cm计算公式：1． 质量均匀分布的圆环，总质量为M ，外径、内径分别为D 1、D 2，则对通过中心与环面垂直的转轴的转动惯量)(812221D D M J +=(15) 2． 若为圆盘试样，上式的D 2=0，即 281MD J =(16) D 为圆盘的直径3．平行轴定理2= (17)J+mdJc刚体对任一转轴的转动惯量等于刚体通过质心并与该轴平行的轴的转动惯量J c，加上刚体的质量与两轴间距离d的二次方的乘积。
数据处理：1．铝环：质量M = kg; D1 = cm; D2 = cm由式（16）可求圆环绕过质心与环面垂直的转轴的转动惯量J环，理= ；与测量值J环，测= ;比较可得：ΔJ环= J环，测 - J环，理 = ;相对误差：E =ΔJ环/J环= %.2．铝圆盘：质量M = kg; D = cm同理，由式（16）可求圆盘绕过质心与环面垂直的转轴的转动惯量J盘，理= ；与测量值J盘，测= ;比较可得：ΔJ盘= J盘，测– J盘，理 = ;相对误差：E =ΔJ盘/J盘= %*3.由[实验步骤]3的测量结果分别计算a., b.两种情况下两移轴砝码对中垂轴OO’的转动惯量J a和J b，并讨论之。
已知两移轴砝码总质量 M = 2×0.167kg砝码直径Φ= 3.0cm思考题：1．简要分析影响本实验测量结果的各种因素是什么？如何减少它们对实验结果的影响？2．本实验测量转动惯量的原理是什么？附录：HMS-2“通用电脑毫秒计”使用说明一、技术性能本仪器由单片机芯片和固有程序等组成。
具有记忆存储功能，最多可记64个脉冲输入的（顺序的）时间，并可随意提取数据，还可以调整为脉冲的编组计时。
它有备用通道，即双通道“或”门输入。
此仪器为可编程记忆式双路毫秒计。
1．输入脉冲宽度：不小于10μs2．计时范围：0-999.999秒3．计时误差：≤0.0005秒4．计时数组：1-645．适用电源：∽220V , 50Hz二、板面（如下图）①为2位脉冲个数数码块；②为6位计时数码块；③为按键数据码盘；④、⑤分别为输入I输入插孔和通断开关；⑥、⑦分别为输入II输入插孔和通断开关；⑧为电源；⑨为复位键。
三、使用方法1．用电缆连接光电门的发光管和输入脉冲，只接通一路（另一路备用）。
2．若只用输入I插孔输入，请将该输入通断开关接通，输入II通断开关断开（切记）。
反之亦然。
若从两输入插孔同时输入信号，请将两通断开关都接通。
3．接通电源：仪器进入自检状态。
板面显示88-888888四次后，显示为P0164，它表明制式（P）为每输入1个（光电）脉冲，计一次时间，最多可记64个时间数据，小于64个也可以被储存和提取数据。
4．按一次“←”或“→”键，面板显示00 000000，此时仪器处于待记时状态。
输入第1个脉冲则开始计时。
5．64个脉冲输入后自动停止（小于64也可）。
取出数据的方法如下：按09两数码键，则显示“***.***”精确到毫秒的第一个脉冲到第九个脉冲之间的时间，依次类推；按01键，则显示“000.000”表示计时开始的时间。
按“→”键一次，则脉冲记时的个数递增1，因此方便地依次提取数据（按“←”键则递减）。
（1）按“9”键两次，仪器又处于新的待记时状态，并把前次数据消除。
（2）按复位键，仪器为在电的重启。
四、调整制式的方法当启动按“←”或“→”键后显示P0164。
这里，01表示制式（P）每一个（光电）脉冲计数一次，64表示计64个数据。
因此，可以通过改变PXXYY中的XX值和YY值，获得不同的计数方式（XX有上限，YY最大值为64）。
例如在P0164制式下，按1，2，3，0键，则面板将显示P1230。
这种制式下，每12个脉冲计数1次，总共计30个数据，提取数据的办法同前。
这样，就能根据不同的实验要求，来选择相应最合适的计数方式，从而大大增强了仪器的适应性。
五、注意事项1．注意光敏管的正、负极性。
2．光敏管电阻小于3KΩ才能正常工作。
3．如果用一路输入插孔输入信号，另一路通断开关必须断开。
