当前位置：文档之家 › 最全的转动惯量的计算ppt课件

最全的转动惯量的计算ppt课件

  • 格式：ppt
  • 大小：1008.00 KB
  • 文档页数：25

下载文档原格式

  / 25

合集下载

转动惯量理论力学

转动惯量理论力学
角用α，β，γ表示 （如图14）。
z
刚体对轴OL的转动惯量
式中
J mrL2
rL2 (OA)2 (OB)2
其中OB是矢 r =OA 在轴OL上的投影。 由矢量投影定理得
OB x cos y cos z cos
因 ( OA )2 x2 y2 z2 ，故
L α B rL A
O
β
y
J x mrx2 m( y2 z2 )
J y mry2 m(z2 x2) J z mrz2 m(x2 y2)
rz
A
O
z
x
rz
y
x
y
图2
转动惯量
§1 转动惯量的概念
4.极转动惯量
对于平面薄板，使平板表面重合于坐标平面Oxy（如图3），
如果薄板内各点的坐标 z 可以忽略，则式简写成
O
z
rz
y
x
x y
图1
在国际单位制中，转动惯量的常用单位是kg·m2 。
转动惯量
§1 转动惯量的概念
2.回转半径
刚体对于某轴z的转动惯量与其质量m之比值的平方根为一 个当量长度，称为刚体对于该轴的回转半径。因此，有关系式
z
Jz , m
J z mz2
可见，如果假想地把刚体的全部质量集中于一点，而不改变 这刚体对于该轴的转动惯量，则这个点到该轴的距离应等于回转 半径。
解：取任一半径为ζ，宽为dζ的圆环，其质量是
dm
m πr2
2πd
2m r2
d
对轴z的转动惯量元素是
dJ z
(dm)
2
2m r2
3d
于是，求得圆盘对轴z转动惯量
y
r

力矩转动定律转动惯量解析课件

力矩转动定律转动惯量解析课件

02
CATALOGUE
转动惯量基础概念
转动惯量的定义
转动惯量
描述刚体绕固定轴转动的惯性大 小的物理量。
定义公式
I = Σ(m * r^2)，其中m为刚体的 质量，r为刚体上任意质点到转动 轴的距离。
转动惯量的性质
转动惯量只与刚体的质量分布 和转动轴的位置有关，与刚体 的运动状态无关。
对于同一刚体，不同的转动轴 位置，其转动惯量可能不同。
力矩转动定律转动 惯量解析课件
contents
目录
• 力矩转动定律概述 • 转动惯量基础概念 • 力矩与转动惯量的关系 • 转动惯量的计算方法 • 转动惯量的应用实例
01
CATALOGUE
力矩转动定律概述
力矩的定义
力矩是描述力的转动效果的物理量，其大小等于力和力臂的乘积。
力矩是一个向量，其大小等于力和力臂的乘积。力臂是从转动轴到力的垂直距离 。在二维平面中，力矩可以表示为M=F×r，其中F是力，r是力臂。
CATALOGUE
转动惯量的应用实例
飞轮的设计与优化
飞轮的设计
飞轮是利用转动惯量储存能量的重要 装置，其设计需要考虑转动惯量的大 小、质量分布、转速等因素。
飞轮的优化
为了提高飞轮的储能效率和稳定性， 需要对飞轮进行优化设计，如采用轻 质高强度的材料、优化飞轮的形状和 尺寸等。
陀螺仪的设计与优化
陀螺仪的设计
陀螺仪是利用角动量守恒原理工作的惯性导 航和姿态测量器件，其设计需要考虑转动轴 的稳定性、转动惯量的大小和分布等因素。
陀螺仪的优化
为了提高陀螺仪的测量精度和稳定性，需要 对陀螺仪进行优化设计，如采用高性能的轴 承材料、减小摩擦力矩等。
电机转子的设计与优化

最全的转动惯量的计算 ppt课件

最全的转动惯量的计算 ppt课件

aCX C
mg
N
NY
求N，N就Y得求maCg
maCY
，即C点的
NX
C 加速度，现在C点作圆周运动， mg 可分为切向加速度和法向加速
度但对一点来说，只有一个加
速度。故这时：
aCX ….实际上正是质心的转动的切向加速度 aCY ….实际上正是质心ppt课的件 转动的法向加速度23
N
XO N
aCX
YZ
当 l > R 2时，f < 0，静摩擦力向前。
ppt课件
16
例一静止刚体受到一等于M0（N.m)的不变力矩的 作用,同时又引起一阻力矩M1， M1与刚体转动的 角速度成正比,即| M1 |= a(Nm),(a为常数)。又
已知刚体对转轴的转动惯量为J,试求刚体角速度
变化的规律。
已知：M0 J M1= –a |t=0=
N YZ
L
已知：m，L
XO
求：，，N 解：1）以杆为研究对
象
mg
受力：mg，N（不产生 对轴的力矩）
建立OXYZ坐标系
ppt课件
19
建立OXYZ坐标系（并以Z轴为转动量的正方向）
N
Y
M
Z
L
XO
r
M mg L sin
r故取JF正值沿。13Z轴m正2L2向，(1)
mg 0则 0
/ 2则 3g / 2L
N
YZ
XO
r
d /2 3g cosd
0
0 2L
1 2
2
3g 2L
sin
0
/
2
3g 2L
mg
3g L
3）求N=？ 轴对杆的力，不影响到杆的转动，但影响质 心的运动，故考虑用p质pt课件心运动定理来解。 22

最全的转动惯量的计算

最全的转动惯量的计算

v R
4m gh 2m M R
例题3 一质量为m、半径为R的均质圆柱，在水 平外力作用下，在粗糙的水平面上作纯滚动，力 的作用线与圆柱中心轴线的垂直距离为l，如图所 示。求质心的加速度和圆柱所受的静摩擦力。 解：设静摩擦力f的方向如 图所示，则由质心运动方程

l ac
F
圆柱对质心的转动定律：
F f maC
f
F l f R JC
纯滚动条件为： aC R
1 2 圆柱对质心的转动惯量为： J C mR 2
联立以上四式，解得：
2F (R l ) aC 3mR
由此可见
R 2l f F 3R
当 l < R 2时， > 0，静摩擦力向后； f
当 l > R 2时， < 0，静摩擦力向前。 f
例一静止刚体受到一等于M0（N.m)的不变力矩的 作用,同时又引起一阻力矩M1， M1与刚体转动的 角速度成正比,即| M1 |= a(Nm),(a为常数)。又 已知刚体对转轴的转动惯量为J,试求刚体角速度 变化的规律。 已知：M0 J M1= –a |t=0= 0 求：（t）=？ 解： 1）以刚体为研究对象； M+ 2）分析受力矩 M0 J M 1 3）建立轴的正方向； 4）列方程：
2）=？
Y Z
2）=？
N YZ



0
XO
r
mg
3g d cosd 0 2L 1 2 3g / 2 3g sin 0 2 2L 2L
/2
3g L
3）求N=？ 轴对杆的力，不影响到杆的转动，但影响质 心的运动，故考虑用质心运动定理来解。

§5转动惯量

§5转动惯量

I
J y I yy y I yx x I yzz
J z Izzz Izx x Izy y
四、惯量椭球
O为刚体定点转动的定点， 在转轴上截取OQ,满足
OQ 1 R 即 R2I 1 I
z

Qx, y, z
O
y
x
R2 I xx 2 I yy 2 I zz 2 2I xy 2I xz 2I yz 1
i
i
对y轴的轴转动惯量 I yy mi xi2 zi2 , i
对z轴的轴转动惯量 Izz mi xi2 yi2 , i
I xz Izx mi xi zi i I yz Izy mi yi zi i
I 2dm
I xx ( y2 z2 )dm I yy ( x2 z2 )dm Izz ( x2 y2 )dm
I yy y I yx x I yz z ˆj I zz z Izxx Izy y kˆ
将W、J代入
T

1

J
2
T 1 2
I
xx
2 x

I
yy
2 y

I
2
zz z

2I xyx y

2I xzxz

2I yz yz
Q点坐标
x R, y R , z R
Q点构成椭球: 惯量椭球
I xx x 2 I yy y2 I zz z 2 2I xy xy 2I xz xz 2I yz yz 1
1.如果定点O正好是刚体的质心或重心，则此椭球称中心惯 量椭球。

最全的转动惯量的计算

最全的转动惯量的计算

F f maC
f
F l f R JC
纯滚动条件为： aC R
1 2 圆柱对质心的转动惯量为： J C mR 2
联立以上四式，解得：
2F (R l ) aC 3mR
由此可见
R 2l f F 3R
当 l < R 2时， f > 0，静摩擦力向后；
当 l > R 2时， f < 0，静摩擦力向前。
（2）当转轴通过棒的一端A并与棒垂直时
A
x
O
l
dx
1 2 J 0 r dm x dx ml 0 3
2 l 2
例题2）半径为R的质量均匀分布的细圆环，质 量均为m，试分别求出对通过质心并与环面垂 直的转轴的转动惯量。
dl
R
例题3 求质量为m、半径为R、厚为h的均质圆盘 对通过盘心并与盘面垂直的轴的转动惯量。
v R
4m gh 2m M R
例题3 一质量为m、半径为R的均质圆柱，在水 平外力作用下，在粗糙的水平面上作纯滚动，力 的作用线与圆柱中心轴线的垂直距离为l，如图所 示。求质心的加速度和圆柱所受的静摩擦力。 解：设静摩擦力 f 的方向如 图所示，则由质心运动方程

l ac
F
圆柱对质心的转动定律：
解：如图所示，将圆盘看成许多薄圆环组成。取 任一半径为r，宽度为dr的薄圆环，此薄圆环的转 动惯量为
dJ r dm
2
dm为薄圆环的质量。以 表示圆盘的质量体密度
dm dV 2rhdr
dJ 2r hdr
3
代入得
1 4 J dJ 2r hdr R h 0 2 m 2 R h

转动惯量课件 PPT

转动惯量课件 PPT

i
a (b c) b(a c) c(a b)
mi[ωri2 ri (ω ri )]
i
ri xiex yiey ziez
(1)
静止系或活
(2)
动系都可以
ω xex yey zez
(3)
(2)(3)代入(1)可得 J J xex J yey J zez
3、5、1 刚体得动量矩
做定点转动的刚体
则点集{Q1,Q2,…,Qn,…}在空间密布成一个椭球 面,此椭球称为此刚体得惯量椭球。
3、5、4 惯量张量与惯量椭球
惯量椭球得概念
求证：定点转动刚体上满足 OQ 1 所有点Q
构成一个椭球面。
I
证明: 在刚体上建立活动系O-xyz, 并设瞬轴l的方
向余弦为 , , 。
令 OQ 1 R
y
ω l 解:如图建立主轴坐
标系。
b
O
a
薄板对对角线l的转 x 动惯量，在主轴坐标
系下的计算式为
Il I1 2 I2 2 I3 2 (1)
其中I1,I2,I3分别是薄板对三个坐标轴的转动惯量， 是对角,线, l的三个方向余弦。
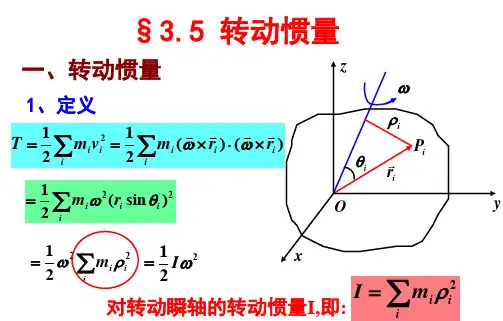
3、5 转动惯量
例题
对角线l得三个方向余弦分别为
y
ωl
cos a
(
I
xx
2 x
I
yy
2 y
I
zz
2 z
2I xyx y
2I yz yz
2I zxzx )
3、5、3 转动惯量得概念
由转动动能引入转动惯量
T 1
2
i
mivi vi
1 2
i
mi (ω ri ) (ω ri )
ez ω

转动惯量PPT课件

转动惯量PPT课件
匀质球体组成的刚体，
m2 R
对Z轴的转动惯量为
Jz J杆 J球

1 3
m1l
2

2 5
m2 R 2

m2
lR
2
21
圆环： 转轴通过中心与环面垂直
薄圆盘： 转轴通过中心与盘面垂直
圆柱体： 转轴沿几何轴
细棒： 转轴通过中心与棒垂直
球体： 转轴沿直径
转轴沿直径
圆筒： 转轴沿几何轴
圆柱体： 转轴通过中心与几何轴垂直
r 2dr
整个圆盘产生的摩擦力矩为

m
M阻 dM阻
ro R
2mg R r2dr
R2 0
dr

2 mgR
3
39
根据转动定律：
M J J d
dt
其中M 为常量，将上式分离变量并积分，则
t
0
M dt J d
0
0
t

J0

1 2
平
刚体运动
动
转 动
A
c
A
c
（质点A既随质心平动又绕质心转动）
刚体运动微分方程式
质心运动定理 刚体质心运动（平动）
角动量定理 刚体的取向与方位（转动）
刚体运动积分方程式
动能定理 刚体的平动和转动 5
作用于刚体上的力
力的 两种效果
使质心平动 绕质心转动
施于刚体的力不是自由矢量
B
A
F
B
F
A
力的作用线过质心 （平动）
即
Lz J

r mi v
2、转动定理 由于刚体的转动惯量为常量，所以有

大学物理转动惯量ppt

大学物理转动惯量ppt

例题6 计算正方形框架ABCD对通过O的转轴的转动 惯量，每一个边的质量为m
每一边对通过一边中心转轴的转动惯量
J1
1 12
ml 2
—— 每一边对ABCD质心转轴 的转动惯量
J1
'
1 12
ml 2
m( 1 2
l)2
1 3
ml 2
四条边对通过ABCD质心转轴的转动惯量 JC 4J1 '
05_03_转动惯量的计算 —— 力学
J mR2
05_03_转动惯量的计算 —— 力学
04/09
例题5 计算半径为R 、质量为M匀质薄圆盘对通过 其中心O并垂直于盘面的Z轴的转动惯量
距离中心r、宽度为dr的同心环对转轴的转动惯量
dJO r2dm r2
dr
圆盘对垂直圆心转轴的转动惯量
JO
R 0
r 3 2
1 3
ML2
05_03_转动惯量的计算 —— 力学
03/09
例题4 计算质量为m，半径为R的均匀薄圆环对通过 圆心垂直于环面轴的转动惯量
圆环上质量元dm对转 轴的转动惯量
dJ R2dm dm m dl
2 R
dJ mR dl
2
薄圆环对通过圆心 垂直环面轴的转动 惯量
J 2 R mR dl
0 2
R12 )
05_03_转动惯量的计算 —— 力学
06/09
平行轴定理
已知刚体对通过质心转轴的转动惯量 J C
另 有 一 个 与 质 心 转 轴 CZ 平行的转轴OZ’，该转轴 与质心转轴的距离为h， 刚体对OZ’转轴的转动惯 量为
JO JC Mh2
05_03_转动惯量的计算 —— 力学

最全的转动惯量的计算

最全的转动惯量的计算
? dl
R
例题3 求质量为m、半径为R、厚为h的均质圆盘 对通过盘心并与盘面垂直的轴的转动惯量。
解：如图所示，将圆盘看成许多薄圆环组成。取 任一半径为 r，宽度为dr的薄圆环，此薄圆环的转 动惯量为
dJ ? r 2dm
dm为薄圆环的质量。以 ? 表示圆盘的质量体密度
dm ? ?dV ? ? ?2?rhdr
M+
2）分析受力矩
M0 J M1
3）建立轴的正方向； 4）列方程：
M 0 ? M1 ? J?
解：4）列方程：
M 0 ? M1 ? J?
? ? M 0 ? M1? M 0 ? a?
M+ M0
M1=–a?
d? ? M 0 ?J a?
dt
J
J
? 1 (ln M0 ? a? ) ? t
分离变量：
a
M0
Jd? dt?源自M0 ? a? J? ? ? d?
t dt ?
0 M 0 ? a?
解：对定滑轮 M ，由转动定律， 对于轴 O，有
RT ? J? ? 1 MR 2 ?
2
对物体 m ，由牛顿第二定律，
mg ? T ? ma
?
RO ?
M
T1
T2 a
mg h
滑轮和物体的运动学关系为 a ? R?
以上三式联立，可得物体下落的加速度为 a? m g m? M 2
物体下落高度 h时的速度
v ? 2ah ? 这时滑轮转动的角速度
? ?v?
R
4mgh 2m ? M
4m gh 2m ? M
R
例题3 一质量为 m、半径为 R的均质圆柱，在水 平外力作用下，在粗糙的水平面上作纯滚动，力 的作用线与圆柱中心轴线的垂直距离为 l，如图所 示。求质心的加速度和圆柱所受的静摩擦力。

最全的转动惯量的计算(教育类别)

最全的转动惯量的计算(教育类别)
求N，就得求 aC ，即C点的
NX
C 加速度，现在C点作圆周运动， mg 可分为切向加速度和法向加速
度但对一点来说，只有一个加
速度。故这时：
aCX ….实际上正是质心的转动的切向加速度 aCY ….实际上正是质心培训类的转动的法向加速度23
N
XO N
aCX
YZ
aCY
C
mg
由角量和线量的关NN系YX :mmgaC23XmgL asiCnY
解:受力分析
取任一状态,由转动定律
M外
1 2
mgl
sin
J
P o
J 1 ml 2 3
3g sin
2l
培训类
11
d d d 3g sin d t d d t 2l
d 3g sind
2l
初始条件为：=0，=0
d
3g
sin d
0
2l 0
3g (1 cos )
2l
培训类
12
例题2 一个质量为M，半径为R的定滑轮（当作均 匀圆盘）上面绕有细绳。绳的一端固定在滑轮边 上，另一端挂一质量为m的物体而下垂。忽略轴处 摩擦，求物体m由静止下落h高度时的速度和此时 滑轮的角速度。
d Z 心Z高处切一厚为dz的薄圆 盘。其半径为
O X
R
Y r R2 Z2
其体积：
dV r2dZ (R2 Z 2 )dZ
其质量： dm dV (R2 Z 2 )dZ
其转动惯量：dJ 1 r2dm 1 (R2 Z 2 )2 dZ
2 2 培训类
7
dJ 1 r 2dm 2
1 (R2 Z 2 )2 dZ
r 2dm l 2 x2dx l3
l 2

《转动惯量的计算》课件

《转动惯量的计算》课件
刚体的转动惯量可以通过对每个质点的转动惯量求和 得到。
常见形状的转动惯量公式
涵盖了圆盘、长棒、球体等常见形状的刚体转动惯量
转动惯量的实验测定
1
二次转动法
通过测量刚体在不同轴上的旋转惯量，判断转Βιβλιοθήκη 惯量的大小。2转动摆法
利用转动摆的运动进行转动惯量的实验测定。
3
牛顿第二定理法
根据牛顿第二定理，实验测定刚体的转动惯量。
总结
1 转动惯量的重要性
转动惯量是研究物体旋转运动的关键参数，对于理解物体的稳定性和运动规律至关重要。
2 转动惯量计算方法的应用
掌握转动惯量计算方法可以帮助我们解决各种旋转运动的问题，推导出物体的运动方程。
3 研究转动惯量的意义和作用
研究转动惯量可以帮助我们深入理解物体的旋转运动规律，拓展我们的物理知识。
质点的转动惯量
定义
质点绕某一轴旋转时的转动惯 量是指质点对该轴的抵抗程度。
计算公式
质点的转动惯量等于质量与离 轴距离之积的总和。
常见形状的转动惯量公式
涵盖了球体、长方体、圆柱体 等常见形状的转动惯量计算公 式。
刚体的转动惯量
定义
刚体的转动惯量是指刚体绕某一轴旋转时，对该轴的 整体抵抗程度。
计算公式
参考文献
本课件参考了相关物理学教材和科研论文。
转轴的平移对转动惯量的影响
平行轴定理
平行轴定理说明了转轴平移时，转动惯量的计算公 式的变化规律。
垂直轴定理
垂直轴定理说明了转轴垂直平移时，转动惯量的计 算公式的变化规律。
应用实例
圆环的转动惯量计算
通过应用公式计算圆环绕垂直直径轴的转动惯量。
圆柱的转动惯量计算
通过应用公式计算圆柱绕其轴线的转动惯量。

最全的转动惯量的计算

最全的转动惯量的计算

取任一状态,由转动定律

P o
1 M 外 mgl sin J 2
1 2 J ml 3
3g sin 2l
d d d 3 g sin d t d d t 2l
3g d sin d 2l
初始条件为：=0，=0


0
3g d 2l
2
3g L
N Y Z XO
aCX
N
aCY
C
代入(1)、（2）式中：
NY mg maCY (2) 3g aCX 0 aCY 2
N X maCX (1)
mg
N X maCX 0 NY mg maCY 3g 5 mg m mg 2 2 5 N mgˆ j 2
1 RT J MR 2 2
M
T1 T2 a mg h
对物体m，由牛顿第二定律，
mg T ma
滑轮和物体的运动学关系为 a R
以上三式联立，可得物体下落的加速度为
m a g mM 2
物体下落高度h时的速度
4m gh v 2ah 2m M
这时滑轮转动的角速度
建立OXYZ坐标系
建立OXYZ坐标系（并以Z轴为转动量的正方向） N
M Y
Z
XO
r
L
0则 0 / 2则 3g / 2 L M mg sin 3g sin 1 2 J 2 L mL 3
mg
r J F mL 故取正值。 3
L M mg sin 2 ( 1 ) 沿1 Z轴正向， 2
例题1 求质量为m，长为l的均匀细棒对下面转轴 的转动惯量：(1)转轴通过棒的中心并和棒垂直； (2) 转轴通过棒的一端并和棒垂直。

最全的转动惯量的计算

最全的转动惯量的计算

3g N sin 2L d d d XO r dt d dt d 3g mg sin( ) d 2 L 2 3g d cos d 2L /2 3g cosd 两边积分： d 2L 0 0
5.3 定轴转动的转动惯量
• 质量离散分布的刚体 • 质量连续分布的刚体
J mi ri
2
J r dm
2
dm为质量元，简称质元。其计算方法如下：
质量为线分布 dm dl
质量为面分布 dm ds 质量为体分布
dm dV
J与质量大小、质量分布、转轴位置有关 演示程序： 影响刚体转动惯量的因素
dl
R
例题3 求质量为m、半径为R、厚为h的均质圆盘 对通过盘心并与盘面垂直的轴的转动惯量。
解：如图所示，将圆盘看成许多薄圆环组成。取 任一半径为r，宽度为dr的薄圆环，此薄圆环的转 动惯量为
dJ r dm
2
dm为薄圆环的质量。以 表示圆盘的质量体密度
dm dV 2rhdr
N Y Z XO
N X maCX 3g NY mg ma sin CY
由角量和线量的关系:
aCX
N
aCY
2L
C
mg
aCX R L 3g sin 0 0 2 2L 2 aCY R
L 3g 3 g 2 L 2



0
sin d
3g (1 cos ) 2l
例题2 一个质量为M，半径为R的定滑轮（当作均 匀圆盘）上面绕有细绳。绳的一端固定在滑轮边 上，另一端挂一质量为m的物体而下垂。忽略轴处 摩擦，求物体m由静止下落h高度时的速度和此时 滑轮的角速度。 解：对定滑轮 M ，由转动定律， R O 对于轴O，有

5.4 转动惯量的计算

5.4 转动惯量的计算
5.4 转动惯量的计算
dm
mr
转轴
分散系统
J
mi
ri
2
连续体
J r2 d m m
J 由质量对轴的分布决定，与转动状态无关。
一. 常见刚体的转动惯量的计算
1、细圆环
z
R C
m
dm
JC mR2
J r2dm m
2、均匀圆盘
z
JC

1 2
mR2
dm
C Rm
r dr
JC

R
R
r 2dm 2rdr
m
0
0
R 2
r2
1 mR2 2
3、均匀细杆 m l
zA
dr
对A轴的转动惯量
A
r dm
JA

1 3
m l2
J A

l 0
r 2dm

l 0
r2
m l
dr

1 ml2 3
AC
m 对过质心C轴的转动惯量l Nhomakorabeal
2
2
zC
JC

1 ml2 12
二、计算转动惯量的几条规律
J Jc md 2
平行轴定理应用
z
zc
求相对于求外任 一轴的转动惯量
JC

2 mR2 5
3、对薄平板刚体的正交轴定理
z
薄板刚体
xi O x
ri
yi
Oxyz 在刚体平面内
y
mi (xi, yi, zi )
J z miri2 mi xi2 mi yi2
Jx mi zi2 mi yi2 J y mi zi2 mi xi2

10-转动惯量PPT

10-转动惯量PPT

转动惯量
设xoy 平面上有n 个质点，它们分别位于),(11y x ，),(22y x ，, ),(n n y x 处，质量分别为n m m m ,,,21 ．则该质点系对于x 轴和y 轴的转动惯量依次为
∑==n i i i x y m I 12， ∑==n i i i y x m I 12
.
1、平面质点系的转动惯量
,),(2
⎰⎰=D
x d y x y I σρ.),(2
⎰⎰=D
y d y x x I σρ 设有一平面薄片，占有xoy 面上的闭区域D ，在点),(y x 处的面密度为),(y x ρ，假定),(y x ρ在D 上连续，平面薄片对于x 轴和y 轴 的转动惯量为
薄片对于轴的转动惯量
x 薄片对于轴的转动惯量y 2、平面薄片的转动惯量
设物体占有空间区域，有连续的密度函数，应用“元素法”，得
Ω),,(z y x ρ对轴的转动惯量是
z ⎰⎰⎰Ω+=dv z y x y x I z ),,()(2
2ρ⎰⎰⎰Ω
+=dv z y x z y I x ),,()(2
2ρ⎰⎰⎰Ω
+=dv z y x x z I y ),,()(2
2ρ轴的转动惯量分别是
轴和对y x
o x
y
D
a a 径的转动惯量
的均匀半圆薄片对其直求半径为例a .3、例题
r r a
d d sin 0302⎰⎰=π
θθμ解: 建立坐标系如图,⎩⎨⎧≥≤+
0:2
22y a y x D y x y I D x d d 2⎰⎰=∴μ⎰⎰=D r r θθμd d sin 23241a M =半圆薄片的质量μπ221a M =。

转动惯量和飞轮矩 PPT

转动惯量和飞轮矩 PPT

R
RGD2 dn
n n0 CeCm 2 TL 375CeCm • dt
(1、21) (1、22)
n ns （nini ns）et/Tm
(1、23)
1、2、5 直流她励电动机传动得动态特 性
描绘出系统动态特性得三要素: 初始值、稳态值与系统得机电时间常数
n ns （nini ns）et/Tm
如图1、1所示, 电动机 带动工作机械得电气传动 系统得运动规律取决于电 机得输出转矩与负载转矩 之间得关系, 并符合刚体 旋转得运动定律 ,即式(1、 1)
TM TL d (J) / dt
图1、1 电气传动系统
（1.1）
1、1、1 基本运动方程式
省略空载转矩时,旋转运动方程式如(1、2)所示。
转动惯量和飞轮矩
第1章 电气传动基础
1、1 电气传动得动力学基础 1、2 直流她励电动机得机械特性及运行方
法 1、3 异步电动机得机械特性及运行方法
1、1 电气传动得动力学基础
1、1、1 基本运动方程式 1、1、2 转矩、飞轮矩得折算 1、1、3 电动机得机械特性与负载转矩特
性
1、1、1 基本运动方程式
I Is （Iini Is）et/Tm
T Ts （Tini Ts）et/Tm
（1.24） （1.25） （1.26）
1、2、5 直流她励电动机传动得动态特 性
2、直流她励电动机启动动态特性
n ns （nini ns）et/Tm
I Is （Iini Is）et/Tm
T Ts （Tini Ts）et/Tm
(1、3)
工程计算中,往往不用转动惯量J,而用飞轮矩 ,两
者之GD间2 得关系如式(1、4)
J m 2 mD2 / 4 GD2 / 4g (1、4)
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

有
l
J0
r 2dm l 2 x2dx l3
l 2
12
将 l m 代入上式，得：
J0

1 12
ml 2
2
（2）当转轴通过棒的一端A并与棒垂直时
A
xO
dx l
J0
r2dm l x2dx 1 ml 2
ቤተ መጻሕፍቲ ባይዱ
0
3
3
例题2）半径为R的质量均匀分布的细圆环，质 量均为m，试分别求出对通过质心并与环面垂 直的转轴的转动惯量。
x
9
常见刚体的转动惯量
J mr 2 J mr2 / 2 J mr2 / 2 J m(r12 r22) / 2
J ml 2 /12
J mr2 / 2
J 2mr 2 / 5 J 2mr 2 / 3
10
例题1 一长为l,质量为m的匀质细杆竖直放置, 其下端与一固定铰链o相连,并可绕其转动.当其 受到微小扰动时,细杆将在重力的作用下由静止
开始绕铰链o转动.试计算细杆转到与铅直线呈
角时的角加速度和角速度.
解:受力分析
取任一状态,由转动定律

M外

1 2
mgl sin

J
P o
J 1 ml2 3
3g sin
2l
11
d d d 3g sin d t d d t 2l
d 3g sind
16
例一静止刚体受到一等于M0（N.m)的不变力矩的 作用,同时又引起一阻力矩M1， M1与刚体转动的 角速度成正比,即| M1 |= a(Nm),(a为常数)。又
已知刚体对转轴的转动惯量为J,试求刚体角速度
变化的规律。
已知：M0 J M1= –a |t=0=
求：（t）=？
0
解： 1）以刚体为研究对象；
M0
J
d dt M 0 a J
d
t dt

0 M 0 a 0 J
M0
a
at
e J
M0
18
例）设一细杆的质量为m，长为L，一端支以
枢轴而能自由旋转，设此杆自水平静止释放。
1
例题1 求质量为m，长为l的均匀细棒对下面转轴 的转动惯量：(1)转轴通过棒的中心并和棒垂直； (2) 转轴通过棒的一端并和棒垂直。
解：(1) 在棒上离轴x处，取一长度元dx（如图所 示），如果棒的质量线密度为，则长度元的质
量为dm=dx，根据转动惯量计算公式：
J r2dm
A
Ox
dx
1 (R2 Z 2 )2 dZ
2
J dJ
R 1 (R2 Z 2 )2 dZ R2
8 R5 2 mR2
15
5
m 4 R3
3
8
（1）平行轴定理
J D JC md 2
JC JD
d
C
z （2）薄板的正交轴定理
o
y
Jz Jx Jy
这时滑轮转动的角速度
4mgh
v 2m M
R
R
14
例题3 一质量为m、半径为R的均质圆柱，在水 平外力作用下，在粗糙的水平面上作纯滚动，力 的作用线与圆柱中心轴线的垂直距离为l，如图所 示。求质心的加速度和圆柱所受的静摩擦力。
解：设静摩擦力f的方向如 图所示，则由质心运动方程
F f maC
解：对定滑轮M，由转动定律， 对于轴O，有
RT J 1 MR2
2
对物体m，由牛顿第二定律，
mg T ma

RO
M
T1
T2 a
mg h
滑轮和物体的运动学关系为 a R
13
以上三式联立，可得物体下落的加速度为 a m g mM 2
物体下落高度h时的速度
v 2ah 4mgh 2m M
2l
初始条件为：=0，=0

d

3g

s in d
0
2l 0
3g (1 cos )
2l
12
例题2 一个质量为M，半径为R的定滑轮（当作均
匀圆盘）上面绕有细绳。绳的一端固定在滑轮边 上，另一端挂一质量为m的物体而下垂。忽略轴处 摩擦，求物体m由静止下落h高度时的速度和此时 滑轮的角速度。
圆柱对质心的转动定律：
Fl f R JC

F l ac f
纯滚动条件为： aC R
圆柱对质心的转动惯量为：
JC

1 mR2 2
15
联立以上四式，解得：
2F(R l) aC 3mR
由此可见
f R 2l F 3R
当l < R 2时，f > 0，静摩擦力向后；
当 l > R 2时，f < 0，静摩擦力向前。
dJ 2r3hdr
J dJ R 2r3hdr 1 R4h
0
2


m
R2h
代入得
J 1 mR2
2
J与h无关
一个质量为m、半径为R的实心圆柱体对其中心 轴的转动惯量也与上述结果相同。
6
例4）求一质量为m的均匀实心球对其一条直径
为轴的转动惯量。
Z
解：一球绕Z轴旋转，离球
M+
2）分析受力矩
M0 J M1
3）建立轴的正方向； 4）列方程：
M 0 M1 J 17
解：4）列方程：
M0 M1 J M 0 M1 M 0 a
M+ M0
M1=–a
d M 0 J a
dt
J
J
1 (ln M 0 a ) t
分离变量：
a
dl
R
4
例题3 求质量为m、半径为R、厚为h的均质圆盘 对通过盘心并与盘面垂直的轴的转动惯量。
解：如图所示，将圆盘看成许多薄圆环组成。取 任一半径为r，宽度为dr的薄圆环，此薄圆环的转 动惯量为
dJ r2dm
dm为薄圆环的质量。以 表示圆盘的质量体密度
dm dV 2rhdr 5
5.3 定轴转动的转动惯量
• 质量离散分布的刚体 J miri2
• 质量连续分布的刚体 J r 2dm
dm为质量元，简称质元。其计算方法如下：
质量为线分布 dm dl 质量为面分布 dm ds
质量为体分布 dm dV
J与质量大小、质量分布、转轴位置有关 演示程序： 影响刚体转动惯量的因素
Zr
d Z 心Z高处切一厚为dz的薄圆 盘。其半径为
O X
R
Y r R2 Z2
其体积：
dV r2dZ (R2 Z 2)dZ
其质量： dm dV (R2 Z 2)dZ
其转动惯量：dJ 1 r2dm 1 (R2 Z 2 )2 dZ
2
2
7
dJ 1 r 2dm 2