1
0
3 y 2 dy 3
5
5 y x3, x 1, x轴
绕y轴旋转一周
1
Vy
0
3 y 2 dy 2
5
y
.,
y=x3 1
y=x3
9
1
◆练习:写出下列旋转体体积的定积分表达式
绕x轴旋转一周
V 2
1
x2 1 2 dx 22
2 1
0
2 x4dx
32 2 3 2
0
1 y x3, x 1, y 0
绕x轴旋转一周
x3, y 1, x 0
绕x轴旋转一周
y=x3 x1
1
Vx
1
dx
0
1
x6dx
6
0
7
.,
y=x3
x
1
8
◆练习:写出下列旋转体体积的定积分表达式
4 y x3, y 1, y 轴
1
绕y轴旋转一周
y
Vy
d x2dy
c
d
c
g( y) 2 dy
.,
c
x=g 5(y)
◆旋转体的体积计算公式
例2 连接坐标原点 O 及点 P( h , r) 的直线,
直线 x=h及 x轴围成一个直角三角形,将它绕
x轴旋转构成一个底半径为 r,高为 h的圆锥,
计算圆锥的体积。
y P(h,r)
解 :如图所示
直线OP的方程为 y r x ,
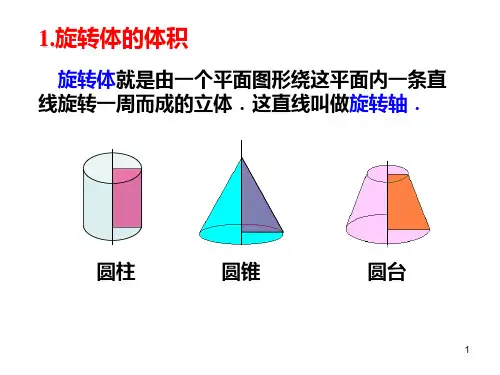
旋转体的定义:旋转体就是由一个平面图形饶 这平面内一条直线旋转一周而成的立体.这直 线叫做旋转轴。
可选取适当坐标系,使旋转轴为x轴或y轴
最基本的情形是曲边梯形绕x轴或y轴旋转的情形。