信与系统课后习题答案汇总

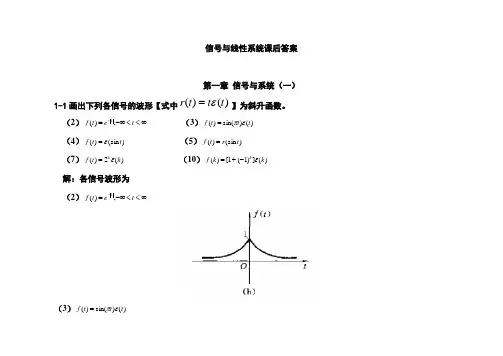
信号与线性系统课后答案第一章 信号与系统（一）1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。

（2）∞<<-∞=-t e t f t ,)( （3）)()sin()(t t t f επ= （4）)(sin )(t t f ε= （5）)(sin )(t r t f = （7）)(2)(k t f k ε= （10）)(])1(1[)(k k f k ε-+= 解：各信号波形为 （2）∞<<-∞=-t e t f t ,)(（3）)()sin()(t t t f επ=（4）)fεt=(sin)(t （5）)tf=r(sin)(t（7）)tf kε(k=(2)（10）)f kεk-=(k+]()1(1[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。

（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ （12）)]()3([2)(k k k f k---=εε 解：各信号波形为 （1）)2()1(3)1(2)(-+--+=t t t t f εεε（2）)2()1(2)()(-+--=t rt rt rtf（5）)2()2()(ttrtf-=ε（8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。

1-4 写出图1-4所示各序列的闭合形式表达式。

1-5 判别下列各序列是否为周期性的。

如果是，确定其周期。

《信号与系统》课后习题参考答案第二章 连续信号与系统的时域分析2-9、（1）解：∵系统的微分方程为：)(2)(3)(t e t r t r '=+'，∴r(t)的阶数与e(t) 的阶数相等，则h(t)应包含一个)(t δ项。

又∵系统的特征方程为：03=+α，∴特征根3-=α∴)()(2)(3t u Ae t t h t -+=δ∴)]()(3[)(2)(33t e t u e A t t h t t δδ--+-+'=')()(3)(23t A t u Ae t t δδ+-'=-将)(t h 和)(t h '代入微分方程（此时e(t)= )(t δ），得：)()(3)(23t A t u Ae t t δδ+-'-+3)(2)]()(2[3t t u Ae t t δδ'=+-∴A=-6则系统的冲激响应)(6)(2)(3t u et t h t --=δ。

∴⎰⎰∞--∞--==t td ue d h t g τττδτττ)](6)(2[)()(3⎰∞-=t d ττδ)(2⎰∞---t d u e τττ)(63 )()(6)(203t u d e u t t ⎰-∞--=τττ )()3(6)(203t u e t u t --=-τ)()1(2)(23t u e t u t -+=- )(23t u e t -=则系统的阶跃响应)(2)(3t u et g t -=。

2-11、解：①求)(t r zi ： ∵系统的特征方程为：0)3)(2(652=++=++αααα，∴特征根：21-=α，32-=α ∴t t zi e C eC t r 3221)(--+= (t ≥0) ②求)(t r zs ：t t e A eA t h 3221)(--+= (t ≥0)，可求得：11=A ，12-=A （求解过程略） ∴)()()(32t u e e t h t t ---=∴)(*)()(*)()]()[(*)()(*)()(3232t u e t u e t u e t u e t u e e t u e t h t e t r t t t t t t t zs --------=-==)()2121()()(21)()(3232t u e e e t u e e t u e e t t t t t t t -------+-=---= ③求)(t r ：)(t r =)(t r zi +)(t r zs ++=--)(3221t te C e C )2121(32t t t e e e ---+- t tt e C e C e 3221)21()1(21---++-+= (t ≥0) ∵)()(t u Ce t r t -=，21=C 21=C ∴ 011=-C ， ∴ 11=C0212=+C 212-=C ∴=-)0(r 21211)0(21=-=+=+C C r zi ， ='-)0(r 2123232)0(21-=+-=--='+C C r zi 2-12、解：（1）依题意，得：)(2)(*)()(t u e t h t u t r tzi -=+)()()(t t h t r zi δ=+∴)(2)]()([*)()(t u e t r t t u t r t zi zi -=-+δ)(2)()()()1(t u e t r t u t r t zi zi --=-+∴)()12()()()1(t u e t r t r t zi zi -=---，两边求导得：)()12()(2)()(t e t u e t r t r t t zi ziδ-+-=-'-- )(2)()()(t u e t t r t r t zi zi--=-'δ ∴)(11)(112)()()1(t p p t p t t r p zi δδδ+-=+-=- ∴)()(11)(t u e t p t r t zi -=+=δ （2）∵系统的起始状态保持不变，∴)()(t u e t r t zi -=∵)()()(t t h t r zi δ=+，∴)()()(t u e t t h t--=δ∴)]()([*)()()(*)()()(33t u e t t u e t u e t h t e t r t r t t t zi ----+=+=δ )()()(t u te t u e t u e tt t ----+=)()2(t u e t t --= 2-16、证：∑∑∞-∞=--∞-∞=--=-=k k t k t k t u e k t t u e t r )3()3(*)()()3(δ∑∞-∞=--=k k t k t u e e )3(3 ∵当t-3k>0即3t k <时：u(t-3k)为非零值 又∵0≤t ≤3，∴k 取负整数，则：3003311)(---∞=∞=----===∑∑e e e e e et r t k k k t k t 则t Ae t r -=)(，且311--=e A 。

信号与系统第三版郑君里课后习题答案第一章习题参考解1，判刑下列信号的类型解：()sin[()];y t A x t = 连续、模拟、周期、功率型信号 。

()()tt y t x e d τττ--∞=⎰ 连续、模拟、非周期、功率型信号。

()(2y n x n =） 离散、模拟、非周期、功率型信号。

()()y n nx n = 离散、模拟、非周期、功率型信号。

1－6，示意画出下列各信号的波形，并判断其类型。

(1) 0()sin()x t A t ωθ=+ 连续、模拟、周期、功率型(2) ()tx t Ae -= 连续、模拟、非周期、只是一个函数，不是物理量。

(3) ()cos 0t x t e t t -=≥ 连续、模拟、非周期、能量型 (4) ()2112,x t t t =+-≤≤ 连续、模拟、非周期、能量型(5) 4()(),0.5kx k k =≥ 离散、模拟、非周期、能量型 (6) 0().j kx k eΩ= 离散、模拟、周期、功率型()sin[()];()()()(2);()()tt y t A x t y t x ed y n x n y n nx n τττ--∞====⎰1－6题，1－4图。

t=-pi:1/200:pi;y1=1.5*sin(2*t+pi/6);subplot(4,1,1),plot(t,y1),title('1.5sin(2*t+pi/6)'),gridy2=2*exp(-t);subplot(4,1,2),plot(t,y2),title('2exp(-t)'),gridt1=0:1/200:2*pi;y3=10*exp(-t1).*cos(2*pi*t1);subplot(4,1,3),plot(t1,y3),title('10exp(-t1)cos(2*pi*t1)'),grid t2=-1:1/200:2;y4=2*t2+1;subplot(4,1,4),plot(t2,y4),title('2x+1'),grid习题1－6 5－6题 n=0:pi/10:2*pi; y=(0.8).^n;subplot(4,1,1),stem(n,y,'fill '),title('(0.8)^n'),grid n1=0:pi/24:2*pi;y1=cos(2*pi*n1);y2=sin(2*pi*n1);subplot(4,1,2),stem3(y1,y2,n1,'fill '),title('exp[2*pi*n1'),grid subplot(4,1,4),stem(n1,sin(2*pi*n1),'fill '),title('sin2pin1'),grid subplot(4,1,3),stem(n1,cos(2*pi*n1),'fill'),title('cos2pin1)'),grid1－8，判断下列系统的类型。

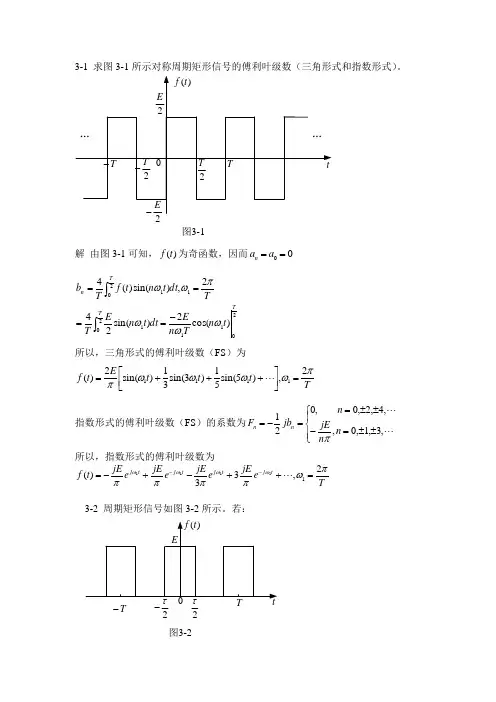
3-1 求图3-1所示对称周期矩形信号的傅利叶级数（三角形式和指数形式）。

图3-1解 由图3-1可知，)(t f 为奇函数，因而00==a a n2112011201)cos(2)sin(242,)sin()(4T T T n t n T n Edt t n E T T dt t n t f T b ωωωπωω-====⎰⎰所以，三角形式的傅利叶级数（FS ）为T t t t E t f πωωωωπ2,)5sin(51)3sin(31)sin(2)(1111=⎥⎦⎤⎢⎣⎡+++=指数形式的傅利叶级数（FS ）的系数为⎪⎩⎪⎨⎧±±=-±±==-= ,3,1,0,,4,2,0,021n n jE n jb F n n π所以，指数形式的傅利叶级数为T e jE e jE e jE e jE t f t j t j t j t j πωππππωωωω2,33)(11111=++-+-=--3-2 周期矩形信号如图3-2所示。

若：图3-22τT-2τ-重复频率kHz f 5= 脉宽 s μτ20=幅度 V E 10=求直流分量大小以及基波、二次和三次谐波的有效值。

解 对于图3-2所示的周期矩形信号，其指数形式的傅利叶级数（FS ）的系数⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛====⎰⎰--22sin 12,)(1112212211τωττωππωττωωn Sa T E n n E dt Ee T T dt e t f T F tjn TT t jn n则的指数形式的傅利叶级数（FS ）为∑∑∞-∞=∞-∞=⎪⎭⎫ ⎝⎛==n tjn n tjn n e n Sa TE eF t f 112)(1ωωτωτ其直流分量为TE n Sa T EF n ττωτ=⎪⎭⎫ ⎝⎛=→2lim100 基波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-2sin 2111τωπEF F 二次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-22sin 122τωπEF F 三次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-23sin 32133τωπE F F 由所给参数kHz f 5=可得s T s rad 441102,/10-⨯==πω将各参数的值代入，可得直流分量大小为V 110210201046=⨯⨯⨯--基波的有效值为())(39.118sin 210101010sin 210264V ≈=⨯⨯⨯- πππ二次谐波分量的有效值为())(32.136sin 251010102sin 21064V ≈=⨯⨯⨯- πππ三次谐波分量的有效值为())(21.1524sin 32101010103sin 2310264V ≈=⨯⨯⨯⨯- πππ3-3 若周期矩形信号)(1t f 和)(2t f 的波形如图3-2所示，)(1t f 的参数为s μτ5.0=，s T μ1= ，V E 1=； )(2t f 的参数为s μτ5.1=，s T μ3= ，V E 3=，分别求：（1）)(1t f 的谱线间隔和带宽（第一零点位置），频率单位以kHz 表示； （2）)(2t f 的谱线间隔和带宽； （3）)(1t f 与)(2t f 的基波幅度之比； （4）)(1t f 基波与)(2t f 三次谐波幅度之比。

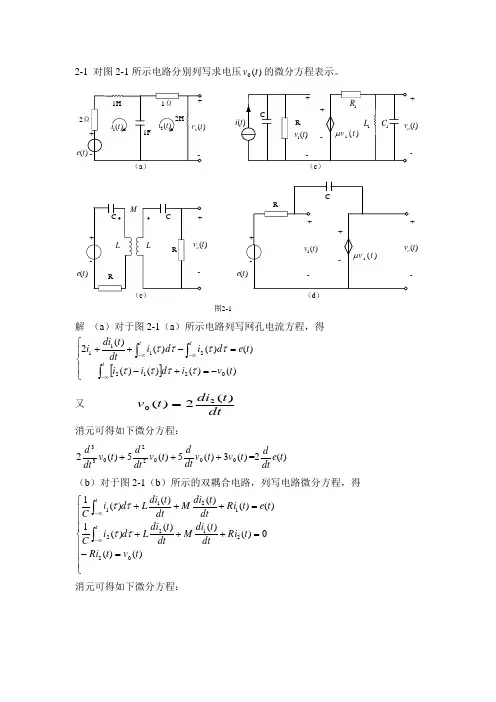
2-1 对图2-1所示电路分别列写求电压)(0t v 的微分方程表示。

2(t ei )(t +-(e )(e )(t +-图2-1解 （a ）对于图2-1（a ）所示电路列写网孔电流方程，得[]⎪⎩⎪⎨⎧-=+-=-++⎰⎰⎰∞-∞-∞-t t t t v i d i i t e d i d i dt t di i )()()()()()()()(202122111ττττττττ 又 dtt di t v )(2)(20= 消元可得如下微分方程：)(3)(5)(5)(200022033t v t v dt dt v dtd t v dt d +++=2)(te dt d（b ）对于图2-1（b ）所示的双耦合电路，列写电路微分方程，得⎪⎪⎪⎩⎪⎪⎪⎨⎧=-=+++=+++⎰⎰∞-∞-)()(0)()()()(1)()()()()(10221221211t v t Ri t Ri dt t di M dt t di L d i Ct e t Ri dtt di M dt t di L d i C ttττττ 消元可得如下微分方程：)()(1)(2)(2)(2)()(22020022203304422t e dtd MR t v C t v dt d C R t v dtd R R L t v dtd RL t v dt d M L =++⎪⎭⎫ ⎝⎛+++- （c ）对于图2-1（c ）所示电路列写电路方程，得⎪⎪⎩⎪⎪⎨⎧=⎥⎦⎤⎢⎣⎡+++=⎰∞-)()()(1)()()()(10101011t v t v dt d C dt t v L R t v R t v t v dt d C t i t μ 消元可得如下微分方程：)()(1)(1)()(101011022110331t i dt dR t v RL t v dt d R R L C t v dt d R C R C t v dt d CC μ=+⎪⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫ ⎝⎛++ （d ）对图2-1（d ）所示电路列写电路方程，电流)(t i 如图2-2所示，得⎪⎪⎩⎪⎪⎨⎧==+=++⎰∞-)()()()()()()()(1)(1011t v t v t e t v t Ri t e t v d i C t Ri t μμττ 消元可得如下微分方程：(t e )(t +-图2-2)()(1)()1(00t e Rt v R t v dt d Cμμ=+-2-2 图2-3所示为理想火箭推动器模型。

第2章 习 题2-1 求下列齐次微分方程在给定起始状态条件下的零输入响应（1）0)(2)(3)(22=++t y t y dt d t y dt d ；给定：2)0(,3)0(==--y dt dy ； （2）0)(4)(22=+t y t y dt d ；给定：1)0(,1)0(==--y dtd y ；（3）0)(2)(2)(22=++t y t y dt d t y dt d ；给定：2)0(,1)0(==--y dt dy ； （4）0)()(2)(22=++t y t y dt d t y dt d ；给定：2)0(,1)0(==--y dtdy ； （5）0)()(2)(2233=++t y dt d t y dt d t y dt d ；给定：2)0(,1)0(,1)0(22===---y dt d y dt d y 。

（6）0)(4)(22=+t y dt d t y dt d ；给定：2)0(,1)0(==--y dtdy 。

解：（1）微分方程的特征方程为：2320λλ++=，解得特征根：121, 2.λλ=-=- 因此该方程的齐次解为：2()t th y t Ae Be --=+.由(0)3,(0)2dy y dt--==得:3,2 2.A B A B +=--=解得:8, 5.A B ==- 所以此齐次方程的零输入响应为:2()85tty t e e--=-.（2）微分方程的特征方程为：240λ+=，解得特征根：1,22i λ=±.因此该方程的齐次解为：()cos(2)sin(2)h y t A t B t =+.由(0)1,(0)1d y y dx --==得:1A =,21B =,解得:11,2A B ==. 所以此齐次方程的零输入响应为:1()cos(2)sin(2)2y t t t =+.（3）微分方程的特征方程为：2220λλ++=，解得特征根:1,21i λ=-± 因此该方程的齐次解为：()(cos()sin())th y t e A t B t -=+.由(0)1,(0)2dy y dx--==得:1,2,A B A =-= 解得:1,3A B ==.所以齐次方程的零输入响应为:()(cos()3sin())ty t e t t -=+.（4）微分方程的特征方程为：2210λλ++=，解得二重根:1,21λ=-.因此该方程的齐次解为：()()th y t At B e -=+. 由(0)1,(0)2dy y dx--==得:1,2,B A B =-=解得:3, 1.A B == 所以该方程的零输入响应为:()(31)ty t t e -=+.（5）微分方程的特征方程为：3220λλλ++=，解得特征根: 1,21λ=-,30λ=. 因此该方程的齐次解为：()()th y t A Bt C e -=++.由22(0)1,(0)1,(0)2d d y y y dx dt---===得:1,1,22A C B C C B +=-=-=. 解得:5,3,4A B C ==-=-.所以方程的零输入响应为:()5(34)ty t t e -=-+.（6）微分方程的特征方程为：240λλ+=，解得特征根:120,4λλ==-. 因此该方程的齐次解为：4()th y t A Be -=+.由(0)1,(0)2d y y dx --==得:1,42A B B +=-=.解得:31,22A B ==-. 所以此齐次方程的零输入响应为:431()22ty t e -=-.2-2 已知系统的微分方程和激励信号，求系统的零状态响应。

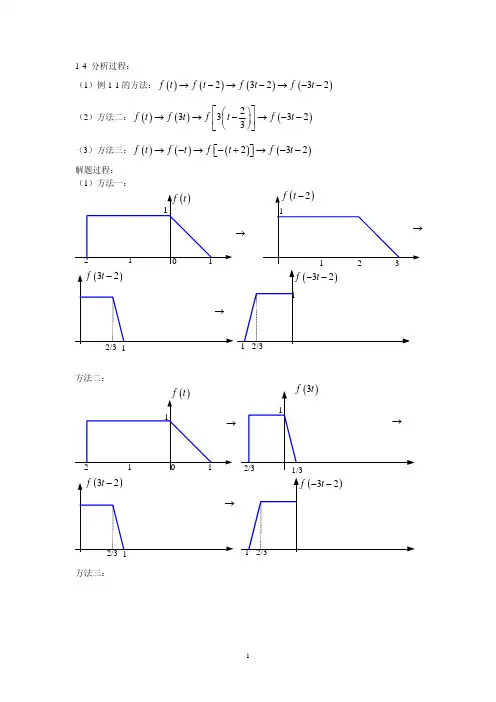
1-4 分析过程：（1）例1-1的方法：()()()()23232f t f t f t f t →−→−→−− （2）方法二：()()()233323f t f t f t f t ⎡⎤⎛⎞→→−→−−⎜⎟⎢⎥⎝⎠⎣⎦（3）方法三：()()()()232f t f t f t f t →−→−+→−−⎡⎤⎣⎦ 解题过程：（1）方法一：方法二：（1）()−f at 左移0t ：()()()000−+=−−≠−⎡⎤⎣⎦f a t t f at at f t at （2）()f at 右移0t ：()()()000−=−≠−⎡⎤⎣⎦f a t t f at at f t at （3）()f at 左移0t a ：()()000⎡⎤⎛⎞+=+≠−⎜⎟⎢⎥⎝⎠⎣⎦t f a t f at t f t at a （4）()f at 右移0t a ：()()000⎡⎤⎛⎞−−=−+=−⎜⎟⎢⎥⎝⎠⎣⎦t f a t f at t f t at a 故（4）运算可以得到正确结果。

注：1-4、1-5题考察信号时域运算：1-4题说明采用不同的运算次序可以得到一致的结果；1-5题提醒所有的运算是针对自变量t 进行的。

如果先进行尺度变换或者反转变换，再进行移位变换，一定要注意移位量和移位的方向。

1-9 解题过程： （1）()()()2tf t eu t −=− （2）()()()232tt f t ee u t −−=+（3）()()()255ttf t e eu t −−=− （4）()()()()cos 1012tf t et u t u t π−=−−−⎡⎤⎣⎦1-12 解题过程：（（（（注：1-9、1-12题中的时域信号均为实因果信号，即()()()=f t f t u t 1-18 分析过程：任何信号均可分解为奇分量与偶分量之和的形式，即()()()()1e o f t f t f t =+其中，()e f t 为偶分量，()o f t 为奇分量，二者性质如下：()()()()()()23e e o o f t f t f t f t =−=−−()()13∼式联立得()()()12e f t f t f t =+−⎡⎤⎣⎦ ()()()12o f t f t f t =−−⎡⎤⎣⎦ 解题过程：(a-1) (a-2)(a-3)(a-4)f t为偶函数，故只有偶分量，为其本身(b) ()(c-1)(c-2)(c-3)(c-4)(d-1)(d-2)(d-3)(d-4)1-20 分析过程：本题为判断系统性质：线性、时不变性、因果性（1）线性（Linearity）：基本含义为叠加性和均匀性即输入()1x t ，()2x t 得到的输出分别为()1y t ，()2y t ，()()11T x t y t =⎡⎤⎣⎦，()()22T x t y t =⎡⎤⎣⎦，则()()()()11221122T c x t c x t c y t c y t +=+⎡⎤⎣⎦（1c ，2c 为常数）。

1试分别指出以下波形是属于哪种信号？题图1-11-2试写出题1-1图中信号的函数表达式。

1-3已知信号)(1t x 与)(2t x 波形如题图1-3中所示，试作出下列各信号的波形图，并加以标注。

题图1-3⑴)2(1-t x ⑵)1(1t x -⑶)22(1+t x⑷)3(2+t x ⑸)22(2-t x ⑹)21(2t x - ⑺)(1t x )(2t x -⑻)1(1t x -)1(2-t x ⑼)22(1t x -)4(2+t x 1-4已知信号)(1n x 与)(2n x 波形如题图1-4中所示，试作出下列各信号的波形图，并加以标注。

题图1-4⑴)12(1+n x ⑵)4(1n x -⑶)2(1n x ⑷)2(2n x -⑸)2(2+n x ⑹)1()2(22--++n x n x⑺)2(1+n x )21(2n x -⑻)1(1n x -)4(2+n x ⑼)1(1-n x )3(2-n x1-5已知信号)25(t x -的波形如题图1-5所示，试作出信号)(t x 的波形图，并加以标注。

题图1-51-6试画出下列信号的波形图：⑴)8sin()sin()(t t t x ΩΩ=⑵)8sin()]sin(211[)(t t t x ΩΩ+= ⑶)8sin()]sin(1[)(t t t x ΩΩ+=⑷)2sin(1)(t tt x = 1-7试画出下列信号的波形图：⑴)(1)(t u e t x t -+=⑵)]2()1([10cos )(---=-t u t u t e t x t π⑶)()2()(t u e t x t --=⑷)()()1(t u e t x t --=⑸)9()(2-=t u t x ⑹)4()(2-=t t x δ1-8试求出以下复变函数的模与幅角，并画出模与幅角的波形图。

⑴)1(1)(2Ω-Ω=Ωj e j X ⑵)(1)(Ω-Ω-Ω=Ωj j e e j X ⑶Ω-Ω---=Ωj j e e j X 11)(4⑷21)(+Ω=Ωj j X 1-9已知信号)]()([sin )(π--=t u t u t t x ，求出下列信号，并画出它们的波形图。