二年级数学乘法估算

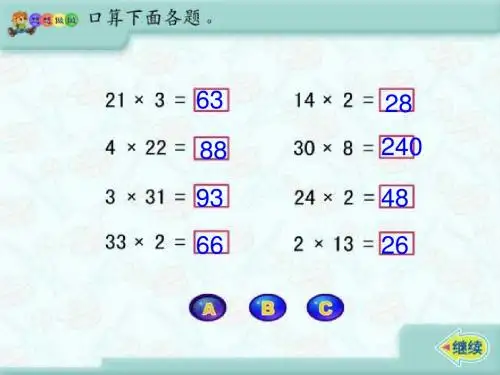
乘法估算怎么估算乘法估算是指在没有计算器或者数字工具的情况下，通过人工进行乘法计算的过程。

这种方法可以在很多场景中使用，例如在购物时计算总价格、在工作中进行预算等等。

下面就介绍一些乘法估算的方法。

一、近似数相乘法近似数相乘法是通过将一个数近似为它的最接近的十位数和个位数的乘积相加得出结果。

例如：计算53 × 47。

可以将53近似为50，47近似为50，然后计算50 × 50 = 2500。

接着，计算50 × 3 + 47 × 0 = 150。

最后将两个结果相加得出2535，这个结果与计算器计算出的结果非常接近。

二、交错相乘法交错相乘法需要对乘数中的每一位先与另一个乘数的各位相乘，然后将结果相加。

例如：计算36 × 27。

首先，将36拆分成30和6，27拆分成20和7。

然后进行相乘计算，得出结果为30 × 20 + 6 × 20 + 30 × 7 + 6 × 7 = 540 + 120 + 210 + 42 = 912。

这种方法也适用于更长的数字乘法计算，只需要逐位相乘并将结果相加即可。

三、倍增法倍增法是将乘数和被乘数不断倍增，直到乘数变为1，然后将所有的中间结果相加得到最终结果。

例如：计算37 × 24。

将37倍增到64，将24倍增到48。

然后将所有中间结果相加得到最终结果。

中间结果为：86 + 172 + 344 + 688 + 1376 = 2666。

这种方法可以大大减少计算次数，适用于大量乘法计算的场景。

总之，乘法估算是一种可以方便地计算乘法的方法，可以在很多生活和工作场景中使用。

其中的方法有很多种，适用于不同的场景和数字大小。

乘法估算的方法
乘法估算是一种在计算过程中快速估算乘法结果的方法。

以下是一些常用的乘法估算方法：
1. 近似估算法：适用于两个较大的数相乘的情况。

首先将乘法运算简化为相对较小的数相乘，然后再进行估算。

例如，要估算68 × 47，可以先将68近似为70，将47近似为50，然后计
算70 × 50 = 3500 来代替估算。

2. 分解估算法：适用于较复杂的乘法运算。

将一个较大的数分解成较小的数的乘积，然后进行分别估算和相加。

例如，要估算145 × 27，可以将145分解为100 + 40 + 5，将27分解为20 + 7，然后计算(100 × 20) + (40 × 20) + (5 × 7) = 2000 + 800 + 35 = 2835 来代替估算。

3. 使用整数的倍数：适用于估算某个数的某个倍数的乘法结果。

例如，要估算247 × 8，可以先计算240 × 8 = 1920，然后再加
上7 × 8 = 56，得到总估算结果为1976。

4. 使用相似性和近似值：适用于含有近似值的乘法运算。

根据数值的相似性，结合已知的近似值进行估算。

例如，要估算23.5 × 4.7，可以将4.7近似为5，然后计算23.5 × 5 = 117.5 来
代替估算。

以上是一些常用的乘法估算方法，通过灵活运用这些方法，我们可以在计算乘法时快速估算结果，提高计算效率。

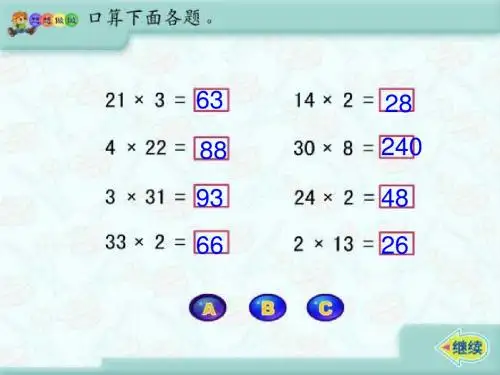
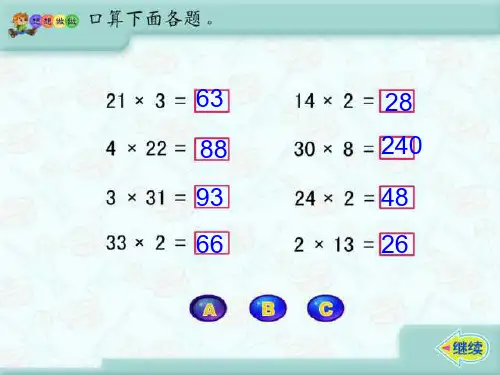
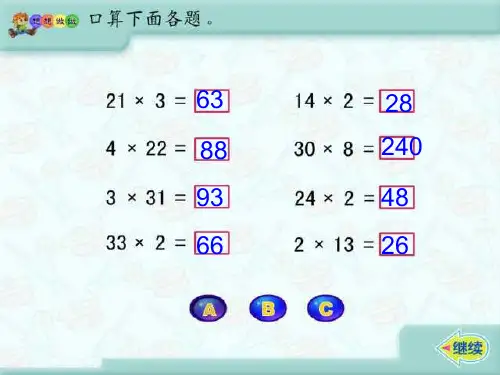
如何快速估算两位数乘法的结果估算在我们的日常生活中非常实用，它能帮助我们在没有计算器的情况下快速得到近似的答案。

在数学中，估算两位数乘法的结果也是非常重要的。

本文将为大家介绍一些快速估算两位数乘法结果的方法和技巧。

1. 相近数相乘法：这是一种广泛使用的估算方法，适用于两个数相差较小的情况。

首先，将两个数分别和10的整数倍相乘，然后将结果相加。

例如，对于56乘以58，我们可以先估算为50乘以60，得到3000，然后再加上6乘以8得到3180，这就是估算的结果。

2. 数位相乘后相加法：这是另一种常用的估算方法，适用于两个数中的某些数位较大，其余数位较小的情况。

首先，将相乘数的各个数位相乘，然后将结果相加。

例如，对于67乘以53，我们可以先估算7乘以3得到21，然后再加上6乘以5得到51，最终得到估算的结果72。

3. 基于十进制的估算法：这种方法通过将两个数分解为十位和个位的形式来估算结果。

首先，将两个数的十位数相乘，得到一个较大的结果。

然后，将两个数的个位数相乘，并将结果加到之前的结果上。

例如，对于73乘以49，我们可以先估算70乘以40得到2800，再加上3乘以9得到27，最终得到估算的结果2827。

4. 估算法则的运用：在估算乘法时，可以根据具体的情况使用估算法则进行综合运用。

例如，对于87乘以56，我们可以先估算80乘以50得到4000，然后再加上7乘以6得到42，最终得到估算的结果4042。

这种方法更加灵活，根据个人的习惯和情况进行调整。

5. 常用乘法口诀的应用：在估算乘法时，熟记乘法口诀可以帮助我们更加快速地估算结果。

例如，对于86乘以52，我们可以利用乘法口诀将它们分解为80乘以50和6乘以2，分别得到4000和12，最终得到估算的结果4012。

以上是一些快速估算两位数乘法的方法和技巧。

通过熟练掌握这些方法，我们可以在没有计算器的情况下快速得到近似的答案，提高计算的效率。

当然，在实际应用中，我们还需要根据具体情况选择合适的估算方法，并结合自己的计算能力进行调整。

两位数乘两位数的估算的算理和算法在日常生活中，我们经常需要进行两位数乘两位数的计算，但是对于一些大型乘法运算，如果直接进行手算，可能会相对复杂和耗时。

估算乘法结果的算理和算法显得十分重要。

本文将从深度和广度两个角度对两位数乘两位数的估算进行全面评估，并据此撰写有价值的文章。

1. 估算的算理估算的算理是指对于乘法运算的结果进行估计时所遵循的一些原则和规律。

在进行两位数乘两位数的估算时，可以根据乘法的性质和规律进行合理的估算。

可以先将两个两位数的数值进行适当的近似，然后再进行乘法运算，最后根据估算结果进行修正。

另外，还可以利用乘法的交换律和结合律来简化估算过程，从而提高计算效率和准确性。

2. 估算的算法估算的算法是指在进行估算时所采用的一些具体的计算方法和步骤。

在进行两位数乘两位数的估算时，可以根据乘法的特点和规律采用不同的算法。

常见的估算算法包括近似相乘法、分步估算法和数字分解法等。

这些算法都可以根据具体的计算需求来灵活应用，从而得到更加准确和有效的估算结果。

总结回顾通过对两位数乘两位数的估算进行全面评估，我们可以发现估算的算理和算法在日常生活中具有重要的应用意义。

合理的估算方法和步骤能够帮助我们快速获得乘法运算的近似结果，并且能够有效提高计算效率和准确性。

在日常生活中，我们应该根据不同的需求，灵活运用估算的算理和算法，从而更加方便和高效地进行乘法运算。

个人观点和理解对于两位数乘两位数的估算，我认为估算的算理和算法是非常重要的。

在实际操作中，我们经常会遇到一些需要快速估算乘法结果的情况，因此掌握合理的估算方法和步骤是十分必要的。

通过学习和掌握估算的算理和算法，我们可以更加轻松地进行乘法运算，同时也能够提高计算的准确性和效率。

在撰写本文时，我深入研究了两位数乘两位数的估算的算理和算法，通过对其深度和广度的评估，能够更好地理解这一主题。

在文章中，我多次提及了“估算”、“算理”和“算法”等主题文字，以便读者能够更加清晰地理解文章内容。

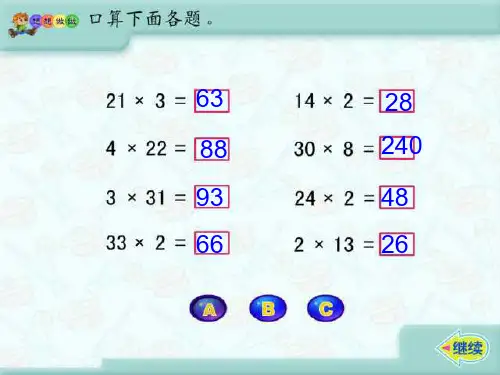
乘法的估算（通用12篇）乘法的估算篇1课题：乘法的估算教学内容：（人教社）教科书第70页例2，练习十五第4～7题。

教学目标：引导学生体验估算的过程，初步了解两、三位数乘一位数的估算方法，培养学生的估算意识。

教具、学具准备：多媒体课件幻灯片。

教学过程：一、提出问题1.用多媒体幻灯片逐一出示各种图片，创设问题情境，引导学生提出用乘法计算的问题。

图片内容是：邮局邮票出售处，有的邮票一枚80分，有的邮票一枚60分。

百货商店鞋柜，一双旅游鞋78元，一双皮鞋164元。

电影院售票处，日场一张电影票15元，夜场一张电影票20元。

小袋鼠蹦跳一次约2米，小袋鼠蹦跳33次。

文具商店柜台，每盒图钉120个，每包本25本。

2.出示课本第70页例2主题图：三年一班29个同学去参观航天航空展览，门票每张8元。

请学生提出问题。

老师在学生提出问题的基础上，补充提出：如果老师这时只带250元钱去，够吗？二、尝试解决教师先请学生猜一猜带250元够不够？再请学生思考怎么知道我们猜得对不对呢？看看小精灵是怎么说的？怎么才能知道8×29大约是多少呢？能不能用我们前面学过的计算方法来解决这个问题？启发学生想出前面我们已经学过整十数乘一位数的乘法口算，我们可以把29看成最接近的整十数来估算。

因为8×30＝240，所以8×29的积比较接近240，我们可以列成算式8×29≈240。

再由小精灵介绍约等号。

可见带250元够买门票。

三、拓展引申估计下列几道乘法算式的积大约是多少？32×6 49×5 218×4 581×2组织学生小组讨论，然后全班交流，说明各应看成几百或几十。

说明因数是三位数时，只要看成最接近的整百数即可。

四、巩固练习1.完成课本第70页“做一做”中的4道题。

先由学生独立计算，然后集体订正答案。

结合订正答案的过程让学生说一说估算的过程。

2.用上课开始时呈现的几个问题情境和学生们提出的问题，让学生估算结果，找出答案。

乘法估算的方法
乘法估算是一种快速近似计算乘法结果的方法，特别适用于没有计算器或需要快速得到近似答案的情况。

以下是乘法估算的几种方法：
1.取整估算：这种方法最简单，即将两个乘数分
别取最接近的整数，然后进行乘法运算。

例如，23 x
18 可以估算为20 x 20 = 400。

2.分段估算：将一个乘数分为容易计算的几部
分，再与另一个乘数相乘。

如27 x 13 可以分为20 x
13 + 7 x 13，即260 + 91 = 351。

3.百分比估算：将一个乘数表示为另一个乘数的
百分比，然后进行计算。

例如，22 x 18 可以估算为
22 x (20 - 10%)，即22 x 20 - 2.2 = 437.8。

4.利用已知乘法事实进行估算：例如，利用
5x2=10, 25x4=100等已知乘法事实，可以快速地估算
出其他乘法的结果。

在进行乘法估算时，需要根据实际情况选择合适的方法，以得到相对准确的结果。

同时，要意识到估算只是一种近似计算，结果可能与精确计算有所差异。

因此，在需要精确答案的场合，还需要使用其他计算方法进行验证。