下载文档原格式
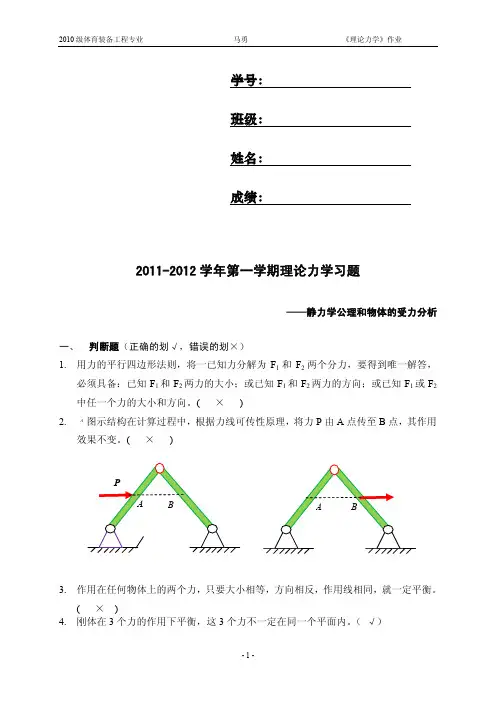
一．填空题（共10分，每空2分）质量为m的均质物体，已知角速度为ω、角加速度为a，如图所示，（1）各点的惯性力向点C简化的结果：主矢的大小是__________，主矩的大小为______________；（2）各点的惯性力向点O简化的结果：主矢的大小是______________，主矩的大小为______________；(3)系统动量为______________。
raωOC二．简答题（共10分）1．半径均为R、重量均为G的两个定滑轮，一个轮上绕过绳子挂一重量为G的重物，另一轮上用一大小为G的力，如右图所示。
则图(a)和图(b)两轮的角加速度相等吗？为什么（5分）(a)GGOO(b)2．在光滑水平在上放置一静止的均质圆盘，当它受一力偶作用时，盘心将如何运动？盘心运动情况与力偶作用位置有关吗？如果圆盘面内受一大小和方向都不变的力作用，盘心将如何运动？盘心运动情况与此力作用位置有关吗？为什么？（5分）三．有重为W的船，长AB=2a，船上有重为P的人，设人最初是在船上A 处，后来沿甲板向右行走，如不计水对于船的阻力。
求：当人走到船上B处时，船向左方移动多少？（20分）A’ A B’ Bb 2ayxl四．质量为2kg 的物块A在弹簧上处于静止，如图所示。
弹簧的刚性系数k为400N/m。
现将质量为4kg的物块B放置在物块A上，刚接触就释放它。
求：（1）弹簧对两物块的最大作用力；（2）两物块得到的最大速度。
（20分）kBA五．圆盘和滑块的质量均为m，圆盘为匀质，其半径为r。
杆OA用铰与圆盘及滑块相连，OA平行于斜面，杆的质量不计。
斜面的倾斜角为θ，滑块与斜面间的滑动摩擦系数为f，圆盘在斜面上作无滑动滚动，求滑块的加速度和杆的内力。
（20分）AOθ六．（用动静法求解，其他方法不给分）质量为m、半径为r的滑轮上绕有软绳，绳的一端固定于点A，令滑轮自由下落，如图所示，不计软绳的质量，试求轮心C的加速度和绳子的拉力。
兴湘12级土木工程理论力学A 卷答案一.选择题（每小题3 分，共15分）1、C2、C3、B4、D5、B二、填空题 (每题4分，共16分)1、该力系的主矢和对于任一点的主矩都等于零；该力偶系中所有各力偶矩矢在三个坐标轴上投影的代数和分别等于零；2、0 , 16KN m ;3、x c =2,y c =274、ω=3/rad s ，ε=392s rad三、判断题（每题2分,共10分） (1)× (2)× (3)× (4)√ (5) √四、作图题（8分）(4分) (4分)五、计算题 （10分）解：如图所示，则 水平方向 =10Ax F kN （2分） 垂直方向 +=3=30A y C F F q k N⨯ （2分） 对A 取矩()0AM F =∑ 33310402CFq ⨯-⨯⨯-⨯= （3分） 综上， 853C F kN = 53Ay F kN = （3分）RA FRB FA BC RC F RBF ' P FD六、计算题 （11分）解：解： 选套筒A 为动点，动系与摇杆B O 2相固连。
（1）求角速度：由动点的速度合成定理r e A a v v v v +==作速度平行四边形，因此有：s m A O v v v A a e /2.0212130sin 11=⨯===ω ，s m v v A r /32.030cos == （3分）摇杆B O 2的角速度/s)(5.04.02.022rad A O v e ===ω（逆时针）。
（1分）（2）求角加速度再由C r ne e B a a a a a a a +++==τ作矢量图投影有τe C A a a a -=030cos ，即030cos A C e a a a -=τ，（3分） 其中：22/32.02s m v a r C ==ω，2121/8.0s m A O a A ==ω因此 2/32.0s m a e -=τ，所以，摇杆B O 2的角加速度为 )s /(2/3222rad AO a e-==τα（逆时针）。
第一章静力学基础一、是非题1．力有两种作用效果，即力可以使物体的运动状态发生变化，也可以使物体发生变形。
（）2．在理论力学中只研究力的外效应。
（）3．两端用光滑铰链连接的构件是二力构件。
（）4．作用在一个刚体上的任意两个力成平衡的必要与充分条件是：两个力的作用线相同，大小相等，方向相反。
（）5．作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。
（）6．三力平衡定理指出：三力汇交于一点，则这三个力必然互相平衡。
（）7．平面汇交力系平衡时，力多边形各力应首尾相接，但在作图时力的顺序可以不同。
（）8．约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。
（）二、选择题1．若作用在A点的两个大小不等的力F1和F2，沿同一直线但方向相反。
则其合力可以表示为。
①F1－F2；②F2－F1；③F1＋F2；2．作用在一个刚体上的两个力F A、F B，满足F A=－F B的条件，则该二力可能是。
①作用力和反作用力或一对平衡的力；②一对平衡的力或一个力偶。
③一对平衡的力或一个力和一个力偶；④作用力和反作用力或一个力偶。
3．三力平衡定理是。
①共面不平行的三个力互相平衡必汇交于一点；②共面三力若平衡，必汇交于一点；③三力汇交于一点，则这三个力必互相平衡。
4．已知F1、F2、F3、F4为作用于刚体上的平面共点力系，其力矢关系如图所示为平行四边形，由此。
①力系可合成为一个力偶；②力系可合成为一个力；③力系简化为一个力和一个力偶；④力系的合力为零，力系平衡。
5．在下述原理、法则、定理中，只适用于刚体的有。
①二力平衡原理；②力的平行四边形法则；③加减平衡力系原理；④力的可传性原理；⑤作用与反作用定理。
三、填空题1．二力平衡和作用反作用定律中的两个力，都是等值、反向、共线的，所不同的是。
2．已知力F沿直线AB作用，其中一个分力的作用与AB成30°角，若欲使另一个分力的大小在所有分力中为最小，则此二分力间的夹角为度。
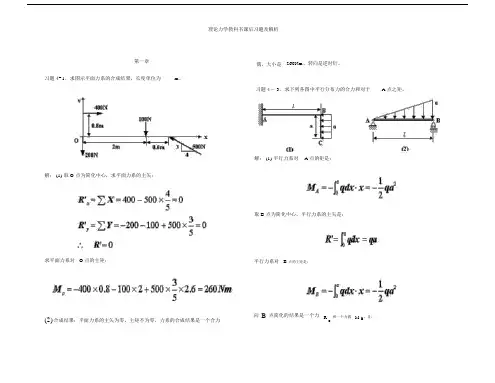
1.1 沿水平方向前进的枪弹，通过某一距离s 的时间为t 1，而通过下一等距离s 的时间为2t .试证明枪弹的减速度（假定是常数）为由题可知示意图如题1.1.1图: {{SSt t 题1.1.1图设开始计时的时刻速度为0v ,由题可知枪弹作匀减速运动设减速度大小为a .则有:()()⎪⎪⎩⎪⎪⎨⎧+-+=-=221210211021221t t a t t v s at t v s 由以上两式得 11021at t s v +=再由此式得 ()()2121122t t t t t t s a +-=1.26一弹性绳上端固定，下端悬有m 及m '两质点。
设a 为绳的固有长度，b 为加m 后的伸长，c 为加m '后的伸长。
今将m '任其脱离而下坠，试证质点m 在任一瞬时离上端O 的距离为解 以绳顶端为坐标原点.建立如题1.26.1图所示坐标系.题1.26.1图设绳的弹性系数为k ,则有 kb mg = ① 当 m '脱离下坠前，m 与m '系统平衡.当m '脱离下坠前，m 在拉力T 作用下上升，之后作简运.运动微分方程为 ()ym a y k mg &&=-- ② 联立①② 得 b b a g y b g y +=+&& ③ 0=+y bg y &&齐次方程通解 t b g A t b g A Y sin cos 211+= 非齐次方程③的特解 b a Y +=0 所以③的通解b a t bg A t b g A Y +++=sin cos 211代入初始条件：0=t 时，,c b a y ++=得0,21==A c A ；故有 b a t b g c y ++=cos 即为m 在任一时刻离上端O 的距离.'1.39 一质点受一与距离23次方成反比的引力作用在一直线上运动。
试证此质点自无穷远到达a 时的速率和自a 静止出发到达4a 时的速率相同。
理论力学教科书课后习题及解析第一章偶，大小是260Nm，转向是逆时针。
习题 4- 1．求图示平面力系的合成结果，长度单位为m。
习题 4－ 3．求下列各图中平行分布力的合力和对于 A 点之矩。
解： (1) 平行力系对 A 点的矩是：解： (1) 取 O 点为简化中心，求平面力系的主矢：取 B 点为简化中心，平行力系的主矢是：求平面力系对O 点的主矩：平行力系对 B 点的主矩是：(2)合成结果：平面力系的主矢为零，主矩不为零，力系的合成结果是一个合力向B点简化的结果是一个力RB和一个力偶M B，且：如图所示；向 A 点简化的结果是一个力R A和一个力偶M A，且：如图所示；将 R B向下平移一段距离d，使满足：最后简化为一个力R ，大小等于R B。
其几何意义是： R 的大小等于载荷分布的将 R A向右平移一段距离d，使满足：矩形面积，作用点通过矩形的形心。
(2)取 A 点为简化中心，平行力系的主矢是：最后简化为一个力R，大小等于R A。
其几何意义是：R 的大小等于载荷分布的三角形面积，作用点通过三角形的形心。
平行力系对 A 点的主矩是：列平衡方程：习题 4-4 ．求下列各梁和刚架的支座反力，长度单位为m。
解方程组：反力的实际方向如图示。
校核：解： (1) 研究 AB 杆，受力分析，画受力图：结果正确。
(2) 研究 AB 杆，受力分析，将线性分布的载荷简化成一个集中力，画受力图：(3) 研究 ABC ，受力分析，将均布的载荷简化成一个集中力，画受力图：列平衡方程：解方程组：列平衡方程：反力的实际方向如图示。
校核：解方程组：结果正确。
反力的实际方向如图示。
校核：结果正确。
习题 4-5 ．重物悬挂如图，已知G=1.8kN ，其他重量不计；求铰链 A 的约束反力和杆 BC 所受的力。
列平衡方程：解方程组：解： (1) 研究整体，受力分析（BC 是二力杆），画受力图：反力的实际方向如图示。
列平衡方程：习题 4-8 ．图示钻井架，G=177kN ，铅垂荷载P=1350kN ，风荷载 q=1.5kN/m ，水平力 F=50kN ；求支座 A 的约束反力和撑杆CD 所受的力。
理论力学作业册学院：专业：学号：年级：班级：姓名：任课老师：前言理论力学是工科高等院校机械、材料、土建、采矿、安全等专业本科生的一门重要的技术基础课。
它是各门力学课的基础，并在工程技术领域有着广泛的应用，并为学习有关的后续课程打好必要的基础。
学习本课程的目的使学生初步学会应用理论力学的理论和方法，分析、解决一些简单的工程实际问题；培养学生的逻辑思维能力和基本工程素质，使学生认知工程中的力学现象与力学问题。
本作业题册是为适应当前我校教学特色而统一筛选出来的题集，入选题目共计83个，可供多学时和少学时学生使用，其中标“*”的题目稍难。
教师可根据学时情况有选择性的布置作业。
本题册中列出的题目仅是学习课程的最基本的作业要求，老师根据情况可适当增加部分作业，部分学生如果有考研或者其他方面更高的学习要求，请继续训练其他题目。
由于时间仓促，并限于编者水平有限，缺点和错误在所难免，恳请大家提出修改建议。
王钦亭2012年10月6日目录第1章静力学基本公理与物体的受力分析 (1)第2章平面汇交力系与平面力偶系 (3)第3章平面任意力系 (7)第4章空间力系、重心 (12)第5章摩擦 (15)第6章点的运动学 (19)第7章刚体的简单运动 (21)第8章点的合成运动 (23)第9章刚体的平面运动 (27)第10章质点动力学基本方程 (31)第11章动量定理 (33)第12章动量矩定理 (37)第13章动能定理 (40)第14章达朗贝尔原理 (44)第15章虚位移原理 (46)答案 (48)第1章静力学基本公理与物体的受力分析L1-1．静力学公理及推论中，哪些公理和推论只适用于刚体？L1-2．三力平衡是否汇交？三力汇交是否平衡？L1-3．画出下面标注符号的物体的受力图：q第2章 平面汇交力系与平面力偶系L2-1(HGDV5-2-2) 如图所示，固定在墙壁上的圆环受三条绳索的拉力作用，力1F 沿水平方向，力3F 沿铅直方向，力2F 与水平线成40°角。
理论力学作业册学院：专业：学号：年级：班级：姓名：任课老师：前言理论力学是工科高等院校机械、材料、土建、采矿、安全等专业本科生的一门重要的技术基础课。
它是各门力学课的基础，并在工程技术领域有着广泛的应用，并为学习有关的后续课程打好必要的基础。
学习本课程的目的使学生初步学会应用理论力学的理论和方法，分析、解决一些简单的工程实际问题；培养学生的逻辑思维能力和基本工程素质，使学生认知工程中的力学现象与力学问题。
本作业题册是为适应当前我校教学特色而统一筛选出来的题集，入选题目共计83个，可供多学时和少学时学生使用，其中标“*”的题目稍难。
教师可根据学时情况有选择性的布置作业。
本题册中列出的题目仅是学习课程的最基本的作业要求，老师根据情况可适当增加部分作业，部分学生如果有考研或者其他方面更高的学习要求，请继续训练其他题目。
由于时间仓促，并限于编者水平有限，缺点和错误在所难免，恳请大家提出修改建议。
王钦亭2012年10月6日目录第1章静力学基本公理与物体的受力分析 (1)第2章平面汇交力系与平面力偶系 (3)第3章平面任意力系 (7)第4章空间力系、重心 (12)第5章摩擦 (15)第6章点的运动学 (19)第7章刚体的简单运动 (21)第8章点的合成运动 (23)第9章刚体的平面运动 (27)第10章质点动力学基本方程 (31)第11章动量定理 (33)第12章动量矩定理 (37)第13章动能定理 (40)第14章达朗贝尔原理 (44)第15章虚位移原理 (46)答案 (48)第1章静力学基本公理与物体的受力分析L1-1．静力学公理及推论中，哪些公理和推论只适用于刚体？L1-2．三力平衡是否汇交？三力汇交是否平衡？L1-3．画出下面标注符号的物体的受力图：q第2章 平面汇交力系与平面力偶系L2-1(HGDV5-2-2) 如图所示，固定在墙壁上的圆环受三条绳索的拉力作用，力1F 沿水平方向，力3F 沿铅直方向，力2F 与水平线成40°角。
三力的大小分别为12000N F =,22500N F =,31500N F =。
求三力的合力。
L2-2(HGDV5-2-6) 物体重P =20kN ，用绳子挂在支架的滑轮B 上，绳子的另一端接在铰车D 上，如图所示。
转动铰车，物体便能升起。
设滑轮的大小、AB 与CB 杆自重及摩擦略去不计，A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时，试求拉杆AB 和支杆CB 所受的力。
p 。
L2-3（HGDV5-2-11) 图为弯管机的夹紧机构的示意图，已知:压力缸直径D=l20mm,压强6MPa 设各杆重量和各处摩擦不计，试求在α=30°位置时所能产生的夹紧力F。
L2-4(HGDV5-2-13) 图示为一拔桩装置。
在木桩的点A上系一绳，将绳的另一端固定在点C，在绳的点B系另一绳BE，将它的另一端固定在点E。
然后在绳的点D用力向下拉，并使绳的BD段水平，AB 段铅直:DE段与水平线、CB段与铅直线间成等角θ=0.lrad(弧度)(当θ很小时，tanθ≈θ)。
如向下的拉力F=800N，求绳AB作用于桩上的拉力。
L2-5(HGDV5-2-27) 已知梁AB上作用一力偶，力偶矩为M，梁长为l，梁重不计。
求在图a、b、c三种情况下，支座A和B的约束反力。
L2-6(HGDV5-2-31) 铰链四杆机构1OABO 在图示位置平衡。
已知:OA=0.4m ，10.6m O B =，作用在OA 上的力偶的力偶矩11Nm M =。
各杆的重量不计。
试求力偶矩2M 的大小和杆AB 所受的力F 。
第3章平面任意力系L3-1(HGDV5-3-1) 己知1150NF=,2200NF=，3300NF=，'200NF F==。
求力系向点Ｏ的简化结果，并求力系合力的大小及其与原点Ｏ的距离d。
L3-2(HGDV5-3-12) 支持窗外凉台的水平梁承受强度为N/mp的均布载荷。
在水平梁的外端从柱上传下载荷P。
柱的轴线到墙的距离为l。
求梁根部的支反力。
L3-3（HGDV5-3-13）在图示刚架中，己知3kN/m q =,F =，10kN m M =，不计刚架自重。
求固定端A 处的约束反力。
L3-4(HGDV5-3-22) 如图所示，行动式起重机不计平衡锤的重为500kN P =，其重心在离右轨1.5m 处。
起重机的起重量为1P =250kN ，突臂伸出离右轨10m 。
跑车本身重量略去不计，欲使跑车满载或空载时起重机均不致翻倒，求平衡锤的最小重量2P 以及平衡锤到左轨的最大距离x 。
L3-5(HGDV5-3-24) 水平梁AB由铰链A和杆BC所支持，如图所示。
在梁上D处用销子安装半径为r=O.lm的滑轮。
有一跨过滑轮的绳子，其一端水平地系于墙上，另一端悬挂有重P=1800N的重物。
如AD=O.2m,BD=0.4m,α=45°，且不计梁、杆、滑轮和绳的重量。
试求铰链A和杆BC对梁的反力。
L3-6(HGDV5-3-27) 由AC和CD构成的组合梁通过铰链C连接。
它的支承和受力如图所示。
已知均布载荷强度q=lOkN/m，力偶矩M=40kN·m，不计梁重。
求支座A、B、D的约束反力和铰链C处所受的力。
L3-7(HGDV5-3-39) 图示构架中，物体P重12OON，由细绳跨过滑轮E而水平系于墙上，尺寸如图。
F。
不计杆和滑轮的重量，求支承A和B处的约束反力，以及杆BC的内力BCL3-8(HGDV5-3-59) 桁架受力如图所示，已知1F =lOkN, 2F =3F =2OkN 。
试求桁架4，5，7，10各杆的内力。
第4章 空间力系、重心L4-1（HGDV7-3-6） 力系中1100N F =，2300N F =，3200N F =，各力作用线的位置如图所示，求将各力系向点O 简化的结果。
L4-2（HGDV7-3-9） 求图示力1000N F =对于z 轴的力矩Z M 。
L4-3（HGDV7-3-12）图示空间架构由三根无重直杆组成，在D端用球铰链连接，如图所示。
A，B和P=，求铰链A，B和C的约束力。
C端则用球铰链固定在水平地板上。
如果挂在D端的物重10kNL4-4（HGDV7-3-14）图示空间桁架由六杆1，2，3，4，5和6构成。
在节点A上作用一力F，此=。
等腰三角形EAK，FBM和NDB 力在矩形ABDC平面内，且与铅直线成45角。
EAK FBMF=，求各杆的内力。
在顶点A，B和D处均为直角，又EC=CK=FD=DM。
若10kNP ，用球铰链A和蝶铰链B固定在墙L4-5（HGDV7-3-18）如图所示，均质长方形薄板重200N上，并用绳子CE维持在水平位置。
求绳子的拉力和支座约束力。
L4-6（HGDV7-3-25）工字钢截面尺寸如图所示，求此截面的几何中心。
第5章 摩擦L5-1（HGDV7-4-1） 如图所示，置于V 型槽中的棒料上作用一力偶，力偶的矩15N m M =⋅时，刚好能转动此棒料。
已知棒料重400N P =，直径0.25m D =，不计滚动磨阻。
求棒料与V 型槽间的动摩擦因数s f 。
L5-2（HGDV7-4-2） 梯子AB 靠在墙上，其重为200N P =，如图所示。
梯长为l ，并与水平面交角 60θ=。
已知接触面间的摩擦因数均为0.25。
今有一重650N 的人沿梯上爬，问人所能达到的最高点C 到A 点的距离s 应为多少?L5-3（HGDV7-4-5） 轧压机由两轮构成，两轮的直径均为 500mm d =，轮间的间隙为5mm a =，两轮反向转动，如图所示。
已知烧红的铁板与铸铁轮间的静摩擦因数为 0.1s f =，问能轧压的铁板厚度 b 是多少?L5-4（HGDV7-4-9） 机床上为了迅速装卸工件，常采用如图所示的偏心轮夹具。
已知偏心轮直径为D ，偏心轮与台面间的静摩擦因数为 s f 。
今欲使偏心轮手柄上的外力去掉后，偏心轮不会自动脱落，求偏心距 e 应为多少? 各铰链中的摩擦忽略不计。
L5-5（HGDV7-4-14）均质长板AD重P，长为 4 m，用一短板BC支撑，如图所示。
若===，BC板的自重不计。
求A，B，C处摩擦角各为多大才能使之保持平衡。
3mAC BC ABf L5-6（HGDV7-4-15）尖劈顶重装置如图所示。
在B上受力P 的作用。
A与B块间的静摩擦因数为s （其他有滚珠处表示光滑）。
如不计A和B块的重量，求使系统保持平衡的力F的值。
*L5-7（HGDV7-4-21）均质圆柱重为P ，半径为r ，搁在不计自重的水平杆和固定斜面之间，杆端A 为光滑铰链，D 端受一铅垂向上的力F ，圆柱上作用一力偶M ，如图所示。
已知F P =，只考虑滑动摩擦且圆柱与杆及斜面间的静滑动摩擦因数皆为0.3s f =，当45θ=时，AB BD =。
求此时能保持系统静止的力偶矩M 的最小值。
第6章 点的运动学L6-1（HGDV7-5-1）图示曲线规尺的各杆，长为200mm OA OB ==，50mm CD DE AC AE ====。
如杆以等角速度rad/s 5πω=绕O 轴转动，并且当运动开始时，杆OA 水平向右。
求尺上点D 的运动方程和轨迹。
L6-2（HGDV7-5-5）套管A 由绕过定滑轮B 的绳索牵引而沿导轨上升，滑轮中心到导轨的距离为l ，如图所示。
设绳索以等速0v 拉下，忽略滑轮尺寸。
求套管A 的速度和加速度与距离x 的关系式。
L6-3（HGDV7-5-7） 图示摇杆滑道机构中的滑块M 同时在固定的圆弧槽BC 和OA 摇杆的滑道中滑动。
如弧BC 的半径为R ，摇杆OA 的轴O 在弧BC 的圆周上。
摇杆绕O 轴以等角速度ω转动，当运动开始时，摇杆在水平位置。
分别用直角坐标法和自然法给出点M 的运动方程，并求其速度和加速度。
L6-4（HGDV7-5-10） 点沿空间曲线运动，在点M 出其速度为43v i j =+，加速度a 与速度v 的夹角30β=，且210m/s a =。
求轨迹在该点密切面内的曲率半径ρ和切向加速度t a 。
L6-5（HTSV3-7-11）已知点的运动方程：50x t =，2500y t =-（长度单位为m ，时间单位为s ），求当0t =时，点的切向加速度、法向加速度及轨迹的曲率半径。
第7章 刚体的简单运动L7-1（HGDV7-6-1） 图示曲柄滑杆机构中，滑杆上有一圆弧形轨道，其半径 100mm R =，圆心1O 在导杆BC 上。
曲柄长 100mm OA =，以等角速度 ω=4 rad/s 绕O 轴转动。
求导杆BC 的运动规律以及当曲柄与水平线间的夹角ϕ为 30 时，导杆BC 的速度和加速度。
L7-2（HGDV7-6-4） 机构如图所示，假定杆AB 以匀速v 运动，开始时 0ϕ=。
