当前位置：文档之家 › 分式全章复习与巩固(基础)PPT课件..

分式全章复习与巩固(基础)PPT课件..

  • 格式：ppt
  • 大小：702.00 KB
  • 文档页数：25

下载文档原格式

  / 25

合集下载

分式-复习课件-(共34张PPT)

分式-复习课件-(共34张PPT)

x2
1 x2
2
9
变: 已知 x2 – 3x+1=0 ,求 x2+
x
x
的1x2值. 的1x2 值.
变:已知 x+ 1=3 ,求
x
x2 /x2 的值. x4+x2+1 /x2
1
x2
1 x2
1
两个分式相乘，把分子相乘的积作为积的分子， 把分母相乘的积作为积的分母。
用符号语言表达： a c ac b d bd
27xy2
-2(a-b)2 -8(b-a)3
关键找出分子和 分母的公因式
m2+4m+4
(3)
m2 - 4
关键找出分母的
2.通分
最简公分母
(1) x 与 y (2)
6a2b
9ab2c
a-1
6
a2+2a+1 与 a2-1
约分与通分的依据都是: 分式的基本性质
整体代入法化简思想：
【【例例11】】已已知知：：1x
a0 1
an
1
an
(a 0)
(1)(3)3 1 (3)3
1 27
(2)(3a)2 b2 (a2b2 )3 解：原式= 32 a2b2 a6b6
6、用科学记数法表示：
例： 0.00065 6.5104
(1) 0.000030
3.0 105
7、约分
:
例(1)
6x2y 12 xy 2
(2) x 1 2x 1 3x 2 x 1 1 x x 1
复习回顾一:
1.解分式方程的思路是：
分式 方程
去分母
整式 方程
2.解分式方程的一般步骤

第三章整理《分式》(复习)ppt课件

第三章整理《分式》(复习)ppt课件

顺水速=静水速+水流速 逆水速=静水速-水流速
设是水流速为xkm/ h
则 水 为 20 + x)km/ h 顺 速 (
逆 速 (20 - x)km/ h 水 为
72 48 = 20 + x 20 − x
A．扩大3倍 B．扩大9倍C．扩大4倍D．不变 扩大3 扩大9 扩大4
3、 填空： x ( x − y ) = ( x − 2
y)
x + xy
x+y
例1：化简求值 ：
a−2 a −1 a−4 ( 2 − 2 )÷ a + 2a a + 4a + 4 a + 2 2 其中a满足：a + 2a − 1 = 0
1. 若分式
A、 A、x≠-1 C、x≠2 、
若有意义， 应满足（ 若有意义，则x应满足（ B ） 应满足
B、 ≠-1且 B、x ≠-1且x ≠2 D、x ≠-1或x ≠2 、 或
x −4 ( x + 1)( x − 2)
若值为0， 应满足（ 若值为 ，则x应满足（ B ） 应满足
A、x=2 、 C、 、
1km
中点 18km }
xkm / h
甲 A
乙 B
甲走了总共20km 甲走了总共
设 乙的速度 xkm / h 则 甲的速度( x + 0.5)km / h
20 18 = x + 0.5 x
1、一项工程，若甲队单独做，恰好在规定的日期 、一项工程，若甲队单独做， 完成，若乙队单独做要超过规定日期3天完成 天完成； 完成，若乙队单独做要超过规定日期 天完成；现 在先由甲、乙合做2天 在先由甲、乙合做 天，剩下的工程再由乙队单独 也刚好在规定日期完成， 做，也刚好在规定日期完成，问规定的日期是多 少天？ 少天？ 1 甲每天的工作量 x 设 天 甲x

最新人教部编版八年级数学上册《第15章 分式【全章】》精品PPT优质课件

最新人教部编版八年级数学上册《第15章 分式【全章】》精品PPT优质课件

• 学习目标： 1．知道并熟记分式乘除法法则. 2．能准确地进行分式的乘除法的计算. 3．通过分式乘除法法则得出体会类比的数学思 想方法.
推进新课
知识点1 分式的乘除法法则
问题1 一个水平放置的长方体容器，其容积
为V，底面的长为a，宽为b，当容器内的水占容 积的 m 时，水面的高度为多少？
n （1）这个长方体容器的高怎么表示？
而分式的分母中含有字母.
3.当x取什么值时，下列分式有意义？
(1) 1 ;(2) 1 ;(3) x 5 ;(4) 1 ;(5) x .
3x
3 x 3x 5
x2 16
x 3
解：(1) x ≠ 0 ;
(2) x ≠ 3 ;
(3) x 5 ;
3
(4) x为全体实数;
(5) x ≠± 3 .
4.当x取何值时，分式
谢谢观赏！
再见！
15.2 分式的运算 15.2.1 分式的乘除 第1课时 分式的乘除
R·八年级上册
新课导入
• 通过前面分式的学习，我们知道分式和分数有 很多的相似性，如性质、约分和通分.事实上， 在运算上它们也有许多的相似性.今天我们一起 类比分数的运算来研究分式的运算，首先学习 分式的乘除.
;
3a2 6ab2
x2 4 x2 4x 4
(3) a
x
x
2
， b
2
y
x
,1 ab
.
解：(3)
ab
bx
x
2
， ab
ay
x
2
, x2 ;
ab x 2
3.
x2 4y2 4x2 8xy
先化简，再求值. 其中x= 1 ，y=1.

教学课件：第五章-分式与分式方程-章末归纳与复习

教学课件：第五章-分式与分式方程-章末归纳与复习
3. 答案
解分式方程的一般步骤包括去分母、去括号、移项合并同类项和系数化 为1等步骤。
03
解析
解分式方程需要运用分式的性质和运算法则，通过去分母、去括号、移
项合并同类项和系数化为1等步骤，将分式方程转化为整式方程进行求
解。
答案与解析
4. 答案
分式方程的应用包括解决比例问题、速度问题、路程问题等 实际问题。例如，已知甲乙两地相距100公里，一辆汽车从 甲地出发，以每小时80公里的速度驶向乙地，求汽车到达乙 地所需时间。
解析
分式方程在解决实际问题中具有广泛的应用，如比例问题、 速度问题、路程问题等。通过建立数学模型，将实际问题转 化为数学问题，利用分式方程进行求解，可以得出实际问题 的解决方案。
THANKS
感谢观看
一元二次分式方程的解法
总结词
通过去分母，将一元二次分式方程转化为可 求解的一元二次方程，然后求解一元二次方 程得到分式方程的解。
详细描述
一元二次分式方程的一般形式为 ax^2+bx+c=0，其中 a、b、c 为已知数，x
为未知数。解一元二次分式方程时，首先去 分母，即将方程两边同时乘以公分母的最小 公倍数，将分式方程转化为整式方程。然后 利用配方法或公式法求解一元二次方程得到 x 的值。最后需要检验解的合理性，即把 x 的
04
分式的应用
分数运算在生活中的应用
日常购物计算折扣
建筑和装修中的比例计算
在购物时，经常需要计算折扣后的价 格，这涉及到分数的运算。
在建筑和装修中，经常需要使用比例 和分数来计算材料用量和布局。
食品分配
在家庭或餐厅中，当需要将食品等物 品均等分配时，需要使用分数运算。
分式方程在实际问题中的应用

《分式方程复习》课件

《分式方程复习》课件
详细描述
在金融和经济领域，分式方程可以用来描述和预测市场行为、投资回报和成本效益分析等。在交通领 域，分式方程可以用来解决交通流量和路线规划问题。在工程领域，分式方程可以用来描述机械运动 、热传导和电路等问题。
04 分式方程的解题 技巧
转化思想
总结词
转化思想是将复杂问题转化为简单问 题，将未知问题转化为已知问题的一 种解题策略。
详细描述
分式方程与整式方程的主要区别在于分母中是否含有未知数。分式方程的分母中 含有未知数，而整式方程的分母中不含有未知数。此外，分式方程的解法通常需 要更多的技巧和注意事项，例如需要处理分母为零的情法
01
02
03
04
直接求解法
通过对方程进行化简，直接求 出方程的解。
详细描述
在解分式方程时，通过对方程进行适 当的变形和转化，可以将分式方程转 化为整式方程或更容易解决的形式， 从而简化解题过程。
整体思想
总结词
整体思想是从整体角度出发，将 问题看作一个整体，从而简化问 题的一种解题策略。
详细描述
在解分式方程时，可以将方程中 的某些项看作一个整体，通过对 方程进行整体变形和运算，从而 简化解题过程。
代数方法
总结词
代数方法是利用代数性质和定理，对方 程进行变形和求解的一种解题策略。
VS
详细描述
在解分式方程时，可以利用代数性质和定 理，如乘法分配律、合并同类项等，对方 程进行变形和简化，从而找到方程的解。
05 分式方程的易错 点分析
概念理解不清
总结词
概念理解不清晰
详细描述
分式方程的基本概念和定义是解题的基础，如果对分式方程的概念理解不清晰，会导致 解题思路出现偏差，甚至无法正确列出方程。

《分式》PPT课件--图文全文

《分式》PPT课件--图文全文
答：甲追上乙需要 时．当a=6，b=５时，甲追上乙需要 ５时．
解：根据题意，乙先行１时的路程是１×b（千米），甲比乙每小时多行（a－b）千米，所以甲追上乙所需的时间是 b÷（a－b）= （时） 当a=6，b=５时，甲追上乙所需的时间是
＝
＝５（时）
代数式
整式
分式
分母中必含有字母
分母不能为零
当分子为零，分母不为零时， 分式值为零。
当x为任意实数时，下列分式一定有意义的是 （ ）
（A）
（B）
( C)
（D）
在分式 中，当x为何值时，分式有意义？分式的值为零？
解：根据题意可知， 该保护区每平方米内灰熊的只数是：７÷p=
文林书店库存一批图书，其中一种图书的原价是每册a元，现降价x元销售，当这种图书的库存全部售出时，其销售额为b元，降价销售开始时，文林书店这种图书 的库存量是 。
甲种糖果每千克价格a元，乙种糖果价格b元，取甲种糖果m㎏，乙种糖果n㎏，混合后，平均每千克价格 元。
像10a+2b， ， ，2a²这样含有字母的数学表达式称为代数式.
整式
单项式:数与字母或字母与字母的积
多项式:几个单项式的和
注意:代数式包括整式，也就是说整式是代数式但代数式就不一定是整式了．
有了这些预备知识，这节课我们将要学习另外一种 代数式！
为了调查珍稀动物资源，动物专家在p平方米的保护区内找到７只灰熊，那么该保护区 每平方米有＿＿＿＿只灰熊．
轮船在静水中每小时走a千米，水流速度为每小时b千米，轮船在逆流中航行s千米，然后又返回出发地，那么轮船需要的时间 是 小时。
一件商品售价x元，利润率为a%（a＞0），则这种商品每件的成 本是 元。
注意：分式中字母的取值不能使分母为零．因为当分母的值为零时，分式就没有意义．

第1章分式章末复习PPT课件


针对训练
6.某市在道路改造过程中，需要甲、乙两个工程队来完成这一工 程。已知甲工程队比乙工程队每天能多铺设20米，且甲工程队 铺设350米所用的天数与乙工程队铺设250米所用的天数相同。 问甲、乙两个工程队每天各能铺设多少米？
解：设乙工程队每天能铺设x米； 则甲工程队每天能铺设（x+20）米， 依题意，得 350 250 ， 解得x=50， x 20 x 经检验，x=50是原方程的解，且符合题意。
解： 由①+ ② +③，得
1 x
1 y
1 z
16
④，
由④- ①，④- ②，④- ③分别得：
1 7, 1 5, 1 4, zxy
x
1 5
,
所以
y
1 4
,
z
1 7
.
归纳拓展
分式方程组的解法也有一定的灵活性，关键是根据每个 问题的特点，选择适当的解答方法，特别提倡“一看，二慢， 三通过”的好习惯。
答：甲工程队每天能铺设70米，乙工程队每天能铺设50米。
考点六 本章数学思想和解题方法
主元法 2a b 例6：已知：a 2b
3 14
，求 a2 b2 的值。
a2 b2
【解析】由已知可以变形为用b来表示a的情势，得 a 4 b ， 5
代入约分即可求值。
解： ∵ 2a b 3 a 2b 14
方法总结
分式有意义的条件是分母不为0；分式无意义的条件是 分母的值为0；分式的值为0的条件是：分子为0而分母不为0.
针对训练
1.若分式 1 无意义，则a的值为 x3
-3 。
2.如果分式 a 2 的值为零，则a的值为 2 。 a2
考点二 分式的有关计算

分式全章复习(第一课时)PPT课件(数学人教版八年级上册)


=a(a+2)
=a2+2a .
初中数学
练习
如果
a2+2a
1=0 ，求代数式 (a
4 a2 a )∙ a 2
的值.
解：原式
=(
a2 a
4 a2 a )∙ a 2
a2 4 a2 = a ∙a 2
(a 2)(a+2) a2 = a ∙a 2
∵ a2+2a 1=0，
∴a2+2a=1. 整体代入
∴原式=1.
国家中小学课程资源
分式全章复习（第一课时）
授课教师：XX 日期：XX年XX月XX日
实 际
列式
分式
类比分 数性质
分式基本性质 类比分 分式的运算 数运算
问 列方程
去分母
题
分式方程
整式方程
目标
实际 问题 的解
目标
解整式方程
分式方程的解
整式方程的解
检验
初中数学
分式的概念
分式
分式基本性质
分式的运算
初中数学
判断:
当a=2时原式= 2+2 2-1
=4 . 取值条件：分式有意义.
a+2 =a 1 .
a≠ ±1且 a≠ ±2 .
初中数学
例
3 a2 先化简 (1+ a 2 )÷a2
1 4
，再选一个你喜欢的值，
代入求出代数式的值.
解：原式
=(
a a
2 3 a2 2 + a 2 ) ∙ a2
4 1
当a=0,
a 2+3 (a+2)(a 2) = a 2 ∙ (a+1)(a 1)

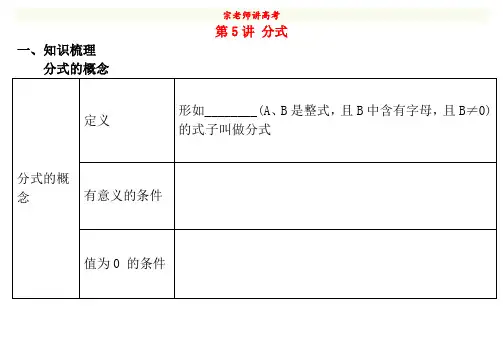
第5讲 分式基础与巩固

第5讲分式一、知识梳理分式的概念的式子叫做分式分式的基本性质及相关概念A B ＝A×B×M，AB＝A÷B÷M(M是不为零的整式)应用注意：通分的关键是确定几个分式的公分母分式的运算除法法则二、题型、技巧归纳考点1 分式的概念例1（1）若分式有意义，则x的取值范围是( ) A．x≠3 B．x＝3 C．x<3 D．x>3(2) 若代数式211x--的值为零，则x＝________.技巧归纳：(1)分式有意义的条件是分母不为零；分母为零时分式无意义．(2)分式的值为零的条件是：分式的分子为零，且分母不为零．(3)分式的值为正的条件是：分子与分母同号；分式的值为负的条件是：分子考点2 分式的基本性质及相关概念例2 下列计算错误的是( )A.0.2a ＋b 0.7a －b ＝2a ＋b 7a －bB.x 3y 2x 2y 3＝x yC.a －b b －a＝－1 D.1c ＋2c ＝3c考点3 分式的运算例3先化简，再求值：其中X=6.技巧归纳：先把括号里的异分母通分变成同分母，进行同分母分式的加减，再把除变乘，进行分式的乘法例4 ⎝⎛⎭⎪⎫1＋1x ÷x 2－1x例5 先化简，再求值：2a －1＋a 2－4a ＋4a 2－1×a ＋1a －2，其中a ＝2＋1.技巧归纳：(1)解有条件的分式化简与求值时，既要瞄准目标，又要抓住条件，既要根据目标变换条件，又要依据条件来调整目标，除了要利用整式化简求值的知识方法外，还常常用到如下的技巧：①取倒数或利用倒数关系；②整体代入；③拆项变形或拆分变形等．(2)化简求值时，近几年出现了一种开放型问题，题目中给定几个数字要考虑三、随堂检测1．在式子，，，，中，分式有（ ） A ．1个 B ．2个 C ．3个 D ．4个2．分式无意义的条件是（ ）A ．x≠—3B ． x=－3C ．x=0D ．x=33．当x= 时，分式值为零.4．计算．= .x y 3πa 13+x 31+x a a 232+x x22x x --2323()a b a b --÷5．若方程无解,则__________________.6．先化简，再求值：，其中. 322x m x x -=--m =211122x x x -⎛⎫-÷ ⎪++⎝⎭2x =。

分式复习课件-图


应用问题
实际问题中的分式
如材料费、工资、均价、生产效率等，均可转 化为分式形式。
解决实际问题中的分式
通过列式、比例、方程等方法，可解决实际问 题中的分式计算与应用。
总结
1
复习内容
本节课程重点回顾分式的定义、性质、运算和应用。
2
重点难点
问题转化、方程解法是本节课程的重点和难点。
结束语
分式是数学的重要内容，也是中考和高考的必考点，希望本节课程对您的学 习有所帮助。
性质2：除法法则
分式除法变为乘法，分子分母分别相乘。
性质3：加减法则
分母相同时，可按分子加减，分母不同时，通分后可加减。
分式的运算
1
乘除运算练习
练习纯分式乘除和分式与整数的乘除。
2
加减运算练习
练习分母相同、分母不同的加减运算。
分式方程
定义
分式方程是含有未知数的分式等式。
解法
可通过通分、移项、消元等方法进行求解。
分式复习ppt课件-图
这份PPT课件将为您介绍分式的基本定义、性质、运算和应用，让您轻松复习 分式。
什么是分式？
定义
分式是指形如$\frac{a}{b}$的表达式，其中a、b为整 数，b≠0.
基本元素
分子、分母、分式线是构成分式的基本元素。
分式的本性质
性质1：乘法法则
分式乘法可交换、结合、分配律。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2018/9/25
知识网络
2018/9/25
要点一、分式的有关概念及性质
2018/9/25
要点二、分式的运算
2018/9/25
2018/9/25
要点三、分式方程
2018/9/25
要点四、分式方程的应用
2018/9/25
经典例题——类型题
提交组内解决不了的问题？
2018/9/25
二、处理重点类型题 1、每组选择一个类型题
例2
例3 5分
例5
例6 6分
4分
5分
2、依据答题要求把责任题的解答过程写在小黑板上。（小组2积分， 讲题人2积分） 要求：答案及思路，规范步骤，考查知识点，所属类型，点评（总 结升华）。 时间：3-8分钟。 3、非责任组注意聆听、纠错、补充（1积分，纠错、补充要等到台 上的同学讲完了才进行纠错，举手回答） 责任组给聆听、纠错、补充最好的小组奖1积分。
2018/9/25
课前就位
• 小组全员到齐 小组+1分
• 小组成员全都提前10分钟 到场。小组+2分
2018/9/25 4
展示与点评
• 优秀/进步学案 • 优秀/进步笔记 • 优秀错题本
2018/9/25
• 分式全章复习与巩固（基础）
2018/9/25
学习目标
• 1. 理解分式的概念，能求出使分式有意义、分式无意义、 分式值为0的条件. • 2．了解分式的基本性质，掌握分式的约分和通分法则． • 3．掌握分式的四则运算． • 4．结合分式的运算，将指数的讨论范围从正整数扩大到 全体整数，构建和发展相互联系的知识体系． • 5．结合分析和解决实际问题，讨论可以化为一元一次方 程的分式方程，掌握这种方程的解法，体会解方程中的化 归思想．
重点奖励
准时到的个人 带学案的个人 带三色笔的个人 带草稿的个人 +1 ~2分 +2分 +2分 +1分
家长签字 +2分
知识回顾 +1分
要点梳理 +1~2分
错题本
+2分
靠旁白
色笔区分
+2 ~3分
+2 ~3分
测评系统 +2 分 典型例+2~3分
英语，语文笔记整理 +2分
2018/9/25
学员积分情况
• • • • • • 江婧婷：161 张之扬：137 徐美玲：0 吴国燚：66 郭亿恬：0 刘超：141 张蕾：34 王源航：162 曹行鹏：93 冯艺：30 耿子涵：0 余姚：80 陈俊宇：45 蔡佳成：147 程远红：158 袁蕴佳：102 谭乐：88 唐钰：168 钱宗源：93 刘俊淏：130 何晨晨：171 孙忻伟：105
2018/9/25
类型一、分式及其基本性质
2018/9/25
2018/9/25
类型二、分式运算
2018/9/25
2018/9/25
2018/9/25
类型三、分式方程的解法
2018/9/25
例5：变式
2018/9/25
类型四、分式方程的应用
2018/9/25
例6：变式
2018/9/25
课后统计、返校要求
下周必带物品：1.作业单
2.错题本
3.语文，英语笔记本 4.数学学案导学
组长统计积分，把积分表交至老师处；
各组同学带走桌位里垃圾；
2018/9/25
25
红 色 部 分 重 点 加 分
!
2018/9/25
12.09—12.16学生登录时长
江婧婷：1.31 张之扬：2.1 徐美玲：0 吴国燚：5.35 郭亿恬：0 刘超：24.52 张蕾：0 王源航：3.19 曹行鹏：0.72 钱宗源：1.02 耿子涵：0 陈俊宇：0.64 程远红：1.57 谭乐：0.59 刘俊淏：1.29 何晨晨：7.14 蔡佳成：2.25 袁蕴佳：2.37 唐钰：6.35 余姚：5.13 孙忻伟：2.46