摆动从动件盘形凸轮机构

第三节 盘形凸轮廓线的设计当根据工作要求和结构条件选定了凸轮机构的类型、从动件的运动规律和凸轮的基圆半径（其确定将在下节中介绍）等结构参数后，就可以设计凸轮的轮廓曲线。

凸轮廓线的设计方法有图解法和解析法，其设计原理基本相同。

本节先简要介绍图解法，后重点介绍解析法设计凸轮廓线。

一、凸轮廓线设计的基本原理图4-13 反转法设计凸轮廓线基本原理图4-13所示为一尖顶对心盘形凸轮机构，设凸轮以等角速度ω逆时针转动，推动从动件2在导路中上、下往复移动。

当从动件处于最低位置时，凸轮轮廓曲线与从动件在A 点接触，当凸轮转过1ϕ角时，凸轮的向径A A 0将转到A A '0位置，而凸轮轮廓将转到图中虚线所示的位置。

从动件尖端从最低位置A 上升至B '，上升的位移为B A S '=1，这是从动件的运动位移。

若设凸轮不动，从动件及其运动的导路一起绕A 0点以等角速度-ω转过1ϕ角，从动件将随导路一起以角速度-ω转动，同时又在导路中作相对导路的移动，如图中的虚线位置，此时从动件向上移动的位移为B A 1。

而且，11S B A B A ='=，即在上述两种情况下，从动件移动的距离不变。

由于从动件尖端在运动过程中始终与凸轮轮廓曲线保持接触，所以从动件尖端的运动轨迹即为凸轮轮廓。

设计凸轮廓线时，可由从动件运动位移先定出一系列的B 点，将其连接成光滑曲线，即为凸轮廓线。

由于这种方法是假设凸轮固定不动而使从动件连同导路一起反转，故称为反转法。

对其它类型的凸轮机构，也可利用反转法进行分析和凸轮廓线设计。

二、图解法设计凸轮廓线1. 移动从动件盘形凸轮廓线的设计（1）尖端从动件 图4-14a 所示为一偏置移动尖端从动件盘形凸轮机构。

设已知凸轮的基圆半径为b r ，从动件导路偏于凸轮轴心A 0的左侧，偏距为e ，凸轮以等角速度ω顺时针方向转动。

从动件的位移曲线如图4-14b 所示，试设计凸轮的轮廓曲线。

图4-14 尖端从动件盘形凸轮廓线设计依据反转法原理，具体设计步骤如下。

第5章凸轮机构1．从动件的运动规律:等速，等加速等减速，余弦加速度，正弦加速度2．动力特性:刚性冲击，柔性冲击3．设计原理:反转法，比例尺，等分基圆，偏置从动件压力角与自锁条件4．基本参数:基圆半径，滚子半径，平底尺寸【思考题】5-1 凸轮机构的应用场合是什么？凸轮机构的组成是什么？通常用什么办法保证凸轮与从动件之间的接触？5-2 凸轮机构分成哪几类？凸轮机构有什么特点？5-3 为什么滚子从动件是最常用的从动件型式？5-4 凸轮机构从动件的常用运动规律有那些？各有什么特点？5-5 图解法绘制凸轮轮廓的原理是什么？为什么要采用这种原理？5-6 什么情况下要用解析法设计凸轮的轮廓？5-7 设计凸轮应注意那些问题？5-8 从现有的机器上找出两个凸轮机构应用实例，分析其类型和运动规律?A级能力训练题1.在凸轮机构的几种基本的从动件运动规律中，运动规律使凸轮机构产生刚性冲击，运动规律产生柔性冲击，运动规律则没有冲击。

2.在凸轮机构的各种常用的推杆运动规律中，只宜用于低速的情况，宜用于中速，但不宜用于高速的情况，而可在高速下应用。

3.设计滚子推杆盘形凸轮轮廓线时，若发现凸轮轮廓线有变尖现象，则在尺寸参数的改变上应采取的措施是或。

4.移动从动件盘形凸轮机构，当从动件运动规律一定时，欲同时降低升程的压力角，可采用的措施是。

若只降低升程的压力角，可采用方法。

5.凸轮的基圆半径是从到的最短距离。

6.设计直动滚子推杆盘形凸轮机构的工作廓线时，发现压力角超过了许用值，且廓线出现变尖现象，此时应采用的措施是__________________________________________。

7.与其他机构相比，凸轮机构的最大优点是。

（1）便于润滑（2）可实现客种预期的运动规律（3）从动件的行程可较大（4）制造方便，易获得较高的精度8.凸轮的基圆半径越小，则凸轮机构的压力角，而凸轮机构的尺寸。

（1）增大（2）减小（3）不变（4）增大或减小9.设计凸轮廓线对，若减小凸轮的基圆半径r b，则凸轮廓线曲率半径将。

凸轮机构基本参数的设计前节所先容的几何法和解析法设计凸轮轮廓曲线，其基圆半径r0、直动从动件的偏距e或摆动从动件与凸轮的中心距a、滚子半径rT等基本参数都是预先给定的。

本节将从凸轮机构的传动效率、运动是否失真、结构是否紧凑等方面讨论上述参数的确定方法。

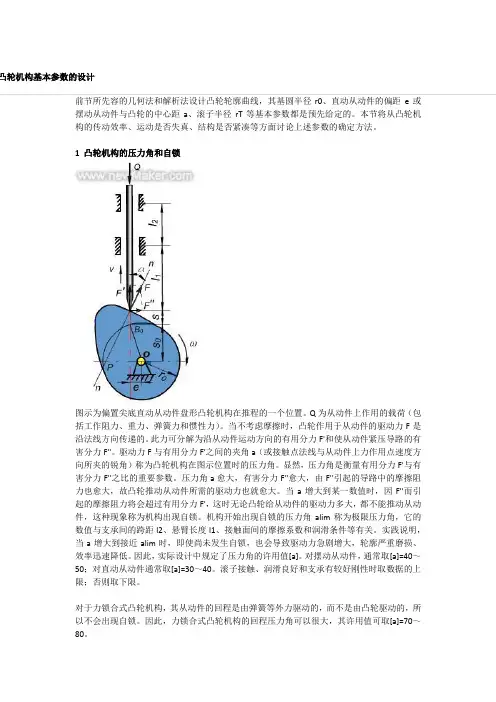
1 凸轮机构的压力角和自锁图示为偏置尖底直动从动件盘形凸轮机构在推程的一个位置。

Q为从动件上作用的载荷（包括工作阻力、重力、弹簧力和惯性力）。

当不考虑摩擦时，凸轮作用于从动件的驱动力F是沿法线方向传递的。

此力可分解为沿从动件运动方向的有用分力F'和使从动件紧压导路的有害分力F''。

驱动力F与有用分力F'之间的夹角a（或接触点法线与从动件上力作用点速度方向所夹的锐角）称为凸轮机构在图示位置时的压力角。

显然，压力角是衡量有用分力F'与有害分力F''之比的重要参数。

压力角a愈大，有害分力F''愈大，由F''引起的导路中的摩擦阻力也愈大，故凸轮推动从动件所需的驱动力也就愈大。

当a增大到某一数值时，因F''而引起的摩擦阻力将会超过有用分力F'，这时无论凸轮给从动件的驱动力多大，都不能推动从动件，这种现象称为机构出现自锁。

机构开始出现自锁的压力角alim称为极限压力角，它的数值与支承间的跨距l2、悬臂长度l1、接触面间的摩擦系数和润滑条件等有关。

实践说明，当a增大到接近alim时，即使尚未发生自锁，也会导致驱动力急剧增大，轮廓严重磨损、效率迅速降低。

因此，实际设计中规定了压力角的许用值[a]。

对摆动从动件，通常取[a]=40～50；对直动从动件通常取[a]=30～40。

滚子接触、润滑良好和支承有较好刚性时取数据的上限；否则取下限。

对于力锁合式凸轮机构，其从动件的回程是由弹簧等外力驱动的，而不是由凸轮驱动的，所以不会出现自锁。

因此，力锁合式凸轮机构的回程压力角可以很大，其许用值可取[a]=70～80。

第5章凸轮机构1．从动件的运动规律:等速，等加速等减速，余弦加速度，正弦加速度2．动力特性:刚性冲击，柔性冲击3．设计原理:反转法，比例尺，等分基圆，偏置从动件压力角与自锁条件4．基本参数:基圆半径，滚子半径，平底尺寸【思考题】5-1 凸轮机构的应用场合是什么？凸轮机构的组成是什么？通常用什么办法保证凸轮与从动件之间的接触？5-2 凸轮机构分成哪几类？凸轮机构有什么特点？5-3 为什么滚子从动件是最常用的从动件型式？5-4 凸轮机构从动件的常用运动规律有那些？各有什么特点？5-5 图解法绘制凸轮轮廓的原理是什么？为什么要采用这种原理？5-6 什么情况下要用解析法设计凸轮的轮廓？5-7 设计凸轮应注意那些问题？5-8 从现有的机器上找出两个凸轮机构应用实例，分析其类型和运动规律?A级能力训练题1.在凸轮机构的几种基本的从动件运动规律中，运动规律使凸轮机构产生刚性冲击，运动规律产生柔性冲击，运动规律则没有冲击。

2.在凸轮机构的各种常用的推杆运动规律中，只宜用于低速的情况，宜用于中速，但不宜用于高速的情况，而可在高速下应用。

3.设计滚子推杆盘形凸轮轮廓线时，若发现凸轮轮廓线有变尖现象，则在尺寸参数的改变上应采取的措施是或。

4.移动从动件盘形凸轮机构，当从动件运动规律一定时，欲同时降低升程的压力角，可采用的措施是。

若只降低升程的压力角，可采用方法。

5.凸轮的基圆半径是从到的最短距离。

6.设计直动滚子推杆盘形凸轮机构的工作廓线时，发现压力角超过了许用值，且廓线出现变尖现象，此时应采用的措施是__________________________________________。

7.与其他机构相比，凸轮机构的最大优点是。

（1）便于润滑（2）可实现客种预期的运动规律（3）从动件的行程可较大（4）制造方便，易获得较高的精度8.凸轮的基圆半径越小，则凸轮机构的压力角，而凸轮机构的尺寸。

（1）增大（2）减小（3）不变（4）增大或减小9.设计凸轮廓线对，若减小凸轮的基圆半径r b，则凸轮廓线曲率半径将。

第四节 凸轮机构基本尺寸设计无论是作图法还是解析法，在设计凸轮廓线前，除了需要根据工作要求选定从动件的运动规律外，还需要确定凸轮机构的一些基本参数，如基圆半径b r 、偏距e 、滚子半径r r 等。

一般来讲，这些参数的选择除了应保证从动件能够准确地实现预期的运动规律外，还应当使机构具有良好的受力状况和紧凑的结构。

本节讨论凸轮机构基本尺寸设计的原则和方法。

一、移动滚子从动件盘形凸轮机构1. 压力角同连杆机构一样，压力角也是衡量凸轮机构传力特性好坏的一个重要参数。

所谓凸轮机构的压力角，是指在不计摩擦的情况下，凸轮对从动件作用力的方向线与从动件上力作用点的速度方向之间所夹的锐角。

对于图4-22所示的移动滚子从动件盘形凸轮机构来说，过滚子中心所作理论廓线的法线nn 与从动件运动方向之间的夹角α就是压力角。

（1）压力角与作用力的关系 由图4-22可以看出，凸轮对从动件的作用力F 可以分解成两个分力，即沿着从动件运动方向的分力F '和垂直于运动方向的分力F ''。

只有前者是推动从动件克服载荷的有效分力，而后者将增大从动件与导路间的摩擦，它是一种有害分力。

压力角α越大，有害分力越大。

当压力角α增大到某一数值时，有害分力所引起的摩擦阻力将大于有效分力F '，这时无论凸轮给从动件的作用力有多大，都不能推动从动件运动，即机构将发生自锁。

因此为减小侧向推力，避免自锁，压力角α应越小越好。

图4-22 凸轮机构的压力角（2）压力角与机构尺寸的关系 设计凸轮时，除了应使机构具有良好的受力状况外，还希望机构结构紧凑。

而凸轮尺寸的大小取决于凸轮基圆半径的大小。

在实现相同运动规律的情况下，基圆半径越大，凸轮的尺寸也越大。

因此，要获得轻便紧凑的凸轮机构，就应当使基圆半径尽可能地小。

但是基圆半径的大小又和凸轮机构的压力角有直接的关系。

下面以图4-22为例来说明这种关系。

图中，过滚子中心B 所作理论廓线的法线nn 与过凸轮轴心0A 所作从动件导路的垂线交于P 点，由瞬心定义可知，该点即为凸轮与从动件在此位置时的瞬心，且ϕωd ds v P A ==0。

凸轮机构一、填空1.凸轮机构主要是由_______、_______和固定机架三个基本构件所组成。

2.按凸轮的外形，凸轮机构主要分为_______凸轮和_______凸轮两种基本类型。

3.从动杆与凸轮轮廓的接触形式有_______、_______和平底三种。

4.以凸轮的理论轮廓曲线的最小半径所做的圆称为凸轮的_______。

5.凸轮理论轮廓曲线上的点的某点的法线方向(即从动杆的受力方向）与从动杆速度方向之间的夹角称为凸轮在该点的_______。

6.随着凸轮压力角α增大，有害分力F2将会_______而使从动杆自锁“卡死”，通常对移动式从动杆，推程时限制压力角α_______。

7.凸轮机构从动杆等速运动的位移为一条_______线，从动杆等加速等减速运动的位移曲线为一条_______线。

8.等速运动凸轮在速度换接处从动杆将产生_______冲击，引起机构强烈的振动。

9.凸轮机构的移动式从动杆能实现_______。

(a 匀速、平稳的直线运动 b 简偕直线运动 c各种复杂形式的直线运动10.从动杆的端部形状有_______、_______和平底三种。

11.凸轮与从动件接触处的运动副属于_______。

(a 高副 b 转动副 c 移动副)12. 要使常用凸轮机构正常工作，必须以凸轮_______。

( a 作从动件并匀速转动 b 作主动件并变速转动 c 作主动件并匀速转动）13.在要求_______的凸轮机构中，宜使用滚子式从动件。

( a 传力较大 b 传动准确、灵敏 c 转速较高）14.使用滚子式从动杆的凸轮机构，为避免运动规律失真，滚子半径r与凸轮理论轮廓曲线外凸部分最小曲率半径ρ最小之间应满足_______。

(a r >ρ最小 b r =ρ最小 c r <ρ最小)15.凸轮与移动式从动杆接触点的压力角在机构运动时是_______。

( a 恒定的 b 变化的 c 时有时无变化的）16.当凸轮转角δ和从动杆行程H一定时，基圆半径r b与压力角α的关系是_______。

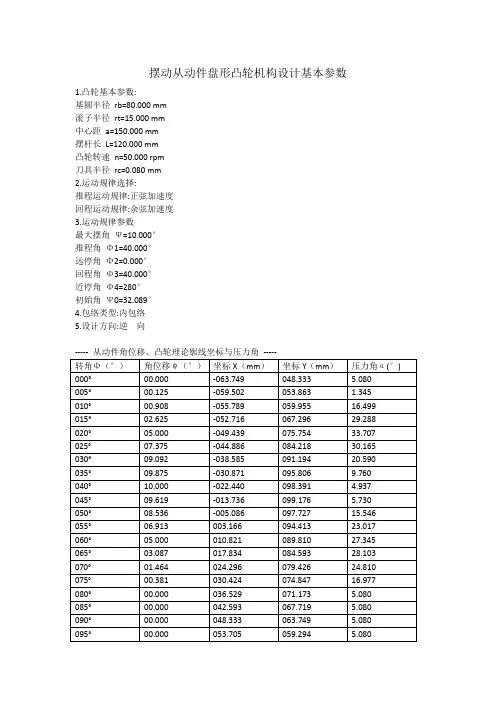
摆动从动件盘形凸轮机构设计基本参数
1.凸轮基本参数:
基圆半径rb=80.000 mm
滚子半径rt=15.000 mm
中心距a=150.000 mm
摆杆长L=120.000 mm
凸轮转速n=50.000 rpm
刀具半径rc=0.080 mm
2.运动规律选择:
推程运动规律:正弦加速度
回程运动规律:余弦加速度
3.运动规律参数
最大摆角Ψ=10.000°
推程角Φ1=40.000°
远停角Φ2=0.000°
回程角Φ3=40.000°
近停角Φ4=280°
初始角Ψ0=32.089°
4.包络类型:内包络
5.设计方向:逆向
推程最大压力角: 033.707 回程最大压力角: 028.257
－－－－－参数说明－－－－－
Φ－凸轮转角(°)
Xa、Ya－实际廓线坐标（mm）
ρb－理论廓线曲率半径（mm）
ρa－实际廓线曲率半径（mm）
曲率半径：“-”曲线外凸，“+”曲线内凹Xc、Yc－刀具中心轨迹坐标（mm）。

机械原理课程设计目录1.设计题目及要求--------------------------------------------------------------------P32.设计目的------------------------------------------------------------------------------P33.设计过程与思路----------------------------------------------------------------------P44.从动件运动规律设计--------------------------------------------------------------P55.凸轮基本尺寸设计-------------------------------------------------------------------P86.凸轮廓线设计------------------------------------------------------------------------P97.校核压力角和凸轮廓线是否出现运动失真现象------------------------P108.改进设计------------------------------------------------------------------------------P119.绘制机构工作图-------------------------------------------------------------------P1110.结束语--------------------------------------------------------------------------------P12 附录及参考文献：机械原理课本机械原理课程ppt，pdf1. 设计题目及要求某技术人员欲设计一台打包机，其推送包装物品的机构如图所示。

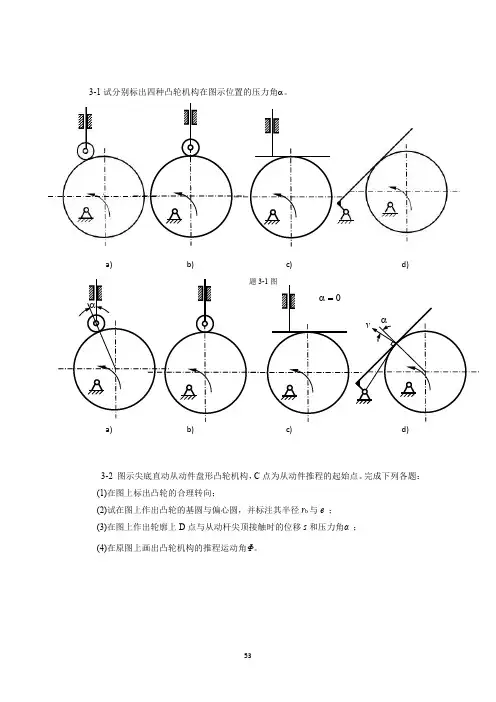
3-1试分别标出四种凸轮机构在图示位置的压力角α。

a)b)c)d)a)b)c)d)3-2图示尖底直动从动件盘形凸轮机构，C 点为从动件推程的起始点。

完成下列各题：(1)在图上标出凸轮的合理转向；(2)试在图上作出凸轮的基圆与偏心圆，并标注其半径r b 与e ；(3)在图上作出轮廓上D 点与从动杆尖顶接触时的位移s 和压力角α；(4)在原图上画出凸轮机构的推程运动角Φ。

题3-2图3-3由图所示直动盘形凸轮的轮廓曲线，在图上画出此凸轮的基圆半径r b、各运动角即推程运动角Φ、远休止角ΦS、回程运动角Φ′和近休止角Φ′S及从动件升程h。

题3-3图3-4图示的对心滚子从动件盘形凸轮机构中，凸轮的实际轮廓为一圆，圆心在A 点，半径R＝40mm，凸轮转动方向如图所示，l OA＝25mm，滚子半径r r＝10mm，试问：(1)凸轮的理论曲线为何种曲线？(2)凸轮的基圆半径r b＝？(3)在图上标出图示位置从动件的位移S，并计算从动件的升距h？(4)用反转法作出当凸轮沿ω方向从图示位置转过90°时凸轮机构的压力角。

题3-4图解：(1)理论轮廓曲线为：以A点为圆心，半径为R＋r r的圆。

(2)此时所求的基圆半径为理论轮廓曲线的r b．r b＝R－OA+r r＝40-25+10＝25mm(3)从动件的位移S如图所示。

升程h＝R+OA+r r-r b＝40+25+10-25＝50mm(4)从动件导路沿-ω方向转过90°到B，压力角α'如图中所示。

3-5如图所示偏置移动滚子从动件盘形凸轮机构。

已知凸轮实际轮廓线为一圆心在O 点的偏心圆，其半径为R ，从动件的偏距为e ，试用图解法：(1)确定凸轮的合理转向；(2)画出凸轮的基圆；(3)标出当从动件从图示位置上升到位移s 时,对应凸轮机构的压力角α；（要求量出具体的数值）题3-5图3-8试以作图法设计一偏置直动滚子推杆盘形凸轮机构。

已知凸轮以等角速度逆时针回转，正偏距e =10mm ，基圆半径r 0=30mm ，滚子半径r r =10mm 。

第9章 凸轮机构一、主要内容：1、根据推杆运动规律利用反转法设计凸轮轮廓曲线2、特定凸轮机构，绘出其实际廓线（理论廓线）、图示位置凸轮机构的压力角，位移、以及凸轮从图示位置转过某个角度后凸轮机构的压力角和位移。

二、作图题 (说明：不必写作图步骤，但必须保留作图线)9-1、图示凸轮机构，凸轮轮廓是一个圆，圆心在A 点，在图上标注：（1）、凸轮的基圆r 0、实际廓线η，理论廓线η’ （2）、图示位置凸轮机构的压力角α，位移s（3）、凸轮从图示位置转过90。

后凸轮机构的压力角α’和位移s ’9-2、图示凸轮机构，凸轮轮廓是一个圆，圆心在A 点，在图上标注图示凸轮机构，要求在图上标注 基园r 0，图示位置压力角α，位移s ，凸轮从图示位置转过90o 后机构的压力角α’和位移s ’9-3 .图示偏心圆盘凸轮机构，圆盘半径R =50mm ， e =25mm ，在图上标注凸轮的基圆r 0、从动件的行程h凸轮从图示位置转过90。

后凸轮机构的压力角α’和位移s ’，并且求出具体数值。

习题9-1 习题9-2 mm)13(2525255030)50/25(sin mm 502)(221-=--=︒====--+=-s e e R e R h α习题9-49-4 图示偏心圆盘凸轮机构，在图上标注（1）凸轮的基圆r 0、实际廓线η，理论廓线η’、偏距园e ；（2）图示位置从动杆的位移S 和压力角α；（3）从动杆由最低位置到图示位置，凸轮已转过的角度δ9-5如图所示为一凸轮机构，凸轮的轮廓为一个圆，圆心为O 1，凸轮的转动中心为O 。

在图上标注（1）凸轮的基圆r 0、实际廓线η，理论廓线η’、偏距园e ；（2）凸轮转过30。

时推杆的位移S 和压力角α ；9-6 图示偏置直动滚子从动件盘形凸轮机构中，凸轮以角速度逆时针方向转动。

试在图上：（1）画出理论轮廓曲线、基圆与偏距圆；（2）标出凸轮从图示位置转过90°时的压力角 和位移 s 。

摆动滚子从动件盘形凸轮机构设计的解析法①0前言摆动滚子从动件盘形凸轮机构的设计主要包括基本尺寸的确定[ 1 ]和凸轮轮廓的设计. 基本尺寸主要是根据压力角确定的, 凸轮轮廓是根据基本尺寸和从动件的运动规律设计的. 过去这两部分的设计常常采用图解法, 虽然图解法简单、直观, 但精度低, 随着计算机技术的发展和数控机床的普及, 凸轮机构设计的解析法[ 2 ]正逐步取代传统的图解法.图1摆动从动件盘形凸轮机构的压力角1机构压力角的计算如图1 所示, 为摆动从动件盘形凸轮机构的压力角示意图. 摆杆长度O 2A = l, 机架长O 1O 2 = a.过瞬心P 作摆杆O 2A 的垂直线, 交O 2A延长线于B 点. 则有:tan A= BAPB=O 2P cos (W0 + W) - lO 2P sin (W0 + W)P 点为机构的瞬心, 则有: X1O 1P = X2O 2PX2X1=O 1PO 2P=d Wd U=O 1PO 1P + a∴O 1P =d Wd U a1 -d Wd UO 2P = O 1P + a = a1 -d Wd U∴tan A=a cos (W0 + W) - l (1 -d Wd U)a sin (W0 + W)上式是按X1 和X2 同向推出的, 否则tan A=a cos(W0 + W) - l (1 +d Wd U)a sin (W0 + W)工程设计中, 必须对凸轮机构的最大压力角加以限制, 凸轮机构的最大压力角应小于许用压力角.2机构基本尺寸的确定图2确定基本尺寸示意图2. 1基本尺寸确定的方法图2 中O 2 为摆杆的回转中心,A 为滚子摆杆的滚子中心. A 0 到A 6 为按给定运动规律W= f (U) 作出的摆杆各个位置, 位置个数可任选. 在摆杆的每位置上截取长为ld Wd U,其中l 为摆杆长, W为摆杆摆角, U为凸轮转角.截取方法为: 若摆杆与凸轮转向相同, 由A 点向着回转中心O 2 取; 若摆杆与凸轮转向相反, 由A 点背着回转中心O 2 取.图2 中凸轮与摆杆的相对转动关系为: 凸轮逆时针转,摆杆推程逆时针转, 回程顺时针转. 若推程许用压力角为[A], 回程许用压力角为[A′], 线段A 1a1,A 2a2, ⋯为对应推程截取的; 线段A 1a′1,A 2a′2, ⋯为对应回程截取的. 过端点a1, A2, ⋯和a′1 , a′2, ⋯作与相应的摆杆成(90°- [A]) 或(90°- [A]) 的直线, 简称a 斜线和a′斜线. 这些线的包络线É , Ê , Ë 所包围的阴影区域为满足许用压力角的前提下, 凸轮回转中心的可选区域. O ′1A 0 为最小基圆半径,O ′1O 2 为对应的中心距.以O 2 为原点,O 2A 0 为x 轴, 使A 1,A 2, ⋯各点y 坐标为正值的方向为y 轴, 建立直角坐标系. 若已知包络线É , Ê , Ë 的方程, 则可知凸轮回转中心O 1 的许用区域.2. 2包络线方程的求法及基本尺寸的确定在图2 中, 任意a 斜线的斜率为k = tan A= cot (- [A] - W) , 各a 点的坐标为:x = l (1 -d Wd U cos W) , y = l (1 -d Wd U) sin W, 由点斜式可写出任意a 斜线的方程. 同理, 对任意a′斜线, 斜率为k′= cot ( [A] - W) , 各a′点的坐标为: x ′= l (1 +d Wd U) cos W, y ′= l (1 +d Wd U) sin W, 同样可写出任意a′斜线的方程.由以上包络线方程相交, 可求出凸轮回转中心O 1 的许用区域, 此过程较繁, 可上机求解. 在O 1 的取值范围内任取一点(x , y ) 作为凸轮的回转中心, 则凸轮的基圆半径可确定:图3反转法设计凸轮的轮廓r0 = ( l - x ) 2 + y 2.3凸轮轮廓的设计图3 中, 直角坐标系的原点位于凸轮的回转中心O 1 点. 机架长为a, 摆杆长为l. 摆动滚子从动件的初始位置在行程起始位置1 时的O 20A 0. 反转U角后, 到达位置2 的O 2A. 凸轮与从动件的接触点A 0 到达A 点,A ′A为对应的弧位移s, 对应从动件的摆角W.从动件O 2A的运动可以看作O 20A 0 绕O 1 点反转U角, 到达O 2A ′位置,O 2A ′再摆动W角到达O 2A 位置. 从动件O 2A 的运动还可以看作O 20A 0 绕O 20 点反转(U+ W) 角, 到达O 20A ″点,O 20A ″再平移到O 2A 位置. 设A 0 点的坐标为(x A 0,第1 期毕艳丽等: 摆动滚子从动件盘形凸轮机构设计的解析法37y A 0) ,A 点的坐标为(x , y ) ,O 2A 的复合运动可用下述的坐标旋转和平移变换来实现.y=cos(U+ W) sin (U+ W)- sin (U+ W) cos (U+ W)x A 0 - x O20y A 0 - y O20+x O2y O2(1)式中: x O 2 = a sin U, y O 2 = a co s U, x O20 = 0, y O20 = a, x A 0 = - l sin W 0, y A 0 = a - l co s WW0 为摆杆的初始位置角, 其值为W0 = arccosa2 + l2 - r202al将其代入方程(1) 并整理, 可得理论廓线方程:x = a sin U- l sin (U+ W+ W0) ; y = a cos U- l cos (U+ W+ W0)则其实际廓线方程[ 2 ] 为:x A= x ±r rd yd Ud xd U2+d yd U2, y A= y ºr rd xd Ud xd U2d yd U2其中r r 为滚子半径; 滚子圆的包络线有两条, 上面一组符号用于求解外凸轮的包络线方程, 下面一组符号用于求解内凸轮的包络线方程.4结束语本文利用解析法设计摆动滚子从动件盘形凸轮机构, 适用于用计算机辅助运算设计凸轮机构, 其精度高, 使用方便, 特别适合高精度凸轮机构的设计.参考文献:[ 1 ]尚锐等. 摆动从动件盘形凸轮机构基本尺寸确定的解析法[J ]. 辽宁工学院学报, 1999, (6) : 29- 32.[ 2 ]邹慧君等. 机械原理[M ]. 北京: 高等教育出版社, 1999, 117- 132.。

摆动滚子从动件盘形凸轮机构设计的解析法①0前言摆动滚子从动件盘形凸轮机构的设计主要包括基本尺寸的确定[ 1 ]和凸轮轮廓的设计. 基本尺寸主要是根据压力角确定的, 凸轮轮廓是根据基本尺寸和从动件的运动规律设计的. 过去这两部分的设计常常采用图解法, 虽然图解法简单、直观, 但精度低, 随着计算机技术的发展和数控机床的普及, 凸轮机构设计的解析法[ 2 ]正逐步取代传统的图解法.图1摆动从动件盘形凸轮机构的压力角1机构压力角的计算如图1 所示, 为摆动从动件盘形凸轮机构的压力角示意图. 摆杆长度O 2A = l, 机架长O 1O 2 = a.过瞬心P 作摆杆O 2A 的垂直线, 交O 2A延长线于B 点. 则有:tan A= BAPB=O 2P cos (W0 + W) - lO 2P sin (W0 + W)P 点为机构的瞬心, 则有: X1O 1P = X2O 2PX2X1=O 1PO 2P=d Wd U=O 1PO 1P + a∴O 1P =d Wd U a1 -d Wd UO 2P = O 1P + a = a1 -d Wd U∴tan A=a cos (W0 + W) - l (1 -d Wd U)a sin (W0 + W)上式是按X1 和X2 同向推出的, 否则tan A=a cos(W0 + W) - l (1 +d Wd U)a sin (W0 + W)工程设计中, 必须对凸轮机构的最大压力角加以限制, 凸轮机构的最大压力角应小于许用压力角.2机构基本尺寸的确定图2确定基本尺寸示意图2. 1基本尺寸确定的方法图2 中O 2 为摆杆的回转中心,A 为滚子摆杆的滚子中心. A 0 到A 6 为按给定运动规律W= f (U) 作出的摆杆各个位置, 位置个数可任选. 在摆杆的每位置上截取长为ld Wd U,其中l 为摆杆长, W为摆杆摆角, U为凸轮转角.截取方法为: 若摆杆与凸轮转向相同, 由A 点向着回转中心O 2 取; 若摆杆与凸轮转向相反, 由A 点背着回转中心O 2 取.图2 中凸轮与摆杆的相对转动关系为: 凸轮逆时针转,摆杆推程逆时针转, 回程顺时针转. 若推程许用压力角为[A], 回程许用压力角为[A′], 线段A 1a1,A 2a2, ⋯为对应推程截取的; 线段A 1a′1,A 2a′2, ⋯为对应回程截取的. 过端点a1, A2, ⋯和a′1 , a′2, ⋯作与相应的摆杆成(90°- [A]) 或(90°- [A]) 的直线, 简称a 斜线和a′斜线. 这些线的包络线É , Ê , Ë 所包围的阴影区域为满足许用压力角的前提下, 凸轮回转中心的可选区域. O ′1A 0 为最小基圆半径,O ′1O 2 为对应的中心距.以O 2 为原点,O 2A 0 为x 轴, 使A 1,A 2, ⋯各点y 坐标为正值的方向为y 轴, 建立直角坐标系. 若已知包络线É , Ê , Ë 的方程, 则可知凸轮回转中心O 1 的许用区域.2. 2包络线方程的求法及基本尺寸的确定在图2 中, 任意a 斜线的斜率为k = tan A= cot (- [A] - W) , 各a 点的坐标为:x = l (1 -d Wd U cos W) , y = l (1 -d Wd U) sin W, 由点斜式可写出任意a 斜线的方程. 同理, 对任意a′斜线, 斜率为k′= cot ( [A] - W) , 各a′点的坐标为: x ′= l (1 +d Wd U) cos W, y ′= l (1 +d Wd U) sin W, 同样可写出任意a′斜线的方程.由以上包络线方程相交, 可求出凸轮回转中心O 1 的许用区域, 此过程较繁, 可上机求解. 在O 1 的取值范围内任取一点(x , y ) 作为凸轮的回转中心, 则凸轮的基圆半径可确定:图3反转法设计凸轮的轮廓r0 = ( l - x ) 2 + y 2.3凸轮轮廓的设计图3 中, 直角坐标系的原点位于凸轮的回转中心O 1 点. 机架长为a, 摆杆长为l. 摆动滚子从动件的初始位置在行程起始位置1 时的O 20A 0. 反转U角后, 到达位置2 的O 2A. 凸轮与从动件的接触点A 0 到达A 点,A ′A为对应的弧位移s, 对应从动件的摆角W.从动件O 2A的运动可以看作O 20A 0 绕O 1 点反转U角, 到达O 2A ′位置,O 2A ′再摆动W角到达O 2A 位置. 从动件O 2A 的运动还可以看作O 20A 0 绕O 20 点反转(U+ W) 角, 到达O 20A ″点,O 20A ″再平移到O 2A 位置. 设A 0 点的坐标为(x A 0,第1 期毕艳丽等: 摆动滚子从动件盘形凸轮机构设计的解析法37y A 0) ,A 点的坐标为(x , y ) ,O 2A 的复合运动可用下述的坐标旋转和平移变换来实现.y=cos(U+ W) sin (U+ W)- sin (U+ W) cos (U+ W)x A 0 - x O20y A 0 - y O20+x O2y O2(1)式中: x O 2 = a sin U, y O 2 = a co s U, x O20 = 0, y O20 = a, x A 0 = - l sin W 0, y A 0 = a - l co s WW0 为摆杆的初始位置角, 其值为W0 = arccosa2 + l2 - r202al将其代入方程(1) 并整理, 可得理论廓线方程:x = a sin U- l sin (U+ W+ W0) ; y = a cos U- l cos (U+ W+ W0)则其实际廓线方程[ 2 ] 为:x A= x ±r rd yd Ud xd U2+d yd U2, y A= y ºr rd xd Ud xd U2d yd U2其中r r 为滚子半径; 滚子圆的包络线有两条, 上面一组符号用于求解外凸轮的包络线方程, 下面一组符号用于求解内凸轮的包络线方程.4结束语本文利用解析法设计摆动滚子从动件盘形凸轮机构, 适用于用计算机辅助运算设计凸轮机构, 其精度高, 使用方便, 特别适合高精度凸轮机构的设计.参考文献:[ 1 ]尚锐等. 摆动从动件盘形凸轮机构基本尺寸确定的解析法[J ]. 辽宁工学院学报, 1999, (6) : 29- 32.[ 2 ]邹慧君等. 机械原理[M ]. 北京: 高等教育出版社, 1999, 117- 132.。