关于地球曲率、大气折射对三角高程测量误差分析共3页
- 格式:doc
- 大小:22.00 KB
- 文档页数:3

三角高程测量的误差分析与大气折光系数的确定随着人们对三角高程测量的研究,在平原或丘陵地区三角高程测量已经能够代替三、四等水准测量、跨河水准;在高山地区甚至可以代替一、二等水准测量。
本文在简要介绍三角高测量的基本原理和误差影响因子的基础上重点阐述如何确定大气折光系数K。
标签:三角高程测量误差分析大气折光系数0引言地面高程传递技术主要包括几何水准测量、三角高程测量、液体静力水准等。
用几何水准求地面点的高程其精度较高,但受大气折光、视距及地形的限制;三角高程测量的基本思想是由测站向照准点所观测的竖角和它们之间的水平距离,计算测站点与照准点之间的高差,其受地形条件的限制较少,使用起来相对灵活、高效,广泛用于控制测量、地形测量和工程测量等领域。
1三角高程测量(Trigonometric height surveying)的基本原理全站仪三角高程测量主要分为单向、对向和中点法三角高程测量,文[1]中指出,对向三角高程测量误差最低、精度最高,下面就以对向三角高程测量为例,简要介绍其基本原理。
对向观测又称往返观测,如图1,将全站仪置于A点,棱镜置于B点,测得A、B两点间的高差hAB,hAB称为往测高差:再将全站仪置于B点,棱镜置于A点,测得B、A两点间的高差hBA,hBA 称为反测高差:往返测高差的平均值即可作为最终的测量结果:这种测量方法在导线测量中使用得比较普遍。
式中:S往、S返、α往和α返分别为往返观测的斜距和竖直角;i往、i返、v往和v返分别为往返观测的仪器高和棱镜高;K往和K返分别为往返观测时的大气折光系数;R为椭球半径。
在全站仪进行往返测量时,如果观测是在相同气象条件下进行的,特别是在同一时间进行,则可假定大气折光系数对于反向观测基本相同,因此K往≈K返。
又S2往·cos2α往和S2返·cos2α返同是A、B两点间的平距的平方,也可近似相等。
从(1)~(3)式可以得出对向观测计算高差的基本公式为:2全站仪对向三角高程测量误差分析根据误差传播定律,对(4)进行微分,并转为中误差关系式,则有:从(5)式可以看出,对向三角高程测量的精度主要受边长误差、竖角观测误差、仪器高和目标高的量测误差等诸多因素的影响具体如下:(1)边长误差的大小决定于测量的方法,当今,先进而精密的测距仪器相继问世并得到广泛推广使用,使测距精度显著提高,如Leica TCA2003的测距标称精度达到了1mm+1ppm,能够显著提高短边的测距精度;(2)竖直角观测误差中有照准误差、读数误差、竖盘指标差等,相对来讲,竖角观测误差对高差测定的影响与推算高差的边长成正比,边长越长,影响越大,实际工作中尽量选取测角精度高、能自动照转的仪器进行测量,如Leica TCA的测角精度达0.5″;(3)仪器高和目标高的测定误差,当用光电测距三角高程测量代替四等水准测量时,仪器高和棱镜高的测定要求达到毫米级,可以采用小钢卷尺认真地量测两次取平均值,在实际工作中,我们可以保持往返测过程中棱镜高不变等措施减少其误差。

全站仪三角高程测量精度分析作者修涛容摘要全站仪三角高程测量具有效率高,实施灵活等优点。
全站仪三角高程测量可以代替水准测量进行高程控制,主要有对向观测法和中间观测法。
在这两种方法中,前者将大气折光系数作为常数考虑,认为各个方向的折光系数相同,这与实际的情况有出入。
而中间观测法则将大气折光系数作为变量处理,并加以改正。
经研究并通过实践验证,在观测结果进行修正的条件下,全站仪三角高程测量完全能达到三、四等水准测量的精度要求,同时可借助Excel强大的数据处理能力,使观测数据的处理更为方便快捷[1]。
文章根据三角高程测量原理及误差传播定律,对全站仪三角高程测量在测量中的应用及精度进行了探讨。
对三角高程测量的不同方法进行了对比、分析总结。
通过试验,对全站仪水准法三角高程测量进行了精度分析。
关键词全站仪;三角高程测量;精度分析Total Station trigonometric leveling accuracy analysisAbstract Total Station trigonometric leveling with high efficiency, the implementation of the advantages of flexible. Total Station trigonometric leveling can replace the standard of measurement for elevation control, mainly on the observation method to the observational method and intermediate. In both methods, the former take into account atmospheric refraction coefficient as a constant, that the refraction coefficient in each direction, this discrepancy with the actual situation. While the rule of the middle observation of atmospheric refraction coefficient as a variable processing and correction. Research and verify through practice, Total Station trigonometric leveling observations amendment can fully meet the accuracy requirements of the third and fourth level measurement, Can take advantage of Excel's powerful data processing capabilities, more convenient to make the processing of observational data.Article based on trigonometric leveling principle and law of error propagation, Total Station trigonometric leveling application and accuracy in the measurement are discussed. Different methods of measurement for triangulation were compared, analyzed and summarized. Trigonometric leveling Total Station Standards test, measurement accuracy analysis.Key words Electronic Total Station;trigonometric leveling;accuracy analysis目录摘要 ..................................................... 错误!未定义书签。

浅谈三角高程测量误差影响因素分析关键词:三角高程误差分析三角高程测量是在地球自然表面进行的。
野外观测时通过量测斜距、垂直角(天顶距)、仪器高、占标高(棱镜高)后利用公式: H=S×Sina+I-V+(1-K)×(S×Cosa)2/2R 其中:H、S、a、I、V分别为高差、斜距、垂直角、仪器高、占标高,K为大气垂直折光系数R为地球平均曲率半径。
对于短程测距而言,垂线偏角和水准面不平行对高差的影响可以不予考虑,坡道弯曲改正也可以忽略不计。
对(1)式进行全微分,并转化为中误差得:m h2=(Sina×m s)2+(S×Cosa/ρ)2×m s2+m i2+ m v2+((S×Cosa)2/(2R))2×m r2下面分别讨论各项误差对三角高程测量误差的影响:1.测距误差对高程误差的影响电磁波测距误差一般可分为仪器系统误差和观测时的对中误差、气象测定误差等,仪器系统误差常指测相误差、加常数的测定误差、光速误差和周期误差等等。
通常情况下,仪器在设计和调试时都可严格控制其数值,但由于运输等原因,造成其值异常。
如果发现其数值较大,可对观测成果进行修正。
对中误差只要作业人员认真操作,一般可以做到:光学对中误差≤±1mm,对一般的测距精度而言对中误差影响不大。
气象因素测定不准,会对大气折射率产生影响,进而影响测距精度。
温度对测距影响最大,其次是大气压,湿度的测定误差对其影响可以忽略不计。
气象参数的测定精度很容易满足测距误差不大于±1mm的要求。
气象参数既可以在测站、镜站分别测定后输入仪器进行自动改正,也可以测记后进行人工改正。
因此,距离的测定误差主要来自仪器的系统误差。
2.垂直角的测定误差垂直角的测定误差主要有照准误差、读数误差、气泡居中误差,当采用全站仪时,由于其水平与垂直度盘采用增量式编码,通过测量莫尔条文的数目,以确定光栅移动的位移量,并经过模数的转换测得微小的角值,仪器竖轴的倾斜误差通过双轴传感器进行自动补偿,因此,其精度稍低于水平角,许多文献研究认为垂直角的观测误差一般比水平角的观测误差大。

三角高程测量1 三角高程测量的基本原理三角高程测量是通过观测两点间的水平距离和天顶距(或高度角)求定两点间的高差的方法。
它观测方法简单,不受地形条件限制,是测定大地控制点高程的基本方法。
目前,由于水准测量方法的发展,它已经退居次要位置,但在山区和丘陵地带依然被广泛采用。
在三角高程测量中,我们需要使用全站仪或者经纬仪测量出两点之间的距离(水平距离或者斜距和高度角,以及测量时的仪器高和棱镜高,然后根据三角高程测量的公式推算出待测点的高程。
三角高程测量由图中各个观测量的表示方法,AB两点间高差的公式为:H=S0tanα+i1-i2①但是,在实际的三角高程测量中,地球曲率、大气折光等因素对测量结果精度的影响非常大,必须纳入考虑分析的范围。
因而,出现了各种不同的三角高程测量方法,主要分为:单向观测法,对向观测法,以及中间观测法。
1.1 单向观测法单向观测法是最基本最简单的三角高程测量方法,它直接在已知点对待测点进行观测,然后在①式的基础上加上大气折光和地球曲率的改正,就得到待测点的高程。
这种方法操作简单,但是大气折光和地球曲率的改正不便计算,因而精度相对较低。
1.2 对向观测法对向观测法是目前使用比较多的一种方法。
对向观测法同样要在A点设站进行观测,不同的是在此同时,还在B点设站,在A架设棱镜进行对向观测。
从而就可以得到两个观测量:直觇:h AB= S往tanα往+i往-v往+c往+r往②反觇:h BA= S返tanα返+i返-v返+c返+r返③S——A、B间的水平距离;α——观测时的高度角;i——仪器高;v——棱镜高;c——地球曲率改正;r——大气折光改正。
然后对两次观测所得高差的结果取平均值,就可以得到A、B两点之间的高差值。
由于是在同时进行的对向观测,而观测时的路径也是一样的,因而,可以认为在观测过程中,地球曲率和大气折光对往返两次观测的影响相同。
所以在对向观测法中可以将它们消除掉。
h=0.5(hAB- hBA=0.5[( S往tanα往+i往-v往+c往+r往-( S返tanα返+i返-v返+c返+r返] =0.5(S 往tanα往-S返tanα返+i往-i返+v返-v往④与单向观测法相比,对向观测法不用考虑地球曲率和大气折光的影响,具有明显的优势,而且所测得的高差也比单向观测法精确。


地球曲率和大气折光对高差的影响
地球曲率对于高差的影响在几乎所有情况下都是显而易见的。
由于地球是一个近似于球体的物体,它的表面是曲率的。
因此,当我们在地球上测量高度差时,需要考虑地球的曲率。
如果我们忽略地球的曲率,那么在较长的距离上测量的高度差可能会显得更大。
例如,当我们站在一个非常大的平地上,远处有一个山峰时,由于地球曲率的影响,我们可能会低估山峰的实际高度。
另一个影响高度差的因素是大气折光。
当光穿过大气层时,由于大气的折射作用,光线会产生偏折。
这种偏折会导致我们在测量高度差时产生误差。
具体来说,大气折光会使得远处的物体看起来比实际位置更高。
这是由于光线在通过大气层时向上弯曲的结果。
因此,在测量高度差时,我们需要考虑大气折光的效应,并进行相应的修正。
总的来说,地球曲率和大气折光都会对高度差产生显著的影响。
为了获得准确的高度差测量结果,我们需要考虑这两个因素,并进行相应的修正。

三角高程测量的精度分析及球气差系数c的确定摘要:本文分析了三角高程在理论与实践中的精度,推证出实际工程测量数据确定C值的方法。
关键词:三角高程;高差;精度;球气差一、前言几何水准测量目前仍是高程测量的主要方法,测量精度高、操作简单是这种方法的优势。
但视线短、速度慢、劳动强度大。
三角高差测量的精度主要受高度角观测精度的限制和大气折光的影响,限制了三角高程测量的应用。
但可在较长的距离上测量。
因此,测量人员一直在研究,提高三角高程测量的精度,在一定的精度范围内,代替几何水准测量。
随着科技的进步、全站仪设备的改变,国内外广泛开展了三角高程测量的研究,研究表明,三角高程测量可以代替四等水准测量,也有的认为三角高程测量已经接近或已达到二等水准测量要求。
这里我们对三角高程测量进行精度分析探讨,以及球气差系数的探讨,使三角高程测量可以达到较高的精度。
二、高差计算三角高程测量的基本思想是根据由测站向照准点所观测的垂直角(或天顶距)和它们之间的水平距离,计算测站点与照准点之间的高差。
在实际测量中三角高程通常是利用在测站上观测目标的垂直角α、平距S0以及量取的仪器高i、目标高v和“两差”改正数f(对于),计算出它们的高差h。
(f主要是地球曲率和大气折光的影响)(1)为了提高所测高差精度,通常都取两点之间的对象观测平均值h平=(hAB+(-hBA))/2, 从上式可以看出影响高差h的精度有测距边S0、垂直角α、仪器高i、目标高v、“两差”改正数f。
三、误差估算全站仪单向三角高程的基本公式:(2)(3)式中:K——大气折光系数;S0——观测时时两点之间的水平距离;R——地球平均曲率半径,一般采用R=6371km。
在一个测区的工作中,当进行桑娇高程测量外业的观测条件近似相同时,一般K与R常分别取一个定值,这样(3)式中得S0随着不同的观测边而变化,因此,可将(3)式变为如下形式:(4)(5)式中:C——三角高程测量“两差”改正系数。

高程测量中的误差分析所谓高程测量,就是根据一点高程与另一点的已知高关,然后按照高差的定义公式,求出测量点的高程。
在测绘工作中,高程测量是最基本、最常见的测量方法,并且在工程施工中发挥着重要的作用,特别是在公路、铁路、隧道、矿井、建筑等工程中。
然而在测量中总是会因为某些因素使测量偏离真值而造成误差。
在高程测量的实际应用中,某些微小误差的积累会影响工程的质量,甚至有可能造成工程事故,因此在高程测量中要十分注意误差存在的因素。
在高程测量中,造成误差的主要因素有人、仪器和客观环境这三方面。
1、人的因素造成误差在任何测量工作中,人的因素都是主导因素,它包括两点:(1)测量方法不理想而造成误差。
在每次高程测量之前,技术人员都要制定测量计划,用什么方法什么步骤都要事先拟定好,不同的方法当然会有不同的效果。
在高程测量中有多种方法,如水准测量、三角高程测量、GPS测高、气压计测高等。
导线选择也有以下几种,如附合导线、闭合导线、支导线、一个结点的导线网、两个或两个以上结点的导线网。
人们可以设想一下,在对一个较大平原地区进行高程测量时,选用的是气压计测高法,那得到的数据是明显不可靠的。
因为气压计测高法的原理是:高程每上升11米,气压约下降1MM,根据气压下降的多少计算高程。
但是在平原地区两点间的高差一般不会超过几米,所以在气压计上的反应是很不明显的,造成的误差当然会很严重。
若是换成水准测量或三角高程测量就能得到比较精确的结果了。
对测量导线的设置若是不理想也会对结果带来不必要的误差,因为当导线长度增加时,横向中误差比纵向中误差增加的快,所以高程测量中应减少导线转折点的数量。
要想避免因方法不理想而带来的误差,就要纵纲全局,因地制宜,注重对细节的处理,从而制定出最理想的方法。
(2)操作人员经验不足或技术不成熟造成误差。
因操作人员的经验不足或技术不成熟而造成误差的例子不胜枚举。
如在水准测量中对仪器的安置不合理,对测量的程序不熟悉,读数不准确以及扶尺不水平,甚至是记录员笔误等等,这些都是容易造成误差的人为因素。

关于地球曲率、大气折射对三角高程测量误差分析一、三角高程测量一般可以替代四等水准测量,也就是说它可以满足四等水准测量的精度要求!二、当地形高低起伏太大,导致高差太大不便于水准测量,可以用三角高程测量原理测量两点间的高差和点位的高程;三、误差来源:由于地球是一不规则椭圆,我们姑且把它看成一个半径为6371km 的圆,我们来看一下水准面的定义:处处与铅垂线(重力线)垂直的连续封闭曲面;而我们假想的是用一个水平面代替水准面(这里大家要注意一下水准面与水平面的区别);受地球曲率影响,导致了一个误差的来源。
所以我们在等级测量中需要计算一个地球曲率改正数对现场测量的高程加以修正。
我们称其为球差改正f=D2/2R(其实这公式也不难推导)1我们来个简单的几何分析:f1=根号下D2+R2-R举例:0.5km误差达到20mm,则有f1=根号下0.52+63712-6771=20mm;由上图我们可以看出,所实测点位的高程偏小,所以用全站仪单向观测时,计算高程时应加上球差改正f1;若进行对向或是中间观测时不必考虑球差改正;等精度观测可以抵消误差(导线测量要求边长大致相等);大气折射对三角高程测量的影响:由于低层空气密度大于高层空气密度,观测竖直角的视线穿越不均匀的介质时,导致竖直角偏大或偏小。
所有我们在计算高程时需要考虑大气折射的影响。
f2(气差改正数)= -k*D2/2R(k为大气垂直折光系数)但水准测量几乎不受大气折射影响,因为水准测量提供的是一条水平的视线;但水准测量计算高程时需要考虑地球曲率的影响;K一般取0.14,由于k受地区、气候、季节等诸多因数的影响,人们很难精确的测定k的值,正是这个原因,《城市测量规范》中规定测量边长不应大于1km。
综合以上:两者误差改正数f=f1+f2=(1-k)*D2/2R;则有;计算高程时:hAB=S*sin&+i-v+f(S为斜距、注意&有正负之分)hAB=D*tan&+i-v+f(D为平距、注意&有正负之分)测量技巧:测量时采用对向观测时可以抵消f;中间观测法能抵消地球曲率影响,但不能抵消大气折射所带来的误差(理论上);qq:1作(个人观点,如有问题,欢迎指教)。

三角高程测量原理误差分析及应用三角高程测量是一种常用的地理测量方法,用于测量地球表面上任意两点之间的高差。
它的原理基于三角形的几何性质,通过测量三角形的边长和角度来计算出高程差。
误差分析是对测量结果进行评估和分析,以确定测量结果的可靠性和精度。
三角高程测量在工程测量、地形测量和地理信息系统等领域有广泛的应用。
三角高程测量的原理是基于几何三角形的性质。
在三角形中,已知两边长度和夹角时,可以通过正弦定理求得第三边的长度。
在实际应用中,使用测量仪器(如全站仪、水准仪)测量两个点的水平距离和夹角,然后根据几何关系计算出两点之间的高差。
对于三角高程测量的误差分析,需要对各种误差进行综合评估和处理。
首先要进行误差源的分析和估计,确定各个误差源对测量结果的影响程度。
然后通过合适的数理统计方法对误差进行处理,例如最小二乘法、平差方法等,以提高测量结果的准确性和可靠性。
最后,通过误差传递的计算,评估最终测量结果的误差范围和可信度。
三角高程测量在地理测量和工程测量中有广泛的应用。
地理测量方面,可以通过三角高程测量来测量地球表面的高程特征,生成数字高程模型,用于地形分析和地图制作。
在工程测量方面,三角高程测量被用于测量任意两点间的高差,如建筑物、道路和管道等的高程差,以支持工程设计和建设。
另外,在地理信息系统中,三角高程测量可以用于数据融合和质量控制,提高地理数据的精度和准确性。
总结而言,三角高程测量是一种常用的地理测量方法,利用三角形的几何性质来测量地表上任意两点的高差。
在测量过程中会存在各种误差,需要进行误差分析和处理,以提高测量结果的准确性和可靠性。
三角高程测量在地理测量和工程测量中有广泛应用,可以用于生成数字高程模型、工程设计和数据质量控制等领域。
三角高程测量精度分析摘要:通常我们主要通过水准与三角高程测量两种主要方法来测量高程。
我们在测量高程的时候一般都是优先选择水准测量的方法来测量。
但是我们都知道,进行水准测量时候的步骤十分繁琐,而且有时候的任务量很大。
地形起伏较大的地区可能不适合水准测量,在这种情况下,我们通常选择三角高程测量来进行高程测量。
本文在阐述一些三角高程测量理论知识的同时,主要研究的内容是三角高程测量精度方面的问题。
然后在案例分析部分着重通过球气差这一主要影响因素分析,其他因素进行辅助分析。
关键词:三角高程测量;精度;球气差;水准测量;影响因素1 绪论我们都知道,测量高程除了水准测量之外,三角高程测量也是一种很好的高程测量方法。
随着测绘行业的不断发展,我们对三角高程测量的研究也越来越重要。
三角高程测量作为一种测量方法,以其简单便捷,受地形条件等影响较小等优势越来越得到普遍运用,在不便于水准测量的山地丘陵地区,三角高程测量就显得比水准测量更加的有优势,也更加被人们所运用。
通过研究分析其精度问题,可以使其适用于不同的施工测量之中。
2 全站仪三角高程测量原理根据如下三角高程测量原理图,根据已知点的高程,求算出未知点的高程。
首先通过量测两点间的高差,步骤为:在A、B两点分别安置全站仪与棱镜,量取仪器高与战舰高i、v。
用全站仪瞄准棱镜中心,点角度测量,测出竖直角α。
又因为A、B水平距离已知,根据三角函数得出倾斜距离D,然后根据如下公式算出A、B两点之间的高差,进而求得两点的高程:(2-1)若A点的高程已知为,则B点高程为:(2-2)图2-1 三角高程测量原理图3 三角高程测量精度实例分析3.1 研究区背景本次研究区选择在山东农业工程学院济北校区内进行,学院内测区整体地势平坦,测量难度较小。
测区内多为水泥路,少植被,通视情况良好,天气干燥少雨,观测条件良好。
3.2影响误差的因子在研究三角高程测量精度的时候,我们首先应该知道有哪些影响三角高程测量精度的因子。
工程测量中三角高程测量的误差分析及解决方法通过对三角高程测量公式的分析,发现影响三角高程测量精度的因子,引进当下较为先进的设备与方法,从而提高三角高程测量的精度,使其可以替代几何水准测量。
该方法的实现可以弥补几何水准受地形条件等因素限制使工作效率慢,测绘成本高,人身、设备安全无法保障等缺点。
标签:三角高程测量;几何水准;误差分析;大气折光系数1 引言一直以来,为保证精度,高等级高程测量都采用几何水准的方法。
而在某些特定环境下,几何水准往往会耗费大量的人力、物力,且受地形等条件因素影响较大!鉴于几何水准在某些特定情形下无法进行的问题,探讨如何提高三角高程测量的精度,以保证其测量成果的可行性和可靠性,使得三角高程测量成果足以替代几何水准。
随着高精度全站仪的问世,结合合理的方式、方法,运用三角高程替代几何水准测量是切实可行的。
三角高程代替几何水准可以解决跨河水准及高边坡、危险地段无法进行精密几何水准测量的难题,保障危险地段测量人员和仪器设备的安全,提高了工作效率,降低了测量成本。
2 三角高程测量误差分析常见的三角高程测量有单向观测法、中间法和对象观测法,对向观测法可以消除部分误差,故在三角高程测量中采用较为广泛。
对向观测法三角高程测量的高差公式为:式中:D为两点问的距离;a为垂直角;(k2-k1)为往返测大气垂直折光系数差;i为仪器高;v为目标高;R为地球曲率半径(6370km);为垂线偏差非线性变化量;令。
对式(1)微分,则由误差传播定律可得高差中误差:(2)由式(2)可知影响三角高程测量精度主要有:1.竖直角(或天顶距)、2.距离、3.仪器高、4.目标高、5.球气差。
第1、2项可以通过试验观测数据分析选择精度合适的仪器及其配套的反光棱镜、温度计、气压表等,我们选择的是徕卡TCA2003及其配套的单棱镜、国产机械通风干湿温度计、盒式气压计;第3、4项,一般要求建立稳定的观测墩和强制对中装置,采用游标卡尺在基座3个方向量取,使3个方向量取的校差小于0.2mm,并在测前、测后进行2次量测;第5项球气差也就是大气折光差,也是本课题的研究重点。
三角测距测量误差影响因素解析三角测距是一种常用的测量方法,通过测量目标物体与测量仪器之间的角度,从而确定目标物体与测量仪器之间的距离。
然而,在实际应用中,由于多种因素的影响,三角测距的测量误差可能会增加。
因此,了解这些误差的影响因素对于提高测量的准确性至关重要。
本文将对影响三角测距测量误差的几个主要因素进行解析和讨论。
第一个影响因素是大气条件。
大气的折射效应是三角测距误差的主要来源之一。
当光线穿过大气层时,由于大气的密度变化,光线会发生折射。
这会导致目标物体的实际位置与测量结果之间存在差异。
此外,大气中的湿度、温度和气压等因素也会对光线的传播速度产生影响,进而影响三角测距的测量结果。
因此,在进行三角测距测量时,需要对大气条件进行适当的校正,以提高测量的准确性。
第二个影响因素是测量仪器的精度和稳定性。
三角测距需要使用一定的测量仪器,比如全站仪或者经纬仪等。
这些仪器的精度和稳定性对于测量结果的准确性起着至关重要的作用。
仪器的精度指的是仪器能够测量的最小间隔,而稳定性指的是在一定时间内,仪器的测量结果的变化程度。
如果仪器的精度较低或者稳定性不好,就会导致测量误差的增加。
因此,在进行三角测距测量时,应选择精度较高且稳定性良好的测量仪器,并保持仪器的正常运行和维护。
第三个影响因素是观测条件的选择。
观测条件包括观测点的选择和观测时间的选择。
观测点的选择应该考虑到目标物体与测量仪器之间的视线通畅程度、观测距离的远近等因素。
如果观测点的选择不合理,可能会导致测量结果的误差增加。
此外,观测时间的选择也是影响三角测距误差的重要因素。
在不同的时间段,大气条件和光线的传播速度会发生不同程度的变化,因此观测时间的选择要尽量避免大气条件变化较大的时段。
选取适当的观测条件可以有效地减小测量误差。
第四个影响因素是观测方法的选择。
在三角测距中,有两种常用的观测方法,即单次观测法和重复观测法。
单次观测法是指观测一次角度,并根据这个角度计算目标物体与测量仪器之间的距离。
三角高程导线测量误差分析三角高程导线测量是一种常见的测量方法,用于测量地表上各点的高程差。
其原理是通过测量三角形的边长和角度,计算出各点的高程差。
然而,由于测量过程中的各种因素影响,会导致测量结果与真实值之间存在误差。
下面将对三角高程导线测量误差进行分析。
首先,仪器设备的误差是导致测量误差的主要原因之一、例如,测量仪器的刻度尺和角度仪的划分误差会导致测量结果的偏差。
此外,仪器本身的精度和稳定性也会引入误差。
为减小这些误差,需要选择精度高、稳定性好的测量仪器,并对其进行定期校准和校验。
其次,环境因素也会对测量结果产生影响。
例如,大气压强、温度、湿度等因素会对光线的折射产生影响,进而影响测量结果。
特别是在野外测量中,气候条件的变化会导致测量结果的不稳定性和误差的增大。
为了减小这些误差,需要在恰当的气象条件下进行测量,并对环境因素进行补偿。
此外,人为因素也是导致误差的重要因素之一、例如,在测量过程中测量员的操作不精确、不稳定,或者读数的误差会导致测量结果的偏差。
测量员的经验和技术水平对测量结果的精度和稳定性也有重要影响。
为减小这些误差,需要进行专门培训,提高测量员的技术水平,并采取规范化的操作方法和读数方法。
最后,地形和地貌的影响也会导致测量误差。
例如,在山区、丘陵等地形复杂的地区,由于地形起伏较大,会导致测量难度增加和测量结果的不准确性增大。
此外,地面的植被、建筑物等也会遮挡观测点,影响测量的可行性和准确性。
为减小这些误差,需要根据具体地形和地貌特点选择合适的测量方法和观测点,并进行合理的数据处理和分析。
综上所述,三角高程导线测量误差是由仪器设备、环境因素、人为因素和地形地貌等多种因素综合影响所致。
为了减小误差,需要选择精度高、稳定性好的测量仪器,并对其进行定期校准和校验;在适当气象条件下进行测量,并对环境因素进行补偿;进行专门培训,提高测量员的技术水平,并采取规范化的操作方法和读数方法;根据具体地形地貌特点选择合适的测量方法和观测点,并进行合理的数据处理和分析。
大气折光在三角高程测量中的反算及精度分析李浩,车国泉(中国水电顾问集团贵阳勘测设计研究院O概述目前,高精度的施工控制网和变形监测网在铁路、公路、水电、火电等测绘部门被广泛使用,其中高程测量是很重要的一项内容。
当前,高程测量的主要方法有水准测量和三角高程测量,但由于地形等因素的限制,水准测量并不能应用于所有的工程,尤其是当测量网需跨越较宽河流、峡谷、海岛或地形起伏很大的山区时更是如此,此时,可采用精密的三角高程测量方法。
随着测绘仪器的飞速发展使得测量方法和精度都有了显著的提高,特别是一批以瑞士Leica公司TCA2003及TCRAI201为代表的智能型全站仪的出现,使高精度的三角高程测量能够成为现实。
但由于很多工程的实际情况不能进行同时往返测取平均值,更多的时候是进行单向测量,因而其测量精度较差。
为提高点位高程测量精度,如何实施有效的大气折光改正,反算大气折光系数,就成为提高三角高程测量精度的关键。
1、三角高程测量原理三角高程测量是利用观测的竖直角、斜距和仪镜高等参数,根据几何三角测量原理计算两点之间高差的一种方法。
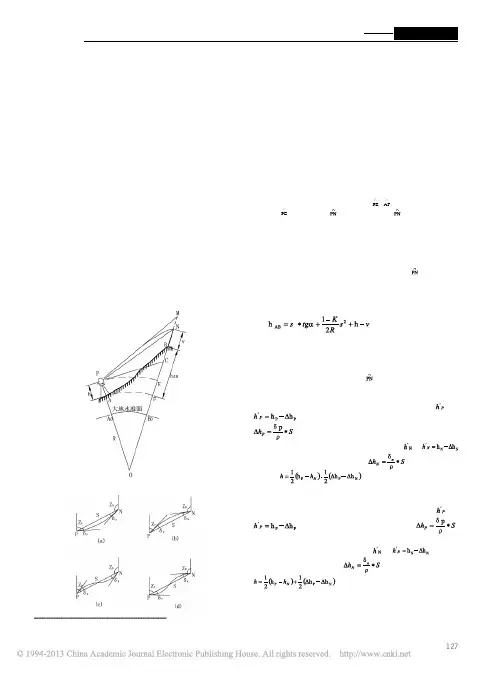
如图1所示。
设:为A, B两点间的实测水平距离,仪器置于A点,仪器高为h,棱镜高为,,R为参考椭球面曲率半径。
PE , AF为过P点和A点的水准面。
PC是PE在P点的切线,PA为光曲线,PM与PN相切。
仪器置于A点测的竖直角为NPC,设为a。
从图中可以看出A, B点间的高差为:Hab=BF=MC十CE十EF一MN一NB(1)式中:EF为仪器高h,NB为棱镜高v;CE及MN为地球曲率和大气折光影响,由式(2)计算:CE=s²/2R MN=s²/2R' (2)式中:R'为光曲线PN的曲率半径;设R/R' = K,则式(2)中MN=Ks²/2R, K称为大气折光系数。
由于A, B两点间的水平距离与曲率半径R之比值很小,故认为PC近似垂直于OM,这样MC就可以用式(3)计算:MC = s * tga ( 3)将式(2)及式(3)代入(1)式,则A, B两地面点间的高差为:(4)式(4)就是单向观测计算高差的基本公式。
关于地球曲率、大气折射对三角高程测量误差分析
一、三角高程测量一般可以替代四等水准测量,也就是说它可以满足四等水准测量的精度要求!
二、当地形高低起伏太大,导致高差太大不便于水准测量,可以用三角高程测量原理测量两点间的高差和点位的高程;
三、误差来源:由于地球是一不规则椭圆,我们姑且把它看成一个半径为6371km的圆,我们来看一下水准面的定义:处处与铅垂线(重力线)垂直的连续封闭曲面;而我们假想的是用一个水平面代替水准面(这里大家要注意一下水准面与水平面的区别);受地球曲率影响,导致了一个误差的来源。
所以我们在等级测量中需要计算一个地球曲率改正数对现场测量的
=D2/2R(其实这公式也不难推导)高程加以修正。
我们称其为球差改正f
1
我们来个简单的几何分析:f1=根号下D2+R2-R
举例:0.5km误差达到20mm,则有f1=根号下0.52+63712-6771=20mm;
由上图我们可以看出,所实测点位的高程偏小,所以用全站仪单向观测时,计算高程时应加上球差改正f1;若进行对向或是中间观测时不必考虑球差改正;等精度观测可以抵消误差(导线测量要求边长大致相等);
大气折射对三角高程测量的影响:由于低层空气密度大于高层空气密度,观测竖直角的视线穿越不均匀的介质时,导致竖直角偏大或偏小。
所有我们在计算高程时需要考虑大气折射的影响。
f2(气差改正数)= -k*D2/2R(k 为大气垂直折光系数)但水准测量几乎不受大气折射影响,因为水准测量提供的是一条水平的视线;但水准测量计算高程时需要考虑地球曲率的影
响;
K一般取0.14,由于k受地区、气候、季节等诸多因数的影响,人们很难精确的测定k的值,正是这个原因,《城市测量规范》中规定测量边长不
应大于1km。
综合以上:两者误差改正数f=f1+f2=(1-k)*D2/2R;
则有;计算高程时:hAB=S*sin&+i-v+f(S为斜距、注意&有正负之分) hAB=D*tan&+i-v+f(D为平距、注意&有正负之分)测量技巧:测量时采用对向观测时可以抵消f;中间观测法能抵消地球曲率影响,但不能抵消大气折射所带来的误差(理论上);
qq:425170631作(个人观点,如有问题,欢迎指教)
2014.1.17
希望以上资料对你有所帮助,附励志名言3条:
1、理想的路总是为有信心的人预备着。
2、最可怕的敌人,就是没有坚强的信念。
——罗曼·罗兰
3、人生就像爬坡,要一步一步来。
——丁玲。