用线段图解答分数应用题

“分数应用题线段图画法”之我见
我们知道线段图能帮助学生直观形象地理解题意,分析数量关系;也等于给学生搭建了一个解决实际问题的平台。

分数应用题是小学高年级教学的一个重点也是一个难点。

如果教会学生迅速正确地画出分数应用题的线段图,那么这道题学生就已经会了百分之五十。

怎样使学生尽快掌握线段图的画法呢?本人积三十年教高年级之经验,总结出了行之有效的方法,不妨称为“中点法”。

不管是传统的教材还是新课改后的课本,分数应用题都是先学了分数乘法应用题后再学分数除法应用题。

这两种类型应用题的数量关系可以分成三种:(一)一种量是另一种量的几分之几。

(二)一种量比另一种量多几分之几。

(三)一种量比另一种量少几分之几。

在审题确定单位“1”的量后,首先用线段表示出这个单位“1”的量,分率的分母是几就把单位“1”的量平均分成几份。

怎样才能分的正确呢?当然可以用直尺画,学生要首先计算把单位“1”的量平均分成几份,然后再画,耗时费力,教学实践证实这样太慢。

怎样才能画得又快又对呢?我们知道初学分数应用题时,题中的分率的分母一般都是除0和1以外的不超过10的自然数,如果分率的分母是2就在所画单位“1”的那条线段的中点估计着点个点,这就把单位“1”的量。

图示法解分数应用题一、夯实基础图示法就是用线段图（或其它图形）把题目中的已知条件和问题表示出来，这样可以把抽象的数量关系具体化，往往可以从图中找到解题的突破口。

运用图示法教学应用题，是培养思维能力的有效方法之一。

图示法不仅可以形象地、直观地反映分数应用题中的“对应量和对应分率”间的关系，启发学生的解题思路，帮助学生找到解题的途径，而且通过画图的训练，可以调动学生思维的积极性，提高学生分析问题和解决问题的能力。

二、典型例题例1．一条鱼重的53加上43千克就是这条鱼的重量，这条鱼重多少千克？ 分析与解：从题意可以知道，这条鱼的重量是单位“1”，用线段图帮助我们分析数量关系从图上可以看出43千克对应的分率是（1－53）。

鱼的重量：43÷（1－53） = 187（千克）。

答：这条鱼重187千克。

例2．一桶油第一次用去51，第二次比第一次多用去20千克，还剩下22千克。

原来这桶油有多少千克？分析与解：从图中可以清楚地看出：这桶油的千克数×（1－51－51）=20+22 则这桶油的千克数为：（20+22）÷（1－51－51）=70（千克）。

答：原来这桶油有70千克。

例3．缝纫机厂女职工占全厂职工人数的207，比男职工少144人，缝纫机厂共有职工多少人？分析与解：解题的关键是找到与具体数量144人的相对应的分率。

从线段图上可以清楚地看出女职工占207，男职工占1－207=2013，女职工比男职工少占全厂职工人数的2013－207=103，也就是144人与全厂人数的103相对应。

全厂的人数为：144÷（1－207－207）=480（人）答：缝纫机厂共有职工480人。

小升初培优冲刺（图示法解分数应用题）一、熟能生巧1．张亮从甲城到乙城，第一天行了全程的40%，第二天行了全程的920，距乙城还有18千米，甲、乙两城相距多少千米？2．李玲看一本书，第一天看了全书的16，第二天看了18页，这时正好看了全书的一半。

分数应用题专项练习(必会）1. 一桶油6千克，用去全部的43，用了多少千克?2. 水果店有苹果640千克,梨是苹果的错误!，梨有多少千克？3. 小刚有玻璃弹子20粒，小强的玻璃弹子是小刚的错误!，两人共有玻璃弹子多少粒?4. 洗衣机厂上月计划生产洗衣机1500台,结果超产错误!，超产了多少台?5. 一本书240页，第一天看了全书的错误!，第二天看了全书的错误!，第三天从第几页开始看?6. 学校植树120棵，其中错误!是梧桐树，错误!是榆树,其余的是樟树，植樟树共多少棵?1. 一桶油，用去错误!千克，正好是全部的错误!，用了多少千克？2. 水果店有梨512千克，梨是苹果的错误!，苹果有多少千克？3. 某校六年级有学生260人,男生是女生的错误!，有男生多少人？4. 今年产鲜鱼20万吨，比去年增产15 ，去年产鲜鱼多少万吨？5. 学校图书馆里，文艺书占错误!,科技书占错误!，已知科技书和文艺书共960本，这个图书馆共有图书多少本？6. 一根铁丝，第一天用去全长的错误!，第二天用去全长的错误!，还剩30米，着根铁丝长多少米?（青铜)签名：7. 自行车厂去年计划生产自行车36万辆,上半年完成59 ，下半年完成错误!,结果超产一部分,超产多少万辆?8. 工厂有水泥120吨,第一天运出错误!，第二天运出错误!,第二天比第一天多运出多少吨?9.六年级有学生256人，有错误!参加了数学兴趣小组，参加数学兴趣小组的学生错误!是男生，求参加数学小组的女生占六年级总人数的几分之几？10.有一堆煤60吨，用去它的错误!还多错误!吨，用去多少吨？11.要修一条公路,第一天修错误!千米，第二天修错误!千米，第三天修的恰好是前两天的错误!，三天一共修多少千米？7.一堆煤，第一次运出错误!，第二次运出120吨，第三次运出这堆煤的错误!正好运完，这堆煤共有多少吨？8.从东城到西城，走了全程的错误!,离全程的中点还有16千米，东西两城相距多少千米？9.体育官买来一些球，买足球20个，足球是篮球的错误!，篮球又是排球的错误!，买来排球多少个？10.学校买回红粉笔比白粉笔少160箱,红粉笔是白粉笔的错误!，有白粉笔多少箱？11.一辆汽车4小时行全程的6/7，行完全程要几小时?（白银）签名综合部分：1.工厂有女工234人，男工比女工的错误!错误!未定义书签。

利用线段图巧教分数乘法两步应用题作者：张飞来源：《新教育时代·教师版》2017年第07期摘要：应用题是小学数学教学的难点，解答应用题的关键在于理解数量关系，数量关系可以用线段图来表达，通过让学生画线段图，再加以分析数量间的关系，使问题迎刃而解，线段图在小学应用题教学中起着重要的作用。

关键词：线段图分数乘法两步应用题小学数学应用题是教学中的重点，分数应用题则是教学中的难点。

有不少的应用题，文字叙述比较抽象，数量关系比较复杂，小学生的思维又处于具体形象向思维抽象、逻辑思维的过渡阶段，对于一些抽象问题理解起来困难较大。

如果教师一味地从字面去分析题意，用语言来表述数量关系，虽然老师讲得口干舌燥，学生却难以理解掌握，事倍功半。

即使是学生理解了，也只局限于会做某个题了。

作为教师不仅要教给学生知识，更重要的是交给学生学习知识的方法。

线段图在小学应用题教学中起到了奇妙的作用，它可以帮助学生轻松、愉快地解决复杂关系的应用题，既培养了学生的能力，又促进了学生思维的发展，是教学中行之有效的教学方法。

稍复杂的求一个数的几分之几是多少的应用题，是在学生学习了求一个数的几分之几是多少的一步应用题的基础上进行教学的。

这类应用题是一个数乘以分数的意义的深化应用。

学生掌握这种应用题的解答方法对今后继续学习分数应用具有重要意义。

人教版小学六年级上册数学课本第17页至23页，在例1（据统计，2003年世界人均耕地面积为2500平方米，我国人均耕地面积仅占世界人均耕地面积的五分之二。

我国人均耕地面积是多少平方米？）理解和掌握了求一个数的几分之几是多少的问题的思路与方法的基础上，学习解决稍复杂的求一个数的几分之几是多少的问题。

例2（噪音对人的健康有害，绿化造林可降低噪音，降低八分之一，人现在听到的声音是多少分贝？）是整体与部分之间的比较，即“知道一个部分量是总量的几分之几，求另一个部分量”的问题，解答一般有两种方法，一种是先求出是总量几分之几的部分量，再用总量减去这个部分量，求出另一个部分量；另一种是先求出要求的部分量占总量的几分之几，再根据分数乘法的意义求出这个部分量是多少。

分数乘法应用题练习1、人的心脏跳动的次数随着年龄而变化。

青少年每分钟约跳75次，婴儿每分钟心跳的次数比青少年多45。

婴儿每分钟心跳多少次？青少年每分钟跳75次婴儿比青少年多45婴儿每分钟跳多少次？法〔一〕婴儿每分钟的心跳=青年每分钟的心跳+婴儿每分钟比青年多跳的次数75+75×45=75+60 =135〔次〕 法〔二〕先求出婴儿所占的比重是青年的几分之几：1+45然后根据分数乘法的意义，求解：75×〔1+45 〕=75×95=135〔次〕 答：婴儿每分钟心跳135次。

2、一个饲养场，养鸭1200只，养的鸡比养的鸭多35，养鸡多少只？鸭：1200只 鸡：多35鸡？只法〔一〕：鸡的只数=鸭的只数+鸡比鸭多的只数1200+1200×35=1200+720 =1920〔只〕法〔二〕：先求出鸡所占的比重是鸭的几分之几：1+35然后根据分数乘法的意义，求出鸡的只数？1200×〔1+35 〕=1200×85=1920〔只〕答：鸡有1920只。

3、学校有20个足球，篮球比足球少 15，篮球多少个？足球：20个 篮球：少15？个 法〔一〕：篮球的个数=足球的个数— 比足球少的个数20-20×15=20-4 =16〔个〕法〔二〕：先求出篮球所占的比重是足球的多少？1-15 =4520×〔1-15 〕=20×45=16〔个〕 答：篮球16个变式训练：一种服装原价105元，现在降价27，现在售价比原价少多少元？分数除法应用题练习题1、一个儿童体内所含水分有28千克，占体重的45。

这个儿童的体重有多少千克？水分占体重的45水分是28千克儿童体重是多少千克？ 法〔一〕：列方程，解之。

解：设这个儿童的体重有X 千克。

45X=28 X=35 法〔二〕：量率对应，求解。

单位“1〞的量=量÷率28÷45=35〔千克〕答：这个儿童的体重有35千克。

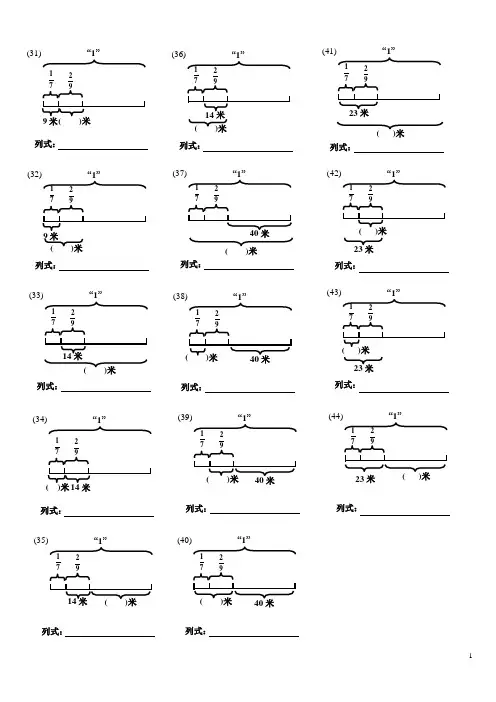
(31)“1”列式： 9米 9271( )米 (32)“1”列式： 9米9271( )米 (34)“1”列式： ( )米 927114米 (33)“1” 列式：( )米927114米(35)“1”列式：( )米 927114米 (36)“1”列式：14米 9271( )米 (37)“1”列式：40米 9271( )米(38)“1”列式： ( )米 927140米(39)“1”列式：( )米 927140米(40)“1”列式：( )米 927140米列式：(41)“1”23米9271( )米列式： (42)“1”23米 9271( )米 列式：(43)“1”23米 9271( )米列式：(44)“1”23米 9271( )米(16) “1”( )吨列式：多25%吨(17)“1”125吨列式：多25% ( )吨(18)吨列式：多25% ( )吨“1”(19) “1”360米列式：少( )米92(20) “1”米列式：少( )米92(23) “1”80米列式：少( )米92(21) “1”360米列式：( )米少92(22) “1”()米列式：少80米92(24) “1”80米列式：( )米少92(20) “1”( )米列式：少280米92(26) “1”()米列式：少280米92(27) “1”280米列式：( )米少92(28) “1”(63)米列式：( )米9271(29) “1”(63)米列式：( )米9271(30) “1”列式：9米9271( )米(1) 52“1”( )米50米列式：(2)52“1”( )米 50列式：(3)52“1”20米( )米列式：(4)52“1”20米 ( )米 列式：(5)52“1”30米( )米列式：(7)53“1”( )米50列式：(6)52“1”30( )米列式：(8)53“1”20米( )米列式：(9)53“1”20米( )米列式：(10)“1”100吨列式：多25%( )吨(11)“1”100吨 列式： 多25%( )吨(12)100吨列式：多25% ( )吨(13)“1”( )吨列式：多25%25吨(14)“1”( )吨列式：多25%25吨(15)25吨列式：多25% ( )吨“1”练 习 题姓名：。

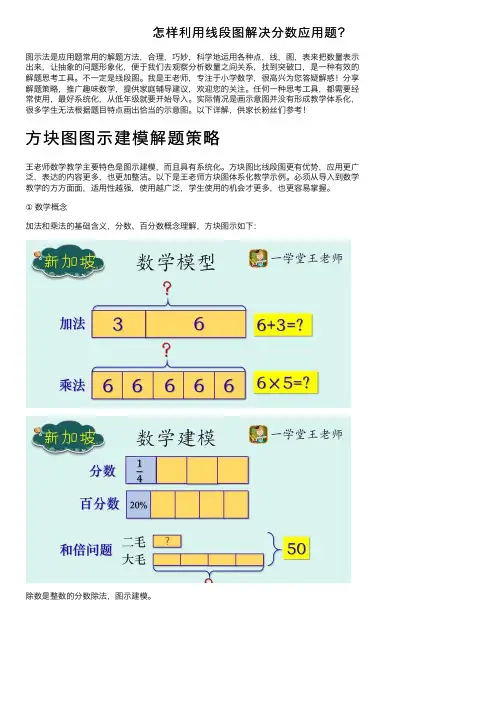
怎样利⽤线段图解决分数应⽤题？图⽰法是应⽤题常⽤的解题⽅法，合理，巧妙，科学地运⽤各种点，线，图，表来把数量表⽰出来，让抽象的问题形象化，便于我们去观察分析数量之间关系，找到突破⼝，是⼀种有效的解题思考⼯具。

不⼀定是线段图。

我是王⽼师，专注于⼩学数学，很⾼兴为您答疑解惑！分享解题策略，推⼴趣味数学，提供家庭辅导建议，欢迎您的关注。

任何⼀种思考⼯具，都需要经常使⽤，最好系统化，从低年级就要开始导⼊。

实际情况是画⽰意图并没有形成教学体系化，很多学⽣⽆法根据题⽬特点画出恰当的⽰意图。

以下详解，供家长粉丝们参考！⽅块图图⽰建模解题策略王⽼师数学教学主要特⾊是图⽰建模，⽽且具有系统化。

⽅块图⽐线段图更有优势，应⽤更⼴泛，表达的内容更多，也更加整洁。

以下是王⽼师⽅块图体系化教学⽰例。

必须从导⼊到数学教学的⽅⽅⾯⾯，适⽤性越强，使⽤越⼴泛，学⽣使⽤的机会才更多，也更容易掌握。

①数学概念加法和乘法的基础含义，分数、百分数概念理解，⽅块图⽰如下：除数是整数的分数除法，图⽰建模。

②整数应⽤题在王⽼师趣味数学专栏系列中，从⼆年级的两步应⽤题开始就导⼊了⽅块图图⽰建模⽅法教学，并延申⾄倍数关系应⽤题，年龄问题，移多补少问题等等分类应⽤题题型。

③分数应⽤题分数应⽤题是研究数量之间份数关系的典型应⽤题，⼀⽅⾯它是在整数应⽤题上的延续和深化，另⼀⽅⾯，它有其⾃⾝的特点和解题规律。

在解这类问题时，分析中数量之间的关系，准确找出“量”与“率”之间的对应是解题的关键。

图⽰不但适合低年级学⽣，⾼年级复杂分数应⽤题依然需要画图来辅助思考。

以下举例，选⾃我的⼩升初真题巧解专栏。

还有其他如⾏程问题。

可以将⽅块图变为路线图。

结语。

线段图巧解分数应用题论文概要：分数应用题的答案可用比的知识、倍数知识等各种方法解答，可以说分数应用题是小学应用题的大熔炉，能从分调动学生的积极性和思维的发展性。

画线段图能形象、生动表露出各种方法的条件，勾勒出各种思维，丰富学生的想象力。

线段图作为辅助解决应用题的一种好的手段，一直贯穿解决问题的教学中。

从小学低年级开始，因此学生感到非常熟悉，在分数应用题的教学时，把线段图加以改进，为解决分数应用题服务，便于学生知识的迁移，做到以旧引新，更容易掌握新的知识。

例如：苹果有100个，梨的个数是苹果的个数的4倍，梨有多少个？通过画线段图，学生很快看出对应的数量，确定解题的方法，从而轻松解答倍数应用题。

这是低年级数学学习的解题手段和技能，把它延伸到解答分数应用题时，有着同样的效果。

如：苹果有100个，梨的个数是苹果的个数的1/4，梨有多少个？通过已有画线段图的技巧，在熟悉旧知识的迁移中，学生很快掌握分数应用题的画图技巧并根据其特点，解答分数应用题。

学生通过化旧为新的学习，不仅形成新的学习技能，并且能锻炼学生灵活多变的思维，发展学生思维的能力。

一、线段图能生动、形象具体突出分数应用题的特点线段图能生动、形象具体突出分数应用题的特点，更便于学生解决分数用题特，提高分数应用题解题能力解决分数应用题的关键：能准确确定整体“1”的量；能找准量与量对应的分率。

当这两个条件具备好了，根据所问题，结合分数应用题的理论，最终确定分数乘、除法应用题。

如：工厂里有一堆煤，烧了它的3/5，还剩下60吨煤没烧，这堆煤原有多少吨？通过画线段图，学生从习惯找整体“1”的量，到最终能准确找出整体“1”的量，顺利突破分数应用题的难点。

接着从线段图学生很容易看出“60吨”这个量的对应的分率不是“3/5”，这个分率不知道，还要学生进一步求出来，是“2/5”，根据问题是求整体“1”的量，还是求部分（一个数的几分之几是多少）量，确定分数应用題的乘、除法。

画线段图解决问题大化县第二小学兰玉珍设计意图：一直以来，较复杂的分数应用题的数量关系较为抽象，难于理解。

在教学中，想让学生通过将生活中的实际问题利用转化的思想抽象成数学问题，利用画线段图的方法分析数量关系，有助于学生理解分数应用题中各数量之间的对比关系，从而能解决不同的问题，帮助他们愉悦地学好数学，树立学数学的信心。

目标：1.通过复习加深理解和掌握单位“1”和各数量之间的数量关系，并能正确解答。

2.通过系统复习，培养学生学会用线段图表示数量关系，培养学生的分析能力和探究能力。

3.通过复习，培养学生认真仔细学习习惯。

重难点：利用线段图，能准确地表示题中的数量关系并能正确解答。

同学们，我们先来回顾一下分数应用题的解题技巧，（课件出示，全班齐读）。

师：分率师谁的，谁就是单位“1”，单位“1”是已知的用乘法计算，求单位“1”的用除法计算。

那我们给下面的式子连线，生口头回答，师连线，（课件出现），这是分数应用题中最常见的类型，在小学阶段中，稍复杂分数应用题对于一些同学来讲，不知从何入手找到正确的数量关系，而通过画线段图的方法可以帮助同学们快速而有效的找到准确的数量关系，得出正确的式子，从而达到事半功倍的效果，那今天我们就来重点复习，用线段图解应用题。

请大家把课题读一遍（用线段图解决分数应用题）。

出示例题：例1，有一条绳子，第一次剪去全长的 1/3 ，第二次剪去3米，这时正好剩下一半，这条绳子原来是多少米？由已知条件可知分率是（），单位“1”是（全长的），剩下一半就是全长的（），那剪去的也是全长的（），请大家尝试画出线段图。

学生尝试后展示结果。

列式计算。

例2，有一桶汽油，第一次取出40%，第二次取出的比第一次少12千克，桶里还剩下28千克，这桶油原有多少千克？请一生读题后问如何画线段图表示。

（课件演示），生说，师画后生自己列式解答，第二次取出的比第一次少12千克，就是第二次也取出这桶油的40%少12KG。

练习：1、李玉看一本书，第一天看了 1/5 ，第二天比第一天多看7页，这时还有56页没有看，这本书有多少页？一生读题目后请一生上台板演，线段图。

分数除法应用题的线段图解浅议
分数除法应用题的线段图解浅议
一、什么是分数除法
所谓的分数除法，就是指把除数和被除数都是分数的情况下的除法。

这个运算是比较复杂的，不像普通的整数除法可以直接用四则运算的
方法进行计算，而是要经历简化步骤和转分母步骤，再进行相应的运
算才能得出结果。

二、分数除法应用题的线段图
分数除法应用题应用线段图是一种简单而有效的方式，通过线段图，
我们可以很直观地把一道分数除法题拆解成两部分，一部分是被除数，另外一部分是除数。

另外，我们可以把每个分数都用一条线段来表示，这样看起来就像是一个真正的线段图。

线段图的关键就是要以最直观的形式来比较被除数和除数的大小，进
而把分数除法题解决掉。

它可以帮助大家快速得出分数除法应用题的
答案，而且还是非常容易的，以上就是关于分数除法应用题的线段图
解浅议。

三、如何应用线段图
首先，我们可以用一条线段来表示被除数，另一条线段来表示除数，
然后比较两条线段的长短。

如果除数比被除数要短，那么答案为商数；如果被除数比除数要短，那么答案为尽数。

最后，我们可以把这个答
案抄写下来作为正确答案。

分数除法应用题的线段图是一种简单而有效的方式，通过这种方式，
我们可以很直观地把一道分数除法题拆解成两部分，从而判断答案为
商数还是尽数，而应用这一方法，则是在最根基上对数字概念进行概
念理解，而不光是死记硬背，以上就是关于分数除法应用题的线段图
解浅议。

用画线段图的方法理解题意，再解答。

1、一种电脑，现价比原价降低了152，正好降低了800元，这种电脑原价多少元？2、某养兔专业户，养的白兔比黑兔多120只，黑兔的只数是白兔的32，这个专业户养白兔多少只？3、甲仓库存粮60吨，乙仓库比甲仓库少52，两个仓库共存粮多少吨？4、普通客车和快车每小时共行132千米，普通客车的速度相当于快车的65，普通客车和快车每小时各行多少千米？5、三个工人一天共做螺钉148个，其中甲做的个数是乙的32，丙做的个数是乙车的54，甲、乙、丙三人各做了多少个螺钉？6、刘师傅第一天做零件80个，第二天比第一天多做了10个，两天共完成了总任务的65，这批零件共有多少个？7、刘星做一批小红花，当做完这批花的83时，再做10朵就完成了一半，刘星应做多少朵？8、张师傅加工一批零件，已经加工了5天，每天加工这批零件的252，已完成了260个，还要加工多少个？9、某车间加工一批零件，已经做好530个，比计划的73多80个，计划加工多少个？10、某商店第一天卖出所有油的51，第二天卖出40千克，第三天卖出所有油的41，三天共卖出124.6千克，这个商店共有油多少千克？11、修一条公路，第一天修了全长的83，第二天修了全长的103，两天修的比全长的一半还多2.8千米，这条公路全长多少千米？某班有学生55人，调出女生人数的61后，这时男女生人数相等，这个班原来有男女生各多少名？初夏早上六点，清亮透明的月儿还躲藏在云朵里，不忍离去，校园内行人稀少，我骑着单车，晃晃悠悠的耷拉着星松的睡眼。

校园内景色如常，照样是绿意盈盈，枝繁叶茂，鸟儿歌唱。

经过西区公园，看那碧绿的草地，飞翔中的亭子，便想起十七那年，在这里寻找春天的日子。

本想就此停车再感受一遍，可惜心中记挂北区的荷塘。

回想起冬日清理完荷塘的枯枝败叶，一片萧条的景色：湖水变成墨绿色，没有鱼儿游动，四处不见了鸟儿的踪影，只有莲藕躺在湖底沉沉睡去。

清洁大叔撑着竹竿，乘一叶扁舟，把一片片黑色腐烂的枯叶残枝挑上船。

30、分数应用题(相遇问题) 姓名一、根据线段图列出算式或方程。

①两人9︰00出发，9︰20同时到达红旗所在地。

②12千米甲？小时？小时乙志明每分行54米小龙每分行52米每小时6千米每小时8千米？米方法1：方法1：方法2：方法2：二、列式解答。

1、小明和小华步行同时从同一地点向相反方向出发，小明每小时行10千米，小华每小时行8千米，50分钟后，两人相距多少千米？2、两个工程队合开一条675米长的隧道，同时各从一端开凿，第一队每天开12.6米，第二队每天开14.4米。

这条隧道要用多少天才能打通？打通时两队各开凿了多少米？3、快、慢两车同时从相距300千米的两地相对开出，快车10小时行完全程，慢车15小时行完全程，经过几小时两车相遇？4、客车和货车同时从相距400千米的两地相对开出，5小时相遇，已知货车每小时行的千米是客车的35，客车每小时行多少千米？5、甲、乙两艘轮船同时从青岛开往上海。

甲船每小时行36.5千米，乙船每小时行43.2千米。

经过8 小时，两船相距多少千米？6、 甲 丙 乙每小时行8千米每小时？千米7、客车和货车同时从相距600千米的两地相对开出，货车每小时行60千米，与客车的速度比是2︰3，两车经过几小时相遇？8、甲、乙两城相距54千米，小张骑自行车从甲城去乙城，每小时行10.7千米，小王骑自行车从乙城去甲城，每小时行11.3千米。

两人同时出发，几小时后两人相距10千米？9、小明和小华同时从家中相对出发，（两人决 定走最近的路线），小明每小时行5.5千米，经过2小时相遇，小华每小时行多少千米？比例尺：1︰400000。