2006年重庆市中考数学真题试卷

2006年普通高等学校招生全国统一考试（重庆卷）数学试题卷（文史类）数学试题（文史类）共5页。

满分150分。

考试时间120分钟。

注意事项：1．答题前，务必将自己的姓名、准考证号填写在答题卡规定的位置上。

2．答选择题时，必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮檫擦干净后，在选涂其他答案标号。

3．答非选择题时，必须用0.5mm 黑色签字笔，将答案书写在答题卡规定的位置上。

4．所有题目必须在答题卡上作答，在试卷上答题无效。

5．考试结束后，将试题卷和答题卡一并交回。

参考公式：如果事件A B 、互斥，那么()()()P A B P A P B +=+如果事件A B 、相互独立，那么()()()P A B P A P B =如果事件A 在一次试验中发生的概率是p ，那么n 次独立重复试验中恰好发生k 次的概率：()(1)k k n k n n P k C p p -=-一．选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个备选项中，只有一项是符合题目要求的。

（1）已知集合{1,2,3,4,5,6,7}U =，{2,4,5,7}A =，{3,4,5}B =，则()()A B =U U 痧（A ）{1,6} （B ）{4,5} （C ）{2,3,4,5,7} （D ）{1,2,3,6,7}（2）在等差数列{}n a 中，若0n a >且3764a a =，5a 的值为（A ）2 （B ）4 （C ）6 （D ）8（3）以点（2，－1）为圆心且与直线3450x y -+=相切的圆的方程为（A ）22(2)(1)3x y -++= （B ）22(2)(1)3x y ++-=（C ）22(2)(1)9x y -++= （D ）22(2)(1)3x y ++-=（4）若P 是平面α外一点，则下列命题正确的是（A ）过P 只能作一条直线与平面α相交 （B ）过P 可作无数条直线与平面α垂直（C ）过P 只能作一条直线与平面α平行 （D ）过P 可作无数条直线与平面α平行（5）()523x -的展开式中2x 的系数为 （A ）－2160 （B ）－1080 （C ）1080 （D ）2160（6）设函数()y f x =的反函数为1()y f x -=，且(21)y f x =-的图像过点1(,1)2，则1()y f x -=的图像必过（A ）1(,1)2 （B ）1(1,)2（C ）(1,0) （D ）(0,1)（7）某地区有300家商店，其中大型商店有30家，中型商店有75家，小型商店有195家。

2006年普通高等学校招生全国统一考试（重庆卷）数学试题卷（理工农医类）一、选择题：本大题共10小题，每小题5分。

在每小题给出的四个备选项中，只有一项是符合题目要求的。

（1）已知集合{}{}{}5,4,3,7,5,4,2,7,6,5,4,3,2,1===B A U ，则()()U U A B ⋃痧＝（ ）（A ）{}6,1 （B ）{}5,4 （C ）{}7,5,4,3,2 （D ）{7,6,3,2,1}（2）在等差数列{}n a 中，若4612a a +=，n S 是数列的{}n a 的前n 项和，则9S 的值为（ ） （A ）48 (B)54 (C)60 （D ）66（3）过坐标原点且与圆2254202x y x y +-++=相切的直线方程为（ ） （A ）x y x y 313=-=或 （B ）x y x y 313-==或（C ）x y x y 313-=-=或 （D ）x y x y 313==或（4）对于任意的直线l 与平面α，在平面α内必有直线m ，使m 与l （ ）（A ）平行 （B ）相交 （C ）垂直 （D ）互为异面直线（5）若nx x ⎪⎪⎭⎫ ⎝⎛-13的展开式中各项系数之和为64，则展开式的常数项为（ ）（A ）－540 （B ）－162 （C ）162 （D ）540（6）为了了解某地区高三学生的身体发育情况，抽查了该地区100名年龄为17.5岁－18岁的男生体重（kg ），得到频率分布直方图如下：根据上图可得这100名学生中体重在[)5.64,5.56的学生人数是（ ） （A ）20 （B ）30 （C ）40 （D ）50（7）与向量7117,,,2222a b ⎛⎫⎛⎫==- ⎪ ⎪⎝⎭⎝⎭的夹角相等，且模为1的向量是（ ）（A ）⎪⎭⎫ ⎝⎛-53,54（B ）⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-53,5453,54或（C ）⎪⎪⎭⎫ ⎝⎛-31,322（D ）⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-31,32231,322或 （8）将5名实习教师分配到高一年级的3个班实习，每班至少1名，最多2名，则不同的分配方案有（ ）（A ）30种 （B ）90种 （C ）180种 （D ）270种（9）如图所示，单位圆中AB 的长为x ，()f x 表示弧 AB 与弦AB 所围成的弓形面积的2倍，则函数()y f x =的图像是（ ）（10）若,,0a b c >且()4a a b c bc +++=-则2a b c ++的最小值为（ ）（A 1 （B 1 （C ）2 （D ）2 二、填空题：本大题共6小题，每小题4分，共24分。

2006年普通高等学校招生全国统一考试（重庆卷）数学（理工农医类）一、选择题：本大题共10小题，每小题5分。

在每小题给出的四个备选项中，只有一项是符合题目要求的。

（1）已经集合{}{}{}5,4,3,7,5,4,2,7,6,5,4,3,2,1===B A U ，则()()U U C A C B ⋃＝ （A ）{}6,1 （B ）{}5,4 （C ）{}7,5,4,3,2 （D ）7,6,3,2,1（2）在等差数列{}n a 中，若a n s a a ,126=+是数列的{}n a 的前n 项和，则a s 的值为（） （A ）48 (B)54 (C)60 （D ）66（3）过坐标原点且与圆0252432=++-+y x y x 相切的直线方程为（） （A ）x y x y 313=-=或 （B ）x y x y 313-==或（C ）x y x y 313-=-=或 （D ）x y x y 313==或（4）对于任意的直线l 与平面α，在平面α内必有直线m ，使m 与l （）（A ）平行 （B ）相交 （C ）垂直 （D ）互为异面直线（5）若nx x ⎪⎪⎭⎫ ⎝⎛-13的展开式中各项系数之和为64，则展开式的常数项为（）（A ）-540 （B ）-162 （C ）162 （D ）540（6）为了了解某地区高三学生的身体发育情况，抽查了该地区100名年龄为17.5岁－18岁的男生体重（kg ），得到频率分布直方图如下：根据上图可得这100名学生中体重在[)5.64,5.56的学生人数是（） （A ）20 （B ）30 （C ）40 （D ）50（7）与向量⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=27,21,21,27b a 的夹角相等，且模为1的微量是（）（A ）⎪⎫ ⎛-3,4 （B ）⎪⎫⎛-⎪⎫ ⎛-3,43,4或（C ）⎪⎪⎭⎫ ⎝⎛-31,322 （D ）⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-31,32231,322或 （8）将5名实习教师分配到高一年级的3个班实习，每班至少1名，最多2名，则不同的分配方案有（） （A ）30种 （B ）90种 （C ）180种 （D ）270种（9）如图所示，单位圆中AB 的长为x ，()f x 表示弧AB 与弦AB 所围成的弓形面积的2倍，则函数y=f(x)的图像是（）（10）若,,0a b c >且()4a a b c bc +++=-则2a b c ++的最小值为（） （A1 （B1 （C）2 （D）2二、填空题：本大题共6小题，每小题4分，共24分。

绝密 * 启用前2006年普通高等学校招生全国统一考试(重庆卷)数学试题卷（理工农医类）数学试题（理工农医类）共5页，满分150分。

考试时间120分钟。

注意事项：1.答题前，务必将自己的姓名、准考证号填写在答题卡规定的位置上。

2.答选择题时，必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦擦干净后，再选涂其他答案标号。

3.答非选择题时，必须使0.5毫米黑色墨水签字笔，将答案书写在答题止规定的位置上。

4.所有题目必须在答题卡上作答，在试题卷上答题无效。

5.考试结束，监考员将试题卷和答题卡一并收回。

参考公式：如果事件A 、B 互斥，那么P （A+B ）－P(A)+P(B) .如果事件A 、B 相互独立，那么P(A ·B)－P(A)·P(B) 如果事件A 在一次试验中发生的概率是P ，那么n 次独立事件重复试验中恰好发生k 次的概率P n (k)=C k n P k (1-P)n-k一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.(1)已知集合U ={1,2,3,4,5,6,7}, A ={2,4,5,7},B ={3,4,5},则(u A )∪(u B )= (A){1,6} (B){4,5}(C){1,2,3,4,5,7} (D){1,2,3,6,7}(2)在等差数列｛a n ｝中，若a a+a b =12,S N 是数列｛a n ｝的前n 项和，则S N 的值为 （A ）48 (B)54 (C)60 (D)66(3)过坐标原点且与x 2｜y 24x ｜2y +25=0相切的直线的方程为 （A ）y =-3x 或y =31x (B) y =-3x 或y =-31x（C ）y =-3x 或y =-31x (B) y =3x 或y =31x(4)对于任意的直线l 与平同a ,在平面a 内必有直线m ,使m 与l(A)平行 （B ）相交(C)垂直 (D)互为异面直线 （5）若(x 3)x1n 的展开式中各项系数之和为64，则展开式的常数项为(A)-540 (B) (c)162 (D)540(6)为了了解某地区高三学生的身体发育情况，抽查了该地区100名年龄为17.5岁－１８岁的男生体重(kg) ,得到频率分布直方图如下：根据上图可得这100名学生中体重在〔56.5,64.5〕的学生人数是 (A)20 (B)30 (C)40 （D ）50(7)与向量a =-⎪⎭⎫ ⎝⎛b ,21,27⎪⎭⎫ ⎝⎛27,21的夹解相等，且模为1的向量是(A) ⎪⎭⎫-⎝⎛53,54 (B) ⎪⎭⎫- ⎝⎛53,54或⎪⎭⎫ ⎝⎛-53,54 （C ）⎪⎭⎫-⎝⎛31,322 （D ）⎪⎭⎫- ⎝⎛31,322或⎪⎭⎫⎝⎛-31,322 （８）将5名实习教师分配到高一年级的３个班实习，每班至少１名，最多２名，则不同的分配方案有（A ）３０种 （B ）９０种 （C ）１８０种 （D ）２７０种（９）如图所示，单位圆中弧AB 的长为x ,f (x )表示弧AB 与弦AB 所围成的弓形面积的２倍，则函数y =f (x )的图象是题 （９）图（１０）若a ,b ,c ＞0且a (a +b +c )+bc =4-23,则2a +b +c 的最小值为 （A ）3-1 (B) 3+1 (C) 23+2 (D) 23-2一、填空题：本大题共6小题，共24分，把答案填写在答题卡相应位置上 （11）复数复数2i321++i的值是_________. (12)∝-n lim=---+++12)12(312n n n _________. (13)已知βα,⎪⎭⎫⎝⎛∈ππ,43，sin(βα+)=－,53 sin ,13124=⎪⎭⎫ ⎝⎛-πβ则os ⎪⎭⎫ ⎝⎛+4πα=________.(14)在数列｛a n ｝中，若a 1=1,a n +1=2a n +3 (n ≥1),则该数列的通项a n =_________.(15)设a ＞0,n ≠1,函数f (x )=a lg (x 2-2n +1) 有最大值.则不等式log n (x 2-5x +7) ＞0的解集为_______. (16)已知变量x ,y 满足约束条件1≤x+y ≤4,-2≤x-y ≤2.若目标函数z =ax +y (其中a ＞0)仅在点(3,1)处取得最大值，则a 的取值范围为___________.二、解答题：本大题共６小题，共７６分解答应写出文字说明，证明过程或演算步骤. （17）（本小题满分13分） 设函数f (x )=3cos 2cos+sin ωrcos ωx+a(其中ω＞0,a ∈R ),且f (x )的图象在y 轴右侧的第一个高点的横坐标为6x. （Ⅰ）求ω的值； （Ⅱ）如果f (x )在区间⎥⎦⎤⎢⎣⎡-65,3ππ上的最小值为3，求a 的值.（１８）（本小题满分13分）某大厦的一部电梯从底层出发后只能在第18、19、20层可以停靠.若该电梯在底层载有 5 位乘客，且每位乘客在这三层的每一层下电梯的概率均为31，用ξ表示这5位乘客在第20层下电梯的人数.求：（Ⅰ）随机变量ξ的分布列； （Ⅱ）随机变量ξ的期望.（１９）（本小题满分１３分）如图，在四棱锥P －ABCD 中，P A ⊥底面ABCD ,∠DAB 为直角，AB ‖CD,AD =CD =24B,E 、F 分别为PC 、CD 的中点.（Ⅰ）试证：CD ⊥平面BEF;（Ⅱ）设P A ＝k ·AB ,且二面角E -BD -C 的平面角大于︒30,求k 的取值范围.（20）(本小题满分13分)已知函数f (x )=(x 2+bx +c )c x ,其中b ,c ∈R 为常数. 图(19)图 （Ⅰ）若b 2＞4(a -1),讨论函数f (x )的单调性； （Ⅱ）若b 2＜4(c -1),且∞→n limxcx f -)(=4,试证：－6≤b ≤2.(21)(本小题满分12分)已知定义域为R 的函数f (x )满足f (f (x )-x 2+y _=f(x )-x 2+x . （Ⅰ）若f (2)-3,求f (1);又若f (0)=a ,求f (a );（Ⅱ）设有且仅有一个实数x 0,使得f(x 0)= x 0,求函数f (x )的解析表达式.(22)(本小题满分12分)已知一列椭圆C n :x 2+22nb y =1. 0＜b n ＜1,n=1,2. .若椭圆C 上有一点P n 使P n 到右准线l n 的距离d .是｜P n F n ｜与｜P n C n ｜的等差中项，其中F n 、C n 分别是C n 的左、右焦点.（Ⅰ）试证：b n ≤23(n ≥1); （Ⅱ）取b n ＝232++n n ，并用S A 表示∆P n F n G n 的面积，试证：S 1＜S 1且S n ＜S n+3 (n ≥3).图(２２)图（20）(本小题满分13分)已知函数f (x )=(x 2+bx +c )c x ,其中b ,c ∈R 为常数. （Ⅰ）若b 2＞4(a -1),讨论函数f (x )的单调性； （Ⅱ）若b 2＜4(c -1),且∞→n limxcx f -)(=4,试证：－6≤b ≤2.(21)(本小题满分12分)已知定义域为R 的函数f (x )满足f (f (x )-x 2+y _=f(x )-x 2+x . （Ⅰ）若f (2)-3,求f (1);又若f (0)=a ,求f (a );（Ⅱ）设有且仅有一个实数x 0,使得f(x 0)= x 0,求函数f (x )的解析表达式.(22)(本小题满分12分)已知一列椭圆C n :x 2+22nb y =1. 0＜b n ＜1,n=1,2. .若椭圆C 上有一点P n 使P n 到右准线l n 的距离d .是｜P n F n ｜与｜P n C n ｜的等差中项，其中F n 、C n 分别是C n 的左、右焦点. （Ⅰ）试证：b n ≤23(n ≥1); （Ⅱ）取b n ＝232++n n ，并用S A 表示∆P n F n G n 的面积，试证：S 1＜S 1且S n ＜S n+3 (n ≥3).图(２２)图(18)(本小题13分) 解法一：（Ⅰ）ξ的所有可能值为０，１，２，３，４，５. 由等可能性事件的概率公式得P (ξ=0)=2532=24332, P (ξ=1)= =∙541532C .24380 P (ξ=2)= =∙532532C =24380, P (ξ=3)==∙542532C .24340P (ξ=4)= =∙54332C =24310, P (ξ=5)= =531.2431（Ⅱ）由（Ⅰ）得ξ的期望为 E ξ=0×24332+１×24380+2×24380+3×24340+4×24310+5×2431=243405=35. 解法二：（Ⅰ）考察一位乘客是否在第20层下电梯为一次试验，这是5次独立重复试验. 故ξ－B ⎪⎭⎫⎝⎛31,5,即有P (ξ=k )=C 25b⎪⎭⎫ ⎝⎛31k-⎪⎭⎫ ⎝⎛532,k =0,1,2,3,4,5.由此计算ξ的分布列如解法一. 解法三： （Ⅰ）同解法一或解二.（Ⅱ）由对称性与等可能性，在三层的任一层下电梯的人数同分布，故期望值相等.即3E ξ=5,从而E ξ=35. （19）（本小题13分） 解法一：（Ⅰ）证：由已知DF ∥AB 且∠DAD 为直角，故ABFD 是矩形，从而CD ⊥BF .又P A ⊥底面ABCD,CD ⊥AD ，故由三垂线定理知CD ⊥PD .在△PDC 中，E 、F 分别PC 、CD 的中点，故EF ∥PD ,从而CD ⊥EF ,由此得CD ⊥面BEF . 第（19）图１（Ⅱ）连结AC 交BF 于G .易知G 为AC 的中点.连接EG ,则在△P AC 中易知EC ∥P A .又因 P A ⊥底面ABCD ,故BC ⊥底面ABCD .在底面ABCD 中，过C 作GH ⊥BD ,垂足为H ,连接EH .由三垂线定理知EH ⊥BD .从而∠EHG 为二面角E -BD -C 的平面角.设AB=a ,则在△P AC 中，有BG =21P A =21ka . 以下计算GH ，考察底面的平面图（如答(19)图２）.连结GD .因S △CBD =21BD ·GH=21GB ·OF . 故GH =BDDFGB ∙.在△ABD中，因为AB ＝a,AD =2A ,得BD =5a第（19）图２ 而GB =21FB =21AD -a.DF-AB ,从而得GH =BD DF GB ∙= aa a 5∙＝.55a因此tan EHG=GH EG =.255521k a ka=由k ＞0知EHG ∠是锐角，故要使EHG ∠＞︒30，必须k 25＞tan ︒30=,33 解之得，k 的取值范围为k ＞.15152解法二：（Ⅰ）如图，以A 为原点，AB 所在直线为x 轴，AD 所在直线为y 轴，AP 所在直线为：轴建立空间直角坐标系，设AB=a ,则易知点A,B,C,D,F 的坐标分别为 A (0,0,0),B (a ,0,0),C (2a ,2a ,0),D (0,2a ,0), F (a ,2a ,0).从而=(2a ,0,0), =(0,2a ,0),DC ·BF =0,故DC ⊥BF .设P A =b ,则P (0,0,b ),而E 为PC 中点.故 第（19）３ E ⎪⎭⎫ ⎝⎛2,,b a a .从而=⎪⎭⎫ ⎝⎛2,,0b a .·=0,故⊥.由此得CD ⊥面BEF . （Ⅱ）设E 在xOy 平面上的投影为G ，过G 作GH ⊥BD 垂足为H,由三垂线定理知EH ⊥BD. 从而∠EHG 为二面角E-BD-C 的平面角. 由PA ＝k ·AB 得P(0,0,ka),E ⎪⎭⎫⎝⎛2,,ka a a ,G(a,a,0). 设H(x,y,0)，则=(x-a,y-a,0), =(-a,2a,0), 由·=0得=a(x-a)+2a(y-a)=0,即 x-2y=-a ①又因BH =(x,a,y,0),且BH 与BD 的方向相同，故a a x -＝ay2，即2x+y=2a ② 由①②解得x =53a,y=54a,从而GH ＝⎪⎭⎫⎝⎛--0,51,52a a ，｜GH ｜＝55a. tan EHG=a Ka552=k 25.由k ＞0知，EHC 是锐角，由∠EHC ＞,30︒得tanEHG ＞tan ,30︒即k 25＞.33 故k 的取值范围为k ＞15152. (20)（本小题13分）解：（Ⅰ）求导得f 2(x )=［x 2+(b +2)x +b+c ］e x ..因b 2＞4(c-1),故方程f 2(x )=0即x 2+(b +2)x +b +c =0有两根；x 1=－2)1(422---+c b cb ＜x 2=－22+b .2)1(42--+c b令f ′（x ）＞0，解得x ＜x 1或x ＞x 1； 又令f ′（x ）＞0，解得x 1＜x ＜x 2.故当x ε（-, x 1）时，f (x )是增函数，当 x ε（x 2，+）时，f(x)也是增函数，但当x ε（x 1 ， x 2）时，f(x)是减函数.（Ⅱ）易知f (0)=c ,f (u )=b +c ,因此e bf xf x f x e x f +==-=-→→)0()0()(lim )(lim00. 所以，由已知条件得b +e =4 b 2≤4(e-1), 因此b 2+4b -12≤0. 解得-6≤b ≤2.(21)（本小题12分） 解：（Ⅰ）因为对任意x εR ，有f (f (x )- x 2 + x )=f (x )- x 2 +x ，所以 f (f (2)- 22+2)=f (2)- 22+2.又由f (2)=3，得f (3-22+2)-3-22+2，即f (1)=1. 若f (0)=a ，则f (a -02+0)=a -02+0，即f (a )=a .（Ⅱ）因为对任意x εR ，有f (f (x ))- x 2 +x )=f (x )- x 2 +x .又因为有且只有一个实数x 0,使得f (x 0)- x 0. 所以对任意x εR ，有f (x )- x 2 +x = x 0.在上式中令x = x 0,有f (x 0)-x 20 + x 0= x 0,又因为f (x 0)- x 0，所以x 0- x 20=0，故x 0=0或x 0=1.若x 0=0，则f (x )- x 2 +x =0，即 f (x )= x 2 –x .但方程x 2 –x =x 有两上不同实根，与题设条件矛质，故x 2≠0.若x 2=1,则有f (x )- x 2 +x =1，即f (x )= x 2 –x +1.易验证该函数满足题设条件. 综上，所求函数为 f (x )= x 2 –x +1（x ∈R ）.（22）（本小题12分）证：（1）由题设及椭圆的几何性质有.1,2||||2==+=n n n n n n d G P F P d 故 设则右准线方程为,12n n b t -= .1xn e x l =因此，由题意n d 应满足.1111+≤≤-xn x e d e 即，＜，解之得：＜＜12110111n n x e e e ≤⎪⎩⎪⎨⎧≤- 即121＜n e ≤, 从而对任意.23,1≤≥n b n （Ⅱ）设点及椭圆方程易知则出）的坐标为（1,,-n n n n d f x P ,11-=nn e x ))11(1)(1()1(22222---=-=nn n n n c c x b y得两极6131±，从而易知f(c)在（21，6131±）内是增函数6131±，1）内是减函数.现在由题设取,,211211,2322c n n n b c n n b n n n +--++=-=++=则是增数列.又易知＜432=c .546131n c =±＜ 故由前已证，知).3(121≥+n S S S S n n ＜，且＜。

2006年闵行区初三调研测试数学试卷（100分钟完成，满分150分）考生注意：除第一，二大题外，其余各题都必须写出主要的计算或论证步骤． 一、填空题：（本题共12题，每题3分，满分36分） 1．计算：32()x =_______________．2．不等式324x ->的解集是_________________． 3．分解因式：228x -=______________________． 4．函数y =______________． 5．如果方程240x mx -+=有两个相等的实数根，那么m =___________． 6．已知：一次函数y k x b =+的图象与直线21y x =-+平行，并且经过点(0,4)，那么这个一次函数的解析式是___________________．7．某校组织初三学生春游，有m 名师生租用45座的大客车若干辆，共有4个空座位，那么租用大客车的辆数是____________（用m 的代数式表示）． 8．如果直角三角形的两条直角边分别等于5cm 和12cm ，那么这个直角三角形斜边上的中线长等于_____________cm ．9．在△ABC 中，边BC 上的中线AD 等于9cm ，那么这个三角形的重心G 到顶点A 的距离是 cm ．10．已知梯形的上底和下底的长分别等于5cm 、11cm ，那么梯形的中位线长等于___________cm ．11．已知D 、E 分别在△ABC 的边AB 、AC 上，//DE BC ，2BD AD =，3DE =，那么BC = ．姓名：_________________________ 登记号：_______________ 座位号：____________ …………………………密○………………………………………封○………………………………………○线…………………………12．已知两圆相切，圆心距等于5cm ，两圆的半径之比为2∶3，那么较大的圆的半径等于_______________cm ．二、选择题：（本题共4题，每题4分，满分16分）【在下列各题的四个备选答案中，只有一个是正确的，请你将正确答案前的字母填在题后的括号内】13是同类二次根式的是…………………………（ ） （A） （B） （C） （D）14．下列方程中，没有实数根的方程是………………………………（ ） （A ）22(3)2x x -+=； （B ）022=+-x x ；（C ）210x x x+=-； （D ）x x -=+2． 15．在Rt △ABC 中，90C ∠=︒，BC a =，CA b =，AB c =，那么下列等式成立的是……………………………………………………………（ ） （A ）sin c a A =⋅； （B ）cos a c A =⋅； （C ）a b tgA =⋅；（D ）a b ctgA =⋅．16．下列判断一定正确的是……………………………………………（ ） （A ）有两角和其中一角的对边对应相等的两个三角形全等； （B ）有一个角和一边对应相等的两个直角三角形全等； （C ）有两边和其中一边的对角对应相等的两个三角形全等； （D ）有两边对应相等，且有一个角为30︒的两个等腰三角形全等．三、（本题共5题，第17、18题每题9分，第19、20、21题每题10分，满分48分） 17．计算：xxx x 1246932-+．18．解不等式组：335(1),4656.33x x x x +>-⎧⎪-⎨-≥⎪⎩19．如图，在Rt △ABC 中，90C ∠=︒，点D 在边BC 上，5AD BD ==，4s i n5A D C ∠=，求cos ABC ∠的值．20．如图，在梯形ABCD 中，//AD BC ，点E 在对角线BD 上，且DCE ADB ∠=∠，如果9BC =，CD ∶BD = 2∶3，求CE 的长．ABCDABCDE21．调查我区某校四个年级学生暑假期间所读课外书的情况．学生分布如图（a ），读书情况的条形图如图（b ），已知该校四个年级共有学生1800人． （1）该校中预年级学生有________人；（2）暑假期间读课外书总量最少的是_______年级学生，共读课外书_______________本．四、（本题共4题，第22、23、24题每题12分，第25题14分，满分50分） 22．如图，AB 是⊙O 的直径，点P 在AB 的延长线上，弦CD AB ⊥，联结OD 、PC ，ODC P ∠=∠，求证：PC 是⊙O 的切线．28%初二中预24%初一22%初三各年级人数分布图（a ）中预 初一 初二 初三 年级各年级人均读书量条形图（b ）ABCDPO23．初中就要毕业了，几位同学准备学业考试结束后结伴去苏州旅游，预计共需费用1200元，后来又有2位同学参加进来，但总的费用不变，于是每人可少分担30元，试求共有几位同学准备结伴去苏州旅游？24．如图，抛物线3482--=mx mx y 与x 轴正半轴交于1(,0)A x 、2(,0)B x两点，且213x x =． （1）求m 的值；（2）抛物线上另有一点C 在第一象限，设BC 的延长线交y 轴于P如果点C 是BP 的中点，求点C 坐标；（3）在（2）的条件下，求证：△OCA ∽△OBC ．25．如图，在矩形ABCD 中，4AB =，3BC =，O 是对角线BD 的中点，点P 在边AB 上，联结PO 并延长，交边CD 于点E ，交边BC 的延长线于点Q ．（1）求证：OP OE =；（2）设BP x =，CQ y =，求y 与x 的函数关系式，并写出自变量x 的取值范围；（3）试判断△CQE 能否成为等腰直角三角形，如果能，请求出x 的值；如果不能，请说明理由．………………………………………………………………………………………………………………………………………………………密 封 线 内 不 准 答 题A BCDPOEQ2006年闵行区初三调研测试数学试卷参考答案以及评分建议一、填空题：（本题共12题，每题3分，满分36分）1．6x ； 2．2x >； 3．2(2)(2)x x +-； 4．1x ≥且2x ≠； 5．4m =±； 6．24y x =-+； 7．445m +； 8．6.5； 9．6； 10．8； 11．9； 12．3或15．二、选择题：（本题共4题，每题4分，满分16分） 13．D ；14．B ；15．C ；16．A ．三、（本题共5题，第17、18题每题9分，第19、20、21题每题10分，满分48分）17．解：原式= ……………………………3分，3分，3分=…………………………………………………………1分 18．解：由① 得28x ->-，…………………………………………………2分 解得 4x <． ……………………………………………………1分由② 得924x ≥， …………………………………………………2分解得 83x ≥． ……………………………………………………2分 所以，原不等式组的解集是843x ≤<． …………………………2分19．解：在Rt △ADC 中，90C ∠=︒，由4sin 5AC ADC AD ∠==，5AD =，解得4AC =．………………3分 由勾股定理得 3CD =．所以358BC CD DB =+=+=．………3分 在Rt △ABC 中，90C ∠=︒，由勾股定理得AB = ……………2分所以，cosBC ABC AB ∠===…………………………2分 20．解：在梯形ABCD 中，//AD BC ，所以ADB DBC ∠=∠， …………2分 因为DCE ADB ∠=∠，所以DCE DBC ∠=∠， …………………2分 又因为CDE BDC ∠=∠，所以△CDE ∽△BDC ， ………………2分 所以CD CEBD BC=，……………………………………………………2分 因为9BC =，CD ∶BD = 2∶3，所以6CE =． …………………2分 21．（1）468；…………4分（2）初三，…………3分．1782．…………3分四、（本题共4题，第22、23、24题每题12分，第25题14分，满分50分） 22．证明：联结OC ，AP 与CD 交于点E ．因为OC 、OD 是⊙O 的半径，所以OC OD =，………………2分 所以OCD ODC ∠=∠． …………………………………………1分 因为ODC P ∠=∠，所以OCD P ∠=∠． ………………………2分 因为CD AB ⊥，所以90PEC ∠=︒，……………………………2分 所以90P PCE ∠+∠=︒，…………………………………………1分 所以90OCD PCE ∠+∠=︒，即90OCP ∠=︒．…………………2分 因为OC 是⊙O 的半径，所以PC 是⊙O 的切线．……………2分 23．解：设共有x 位同学准备结伴去苏州旅游． …………………………1分 根据题意，得12001200302x x-=-，…………………………………5分 整理后，得 22800x x --=，……………………………………2分 解得 110x =，28x =-（不合题意，舍去）． …………2分 经检验：10x =是原方程的解，且符合题意．所以，原方程的解是10x =． ……………………………………1分答：共有10位同学准备结伴去苏州旅游．………………………1分24．解：（1）由题意得128x x +=，12x x m⋅=-1分 于是由213x x =，解得12x =，26x =，………………………1分所以，3m =-． ……………………………………………1分 （2）由（1）得点B 的坐标是(6,0)B ，233y x x =-+- …………………………………2分 当点C 是BP 的中点时，得点C 的横坐标是3， …………1分于是，当3x =时，得93y =-= …1分所以，点C 的坐标是(3,C ．……………………………1分 （3）由（1）得点A 的坐标是(1,0)A ．…………………………1分于是，1OA =，6OB =，OC ==1分 所以，OC OAOB OC=，……………………………………………1分 又因为AOC COB ∠=∠，所以△OCA ∽△OBC ． …………1分25．（1）证明：在矩形ABCD 中，//AB CD ，所以PBO EDO ∠=∠， …1分 因为O 是对角线BD 的中点，所以OB OD =， …………1分 又因为BOP DOE ∠=∠，所以△BOP ≌△DOE ， ………1分 所以OP OE =． ……………………………………………1分 （2）解：因为CQ y =，3BC =，所以3BQ y =+． …………………1分 因为△BOP ≌△DOE ，所以BP DE x ==，于是，由4AB =得4CE x =-．………………………………1分因为//BP CE，所以CE QCBP QB=，……………………………1分即43x yx y-=+，所以1232(2)xyx-=-，24x<≤．…………2分（3）解：当△CQE是等腰直角三角形时，得CE CQ=，即4x y-=，…………………………………………………1分于是由1232(2)xyx-=-，得12342(2)xxx-=--，…………………1分解得17 2x=，24x=（舍去）．………………………………1分所以，当72x=时，△CQE是等腰直角三角形．…………1分。

2006年普通高等学校招生全国统一考试（重庆卷）数学试题卷（文史类）数学试题（文史类）共5页。

满分150分。

考试时间120分钟。

注意事项：1．答题前，务必将自己的姓名、准考证号填写在答题卡规定的位置上。

2．答选择题时，必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮檫擦干净后，在选涂其他答案标号。

3．答非选择题时，必须用0.5mm 黑色签字笔，将答案书写在答题卡规定的位置上。

4．所有题目必须在答题卡上作答，在试卷上答题无效。

5．考试结束后，将试题卷和答题卡一并交回。

参考公式：如果事件A B 、互斥，那么()()()P A B P A P B +=+ 如果事件A B 、相互独立，那么()()()P A B P A P B =如果事件A 在一次试验中发生的概率是p ，那么n 次独立重复试验中恰好发生k 次的概率：()(1)k kn k n n P k C p p -=-一．选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个备选项中，只有一项是符合题目要求的。

（1）已知集合{1,2,3,4,5,6,7}U =，{2,4,5,7}A =，{3,4,5}B =，则()()A B = U U痧（A ）{1,6} （B ）{4,5} （C ）{2,3,4,5,7} （D ）{1,2,3,6,7} （2）在等差数列{}n a 中，若0n a >且3764a a =，5a 的值为 （A ）2 （B ）4 （C ）6 （D ）8（3）以点（2，－1）为圆心且与直线3450x y -+=相切的圆的方程为 （A ）22(2)(1)3x y -++= （B ）22(2)(1)3x y ++-= （C ）22(2)(1)9x y -++= （D ）22(2)(1)3x y ++-=（4）若P 是平面α外一点，则下列命题正确的是（A ）过P 只能作一条直线与平面α相交 （B ）过P 可作无数条直线与平面α垂直 （C ）过P 只能作一条直线与平面α平行 （D ）过P 可作无数条直线与平面α平行 （5）()523x -的展开式中2x 的系数为（A ）－2160 （B ）－1080 （C ）1080 （D ）2160 （6）设函数()y f x =的反函数为1()y fx -=，且(21)y f x =-的图像过点1(,1)2，则1()y f x -=的图像必过（A ）1(,1)2 （B ）1(1,)2（C ）(1,0) （D ）(0,1)（7）某地区有300家商店，其中大型商店有30家，中型商店有75家，小型商店有195家。

2006年普通高等学校招生全国统一考试（重庆卷）
数学试题卷（理工农医类）
一、选择题：本大题共10小题，每小题5分。在每小题给出的四个备选项中，只有一项是符合题目要求的。
（1）已知集合 ，则 ＝（）
（A） （B） （C） （D）{ }
（2）在等差数列 中，若 ， 是数列的 的前n项和，则 的值为（）
（A）48 (B)54 (C)60（D）66
（15）设 ，函数 有最大值，∵ 有最小值，∴0<a<1，则不等式 的解为 ，解得2<x<3，所以不等式的解集为 .
（16）已知变量 满足约束条件 在坐标系中画出可行域，如图为四边形ABCD，其中A(3，1)， ，目标函数 （其中 ）中的z表示斜率为－a的直线系中的截距的大小，若仅在点 处取得最大值，则斜率应小于 ，即 ，所以 的取值范围为(1，+∞)。
（II）若 ，且 ，试证：
（21）（本小题满分12分）
已知定义域为R的函数 满足
（I）若 ，求 ;又若 ，求 ;
（II）设有且仅有一个实数 ，使得 ，求函数 的解析表达式
（22）（本小题满分12分）
已知一列椭圆 。 ……。若椭圆 上有一点 ，使 到右准线 的距离 是 与 的等差中项，其中 、 分别是 的左、右焦点。
二、填空题：本大题共6小题，每小题4分，共24分。把答案填写在答题卡相应位置上
（11）复数 的值是。
（12） 。
（13）已知 ，则 。
（14）在数列 中，若 ，则该数列的通项 。
（15）设 ，函数 有最大值，则不等式 的解集为。
（16）已知变量 满足约束条件 若目标函数 （其中 ）仅在点 处取得最大值，则 的取值范围为。
（7）与向量 的夹角相等，且模为1的向量为(x，y)，则 ，解得 或 ，选B.

部门经理2006年全国中考数学应用题集锦1、（2006重庆）机械加工需要拥有进行润滑以减少摩擦，某企业加工一台大型机械设备润滑用油90千克，用油的重复利用率为60%，按此计算，加工一台大型机械设备的实际耗油量为36千克.为了建设节约型社会，减少油耗，该企业的甲、乙两个车间都组织了人员为减少实际耗油量进行攻关.（1） 甲车间通过技术革新后，加工一台大型机械设备润滑用油量下降到70千克，用油的重复利用率仍然为60%.问甲车间技术革新后，加工一台大型机械设备的实际耗油量是多少千克？（2） 乙车间通过技术革新后，不仅降低了润滑用油量，同时也提高了用油的重复利用率，并且发现在技术革新的基础上，润滑用油量每减少1千克，用油量的重复利用率将增加1.6%. 这样乙车间加工一台大型机械设备的实际耗油量下降到12千克. 问乙车间技术革新后，加工一台大型机械设备润滑用油量是多少千克?用油的重复利用率是多少？2（1）该公司“高级技工”有 名；（2）所有员工月工资的平均数x 为2500中位数为 元，众数为 元； （3）小张到这家公司应聘普通工作人员．请你回答右图中小张的 问题，并指出用（2）中的哪个数据向小张介绍员工的月工资 实际水平更合理些；（4）去掉四个管理人员的工资后，请你计算出其他员工的月平均工资y （结果保留整数），并判断y 能否反映该公司员工的月工资实际水平．3、（2006河北）有两段长度相等的河渠挖掘任务，分别交给甲、乙两个工程队同时进行挖掘．图11是反映所挖河渠长度y （米）与挖掘时间x （时）之间关系的部分图象．请解答下列问题：（1）乙队开挖到30米时，用了_____小时．开挖6小时时，甲队比乙队多挖了______米；（2）请你求出：①甲队在0≤x ≤6的时段内，y 与x 之间的函数关系式；②乙队在2≤x ≤6的时段内，y 与x 之间的函数关系式；③开挖几小时后，甲队所挖掘河渠的长度开始超过乙队？（3）如果甲队施工速度不变，乙队在开挖6小时后，施工速度增加到12米/时，结果两队同时完成了任务．问甲队从开挖到完工所挖河渠的长度为多少米？4、（2006山东日照）在我市南沿海公路改建工程中，某段工程拟在30天内（含30天）完成．现有甲、乙两个工程队，从这两个工程队资质材料可知：若两队合做24天恰好完成；若两队合做18天后，甲工程队再单独做10天，也恰好完成．请问：（1）甲、乙两个工程队单独完成该工程各需多少天？（2）已知甲工程队每天的施工费用为0．6万元，乙工程队每天的施工费用为0．35万元，要使该工程的施工费用最低，甲、乙两队各做多少天（同时施工即为合做）？最低施工费用是多少万元？5、（2006四川资阳）某乒乓球训练馆准备购买n副某种品牌的乒乓球拍，每副球拍配k(k≥3)个乒乓球. 已知A、B两家超市都有这个品牌的乒乓球拍和乒乓球出售，且每副球拍的标价都为20元，每个乒乓球的标价都为1元. 现两家超市正在促销，A超市所有商品均打九折(按原价的90%付费)销售，而B超市买1副乒乓球拍送3个乒乓球. 若仅考虑购买球拍和乒乓球的费用，请解答下列问题：(1) 如果只在某一家超市购买所需球拍和乒乓球，那么去A超市还是B超市买更合算？(2) 当k=12时，请设计最省钱的购买方案.6、（2006浙江舟山）近阶段国际石油价格猛涨，中国也受其影响，为了降低运行成本，•部分出租车进行了改装，改装后的出租车可以用液化气来代替汽油．假设一辆出租车日平均行程为300千米．（1）使用汽油的出租车，假设每升汽油能行驶12千米．当前的汽油价格为4.6•元/升，当行驶时间为t天时，所耗的汽油费用为p元，试写出p关于t的函数关系式．（2）使用液化气的出租车，假设每千克液化气能行驶15～16千米，•当前的液化气价格为4.95元/千克，当行驶时间为t天时，所耗的液化气费用为w元，试求w•的取值范围（用t表示）．（3）若出租车要改装为使用液化气，每辆需配置成本为8000元的设备，•根据近阶段汽油和液化气的价位，请在（1）、（2）的基础上，计算出最多几天就能收回改装设备的成本？•并利用你所学的知识简单说明使用哪种燃料的出租车对城市的健康发展更有益（用20左右字谈谈感想）．7、（2006山东济宁）随着大陆惠及台胞政策措施的落实，台湾水果进入了大陆市场。

重庆六十四中 张辅忠 E-mail ：zfzjhyzsc@重庆64中初2006级中考模拟考试数学 试卷 2006.4（本卷共五个大题，满分150分，考试时间：120分钟）一、细心填一填（本大题共有10小题，每小题3分，共30分） 1.3-的相反数是 ，9的平方根是 .2. 1）计算： =⋅23x x ，2）因式分解：=-92x . 3.太湖的面积约为36000顷，这个数据用科学记数法可表示为 顷. 4.已知抛物线3)1(2+--=x y 的顶点坐标为 . 5.函数21+=x y 中自变量x 的取值范围是 ，函数3-=x y 中x 自变量的取值范围是 .6.设1x 、2x 是一元二次方程0532=--x x 的两根，则=+21x x ，=⋅21x x .7.已知反比例函数xky =的图象经过点（-2，-3），则=k . 8.如图，已知AB 是⊙O 的一条弦，OC ⊥AB 于C ，若AB=36，r=6，则弦心距OC= ，∠AOB= .9.右表是近6届奥运会中国体育代表团获得的金牌数，在这组数据中，众数是 ，中位数是 .10.某体育馆用大小相同的长方形木块镶嵌地面，第一次铺2块（如图1）第二次把第一次铺的完全围起来（如图2）；第三次再把第二次铺的完全围起来（如图3）；……依次类推，第n 次铺完后，用字母n 表示第n 次镶嵌所使用的木板数是 .二、精心选一选（本大题共有8小题，每小题4分，共40分。

在每小题给出的四个选项中，只有一项是正确的；请把正确选项前字母代号填在题后的括号内，只要你掌握概念，认真思考，相信你一定会选对的！）11.下列二次根式不能再化简的是--------------------------------------（ ）A. B. C. D.12. 已知两圆半径分别是1和3，圆心距为2，则两圆的位置关系是----------（ ） A.相离 B.外切 C.内切 D.相交13.下列调查中适合用普查方法的是-------------------------------------（ ） A.要了解本班同学的身高 B.要了解一批灯泡的使用寿命C.要了解全国人口老龄化的情况D.要了解电视台某娱乐节目的收视率14.下列事件中，属于随机事件的是-------------------------------------（ ） A.掷一枚骰子所得点数不超过6 B.买彩票中奖C.抛出的篮球会下落D.口袋中装有10个红球，从中摸出一个白球8y x 23122y x +学校________________班级____________姓名____________考场____________座位号__________ …………………………密…………封…………线…………内…………不…………要…………答…………题…………………………15.如图是一个等腰梯形，若在该梯形中添加一条线段,可把这个梯形分成一个平行四边形和一个三角形，则这个三角形一定是--------------------（ ） A.等边三角形 B.等腰三角形 C.直角三角形 D.等腰直角三角形 16.一空间几何体的三视图如图所示，则这个几何体是--------------------（ ）A.圆柱B.圆锥C.球D.三棱锥17.如图，小正方形的边长均为1，则下列图中的三角形（阴影部分）与△ABC 相似的是（ ）18.为测量被池塘相隔的两棵树A 、B 的距离，数学课外兴趣小组的同学们设计了如图所示的测量方案：从树A 沿着垂直于AB 的方向走到E ，再从E 沿着垂直于AE 的方向走到F ，C 为AE 上一点，其中3位同学分别测得三组数据：1）AC ，∠ACB 2）CD ，∠ACB ，∠ADB 3）EF ，DE ，AD 其中能根据所测数据求得A 、B 两树距离的有-----（ ） A.0组 B.一组 C.二组 D.三组19. 刘翔在出征雅典奥运会前刻苦进行110米跨栏训练，教练对他10次的训练成绩进行统计分析，判断他的成绩是否稳定，则教练需要知道刘翔这10次成绩的（ ）A ．众数B ．方差C ．平均数D ．频数20. 如图，△ABC 和△DEF 是两个形状大小完全相同的等腰直角三角形，∠B=∠DEF=90°，点B 、C 、E 、F 在同一直线上．现从点C 、E 重合的位置出发，让△ABC 在直线EF 上向右作匀速运动，而△DEF 的位置不动．设两个三角形重合部分的面积为y ，运动的距离为x ．下面表示y 与x 的函数关系式的图象大致是（ ）三、认真答一答（本大题共60分，解答需写出必要的文字说明，演算步骤或证明过程，只要你积极思考，细心计算，你一定会解答正确的。

2006年普通高等学校招生全国统一考试（重庆卷）数学试题卷（理工农医类）一、选择题：本大题共10小题，每小题5分。

在每小题给出的四个备选项中，只有一项是符合题目要求的。

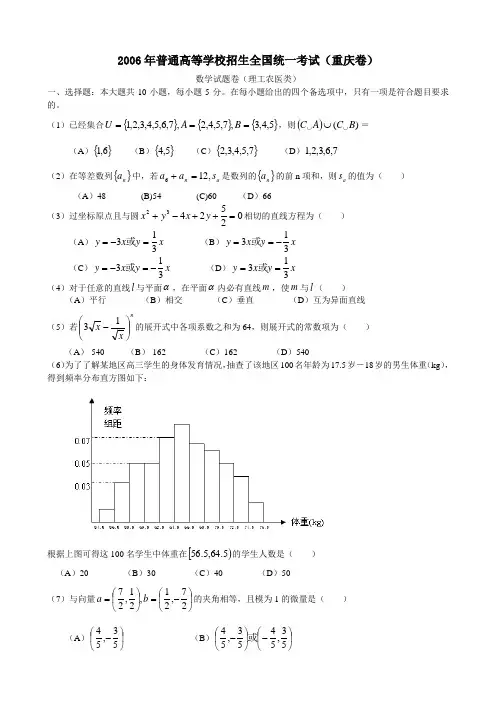
（1）已经集合{}{}{}5,4,3,7,5,4,2,7,6,5,4,3,2,1===B A U ，则())(B C A C ⋃⋃⋃＝（A ）{}6,1 （B ）{}5,4 （C ）{}7,5,4,3,2 （D ）7,6,3,2,1（2）在等差数列{}n a 中，若a n s a a ,126=+是数列的{}n a 的前n 项和，则a s 的值为（ ） （A ）48 (B)54 (C)60 （D ）66 （3）过坐标原点且与圆0252432=++-+y x y x 相切的直线方程为（ ）（A ）x y x y 313=-=或 （B ）x y x y 313-==或 （C ）x y x y 313-=-=或 （D ）x y x y 313==或（4）对于任意的直线l 与平面α，在平面α内必有直线m ，使m 与l （ ）（A ）平行 （B ）相交 （C ）垂直 （D ）互为异面直线 （5）若nx x ⎪⎪⎭⎫⎝⎛-13的展开式中各项系数之和为64，则展开式的常数项为（ ）（A ）-540 （B ）-162 （C ）162 （D ）540（6）为了了解某地区高三学生的身体发育情况，抽查了该地区100名年龄为17.5岁－18岁的男生体重（kg ），得到频率分布直方图如下：根据上图可得这100名学生中体重在[)5.64,5.56的学生人数是（ ） （A ）20 （B ）30 （C ）40 （D ）50 （7）与向量⎪⎭⎫ ⎝⎛-=⎪⎭⎫⎝⎛=27,21,21,27b a 的夹角相等，且模为1的微量是（ ）（A ）⎪⎭⎫⎝⎛-53,54 （B ）⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-53,5453,54或（C）⎪⎪⎭⎫⎝⎛-31,322（D）⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫⎝⎛-31,32231,322或（8）将5名实习教师分配到高一年级的3个班实习，每班至少1名，最多2名，则不同的分配方案有（）（A）30种（B）90种（C）180种（D）270种（9）如图所示，单位圆中 AB的长为x，()f x表示弧 AB与弦AB所围成的弓形面积的2倍，则函数y=f(x)的图像是（）（10）若,,0a b c>且()4a abc bc+++=-则2a b c++的最小值为（）（A）1（B）1（C）2（D）2二、填空题：本大题共6小题，每小题4分，共24分。

一．选择题：本大题共 10 小题，每小题 5 分，共 50 分。在每小题给出的四个备选项中， 只有一项是符合题目要求的。
（1）已知集合U {1, 2,3, 4,5, 6, 7} ， A {2, 4,5, 7} ， B {3, 4,5} ，则 (ðU A) (ðU B)
（A）{1, 6} （B）{4,5} （C）{2,3, 4,5, 7} （D）{1, 2,3, 6, 7}
（A） 2 3 （B）3 （C）2 （D） 3
, sin(
二．填空题：本大题共 4 小题，每小题 4 分，共 24 分。把答案填写在答题卡相应位置上。
（13）已知 sin 2
5

，
52


（14）在数列{an}中，若 a1 1， an1 an 2(n 1) ，则该数列的通项 an
如果事件 A、B 互斥，那么 P( A B) P( A) P(B)
如果事件 A、B 相互独立，那么 P( A:B) P( A):P(B)
如果事件 A 在一次试验中发生的概率是 p ，那么 n 次独立重复试验中恰好发生 k 次的概率： Pn (k ) Cnk pk (1 p)nk
（15）设 a 0, a 1 ，函数 f (x) loga (x2 2x 3) 有最小值，则不等式
loga (x 1) 0 的解集为
，则 tan
。
对全部高中资料试卷电气设备，在安装过程中以及安装结束后进行高中资料试卷调整试验；通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关，系电通，力1根保过据护管生高线产中0不工资仅艺料可高试以中卷解资配决料置吊试技顶卷术层要是配求指置，机不对组规电在范气进高设行中备继资进电料行保试空护卷载高问与中题带资2负料2，荷试而下卷且高总可中体保资配障料置各试时类卷，管调需路控要习试在题验最到；大位对限。设度在备内管进来路行确敷调保设整机过使组程其高1在中正资，常料要工试加况卷强下安看与全22过，22度并22工且22作尽22下可护都能1关可地于以缩管正小路常故高工障中作高资；中料对资试于料卷继试连电卷接保破管护坏口进范处行围理整，高核或中对者资定对料值某试，些卷审异弯核常扁与高度校中固对资定图料盒纸试位，卷置编工.写况保复进护杂行层设自防备动腐与处跨装理接置，地高尤线中其弯资要曲料避半试免径卷错标调误高试高等方中，案资要，料求编试技5写、卷术重电保交要气护底设设装。备备置管4高调、动线中试电作敷资高气，设料中课并技3试资件且、术卷料中拒管试试调绝路包验卷试动敷含方技作设线案术，技槽以来术、及避管系免架统不等启必多动要项方高方案中式；资，对料为整试解套卷决启突高动然中过停语程机文中。电高因气中此课资，件料电中试力管卷高壁电中薄气资、设料接备试口进卷不行保严调护等试装问工置题作调，并试合且技理进术利行，用过要管关求线运电敷行力设高保技中护术资装。料置线试做缆卷到敷技准设术确原指灵则导活：。。在对对分于于线调差盒试动处过保，程护当中装不高置同中高电资中压料资回试料路卷试交技卷叉术调时问试，题技应，术采作是用为指金调发属试电隔人机板员一进，变行需压隔要器开在组处事在理前发；掌生同握内一图部线纸故槽资障内料时，、，强设需电备要回制进路造行须厂外同家部时出电切具源断高高习中中题资资电料料源试试，卷卷线试切缆验除敷报从设告而完与采毕相用，关高要技中进术资行资料检料试查，卷和并主检且要测了保处解护理现装。场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况，然后根据规范与规程规定，制定设备调试高中资料试卷方案。

重庆市2006年初中毕业生学业暨高中招生考试数学试卷（全卷共四个大题 满分：150分 考试时间：120分钟）注意：凡同一题号下注有“课改实验区考生做”的题目供课改实验区考生做，注有“非课改实验区考生做”的题目供非课改实验区考生做，没有注明的题目供所有考生做．一、选择题：（本大题10个小题，每小题4分，共40分）每个小题都给出了代号为Ａ，Ｂ，Ｃ，Ｄ的四个答案，其中只有一个是正确的，请将正确答案的代号填入题后的括号中． 1．3的倒数是（ ） Ａ．3-Ｂ．3Ｃ．13Ｄ．13-2．计算232(3)x x -·的结果是（ ）Ａ．56x - Ｂ．56x Ｃ．62x - Ｄ．62x3．O 的半径为4，圆心O 到直线l 的距离为3，则直线l 与O 的位置关系是（ ） Ａ．相交 Ｂ．相切 Ｃ．相离 Ｄ．无法确定4．使分式24xx -有意义的x 的取值范围是（ ） Ａ．2x = Ｂ．2x ≠ Ｃ．2x=- Ｄ．2x ≠-5．不等式组2030x x ->⎧⎨-<⎩，的解集是（ ）Ａ．2x >Ｂ．3x < Ｃ．23x << Ｄ．无解6．如图，O 的直径CD 过弦EF 的中点G ，40EOD ∠=， 则DCF ∠等于（ ）Ａ．80 Ｂ．50 Ｃ．40 Ｄ．20 7．（课改实验区考生做）如图是由几个相同的小正方体搭成的几何体的三种视图，则搭成这个几何体的小正方体的个数是（ ） Ａ．3 Ｂ．4 Ｃ．5 Ｄ．6（非课改实验区考生做）分式方程1421x x x -=+-的解是（） Ａ．17x =，21x = Ｂ．17x =，21x =- Ｃ．17x =-，21x =-Ｄ．17x =-，21x =8．观察市统计局公布的“十五”时期重庆市农村居民年人均收入每年比上年增长率的统计图，下列说法中正确的是（ ）俯视图左视图主视图7题图6题图O C FGDEＡ．2003年农村居民年人均收入低于2002年Ｂ．农村居民年人均收入每年比上年增长率低于9%的有2年 Ｃ．农村居民年人均收入最多的是2004年 Ｄ．农村居民年人均收入每年比上年的增长率有大有小，但农村居民年人均收入在持续增加9．免交农业税，大大提高了农民的生产积极性，镇政府引导农民对生产的某种土特产进行春节期间，这三种不同包装的土特产都销售了12000千克，那么本次销售中，这三种包装的土特产获得利润最大的是（ ） Ａ．甲 Ｂ．乙 Ｃ．丙 Ｄ．不能确定 10．（课改实验区考生做）现有A B ，两枚均匀的小立方体（立方体的每个面上分别标有数字1，2，3，4，5，6）．用小莉掷A 立方体朝上的数字为x ，小明掷B 立方体朝上的数字为y 来确定点()P x y ，，那么他们各掷一次所确定的点P 落在已知抛物线24y x x =-+上的概率为（ ） Ａ．118Ｂ．112Ｃ．19Ｄ．16（非课改实验区考生做）已知α，β是关于x 的一元二次方程22(23)0x m x m +++=的两个不相等的实数根，且满足111αβ+=-，则m 的值是（ ）Ａ．3或1- Ｂ．3 Ｃ．1 Ｄ．3-或1 二、填空题：（本大题10个小题，每小题3分，共30分）请将正确答案直接填写在题中的横线上．11．重庆市某天最高气温是17℃，最低气温是5℃，那么当天的最大温差是 ℃．12．分解因式：24x -= ．（年） 200520042003200220018题图13．如图，已知直线12l l ∥，140∠=，那么2∠= 度．14．圆柱的底面周长为2π，高为1，则圆柱侧面展开图的面积为 ．15．废旧电池对环境的危害十分巨大，一粒钮扣电池能污染600立方米的水（相当于一个人一生的饮水量）．某班有50名学生，如果每名学生一年丢弃一粒钮扣电池，且都没有被回收，那么被该班学生一年丢弃的钮扣电池能污染的水用科学计数法表示为 立方米． 16．（课改实验区考生做）如图，已知函数y ax b =+和y kx =的图象交于点P ，则根据图象可得，关于()x y ，的二元一次方程组y ax b y kx=+⎧⎨=⎩，的解是 ．2)-= ．17．如图所示，A ，B 是4×5网格中的格点，网格中的每个小正方形的边长都是1．请在图中清晰标出使以A ，B ，Ｃ为顶点的三角形是等腰三角形的所有格点Ｃ的位置．18．按一定规律排列的一列数依次为：1111112310152635，，，，，……，按此规律排列下去，这列数中的第7个数是 ．2113题图1l2l17题图BAxy16题图b19．如图，矩形AOCB 的两边OC OA ，分别位于x 轴，y 轴上，点B 的坐标为2053B ⎛⎫- ⎪⎝⎭，，D 是AB 边上的一点．将ADO △沿直线OD 翻折，使A 点恰好落在对角线OB 上的点E 处，若点E 在一反比例函数的图象上，那么该函数的解析式是 ．20．如图，ABC △内接于O ，A ∠所对弧的度数为120．ABC ACB ∠∠，的平分线分别交AC AB ，于点D E CE BD，，，相交于点F ．以下四个结论：①1cos 2BFE ∠=；②BC BD =；③EF FD =；④2BF DF =．其中结论一定正确的序号数是 ．三、解答题（本大题6个小题，共60分）下列各题解答时必须给出必要的演算过程或推理步骤． 21．（每小题5分，共10分） （1）计算：102tan 60(51)--++；（2）解方程组：2328y x y x =⎧⎨+=⎩， ①．②22．（10分）如图，A D F B ，，，在同一直线上，AD BF =，AE BC =，且AE BC ∥． 求证：（1）AEF BCD △≌△；（2）EF CD ∥．20题图19题图xEDBCBCFD AE22题图23．（10分）在暑期社会实践活动中，小明所在小组的同学与一家玩具生产厂家联系，给该厂组装一部分玩具，该厂同意他们组装240套玩具．这些玩具分为A B C ，，三种型号，它们的数量比例以及每人每小时组装各种型号玩具的数量如图所示：若每人组装同一种型号玩具的速度都相同，根据以上信息，完成下列填空： （1）从上述统计图可知，A 型玩具有 套，B 型玩具有 套，C 型玩具有 套． （2）若每人组装A 型玩具16套与组装C 型玩具12套所花的时间相同，那么a 的值为 ，每人每小时能组装C 型玩具 套． 24．（10分）农科所向农民推荐渝江Ⅰ号和渝江Ⅱ号两种新型良种稻谷．在田间管理和土质相同的条件下，Ⅱ号稻谷单位面积的产量比Ⅰ号稻谷低20%，但Ⅱ号稻谷的米质好，价格比Ⅰ号高．已知Ⅰ号稻谷国家的收购价是1.6元／千克．（1）当Ⅱ号稻谷的国家收购价是多少时，在田间管理、土质和面积相同的两块田里分别 种植Ⅰ号，Ⅱ号稻谷的收益相同？（2）去年小王在土质、面积相同的两块田里分别种植Ⅰ号，Ⅱ号稻谷，且进行了相同的 田间管理．收获后，小王把稻谷全部都卖给国家．卖给国家时，Ⅱ号稻谷的国家收购价定为2.2元／千克，Ⅰ号稻谷国家的收购价未变，这样小王卖Ⅱ号稻谷比卖Ⅰ号稻谷多收入1040元，那么小王去年卖给国家的稻谷共有多少千克？25．（10分）如图，在梯形ABCD 中，AB DC ∥，90BCD ∠=， 且1AB =，2BC =，tan 2ADC ∠=． （1）求证：DC BC =；（2）E 是梯形内一点，F 是梯形外一点，且EDC FBC ∠=∠，DE BF =，试判断ECF △的形状，并证明你的结论；（3）在（2）的条件下，当:1:2BE CE =，135BEC ∠=时，求sin BFE ∠的值．Ｃ型25%Ｂ型 Ａ型55%2a -项目 套／小时 23题图26．（10分）机械加工需用油进行润滑以减小摩擦，某企业加工一台大型机械设备润滑用油．．量．为90千克，用油的重复利用率为60%，按此计算，加工一台大型机械设备的实际耗油．．．．量．为36千克．为了建设节约型社会，减少油耗，该企业的甲、乙两个车间都组织了人员为减少实际耗油量．．．．．进行攻关． （1）甲车间通过技术革新后，加工一台大型机械设备润滑用油量．．．下降到70千克，用油的 重复利用率仍然为60%．问甲车间技术革新后，加工一台大型机械设备的实际耗油量．．．．．是多少千克？（2）乙车间通过技术革新后，不仅降低了润滑用油量．．．，同时也提高了用油的重复利用率， 并且发现在技术革新前的基础上，润滑用油量．．．每减少1千克，用油的重复利用率将增加1.6%．这样乙车间加工一台大型机械设备的实际耗油量．．．．．下降到12千克．问乙车间技术革新后，加工一台大型机械设备的润滑用油量．．．是多少千克？用油的重复利用率是多少？四、解答题：（本大题2个小题，共20分）下列各题解答时必须给出必要的演算过程或推理步骤．27．（10分）已知：m ，n 是方程2650x x -+=的两个实数根，且m n <，抛物线2y x bx c =-++的图象经过点A (0m ，)，B (0n ，)． (1) 求这个抛物线的解析式；(2) 设（1）中的抛物线与x 轴的另一交点为C ，抛物线的顶点为D ，试求出点C ，D 的坐标和BCD △的面积；（注：抛物线2y ax bx c =++(0)a ≠的顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭，）； (3) P 是线段OC 上的一点，过点P 作PH x ⊥轴，与抛物线交于H 点，若直线BC 把EB FC DA 25题图PCH △分成面积之比为2:3的两部分，请求出P 点的坐标．28．（10分）如图281-所示，一张三角形纸片ABC ，ACB ∠90=,86AC BC ==，．沿斜边AB 的中线CD 把这张纸片剪成11AC D △和22BC D △两个三角形（如图282-所示）．将纸片11AC D △沿直线2D B （AB ）方向平移（点12A D D B ，，，始终在同一条直线上），当点1D 与点B 重合时，停止平移．在平移的过程中，11C D 与2BC 交于点E ，1AC 与22C D ，2BC 分别交于点F ，P ．（1）当11AC D △平移到如图283-所示的位置时，猜想图中1D E 与2D F 的数量关系，并证明你的猜想；（2）设平移距离21D D 为x ，11AC D △与22BC D △重叠部分的面积为y ，请写出y 与x 的函数关系式，以及自变量x 的取值范围；（3）对于（2）中结论是否存在这样的x ，使得重叠部分面积等于原ABC △纸片面积的14？若存在，请求出x 的值；若不存在，请说明理由．27题图28-1图28-3图28-2图CB DA 2D2C1C B1D A1D2D1C重庆市2006年初中毕业生学业暨高中招生考试数学试题参考答案与评分意见一、选择题：（每小题4分，共40分） 1－5 ＣＡＡＢＣ 6－10 ＤＢＤＣＢ 二、填空题：（每小题3分，共30分） 11．12；12．()()22x x +-；13．40；14．2π；15．4310⨯；16．（课改）42x y =-⎧⎨=-⎩，，（非课改）；17．18．150； 19．12y x=-； 20．①③．三、解答题：（本大题6个小题，共80分） 21．（每小题5分，共10分） 解：（1）原式112=+················································································· （4分） 32=． ······································································································ （5分）（2）将①代入②，得38y y +=． ········································································ （2分） 解之，得2y =． ··························································································· （3分） 将2y =代入①，得1x =． ·········································································· （4分）所以，原方程的解为12x y =⎧⎨=⎩，．········································································· （5分）22．（10分） 证明：（1）因为AE BC ∥，所以A B =∠∠． ························································· （2分） 又因AD BF =，所以AF AD DF BF FD BD =+=+=． ················· （5分） 又因AE BC =，所以AEF BCD △≌△． ············································ （7分） （2）因为AEF BCD △≌△，所以EFA CDB =∠∠． ································ （9分） 所以EF CD ∥． ····················································································· （10分）17题答图23．（10分）（每空各2分）（1） 132 ， 48 ， 60 （2） 4 ， 6 24．（10分）解：（1）由题意，得1.62120%=-（元）； ··································································· （2分）（2）设卖给国家的I 号稻谷为x 千克， ································································ （3分）根据题意，得()120% 2.2 1.61040x x -⨯=+． ········································· （6分） 解得，6500x =（千克） ············································································· （7分） ()120% 1.811700x x x +-==（千克）． ··················································· （9分） 答：（1）当II 号稻谷的收购价是2元时，种植I 号，Ⅱ号稻谷的收益相同； （2）小王去年卖给国家的稻谷共为11700千克． ·········································· （10分） 25．（10分） 解：（1）过A 作DC 的垂线AM 交DC 于M ．则2AM BC ==． ································· （1分）又tan 2ADC =∠，所以212DM ==． ·································································· （2分）因为1MC AB ==，所以2DC DM MC =+=． 即DC BC =． ········································ （3分） （2）等腰直角三角形． ·························································································· （4分）证明：因为DE BF =，EDC FBC =∠∠，DC BC =， 所以，DEC BFC △≌△． ········································································· （5分） 所以CE CF =，ECD BCF =∠∠．所以90ECF BCF BCE ECD BCE BCD =+=+==∠∠∠∠∠∠．即ECF △为等腰直角三角形．····································································· （6分）（3）设BE k =，则2CE CF k ==．所以EF =． ································· （7分） 因为135BEC =∠，又45CEF =∠，所以90BEF =∠． ·················· （8分） 所以3BF k ==． ······························································· （9分）所以1sin 33k BFE k ==∠． ········································································ （10分） 26．（10分）解：（1）由题意，得()70160%7040%28⨯-=⨯=（千克）．······························· （2分） （2）设乙车间加工一台大型机械设备润滑用油量．．．为x 千克． ····························· （3分） 由题意，得()190 1.6%60%12x x ---=⎡⎤⎣⎦． ········································ （6分） 整理，得2657500x x --=．A B E FM D25题答图解得：175x =，210x =-（舍去）． ··························································· （8分）()9075 1.6%60%84%-⨯+=． ································································ （9分） 答：（1）技术革新后，甲车间加工一台大型机械设备的实际耗油量．．．．．是28千克． （2）技术革新后，乙车间加工一台大型机械设备润滑用油量．．．为75千克，用油的重复利用率为84%． ·········································································································· （10分） 四、解答题：（本大题2个小题，共20分） 27．（10分） 解：（1）解方程2650x x -+=，得15x =，21x =． ·············································· （1分） 由m n <，有1m =，5n =．所以点A ，B 的坐标分别为()10A ，，()05B ，． ········································ （2分） 将()10A ，，()05B ，的坐标分别代入2y x bx c =-++，得105b c c -++=⎧⎨=⎩，．解这个方程组，得45b c =-⎧⎨=⎩，．所以抛物线的解析式为245y x x =--+． ·················································· （3分） （2）由245y x x =--+，令0y =，得245x x --+= 解这个方程，得15x =-，21x =． 所以C 点的坐标为()50-，．由顶点坐标公式计算，得点()29D -，．···························································· （4分）过D 作x 轴的垂线交x 轴于M ，则()12795222DMC S =⨯⨯-=△， ()1295142MDBO S =⨯⨯+=梯形， ································································· （5分）1255522BOC S =⨯⨯=△．所以2725141522BCD DMC BOC MDBO S S S S =+-=+-=梯形△△△． ·············· （6分） （3）设P 点的坐标为()0a ，，因为线段BC 过B ，C 两点，所以BC 所在的直线方程为5y x =+．27题答图那么，PH 与直线BC 的交点坐标为()5E a a +，， ································· （7分）PH 与抛物线245y x x =--+的交点坐标为()245H a a a --+，． ······· （8分） 由题意，得①32EH EP =，即()()()2345552a a a a --+-+=+． 解这个方程，得32a =-或5a =-（舍去）． ··············································· （9分） ②23EH EP =，即()()()2245553a a a a --+-+=+． 解这个方程，得23a =-或5a =-（舍去）． P 点的坐标为302⎛⎫- ⎪⎝⎭，或203⎛⎫- ⎪⎝⎭，． ························································· （10分） 28．（10分）解：（1）12D E D F =． ································································································ （1分） 因为1122C D C D ∥，所以12C AFD =∠∠，又因为90ACB =∠，CD 是斜边AB 的中线，所以DC DA DB ==，即112221C D C D BD AD ===． 所以1C A =∠∠，所以2AFD A =∠∠． ···················································· （2分） 所以22AD D F =．同理：11BD D E =．又因为12AD BD =，所以21AD BD =．所以12D E D F =． ······················ （3分）（2）因为在Rt ABC △中，8AC =，6BC =，所以由勾股定理，得10AB =． 即1211225AD BD C D C D ====．又因为21D D x =，所以11225D E BD D F AD x ====-．所以21C F C E x ==． 在22BC D △中，2C 到2BD 的距离就是ABC △的AB 边上的高，为245． 设1BED △的1BD 边上的高为h ，由探究，得221BC D BED △∽△， 所以52455h x -=． 所以()24525x h -=，()1211125225BED S BD h x ==-△． ·························· （5分） 2 11 28题答图又因为1290C C +=∠∠，所以290FPC =∠．又因为2C B =∠∠，4sin 5B =，3cos 5B =．所以235PC x =，45PF x =，22216225FC P S PC PF x ==△． ················· （7分）而()2212221126522525BC D BED FC P ABC y S S S S x x =--=---△△△△．所以()2182405255y x x x =-+≤≤． ······················································· （8分）（3）存在．当14ABC y S =△时，即218246255x x -+=．整理，得2320250x x -+=．解得，153x =，25x =． 即当53x =或5x =时，重叠部分面积等于原ABC △面积的14． ··········· （10分）。

则“ AF , BF , CF 成等差数列”是“ x1 x2 8 ”的
（A）充要条件 （C）充分不必要条件
3
22 2
1
（C）
2
（B）必要不充分条件 （D）既非充分也非必要
（12）若 a,b, c 0 且 a2 2ab 2ac 4bc 12 ，则 a b c 的最小值是
一．选择题：本大题共 10 小题，每小题 5 分，共 50 分。在每小题给出的四个备选项中， 只有一项是符合题目要求的。
（1）已知集合U {1, 2,3, 4,5, 6, 7} ， A {2, 4,5, 7} ， B {3, 4,5} ，则 (ðU A) (ðU B)
（A）{1, 6} （B）{4,5} （C）{2,3, 4,5, 7} （D）{1, 2,3, 6, 7}
AB 1, BB1 3 1 ， E 为 BB1 上使 B1E 1的点。
平面 AEC1 交 DD1 于 F ，交 A1D1 的延长线于 G ，
求：
（Ⅰ）异面直线 AD 与 C1G 所成角的大小；
（Ⅱ）二面角 A C1G A1 的正切值；
（21）（本小题满分 12 分）
已知定义域为
（2）在等差数列an中，若 an 0 且 a3a7 64 ， a5 的值为
（A）2 （B）4 （C）6 （D）8
（3）以点（2，－1）为圆心且与直线 3x 4 y 5 0 相切的圆的方程为
（A） (x 2)2 ( y 1)2 3 （B） (x 2)2 ( y 1)2 3
设函数 f (x) 3 cos2 x sin x cosx a （其中 0, a R ）。且 f (x) 的图像在

2006年普通高等学校招生全国统一考试（重庆卷）数学试题卷（理工农医类）一、选择题：本大题共10小题，每小题5分。

在每小题给出的四个备选项中，只有一项是符合题目要求的。

（1）已知集合{}{}{}5,4,3,7,5,4,2,7,6,5,4,3,2,1===B A U ，则()()UU A B ⋃＝（ ）（A ）{}6,1 （B ）{}5,4 （C ）{}7,5,4,3,2 （D ）{7,6,3,2,1} （2）在等差数列{}n a 中，若4612a a +=，n S 是数列的{}n a 的前n 项和，则9S 的值为（ ） （A ）48 (B)54 (C)60 （D ）66（3）过坐标原点且与圆2254202x y x y +-++=相切的直线方程为（ ） （A ）x y x y 313=-=或 （B ）x y x y 313-==或（C ）x y x y 313-=-=或 （D ）x y x y 313==或（4）对于任意的直线l 与平面α，在平面α内必有直线m ，使m 与l （ ）（A ）平行 （B ）相交 （C ）垂直 （D ）互为异面直线（5）若nx x ⎪⎪⎭⎫ ⎝⎛-13的展开式中各项系数之和为64，则展开式的常数项为（ ）（A ）－540 （B ）－162 （C ）162 （D ）540根据上图可得这100名学生中体重在[)5.64,5.56的学生人数是（ ） （A ）20 （B ）30 （C ）40 （D ）50 （7）与向量7117,,,2222a b ⎛⎫⎛⎫==-⎪ ⎪⎝⎭⎝⎭的夹角相等，且模为1的向量是（ ） （A ）⎪⎭⎫ ⎝⎛-53,54（B ）⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-53,5453,54或（C ）⎪⎪⎭⎫ ⎝⎛-31,322（D ）⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-31,32231,322或 （8）将5名实习教师分配到高一年级的3个班实习，每班至少1名，最多2名，则不同的分配方案有（ ）（A ）30种 （B ）90种 （C ）180种 （D ）270种 （9）如图所示，单位圆中AB 的长为x ，()f x 表示弧AB 与弦AB 所围成的弓形面积的2倍，则函数()y f x =的图像是（ ）（10）若,,0a b c >且()43,a a b c bc +++=-则2a b c ++的最小值为（ ）（A ）31 （B ）31（C ）232 （D ）232二、填空题：本大题共6小题，每小题4分，共24分。

新世纪教育网
精品资料
版权所有@新世纪教育网
一、填空题 第 1 题答案.
40
第 2 题答案.
25°
第 3 题答案.
135
第 4 题答案.
17 17
第 5 题答案. 55 第 6 题答案.
OCP 40 ； ①存在； ②符合条件的点 P 共有 3 个： 当点 P 在线段 AO 上时， 当点 P 在 OB

的延长线上时， OCP 20 ；当点 P 在 OA 的延长线上时， OCP 100 ．

第 7 题答案. ①②④
第 8 题答案.
9 5
第 9 题答案. 40° 第 10 题答案. 48 第 11 题答案. 40 第 12 题答案. 64º 第 13 题答案. 4 第 14 题答案. 10 第 15 题答案.
新世纪教育网 精品资料 版权所有@新世纪教育网
新世纪教育网
精品资料
版权所有@新世纪教育网
90 第 16 题答案. 4 第 17 题答案. 19° 第 18 题答案. 45 第 19 题答案. 90 第 20 题答案. 30
新世纪教育网 精品资料来自版权所有@新世纪教育网

2006年全国中考数学压轴题全析全解1、（2006重庆）如图1所示，一张三角形纸片ABC ，∠ACB=90°,AC=8,BC=6.沿斜边AB 的中线CD 把这张纸片剪成11AC D ∆和22BC D ∆两个三角形（如图2所示）.将纸片11AC D ∆沿直线2D B （AB ）方向平移（点12,,,A D D B 始终在同一直线上），当点1D 于点B 重合时，停止平移.在平移过程中，11C D 与2BC 交于点E,1AC 与222C D BC 、分别交于点F 、P.(1) 当11AC D ∆平移到如图3所示的位置时，猜想图中的1D E 与2D F 的数量关系，并证明你的猜想；(2) 设平移距离21D D 为x ，11AC D ∆与22BC D ∆重叠部分面积为y ，请写出y 与x 的函数关系式，以及自变量的取值范围；（3）对于（2）中的结论是否存在这样的x 的值，使重叠部分的面积等于原ABC ∆面积的14. 若存在，求x 的值；若不存在，请说明理由.[解]（1）12D E D F =.因为1122C D C D ∥，所以12C AFD ∠=∠.又因为90ACB ∠=︒，CD 是斜边上的中线，所以，DC DA DB ==，即112221C D C D BD AD === 所以，1C A ∠=∠，所以2AFD A ∠=∠ 所以，22AD D F =.同理：11BD D E =.CBDA 图1122图3C 2D 2C 1BD 1A图2PCQB又因为12AD BD =，所以21AD BD =.所以12D E D F =（2）因为在Rt ABC ∆中，8,6AC BC ==，所以由勾股定理，得10.AB = 即1211225AD BD C D C D ====又因为21D D x =，所以11225D E BD D F AD x ====-.所以21C F C E x == 在22BC D ∆中，2C 到2BD 的距离就是ABC ∆的AB 边上的高，为245. 设1BED ∆的1BD 边上的高为h ，由探究，得221BC D BED ∆∆∽，所以52455h x-=. 所以24(5)25x h -=.121112(5)225BED S BD h x ∆=⨯⨯=- 又因为1290C C ∠+∠=︒，所以290FPC ∠=︒.又因为2C B ∠=∠，43sin ,cos 55B B ==. 所以234,55PC x PF x == ，22216225FC P S PC PF x ∆=⨯=而2212221126(5)22525BC D BED FC P ABC y S S S S x x ∆∆∆∆=--=--- 所以21824(05)255y x x x =-+≤≤ (3) 存在. 当14ABC y S ∆=时，即218246255x x -+= 整理，得2320250.x x -+=解得，125,53x x ==.即当53x =或5x =时，重叠部分的面积等于原ABC ∆面积的142、（2006浙江金华）如图,平面直角坐标系中,直线AB 与x 轴,y 轴分别交于A (3,0),B (0,3)两点, ,点C 为线段AB 上的一动点,过点C 作CD ⊥x 轴于点D .(1)求直线AB 的解析式; (2)若S 梯形OBCD,求点C 的坐标; (3)在第一象限内是否存在点P ,使得以P,O,B 为顶点的 三角形与△OBA 相似.若存在,请求出所有符合条件 的点P 的坐标;若不存在,请说明理由.[解] （1）直线AB 解析式为：y=33-x+3．（2）方法一：设点Ｃ坐标为（x ，33-x+3），那么OD ＝x ，CD ＝33-x+3． ∴OBCD S 梯形＝()2CD CD OB ⨯+＝3632+-x ． 由题意：3632+-x ＝334，解得4,221==x x （舍去） ∴ Ｃ（２，33） 方法二：∵ 23321=⨯=∆OB OA S AOB ,OBCD S 梯形＝334，∴63=∆ACD S ． 由OA=3OB ，得∠BAO ＝30°，AD=3CD ．∴ ACD S ∆＝21CD ×AD ＝223CD ＝63．可得CD ＝33． ∴ AD=１，OD ＝２．∴C （２，33）． （３）当∠OBP ＝Rt ∠时，如图①若△BOP ∽△OBA ，则∠BOP ＝∠BAO=30°，BP=3OB=3，∴1P （3，33）． ②若△BPO ∽△OBA ，则∠BPO ＝∠BAO=30°,OP=33OB=1． ∴2P （1，3）．当∠OPB ＝Rt ∠时③ 过点P 作OP ⊥BC 于点P(如图)，此时△PBO ∽△OBA ，∠BOP ＝∠BAO ＝30°过点P 作PM ⊥OA 于点M ．方法一： 在Rt △PBO 中，BP ＝21OB ＝23，OP ＝3BP ＝23． ∵ 在Rt △P ＭO 中，∠OPM ＝30°， ∴ OM ＝21OP ＝43；PM ＝3OM ＝433．∴3P （43，433）．方法二：设Ｐ（x ，33-x+3），得OM ＝x ，PM ＝33-x+3 由∠BOP ＝∠BAO,得∠POM ＝∠ABO ．∵tan ∠POM==OMPM =x x 333+-，tan ∠ABOC=OBOA =3．∴33-x+3＝3x ，解得x ＝43．此时，3P （43，433）．④若△POB ∽△OBA(如图)，则∠OBP=∠BAO ＝30°，∠POM ＝30°． ∴ PM ＝33OM ＝43． ∴ 4P （43，43）（由对称性也可得到点4P 的坐标）． 当∠OPB ＝Rt ∠时，点P 在ｘ轴上,不符合要求. 综合得，符合条件的点有四个，分别是：1P （3，33），2P （1，3），3P （43，433），4P （43，43）．3、（2006山东济南）如图1，已知Rt ABC △中，30CAB ∠=，5BC =．过点A 作AE AB ⊥，且15AE =，连接BE 交AC 于点P ．（1）求PA 的长；（2）以点A 为圆心，AP 为半径作⊙A ，试判断BE 与⊙A 是否相切，并说明理由； （3）如图2，过点C 作CD AE ⊥，垂足为D ．以点A 为圆心，r 为半径作⊙A ；以点C 为圆心，R 为半径作⊙C ．若r 和R 的大小是可变化的，并且在变化过程中保持⊙A 和⊙C 相．切．，且使D 点在⊙A 的内部，B 点在⊙A 的外部，求r 和R 的变化范围．CABＤ[解]（1） 在Rt ABC △中，305CAB BC ∠==，， 210AC BC ∴==．AE BC ∥，APE CPB ∴△∽△． ::3:1PA PC AE BC ∴==． :3:4PA AC ∴=，3101542PA ⨯==． （2）BE 与⊙A 相切．在Rt ABE △中，AB =15AE =，tanAE ABE AB ∴∠===60ABE ∴∠= ． 又30PAB ∠=，9090ABE PAB APB ∴∠+∠=∴∠=，， BE ∴与⊙A 相切．（3）因为5AD AB ==，r 的变化范围为5r <<当⊙A 与⊙C 外切时，10R r +=，所以R 的变化范围为105R -<<；当⊙A 与⊙C 内切时，10R r -=，所以R 的变化范围为1510R <<+ 4、（2006山东烟台）如图，已知抛物线L 1: y=x 2-4的图像与x 有交于A 、C 两点， （1）若抛物线l 2与l 1关于x 轴对称，求l 2的解析式；（2）若点B 是抛物线l 1上的一动点（B 不与A 、C 重合），以AC 为对角线，A 、B 、C 三点为顶点的平行四边形的第四个顶点定为D ，求证：点D 在l 2上；（3）探索：当点B 分别位于l 1在x 轴上、下两部分的图像上时，平行四边形ABCD 的面积是否存在最大值和最小值？若存在，判断它是何种特殊平行四边形，并求出它的面积；若不存在，请说明理由。