圆和扇形

容提要本讲主要讲解与圆和扇形有关的概念 .及周长、面积公式等.下面我们来说说这方面的基础知识. 圆是我们在生活中经常见到的图形.它也是最完美的平面图形：有无数条通过圆心的对称轴.绕圆心旋转任何角度还保持原状.而且.所有的平面图形在周长相同的情况下.圆的面积是最大的.我们知道.圆的周长和直径的比值是一个固定不变的数 .这正是圆周率.用兀表示.另外.一般把直径记作d.半径记作r.如图1所示.所以.圆的周长|Cd 2r |.圆的面积|Sr 2.如图3.由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫扇形. 它是圆的一部分.所以关于扇形的各种计算可以应用圆里面的结论.扇形的圆心角为n 。

时它的弧长和面积应该分别是圆周长和圆面积的 所以.扇形弧长=—2 r .面积=—r 2360 360我们先来熟悉一下这些公式. 练习:圆与扇形公式与割补n 3601.半径是2的圆的面积和周长分别是多少？2.直径是5的圆的面积和周长分别是多少？3.周长是10兀的圆的面积是多少？4.面积是9兀的圆的周长是多少？例题一、基本公式运用例题1.已知扇形的圆心角为120。

.半径为2.则这个扇形的面积和周长各是多少？（圆周率按 3.14计算）例题2.已知扇形面积为18.84平方厘米.圆心角为60。

.则这个扇形的半径和周长各是多少？（圆周率按3.14计算）随堂练习：1.已知一个扇形的弧长为0.785厘米.圆心角为45° .这个扇形的半径和周长各是多少?2.扇形的面积是31.4平方厘米，它所在圆的面积是157平方厘米，这个扇形的圆心角是多少?例题3.如图.直角三角形 ABC 的面积是45.分别以BC 为圆心.3为半径画圆.已知图中阴影部分的面积是 35.58.请问：角 A 是多少度？（兀取3.14）圆中方.方中圆例题4.如图.左下图和右下图中的正方形边长都是2.那么大圆、小圆的面积分别为随堂练习：1.已知外面大圆的半径是 4.里面小圆的面积是多少？（答案用兀表示）二、割补法例题5.求下列各图中阴影部分的面积（图中长度单位为厘米.圆周率按3.14计算）:A2随堂练习:求下图中阴影部分的面积（图中长度单位为厘米.圆周率按3.14计算）：(2)例题6.求下列各图中阴影部分的面积（图中长度单位为厘米.圆周率按3.14计算）：(1)例题7.已知图中正方形的边长为 2.分别以其四个顶点为圆心的直角扇形恰好交于正方形中心.那么图中阴影部分的面积为（答案用表示）3.14)2(2)例题8.根据图中所给数值.求下面图形的外周长和总面积分别是多少？（兀取Js——4 —■随堂练习：1.根据下图中给出的数值.求这个图形的外周长和面积. （搬3.14）例题9.求图中阴影部分的面积.（圆周率取3.14）思考题图中的4个圆的圆心是正方形的4个顶点.它们的公共点是该正方形的中心. 如果每个圆的半径都是那么阴影部分的总面积是多少平方厘米？1厘米.20厘米作业：1. 半径为4厘米的圆的周长是米.面积是:方厘米;2,半径为4厘米.圆心角为90的扇形周长是米.面积是方厘米.（取3.14）3.家里来客人了 ,淘气到超市买了4瓶啤酒.售货员阿姨将4瓶啤酒捆扎在一起（如卜图所示）,捆4圈至少要用绳子厘米.（取3.14.接头处忽略不计）4.,圆周率按3.14计算）：5.卜列图形中的正方形的边长为2,则下图中各个阴影部分面积的大小分别为（取3.14）求下列各图中阴影部分的面积（图中长度单位为厘米1010用一块面积为36平方厘米的圆形铝板下料,从中裁出了7个同样大小的圆铝板.问：所余下的边角料的总面积是多少平方厘米？圆与扇形旋转与重叠知识总结：学习如何利用割补法和包含排除的思想计算图形中特定部分的面积；学会分析几何图形的运动过程并由此得出点的轨迹和图形扫过的区域.例题：一、重叠问题例题1.下图中甲区域比乙区域的面积大57平方厘米.且半圆的半径是10厘米.那么其中直角三角形的另一条直角边的长度是多少？（圆周率取3.14）例题2.下图中有一个等腰直角三角形ABC.一个以AB为直径的半圆.和一个以BC为半径的扇形.已知AB BC 10厘米.图中阴影部分的面积为多少平方厘米？（< 3.14）随堂练习1.如图17-13.以AB为直径做半圆.三角形ABC是直角三角形.阴影部分①比阴影部分②的面积小28平方厘米AB长40厘米.求BC的长度.（取3.14.）6.例题3.如图.直角三角形的两条直角边分别为3和5.分别以三条边做了3个半圆（直角顶点在以斜边为直径的半圆上）.那么阴影部分的面积为5例题4.图1是一个直径是3厘米的半圆.AB是直径.如图2所示.让A点不动.把整个半圆逆时针转60°.此时B点移动到C点.请问：图中阴影部分的面积是多少平方厘米？（兀取 3.14）A B图2二、动态扫面积问题例题5.如图.正方形ABCD边长为1厘米.依次以A、B、C、D为圆心.以AD、BE、CF、DG为半径画出四个直角扇形.那么阴影部分的面积为方厘米.（取3.14）EG例题6.如图所示.以等边三角形的B、C、A三点分别为圆心.分别以AB、CD、AE为半径画弧.这样形成的曲线ADEF被称为正三角形ABC的渐开线.如果正三角形ABC的边长为3厘米.那么此渐开线的长度为多少厘米.图中I、II、III三部分的面积之和是多少平方厘米？三、运动圆扫面积例题7.图中正方形的边长是4厘米.而圆环的半径是1厘米.当圆环绕正方形无滑动地滚动一周又回到原来位置时.其扫过的面积有多大？（兀取3.14）随堂练习1.图中长方形的长是10厘米.宽是4厘米.而圆环的半径是1厘米.当圆环绕正方形无滑动地滚动一周又回到原来位置时.其扫过的面积有多大？（兀取3.14）例题8.图中等边三角形的边长是3厘米.而圆环的半径是1厘米.当圆环绕等边三角形无滑动地滚动一周又回到原来位置时.其扫过的面积有多大？（澈3.14）思考题如图所示.一只小狗被拴在一个边长为4米的正五边形的建筑物的一个顶点处.四周都是空地.绳长刚好够小狗走到建筑物外墙边的任一位置. 小狗的活动围是多少平方米？（建筑外墙不可逾越.小狗身长忽略不计作业：1.图17-14由一个长方形与两个90角的扇形构成.其中阴影部分的面积是方厘米.（取3.14 .)图17-142.图中有一个矩形和两个半径分别为5和2的直角扇形.那么两个阴影部分的面积相差为取 3.14)如图.直角三角形的两条直角边长分别是10cm 和6cm.分别以直角边为直径作出两个半圆.这两个（17 30）5.图中正方形的边长是 6厘米.而圆环的半径是1厘米.当圆环绕正方形无滑动地滚动一周又回到原来位置时.其扫过的面积有3. 半圆的交点恰好落在斜边上.那么阴影部分的面积是 2cm .（取 3.14）4. 图1是一个直径是 3厘米的半圆.AB 是直径.如图2所示让A 点不动.把整个半圆逆时针转60 °.此时B 点移动到C 点.请问：图中阴影部分的面积是手方厘米（兀取3.14）6 cm10cm图25厘米.圆形的半径是1厘米.当圆形绕等边三角形滚动一周又回到原来6.图中等边三角形的边长是位置时.扫过的面积有（橄3.14）几何计数知识总结:例题：一、枚举或分类解题利用枚举法以及分类的方法进行几何计数.特别是对于正方形和三角形的计数问题. 通常按照面积的大小或者包含基本图形的多少来对图形进行分类.例题1.小杰瑞把巧克力棒摆成了如图所示的形状.其中每一条小短边代表一个巧克力棒.请问：(1)一共有多少个巧克力棒？(2)这些巧克力棒共构成了多少个三角形？(3)嘴馋的小杰瑞吃掉一个巧克力棒后(图中两端带有箭头的小边) .剩下的图形中还有多少个三角形？随堂练习1.例题2.如图.它是由18个大小相同的小正三角形拼成的四边形.其中某些相邻的小正三角形可以拼成较大的正三角形.图中包含""的各种大小的正三角形一共有例题3.如图AB.CD.EFMN互相平行.则图中三角形个数是例题4.图中有多少个正方形?二、与排列组合有关的计数利用排列组合的方法进行几何计数.特别是对于矩形和四边形的计数问题例题5.如图线段AB.BCCD.DE的长度都是3厘米.请问：(1)图中一共有多少条线段？(2)这些线段的长度之和是多少厘米？3厘米3厘米3厘米3厘米人_一_ 人___ 人___ 人f Y Y Y >A B C D E随堂练习1.求图中一共有多少条线段.例题6.求图中一共有多少条线段.求图中一共有多少个矩形.随堂练习1.如图.四条边长度都相等的四边形称为菱形.用16个同样大小的菱形组成如图的一个大菱形.数一数图中共有多少个菱形?例题7.右图是一个长为9.宽为4的长方形网格.每一个小格都是一个正方形.那么:1)从中可以数出矩形.2)从中可以数出正方形.3)从中可以数出包含 .正方形有随堂练习(1)图中包含★的长方形有 .包含？的正方形又有(2)图中同时包含？和★的长方形有 .三、 与容斥原理有关的几何计数例题8.图中一共包含多少个矩形？多少个正方形?思考题用16个边长为1的等边三角形拼成一个边长为 4的大等边三角形.那么组成的图形中可以找出多少个平行作业1. 数一数图中一共有多少条线段?2.图中共有 个三角形.1.四边形?【分析与解】按边长分类数 .图中共有9 3 1 13个三角形；平行四边形共有 3 3 3 2 15个.3.在图中.包含※的长方形共有 _________ 企.【分析与解】图中共有 7 1 8个正方形.19个长方形.这道题适合按大小分类数. 图中有三角形 个.梯形 个.【分析与解】三角形有 3 12 3 18个.梯形有121 2 3 18个.【分析与解】答案是38.144 .长方形有 123 1 2 3 4 5 2 1 2 3 1 2 3 144个. 正方形有 3 5 2 4 1 3 2 9 4 1 38个（这里给出正方形的求法比较巧妙 .如果不合适 请按 正方形的边长分类枚举）.5. 个长方形.4.A6.当运动的速度相同时 .时间的倍数关系等于路程的倍数关系; 当运动的时间相同时 .速度的倍数关系等于路程的倍数关系;当运动的路程相同时 .时间的倍数关系等于速度的倍数关系.但注意时间长的速度慢.时间短的速度快.例题1. )甲、乙两地间的路程是 600千米.上午8点客车以平均每小时 60千米的速度从甲地开往乙地.货车以平均每小时 50千米的速度从乙地开往甲地.要使两车在全程的中点相遇 .货车必须在上午几点出发?例题2. )某学校组织学生去春游.以2米/秒的速度前进.一名学生以 头.再回到队尾.共用6分钟.那么队伍的总长为多少米？4米/秒的速度从队尾跑到队例题3. A 城在一条河的上游.B 城在这条河的下游. A 、B 两城的水路距离为396千米.一艘在静水中速 度为每小时12千米的渔船从B 城往A 城开.一艘在静水中速度为每小时 30千米的治安巡逻艇从 A 城 往B 城开.已知河水的速度为每小时6千米.从A 流向B.两船在距离A 城180千米的地方相遇.巡 逻艇在到达B 城后得到消息说他们刚才遇到的那艘渔船上有一名逃犯船.请问巡逻艇能不能在渔船到达 A 城之前追上渔船？如果能的话 .请问巡逻艇在距 .于是巡逻艇立刻返回去追渔A 城多远的地方追上渔船；如果不能的话.请算出巡逻艇比渔船慢多少小时到A 城.例题4.蜗牛沿着公路前进.对面来了一只兔子.他问兔子：“后面有乌龟吗？ ”.兔子回答说:"10分钟前我超 过了一只乌龟”.接着蜗牛继续爬了 10分钟.遇到了乌龟.已知乌龟的速度是蜗牛速度的10倍.那么兔知识总结:行程.行程问题主要有三组共 9个基本公式:本讲重点学习在小升初中和各个杯赛中的较复杂的行程问题(1)路程速度时间；速度路程时间；时间路程速度；(2)相遇路程速度和时间；速度和相遇路程时间；时间相遇路程速度和；(3) 追及路程速度差时间；速度差追及路程时间；时间追及路程速度差要会灵活运用公式.通过已知的条件求出未知的路程、速度或时间.此时.我们还经常需要用到以下这三个基本倍数关系:子速度是乌龟速度的.............例题5.甲、乙二人相距100米的直路上来回跑步，甲每秒钟跑2.8米，乙每秒钟跑2.2米.他们同时分别在直路两端出发，当他们跑了30分钟时，这段时间相遇了几次？例题6.甲乙两车同时从A、B两地出发相向而行.两车在距离B地64千米的地方第一次相遇.相遇后两车继续原速前进.并且在到达对方出发点之后.立即沿原路返回.途中在距离A点48千米处第二次相遇问：两次相遇点距离是多少千米？例题7.甲、乙两车分别从A、B两地出发.在A、B之间不断往返行驶.已知甲车的速度是每小时15千米.乙车的速度是每小时35千米.并且甲、乙两车第三次相遇（这里特指面对面的相遇）的地点与第四次相遇的地点恰好相距120千米.那么.A、B两地之间的距离等于米.例题8.快、中、慢3辆车同时从同一地点出发.沿同一公路追赶前面的一个骑车人.这3辆车分别用6 分钟、10分钟、12分钟追上骑车人.现在知道快车每小时走24千米.中车每小时走20千米.那么.慢车每小时走多少千米？例题9.有甲乙丙三车各以一定的速度从A到B.乙比丙晚出发10分钟.出发后40分钟追上丙.甲比乙又晚出发10分钟.出发后60分钟追上丙.问.甲出发后多少分钟可以追上乙？思考题一次越野赛跑中.当小明跑了1600米时.小刚跑了1450米.此后两人分别以每秒a米和每秒b米匀速跑.又过100秒时小刚追上小明.200秒时小刚到达终点.300秒时小明到达终点.这次越野赛跑的全程为多少？作业1.现有两列火车同时同方向齐头行进.快车每秒行18米.慢车每秒行10米.行12秒后快车超过慢车.如果这两辆火车车尾相齐同时同方向行进.则9秒后快车超过慢车.那么快慢两车的车长分别是几米？2.一辆中巴车6点（24小时制）从A城出发.以每小时40千米的速度向B城驶去.3小时后一辆小轿车以每小时75千米的速度也从A出发到B.当小轿车到达B后.中巴车离B还有90千米.那么中巴车是几点几分到达B的？3.甲、乙两人从相距为46千米的A、B两地出发相向而行.甲比乙先出发一个小时.他们两人在乙出发后4小时相遇.又已知甲比乙每小时快2千米.那么乙的速度为每小时多少千米？4.甲、乙两人分别从南北两地相对而行. 已知甲每分钟走50米.乙走完全程要30分钟.相对而行10分钟后.甲、乙仍相距100米.那么还要过多少秒钟.甲、乙第一次相遇？5.（第三届“走进美妙的数学花园”团体对抗赛第22题）一个和尚每天早晨都到河边去提一桶水.他提空桶时每秒走3米.提满桶时每秒2米.来回一趟需10分钟。

圆和扇形知识要点
圆和扇形是初中数学中重要的几何概念，它们在实际生活中广泛应用于计算和测量。

以下是圆和扇形的一些重要知识要点。

一、圆：
1.圆的定义：圆是由平面上与一个确定点的距离相等的所有点构成的图形。

这个确定点叫做圆心，到圆心的距离叫做半径。

2.圆的性质：
a.圆心角：圆心角是由圆上两条弧所对的圆心角度。

圆心角的度数等于其所对弧的弧度数。

b.圆的周长：圆的周长等于圆周上的任意一条弧的长度乘以360度除以该弧所对的圆心角的度数。

c.圆的面积：圆的面积等于半径的平方乘以π（即πr²）。

d.弧长和扇形面积：弧长是圆周上的一段弧的长度，扇形是由圆心角和圆弧组成的图形。

弧长等于半径乘以圆心角的弧度数，扇形的面积等于半径的平方乘以圆心角的弧度数除以2
二、扇形：
1.扇形的定义：扇形是由一条弧和两条半径所围成的图形。

2.扇形的性质：
a.扇形角：扇形角是由扇形的两条半径所对的角。

b.扇形的面积：扇形的面积等于半径的平方乘以扇形角的度数除以360。

c.扇形的周长：扇形的周长等于半径乘以扇形的弧度数。

三、圆和扇形的应用：
1.圆和扇形经常应用于计算圆的周长、面积、弧长，以及扇形的面积和周长。

2.圆和扇形的概念也可以应用于计算圆柱的表面积和体积，以及球的表面积和体积。

3.圆和扇形在建筑设计、制造业、地理测量、机械制造等领域也有广泛的应用。

以上是圆和扇形的一些重要知识要点。

深入理解和掌握这些知识，可以帮助学生在数学学习中更好地应用几何概念，解决实际问题。

( 圆心角)的大小有关。
同学们，你了解圆心角了吗？加油！
1.选择题。
（1）圆心角是由两条（ A ）组成的。
A 半径
B 直径
（2）扇形圆心角的度数是（ C ）。
A 大于0° C 大于0°，小于360°
B 大于0°，等于360° D 任意度
同学们，这些题你都明白为什么了吗？
2.判断题。 （1）扇形总是比圆小。
5 如图是小红家去年的支出情况统计图。如果小红家去年全年支 出10000元，那么教育支出有多少元?
10000×25%=2500（元）
答：教育支出有2500元。
扇形统计图是用整个圆的面积表示总数，用圆
认 识
内的扇形面积表示各部分占总数的百分比。
扇
形
统 计
扇形统计图的作用：扇形统计图可以清楚地表示出
从图上直接可以了解到哪些情况？
从图上直接可以看出部分占整体的百分比。 扇形统计图可以很清楚地表示部分和整体之间的关系。
这样的统计图 叫做扇形统计
图。
1 根据统计图（4）回答问题。
篮球 （2）如果你是六（1）班的体育委员，班里要组 织球类比赛，你打算组织什么比赛？为什么？
篮球，因为喜欢篮球的人数最多。
玉
米
大豆
50
12.5
%
谷%
子
10
%
答：李庄种植大豆50公 （3）顷自。己提出问题并解答。
李庄种植谷子多少公顷？
400×10%=40（公顷）
答：李庄种植谷子40公 顷。
4 黄豆的成分如下面的统计图所示，自己提出问题并解答。 100千克黄豆中含脂肪多少千克？ 100×16%=16（千克） 答：100千克黄豆中含脂肪16千克。

设计图案
2023-11-04
目 录
•圆 • 扇形 • 圆和扇形的制作技巧 • 圆和扇形在平面设计中的应用 • 圆和扇形在空间设计中的应用 • 圆和扇形在产品设计中的应用
01
圆
圆的定义
01
02
03
圆的定义
圆是一种几何图形，由一 条线段围绕其一个端点旋 转一周所形成的闭合曲线 构成。
圆心
圆的中心点称为圆心，用 字母O表示。
使用几何画板制作圆
确定中心点
确定一个明确的中心点，并使用该点作为圆心的位置。
确定半径
确定圆的半径，即从圆心到圆周的距离。
绘制圆形
在几何画板中选择“圆形”工具，然后根据中心点和半径进行绘 制。
使用几何画板制作扇形
确定中心点
01
确定一个明确的中心点，并使用该点作为扇形的中心。
确定半径和角度
02
确定扇形的半径和所包含的角度。
圆和扇形在包装设计中的应用
01
突出主题
利用圆形和扇形元素可以突出包装的主题和特色，使产品在货架上脱
颖而出。
02
吸引目光
独特的圆形或扇形设计可以吸引消费者的目光，提高产品的关注度和
购买意愿。
03
环保意识
圆形和扇形包装设计可实现更好的空气流通和废物回收，符合现代人
的环保意识。
感谢您的观看
THANKS
绘制扇形
03
在几何画板中选择“扇形”工具，然后根据中心点、半径和角
度进行绘制。
使用Photoshop或Illustrator制作圆和扇形
使用Photoshop或Illustrator等图形编辑软件，可以方便地创建和编辑圆形和扇 形。
选择软件中的形状工具，如椭圆工具或弧线工具，然后根据需要调整形状的大小 和角度。

扇形面积就占整个圆面积的几分之几
45˚
我的收获：
圆上A、 B两点间的部分叫做弧，读作弧AB
一条弧和经过这条弧两端的两条半径所围
成的图形叫做扇形，扇形是圆的一部分
扇形都有一个角，角的顶点在圆心。
顶点在圆心的角叫圆心角
判断一个角是不是圆心角必须满足两个条件：
1.顶点必须在圆心。
2.角的两边必须是圆的两条半径。
①以圆心为顶点构成圆心角；
②角的两边是半径；
③曲线是圆上的一段弧。
4.在同一个圆中，扇形的大小与其圆心角的大小有关。
练一练
1.下面哪个图形中的涂色部分是扇形？
第三、四个图形中的涂色部分是扇形。
2. 下面图形中哪些角是圆心角？在（ ）里画√。




（√）
⌒








（
）
（
）
根据圆心角的定
义特征来判断。
A 30°
①画一个圆。
②画30°、60°、90°、120°的圆心角。
D
120°
结论：在同一个圆中，扇形的大小与其圆心角的大
小有关。圆心角大，所对应的扇形就大；圆心角小，
所对应的扇形就小。
1.扇形是由两条半径和圆上的一段曲线围成的图形。
2.扇形都有一个角，角的顶点是圆心，即圆心角。
3.判定一个图形是扇形，要牢记以下三点：
圆和扇形
扇 形
1.经历观察、讨论等初步认识扇形的过程。
2.知道扇形，初步了解扇形的特征，能在圆中画出扇形。
3.体会扇形和圆的关系，感受扇形图与名称的联系，发展空间
观念。
重难点
能在圆中画出扇形。
观察各圆中涂色的部分，说一说它们的形状像什么。

扇形与其他图形的组合
扇形可以与其他图形进行组合，形成更复杂的几何图形，如圆锥、 圆柱等。
扇形的变形和拓展
通过对扇形的变形和拓展，可以得到更多有趣的几何图形，如弓形、 环形等。
25
思考题与练习题
2024/1/29
思考题
请思考扇形面积和周长的计算公式是 如何推导出来的？这些公式在实际应 用中有哪些限制？
扇形与相交圆的组合
两个相交圆的交点位于扇形的弧上，通过计算扇形的面积和两个相交圆的面积，可 以得到组合图形的总面积。同时，还可以利用相交圆的性质求解一些与扇形相关的 几何问题。
22
PART 06
总结回顾与拓展延伸
REPORTING
2024/1/29
23
总结回顾本次课程重点内容
扇形的定义和性质
扇形是由两个半径和一个圆弧所围成的图形，具有特定的面积和 周长计算公式。
圆心角和弧度的关系
圆心角的大小决定了扇形的面积和周长，而弧度则是圆心角的度量 单位。
扇形的面积和周长计算
通过给定的圆心角和半径，可以计算出扇形的面积和周长。
2024/1/29
24
拓展延伸：探索更多扇形相关的知识领域
2024/1/29
扇形的应用
扇形在日常生活和工业生产中有着广泛的应用，如风扇叶片、汽 车轮胎等。
练习题
请计算给定半径和圆心角的扇形的面 积和周长，并比较不同半径和圆心角 对扇形面积和周长的影响。同时，尝 试探索扇形面积和周长与半径和圆心 角之间的函数关系。
26
THANKS
感谢观看
REPORTING
2024/1/29
27
扇形面积公式的应用 利用扇形面积公式可以计算出任意大小、任意中心角的扇 形的面积，为几何学和物理学等领域的研究提供了便利。

圆和扇形（一）【知识概述】1、圆：（1）圆心决定圆的位置，圆的半径决定圆的大小。

（2）圆是轴对称图形，任何一条直径所在的直线都是圆的对称轴，一个圆有无数条对称轴。

圆周长公式：C=πd 或C=2πr 。

圆面积公式：2r S π=。

圆环面积：)(22r R S -=π环图一 图二 图三2、扇形：如上图二，连接两条半径OA 、OB ，就可得到一个扇形OAB ，扇形面积公式是：S=3602r n π。

扇形的圆弧长=所在圆周长的。

其中r 是指扇形的在圆的面积，n 指的是圆心角的度数。

【例1】一个大圆内有三个大小不等的小圆．这些小圆的圆心在大圆的同一条直径上，连同大圆在内每相邻的两个圆都相切．已知大圆的周长是10厘米，求这三个小圆的周长之和．【例2】右面图形的周长是多少厘米？O12厘米【例3】街心花园中圆形花坛的周长是18.84米。

花坛的面积是多少平方米？【例4】图二中n=60°，半径为6厘米，扇形面积是多少？弧AB 是多少？【例5】、图三中，直角三角形AOC 的直角边OA= 6厘米，求弓形AC 的面积。

【例5】如图，圆的周长是24厘米，圆的周长与长方形ABCO 的周长恰好相等，求阴影部分的周长。

A B CD O【例6】半径分别为2厘米和3厘米两个半圆摆放如下图，求阴影部分的周长。

4厘米6厘米【例7】正方形ABCD的边长为1厘米，依次以A、B、C、D为圆心，以AD、BE、CF、DG为半径画出扇形，求阴影部分的周长。

【例8】计算下图阴影部分的面积．(单位：厘米)【例9】在一块长4.5米，宽2米的长方形铁板上截下2个最大的圆形后，剩下的铁板面积是多少平方米？【例10】从一块边长10厘米的正方形铁皮上剪下一个最大的圆，这块圆形铁皮的面积是多少平方厘米？剩下的面积是多少？【例11】从一个直径为10厘米的圆中，剪去一个最大的正方形，正方形面积是多少？【例12】求下图的面积和周长。

(单位：厘米)练一练:求下面组合图形的面积和周长．(长度单位：厘米)练习一、基本题1、一个圆形花坛的周长是25.12米。

圆扇形面积公式圆是数学中的一个重要概念，它是指平面上距离一点固定距离的所有点的集合。

圆的面积公式是数学中的基本公式之一，用来计算圆的面积。

在圆的面积公式中，另一个与之密切相关的公式是扇形的面积公式。

下面将分别对圆和扇形的面积公式进行详细介绍。

接下来，我们来讨论扇形的面积公式。

扇形是圆中的一部分，它是由一条弧和两条半径所夹的区域组成。

扇形的面积公式可以通过圆的面积公式来计算。

假设圆的半径为r，扇形的圆心角为θ（单位为弧度），那么扇形的面积公式可以表示为：A=（θ/2π）πr²，其中A表示扇形的面积，θ表示扇形的圆心角。

根据这个公式，我们可以通过圆的半径和扇形的圆心角来计算扇形的面积。

在实际应用中，圆和扇形的面积公式经常被用到。

例如，在建筑设计中，通过圆形的面积可以计算出需要铺设的地板面积；在工程测量中，通过扇形的面积可以计算出需要开挖的土方量。

这些实际问题都可以通过圆和扇形的面积公式来解决。

除了面积公式，圆和扇形还有其他一些重要的性质和公式。

例如，圆的周长公式是：C=2πr，其中C表示圆的周长。

扇形的弧长公式是：L=（θ/2π）2πr，其中L表示扇形的弧长。

这些公式在实际应用中同样经常被用到。

总结起来，圆的面积公式是通过半径来计算圆的面积的，扇形的面积公式是通过圆的面积公式来计算扇形的面积的。

圆和扇形的面积公式在实际应用中有着广泛的用途，可以帮助我们解决各种问题。

在学习和应用中，我们需要深入理解并掌握圆和扇形的面积公式，以便更好地应用于实际问题中。

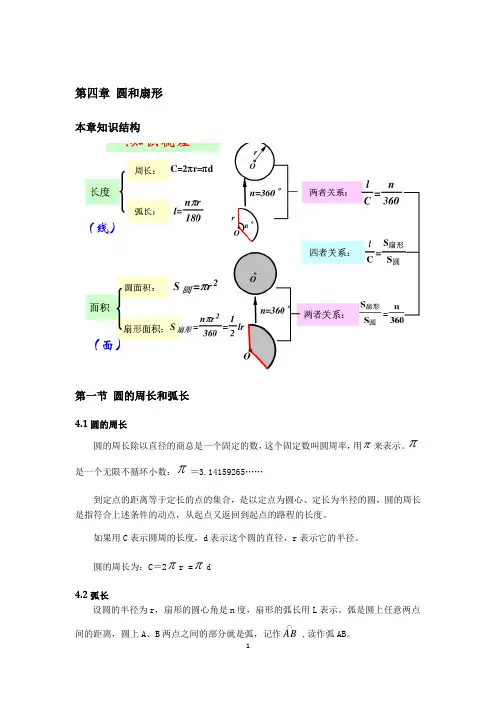
第四章圆和扇形本章知识结构第一节圆的周长和弧长4.1圆的周长圆的周长除以直径的商总是一个固定的数，这个固定数叫圆周率，用π来表示。

π是一个无限不循环小数：π＝3.14159265……到定点的距离等于定长的点的集合，是以定点为圆心、定长为半径的圆，圆的周长是指符合上述条件的动点，从起点又返回到起点的路程的长度。

如果用C表示圆周的长度，d表示这个圆的直径，r表示它的半径。

圆的周长为：C＝2πr =πd4.2弧长设圆的半径为r，扇形的圆心角是n度，扇形的弧长用L表示。

弧是圆上任意两点间的距离，圆上A、B两点之间的部分就是弧，记作⋂AB ,读作弧AB。

1802360110r r ππ=⨯=圆心角所对的弧长； 18023600rn r n L n ππ=⨯=圆心角所对的弧长。

第二节 圆和扇形的面积4.3圆的面积2r S π=圆的面积4.4扇形的面积由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形。

设组成扇形的半径为r ，圆心角为0n ，弧长为l ，扇形的面积:S ＝360n ×πr 2＝21Lr本章最重点内容本章是圆与扇形，掌握圆的周长的计算公式和弧长的概念，会计算圆的面积及扇形的面积，是我们学习的重点。

1．圆的周长公式：r d C ⋅=⋅=ππ2． 2．弧长公式：180360rdl ⋅=⋅=ππ．3．圆的面积公式：2r S ⋅=π 4．扇形面积公式：lr r n S 213602=⋅=π扇． 5．特别地：360n C l =，360n S S =扇，即：SSC l 扇=． 本章错题集【结合个人平时作业具体情况总结、整理、添加】1．如图，一个半径为1厘米的小圆盘沿着一个半径为4厘米的大圆盘外侧做无滑动的滚动。

当小圆盘的中心围绕大圆盘中心转动90度后，小圆盘运动过程中扫过的面积是多少平方厘米？(3π=)【答案】：小圆盘运动过程中扫过的面积由两部分组成，即两半圆加四分之一环形。

2221(64)418S πππ=⨯+⨯-⨯÷=平方厘米。

圆面积扇形面积公式圆是几何中的基本图形之一，它有许多重要的性质和公式。

其中，圆的面积和扇形的面积是我们经常需要计算的。

本文将介绍圆的面积和扇形的面积公式，以及它们的应用。

1. 圆的面积公式圆的面积公式是数学中最基本且最重要的公式之一。

在计算圆的面积时，我们需要知道圆的半径。

圆的半径是从圆心到圆上任意一点的距离，通常用字母r表示。

圆的面积公式为：S = πr^2，其中π是一个常数，约等于3.14159。

例如，如果一个圆的半径是5厘米，那么它的面积就是：S = 3.14159 * 5^2 = 78.54平方厘米。

2. 扇形的面积公式扇形是圆的一部分，它由圆心、圆弧和两条半径组成。

计算扇形的面积时，我们需要知道扇形的圆心角和圆的半径。

扇形的面积公式是：S = (θ/360) * πr^2，其中θ是扇形的圆心角，可以用度数或弧度表示。

例如，如果一个扇形的圆心角是60度，半径是5厘米，那么它的面积就是：S = (60/360) * 3.14159 * 5^2 = 13.09平方厘米。

3. 圆与扇形的应用圆和扇形的面积公式在日常生活和工作中有广泛的应用。

以下是一些例子：(1) 建筑设计：在建筑设计中，圆和扇形的面积公式可以用来计算房间的面积、花坛的面积等。

(2) 圆桌布料：如果我们知道圆桌的直径或半径，可以利用圆的面积公式计算所需的桌布面积，以便购买合适尺寸的桌布。

(3) 园艺设计：在园艺设计中，扇形的面积公式可以用来计算花坛或草坪的面积，以便购买足够的土壤或草坪。

(4) 圆形广告牌：如果我们想在一个圆形广告牌上放置广告，可以利用扇形的面积公式计算广告的面积，帮助我们确定广告的尺寸和设计。

总结：圆的面积和扇形的面积是几何中重要的概念和公式。

圆的面积公式是S = πr^2，扇形的面积公式是S = (θ/360) * πr^2，其中θ是扇形的圆心角。

这些公式在日常生活和工作中有广泛的应用，可以帮助我们计算房间面积、购买桌布、设计花坛等。

冀教版数学六年级上册第一单元
圆和扇形
1.量一量圆的半径和直径。
2.圆中心的一点叫做（ 圆心 ），用 字母（ O ）表示，它到圆上任意
一点的距离都（ 相等 ）。
3.画圆时，圆规两脚间的距离是圆 的（ 半径 ）。
4.要画一个直径是5厘米的圆，圆规
两尖端之间的距离应定为（ 2.5 ） 厘米。
5.用圆规或其他工具画圆。
挫折的名言 1、 我觉得坦途在前，人又何必因为一点小障碍而不走路呢？——鲁迅 2、 “不耻最后”。即使慢，弛而不息，纵会落后，纵会失败，但一定可以达到他所向的目标。——鲁迅 3、 故天将降大任于是人也，必先苦其心志，劳其筋骨，饿其体肤，空乏其身，行拂乱其所为，所以动心忍性，曾益其所不能。 战胜挫折的名言 1、卓越的人一大优点是：在不利与艰难的遭遇里百折不饶。——贝多芬 2、每一种挫折或不利的突变，是带着同样或较大的有利的种子。——爱默生 3、我以为挫折、磨难是锻炼意志、增强能力的好机会。——邹韬奋 4、斗争是掌握本领的学校，挫折是通向真理的桥梁。——歌德 激励自己的座右铭 1、 请记得，好朋友的定义是：你混的好，她打心眼里为你开心；你混的不好，她由衷的为你着急。 2、 要有梦想，即使遥远。 3、 努力爱一个人。付出，不一定会有收获；不付出，却一定不会有收获，不要奢望出现奇迹。 4、 承诺是一件美好的事情，但美好的东西往往不会变为现实。 工作座右铭 1、 不积跬步，无以至千里；不积小流，无以成江海。——《荀子劝学》 2、 反省不是去后悔，是为前进铺路。 3、 哭着流泪是怯懦的宣泄，笑着流泪是勇敢的宣言。 4、 路漫漫其修远兮，吾将上下而求索。——屈原《离骚》 5、 每一个成功者都有一个开始。勇于开始，才能找到成功的路。 国学经典名句 1、知我者，谓我心忧，不知我者，谓我何求。（诗经王风黍离） 2、人而无仪，不死何为。 （诗经风相鼠） 3、言者无罪，闻者足戒。 （诗经大序） 4、他山之石，可以攻玉。 （诗经小雅鹤鸣） 5、投我以桃，报之以李。 （诗经大雅抑） 6、天作孽，犹可违，自作孽，不可活。（尚书） 7、满招损，谦受益。 （尚书大禹谟） 青春座右铭 1、爱的力量大到可以使人忘记一切，却又小到连一粒嫉妒的沙石也不能容纳。 2、把手握紧，什么也没有；把手伸开，你就拥有了一切。 3、不在打击面前退缩，不在困难面前屈服，不在挫折面前低头，不在失败面前却步。勇敢前进！ 4、当你能飞的时候就不要放弃飞。 5、当你能梦的时候就不要放弃梦。 激励向上人生格言 1、实现自己既定的目标，必须能耐得住寂寞单干。 2、世界会向那些有目标和远见的人让路。 3、为了不让生活留下遗憾和后悔，我们应该尽可能抓住一切改变生活的机会。 4、无论你觉得自己多么的不幸，永远有人比你更加不幸。 5、无论你觉得自己多么的了不起，也永远有人比你更强。 6、打击与挫败是成功的踏脚石，而不是绊脚石。 激励自己的名言 1、忍别人所不能忍的痛，吃别人所别人所不能吃的苦，是为了收获得不到的收获。 2、销售是从被别人拒绝开始的。 3、好咖啡要和朋友一起品尝，好机会也要和朋友一起分享。 4、生命之灯因热情而点燃，生命之舟因拼搏而前行。 5、拥有梦想只是一种智力，实现梦想才是一种能力。 6、有识有胆，有胆有识，知识与胆量是互相促进的。 7、体育锻炼可以（有时可以迅速）使人乐观（科学实验证明）。 8、勤奋，机会，乐观是成功的三要素。（注意：传统观念认为勤奋和机会是成功的要素，但是经过统计学和成功人士的分析得出，乐观是成功的第三要素） 9、自信是人格的核心。 10、获得的成功越大，就越令人高兴。

圆和扇形九年级知识点圆和扇形是九年级数学中的重要知识点之一，下面我们来详细了解一下。

一、圆的基本概念1. 圆的定义：圆是平面上所有到圆心距离相等的点的集合。

2. 圆的元素：圆心、半径、直径、弧、弦、圆周等。

3. 圆的性质：a. 圆心角：以圆心为顶点的角，圆心角的度数为所对弧的度数。

b. 弧度制和角度制：弧度制是角度的另一种计量单位，360度对应2π弧度。

c. 圆周角：等于360度或2π弧度。

d. 弧长：圆的一部分弧的长度。

e. 弦长：连接圆上两点的线段长度。

二、扇形的性质和计算1. 扇形的定义：由圆心角和弧段组成的图形称为扇形。

a. 扇形圆心角的度数等于对应的弧的度数。

b. 扇形的面积等于圆的面积乘以扇形圆心角的度数除以360。

c. 扇形的弧长等于圆的周长乘以扇形圆心角的度数除以360。

3. 扇形的计算实例：如图所示，已知半径为r的圆的圆心角为θ，求扇形的面积和弧长。

解：扇形的面积等于πr²乘以θ的度数除以360，即S=πr²(θ/360)。

扇形的弧长等于2πr乘以θ的度数除以360，即L=2πr(θ/360)。

三、九年级数学应用题中的圆和扇形1. 圆的周长和面积的应用：a. 计算圆的周长：C = 2πr，其中r为圆的半径。

b. 计算圆的面积：S = πr²，其中r为圆的半径。

c. 解决与圆的周长和面积相关的实际问题，如园艺设计、建筑规划等。

a. 计算扇形的面积：S = (θ/360)πr²，其中θ为扇形圆心角的度数，r为扇形的半径。

b. 计算扇形的弧长：L = (θ/360) × 2πr，其中θ为扇形圆心角的度数，r为扇形的半径。

c. 解决与扇形面积、扇形弧长相关的实际问题，如计算扇形区域的面积和绳索的长度等。

综上所述，圆和扇形是九年级数学中的重要知识点，通过深入了解圆和扇形的定义、性质以及应用，我们可以更好地解决与它们相关的数学问题，同时也能在实际生活中灵活运用这些知识。

1. 圆的半径长扩大到原来的3倍，圆的面积也扩大到原来的3倍2. 半径长为2厘米的圆的周长与面积相等3. 若甲圆的周长是乙圆周长的13，那么甲圆的面积也是乙圆面积的13练习：1. 一个圆的半径扩大3倍，则下列结论正确的是（）A 圆直径扩大6倍B圆周长扩大6倍C圆面积扩大3倍D圆面积扩大9倍2. 如果大圆的半径是小圆的直径，则小圆的面积是大圆面积的（填几分之几）例4如图，已知外圈的周长是内圈的4倍，外圆的周长是50.24cm，求阴影部分的面积。

练习：1. 已知两圆周长之和是40 厘米，且小圆半径是大圆半径的23，求两圆的面积2. 环形的外圆周长是18.84厘米，内圆直径是4厘米，则环形的面积是例5用三根同样长的铁丝分别围成圆、正方形、长方形，这三个图形中，面积最大的是（）A 圆 B 正方形 C 长方形 D三者相等练习：1. 一张长方形纸片长10厘米，宽9厘米，在这张纸片中剪出一个最大的圆，这个圆的面积是。

例6以三角形ABC的三个顶点为圆心，以10毫米长为半径，在三角形ABC内画弧可得三条弧，阴影部分的面积是例7 已知小圆的半径是6，大圆的半径是8，AOC BOC AOB ∠∠∠,,都为120°，三角形面积为93，且被均匀的分成了3份，求阴影部分的面积。

（π取3）练习：已知下图圆C 的半径与圆B 的半径相加正好是圆A 的半径，若圆C 与圆B 的半径比试3:4，求白色部分的面积与阴影部分的面积之比是多少（π取3）考点2 扇形面积例1 圆心角为n °的扇形的面积是它所在圆面积的 （填几分之几）CE1D1考点4 扇形图例：一所中学准备搬迁到新校舍，在迁入新校舍之前就该校500名学生如何到新校舍的问题进行了一次调查，得到如下数据：步行90人，骑自行车160人，坐公共汽车220人，其他30人，请算出各部分学生数占学生总数的百分比，并用扇形统计图表示。

考点5综合性应用题例1钟表问题台钟的时针长10厘米，从早上7点到中午12点，则时针扫过的面积是练习：1. 三点十五分，时针与分针的夹角是2. 时针长5厘米，分针长8厘米，秒针长1分米，从上午9点到上午10点40分，时针、分针扫过的面积分别是多少平方厘米？例2 箭靶问题射箭运动的箭靶由10个同心圆组成，两个相邻的同心圆半径之差等于最里面小圆的半径，最里面的小圆是10环，最外面的圆环是1环，问：（1）10环面积是1环面积的几分之几？（2）9环面积是1环面积的几分之几？例3 图形运动1. 如图，一只羊被栓在边长均为3米的三角形建筑物墙角A处，周围都是草地，绳长4米，（1）求羊所能吃到草的地方的总面积；（2）如果有一堆鲜草距A处有4.1米，请问这只羊能够吃到这堆鲜草吗？【自我测试】1. 在一个周长为100毫米的硬纸正方形内，要剪下一个最大的圆，这个圆的周长和面积分别是_______。

A BO圆和扇形章节复习内容分析圆和扇形是初中数学六年级第四章的内容，同学们需要学会用圆的周长、面积、弧长和扇形面积公式进行简单的计算，并体会近似与精确的数学思想．难点是圆的组合图形的面积计算，同学们需要灵活运用各个基本图形面积的计算方法，并能看出组合图形是由哪些基本图形组成，从而进行相关的计算． 知识精讲基本内容注意点4.1 圆的周长 1、圆的周长公式及应用． 4.2 弧长 1、弧长公式及应用． 4.3 圆的面积 1、圆的面积公式及应用． 4.4 扇形的面积1、扇形的面积公式及应用；2、*圆的组合图形的面积计算．圆一：圆的周长1、 圆的周长通过操作和计算，我们发现圆的周长都是直径的固定的倍数，我们把这个倍数叫做圆周率，用字母π表示，π读作“pai”；圆周率π是个无限不循环小数， 3.14π≈．圆的周长÷直径 = 圆周率．用字母C 表示圆的周长，d 表示直径，r 表示半径，那么：C d π=或2C r π=二：弧长1、弧和圆心角的概念如图，圆上A 、B 两点之间的部分就是弧，记作：AB ，读作：弧AB ；AOB ∠称为圆心角．ABO2、弧长公式设圆的半径长为r ，n °圆心角所对的弧长是l ，那么：180nl r π=． 三：圆的面积1、 圆的面积圆所占平面的大小叫做圆的面积．设圆的半径长为r ，面积为S ，那么：圆的面积2S r r r ππ=⨯=．四：扇形的面积1、 扇形的概念由组成圆心角的两条半径和圆心角所对的弧围成的图形，叫做扇形． 如图，空白部分记作扇形AOB ． 2、 扇形的面积设组成扇形的半径为r ，圆心角为n °，弧长为l ，那么：213602n S r lr π==扇形．五：圆的组合图形1、三角形的面积 =2⨯底高． 2、等腰直角三角形的面积 =24=直角边的平方斜边的平方． 3、长方形的面积 =⨯长宽． 4、正方形的面积 = 边长的平方 = 2对角线的平方．5、菱形的面积 =2对角线之积．6、梯形的面积 =()2⨯上底+下底高．7、圆的面积 =π⨯半径的平方． 8、扇形的面积 =360π⨯⨯︒圆心角半径的平方．例题解析【例1】 圆的周长是这个圆半径的（ ）倍A ．6B ．2πC ．3.14D ．6.28【难度】★【答案】B 【解析】圆的周长公式2l r π=，所以周长是半径的2π倍． 【总结】考查圆的周长与半径的关系．【例2】 同一个圆里，直径与半径的比是______．【难度】★【答案】2:1．【解析】直径是半径的两倍，所以比是2:1． 【总结】考查同一个圆的直径与半径的关系．【例3】 要画一个周长为18.84厘米的圆，它的半径应取______厘米． 【难度】★【答案】3．【解析】18.84 3.1423÷÷=厘米． 【总结】考查圆的周长公式的应用．【例4】 如果圆的半径缩小到它的13，那么圆的周长缩小到原来的______．【难度】★【答案】13．【解析】由2l r π=可知圆的周长与半径成正比，所以周长也缩小到原来的13．【总结】考查圆的周长的计算．【例5】 如果圆上一条弧长占圆周长的15，那么这条弧所对的圆心角占圆的周角的______．【难度】★【答案】72︒．【解析】由180n r l π=可知，弧长与圆心角成正比，故圆心角为：1360725⨯=．【总结】考查弧长公式的运用．【例6】 圆心角为45°的扇形，如果拼成一个圆，需要这样的扇形至少____个． 【难度】★【答案】8．【解析】360458÷=． 【总结】考查扇形与圆的关系．【例7】 下列叙述中正确的个数是（ ） （1）弧的长度只取决于弧所在圆的半径大小；（2）两条弧的长度相等，则它们所对的圆心角相等；（3）圆心角扩大3倍，而圆的半径缩小13，那么原来的弧长不变．A ．0B ．1C ．2D ．3【难度】★【答案】B【解析】由180n rl π=，可知弧长取决于圆心角和半径，所以（1）、（2）都错，弧长与半径和圆心角都成正比，所以（3）对．【总结】考查对弧长公式的理解及决定弧长的量．【例8】 一个扇形的面积是它所在圆面积的79，这个扇形的圆心角是______度． 【难度】★【答案】280．【解析】因为213602n S r lr π==扇形，所以°°73602809n =⨯=． 【总结】考查扇形的面积与圆心角的关系．【例9】 一个圆的周长为9.42厘米，那么这个圆的面积是______平方厘米． 【难度】★★ 【答案】27.065cm ．【解析】9.42 3.142 1.5r cm =÷÷=半径，所以面积为：23.14 1.5 1.57.065cm ⨯⨯=． 【总结】考查圆的周长与面积的计算．【例10】 把一根长314厘米的细钢丝绕在一个圆筒上，正好绕10周，这个圆筒的半径是（ ）A ．5B ．10C ．20D ．3.14【难度】★★【答案】A 【解析】31410 3.1425÷÷÷=． 【总结】考查圆的周长在实际问题中的应用．【例11】 在一个边长为8厘米的正方形内画一个最大的圆，这个圆的周长是______厘米． 【难度】★★【答案】8π．【解析】圆的直径等于正方形的边长，所以周长是8d ππ=． 【总结】考查圆的周长的计算．【例12】 有一个直径是8厘米的半圆形铁片，这个铁片的周长是______厘米． 【难度】★★【答案】20.56cm ．【解析】28 3.1482820.56d cm π÷+=⨯÷+=． 【总结】考查半圆的周长，半圆的周长等于半圆加上直径的长．．【例13】 一个环形纸板，内圆半径是3厘米，外圆直径是10厘米，这个环形纸板的面积是3厘米______平方厘米．【难度】★★【答案】16π．【解析】外圆半径是5厘米，故圆环面积为：225316ππ-=（）平方厘米． 【总结】考查圆环的面积的计算，大圆面积减去小圆面积．【例14】 下列说法正确的是（ ） A ．扇形是圆的一部分，圆的一部分是扇形 B ．圆中任意画两条半径，一定能构成两个扇形 C ．如果圆的面积扩大9倍，那么圆的直径扩大9倍D ．在所有扇形中，圆半径大的面积大【难度】★★【答案】B【解析】圆的一部分不一定是扇形；圆的面积扩大9倍，直径扩大3倍；扇形的面积与圆心角和半径都有关．【总结】考查圆和扇形的关系及圆的面积与直径的关系．【例15】 已知大扇形的面积是小扇形面积的94倍，如果它们的圆心角相等，那么小扇形的半径是大扇形半径的______．【难度】★★【答案】23．【解析】扇形的面积与半径的平方成正比，所以小扇形的半径是大扇形半径的23． 【总结】考查扇形的面积与半径的关系．【例16】 已知扇形的弧长是9.42厘米，圆心角是270°，那么这个扇形的面积是______平方厘米【难度】★★【答案】237.68cm ．【解析】扇形的半径为：9.42180270 3.142cm ⨯÷÷=， 故扇形的面积为：22703.1429.42360⨯⨯=2cm ． 【总结】考查扇形的弧长与扇形的面积的计算，注意公式的准确运用．【例17】 图中的三角形是等边三角形，阴影部分是一个扇形，那么阴影部分的面积是______平方厘米．【难度】★★【答案】152π平方厘米． 【解析】23001533602S ππ=⨯⨯=阴影平方厘米． 【总结】考查扇形的面积，注意本题中圆心角度数为300°．【例18】 ．下面两个图形中，其中正方形的面积相等，那么阴影部分面积大小关系是（ ） A ．甲 > 乙 B ．甲 < 乙C ．甲 = 乙D ．无法比较【难度】★★【答案】C【解析】乙的四个扇形恰好组成一个圆． 【总结】本题主要考查对阴影部分的面积的计算．【例19】 要画一个面积是3.14平方厘米的圆，圆规两脚之间的距离要取______厘米． 【难度】★★【答案】1．【解析】圆规两脚间的距离就是圆的半径，2 3.14 3.1411r r =÷==，所以厘米． 【总结】考查利用圆的面积求圆的半径．【例20】 在周长为24厘米的正方形纸片上剪去一个最大的圆，则剩余部分的周长是______厘米，面积是______平方厘米．（结果保留π）．【难度】★★【答案】42.84；7.74．【解析】剩余部分的周长是正方形的周长加上圆的周长，剩余部分的面积是正方形面积减去圆的面积，而最大圆的直径为正方形的边长，因为正方形的周长为24厘米，故边长为6厘米，即636d r C d ππ====圆，，故厘米，24C =正方形厘米， 所以剩余部分周长为：62418.842442.84π+=+=厘米，面积为226633697.74r πππ=⨯-⨯=-=平方厘米．【总结】考查圆的周长与面积的计算，注意正方形中剪出的最大圆的直径即为正方形的边长．【例21】 如图，阴影部分周长相同的有（ ） A ．1个 B ．2个 C ．3个 D ．4个【难度】★★【答案】D【解析】阴影部分的周长都等于大半圆的长加小半圆的长，每个图中都只有一个大半圆， 所有的小半圆周长也相等，所以四个阴影部分周长都相等，故选D ． 【总结】考查阴影部分的周长的计算．【例22】 如图，正方形中，分别以两个对角顶点为圆心，以正方形的边长6为半径画弧，形成树叶形的图案（阴影部分），求树叶形图案的周长．【难度】★★【答案】18.84．【解析】树叶形的周长是半径为6的半圆的周长，所以618.84C r ππ===．ABCD A B CD【总结】考查阴影部分的周长的计算，注意认真分析图形的特征．【例23】 扇形的面积是314平方厘米，扇形所在的圆的面积是1256平方厘米，这个扇形的圆心角是多少度？【难度】★★【答案】90︒．【解析】扇形的面积与圆心角成正比，所以314360901256⨯=︒．【总结】考查扇形的面积与圆心角的关系．【例24】 如图，AB = BC = CD = 2厘米，分别求出大、中、小圆的周长和面积． 【难度】★★【答案】642C C C πππ===小大中厘米，厘米，厘米；94S S S πππ===小大中平方厘米，平方厘米，平方厘米． 【解析】64C d C d ππππ====大大中中厘米，厘米， 2C d ππ==小小厘米，2r S ππ==小小平方厘米，22r 9r 4S S ππππ====大大中中平方厘米，平方厘米．【总结】考查圆的周长和面积的计算．【例25】 如图，四边形ABCD 是长方形，AB = 12 cm ，求图中阴影部分的面积． 【难度】★★ 【答案】28.26cm 2． 【解析】6AD BC cm ==， 212672cm S S =⨯==长半圆，226218cm ππ⨯÷=，()()211367218928.26cm 22ABD S S S S ππ=--=--==△阴影长半圆． 【总结】考查阴影部分面积的计算，注意用规则图形的面积去表示不规则图形的面积． 【例26】 一辆自行车轮胎的外直径是0.7米，如果车轮每分钟转90周，40分钟能行多远？通过一座567米的大桥需要多少分钟？（π取3）【难度】★★【答案】76503米，分．【解析】40分钟能行：30.790407560⨯⨯⨯=米，需要时间：5671893÷=分．【总结】考查圆的周长的在实际问题中的应用．【例27】 在长19厘米，宽9厘米的长方形纸片中，剪半径都是1.5厘米的小圆，共可剪出小圆多少个？剪去这些小圆后，剩下的边角料的总面积是多少？．【难度】★★【答案】43.83平方厘米． 【解析】9 1.523÷⨯=（）， 19 1.5261÷⨯=（），所以可剪出3618⨯=个圆，剩下的面积是：219918 1.517140.543.83ππ⨯-⨯⨯=-=平方厘米． 【总结】考查长方形中剪出圆的问题，注意认真分析．【例28】 四个半径为2厘米的圆围成的图形中，求阴影部分的面积和周长．【难度】★★【答案】3.44平方厘米，12.56厘米．【解析】面积：2442164 3.44ππ⨯-⨯=-=平方厘米； 周长：222412.56r πππ=⨯⨯==厘米．【总结】考查阴影部分的周长与面积的计算，注意观察阴影部分图形的特征．【例29】 如图，圆的周长为6.28厘米，圆的面积与长方形的面积正好相等，图中阴影部分的周长是______厘米．【难度】★★★ 【答案】7.85厘米．【解析】圆的半径为：6.28 3.1421÷÷=厘米，则2r 3.14S S π===圆长方形平方厘米， 故长方形的长为：3.141 3.14÷=厘米，所以阴影部分的周长为：()3.1412 6.28427.85cm +⨯+÷-=厘米．【总结】考查阴影部分的周长的计算，注意此周长包含了四分之一的弧长和三条线段长． 【例30】 两个连在一起的皮带轮，其中一个轮子直径是3 dm ，当它旋转7周时，另一个轮子转了5周，则另一个轮子的半径是______dm ．【难度】★★★【答案】4.2．【解析】由题意，可得另一个轮子的半径为：375 4.2⨯÷=dm ． 【总结】本题中要找到两个轮子转动的距离的关系，然后再计算即可．【例31】 将一个圆沿半径剪开，再拼成一个近似长方形，已知这个长方形的周长是41.4厘米，那么，这个圆的周长和面积各是多少？【难度】★★★【答案】31.4厘米，78.5平方厘米．【解析】圆的半径为：41.42 3.1415÷÷+=（）厘米，故圆的周长为：2 3.14531.4⨯⨯=厘米，圆的面积为：3.145578.5⨯⨯=平方厘米．【总结】考查圆的周长与面积的计算．拥有2台拥有1台20% 其他【例32】 在一次对某小区500户家庭拥有电视机的数量的调查中，调查结果如图所示，根据图中所给的信息回答问题：（1）家中拥有一台电视机的家庭有几户？（2）如果拥有一台电视机的家庭数正好是拥有2台电视机的家庭数的27，那么拥有2台电视机的家庭有几户？（3）图中的“其他”的扇形的圆心角是几度？【难度】★★★【答案】（1）100户；（2）350户；（3）36． 【解析】（1）()50020%100⨯=户； （2）21003507÷=（户）； （3）()35050070%360120%70%36÷=⨯--=︒，． 【总结】考查有关扇形图的简单计算．课后作业【作业1】 若一弧的长是它所在圆的周长的15，则此弧所对的圆心角是______度．【难度】★【答案】72．【解析】弧长与圆心角成正比，1360725⨯=．【总结】考查弧长与圆心角的关系．【作业2】 如果一条弧所对的圆心角缩小为原来的14，所在圆的半径扩大为原来的3倍，那么所得的新弧长与原来的弧长之比是______．【难度】★【答案】3:4．【解析】180nl r π=，弧长与圆心角、半径成正比，所以比为3:4． 【总结】考查弧长与圆心角和半径的关系．【作业3】 甲圆与乙圆的半径之比是 2 : 3，则甲与乙的直径之比是______，周长之比是______，面积之比是______．【难度】★【答案】2：3，2：3，4：9．【解析】半径比等于直径比等于周长比，面积比等于半径比的平方． 【总结】考查圆中各个基本量之间的关系． 【作业4】 下列说法正确的个数是（ ） （1）半径越大，圆的面积越大； （2）半径越大，所对的弧越长； （3）弧是圆上两点间的一条线段； （4）圆心角相等，它们所对的弧长也相等．A ．1个B ．2个C ．3个D ．4个【难度】★★【答案】A【解析】2S r π=，圆的面积只与半径有关，（1）√；180nl r π=弧长与半径和圆心角都有关系；（2）×； （3）×； （4）×，弧长与半径和圆心角都有关．【总结】考查弧长的影响因素． 【作业5】 求下列各圆的周长和面积： （1）r = 3，C =______，S =______； （2）d = 8，C =______，S =______；（3）l = 5，n = 72°，S =______．【难度】★★【答案】（1）C = 9.42，S = 28.26；（2）C = 25.12，S = 50.24； （3）S = 49.76．【解析】222360nC r S r S r πππ===，，．【总结】考查圆的周长与面积的计算．【作业6】 求下列弧的弧长：（1）r = 4，n = 90°，l =______；（2）d = 9，n = 120°l =______； （3）C = 20，n = 175°l =______．【难度】★★【答案】（1）6.28；（2）9.42；（3）9.72．【解析】（1）9042180180n l r πππ==⨯==6.28，（2）91209239.4221802r d l ππ=÷==⨯==，； （3）10175101759.72218018C r l ππππ===⨯=≈，．【总结】考查弧长的计算． 【作业7】 在长是6厘米，宽是4厘米的长方形内剪一个最大的圆，则圆的面积是______平方厘米【难度】★★【答案】12.56．【解析】圆的直径等于4厘米，2412.56S r ππ===平方厘米．【总结】考查圆的面积的计算．【作业8】 用一根长为37.68厘米的铅丝围成一个圆，圆的面积是______平方厘米．【难度】★★【答案】113.04平方厘米．【解析】237.68 3.142636113.04r S r ππ=÷÷====厘米，平方厘米．【总结】本题中铁丝的总长度就是所围成的圆的周长，从而算出半径和面积．【作业9】 一个圆环形纸片，外环半径6厘米，内环半径5厘米，这个圆环的面积是______平方厘米，周长是______厘米．【难度】★★【答案】34.54；69.08．【解析】221236251134.54S r r πππππ=-=-==圆环平方厘米；()1222269.08C r r ππ=+==圆环厘米．【总结】考查圆环的面积与周长的计算．【作业10】 已知一个扇形的半径是6厘米，圆心角是120°，则此扇形的周长是______厘米．【难度】★★【答案】24.56厘米． 【解析】1202261241224.56180180n C l r r r πππ=+=+=⨯+=+=扇厘米． 【总结】考查扇形周长的计算，注意扇形的周长还要包含两条半径的长．【作业11】 扇形的半径是6分米，扇形的弧长是4π分米，这段弧所对的圆心角是______度，这个扇形的面积是______平方分米．（结果保留π）【难度】★★【答案】120，12π． 【解析】180********l n r πππ⨯===，212012360S r ππ==平方分米． 【总结】考查扇形的圆心角和面积的计算．A B O A BCD B C D 【作业12】 一个时钟的时针长5厘米，它从上午8点到下午4点，时针针尖走过的距离是（ ）．A ．203πB ．103πC ．60πD ．30π【难度】★★【答案】203π．【解析】2402051801803n l r πππ==⨯=． 【总结】考查弧长在计算时针所走过的路程中的计算．【作业13】 已知一条弧长等于1，它的半径为R ，这条弧所对的圆心角增加1°，则它的弧长增加（ ）A ．1nB ．180Rπ C ．180R π D ．1360【难度】★★【答案】B【解析】由弧长公式1800n R l π=可知，当圆心角增加1°时，弧长则增加180R π． 【总结】考查对弧长公式中每个量的理解．【作业14】 如图，半径r = 12，60AOB ∠=︒，求这个图形的周长．【难度】★★【答案】86.8厘米． 【解析】30012122202486.8180C ππ=⨯+⨯=+=厘米． 【总结】此图的周长包含了弧长和两条半径的长．【作业15】 如图，正方形ABCD 的边长为4，求阴影部分的面积和周长．【难度】★★【答案】面积为16，周长为18.84．【解析】阴影部分的面积是正方形的面积加上圆的面积，再减去扇形的面积；阴影部分的周长则是三段弧的长的和．故2244441624S ππ⨯⎛⎫=⨯+⨯-= ⎪⎝⎭阴影， 12242618.844C r R πππππ=+⨯=+==阴影． 【总结】考查阴影部分的面积和周长的计算，认真分析阴影图形的特征．【作业16】 如图，四边形ABCD 是长方形，AB = 10 cm ，BC = 6 cm ，求阴影部分的周长．【难度】★★【答案】33.12厘米．【解析】()121026448833.124C πππ=⨯+⨯++=+=厘米． 【总结】考查阴影部分周长的计算，注意包含了每一段弧和线段的长．AB C A BCD 【作业17】 如图，一个边长是1厘米的等边三角形，将它沿直线作顺时针方向翻动，到达图示中最右边三角形的位置，点B 所经过的路程是______厘米．（结果保留π）【难度】★★★【答案】2π．【解析】分析整个运动过程，可知B 经过的路程恰好为一个圆周，所以B 所经过的路程 是22r ππ=．【总结】考查图形在翻转过程中，图形上每个一点的运动轨迹，综合性较强，教师要带领学 生共同分析．【作业18】 如图所示，已知正方形ABCD 的边长为3.2厘米，在这个正方形中有个半径为0.4厘米的圆沿着它的四条边滚动一周，求圆滚动时扫过的面积．（保留π）【难度】★★★【答案】7.040.16π+． 【解析】经过分析可知圆扫过的面积为，大正方形的面积减去中间空白处的小正方形的面积再减去四个弯角的面积．一个弯角的面积是：210.40.40.40.160.044ππ⨯-⨯⨯=-， 则4个弯角的面积是：(0.160.04)40.640.16ππ-⨯=-， 而中间空白部分的正方形的面积是：(3.20.80.8)(3.20.80.8) 1.6 1.6 2.56--⨯--=⨯=， 故圆扫过的面积为：3.2 3.2 2.56(0.640.16)7.040.16ππ⨯---=+．【总结】本题综合性较强，主要是要分析清楚圆在滚动时扫过的面积的状态．。

圆和扇形的相关知识点总结一、圆的基本概念圆是平面上一组到一点距离相等的所有点的集合。

它由一个中心点和一个半径组成。

圆的半径是从中心点到圆上任意一点的距离。

二、圆的性质 1. 圆的周长：圆的周长是圆上一点到另一点的距离。

圆的周长公式为C = 2πr，其中C表示圆的周长，r表示圆的半径，π是一个常数，约等于3.14159。

2. 圆的面积：圆的面积是圆内部的平面面积。

圆的面积公式为A = πr^2，其中A表示圆的面积，r表示圆的半径。

3. 圆的直径：圆的直径是通过圆心并且两端点都在圆上的线段。

直径是半径的两倍，即d = 2r。

4. 圆的弧长：圆的弧长是圆上一段弧的长度。

弧长的公式为L = 2πr(θ/360°)，其中L表示弧长，r表示圆的半径，θ表示弧度的角度。

5. 圆的弧度：圆的弧度是圆上一段弧所对应的圆心角的度量。

弧度和角度之间的转换关系为：1弧度≈ 57.3°。

6. 圆的切线：圆上一点的切线是与圆相切且与半径垂直的直线。

三、扇形的基本概念扇形是由圆心、圆弧和两条半径所围成的图形。

扇形可以看作是一个圆心角所对应的圆弧和两条半径组成的图形。

四、扇形的性质 1. 扇形的圆心角：扇形的圆心角是扇形两条边所夹的角度。

圆心角的度数可以用扇形的圆心角度量来表示。

2. 扇形的弧长：扇形的弧长是扇形圆弧的长度。

弧长的计算公式为L = 2πr(θ/360°)，其中L表示弧长，r表示扇形的半径，θ表示圆心角的度数。

3. 扇形的面积：扇形的面积是扇形所覆盖的圆形面积的一部分。

扇形的面积计算公式为A = πr^2(θ/360°)，其中A表示扇形的面积，r表示扇形的半径，θ表示圆心角的度数。

五、常见应用场景 1. 扇形在地理上用于表示地球表面上的各种区域，如时区和地域划分。

2. 扇形在建筑设计中用于确定某个区域的角度和面积，如窗户的设计和阳台的布局。

3. 扇形在机械制造中用于设计和制造各种旋转部件，如轮胎和齿轮。

练一练 1.下面哪个图形中的涂色部分是扇形？
2.在下面的圆中画出大小不同的扇形 并涂色。
看轻别人很容易，要摆平自己却很困难。 种子牢记着雨滴的叮嘱,增强了发芽的勇气；泉水经过一路曲折，才唱出美妙的歌。——成文之 你不能左右天气，但你能转变你的心情。
我们不希望自己是什么天才。没有从天而降的成功，每从跌倒里站起来一次，成功就近了一寸。也没有平白无故的威信。每正确一次，威信就 增加一分。 不管失败多少次，都要面对生活，充满希望。 “不可能”只存在于蠢人的字典里。 成功就是你被击落到失望的深渊之后反弹得有多高。
冀教版数学六年级上册第一单元
扇形的认识
教学目标
1、在观察、讨论、判断等活动中，经历初步认 识扇形的过程。 2、知道扇形，初步了解扇形的特征，能在圆中 画出扇形。 3、体会扇形和圆的关系，知道扇形的各部分名 称。
观Байду номын сангаас各圆中涂色的部分，说一说它们 的形状像什么？
说一说
扇形有什么特征？
扇形都有一个角， 角的顶点是圆心。
扇形是由两条半径 和圆上的一段曲线围 成的。
左图中，圆上A、B 两点之间的部分叫做弧。 读作：弧AB。
顶点在圆心，两条半 径组成的∠AOB，叫做 圆心角。
圆心角与扇形的大小有什么关系？
（1）画圆心角不同的扇形：在同一个圆中分别画 出圆心角是30°、60°、90°和120°的扇形。
C
90°
●
B 60°
A 30°
D
120°
①画一个圆。
②画30°、60°、 90°120°的圆心角。
结论：在同一个圆中，扇形的大小与其 圆心角的大小有关。圆心角大，所对应的 扇形就大；圆心角小，所对应的扇形就小。

圆和扇形知识点归纳圆和扇形是几何学中的基本图形，广泛应用于建筑、工程、地理测量等领域。

它们具有一些重要的特性和性质，下面将对圆和扇形的知识点进行归纳。

一、圆的基本概念：1.圆的定义：由平面上所有与给定点（圆心）的距离等于常数（半径）的点的集合所组成的图形叫做圆。

2.圆心和半径：圆心是圆上任意两点的连线的中点，圆半径是圆心到圆上任意一点的距离。

3.圆的重要性质：(1)圆上任意两点与圆心的距离相等；(2)圆的直径是圆的一条由圆心到圆上的点的线段，它的长度等于半径的两倍；(3)圆的弦是圆上的两点间的线段，弦的长度小于等于直径；(4)圆的弧是圆上的一段弦；(5)圆的面积公式为S=πr²，其中S是圆的面积，r是圆的半径。

二、扇形的基本概念：1.扇形的定义：由圆心和圆上一条弧段所组成的图形叫做扇形。

2.扇形的重要性质：(1)扇形的弧长是扇形弧的长度，可以通过圆的周长与圆心角的比例得到；(2)扇形的面积是扇形所占圆的面积的比例，可以通过圆的面积与圆心角的比例得到；(3)扇形弧的度数是指扇形所对的圆心角的度数，单位为度或弧度；(4)扇形所对的圆心角的度数等于其所包含的弧长与半径的比例。

三、圆和扇形之间的关系：1.扇形是圆的一部分，是圆的一个划分区域。

2.扇形的度数与其所对的圆心角的度数相等。

3.扇形的面积是圆的面积的一部分，可以通过圆的面积与圆心角的比例计算得到。

4.扇形的弧长是圆的周长的一部分，可以通过圆的周长与圆心角的比例计算得到。

四、圆和扇形的应用：1.圆和扇形在建筑领域中用于设计圆形建筑物、广场等。

2.圆和扇形在地理测量中用于计算球面上的角度和弧长。

3.圆和扇形在制图中用于画圆形或弧形的路径。

4.圆和扇形在机械工程中用于设计齿轮、曲柄等圆形传动装置。

5.圆和扇形在电子学中用于设计电路板上的圆形路径。

综上所述，圆和扇形是几何学中的基本图形，具有一些重要的特性和性质。

它们的应用广泛，涉及到建筑、工程、地理测量等多个领域。