第四章 投入产出分析

环境—经济系统的投入产出分析一、概论投入产出分析技术是美国经济学家瓦西里·里昂惕夫（W. Leontief ）于1936年发明的一种科学的经济分析方法。

投入产出分析技术利用现代数学方法，分析国民经济各部分之间在生产数量上的互相依存关系，用于预测及平衡再生产的综合比例，有时称为部门联系平衡分析。

环境—经济系统的投入产出分析是把自然环境资源、能源和生产排出的废弃物作为经济活动的投入物和产出物，并利用能量与物质恒定律和生态经济学的原理，分析改善环境质量带来的效益与支付的费用以及经济发展对环境的影响。

20世纪70年代以来，环境—经济系统的投入产出分析应用迅速发展，已成为目前分析和预测经济发展与环境保护协调平衡的一种有效手段。

二、基本原理1、概述（1）投入产出分析是对经济系统各部门间的数量依存关系进行研究，以确定国民经济各部门错综复杂的联系和在生产的重要比例关系的方法和技术。

其中：投入是指生产过程中消耗的原材料、燃料、动力和劳动；产出是指从事经济活动的结果及产品的分配去向，使用方式和数量。

（2）投入产出分析的基础是投入产出模型或投入产出表，其是一种特殊的线性模型，模拟了某地区或某企业各生产部门之间的相互关系，是生产部门对社会最终需要量变化的反映。

（3）在现代经济活动中，各生产部门之间存在着复杂而密切的联系，并且整个经济系统是处于平衡状态的。

其中经济系统中任一部门发生变化，都将引起其它部门的供求变化，这种连锁反应，结果是破坏原有的平衡。

投入产出分析就是依照经济按比例发展的客观规律，描述经济系统中各部门的平衡关系。

（4）里昂惕夫（美国经济学家）在上世纪30年代提出了投入产出模型，其将各种经济流归结在一个表中，为某一国家和地区的整个经济活动提供了一个简明而又系统的结构关系—投入产出表，奠定了投入产出模型的方法论基础。

2、投入产出表的结构投入产出表主要是中间产品交流表，后来发展为直接消耗系数表和完全消耗系数表。

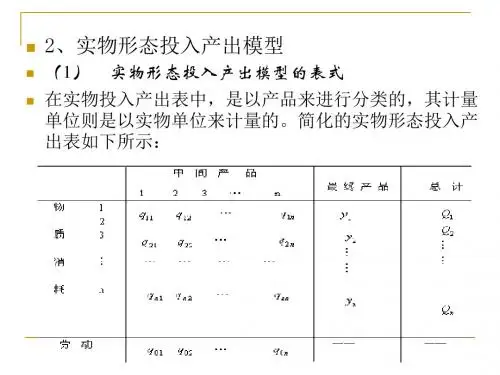
投入产出模型应用与分析一、投入产出分析简介投入产出分析，是研究经济系统各个部分间表现为投入与产出的相互依存关系的经济数量方法。

投入是进行一项活动的消耗。

如生产过程的消耗包括本系统内各部门产品的消耗（中间投入）和初始投入要素的消耗（最初投入）。

产出是指进行一项活动的结果。

如生产活动的结果是为本系统各部分生产的产品（物质产品和劳务）。

瓦西里·列昂剔夫（Wassily W.Leontief，1906—1999）是投入产出账户的创始人。

投入产出表同时表现了社会产品的实物分配和价值构成，全面反映了社会再生产中各部门的经济联系。

利用投入产出表及其数学模型，通过确定一些十分重要的经济参数，可以深入分析国民经济的各种重大比例和经济结构，这就对社会再生产过程进行系统的经济分析提供了非常有用的工具。

价值型投入产出表是根据国民经济各产品部门本期生产活动的产品与服务的分配去向和消耗来源排列而成的一张棋盘式平衡表。

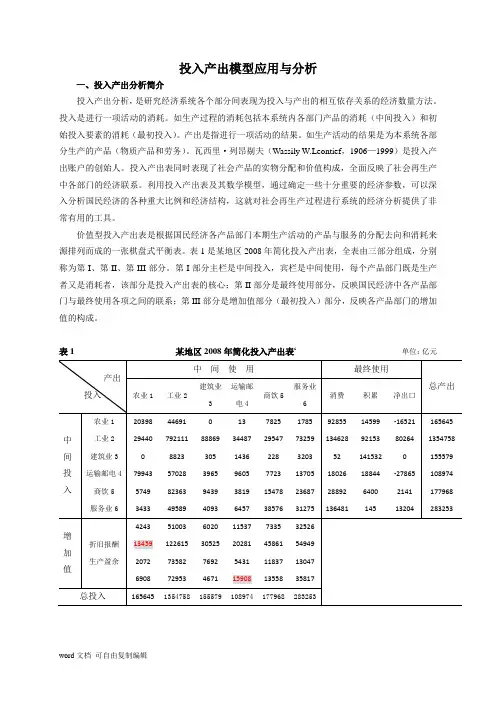
表1是某地区2008年简化投入产出表，全表由三部分组成，分别称为第I、第II、第III部分。

第I部分主栏是中间投入，宾栏是中间使用，每个产品部门既是生产者又是消耗者，该部分是投入产出表的核心；第II部分是最终使用部分，反映国民经济中各产品部门与最终使用各项之间的联系；第III部分是增加值部分（最初投入）部分，反映各产品部门的增加值的构成。

表1 某地区2008年简化投入产出表i单位：亿元二、投入产出模型(一)建立模型 1.行模型（1）建立行模型：i i X y nj ij x =+∑=1 (i =1,2,．．．,n) 引入直接消耗系数 ij a ，即：ij a ＝ij x ／j X可得：i i X y jX nj ij a =+∑=1即用矩阵表示为: AX+Y=X化简后可得价值型行数学模型： X=(I-A)-1Y 或 X=B Y （2）计算相关矩阵A ，B=(I-A)-1-I ，B =(I-A)-1 =B+I直接消耗系数矩阵：A=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 0.1104 0.21680.05930.0263 0.0366 0.0207 0.0836 0.0870 0.0350 0.0607 0.0608 0.0347 0.0484 0.0434 0.0881 0.0255 0.0421 0.4826 0.0113 0.00130.0132 0.0020 0.0065 0.0000 0.2586 0.1660 0.3165 0.5712 0.5847 0.1777 0.0063 0.04400.0001 0.0000 0.03301231.0完全消耗系数矩阵：B=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 0.22350.34120.16110.1660 0.1902 0.1696 0.1885 0.1958 0.1385 0.2087 0.2227 0.1731 0.1508 0.1664 0.1908 0.1689 0.2174 0.7095 0.02270.0133 0.0250 0.0178 0.0240 0.0197 1.00730.87641.11911.7485 1.8655 1.25510.0562 0.0955 0.0504 0.0775 0.12040.1976完全需要系数矩阵：B =⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 1.2235 0.3412 0.1611 0.1660 0.1902 0.1696 0.1885 1.1958 0.1385 0.2087 0.2227 0.1731 0.1508 0.1664 1.1908 0.1689 0.2174 0.7095 0.0227 0.0133 0.0250 1.0178 0.0240 0.0197 1.0073 0.8764 1.1191 1.7485 2.8655 1.25510.0562 0.0955 0.0504 0.0775 0.12041.1976（3）价值型行数学模型 X=(I-A)-1Y=B Y⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛654321X X X X X X =⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 1.2235 0.3412 0.1611 0.1660 0.1902 0.1696 0.1885 1.1958 0.1385 0.2087 0.2227 0.17310.1508 0.1664 1.1908 0.1689 0.2174 0.7095 0.0227 0.0133 0.0250 1.0178 0.0240 0.0197 1.0073 0.8764 1.1191 1.7485 2.8655 1.25510.0562 0.0955 0.0504 0.0775 0.1204 1.1976⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛654321Y Y Y Y Y Y2列模型 （1）建立列模型j j j j j X s t v d ni ij x =++++∑=1 (j =1,2,．．．,n)引入直接消耗系数 ij a 可得：j j j j j X s t v d j X ni ij a =++++∑=1即用矩阵表示为：AcX+N=X化简后可得价值型列数学模型： X=(I-Ac)-1N （2）计算相关矩阵A C ，(I-Ac)-1物耗系数矩阵：Ac=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 0.5187000000 0.5584000000 0.5122000000 0.6856000000 0.76370000000.8389增加值系数矩阵：(I-Ac)-1=⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ 2.0775*******.26440000002.0500000003.181********.231590000006.2081（3）价值型列数学模型 X=(I-Ac)-1N⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛654321X X X X X X =⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛ 2.0775*******.26440000002.05000000003.181********.231590000006.2081⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛654321N N N N N N ij x :第i 部门（行部门）生产的产品或服务分配给第j 部门（列部门）用于生产消耗的产品产值；第j 部门（列部门）生产过程中直接消耗第i 部门的产品或服务的产品产值；i y :第i 部门在本期产品中提供的最终使用额，包括消费和积累；j d 、j v 、j t 、j s :分别为第j 部门的折旧，劳动报酬，生产税净额，和营业盈余； j m :为第j 部门的社会纯收入，等于j t +j s ； j N :为第j 部门的增加值，等于j d +j v +j t +j s ；i X :第i 部门总产出 ；j X :第j 部门总投入；A :直接消耗系数矩阵（ij a ）n n ⨯X=（X 1 X 2.......X N )T —总产出的列向量；Y=（y 1 y 2.......y N )T —最终使用的列向量；j i ,=1,2,3,4,5,6分别表示农业部门、工业部门、建筑业部门、运输邮电部门、商饮部门和服务业部门；n =6。

投入产出分析经济学引言投入产出分析是一种经济学工具，用于评估一个国家、地区或产业的经济活动。

它通过衡量产出与投入之间的关系，揭示了经济系统的结构和运作方式。

投入产出分析广泛应用于政府决策、产业规划和经济发展的研究中。

本文将介绍投入产出分析经济学的基本概念、原理和应用，以及其在经济学研究和实践中的重要性。

基本概念投入在投入产出分析中，投入通常指的是生产过程中使用的资源和要素，包括劳动力、资本、土地和原材料等。

这些投入会被用于生产过程中，从而产生最终的产品或服务。

产出产出是指经济活动中所得到的最终产品或服务。

在投入产出分析中，产出通常指的是一个国家、地区或产业的总产出，可以用来衡量经济活动的规模和质量。

产出可以是实物产品，也可以是服务。

投入产出表投入产出表是投入产出分析的核心工具，用于描述一个经济系统中各个部门间的投入产出关系。

它包含了各个产业的投入和产出数据，可以用来计算产业间的关联度、乘数效应和经济影响等指标。

原理和方法帕累托优化投入产出分析经济学中的帕累托优化原理是指通过合理分配资源和要素，使得经济系统的产出最大化。

帕累托优化的目标是在满足资源有限的情况下，最大化社会总产出和福利。

投入产出矩阵投入产出矩阵是投入产出分析中的一个重要概念，用于描述各个产业间的投入和产出关系。

投入产出矩阵是一个方阵，其中的每一个元素表示一个产业的投入或产出量。

通过矩阵运算，可以计算产业间的关联度和乘数效应等指标。

乘数效应乘数效应是指投入产出分析中的一种经济影响指标。

它描述了一个单位的增加在一个经济系统中所能带来的总产出增加量。

乘数效应可以用来评估政府政策、产业发展和经济增长等方面的影响。

应用领域投入产出分析经济学广泛应用于各个领域的经济研究和实践中。

以下是几个主要的应用领域：政府决策投入产出分析经济学可以帮助政府制定经济政策和决策。

通过分析投入产出关系，政府可以评估政策的影响，预测经济活动的变化，并制定相应的措施和政策。

投入产出分析原理及应用投入产出分析是一种衡量经济活动效率的方法，主要用于度量一个经济体的产出与投入之间的关系。

它可以帮助决策者了解经济活动的效率水平，以及优化资源配置。

本文将介绍投入产出分析的原理、计算方法和应用。

投入产出分析的核心原理是通过建立产出与投入的关系模型，来衡量经济体所需的投入资源与其产出之间的关系。

一般来说，投入产出模型包括产出矩阵和投入矩阵。

产出矩阵以列向量的形式表示一个经济体所产出的各种产品或服务。

而投入矩阵则以行向量的形式表示经济体所使用的各种资源或要素。

这些矩阵之间的乘积将得出一个产出向量，它表示了经济体所能产出的各种产品或服务。

投入产出分析的关键在于计算投入产出矩阵。

一般情况下，投入产出矩阵可以通过调查和统计数据获得。

在计算投入产出矩阵时，我们需要注意考虑到投入产出关系的复杂性，例如资源之间的相互依赖关系和技术进步的影响。

利用投入产出矩阵，我们可以计算出一系列有关经济体效率的指标。

其中最重要的指标是生产率。

生产率是指单位投入资源所产出的产出量。

在投入产出分析中，我们可以通过计算产出矩阵与投入矩阵的乘积，再与投入矩阵相除得到一个生产率矩阵，从而衡量各种经济活动的效率水平。

投入产出分析的应用非常广泛。

首先，它可以用于优化资源配置。

通过衡量各种经济活动的效率，我们可以发现资源配置中的问题，并调整产业结构，实现资源的最佳利用。

例如，当某一部门的生产率较低时，我们可以考虑增加该部门的资源投入，以提高其产出。

而当某一部门的生产率过高时，我们可以减少其资源投入，以优化整体资源利用效率。

其次，投入产出分析可以用于预测和规划经济活动。

通过对历史数据的分析和对未来的预测，我们可以建立模型来预测某一经济体在特定条件下的产出和投入状况。

这对经济决策者来说非常重要，因为他们可以根据这些预测结果来制定合理的经济政策和规划。

此外，投入产出分析还可以用于评估政策和项目的影响。

通过建立一个投入产出模型，我们可以评估某一政策或项目对经济体的影响。

投入产出分析投入产出分析是一种经济学工具，用于评估生产过程中资源投入和产出之间的关系。

它可以帮助企业和政府机构决策，优化资源配置，提高生产效率。

本文将探讨投入产出分析的概念、方法和应用，并结合实际案例进行解析。

首先，我们来了解一下投入产出分析的基本概念。

投入产出分析是一种宏观经济学方法，旨在分析一个经济体中各个部门之间的关联关系和相互依赖程度。

它通过测算一个单位资源投入时所创造的产出，并以此为基础，推算整个经济体的资源配置和产出情况。

投入产出分析的核心是构建一个投入产出表，记录各个部门的资源投入和产出情况。

在具体的方法上，投入产出分析采用了线性代数和矩阵分析的技术。

首先，我们需要将经济体划分为不同的部门，例如农业、工业、服务业等。

然后，我们通过调查和统计数据，确定各个部门的资源投入和产出情况，包括劳动力、物资、资本等。

接下来，我们构建一个投入产出矩阵，将各个部门之间的关系用矩阵表示。

通过矩阵运算，我们可以计算出每个部门的资源利用率、就业效益、生产乘数等指标，从而评估整个经济体的效益和可持续发展性。

投入产出分析的应用领域广泛。

首先，它可以用于评估政府政策的效果。

政府决策往往涉及资源配置和经济发展问题，投入产出分析可以帮助政府机构预测政策的影响，优化政策设计，实现经济可持续增长。

其次，它可以用于企业的经营决策。

企业在生产过程中面临资源投入和产出之间的权衡，投入产出分析可以帮助企业优化生产方案，提高资源利用效率，增加利润。

另外，投入产出分析还可以用于评估经济发展项目的可行性，研究产业链的发展潜力，支持区域经济发展规划等。

为了更好地理解投入产出分析的实际应用，我们以汽车制造业为例进行解析。

汽车制造业是一个典型的多部门产业，涉及到冶金、机械、橡胶、塑料、电子等多个部门之间的关系。

通过投入产出分析，我们可以评估汽车制造业对其他部门的资源需求，以及对就业和产出的影响。

同时，我们还可以估算汽车制造业在整个经济体中的比重，以及其对国内生产总值和出口收入的贡献。

第四章投入-产出分析1、教学目标和要求:①了解生产函数概念,理解管理经济学中短期与长期的区别;②掌握总产量、平均产量、边际产量概念、相互关系及计算公式;③掌握边际收益递减规律以及单一可变要素下企业合理投入目标的确定.④了解等产量曲线、等成本曲线、边际技术替代率和生产扩张线概念;⑤理解两种可变要素最优组合条件和规模收益规律;⑥了解技术进步性质、作用、类型、实现机制2、重点:不同风格的谈判者策略;难点: 不同性格的谈判者策略.3、授课方法:讲授,分析与讨论4、课时安排:8课时5、内容要点及过程:第一节生产与生产函数一、生产生产,就是指一切创造价值的活动.它不仅包括物质产品的有形加工或制造,也包括运输服务、法律咨询、医疗服务和发明创造等各类服务性活动.二,生产函数.在既定生产技术条件下,一定时期内各种可行的生产要素组合和可能达到的最大产出量之间的数量关系. 公式为Q=f(X1,X2,X3, …,X n)三、生产函数的分类1、短期生产函数2、长期生产函数这里的短期和长期,并不是指一个具体的时间跨度,而是指企业能否来得及调整生产规模所需时间长度.第二节单一可变要素的合理投入一、总产量、平均产量、边际产量1、总产量、平均产量、边际产量的概念总产量是指,投入一定量生产要素所得到的总产出量.平均产量,是指平均每单位生产要素投入的产出量.边际产量,是指增加或减少一单位生产要素投入量所带来的产出量变化.2、总产量、平均产量、边际产量的相互关系二、边际收益递减规律在一定技术水平条件下,若其他生产要素不变,连续增加某种生产要素投入量,在经过一定点之后,增加的产量必定会出现逐渐递减趋势.三、生产的三个阶段:第三节两种可变要素的最优组合一.等产量曲线:在其他条件不变时,为生产一定产量所需投入的两种生产要素之间的各种可能组合的轨迹.1、边际技术替代率:在维持产量不变前提下,减少一种生产要素数量与增加另一种生产要素数量之比.二、等成本曲线生产要素价格一定时,花费一定总成本所能购买的两种生产要素组合的轨迹.三、两种投入要素最优组合1、产量既定,成本最小的要素组合2、成本既定,成本最小的要素组合四、生产扩张线在生产要素价格既定条件下,不同产量水平的最优投入组合点的轨迹.五、规模收益1、规模收益递增;2、规模收益不变;3、规模收益递减第四节技术进步与生产函数一、技术进步导致生产函数改变1、技术进步,就是新的生产方法以及新的管理组织方式.二、技术进步的类型1、资本使用型技术进步2、劳动使用型技术进步3、中性型技术进步三、技术进步实现途径1、研究与开发研究,包括基础性研究和应用性研究.开发,是把研究提供的知识结果或发现运用到商业经营活动中,是知识产业化或商业化的过程.2、发明和创新发明,是指创造出全新的事物或方法.在与经济、商业活动相关意义上,发明一般指全新技术、工艺或者全新管理和组织资源方式的产生或提供,它往往表现为应用性研究的结果形态,并有可能得到专利的保护.创新,指把某项发明成果第一次运用到商业、经营活动中.创新,是开发实施过程中的一个关键性环节.6、小结生产函数,是指在既定生产技术条件下,一定时期内各种可行的生产要素组合和可能达到的最大产出量之间的数量关系. 公式为Q=f(X1,X2,X3, …,X n)管理经济学中的短期和长期,并不是指一个具体的时间跨度,而是指企业能否来得及调整生产规模所需时间长度.总产量是指,投入一定量生产要素所得到的总产出量.平均产量,是指平均每单位生产要素投入的产出量.边际产量,是指增加或减少一单位生产要素投入量所带来的产出量变化.边际收益递减规律,是指在一定技术水平条件下,若其他生产要素不变,连续增加某种生产要素投入量,在经过一定点之后,增加的产量必定会出现逐渐递减趋势.等产量曲线,是指在其他条件不变时,为生产一定产量所需投入的两种生产要素之间的各种可能组合的轨迹.规模收益问题,有1、规模收益递增;2、规模收益不变;3、规模收益递减技术进步实现途径有,1、研究与开发.研究,包括基础性研究和应用性研究.开发,是把研究提供的知识结果或发现运用到商业经营活动中,是知识产业化或商业化的过程.2、发明和创新.发明,是指创造出全新的事物或方法.在与经济、商业活动相关意义上,发明一般指全新技术、工艺或者全新管理和组织资源方式的产生或提供,它往往表现为应用性研究的结果形态,并有可能得到专利的保护. 创新,指把某项发明成果第一次运用到商业、经营活动中.创新,是开发实施过程中的一个关键性环节.。

南京中天国际大酒店酒店简介南京,山水城林，钟灵毓秀。

南京中天国际大酒店，是一家按照国际五星级酒店标准豪华装修的商务酒店。

距机场50公里；距市中心6公里，车程约15分钟；距总统府风景区1公里；距大行宫地铁站约10分钟路程。

南京中天国际大酒店建筑面积10000平方米。

拥有各类不同款式的客房400多间，并配备了先进的房内设施。

南京中天国际酒店中餐厅拥有各类豪华包厢50间、以及可以容纳千人同时用餐的豪华宴会厅，火锅餐厅，阳光咖啡厅，特聘多次荣获全国厨艺大奖的烹饪名师主理，经营以燕、鲍、翅为主轴的粤菜、和以“佛跳墙”为灵魂的闽菜等各色菜肴。

南京中天国际酒店详细信息酒店星级：五星级开业时间：2012年开业客房数量：客房400间/套详细地址：南京市白下区长白街88号交通情况：距离市中心2公里、距离大行宫地铁站：3公里、距离机场50公里、距离总统府风景区1公里服务设施：叫醒服务、行李存放支持卡类：国际信用卡万事达(Master)、国际信用卡威士(VISA)、国际信用卡运通(AMEX)、国际信用卡大莱(Diners Club)、国际信用卡JCB、国内发行银联卡附近景点：总统府风景区，1912酒吧街区上网情况：所有房间免费宽带上网配套设施餐饮设施（七大镇宝）璇宫餐厅、香江餐厅、太平洋餐厅、金海湾餐厅、梅苑餐厅、樱花苑餐厅、金淼餐厅会议设施小会议室7个可容纳8-30人、扬子厅可容纳40-380人、钟山厅可容纳200-1200人休闲设施游泳、健身、桑拿、按摩、棋牌、台球、乒乓球、夜总会服务设施金钥匙、会议厅、商务中心、停车场、外币兑换、票务服务、DDD、IDD、洗衣服务、商场、医务室、美容美发、出租车、宽带上网、残疾人客房、婴儿看护、茶座。

投入分析1.土地：本酒店采用租赁形式，由于位于南京最繁华的市中心，因此在租金方面是比较昂贵的，在权衡各方面的因素之后，我们确定我们的租金在500万.2.人力：我们酒店人力资源岗位等级分为四个等级。