八年级数学上册198直角三角形的性质练习无答案沪教版五四制

19.8（1）直角三角形的性质一、填空题1．若直角三角形的两个锐角之差为24度，则较大的锐角的度数是_________ ． 2. 如图，在Rt △ABC 中，∠ACB ＝90°，CD ⊥AB 于D ， (1)若∠B ＝50°，则∠A ＝__________； (2)若∠B －∠A ＝50°，则∠A ＝__________； (3)与∠A 互余的角有________________；(4)与∠A 相等的角有________________． 第2题图3．已知直角三角形面积等于24平方厘米，斜边上的高为4厘米，则斜边上的中线长 为 厘米．4．等腰直角三角形中，若斜边和斜边上的高的和是6cm ，则斜边长是 cm ． 5. 若直角三角形的斜边上的高与斜边上的中线长分别为2 cm 和3 cm ，则这个直角三角形的面积为__________cm 2.6. 在Rt △ABC 中，∠C ＝90°，周长为24 cm ，三边长的比为3∶4∶5，则斜边上的中线长为__________cm ，斜边上的高为__________cm.二、解答题7．如图，已知△ABC 中，∠ ABC=∠ ACB ，D 、E 为△ABC 外两点，AD ⊥BD ，AE ⊥CE ，F 、G 分别为AB 、AC 的中点．求证：DF ＝GE .8．如图，已知：在ABC ∆中，D BC AC AD C B 于交，，⊥=∠=∠2040． 求证：AB CD 2=．ABCD9. 如图，已知在Rt △ABC 中，∠C ＝90°，M 是AB 的中点，AM ＝AN ，MN ∥AC . 求证：MN ＝AC .10. 如图，已知HE 、AG 相交于点D ，点B 、C 、F 分别是线段DG 、HD 、AE 的中点，若AH ＝AD ，DE ＝EG .求证：CF ＝BF .三、提高题11．如图，已知：在ΔABC 中, ∠ABC=2∠C,AD ⊥BC 于D,E 是AC 中点,ED 的延长线与AB 的延长线交于点F ．求证：BF=BD ．ＣＢＡＥＤＦ19.8（2）直角三角形的性质一、填空题1. 在Rt△ABC中，∠C＝90°，∠B＝60°，若BC＝4 cm，则AB＝__________cm.2. 在△ABC中，若∠C∶∠B∶∠A＝1∶2∶3，BC＝16,则AB＝__________.3.在Rt△ABC中，若∠ACB＝90°，CD⊥AB于D，∠A＝30°，若BD＝4cm，则BC＝__________cm，AD＝__________cm.4. 等腰三角形的顶角为30°，腰长为4 cm，则这个等腰三角形的面积为__________cm 5．△ABC中,AB=AC,∠BAC=120°,AB=12cm,则BC边上的高AD= cm.．6.等腰三角形一腰上的高等于腰长的一半，则此等腰三角形的顶角度数是__________．7.如图，在Rt△ABC中，∠A<∠B，CM是斜边AB上的中线，将△ACM沿CM翻折，点A落在点D处，如果CD恰好与AB垂直，那么∠A＝__________度．二、解答题8．已知：如图，△ABC中，AB=AC，点D在BC边上，∠DAC=90° , AD= 12 CD．求：∠BAC的度数．9．已知：如图，在△ABC中，BD＝DC，若AD⊥AC，∠BAD＝30°．求证：AC＝12 AB．AB CDAB CD10. 如图，已知等边三角形中，E 是AC 上的一点，CE ＝14AC ，过E 作DE ⊥AC 交BC 于点D . 求证：D 是BC 的中点．11. 如图，已知△ABC 中，∠ACB ＝90°，CD ⊥AB 于D ，CE 为AB 边上的中线，若AC ＝AE .求证：BC ＝2CD .三、提高题12．已知：等腰三角形一腰上的高是另一腰长度的12，求这个等腰三角形的底角的度数。

19.8（1）直角三角形的性质一、填空题1．若直角三角形的两个锐角之差为24度，则较大的锐角的度数是_________ ．2. 如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB于D，(1)若∠B＝50°，则∠A＝__________；(2)若∠B－∠A＝50°，则∠A＝__________；(3)与∠A互余的角有________________；(4)与∠A相等的角有________________．第2题图3．已知直角三角形面积等于24平方厘米，斜边上的高为4厘米，则斜边上的中线长为厘米．4．等腰直角三角形中，若斜边和斜边上的高的和是6cm，则斜边长是 cm．5. 若直角三角形的斜边上的高与斜边上的中线长分别为2 cm和3 cm，则这个直角三角形的面积为__________cm2.6. 在Rt△ABC中，∠C＝90°，周长为24 cm，三边长的比为3∶4∶5，则斜边上的中线长为__________cm，斜边上的高为__________cm.二、解答题7．如图，已知△ABC中，∠ ABC=∠ ACB，D、E为△ABC外两点，AD⊥BD，AE⊥CE，F、G 分别为AB、AC的中点．求证：DF＝GE.8．如图，已知：在ABC ∆中，D BC AC AD C B 于交，，⊥=∠=∠2040． 求证：AB CD 2=．9. 如图，已知在Rt △ABC 中，∠C ＝90°，M 是AB 的中点，AM ＝AN ，MN ∥AC . 求证：MN ＝AC .10. 如图，已知HE 、AG 相交于点D ，点B 、C 、F 分别是线段DG 、HD 、AE 的中点，若AH ＝AD ，DE ＝EG .求证：CF ＝BF .ABCD三、提高题11．如图，已知：在ΔABC 中, ∠ABC=2∠C,AD ⊥BC 于D,E 是AC 中点,ED 的延长线与AB 的延长线交于点F ．求证：BF=BD ．19.8（2）直角三角形的性质一、填空题1. 在Rt △ABC 中，∠C ＝90°，∠B ＝60°，若BC ＝4 cm ，则AB ＝__________cm.2. 在△ABC 中，若∠C ∶∠B ∶∠A ＝1∶2∶3，BC ＝16,则AB ＝__________.3.在Rt △ABC 中，若∠ACB ＝90°，CD ⊥AB 于D ，∠A ＝30°，若BD ＝4cm ，则BC ＝__________cm ，AD ＝__________cm.4. 等腰三角形的顶角为30°，腰长为4 cm ，则这个等腰三角形的面积为__________cm 5．△ABC 中,AB=AC,∠BAC=120°,AB=12cm,则BC 边上的高AD= cm.．ＣＢＡＥＤＦ6.等腰三角形一腰上的高等于腰长的一半，则此等腰三角形的顶角度数是__________．7.如图，在Rt△ABC中，∠A<∠B，CM是斜边AB上的中线，将△ACM沿CM翻折，点A落在点D处，如果CD恰好与AB垂直，那么∠A＝__________度．二、解答题8．已知：如图，△ABC中，AB=AC，点D在BC边上，∠DAC=90° , AD= 12 CD．AB CD1 2AB．9．已知：如图，在△ABC中，BD＝DC，若AD⊥AC，∠BAD＝30°．求证：AC＝AB CD10. 如图，已知等边三角形中，E 是AC 上的一点，CE ＝14AC ，过E 作DE ⊥AC 交BC 于点D . 求证：D 是BC 的中点．11. 如图，已知△ABC 中，∠ACB ＝90°，CD ⊥AB 于D ，CE 为AB 边上的中线，若AC ＝AE .求证：BC ＝2CD .三、提高题12．已知：等腰三角形一腰上的高是另一腰长度的12，求这个等腰三角形的底角的度数。

19.8 直角三角形的性质 同步练习一、选择题1. 在Rt △ABC 中，∠C ＝90°，a ＝12，b ＝16，则c 的长为（ ）A 、26B 、18C 、20D 、21 2．图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形．若正方形A 、B 、C 、D 的边长分别是3、5、2、3，则最大正方形E 的面积是( )A ．13B ．26C ．47D ．94 3． “赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形．如图，是一“赵爽弦图”飞镖板，其直角三角形的两条直角边的长分别是2和4．小明距飞镖板一定距离向飞镖板投掷飞镖（假设投掷的飞镖均扎在飞镖板上）, 则投掷一次飞镖扎在中间小正方形区域（含边线）的概率是( )A ．B ．C ．D ． 4. 一个等腰三角形的腰长为17，底边长为16，则该等腰三角形的面积为（ ）A 、112B 、120C 、128D 、136 5． 如图，矩形ABCD 沿着直线BD 折叠，使点C 落在C ′处，BC ′交AD 于E ，AD ＝16，AB ＝8，则DE 的长为（ ）121415110赵爽弦图A 、12B 、10C 、8D 、6 二、填空题6．如图所示，以Rt △ABC 中的三边向 外作正方形，其面积分别为,则S 3=________；7．直角三角形两条直角边的长分别为6、8，则斜边上的高为_________.8．一个长方形的长为12cm ，对角线长为13cm ，则该长方形的周长为__________. 9．如图，某人欲横渡一条河，由于水流的影响，实际上岸地点C 偏离欲到达点B200m ，结果他在水中实际游了520m ，求该河流的宽度为_________.10. 在Rt △ABC 中，∠C =90°，AB =15，BC : AC =3:4，则BC =___________. 三、解答题11．如图所示，有一条小路穿过长方形的草地ABCD ，若AB =60m ，BC =84m ，AE =100m ，则这条小路的面积是多少?C 'EDCB A8,4,,,21321==S S S S S且12. 已知等腰三角形的一条腰长是5，底边长是6，求它底边上的高13．如图，小明在广场上先向东走10米，又向南走40米，再向西走20米，又向南走40米，再向东走70米.求小明到达的终止点与原出发点的距离.14. 在长方形纸片ABCD 中，AD ＝4cm ，AB ＝10cm ，按如图方式折叠，使点B 与点D 重合，折痕为EF ，求DE .EFDCBA104020 40出发点 70终止点15．AB是一个12米长的墙，用18米长的网围成一个如图所示的鸡舍，求鸡舍的面积.参考答案1． C 2． C 3． C 4． B 5． B 6． 12 7． 4.8 8． 34cm 9． 480cm 10．911．解：（1）RT △ABE 中，AE 2=AB 2+BE 2 ,所以1002=602+BE 2，BE=80,CE=4路的面积=EC×AB=4×60=240m 2.12．解：等腰△ABC 中.AD 是BC 上的高，所以BD=CD=3.RT △ABD 中，AB 2=AD 2+BD 2 ,所以52=AD 2+32，AD=4.13．解：解：BA ⊥AC 于点A ，Rt △ACB 中，BC 2=AC 2+AB 2 ,所以BC 2=602+802，BC=100.ACBD14．解：设DE=x,则DE=BE=x,AE=10－x.∠DAE=900，Rt△ADE中，DE2=AD2+AE2,所以x2=42+(10－x)2，x=5.8,所以DE=5.8.15．解：解：设BC=x,则AC=18－x.∠ABC=900，Rt△ABC中，AC2=AB2+BC2,所以(18－x)2=122+x2，x=5,所以BC=5,S△ABC=1/2 BC×AB=1/2×12×5=3010402040出发点70终止点A BC。

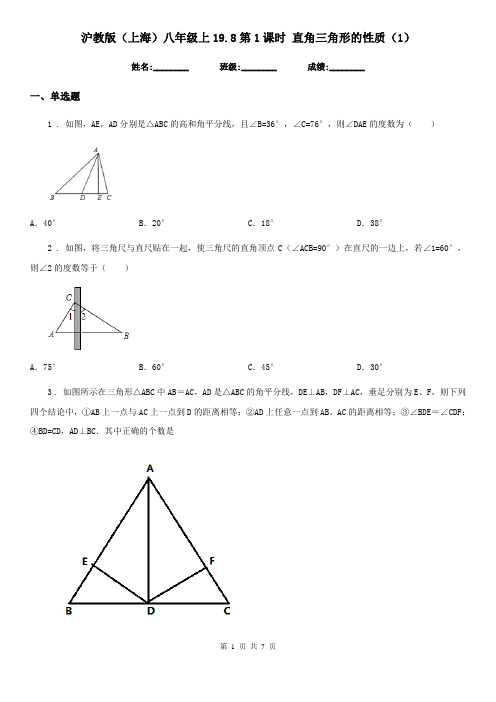
沪教版（上海）八年级上19.8第1课时直角三角形的性质（1）姓名:________ 班级:________ 成绩:________一、单选题1 . 如图，AE，AD分别是△ABC的高和角平分线，且∠B=36°，∠C=76°，则∠DAE的度数为（）A．40°B．20°C．18°D．38°2 . 如图，将三角尺与直尺贴在一起，使三角尺的直角顶点C（∠ACB=90°）在直尺的一边上，若∠1=60°，则∠2的度数等于（）A．75°B．60°C．45°D．30°3 . 如图所示在三角形△ABC中AB＝AC，AD是△ABC的角平分线，DE⊥AB，DF⊥AC，垂足分别为E、F，则下列四个结论中，①AB上一点与AC上一点到D的距离相等；②AD上任意一点到AB、AC的距离相等；③∠BDE＝∠CDF；④BD=CD，AD⊥BC．其中正确的个数是A．1个B．2个C．3个D．4个4 . 如图，AB＝AC，∠BAC＝120°，AB的垂直平分线交BC于点D，那么∠ADC的度数为（）A．120°B．30°C．60°D．80°二、填空题5 . 如图，射线OE方向表示北偏西53°17′，则∠DOE的度数是___．6 . 如图,BC⊥ED于O,∠A=43∘,∠D=20∘,则∠B=______.7 . 如图，△ABC中，CD⊥AB于D，E是AC的中点．若AD=5，DE=6.5，则CD的长等于_______.8 . •用加减法解二元一次方程组时，••两个方程中同一个未知数的系数必须________•或_______，•即它们的绝对值______．•当未知数的系数的符号相同时，•用_______；当未知数的系数的符号相反时，用_______．•当方程组里两个方程的同一个未知数的系数成整数倍时，可以利用________性质，将方程经过简单变形，•使这个未知数的系数的绝对值________，再用加减法消元，进一步求得方程组的解．9 . 如图，EF⊥AB于点F，CD⊥AB于点D，E是AC上一点，∠1=∠2，则图中互相平行的直线有________对.10 . 在直角三角形中，两个锐角的度数比为2：3，那么较小锐角的度数是_____．11 . 如图，DE为△ABC的中位线，点F在DE上，且∠AFB＝90°，若AB＝6，BC＝8，则EF的长为______．12 . 如图，在△ABC中，AB＝AC＝30cm，DE是AB的垂直平分线，分别交AB、AC于D、E两点．（1）若∠C＝70°，则∠BEC＝_____；（2）若BC＝20cm，则△BCE的周长是_____cm．三、解答题13 . 如图，在中，已知，的垂直平分线交于点，交于点，连接（1）若，则的度数是度（2）若，的周长是①求的长度；②若点为直线上一点，请你直接写出周长的最小值14 . 在中，，，求的各个内角的度数．15 . 已知：如图∠ABC＝∠ADC＝90°，M，N分别是AC、BD的中点．（1）求证：MN⊥BA．（2）若∠BAD＝45°，连接MB、MD，判断△MBD的形状，并说明理由．16 . 如图所示，AD，AE是三角形ABC的高和角平分线，∠B=36°，∠C=76°，求∠DAE的度数．17 . 如图1所示，在中，，点是线段延长线上一点，且，点是线段上一点，连接，以为斜边作等腰，连接，满是条件.（1）若，，，求的长度；（2）求证：；（3）如图2，点是线段延长线上一点，其余条件与题干一致，探究、、之间的数量关系，并证明你的结论.参考答案一、单选题1、2、3、4、二、填空题1、2、3、4、5、6、7、8、三、解答题1、2、3、4、5、。

泸科版2020秋八年级数学上册专练：直角三角形的性质定理（含答案）一．选择题（共8小题）1．如图，△ABC中，∠C=90°，AC=3，∠B=30°，点P是BC边上的动点，则AP长不可能是（）A． 3.5 B． 4.2 C． 5.8 D． 7第1题第2题第3题2．如图，在△ABC中，∠B=30°，BC的垂直平分线交AB于E，垂足为D．若ED=5，则CE 的长为（）A． 10 B． 8 C． 5 D． 2.53．如图，Rt△ABC中，∠C=90°，以点B为圆心，适当长为半径画弧，与∠ABC的两边相交于点E，F，分别以点E和点F为圆心，大于的长为半径画弧，两弧相交于点M，作射线BM，交AC于点D．若△BDC的面积为10，∠ABC=2∠A，则△ABC的面积为（）教育精A． 25 B． 30 C． 35 D． 404．在Rt△ABC中，∠C=90°，∠B=30°，斜边AB的长为2cm，则AC长为（）A．4cm B． 2cm C． 1cm D．m5．如图，△ABC中，∠ACB=90°，CD是高，∠A=30°，则BD与AB的关系是（）A． BD=AB B． BD=AB C． BD=AB D． BD=AB第5题第6题第7题第8题6．如图是屋架设计图的一部分，立柱BC垂直于横梁AC，AB=10m，∠A=30°，则立柱BC的长度是（）A． 5m B． 8m C． 10m D． 20m7．如图，一棵树在一次强台风中于离地面3米处折断倒下，倒下部分与地面成30°角，这棵树在折断前的高度为（）A． 6米B． 9米C． 12米D． 15米8．如图，已知∠ABC=60°，DA是BC的垂直平分线，BE平分∠ABD交AD于点E，连接CE．则下列结论：①BE=AE；②BD=AE；③AE=2DE；④S△ABE=S△CBE，其中正确的结论是（）A．①②③B．①②④C．①③④D．②③④二．填空题（共10小题）9．如图，在Rt△ABC中，∠ACB=90°，AB的垂直平分线DE交AC于E，交BC的延长线于F，若∠F=30°，DE=1，则BE的长是_________ ．10．如图，∠AOE=∠BOE=15°，EF∥OB，EC⊥OB，若EC=1，则EF= _________ ．11．如图，在△ABC中，∠C=90°，∠B=60°，AB=10，则BC的长为_________ ．12．如图，在等腰三角形ABC中，AB=AC=12cm，∠ABC=30°，底边上的高AD= _______cm．第9题第10题第11题第12题教13．如图，在△ABC中，AB=BC，∠B=120°，AB的垂直平分线交AC于点D．若AC=6cm，则AD= _________ cm．。

直角三角形的性质从具体的数据表示长度到字母表示长度，上升一个层次.交换条件和结论,可能会出现多解,体现分类思想。

尝试添加辅助线，构造运用角平分线性质所需的图形,再运用直角三角形的性质、线段垂直平分线性质进行证明.知识呈现:新课探索课内练习课堂小结：线段垂直平分线的性质，角平分线的性质,直角三角形的性质定理1、2及推论1、2的综合运用。

课外作业练习册，堂堂练预习要求18。

9（1）勾股定理勾股定理的内容及简单应用教学后记与反思1、课堂时间消耗:教师活动分钟；学生活动分钟）2、本课时实际教学效果自评（满分10分）: 分3、本课成功与不足及其改进措施：尊敬的读者：本文由我和我的同事在百忙中收集整编出来，本文档在发布之前我们对内容进行仔细校对，但是难免会有不尽如人意之处，如有疏漏之处请指正，希望本文能为您解开疑惑,引发思考。

文中部分文字受到网友的关怀和支持，在此表示感谢！在往后的日子希望与大家共同进步，成长。

This article is collected and compiled by my colleagues and I in our busy schedule. We proofread the content carefully before the release of this article, but it is inevitable that there will be some unsatisfactory points. If there are omissions, please correct them. I hope this article can solve your doubts and arouse your thinking. Part of the text by the user's care and support, thank you here! I hope to make progress and grow with you in the future.。

数学八年级上 第十九章 几何证明19.8 直角三角形的性质（1）一、选择题1．如图，在Rt △ABC 中，∠ACB =90°，BC 的垂直平分线交斜边AB 于D ，AB =12 cm ，AC =6 cm ，则图中等于60°的角共有 （ ） A ．2个 B ．3个 C ．4个 D ．5个第1题 第2题 第3题 第8题 第9题 2. 如图，Rt △ABC 中，∠B=90°，∠ACB=60°，延长BC 到D ，使CD=AC 则AC ：BD= （ ）A ．1：2B ．1：3C ．2：3D ．3:43. 如图，在Rt △ABC 中，∠ACB=90°，CD 、CE ，分别是斜边AB 上的高与中线，CF 是∠ACB 的平分线.则∠1与∠2的关系是 （ ） A ．∠1<∠2 B ．∠1=∠2; C ．∠1>∠2 D ．不能确定4. 在直角三角形ABC 中，若∠C=90°，D 是BC 边上的一点，且AD=2CD ，则∠ADB 的度数是 （ ）A ．30°B ．60°C ．120°D ．150°5、在△ABC 中, ∠A: ∠B: ∠C=1:2:3,CD ⊥AB 于D,AB=a ,则DB 等于 ( ) A.2a B.3a C. 4aD. 52a6下列命题错误的是 （ ）A ．有两个角互余的三角形一定是直角三角形；B ．三角形中，若一边等于另一边一半，则较小边对角为30°C ．直角三角形斜边上的中线等于斜边的一半；D ．△ABC 中，若∠A ：∠B ：∠C=1：4：5，则这个三角形为直角三角形。

7、如果三角形的两条边上的垂直平分线的交点在第三条边上，那么这个三角形是 ( ) A.锐角三角形 B.等腰三角形 C.直角三角形 D.钝角三角形8、将一张长方形纸片ABCD 如图所示折叠，使顶点C 落在C ′点. 已知AB=2,∠DEC ′=30°,则折痕DE 的长为 （ ）A 、4B 、32C 、2D 、19、如图，∠B C A =90，C D ⊥A B ，则图中与∠A 互余的角有 （ ） A ．1个 B 、2个 C 、3个 D 、4个10. 具有下列条件的△ABC 中，不是直角三角形的是 （ ） A ．∠A -∠B =∠C B 、∠A =3∠C ，∠B =2∠C C 、∠A =∠B =21∠C D 、∠A =∠B =2∠C二、填空题11、“直角三角形两锐角互余”逆定律(填:“有”或“没有”)12、直角三角形中一个锐角为30°,斜边和最小的边的和为12cm,则斜边长为 .13、等腰直角三角形的斜边长为3,则它的面积为 .14、等腰三角形一腰上的高等于该三角形一条边长度的一半,则其顶角为 .15、已知在△ABC中，∠ACB=90°，CD是高，∠A=30°，AB=4cm,则BC=_______cm,∠BCD=_______，BD=_______cm，AD=________cm；16、已知三角形的的三个内角的度数之比为1：2：3，且最短边是3厘米，则最长边上的中线等于____________；17、在△ABC中，∠C=90°，∠A、∠B的平分线相交于O，则∠AOB=_________；18、等边三角形的高为2，则它的面积是。

板块一：直角三角形的基本性质有一个角是90︒的三角形叫做直角三角形。

性质一：直角三角形的两个锐角互余性质二：直角三角形斜边上的中线等于斜边的一半推论一：在直角三角形中，如果一个锐角等于30︒，那么它所对的直角边等于斜边的一半； 推论二：在直角三角形中，如果一条直角边等于斜边的一半，那么这条直角边所对的角等于30︒。

重要结论：直角三角形两直角边的乘积等于斜边与斜边上的高的乘积。

【例题1】 【基础、提高】请证明下列命题：1、直角三角形的斜边中线等于斜边的一半2、如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形. 【尖子】在ABC ∆中，=30B ∠︒，2AB AC =，求证 ：ABC ∆为直角三角形.第二讲 直角三角形之基础【例题2】 【提高】在ABC ∆中，BD DC =，若AD DC ⊥，30BAD ∠=︒，求证：12AC AB =. DCBA【尖子】在Rt ABC ∆中，90ACB ∠=︒，AC BC <，若214BC AC AB =，则_______B ∠=. CBA【例题3】 在ABC ∆中，点D 在边AC 上，DB BC =，点E 是CD 的中点，点F 是AB 的中点，（1）求证：12EF AB =（2）过点A 作AG 平行于EF ，交BE 的延长线于点G ，求证：ABE ∆≌AGE ∆ FED CBA【例题4】 （1）AC 、BD 相交于点E ，且BA BE =，CE CD =，M 、N 、P 分别是AE 、DE 、BC 的中点，求证：MP NP =.NMEDCBA（2）在ABC ∆中，点D 在AC 上，且BD AB ⊥，2C A ∠=∠，求证：2AD BC =CDAB【例题5】 【基础、提高】在ABC ∆中，AD BC ⊥，BE AC ⊥，45ABC ∠=︒，M 是BF 的中点，N 是AC的中点，那么线段DM 、DN 有何关系？并说明理由.NMFE DCBA【尖子】AD 是ABC ∆的BAC ∠内部的任意一条射线，BD AD ⊥，CE AD ⊥，垂足分别为D 、E ，M 是BC 的中点，求证：MD ME =MECDBA【例题6】 （1）在ABC ∆中，CD AB ⊥，垂足为D ，BE AC ⊥,垂足为E ，联结DE ，点G F 、分别是BC 、DE 的中点，求证：GF DE ⊥EFGDCBA（2）如图，在ABC ∆中，D 是BC 边上一点，过D 点作DE AB ⊥于E ，DF AC ⊥于F ，M 、N 分别是AD 、EF 的中点，求证：MN EF ⊥.NMF DECBA板块二：等腰直角三角形两条直角边相等的直角三角形，叫做等腰直角三角形 性质一：等腰直角三角形的三个角分别为45︒，45︒，90︒ 性质二：等腰直角三角形的三边比为性质三：等腰直角三角形底边上的中线等于底边的一半，同时也是底边上的高和顶角平分线.另外，等腰直角三角形还可以看成是正方形的“半成品”，因此“还原正方形”也是等腰直角三角形常用的辅助线做法之一.【例题7】 在MNP ∆中，45MNP ∠=︒，H 是高MQ 和NR 的交点，求证：HN PM =PQRHNM【例题8】 两个全等的含30︒、60︒角的三角板ADE 和三角板ABC ，如图所示放置，E 、A 、C 三点在一条直线上，连结BD ，取BD 的中点M ，连结ME 、MC ，试判断EMC ∆的形状，并说明理由.EMDCBA【例题9】 在Rt ABC ∆中，AB AC =，90A ∠=︒，D 为BC 上任意一点，且DF AB ⊥于F ，DE AC ⊥于E ，M 为BC 的中点，试判断MEF ∆是什么形状的三角形，并证明你的结论.MF ECBA【例题10】 已知，ABC ∆中，AB AC =，90BAC ∠=︒，D 是AC 的中点，AF BD ⊥于E ，交BC 于F ，连接DF ，求证：ADB CDF ∠=∠.EFDCBA【例题11】 【基础、提高】已知ABC ∆和AEF ∆是以A 为直角顶点的等腰直角三角形，A 、C 、F 在同一条直线上，求证：BF CE =，BF CE ⊥.E【尖子】已知AB AC =,AE AF =,90BAC EAF ∠=∠=︒,BF 、CE 交于点M ，连接AM ， 求证：BF CE =，BF CE ⊥；求：AMC ∠的度数.EBMF C A【练习1】 在ABC ∆中，AB AC =，120BAC ∠=︒，EF 为线段AB 的垂直平分线，求证：2FC BF =CFEBA【练习2】 三个正方形如图中排列，AC 、AD 、AE 为三条对角线，求123∠+∠+∠的度数321EDA【练习3】 已知，所图所示，Rt ABC ∆中，AB AC =，90BAC ∠=︒，O 为BC 的中点，（1）写出点O 到ABC ∆的三个顶点A 、B 、C 的距离的关系（不要求证明）（2）如果点M 、N 分别在线段AC 、AB 上移动，且在移动中保持AN CM =，试判断OMN ∆ 的形状，并证明你的结论.N MOCBA【练习4】 小华将一条直角边为1的一个等腰直角三角形纸片（如图1），沿它的对称轴折叠1次后得到一个等腰直线三角形（如图2），再将图2的等腰直角三角形沿它的对称轴折叠后得到一个等腰直三角形（如图3），则图3中的等腰直角三角形的一条腰长为 ；同上操作，若小华连续将图1的等腰直角三角形折叠n 次后所得到的等腰直角三角形（如图1n +）的一条腰长为 .图n +1. . .图1【练习5】 已知在ABC ∆中，90BAC ∠=︒，AB AC =，D 、E 在BC 上，45DAE ∠=︒，2BD =，3CE =，求DE 的长ED CBA【练习6】 已知在ABC ∆中，90BAC ∠=︒，AB AC =，AD BC ⊥于D ，E 为AC 上一点，BE 交AD 于H ，AF BE ⊥于G ，求证：DH DF =，FH 平行于AC .G E FHDCBA【练习7】 在等腰Rt ABC ∆中，90A ∠=︒，P 为BC 延长线上一点，PE AB ⊥，PF AC ⊥，M 为BC 中点，联结ME 、MF ，求证：ME MF =，ME MF ⊥.FE PMCBA。

教学设计表进行线段转化，试着想一想，还有没有别的方法？3、几何画板演示辅助线添法，引导学生进行证明5、小总结：根据之前的学习，我们知道当遇到线段的倍分问题时，可以使用线段的转化来解决，那么推论1给我们提供了什么新思路？题还可以使用特殊角转化（推论1）（板书）例题讲解，巩固运用（1）13’30”-19’40”掌握例题11、让我们来看看这道例题能不能使用我们学习的新思路去解决？题目（板书）：已知：AB=AC，∠B=30°，AD⊥AC求证：1=2BD DC请学生在导学单上先标出已知条件（一位同学上台标记），并思考如何证明3、讲解例题（板2、一位学生用粉笔标出已知条件，效果图：全体学生思考如何证明书）深化理解，变式训练19’40”-27’30”完成导学单上练习部分第1题1、通过用特殊角转化线段的倍分关系，我们已经解决了一道例题，现在请你们自主完成练习部分第一题：3、巡场进行个别辅导（①指出这题是例题1的变式②提示学生将已知在图上进行标记），请完成得快的同学上台分享思路2、完成导学单上练习部分第一题4、一位学生上台讲练习1（通过垂直平分线的定义得到BD=AD，得∠B=∠BAD=30°，从而∠DAC=∠BAC-∠BAD=120°-30°=90°，于是CD=2AD=2BD）几何画板操作简单、绘图精准直观，可以很好地辅助几何题的讲解。

辅以电子白板取代传统黑板，ActivInspire电子白板笔取代粉笔，如虎添翼。

自主梳理，证明推论227’30”-32’00”由推论1的逆命题得到推论2，理解推论2的证明1、回忆之前我们学习的垂直平分线定理和角平分线定理都有逆定理，那请一位同学用文字语言试着说说看推论1的逆命题？3、转化为几何语言？5、思考这个命题2、一位同学回答：在直角三角形中，如果一条直角边等于斜边的一半，那么这条直角边所对的角等于30°4、学生回答：已知：在Rt△ABC中，∠ACB=90°，12BC AB，求运用几何画板演示定理的推理过程，清晰直观，大大提升了课堂教学的效率。