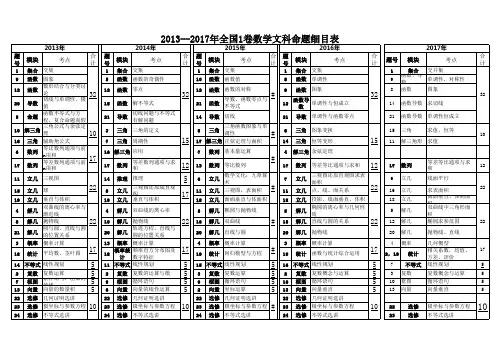
2013至2017年全国一卷高考数列

数列专题高考真题(2014·I) 17. (本小题满分12分) 已知数列{}的前项和为，=1，，，其中为常数.（Ⅰ）证明：；（Ⅱ）是否存在，使得{}为等差数列并说明理由.(2014·II) 17.（本小题满分12分） 已知数列满足=1，.（Ⅰ）证明是等比数列，并求的通项公式；（Ⅱ）证明： .(2015·I)（17）（本小题满分12分）为数列的前项和.已知，（Ⅰ）求的通项公式：（Ⅱ）设 ,求数列的前项和。

(2015·I I)（4）等比数列满足，135a a a ++ =21，则357a a a ++= ( )（A ）21 （B ）42 （C ）63 （D ）84(2015·I I)（16）设n S 是数列{}n a 的前n 项和，且11a =-，11n n n a S S ++=，则n S =________． (2016·I)（3）已知等差数列前9项的和为27，，则（A ）100 （B ）99 （C ）98 （D ）97(2016·I)（15）设等比数列满足的最大值为__________。

(2016·II)（17）（本题满分12分）S n 为等差数列的前项和，且=1 ，=28 记，其中表示不超过的最大整数，如.（I ）求，，；（II ）求数列的前1 000项和.(2016·III)（12）定义“规范01数列”如下：共有项，其中项为0，项为1，且对任意，中0的个数不少于1的个数.若，则不同的“规范01数列”共有 （A ）18个（B ）16个（C ）14个（D ）12个(2016·III)（17）（本小题满分12分）已知数列的前项和，其中（I ）证明是等比数列，并求其通项公式；（II ）若 ，求.(2017·I)4．记n S 为等差数列{}n a 的前n 项和．若4524a a +=，648S =，则{}n a 的公差为A ．1B ．2C ．4D ．8(2017·I)12．几位大学生响应国家的创业号召，开发了一款应用软件。

1、（2016全国I 卷17题）（本题满分12分）已知{}n a 是公差为3的等差数列，数列{}n b 满足12111==3n n n n b b a b b nb +++=1，，，. （I ）求{}n a 的通项公式； （II ）求{}n b 的前n 项和.【答案】（I ）；（II ）考点：等差数列与等比数列 2、（2015全国I 卷7题）已知是公差为1的等差数列，则=4，=（A ） （B ） （C ）10 （D ）12解析：18141110(1)1119,82844(46),,92222n n n S na S a S a a a -=+=+==+==+=，故答案选B.3、（2015全国I 卷13题）在数列{a n }中， a 1=2,a n+1=2a n , S n 为{a n }的前n 项和。

若S n =126，则n=.答案：6 解析：由a 1=2,a n+1=2a n ,可得1172,22126,22,6n n n n n a S n ++==-===4、（2014全国I 卷17题）（本小题满分12分）已知{}n a 是递增的等差数列，2a ，4a 是方程2560x x -+=的根。

（I ）求{}n a 的通项公式； （II ）求数列2n n a ⎧⎫⎨⎬⎩⎭的前n 项和. 【解析】：（I ）方程2560x x -+=的两根为2,3,由题意得22a =，43a =，设数列{}n a 的公差为 d ,，则422a a d -=，故d=12，从而132a =， 所以{}n a 的通项公式为：112n a n =+ …………6 分 (Ⅱ)设求数列2n n a ⎧⎫⎨⎬⎩⎭的前n 项和为S n ,由(Ⅰ)知1222n nn a n ++=， 则：23413451222222n n n n n S +++=+++++ 34512134512222222n n n n n S ++++=+++++ 两式相减得 341212131112311212422224422n n n n n n n S ++++++⎛⎫⎛⎫=++++-=+-- ⎪ ⎪⎝⎭⎝⎭ 所以1422n n n S ++=-………12分 5、（2013全国I 卷6题）设首项为1，公比为23的等比数列{}n a 的前n 项和为n S ，则（ ）（A ）21n n S a =- （B ）32n n S a =- （C ）43n n S a =- （D ）32n n S a =-6、（2013全国I 卷17题）（本小题满分12分）已知等差数列{}n a 的前n 项和n S 满足30S =，55S =-。

2013年高考真题——数列0.（2013·湖南高考文科）.对于E={a 1，a 2,….a 100}的子集X={k i i i a a a ,,21},定义X 的“特征数列”为x 1,x 2…,x 100,其中121===k i i i x x x .其余项均为0，例如子集{a 2，a 3}的 “特征数列”为0，1，1，0，0，…,0（1）子集{a 1,a 3,a 5}的“特征数列”的前3项和等于________________;（2）若E 的子集P 的“特征数列”P 1，P 2，…,P 100 满足11=p ，P i +P i+1=1, 1≤i ≤99;E 的子集Q 的“特征数列” q 1，q 2，q 100 满足q 1=1，q 1+q j+1+q j+2=1，1≤j ≤98，则P∩Q 的元素个数为___________.1. （2013·新课标Ⅰ高考理科）设等差数列}{n a 的前n 项和为n S ，若21-=-m S ,0=m S ,31=+m S ，则=m （ ） A.3 B.4C.5D. 62.（2013·安徽高考文科）设S n 为等差数列｛a n ｝的前n 项和，837=4,2S a a =-，则a 9=（ ）A.-6B.-4C.-2D.23. （2013·辽宁高考文科）下面是关于公差0d >的等差数列{}n a 的四个命题：1:p 数列{}n a 是递增数列；2:p 数列{}n na 是递增数列；3:p 数列n a n ⎧⎫⎨⎬⎩⎭是递增数列；4:p 数列{}3n a nd +是递增数列；其中的真命题为（ ）12342314.,.,.,.,A p p B p p C p p D p p4. （2013·重庆高考文科）若2、a 、b 、c 、9成等差数列，则c a -= ． 5．（2013·上海高考文科）在等差数列{}n a 中，若a 1+ a 2+ a 3+ a 4=30，则a 2+ a 3= . 6. （2013·广东高考理科）在等差数列{}n a 中，已知3810a a +=，则573a a +=___ 7.(2013·新课标全国Ⅱ高考理科)等差数列{a n }的前n 项和为S n ,已知S 10=0,S 15=25,则n S n 的最小值为 .8.（2013·安徽高考理科））如图，互不相同的点A 1,A 2,…,A n ,…和B 1,B 2,…,B n ,…分别在角O 的两条边上，所有n n A B 相互平行，且所有梯形A n B n B n+1A n+1的面积均相等。

2013---2017年全国1卷高考理科数学分类汇编---数列（2017全国1.理数.4）记n S 为等差数列{}n a 的前n 项和．若4524a a +=，648S =，则{}n a 的公差为 A.1B.2C.4D.8【考点】：等差数列，难度较小。

【思路】：将求和公式化简即可得到公差。

【解析】：()16616648162a a S a a +==⇒+=，451824a a a a +=+=，作差86824a a d d -==⇒=故而选C 。

（2017全国1.理数.12）几位大学生响应国家的创业号召，开发了一款应用软件.为激发大家学习数学的兴趣，他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案：已知数列1，1，2，1，2，4，1，2，4，8，1，2，4，8，16，…，其中第一项是20，接下来的两项是20，21，再接下来的三项是20，21，22，依此类推.求满足如下条件的最小整数N ：N >100且该数列的前N 项和为2的整数幂.那么该款软件的激活码是 A.440B.330C.220D.110【考点】：行列式（杨辉三角）求和问题，计算量较大。

【思路】：将已知的数列列举成行列式的形式，02第一行，1个数，求和为121-0212 第二行，2个数，求和为221- 021222第三行，3个数，求和为321-02122232第四行，4个数，求和为421-021*******第五行，5个数，求和为521-故而可得，第n 行，n 个数，求和为21n-，因此前n 行，一共有()12n n +个数，求和为122n n +--【解析】：根据上面的分析，我们可以类推得到，前14行，有105个数，求和为15216-，当110N =时，求和为15515216212172n -+-=-≠前20行，有210个数，求和为21222-，当220N =时，求和为211021102222122232n -+-=+-≠前25行，有225个数，求和为26226-，当330N =时，求和为2652652262122272n -+-=+-≠前29行，有435个数，求和为30231-，当440N =时，求和为30530231212-+-=，故而选A 。

2013年全国各省市文科数学—数列1、2013大纲文T7.已知数列{}n a 满足{}12430,,103n n n a a a a ++==-则的前项和等于（A ）()-10-61-3（B ）()-1011-39（C ）()-1031-3 （D ）()-1031+3 2、2013陕西文T13. 观察下列等式: 23(11)21(21)(22)213(31)(32)(33)2135+=⨯++=⨯⨯+++=⨯⨯⨯…照此规律, 第n 个等式可为 .3、2013辽宁文T4.下面是关于公差0d >的等差数列()n a 的四个命题：{}1:n p a 数列是递增数列； {}2:n p na 数列是递增数列；3:n a p n ⎧⎫⎨⎬⎩⎭数列是递增数列；{}4:3n p a nd +数列是递增数列； 其中的真命题为（A ）12,p p （B ）34,p p （C ）23,p p （D ）14,p p 4、2013安徽文T7.设n S 为等差数列{}n a 的前n 项和，8374,2S a a ==-，则9a = （A ）6- （B ）4- （C ）2- （D ）2 5、2013重庆文T12.若2、a 、b 、c 、9成等差数列，则c a -= ． 6、2013上海文T2.在等差数列{}n a 中，若a 1+ a 2+ a 3+ a 4=30，则a 2+ a 3= . 7、2013新课标文T6.设首项为1，公比为23的等比数列{}n a 的前n 项和为n S ，则（ ）（A ）21n n S a =- （B ）32n n S a =- （C ）43n n S a =- （D ）32n n S a =- 8、2013辽宁理T14.已知等比数列{}n a 是递增数列，n S 是{}n a 的前n 项和.若1a ，3a 是方程26540x x S -+==的两个根，则 .9、2013北京文T11．若等比数列{}n a 满足2420a a +=，3540a a +=，则公比q = ；前n 项和n S = 。

第六章 数列第一节 等差数列与等比数列题型67 等差（等比）数列的公差（公比）1.（2013辽宁4）下面是关于公差>0d 的等差数列{}n a 的四个命题：1:p 数列{}n a 是递增数列； 2:p 数列{}n na 是递增数列； 3:p 数列n a n ⎧⎫⎨⎬⎩⎭是递增数列； 4:p 数列{}3n a nd +是递增数列；其中的真命题为( ).A. 12p p ，B. 34p p ，C. 23p p ，D. 14p p ， 2.（2013江西理3）等比数列x ，33x +，66x +，⋅⋅⋅的第四项等于（ ）. A ．24- B ．0 C ．12 D ．243. (2013全国新课标卷理3）等比数列{}n a 的前n 项和为n S ，已知3215109S a a a =+=，，则1a =（ ）. A.13 B. 13- C. 19 D. 19- 4. (2013福建理9）已知等比数列{}n a 的公比为q ，记m n m n m n m n a a a b +-+-+-+⋅⋅⋅++=)1(2)1(1)1(，m n m n m n m n a a a b +-+-+-*⋅⋅⋅**=)1(2)1(1)1(，()*,m n ∈N ，则以下结论一定正确的是（ ）A. 数列{}n b 为等差数列，公差为m qB. 数列{}n b 为等比数列，公比为m q 2C. 数列{}n c 为等比数列，公比为2m q D. 数列{}n c 为等比数列，公比为mm q 5.（2014 北京理 5）设{}n a 是公比为q 的等比数列，则“1q >”是“{}n a ”为递增数列的（ ）.A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件6.（2014 福建理 3）等差数列{}n a 的前n 项和n S ，若132,12a S ==，则6a =( ). A.8 B.10 C.12 D.147.（2014 辽宁理 8）设等差数列{}n a 的公差为d ，若数列{}12n a a 为递减数列，则（ ）. A ．0d < B ．0d > C ．10a d < D ．10a d >8.（2014 重庆理 2）对任意等比数列{}n a ，下列说法一定正确的是（ ）. A. 139,,a a a 成等比数列 B. 236,,a a a 成等比数列 C. 248,,a a a 成等比数列 D. 369,,a a a 成等比数列9.（2014 安徽理 12）数列{}n a 是等差数列，若11a +，33a +，55a +构成公比为q 的等比数列，则q = .10.（2015湖南理14）设n S 为等比数列{}n a 的前项和，若11a =，且13S ，22S ，3S 成等差数列，则n a =.10.解析 因为13S ，22S ，3S 成等差数列，所以21343S S S =+， 即12112322()3a a a a a a ⨯+=+++，得323a a =，所以3q =.又因为}{n a 为等比数列，所以1113--==n n n q a a .11.（2015陕西理13）中位数为1010的一组数构成等差数列，其末项为2015，则该数列的首项为 ．11.解析 当项数2n k =时，中位数11101022k k na a a a +++===， 所以121010202020155n a a =⨯-=-=； 当项数21n k =-时，中位数110102nk a a a +===， 所以121010202020155n a a =⨯-=-=. 综上所述，首项为5.12.（2015浙江理3）已知{}n a 是等差数列，公差d 不为零，前n 项和是n S ，若348,,a a a 成等比数列，则（ ）．A.140,0a d dS >>B.140,0a d dS <<C.140,0a d dS ><D.140,0a d dS <>12.解析 因为348,,a a a 成等比数列，所以2438a a a =⋅，即()()()2111327a d a d a d +=+⋅+，所以21350a d d +=．因为0d ≠，所以135a d =-，所以21503a d d =-<．又414320246233S a d d d d ⨯=+=-+=- ， 所以24203dS d =-<．故选B ．13.（2015重庆理2）在等差数列{}n a 中，若24a =，42a =，则6a =（ ）. A. 1- B. 0 C. 1 D. 6 13.解析 由等差中项知：4262a a a =+，所以64220a a a =-=.故选B.14.（2016全国乙理3）已知等差数列前项的和为，，则（ ）. A. B. C. D. 14.C 解析 设等差数列的公差为，由，得.又，则，得.故.故选C. 15.（2016天津理5）设是首项为正数的等比数列，公比为，则”“是”对任意的正整数，“的（ ）.A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件15. C 解析 由题意得，.由，故是必要不充分条件.故选C.16.（2016江苏8）已知是等差数列，是其前项和．若，，则的值是 ．16. 解析 设公差为，则由题意可得，解得，则．17.（2016北京理12）已知为等差数列，为其前项和，若，，则__________. 17. 解析 设等差数列的公差为d ，由题设得，解得，所以. 18.(2017北京理10)若等差数列和等比数列满足，，则{}n a 92710=8a 100=a 100999897{}n a d 95279S a ==53a =108a =10555d a a =-=1d =100109089098a a d =+=+={}n a q 0q <n 2120n n a a -+<()2221212100n n n na a a q q ---+<⇔+<⇔()()2(1)10,1n q q q -+<⇔∈-∞-()(),1,0-∞-⊆-∞{}n a n S n 2123a a +=-510S =9a 20d ()2111351010a a d a d ⎧++=-⎪⎨+=⎪⎩143a d =-⎧⎨=⎩948320a =-+⨯={}n a n S n 16a =350a a +=6S =6{}n a 1116(2)(4)0aa d a d =⎧⎨+++=⎩162a d =⎧⎨=-⎩6165662S a d ⨯=+={}n a {}n b 11–1a b ==448a b ==_______. 18.解析 由，，则，由，，则，则.故. 19.（2017全国1理4）记为等差数列的前项和．若，，则的公差为（ ）.A ．1B ．2C ．4D ．819.解析 ，，联立，得，即，所以.故选C.20.（2017全国2理3）我国古代数学名著《算法统宗》中有如下问题：“远望巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯？”意思是：一座7层塔共挂了盏灯，且相邻两层中的下一层灯数是上一层灯数的2倍，则塔的顶层共有灯（ ）. A ．1盏 B ．3盏 C ．5盏 D ．9盏 20.解析 设顶层灯数为，，，解得．故选B.21.（2017全国3理14）设等比数列满足， ，则 ___________．21.解析 因为为等比数列，设公比为．由题意得，即 显然，，，得，即，代入式可得， 所以．题型68 等差、等比数列求和问题的拓展22．（2013江西理17）正项数列{}n a 的前n 项和n S 满足：222(1)()0n n S n n S n n -+--+=． (1) 求数列{}n a 的通项公式n a ； (2) 令221(2)n n n b n a +=+，数列{}n b 的前n 项和为n T ．证明：对于任意的n *∈Ν，都有564n T <． 22a b =11a =-48a =21132a a d =+=-+=11b =-48b =2q =-212b b q ==22212a b ==n S {}n a n 4524a a +=648S ={}n a 45113424a a a d a d +=+++=61656482S a d ⨯=+=112724 61548 a d a d +=⎧⎪⎨+=⎪⎩①②3⨯-①②()211524-=d 624d =4d =3811a 2=q ()7171238112-==-a S 13a ={}n a 12–1a a +=13––3a a =4a ={}n a q 121313a a a a +=-⎧⎨-=-⎩112111 3 a a q a a q +=-⎧⎪⎨-=-⎪⎩①②1q ≠10a ≠式式②①13q -=2q =-①11a =()3341128a a q ==⨯-=-23. （2013江苏19）设{}n a 是首项为a ，公差为d 的等差数列)0(≠d ，n S 是其前n 项和.记cn nS b n n +=2，n *∈Ν，其中c 为实数. （1）若0=c ，且421b b b ，，成等比数列，证明：k nk S n S 2=（,k n *∈Ν）；（2）若{}n b 是等差数列，证明：0=c .24.（2017全国1理12）几位大学生响应国家的创业号召，开发了一款应用软件.为激发大家学习数学的兴趣，他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案：已知数列1，1，2，1，2，4，1，2，4，8，1，2，4，8，16 ，…，其中第一项是，接下来的两项是，，再接下来的三项是，，，依此类推.求满足如下条件的最小整数且该数列的前项和为2的整数幂.那么该款软件的激活码是（ ）. A.B.C.D.24.解析 设首项为第1组，接下来两项为第2组，再接下来三项为第3组，以此类推． 设第组的项数为，则组的项数和为，由题意得，.令，得且，即出现在第13组之后，第组的和为，组总共的和为，若要使前项和为2的整数幂，则项的和应与互为相反数，即，，得的最小值为，则.故选A.25.(2017山东理19）已知是各项均为正数的等比数列，且，， （1）求数列的通项公式；（2）如图所示，在平面直角坐标系中，依次联结点，，…，得到折线，求由该折线与直线，，所围成的区域的面积.020212021222100N N >：N 440330220110n n n ()12n n +100N >()11002n n +>14n ≥*n ∈N N n 122112nn -=--n ()12122212n n n n +--=---N ()12n n N +-21k -2n --()*21214k n k n -=+∈N ，≥()2log 3k n =+n 295n k ==，()2912954402N ⨯+=+={}n x 123x x +=322x x -={}n x xOy ()111P x ，()222P x ，()11,1n n P x n +++121n PPP +0y =1x x =1n x x +=n T25.解析 （1）设数列的公比为，由已知.由题意得，所以，因为，所以，因此数列的通项公式为（2）过向轴作垂线，垂足分别为，由（1）得记梯形的面积为. 由题意，所以 ①又②，得 所以26.（2014 大纲理 10）等比数列{}n a 中，4525a a ==，，则数列{}lg n a 的前8项和等于（ ）.A ．6B ．5C ．4D ．3{}n x q 0q >1121132x x q x q x q +=⎧⎨-=⎩23520q q --=0q >12,1q x =={}n x 12.n n x -=1231,,,,n P P P P +x 1231,,,,n Q Q Q Q +111222.n n n n n x x --+-=-=11n n n n P P Q Q ++n b 12(1)2(21)22n n n n n b n --++=⨯=+⨯123n n T b b b b =++++=10132325272(21)2(21)2n n n n ---⨯+⨯+⨯++-⨯++⨯012212325272(21)2(21)2n n n T n n --=⨯+⨯+⨯++-⨯++⨯-①②121132(222)(21)2n n n T n ----=⨯++++-+⨯=1132(12)(21)2.212n n n ---+-+⨯-(21)21.2n n n T -⨯+=题型69 等差、等比数列的性质及其应用26.（2013广东12）在等差数列{}n a 中，已知3810a a +=，则573a a += ． 27. （2013江苏14）在正项等比数列}{n a 中，215=a ，376=+a a ，则满足n n a a a a a a 2121>+++的最大正整数n 的值为 .28. （2013浙江18）在公差为d 的等差数列{}n a 中，已知101=a ，且3215,22,a a a +成等比数列. （1）求n a d ,；（2）若0<d ，求.||||||||321n a a a a ++++29.（2014 天津理 11）设{}n a 是首项为1a ，公差为1-的等差数列，n S 为其前n 项和.若124,,S S S 成等比数列，则1a 的值为__________.30.（2014 江苏理 20）设数列{}n a 的前n 项和为n S ．若对任意正整数n ，总存在正整数m ，使得n m S a =，则称{}n a 是“H 数列”．（1）若数列{}n a 的前n 项和2nn S = ()*n ∈N ，证明：{}n a 是“H 数列”；（2）设{}n a 是等差数列，其首项11a =，公差0d <．若{}n a 是“H 数列”，求d 的值； （3）证明：对任意的等差数列{}n a ，总存在两个“H 数列”{}n b 和{}n c ，使得n n na b c =+()*n ∈N 成立．31.（2014 天津理 19）已知q 和n 均为给定的大于1的自然数.设集合{}0,1,2,,1M q =-，集合{}112,,1,2,,n n i A x x x x q x q x M i n -+∈===++.（1）当2q =，3n =时，用列举法表示集合A ； （2）设,s t A Î，112n n s a a q a q -=+++，112n n t b b q b q -=+++，其中,i i a b M ∈，1,2,i n =.证明：若n n a b <，则s t <.32.（2014 北京理 12）若等差数列{}n a 满足7890a a a ++>，7100a a +<，则当n =________时，{}n a 的前n 项和最大.33.（2015安徽理14）已知数列{}n a 是递增的等比数列，14329,8a a a a +==，则数列{}n a 的前n 项和等于 .34.解析 设等比数列的公比为()1q q >，则31123198a a q a q ⎧+=⎪⎨=⎪⎩①②，解得112a q =⎧⎨=⎩或1812a q =⎧⎪⎨=⎪⎩（舍去），所以122112nn n S -==--． 35.（2015北京理6）设{}n a 是等差数列，下列结论中正确的是（ ）. A.若120a a +>，则230a a +> B.若130a a +<，则120a a +< C.若120a a <<，则2a >D.若10a <，则()()21230a a a a -->36.解析 依题意，{}n a 是等差数列，若120a a +>，并不能推出230a a +>； 故选项A 不正确.对于B 选项，若130a a +<，并不能推出120a a +<；故选项B 不正确.对于C 选项，若120a a <<，则210d a a =->，()()22213222a a a a a d a d -=--+=()2222220a a d d --=>，因此2a >C 正确.对于D 选项，若10a <，则()()221230a a a a d--=-…，并不能推出()()21230a a a a -->.故选C.37.（2015福建理8）若,a b 是函数()()20,0f x x px q p q =-+>>的两个不同的零点，且,,2a b -这三个数可适当排序后成等差数列，也可适当排序后成等比数列，则=p q +（ ）.A ．6B ．7C ．8D ．9 37.解析 由韦达定理得a b p +=，ab q =，则0a >，0b >，当a ，b ，2-适当排序后 成等比数列时，2-必为等比中项，故4ab q ==，此时4b a=．当适当排序后成等差数列时，2-必不是等差中项，当a 是等差中项时，422a a =-，解得1a =，4b =；当4a是等差中项时，82a a=-，解得4a =，1b =． 综上所述，5a b p +==，所以9p q +=．故选D ．38.（2015广东理10）在等差数列{}n a 中，若3456725a a a a a ++++=，则28a a +=．38.解析 因为{}n a 是等差数列，所以37462852a a a a a a a +=+=+=，345a a a +++6a +7a =5525a =，即55a =，所以285210a a a +==．故应填10． 39.（2015全国Ⅱ理4）等比数列{}n a 满足13a =，13521a a a ++=，则357a a a ++=（ ）．A.21B. 42C. 63D. 84 39.解析 由题意可设等比数列的公比为q ，则由13521a a a ++=得，2411121a a q a q ++=.又因为13a =，所以4260q q +-=.解得22q =或23q =-（舍去），所以()235713521242a a a a a a q ++=++=⨯=.故选B.40.（2016全国乙理15）设等比数列满足，，则的最大值为 .40. 解析 由，得. 又，得.故.解法一：由，得，得，且.故当或时，取得最大值，即.解法二：.故当或时，{}n a 1310a a +=245a a +=12n a a a ⋅⋅⋅64()241313105a a qa qa q a a q +=+=+==12q =()222131111111102a a a a q a q a ⎡⎤⎛⎫+=+=+=+=⎢⎥ ⎪⎝⎭⎢⎥⎣⎦18a =()14*11822n n n a n --⎛⎫⎛⎫==∈ ⎪⎪⎝⎭⎝⎭N 1n a (4)112n -⎛⎫⎪⎝⎭…4n …41a =3n =412n a a a ()321121231234max11164222n a a a a a a a a a a ---⎛⎫⎛⎫⎛⎫==== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭()()211720121221211822n n n n n n nn a a a a q--+++++-⎛⎫==⋅= ⎪⎝⎭3n =4取得最大值.41.（2016全国甲理17）为等差数列的前项和，且，．记，其中表示不超过的最大整数，如，． （1）求，，；（2）求数列{}n b 的前1000项和．42.解析 （1）设的公差为，，所以，所以，所以．所以，，．（2）当时，；当时，； 当时，；当时，． 所以． 43.（2017江苏09）等比数列的各项均为实数，其前项的和为，已知，，则 ． 43.解析 解法一：由题意等比数列公比不为，由，因此，得． 又，得，所以． 故填．解法二（由分段和关系）：由题意，所以，即．下同解法一．12n a a a 6264=n S {}n a n 11a =728S =[]lg n n b a =[]x []0.90=[]lg 991=1b 11b 101b {}n a d 74728S a ==44a =4113a a d -==1(1)n a a n d n =+-=[][]11lg lg10b a ===[][]1111lg lg111b a ===[][]101101lg lg1012b a ===0lg 1n a <≤129n =⋅⋅⋅，，，1lg 2n a <≤101199n =⋅⋅⋅，，，2lg 3n a <≤100101999n =⋅⋅⋅，，，lg 3n a =1000n =1000121000=T b b b =++⋅⋅⋅+[][][]121000lg lg lg =a a a ++⋅⋅⋅+091902900311893⨯+⨯+⨯+⨯={}n a n n S 374S =6634S =8a =1()()313616171416314a q S q a q S q ⎧-==⎪-⎪⎨-⎪==⎪-⎩36319S q S =+=2q =3123S a a a =++()2117174a q q a =++==114a =78132a a q ==323363374634S S S q S ⎧=⎪⎪⎨⎪=+=⎪⎩38q =2q =44.（2017全国2理15）等差数列的前项和为，，，则． 44.解析 设首项为，公差为．由，，得，，所以，，. 题型70 判断或证明数列是等差、等比数列1.（2014 新课标1理17）已知数列{}n a 的前n 项和为n S ，11a =，0n a ≠，11n n n a a S λ+=-，其中λ为常数.（1）证明：2n n a a λ+-=；（2）是否存在λ，使得{}n a 为等差数列？并说明理由.2.（2014 新课标2理17）已知数列{}n a 满足11a =，131n n a a +=+. （1）证明12n a ⎧⎫+⎨⎬⎩⎭是等比数列，并求{}n a 的通项公式； （2）证明：1211132n a a a ++<…+. 3.（2015湖南理21）已知0a >，函数()[)()e sin 0,ax f x x x =∈+∞. 记n x 为()f x 的从小到大的第n ()*n ∈N 个极值点.证明： （1）数列(){}nf x 是等比数列；（2）若a ，则对一切*n ∈N ，()n n x f x <恒成立.4.解析 证明 (1) '()e sin e cos e (sin cos )ax ax axf x a x x a x x =+=+e sin()ax x ϕ=+，其中a 1tan =ϕ，π02ϕ<<. {}n a n n S 33a =410S =11nk kS ==∑{}n a 1a d 3123a a d =+=414610S a d =+=11a =1d =n a n =()12n n n S +=()()112222122311nk kS n n n n ==++++=⨯⨯-+∑11111112122311n n n n ⎛⎫-+-++-+-= ⎪-+⎝⎭122111n n n ⎛⎫-= ⎪++⎝⎭令 0)('=x f ，由0x …得 πx m ϕ+=，即*π,x m m ϕ=-∈N .对k ∈N ，若2π(21)πk x k ϕ<+<+，即2π(21)πk x k ϕϕ-<<+-，则0)('>x f ； 若(21)π(22)πk x k ϕ+<+<+，即(21)π(22)πk x k ϕϕ+-<<+-，则0)('<x f . 因此，在区间((1)π,π)m m ϕ--与(π,π)m m ϕ-上，)('x f 的符号总相反，于是，当*π,x m m ϕ=-∈N 时，)(x f 取得极值，所以*π,n x n n ϕ=-∈N . 此时，()1()()esin(π)(1)e a n n a n n f x n πϕπϕϕ-+-=-=-，易知0)(≠n x f ， 且 2[(1)π]π11(π)()(1)e e ()(1)en a n a n n a n n f x f x ϕϕ++-++--==--是常数， 故数列)}({n x f 是首项为(π)1()esin a f x ϕϕ-=，公比为πe a -的等比数列. (2) 由(1)知，sin ϕ=，于是对一切*n ∈N ，|)(|n n x f x <恒成立，即(π)πa n n ϕϕ--<恒成立，(π)e (π)a n a n ϕϕ-<- （*）恒成立（因为>0a ）. 设e ()(0)tg t t t=>，则2e (1)'()t t g t t -=.令()'0g t =得1=t . 当10<<t 时，0)('<t g ，所以)(t g 在)1,0(上单调递减； 当1>t 时，0)('>t g ，所以)(t g 在),1(∞+上单调递增. 从而当1=t 时，函数)(t g 取得最小值(1)e g =.因此，要使（*）式恒成立，只需(1)e g a <=，即只需a >.而当a =时，由1tan a ϕ==>π02ϕ<<知，ππ32ϕ<<.于是2ππ3ϕ-<<2n …时，3ππ2π2n ϕϕ-≥->>， 因此，对一切*n ∈N，1n ax =≠，所以()(1)e n g ax g a >==， 故（*）式也恒成立.综上所述，若a ，则对一切*n ∈N ，|)(|n n x f x <恒成立.5.（2015江苏卷20）设1234,,,a a a a 是各项为正数且公差为d ()0d ≠的等差数列．（1）证明：31242,2,2,2aaaa依次成等比数列；（2）是否存在1,a d ，使得2341234,,,a a a a 依次构成等比数列？并说明理由；（3）是否存在1,a d 及正整数,n k ，使得351234,,,n n k n k n ka a a a +++依次成等比数列，并说明理由．5.解析（1）由题意11a a =，21a a d =+，312a a d =+，413a a d =+，故121122222a d d a a a +==，3211222222a d d d a a a ++==，31413222222d d a a a a d ++==，而120a ≠且20d≠，从而31242,2,2,2a a a a 时以12a为首项，2d 为公比的等比数列．（2）解法一：假设存在满足条件的1,a d ， 从而11a a =，()2221a a d =+，()33312a a d =+，()44413a a d =+，若满足题意，的须使43213624324a a a a a a ⎧=⎪⎨=⎪⎩，即4321332324a a a a a a ⎧=⎪⎨=⎪⎩， 即()()()()()4311132111223a d a a d a d a d a d ⎧+=+⎪⎨+=++⎪⎩①②，化简得3223411122311264030a d a d a d d a d a d d ⎧++-=⎪⎨++=⎪⎩， 因为0d ≠，故32231112211264030a a d a d d a a d d ⎧++-=⎪⎨++=⎪⎩，不妨设1a t d =， 从而转化为32226410310t t t t t ⎧++-=⎪⎨++=⎪⎩③④，由④得231t t =--，代入③得()22316410t t t t --++-=，化简得到210t -=，即12t =， 易见12t =不满足④式，故方程组无解，即不存在满足条件的1,a d ． 解法二：假设存在满足条件的1,a d ，若需满足条件，则必有43213a a a =成立，即为了方便，不妨设1a a d =-，2a a =，3a a d =+， 易知10a a d =->，即a d >，从而()()34a a d a d =-+，即()()422222aa d a ad d =-++4322223422a a d a d a d ad d =++---，整理得334220ad ad d --=，因为0d ≠，故设a t d=，则32210t t --=，构造()3221g t t t =--，则()2'320g t t =->对()1,t ∈+∞恒成立，由()110g =-<，()2110g =>知()1,2t ∈．另外，还需有624324a a a =，即32324a a a =，即()()322a d a a d +=+，整理得2230a d ad d +-=，仿照上面的步骤即210t t +-=，解得()111,22t -=∉或()211,22t -+=∉，因此不满足题意． 综上论证：不存在满足条件的1,a d ．解法三（取对数降为线性）：假设存在满足条件的1,a d ，由1a ，2a ，3a ，4a 均为正数， 因此2341234,,,a a a a 均为正数，所以2341234ln ,ln ,ln ,ln a a a a 构成等差数列，即1234ln ,2ln ,3ln ,4ln a a a a 构成等差数列，不妨设通项为pn q +，1,2,3,4n =， 由于1234,,,a a a a 构成等差数列，且公差为d ()0d ≠， 故设其通项为n a dn a =+，1,2,3,4n =， 从而()ln n dn a pn q +=+，即()ln qdn a p n+=+对1,2,3,4n =均成立， 不妨设()()ln q f x dx a p x =+--，从而()()222'd q dx pdx qaf x dx a x dx a x ++=+=++， 因为0d ≠，0x >，0dx a +>，所以函数()'f x 至多有两个零点，即()f x 在()0,x ∈+∞上至多有三个单调区间， 从而()f x 至多会有三个零点，这与1,2,3,4x =都是()f x 的零点相矛盾， 因此不存在满足条件的1,a d ．（3）解法一（取对数降为线性）：假设存在满足条件的1,a d 及正整数,n k ，使得231234,,,n n k n k n k a a a a +++依次成等比数列，因为231234,,,n n k n k n ka a a a +++都是整数， 所以231234ln ,ln ,ln ,ln n n k n k n ka a a a +++构成等差数列，即()()()1234ln ,ln ,2ln ,3ln n a n k a n a n k a +++构成等差数列， 设其通项为sm t +，1,2,3,4m =，不妨设数列1234,,,a a a a 的通项为m a dm a =+，1,2,3,4m =，0d ≠， 所以()()1ln n m k dm a sm t +-+=+⎡⎤⎣⎦，即()ln sm tdm a km n k++=+-对1,2,3,4m =恒成立，不妨设n k c -=，令()()ln sx tg x dx a kx c+=+-+，则()()()()2's kx c k sx t dg x dx a kx c +-+=-++()2d sc kt dx a kx c -=-++ ()()()()()22d kx c kt sc dx a dx a kx c ++-+=++()()()()22222dk x dkc ktd scd x c d kt sc adx a kx c ++-++-=++，因为0d ≠，0x >，0dx a +>，0kx c +≠，所以函数()'g x 至多有两个零点，即()g x 在()0,x ∈+∞上至多有三个单调区间， 从而()g x 至多会有三个零点，这与1,2,3,4x =都是()g x 的零点相矛盾，因此不存在满足条件的1,a d ，使得231234,,,n n k n k n ka a a a +++依次成等比数列．解法二（多次求导，省考试院提供）：假设存在满足条件的1,a d 及正整数,n k ，使得231234,,,n n k n k n ka a a a +++依次成等比数列，则()()()()()()()22111322111232n k n k n n k n k n k a a d a d a d a d a d +++++⎧+=+⎪⎨++=+⎪⎩，分别在上述两个等式的两边同时除以()21n k a +及()221n k a +，并令1d t a =1,03t t ⎛⎫>-≠ ⎪⎝⎭，则()()()()()()()2232212111312n k n k n k n k n k t t t t t +++++⎧+=+⎪⎨++=+⎪⎩， 将上述两个等式两边取对数，得()()()()()()()()()()2ln 122ln 1ln 13ln 1322ln 12n k t n k t n k t n k t n k t ++=++⎧⎪⎨+++++=++⎪⎩化简得()()()()()()()()2ln 12ln 12ln 1ln 123ln 13ln 13ln 1ln 13k t t n t t k t t n t t ⎧+-+=+-+⎡⎤⎡⎤⎪⎣⎦⎣⎦⎨+-+=+-+⎡⎤⎡⎤⎪⎣⎦⎣⎦⎩，上述两式相除得()()()()()()()()ln 12ln 12ln 1ln 12ln 13ln 12ln 1ln 12t t t t t t t t +-++-+=+-++-+， 化简得()()()()()()ln 13ln 123ln 12ln 14ln 13ln 1t t t t t t +++++=++（*）， 令()()()()()()()4ln 13ln 1ln 13ln 123ln 12ln 1g t t t t t t t =++-++-++，则()()()()()()()()()()222213ln 13312ln 1231ln 1'11213t t t t t t g t t t t ⎡⎤++-+++++⎣⎦=+++， 令()()()()()()()22213ln 13312ln 1231ln 1ht t t t t t t =++-+++++，则()()()()()()()'613ln 13212ln 121ln 1h t t t t t t t =++-+++++⎡⎤⎣⎦.令()()()()()()()()'613ln 13212ln 121ln 1mt h t t t t t t t ==++-+++++⎡⎤⎣⎦， 则()()()()'63ln 134ln 12ln 1m t t t t =+-+++⎡⎤⎣⎦，令()()()()()'63ln 134ln 12ln 1nt m t t t t ==+-+++⎡⎤⎣⎦，则()()()()12'011213n t t t t =>+++，由()()()()00000g h m n ====，()'0n t >，知()n t ，()m t ，()h t ，()g t 在1,03⎛⎫- ⎪⎝⎭和()0,+∞上均单调，故()g t 只有唯一的零点0t =，即方程（*）只有唯一解0t =，故假设不成立．所以不存在满足条件的1,a d 及正整数,n k ，使得231234,,,n n k n k n ka a a a +++依次成等比数列．评注 第（1）问可以探究并证明2n an b =是等比数列．证明：因为112222n n nn a a a d a ++-==，因此2na nb =以112a b =为首项，2d 为公比的等比数列． 第（2）问解法一其实就是通过两元关系找到方程组的解，解高次方程最好的办法就是不断降幂迭代，衔接教材中有一道题就是降幂迭代思维，例：设12x -=，求4221x x x ++-的值．解析因为264x -=32-=，故()223321x x ==-+，即210x x +-=.即12x =是方程210x x +-=的一个根， 故4221xx x ++-()22121x x x =-++-22x =()21x =-22x =-)21=-3=-【1】或者也可以对方程组()()()()()4311132111223a d a a d a d a d a d ⎧+=+⎪⎨+=++⎪⎩①②， 将②代入①得()()()4211113a d a a d a d +=++，化简即()()321113a d a a d +=+，进而探求1a 与d 的关系，由②可直接得到1a 与的关系，验证关系不一致即可证明不存在，如同解法二类似． 【2】为了简化运算，参考标准可以选为2a 与d ，如同解法二类似．但解法二也可以利用迭代，例如解法二涉及32221010t t t t ⎧--=⎪⎨+-=⎪⎩，转换后即()21210t t t ---=，即2210t --=，方程无解．【3】降幂迭代的方向可以不同（部分迭代和全部迭代），仅是步骤复杂程度变化，但结论不变，如处理解法一得到的式子还可以是32226410310t t t t t ⎧++-=⎪⎨++=⎪⎩③④，由④得231t t =--，代入③得()()231631410t t t t --+--+-=，即261670t t ++=，再次迭代，即()6311670t t --++=，解得12t =，同理推翻． 【4】如果直接由624324a a a =可以推证2310t t ++=，其中1a t d=．解得t =1a =或1a =，当1302a d --=>时，易知0d <，此时413302a a d -=+=<，不满足题意；当1302a -+=>时，易知0d <，此时413302a a d +=+=<，不满足题意． 可以直接推翻结论．【5】构造的时候也可以构造成1dt a =，如省考试院公布的标准答案． 解法二是通过论证判定方程组解的范围不一致（一个求解范围，一个是确定值）进行否定，具有一定的风险，因为对解的限制要求较高，若两解差的精度较小，则难以通过此法判定． 因此，往后此类试题也可以考查两方程均无法解出确定则，则我们可以通过降幂迭代或者判定解得范围解决．解法三是从构造方程研究函数零点角度解决．但数学翻译语言：“函数()'f x 至多有两个零点，则()f x 至多有三个单调区间”是不成立的，因为()f x 在无定义的地方可能会间断，将某一单调区间拆成两个，但此题有限制，因此成立．数学翻译语言：“()f x 至多有三个单调区间，则()f x 至多会有三个零点”是正确的． 【6】也有老师从函数的凹凸性给予解释．（2）假设存在参数可以是其成等比数列，那么我们可以构造出下面的对应等式关系：1a bq =，222a bq =，333a bq =，444a bq =，,0q b >，1b ≠，所以1nn a qb =()1,2,3,4n =关于n 的函数是一致凹或凸的，所以()11,a 与()44,a 的连线必不与()22,a ，()33,a 的连线重合． 这是与等差数列对应点在直线上是矛盾的，故不存在1,a d 满足要求． （3）依据题意构造等式关系如下：1n n a bq =，2'n k n k a b q ++=，233'n k n k a b q ++=，354'n kn k a b q ++=，'k b bq =， 所以11'n a qb =，12'n ka qb +=，133'n ka qb +=，154'n ka qb +=，假设存在，那么坐标上三点()2,n k a +，()33,n k a +，()45,n k a +共线， 依据函数图像凹凸性，知其不成立，因此不存在．6.（2016浙江理6）如图所示，点列分别在某锐角的两边上，且{}{},n n A B 1n n A A +=，，，，，（表示点与点不重合）.若，为的面积，则（ ）.A.是等差数列B.是等差数列C.是等差数列D.是等差数列6.A 解析 设点到对面直线的距离为，则. 由题目中条件可知的长度为定值，则.那么我们需要知道的关系式，过点作垂直得到初始距离，那么和两个垂足构成了直角梯形，那，其中为两条线的夹角，那么.由题目中条件知，则.所以，其中为定值，所以为等差数列.故选A. 7.（2016全国丙17）已知数列的前项和，.其中. （1）证明是等比数列，并求其通项公式；（2）若，求. 7.解析 （1）由题意得，故，，. 由，，得，即.由，，得，所以.因此是首项为，公比为的等比数列.于是.12n n A A ++2n n A A +≠n ∈*N 112n n n n B B B B +++=2n n B B +≠n ∈*N P Q ≠P Q nn n d A B =n S 1n n n A B B +△{}n S 2{}nS {}n d 2{}n d n A n h 112n n n n+S h B B =1n n B B +1212n n S h B B =n h 1A 1h 1,n A A 11tan n n h h A A θ=+⋅θ11121(tan )2n n S h A A B B θ=+⋅112n n n n A A A A +++=()1121n A A n A A =-()1121211tan 2n S h n A A B B θ=⎡+-⋅⎤⎣⎦θn S {}n a n 1n S a =+1n n S a λ=+0λ≠{}n a 53132S =λ1111a S a λ==+1λ≠111a λ=-10a ≠1n n S a λ=+111n n S a λ++=+11n n n a a a λλ++=-()11n n a a λλ+-=10a ≠0λ≠0n a ≠11n n a a λλ+=-{}n a 11λ-1λλ-()1*111n n a n λλλ-⎛⎫=∈ ⎪--⎝⎭N •••（2）由（1）得.由，得，即，解得.8.（2017江苏19）对于给定的正整数，若数列满足对任意正整数总成立，则称数列是“数列”．（1）证明：等差数列是“数列”；（2）若数列既是“数列”，又是“数列”，证明：是等差数列． 8.解析 （1）因为是等差数列，设其公差为，则，从而当时， ，，所以，因此等差数列是“数列”． （2）由数列既是“数列”，又是“数列”，因此，当时， ① 当时， ② 由①知， ③④将③④代入②，得，其中， 所以是等差数列，设其公差为．在①中，取，则，所以， 在①中，取，则，所以， 从而数列是等差数列．评注 这是数列新定义的问题，其实类似的问题此前我们也研究过，给出仅供参考．11n n S λλ⎛⎫=- ⎪-⎝⎭53132S =5311132λλ⎛⎫-= ⎪-⎝⎭51132λλ⎛⎫= ⎪-⎝⎭1λ=-k {}n a 1111+n k n k n n n k a a a a a --+-++-++⋅⋅⋅+++⋅⋅⋅+2n k n a ka +=n ()n k >{}n a ()P k {}n a ()3P {}n a ()2P ()3P {}n a {}n a d ()11n a a n d =+-4n …()()1111=n k n k a a a n k d a n k d -++=+--+++-()12212n a n d a +-=1,2,3k =321123+++6n n n n n n n a a a a a a a ---+++++={}n a ()3P {}n a ()2P ()3P 3n …21124n n n n n a a a a a --+++++=4n …3211236n n n n n n n a a a a a a a ---++++++++=()()321144n n n n n a a a a a n ---++=-+≥()()231142n n n n n a a a a a n +++-+=-+≥112n n n a a a -++=4n …345,,,a a a ⋅⋅⋅d '4n =235644a a a a a +++=23a a d '=-3n =124534a a a a a +++=312a a d '=-{}n a（2015南通基地密卷7第20题）设数列的各项均为正数，若对任意的，存在，使得成立，则称数列为“型”数列．（1）若数列是“型”数列，且，，求；（2）若数列既是“型”数列，又是“型”数列，证明数列是等比数列． 解析 （1）由题意得，成等比数列，且公比，所以．（2）由是“型”数列得成等比数列，设公比为， 由是“型”数列得成等比数列，设公比为；成等比数列，设公比为； 成等比数列，设公比为； 则，，， 所以，不妨令，则． 所以，，所以，综上，从而是等比数列．9.(2017北京理20)设和是两个等差数列，记，其中表示这个数中最大的数．（1）若，，求的值，并证明是等差数列； （2）证明：或者对任意正数，存在正整数，当时，；或者存在正整数，使得是等差数列．{}n a *n ∈N *k ∈N 22n k n n k a a a ++={}n a k J {}n a 2J 28a =81a =2n a {}n a 3J 4J {}n a 2468,,,,a a a a ⋅⋅⋅138212a q a ⎛⎫== ⎪⎝⎭412212n n n a a q --⎛⎫== ⎪⎝⎭{}n a 4J 159131721,,,,,,a a a a a a ⋅⋅⋅t {}n a 3J 1471013,,,,,a a a a a ⋅⋅⋅1α2581114,,,,,a a a a a ⋅⋅⋅2α3691215,,,,,a a a a a ⋅⋅⋅3α431311a t a α==431725a t a α==432139a t a α==123ααα==123αααα===43t α=()32113211k k k a a a α----==()2311223315111k k k k k aa a t a a ααα------====131323339111k k k k kaa a t a a ααα----====11n n a a -={}n a {}n a {}n b 1122max{,,,}n n n c b a n b a n b a n =--⋅⋅⋅-(1,2,3,)n =⋅⋅⋅12max{,,,}s x x x ⋅⋅⋅12,,,s x x x ⋅⋅⋅s n a n =21n b n =-123,,c c c {}n c M m n m ≥nc M n>m 12,,,m m m c c c ++⋅⋅⋅9.解析 （1），，. 当时，， 所以关于单调递减. 从而，将代入，满足此式，所以对任意，，于是， 得是等差数列.（2）设数列和的公差分别为，则. 所以. ①当时，取正整数，则当时，，因此. 此时，是等差数列.②当时，对任意， .此时，是等差数列.③当时，当时，有，所以 .对任意正数，取正整数，111110c b a =-=-={}{}21122max 2,2max 121,3221c b a b a =--=-⨯-⨯=-{}{}3112233max 3,3,3max 131,332,5332c b a b a b a =---=-⨯-⨯-⨯=-3n …()()()()111120k k k k k k k k b na b na b b n a a n ++++---=---=-<k k b na -*k ∈N {}112211max ,,,1n n n c b a n b a n b a n b a n n =---=-=-1,2,3n =1n …1n c n =-11n n c c +-=-{}n c {}n a {}n b 12,d d ()[]()()121111211(1)1k k b na b k d a k d n b a n d nd k -=+--+-=-+--()()11212111211,,n b a n n d nd d nd c b a n d nd ⎧-+-->⎪=⎨-⎪⎩当时当时…10d >21d m d >n m …12nd d >11n c b a n =-12,,,m m m c c c ++10d =1n …(){}(){}()11211211max ,01max ,0n c b a n n d b a n d a =-+-=-+--123,,,,,n c c c c 10d <21d n d >12nd d <()()()11211211121n b a n n d nd c b d n d d a d n n n-+---==-+-++…()111212||n d d a d b d -+-+--M 12112211||max ,M b d a d d d m d d ⎧⎫+-+-->⎨⎬-⎩⎭OB 3A 3B 2A 2B 1A 1故当时，. 题型71 等差数列与等比数列的交汇问题——暂无 第二节 数列的通项公式与求和 题型72 数列通项公式的求解1. (2013安徽理14） 如图，互不相同的点12n A A A ，，，，和12n B B B ，，，，分别在角O 的两条边上，所有n n A B 相互平行，且所有梯形11n n n n A B B A ++的面积均相等. 设n n OA a =.若1212a a ==，，则数列{}n a 的通项公式是 . 2．（2013湖北理18）已知等比数列{}n a 满足： 23||10a a -=，123125a a a =． (1) 求数列{}n a 的通项公式；(2) 是否存在正整数m ，使得12111....1ma a a ++…？若存在，求m 的最小值；若不存在，说明理由．3．（2013广东19）设数列{}n a 的前n 项和为n S .已知11a =，2121233n n S a n n n +=---，*n ∈N(1) 求2a 的值；(2) 求数列{}n a 的通项公式；(3) 证明:对一切正整数n ，有1211174n a a a +++<. 4．(2013天津理19） 已知首项为32的等比数列{}n a 不是递减数列，其前n 项和为()n S n *∈Ν，且33S a +，55S a +，44S a +成等差数列．(1) 求数列{}n a 的通项公式； (2) 设1()n n nT S S n *-∈=Ν， 求数列{}n T 的最大项的值与最小项的值． 5.（2014 江苏理 7）在各项均为正数的等比数列{}n a 中，21a =，8642a a a =+，则6a 的值是 ．6.（2014 广东理 19）（14分）设数列{}n a 的前n 项和为n S ，满足2*1234,n n S na n n n +=--∈N ，且315S =.（1）求123,,a a a 的值;n m …nc M n>（2）求数列{}n a 的通项公式.7.（2014 湖南理 20）已知数列{}n a 满足11a =，1nn n a a p +-=，*N n ∈.（1）若{}n a 为递增数列，且123,2,3a a a 成等差数列，求p 的值； （2）若12p =，且{}21n a -是递增数列，{}2n a 是递减数列，求数列{}n a 的通项公式. 8.（2015安徽理17）设*n ∈N ，n x 是曲线221n y x +=+在点()1,2处的切线与x 轴交点的横坐标．（1）求数列{}n x 的通项公式；（2）记2221321n n T x x x -=，求证：14n T n…. 8.解析 （1）()()2221122n n y xn x ++''=+=+，所以曲线221n y x +=+在点()1,2处的切线斜率为22n +，从而切线方程为()()2221y n x -=+-．令0y =，解得切线与x 轴的交点的横坐标1111n nx n n =-=++． （2）证法一：证明：由题设和（1）中的计算结果知：22222213211321242n n n T x x x n --⎛⎫⎛⎫⎛⎫== ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭．当1n =时，114T =； 当2n …时，因为()()()()222221222121121222n n n n xn n n -----⎛⎫==>= ⎪⎝⎭2212n n n n --=， 所以2112112234n n T n n-⎛⎫>⨯⨯⨯⨯=⎪⎝⎭． 综上可得对任意的*n ∈N ，均有14n T n…． 证法二：分析 证明数列不等式时，对于不等式两端含n 且一端是积的形式()()1n i i a f n =⎛⎫<> ⎪⎝⎭∏，可采用对称的思想，使其化为两个数列积的形式，再通过比较通项 的大小，最后根据不等式“同向同正可乘”的基本性质，叠乘得以证明． 证明：设14n G n =是数列{}n b 的前n 项积，则当1n =时，114b =； 当2n …时，()141n G n =-，所以11n n n G n b G n--==．由（1）可得，当1n =时，22111124x b ⎛⎫=== ⎪⎝⎭；当2n …时，22212112n n n n x b n n ---⎛⎫-=-= ⎪⎝⎭()()223221411044n n n n n n---=>， 所以此时221n n x b ->，所以可得222352123n n x x x b b b ->，综上可得22221352112314n n x x x x b b b b n -=…，即14n T n…． 9.（2015北京理20）已知数列{}n a 满足：*1a ∈N ，136a …，且()12,18,1,2,236,18n n n nn a a a n a a +⎧==⎨->⎩…，记集合{}*n M a n =∈N .（1）若16a =，写出集合M 的所有元素；（2）若集合M 存在一个元素时3的倍数，证明：M 的所有元素都是3的倍数； （3）求集合M 的元素个数的最大值. 9.解析（1）6，12，24.（2）因为集合M 存在一个元素是3的倍数，所以不妨设k a 是3的倍数.由12,18236,18n n n nn a a a a a +⎧=⎨->⎩…，可归纳证明对任意n k …，n a 是3的倍数.如果1k =，则M 的所有元素都是3的倍数；如果1k >，因为12k k a a -=或1236k k a a -=-，所以12k a -是3的倍数，或1236k a --是3的倍数，于是1k a -是3的倍数.类似可得，2k a -，…，1a 都是3的倍数.从而对任意1n …，n a 是3的倍数，因此M 的所有元素都是3的倍数. 综上，若集合M 存在一个元素是3的倍数，则M 的所有元素都是3的倍数.（3）由136a …，*1a ∈N ，11112,18236,18n n n n n a a a a a ----⎧=⎨->⎩…，可归纳证明()362,3,n a n =….因为1a 是正整数，112112,18236,18a a a a a ⎧=⎨->⎩…，所以2a 是2的倍数.从而当3n …时，n a 是4的倍数.如果1a 是3的倍数，由（2）知对所有正整数n ，n a 是3的倍数，因此当3n …时，{}12,24,36n a ∈，这时，M 中的元素的个数不超过5.如果1a 不是3的倍数，由（2）知，对所有的正整数n ，n a 不是3的倍数，因此当3n …时，{}4,8,16,20,28,32n a ∈，这时M 的元素的个数不超过8.当11a =时，{}1,2,4,8,16,20,28,32M =有8个元素. 综上可知，集合M 的元素个数的最大值为8.10.（2016浙江理13）设数列的前项和为.若，，，则， .10. ； 解析 由，，解得.由，两式相减得，即.又，所以，，所以. 题型73 数列的求和1. (2013全国新课标卷理16）等差数列{}n a 的前n 项和为n S ，已知1015025S S ==，，则n nS 的最小值为 .2.（2013辽宁14）已知等比数列{}n a 是递增数列，n S 是{}n a 的前n 项和.若13a a ，是方程2540x x -+=的两个根，则6S = .3.(2013重庆理12）已知{}n a 是等差数列，11a =，公差0d ≠，n S 为其前n 项和，若125,,a a a 成等比数列，则8S = .4．(2013湖南理15）设n S 为数列{}n a 的前n 项和，1(1),,2n n n n S a n *=--∈Ν则 （1）3a =_____；（2）12100S S S ++⋅⋅⋅+=___________.5．（2013四川理16）在等差数列{}n a 中，138a a +=，且4a 为2a 和9a 的等比中项，求数{}n a n n S 24S =121n n a S +=+*n ∈N 1a =5S =11212124S a a =+=2121a a =+1213a a ==，1121,21(2)n n n n a S a S n +-=+=+…12n n n a a a +-=13(2)n n a a a +=…213a a =13(1)n n a a n +=…13n n a -=551312113S -==-。

2013 年高考数学全国卷1(完整版试题 +答案 +解析 )2013 年普通高等学校招生全国统一考试（全国卷）理科数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共 6 页．考试时间120 分钟．满分150 分．答题前，考生务必用0.5 毫米的黑色签字笔将自己的姓名、座号、考号填写在第Ⅰ 卷答题卡和第Ⅱ 卷答题纸规定的位置．参考公式：样本数据x1 , x2 ,x n的标准差( x1x) 2(x2x) 2( x n x)2s n其中 x 为样本平均数球的面积公式S 4 R2第Ⅰ卷（选择题共 60 分）注意事项：1．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上．2．第Ⅰ卷只有选择题一道大题．一、选择题：本大题共12 小题，每小题 5 分，共 60 分．在每小题给出的四个选项中，只有一项是符合题目要求的．1. 复数12i（i是虚数单位）的虚部是1 iA ．31C．3 D ．1 B．222. 已知R是实数集，M x 21 , N y y x 1 1 ，则N C R M xA．(1,2)B．0,2 C.D．1,23.现有 10 个数，其平均数是 4 ，且这 10 个数的平方和是 200 ，那么这个数组的标准差是A．1B．2C．3D．44.设 S n为等比数列 { a n } 的前 n 项和， 8a2a50，则S4 S2A．5B．8C．8D． 155.已知函数 f ( x)sin(2x) ，若存在a(0,) ，使得 f (x a) f (x a) 恒成立，则 a6的值是A ．B ．3C ．4 D ．626. 已知 m 、 n 表示直线， , , 表示平面，给出下列四个命题，其中真命题为（ 1） m,n , nm, 则（ 2） , m,n,则 nm（ 3） m , m , 则 ∥（ 4） m, n, mn,则A ．（ 1）、（2）B ．（3）、（ 4）C ．（2）、（ 3）D ．（2）、（ 4）7. 已知平面上不共线的四点O, A, B, C ，若 OA 3OB2OC,则| AB |等于|BC |A ． 1B ． 2C ． 3D ． 48. 已知三角形ABC 的三边长成公差为 2 的等差数列，且最大角的正弦值为3，则这个三2角形的周长是A ． 18B ． 21C ． 24D ． 159. 函数 f ( x)lg x1的零点所在的区间是xA ． 0,1B ． 1,10C ． 10,100D ． (100, )10. 过直线 yx 上一点 P 引圆 x 2y 26x 7 0 的切线，则切线长的最小值为23210 D ． 2A ．B ．2C ．2211. 已知函数 f ( x)x 2 ax 2b . 若 a,b 都是区间 0,4 内的数，则使 f (1)0 成立的概率是3B ．13 5A ．4C ．D ．48812. 已知双曲线的标准方程为x 2 y 2 1 ，F 为其右焦点， A 1 , A 2 是实轴的两端点， 设 P 为9 16双曲线上不同于A 1 , A 2 的任意一点， 直线 A 1 P, A 2 P 与直线 xa 分别交于两点 M , N , 若FM FN0 , 则 a 的值为16B ．925 16A ．5C ．D ．995第Ⅱ卷（非选择题共90分）注意事项：1．请用 0.5 毫米的黑色签字笔将每题的答案填写在第Ⅱ 卷答题纸的指定位置．书写的答案如需改动，要先划掉原来的答案，然后再写上新答案．2．不在指定答题位置答题或超出答题区域书写的答案无效．在试题卷上答题无效．3．第Ⅱ 卷共包括填空题和解答题两道大题．二、填空题：本大题共 4 小题，每小题 4 分，共 16 分．开始13. 如图所示的程序框图输出的结果为__________.a2, i 1 否14. 若一个底面是正三角形的三棱柱的正视图如下图所示，其顶点都在一个球面上，则该球的表面积为__________.i 10是1a1输出 aa111第14 题图i i1结束第13题图15. 地震的震级 R 与地震释放的能量 E 的关系为R 2(lg E 11.4)．2011 年 3 月 11日，日3本东海岸发生了9.0 级特大地震， 2008 年中国汶川的地震级别为8.0 级，那么 2011年地震的能量是 2008年地震能量的倍．16.给出下列命题：①已知都是正数，且a1a，则a b；1bb②已知 f ( x) 是 f ( x) 的导函数，若x R , f (x) 0 ，则 f (1) f (2)一定成立；③命题“x R ，使得x2 2 x 1 0 ”的否定是真命题；④“ x1, 且 y 1 ”是“ x y 2 ”的充要条件.其中正确命题的序号是.(把你认为正确命题的序号都填上)三、解答题：本大题共６小题，共 74 分．解答应写出文字说明，证明过程或演算步骤．17．（本小题满分 12 分）已知向量 a(1, cos x ) 与 b ( 3 sin x cos x, y) 共线，且有函数 yf ( x) ．2 2 2（Ⅰ）若 f ( x) 1，求 cos(22x) 的值；3（Ⅱ）在ABC 中，角 A, B, C ,的对边分别是 a, b, c ，且满足 2a cosC c 2b ，求函数f ( B) 的取值范围 .18．（本小题满分 12 分）已知等差数列a n的前 n 项和为n ，公差d 0,且3 5 1413 成等比数列．SS S50, a , a , a（Ⅰ）求数列a n 的通项公式；（Ⅱ）设b n 是首项为 1，公比为 3 的等比数列，求数列b n 的前 n 项和 T n .a n19.（本小题满分 12 分）已知四棱锥A BCDE ，其中AB BC AC，2，CD面ABC ，BE 1CD BE∥CD，F 为 AD的中点.D（Ⅰ）求证：EF ∥面 ABC ；（Ⅱ）求证：面ADE面ACD ；F（ III）求四棱锥 A BCDE 的体积.EC AB20. （本小题满分 12 分）在某种产品表面进行腐蚀性检验，得到腐蚀深度y 与腐蚀时间x之间对应的一组数据：时间 x （秒）51015203040深度 y （微米）61010131617现确定的研究方案是：先从这 6 组数据中选取 2 组，用剩下的 4 组数据求线性回归方程，再对被选取的 2 组数据进行检验．（Ⅰ）求选取的 2 组数据恰好不相邻的概率；（Ⅱ）若选取的是第 2 组和第 5 组数据，根据其它 4 组数据，求得y 关于x的线性回归方程 y?4 x 139，规定由线性回归方程得到的估计数据与所选出的检验数据的误1326差均不超过 2 微米，则认为得到的线性回归方程是可靠的，判断该线性回归方程是否可靠．21.（本小题满分 12 分）已知函数ax b1, f ( 1)) 的切线方程为x y 3 0 .f (x)2在点 (x1（Ⅰ）求函数 f ( x) 的解析式；（Ⅱ）设 g ( x) ln x ，求证： g (x) f ( x) 在 x [1, ) 上恒成立.22. （本小题满分14 分）实轴长为 4 3 的椭圆的中心在原点，其焦点F1,, F2在x轴上.抛物线的顶点在原点O ，对称轴为 y 轴，两曲线在第一象限内相交于点 A ,且AF1AF2，△ AF1 F2的面积为3.（Ⅰ）求椭圆和抛物线的标准方程；（Ⅱ）过点 A 作直线 l 分别与抛物线和椭圆交于B,C ,若 AC 2 AB ,求直线l的斜率k.yAF1 B o F2xC参考答案及评分标准一．选择题（本大题共12 小题，每小题 5 分，共 60 分．）BDBADBBDBC CB二．填空题（本大题共4 小题，每小题 4 分，共 16 分．）313． 214.1915. 10216. ①③3三．解答题17．（本小题满分 12 分）解：（Ⅰ）∵ a 与 b 共线1cos x∴xy 23 sin x cos2 2y3 sin x cosxcos 2x3sin x1(1 cos x) sin( x) 1 ⋯⋯⋯⋯ 3 分22 2226 2∴ f ( x)sin( x ) 1 1 ，即 sin(x) 1 ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 4 分62 2 cos(26 12x) cos2( x) 2cos 2 ( x) 1 2sin 2 ( x ) 1 33 3 62⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6 分（Ⅱ）已知2a cosC c2b由正弦定理得：2sin A cosC sin C2sin B 2 sin( A C )2sin A cosC sin C2sin A cosC2 cos Asin C∴ cosA1 ，∴在ABC 中 ∠ A231f (B)sin(B)26 25 ∵∠ A∴ 0 B ,B3 3 666∴1sin(B) 1, 1 f ( B) 32623∴函数f (B) 的取值范围为 (1, ]⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯8 分10 分12 分2013 年高考数学全国卷1(完整版试题 +答案 +解析 )18．（本小题满分12 分）解：（Ⅰ）依题意得3a132d5a1455022d⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2 分( a13d ) 2a1 ( a112d )解得 a13，⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 4 分d2a n a1，即2n 1． 6 分⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( Ⅱ) bn3n1， bn a n3n1(2n 1) 3n 1⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯7 分a nT n353732(2n 1) 3n 13T n 3 3 5327 33(2n 1) 3n 1(2n 1) 3n⋯⋯⋯⋯⋯⋯⋯⋯9分2T n 3 2 3 2 32 2 3n 1(2n1)3n32 3(13n 1 )( 2n 1)3n132n 3n∴ T n n 3n⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 12 分19．（本小题满分12 分）解：（Ⅰ）取AC 中点 G,连结 FG、 BG，∵F,G分别是 AD,AC的中点D1∴FG∥ CD,且 FG= DC=1 ．2∵ BE∥ CD ∴ FG 与 BE 平行且相等F∴ EF∥ BG．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 2 分EEF 面 ABC, BG面 ABC GC ∴ EF ∥面 ABC A⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 4 分（Ⅱ）∵△ ABC 为等边三角形∴ BG⊥ AC B 又∵ DC⊥面 ABC,BG面 ABC∴ DC⊥ BG2013 年高考数学全国卷1(完整版试题 +答案 +解析 )∴ BG 垂直于面 ADC 的两条相交直线AC,DC，∴ BG⊥面 ADC．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 6 分∵EF∥ BG∴EF⊥面 ADC∵ EF面 ADE，∴面 ADE⊥面 ADC ．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 8 分（Ⅲ）连结 EC,该四棱锥分为两个三棱锥E－ABC和 E－ ADC ．V A BCDE V E ABC V E ACD131113333．⋯⋯⋯⋯⋯⋯⋯⋯⋯ 12 分34321264另法：取 BC 的中点为 O ，连结AO ，则 AO BC ，又 CD平面ABC ,∴CD AO, BC CD C , ∴AO平面，∴AO为V A BCDE的高，BCDEAO 3, S BCDE(12)1 3 ,V A BCDE1333．222322420．（本小题满分12 分）解：（Ⅰ）设 6 组数据的编号分别为1,2,3,4,5,6.设抽到不相邻的两组数据为事件A，从 6组数据中选取 2 组数据共有15 种情况：（ 1,2 ）（ 1,3 ）（1,4 ）（ 1,5 ）（ 1,6 ）（ 2,3 ）（ 2,4 ）（ 2,5 ）（ 2,6 ）（ 3,4 ）（ 3,5 ）（ 3,6 ）（ 4,5）（ 4,6）（ 5,6），其中事件A包含的基本事件有10种．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 3 分所以P( A)102．所以选取的 2 组数据恰好不相邻的概率是2．⋯⋯⋯⋯⋯⋯⋯⋯⋯ 6 分1533( Ⅱ )当 x10时， ?413921921910 |2;⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯9 分26261326当x30时， ?413937937916 |2;2626132612 分所以，该研究所得到的回归方程是可靠的．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯21．（本小题满分12 分）解：（Ⅰ）将 x 1 代入切线方程得y2∴ f ( 1)b a2 ，化简得 b a 4 ．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 2 分11f ( x)a( x21)(ax b) 2 x(1x 2 ) 22013 年高考数学全国卷1(完整版试题 +答案 +解析 )f ( 1)2a2(b a)2b b1 ．442解得： a2, b2∴ f ( x)2x2x 2．12x2（Ⅱ）由已知得ln x在 [1,) 上恒成立x21化简得 ( x21) ln x2x2即 x2 ln x ln x 2 x20在 [1,) 上恒成立．设 h(x)x 2 ln x ln x 2x 2 ，⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4分6分8分h (x)2xln x x 12x1∵ x 1∴ 2x ln x0,2，即 h ( x) 0 ．10 分x⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯x∴ h(x) 在 [1,) 上单调递增， h( x)h(1) 0∴ g(x) f (x) 在 x[1,) 上恒成立．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯12 分22．（本小题满分 14分）解（ 1）设椭圆方程为x2y21 (a b 0) ， AF1 m, AF2 n a2b2m 2n24c2由题意知m n 4 3⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 2 分mn 6解得 c 29 ，∴ b 212 9 3 ．∴椭圆的方程为x 2y2⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 4 分1213∵ y A c3，∴ y A1,代入椭圆的方程得x A 2 2 ，将点 A 坐标代入得抛物线方程为x 28 y ．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 6 分（ 2）设直线l的方程为y 1 k ( x 2 2 ) ， B(x1, y1 ), C (x2 , y2 )---2013 年高考数学全国卷1(完整版试题 +答案 +解析 )由 AC 2AB得 x22 22( x 2 2)，1化简得 2x1x222⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯8 分联立直线与抛物线的方程y1k( x 2 2)，x 28 y得 x28kx162k80∴ x1 2 28k ①⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯10 分联立直线与椭圆的方程y1k( x2 2 )x 24y 212得2)2(8 1622)32216 28 0k x k x k kk∴ x2 2 2162k 28k②⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯12 分14k2∴ 2x1x22(8k2 2 )162k 28k2 2 2 214k 2整理得： (16k42)(112k)0 4k 2∴ k2，所以直线 l的斜率为2．⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 14 分44-11-/11。

2013---2017年全国1卷高考理科数学分类汇编---不等式（2017全国 1.理数.14）设x ，y 满足约束条件21210x y x y x y +≤⎧⎪+≥-⎨⎪-≤⎩，则32z x y =-的最小值为_____________ .【考点】：简单的线性规划。

【思路】：根据约束条件，画出可行域即可。

【解析】：如图所示，可行域为阴影部分，令03320:2z x y l y x =-=⇒=为初始直线，当0l 向上平移时，32z x y =-逐渐变小，故而在点()1,1F -处取到最小值-5。

（2016全国1.理数.16）某高科技企业生产产品A 和产品B 需要甲、乙两种新型材料．生产一件产品A 需要甲材料1.5kg ，乙材料1kg ，用5个工时；生产一件产品B 需要甲材料0.5kg ，乙材料0.3kg ，用3个工时．生产一件产品A 的利润为2100元，生产一件产品B 的利润为900元．该企业现有甲材料150kg ，乙材料90kg ，则在不超过600个工时的条件下，生产产品A 、产品B 的利润之和的最大值为 元． 【答案】216000作出二元一次不等式组②表示的平面区域（如图）,即可行域.考点：线性规划的应用【名师点睛】线性规划也是高考中常考的知识点,一般以客观题形式出现,基本题型是给出约束条件求目标函数的最值,常见的结合方式有：纵截距、斜率、两点间的距离、点到直线的距离,解决此类问题常利用数形结合.本题运算量较大,失分的一个主要原因是运算失误.（2015全国1.理数.15）若x ，y 满足约束条件10040x x y x y -≥⎧⎪-≤⎨⎪+-≤⎩，则y x 的最大值为 .【解析】试题分析：作出可行域如图中阴影部分所示，由斜率的意义知，yx是可行域内一点与原点连线的斜率，由图可知，点A （1,3）与原点连线的斜率最大，故yx的最大值为3.考点：线性规划解法（2014全国1.理数.9）不等式组124x y x y +⎧⎨-⎩……的解集记为D .有下面四个命题：1p ：(),x y D ∀∈，22x y +-…；2p ：(),x y D ∃∈，22x y +…； 3p ：(),x y D ∀∈，23x y +…； 4p ：(),x y D ∃∈，21x y +-…. 其中真命题是（ ）A. 2p ，3pB. 1p ，2pC. 1p ，4pD. 1p ，3p解析 不等式组1,24x y x y +⎧⎨-⎩……表示的平面区域D 如图阴影区域所示.设2z x y =+，作出基本直线0l ：20x y +=，经平移可知直线l ：2z x y =+经过点()2,1A-时z 取得最小值0，无最大值.对于命题1p ：由于z 的最小值为0，所以(),x y D ∀∈，20x y +…恒成立，故22x y +-…恒成立，因此命题1p 为真命题；由于(),20x y Dx y ∀∈+…，故(),x y D ∃∈，22x y +…，因此命题2p 为真命题；由于2z x y =+的最小值为0，无最大值，故命题3p 和4p 错误，故选B.2y =0x-2y=4。

2013年全国各省市文科数学—数列1、2013大纲文T17．（本小题满分10分） 等差数列{}n a 中，71994,2,a a a == （I ）求{}n a 的通项公式； （II ）设{}1,.n n n nb b n S na =求数列的前项和2、2013新课标1文T17.（本小题满分12分）已知等差数列{}n a 的前n 项和n S 满足30S =，55S =-。

（Ⅰ）求{}n a 的通项公式； （Ⅱ）求数列21211{}n n a a -+的前n 项和。

3、2013新课标Ⅱ文T17.（本小题满分12分）已知等差数列{}n a 的公差不为零，125a =，且11113,,a a a 成等比数列。

（Ⅰ）求{}n a 的通项公式； （Ⅱ）求14732+n a a a a -++⋅⋅⋅+；4、2013山东文(20)(本小题满分12分)设等差数列{}n a 的前n 项和为n S ，且244S S =,122+=n n a a (Ⅰ)求数列{}n a 的通项公式(Ⅱ)设数列{}n b 满足*121211,2n n n b b b n N a a a +++=-∈ ，求{}n b 的前n 项和n T5、2013北京文T20．（本小题共13分）给定数列1a ，2a ， ，n a 。

对1,2,3,,1i n =- ，该数列前i 项的最大值记为i A ，后n i -项1i a +，2i a +， ，n a 的最小值记为i B ，i i i d A B =-。

（1）设数列{}n a 为3，4，7，1，写出1d ，2d ，3d 的值。

（2）设1a ，2a ， ，n a （4n ≥）是公比大于1的等比数列，且10a >，证明1d ，2d ， ，1n d -是等比数列。

（3）设1d ，2d ， ，1n d -是公差大于0的等差数列，且10d >，证明1a ，2a ，，1n a -是等差数列。

6、2013重庆文T16.（本小题满分13分，（Ⅰ）小问7分，（Ⅱ）小问6分）设数列{}n a 满足：11a =，13n n a a +=，n N +∈． （Ⅰ）求{}n a 的通项公式及前n 项和n S ；（Ⅱ）已知{}n b 是等差数列，n T 为前n 项和，且12b a =，3123b a a a =++，求20T ．7、2013四川文T16.(本小题满分12分)在等比数列{}n a 中，212a a -=，且22a 为13a 和3a 的等差中项，求数列{}n a 的首项、公比及前n 项和。

11ma ++≥2．（本小题满分16分）(2013江苏卷)设}{n a 是首项为a ，公差为d 的等差数列)0(≠d ，n S 是其前n 项和．记cn nS b nn +=2， *N n ∈，其中c 为实数．（1）若0=c ，且421b b b ，，成等比数列，证明：k nk S n S 2=（*,N n k ∈）； （2）若}{n b 是等差数列，证明：0=c ． 证：（1）若0=c ，则d n a a n )1(-+=，2]2)1[(a d n n S n +-=，22)1(ad n b n +-=．当421b b b ，，成等比数列，4122b b b =，即：⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+2322d a a d a ，得：ad d 22=，又0≠d ，故a d 2=．由此：a n S n 2=，a k n a nk S nk 222)(==，a k n S n k 222=． 故：k nk S n S 2=（*,N n k ∈）．（2）cn a d n n c n nS b n n ++-=+=22222)1(， c n a d n ca d n c a d n n ++--+-++-=2222)1(22)1(22)1( cn a d n ca d n ++--+-=222)1(22)1(． (※) 若}{n b 是等差数列，则Bn An b n +=型． 观察(※)式后一项，分子幂低于分母幂，故有：022)1(2=++-cn ad n c，即022)1(=+-a d n c ，而(1)202n d a -+≠， 故0=c ．经检验，当0=c 时}{n b 是等差数列．3.(本题满分14分)(2013浙江.理)在公差为d 的等差数列{a n }中，已知a 1=10，且a 1，2a 2+2，5a 3成等比数列.（Ⅰ）求d ，a n ；（Ⅱ) 若d<0，求|a 1|+|a 2|+|a 3|+…+|a n | .解.本题主要考查等差数列、等比数列的概念，等差数列通项公式、求和公式等基础知识，同时考查运算求解能力。

2013-2017年浙江高考理科数学历年真题之数列大题（教师版）1、（2013年）在公差为d 的等差数列{}n a 中，已知112310,,22,5a a a a =+且成等比数列.(Ⅰ)求d ，n a ； ⅠⅠ()120,|||||.n da a a <+++ 若求|(Ⅰ) 解;：由题意得223125(22)34014a a a d d d d ⋅=+⇒--=⇒=-=或所以 11,*46,*.n n a n n N a n n N =-∈=+∈或ⅠⅠ()设数列{}n a 的前n 项和为n S ，因为0,d <由(Ⅰ)得1,11,n da n =-=-则当11n ≤时，212121||||||.22n n a a a S n n +++==-+ 当12n ≥时，21211121||||||2110.22n n a a a S S n n +++=-+=-+ 综上即得212212111,22||||||12111012.22n n n n a a a n n n ⎧-+≤⎪⎪+++=⎨⎪-+≥⎪⎩2、（2014年）已知数列{}n a 和{}n b 满足()()*∈=N n a a a nb n 221 .若{}na 为等比数列，且.6,2231b b a +==(Ⅰ)求n a 与n b ； ⅠⅠ()设()*∈-=N n b a c nn n11。

记数列{}n c 的前n 项和为n S . （i ）求n S ；（ii ）求正整数k ，使得对任意*∈N n ，均有n k S S ≥． 解析：（I ）由题意，()()*∈=N n a a a nb n 221 ，326b b-=，知3238b b a -==，又由12a =，得公比2q =（2q =-舍去），所以数列{}n a 的通项公式为2()n n a n N *=∈，所以()()1121232n n n n n a a a a ++==，故数列{}n b 的通项公式为，()1()n b n n n N *=+∈；（II ）（i ）由（I ）知，11111()21n n n n c n N a b n n *⎛⎫=-=--∈ ⎪+⎝⎭，所以11()12n nS n N n *=-∈+； （ii ）因为12340,0,0,0c c c c =>>>；当5n ≥时，()()11112n n n n c n n +⎡⎤=-⎢⎥+⎣⎦，而()()()()()11112120222n n n n n n n n n ++++++--=>，得()()51551122n n n ++≤<，所以当5n ≥时，0n c <，综上对任意n N *∈恒有4n S S ≥，故4k =．3、（2015年）已知数列{a n }满足a 1=21, 且1n a +=n a -2n a (n ∈N*) (I)证明：1≤1+n na a ≤2 (n ∈N*) (II)设数列{2n a }的前n 项和为S n , 证明)2(21+n ≤nSn ≤)1(21+n (n ∈N*)解: (I)∵a n -a n +1=2n a ≥0 ∴a n +1≤a n ∴a n ≤a 1=21由a n =11)1(---n n a a 得a n =0)1()1)(1(1121>-----a a a a n n , 故0< a n ≤21 从而n n n n n n a a a a a a -=-=+11)1(1∈[1, 2] 即1≤1+n n a a ≤2 法二: 在0< a n ≤21基础上证a n ≤2a n +1可用分析法 要使a n ≤2a n +1, 只要a n ≤2(a n -2n a )⇔22n a ≤a n ⇔0< a n ≤21, 故a n ≤2a n +1成立 (II)∵2n a =a n -a n +1 ∴S n =a 1-a 2+a 2-a 3+…+a n -a n +1=a 1-a n +1=21-a n +1 由a n +1=a n (1-a n ) ∴n n n a a a -+=+11111∴n n n a a a -=-+11111∈[1, 2], 0<a n ≤21 故1≤n n a a 111-+≤2, n ∈N*, 累加得n ≤1111a a n -+≤2n 即n +2≤11+n a ≤2n +2即221+n ≤a n +1≤21+n ,从而)2(2+n n ≤S n =21-a n +1≤)1(2+n n因此,)2(21+n ≤nSn ≤)1(21+n (n ∈N*) (n n n a a a -=-+11111=1+n n a a , (I)(II)关联在此)法二: (用数学归纳法)∵2n a =a n -a n +1 ∴S n =a 1-a 2+a 2-a 3+…+a n -a n +1=a 1-a n +1=21-a n +1 要使)2(21+n ≤nS n ≤)1(21+n 成立, 只须且必须221+n ≤a n +1≤21+n (n ∈N*)当n =1时, a 2=41, 可得41≤a 2≤31, 结论成立假设当n =k 时, 结论成立, 即221+k ≤a k +1≤21+k , k ∈N*,则当n =k +1时, 注意到x -x 2在[0,21]上是增函数,∴a k +2=a k +1-21+k a ≤22)2(1)2(121++=+-+k k k k ≤313412+=+++k k k k且a k +2=a k +1-21+k a ≥22)1(412)22(1221++=+-+k k k k ≥421+k (事实上, ∵(2k +1)(2k +4)-4(k +1)2=2k ≥0 ∴2)1(412++k k ≥421+k ) 也就是说, 当n =k +1时, 结论也成立 因此, 原命题得证4、（2016年）设数列{}n a 满足112n n a a +-…，n *∈N ． （1）求证：()1122n n a a--…，n *∈N ；（2）若32n n a ⎛⎫ ⎪⎝⎭…，n *∈N ，证明：2n a …，n *∈N ．解析：5、 (2017年) 已知数列{x n }满足x 1=1，x n =x n +1+ln(1+x n +1)（n ∈N *）．证明：当n ∈N *时， （1）0＜x n +1＜x n ； （2）2x n +1− x n ≤x n x n +12；（3）12n-1≤x n ≤12n-2．解析：。

2011………2017高考全国卷（Ⅰ、Ⅱ、Ⅲ）各年分类汇编（数列） （2017、Ⅰ卷）4．记为等差数列的前项和．若，，则的公差为A ．1B ．2C ．4D ．812．几位大学生响应国家的创业号召，开发了一款应用软件。

为激发大家学习数学的兴趣，他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案：已知数列1，1，2，1，2，4，1，2，4，8，1，2，4，8，16，…，其中第一项是20，接下来的两项是20，21，再接下来的三项是20，21，22，依此类推。

求满足如下条件的最小整数N ：N >100且该数列的前N 项和为2的整数幂。

那么该款软件的激活码是 A ．440B ．330C ．220D ．110（2017、Ⅱ卷）3．我国古代数学名著《算法统宗》中有如下问题：“远望巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯？”意思是：一座7层塔共挂了381盏灯，且相邻两层中的下一层灯数是上一层灯数的2倍，则塔的顶层共有灯（）A 、1盏B 、3盏C 、5盏D 、9盏 15．等差数列{}n a 的前n 项和为n S ，33=a ，104=S ，则=∑=nk kS 11. （2017、Ⅲ卷）9.等差数列{}n a 的首项为1，公差不为0.若a 2，a 3，a 6成等比数列，则{}n a 前6项的和为（ ）A . -24 B . -3 C . 3 D . 814. 设等比数列{}n a 满足12131,3a a a a +=--=-，则4_______.a = （2016、Ⅰ卷）3、已知等差数列{}n a 前9项的和为27，810=a ，则=100a（A ）100 （B ）99 （C ）98 （D ）97 15、 设等比数列{}n a 满足1031=+a a ，542=+a a ，则n a a a ⋯21的最大值为． （2016、Ⅱ卷）17（本小题满分12分）n S 为等差数列{}n a 的前n 项和，且11a =，728S =．记[]lg n n b a=，其中[]x 表示不超过x 的最大整数，如[]0.90=，[]lg991=．（Ⅰ）求1b ，11b ，101b ；n S {}n a n 4524a a +=648S ={}n a（Ⅱ）求数列{}n b的前1000项和．（2016、Ⅲ卷）12、定义“规范01数列”{}n a 如下：{}n a 共有2m 项，其中m 项为0，m 项为1，且对任意2k m ≤，12,,,k a a a 中0的个数不少于1的个数.若4m =，则不同的“规范01数列”共有（ ） A ．18个B ．16个C ．14个D ．12个17、已知数列{}n a 的前n 项和1n n S a λ=+，其中0λ≠．（I ）证明{}n a 是等比数列，并求其通项公式； （II ）若53132S = ，求λ． （2015、Ⅰ卷）17）（本小题满分12分）n S 为数列{}n a 的前n 项和.已知20,243n n n n a a a S >+=+，（Ⅰ）求{}n a 的通项公式： （Ⅱ）设11n n n b a a += ,求数列{}n b 的前n 项和。

一、集合（2017全国1.理数.1）1.已知集合A ={x |x <1}，B ={x |31x <}，则A.{|0}A B x x =<B.A B =RC.{|1}A B x x => D.A B =∅ 【考点】：集合的简单运算，指数函数【思路】：利用指数函数的性质可以将集合B 求解出来，之后利用集合的计算求解即可。

【解析】：由310x x <⇒<，解得{}0B x x =<，故而{}{}0,1A B B x x A B A x x ⋂==<⋃==<，选A.（2016全国1.理数.1）设集合{}2430A x x x =-+<，{}230x x ->,则A B = （A ）33,2⎛⎫-- ⎪⎝⎭ （B ）33,2⎛⎫- ⎪⎝⎭ （C ）31,2⎛⎫ ⎪⎝⎭ （D ）3,32⎛⎫⎪⎝⎭【答案】D考点：集合的交集运算【名师点睛】集合是每年高考中的必考题,一般以基础题形式出现,属得分题.解决此类问题一般要把参与运算的集合化为最简形式再进行运算,如果是不等式解集、函数定义域及值域有关数集之间的运算,常借助数轴进行运算.（2014全国1.理数.1）已知集合{}2230A x x x =--…，{}22B x x =-<…，则A B = （ ） A.[]2,1-- B.[)1,2- C.[]1,1- D. [)1,2【解析】：∵A={x |2230x x --≥}={}13x x x ≤-≥或，B={}22x x -≤<， ∴A B ⋂={}21x x -≤≤，选A（2013全国1.理数. 1）已知集合{}{2|20,|A x x x B x x =->=<，则A.A ∩B=∅B.A ∪B=RC.B ⊆AD.A ⊆B【命题意图】本题主要考查一元二次不等式解法、集合运算及集合间关系，是容易题.【解析】A=(-∞,0)∪(2,+∞), ∴A ∪B=R,故选B.。

2013年全国各省市理科数学—数列1、2013大纲理T17．（本小题满分10分）等差数列{}n a 的前n 项和为n S ，已知232=S a ，且124,,S S S 成等比数列，求{}n a 的通项式。

求数列｛c n ｝的前n 项和R n .3、2013四川理T16.(本小题满分12分)在等差数列{}n a 中，138a a +=，且4a 为2a 和9a 的等比中项，求数列{}n a 的首项、公差及前n 项和。

4、2013天津理T19. (本小题满分14分)已知首项为32的等比数列{}n a 不是递减数列, 其前n 项和为(*)n S n ∈N , 且S 3 + a 3, S 5 + a 5, S 4 + a 4成等差数列.(Ⅰ) 求数列{}n a 的通项公式; (Ⅱ) 设*()1n n nT S n S ∈=-N , 求数列{}n T 的最大项的值与最小项的值.5、2013浙江理T18.在公差为d 的等差数列}{n a 中，已知101=a ，且3215,22,a a a +成等比数列。

（1）求n a d ,；（2）若0<d ，求.||||||||321n a a a a ++++6、2013广东理T19．（本小题满分14分） 设数列{}n a 的前n 项和为n S .已知11a =,2121233n n S a n n n +=---,*n ∈N . (Ⅰ) 求2a 的值；(Ⅱ) 求数列{}n a 的通项公式；(Ⅲ) 证明:对一切正整数n ,有1211174n a a a +++< .7、2013安徽理T20.（本小题满分13分）设函数22222()1(,)23n nn x x x f x x x R n N n=-+++++∈∈ ，证明：（Ⅰ）对每个nn N ∈，存在唯一的2[,1]3n x ∈，满足()0n n f x =； （Ⅱ）对任意np N ∈，由（Ⅰ）中n x 构成的数列{}n x 满足10n n p x x n+<-<。

2013---2017年全国1卷高考理科数学分类汇编---统计（2015全国1.理数.19）(本小题满分12分)某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x (单位：千元)对年销售量y (单位：t )和年利润z (单位：千元)的影响，对近8年的年宣传费x i 和年销售量y i (i ＝1，2，···，8)数据作了初步处理，得到下面的散点图及一些统计量的值.表中i w =8118i i w w ==∑(Ⅰ)根据散点图判断，y ＝a ＋bx 与y ＝c ＋y关于年宣传费x 的回归方程类型？(给出判断即可，不必说明理由)(Ⅱ)根据(Ⅰ)的判断结果及表中数据，建立y 关于x 的回归方程；(Ⅲ)已知这种产品的年利润z 与x ，y 的关系为z ＝0.2y －x .根据(Ⅱ)的结果回答下列问题： （ⅰ）年宣传费x ＝49时，年销售量及年利润的预报值是多少？ （ⅱ）年宣传费x 为何值时，年利率的预报值最大？附：对于一组数据(u 1 v 1)，(u 2 v 2)…….. (u n v n )，其回归线v ＝αβ+u 的斜率和截距的最小二乘估计分别为：121()(),()niii nii u u v v v u u u βαβ==--==--∑∑19．（本小题满分12分）解：（Ⅰ）由散点图可以判断，y c =+适宜作为年销售量y 关于年宣传费x 的回归方程类型．……2分（Ⅱ）令w=先建立y关于w的线性回归方程．由于()()()81821108.8681.6i iiiiw w y ydw w==--===-∑∑，56368 6.8100.6c y dw=-=-⨯=，所以y关于w的线性回归方程为100.668y w=+，因此y关于w的线性回归方程为100.6y=+6分（Ⅲ）（ⅰ）由（Ⅱ）知，当49x=时，年销售量y的预报值100.6576.6y=+=，年利润z的预报值0.2576.64966.32z=⨯-=．……9分（ⅱ）根据（Ⅱ）的结果知，年利润z的预报值(0.2100.620.12z x x=⨯+-=-+．13.66.82==，即46.24x=时，z取得最大值．故年宣传费为46.24千元时，年利润的预报值最大．……12分（2013全国1.理数.3）为了解某地区的中小学生视力情况，拟从该地区的中小学生中抽取部分学生进行调查，事先已了解到该地区小学、初中、高中三个学段学生的视力情况有较大差异，而男女生视力情况差异不大.在下面的抽样方法中，最合理的抽样方法是A.简单随机抽样B.按性别分层抽样C.按学段分层抽样D.系统抽样【命题意图】本题主要考查分层抽样方法，是容易题.【解析】因该地区小学、初中、高中三个学段学生的视力情况有较大差异，故最合理的抽样方法是按学段分层抽样，故选C.。