三视图讲解

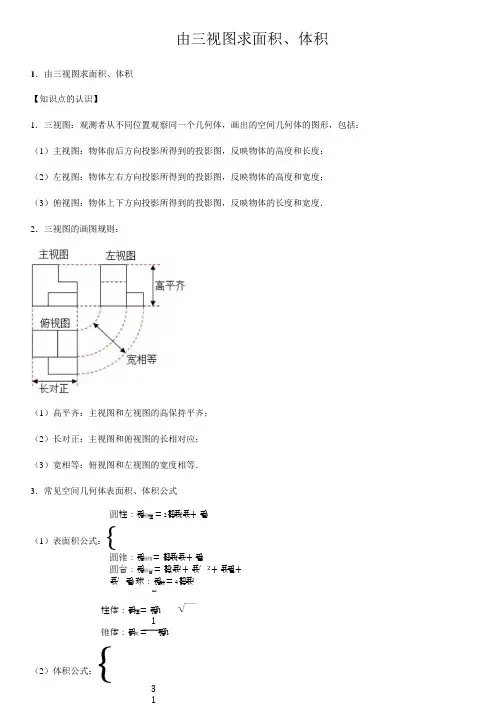
由三视图求面积、体积1．由三视图求面积、体积【知识点的认识】1．三视图：观测者从不同位置观察同一个几何体，画出的空间几何体的图形，包括：（1）主视图：物体前后方向投影所得到的投影图，反映物体的高度和长度；（2）左视图：物体左右方向投影所得到的投影图，反映物体的高度和宽度；（3）俯视图：物体上下方向投影所得到的投影图，反映物体的长度和宽度．2．三视图的画图规则：（1）高平齐：主视图和左视图的高保持平齐；（2）长对正：主视图和俯视图的长相对应；（3）宽相等：俯视图和左视图的宽度相等．3．常见空间几何体表面积、体积公式圆柱：푆圆柱=2휋푟(푟+푙)（1）表面积公式：{圆锥：푆圆锥=휋푟(푟+푙)圆台：푆圆台=휋(푟2+푟′2+푟푙+푟′푙) 球：푆球=4휋푟2柱体：푉柱=푆ℎ1锥体：푉锥=푆ℎ（2）体积公式：{台体：푉台=(푆+푆푆′+푆′)ℎ33球：푉球=4휋푟31/ 3【解题思路点拨】1．解题步骤：（1）由三视图定对应几何体形状（柱、锥、球）（2）选对应公式（3）定公式中的基本量（一般看俯视图定底面积，看主、左视图定高）（4）代公式计算2．求面积、体积常用思想方法：（1）截面法：尤其是关于旋转体及与旋转体有关的组合体问题，常用轴截面进行分析求解；（2）割补法：求不规则图形的面积或几何体的体积时常用割补法；（3）等体积转化：充分利用三棱锥的任意一个面都可以作为底面的特点，灵活求解三棱锥的体积；（4）还台为锥的思想：这是处理台体时常用的思想方法．【命题方向】三视图是新课标新增内容之一，是新课程高考重点考查的内容．解答此类问题，必须熟练掌握三视图的概念，弄清视图之间的数量关系：正视图、俯视图之间长相等，左视图、俯视图之间宽相等，正视图、左视图之间高相等（正俯长对正，正左高平齐，左俯宽相等），要善于将三视图还原成空间几何体，熟记各类几何体的表面积和体积公式，正确选用，准确计算．例：某几何体三视图如图所示，则该几何体的体积为（）A.8﹣2πB.8﹣πC.8 ―휋2D.8 ―휋41分析：几何体是正方体切去两个圆柱，根据三视图判断正方体的棱长及切去的圆柱的底面半径和高，把数据代入4正方体与圆柱的体积公式计算．1解答：由三视图知：几何体是正方体切去两个圆柱，4正方体的棱长为 2，切去的圆柱的底面半径为 1，高为 2，∴几何体的体积V＝23﹣2 ×14×π×12×2＝8﹣π．故选：B．点评：本题考查了由三视图求几何体的体积，根据三视图判断几何体的形状及数据所对应的几何量是解题的关键．。

立体几何和三视图一、知识点回顾1、空间几何体的三视图定义三视图：正视图（光线从几何体的前面向后面正投影）；侧视图（从左向右）、 俯视图（从上向下）注：正视图反映了物体上下、左右的位置关系，即反映了物体的高度和长度； 俯视图反映了物体左右、前后的位置关系，即反映了物体的长度和宽度；侧视图反映了物体上下、前后的位置关系，即反映了物体的高度和宽度。

▲长对正，高平齐 ，宽相等2、柱体、锥体、台体的表面积与体积（1）几何体的表面积为几何体各个面的面积的和。

（2）特殊几何体表面积公式（c 为底面周长，h 为高，'h 为斜高，l 为母线）ch S =直棱柱侧面积 rh S π2=圆柱侧 '21ch S =正棱锥侧面积 rl S π=圆锥侧面积')(2121h c c S +=正棱台侧面积l R r S π)(+=圆台侧面积()l r r S +=π2圆柱表 ()l r r S +=π圆锥表 ()22R Rl rl r S +++=π圆台表（3）柱体、锥体、台体的体积公式V Sh =柱 2V S h r h π==圆柱 13V S h=锥 h r V 231π=圆锥'1()3V S S h =+台'2211()()33V S S h r rR R h π=++=++圆台二、专题讲解1、空间角问题（1）直线与直线所成的角 ①两平行直线所成的角：规定为 0。

②两条相交直线所成的角：两条直线相交其中不大于直角的角，叫这两条直线所成的角。

③两条异面直线所成的角：过空间任意一点O ，分别作与两条异面直线a ，b 平行的直线b a '',，形成两条相交直线，这两条相交直线所成的不大于直角的角叫做两条异面直线所成的角。

（2）直线和平面所成的角①平面的平行线与平面所成的角：规定为 0。

②平面的垂线与平面所成的角：规定为90。

③平面的斜线与平面所成的角：平面的一条斜线和它在平面内的射影所成的锐角，叫做这条直线和这个平面所成的角。

1、《三视图》一等奖说课稿范文一、教材分析1、本堂课在教材中的地位和作用：人们在日常生活中接触到的是立体图形，而要研究它，往往把它转化成平面图形来研究。

图形的三视图是立体图形转化成平面图形的一种形式，而下一节的“立体图形的表面展开图”是由立体图形转化成平面图形的另一种形式。

而整个初中数学教材的编排顺序也是按立体图形—平面图形——多边形——四边形——三角形的编排顺序。

因此，本节内容将是由立体图形到平面图形的一个纽带，学好它至关重要。

2、教学内容分析：本节课由学生日常生活引入，由浅入深，循序渐进。

由生活中的立体图形——视图——利用图纸制作工件。

让学生经历探索三视图画法的过程，让学生深切体会到数学知识来源于生活，运用于生活。

3、教学目标：（1）知识目标：让学生能画出简单立体图形的三视图。

（2）能力目标：培养学生多角度观察事物的能力以及空间想象能力、渗透数学转化思想。

（3）情感目标：通过学生对“三视图”的学习应用，激发学生热爱生活、热爱数学的情感。

4、教学重点：画简单立体图形的三视图。

5、教学难点：三视图与美术作图的区别。

二、学情分析七年级学生对身边有趣的事物充满好奇，对一些有规律性的问题充满探求的欲望，他们非常乐意动手操作，有很强的好胜心和表现欲，有一定的归纳能力。

但是他们开始接触几何知识，空间想象力太弱，缺乏从多角度观察事物的经验。

三、教学方法依据新的课程标准精神及建构主义学习理论，学生学习不是教师向学生传递知识的过程，而是学生建构自已的知识和能力的过程。

根据以上教材的特点和学生的具体情况，我将采取以下教学方法进行教学。

1、情景教学法：通过各种情景的设置，让学生溶入到生活中去。

通过在生活情景中体验、掌握数学知识，让学生深切体会到，数学就在我们身边。

2、直观教具演示教学法通过直观教具的演示，以及学生利用学具亲自操作，培养学生从多角度观察事物的.能力。

满足学生的探求欲望。

3、多媒体辅助教学法。

通过多媒体动画演示，针对学生缺乏空间想象力的弱点化难为易。

29.2 三视图1.三视图概念：物体的正投影从一个方向反映了物体的形状和大小，为了全面地反映一个物体的形状和大小，我们常常再选择正面和侧面两个投影面，画出物体的正投影。

如图 (1)，我们用三个互相垂直的平面作为投影面，其中正对着我们的叫做正面，正面下方的叫做水平面，右边的叫做侧面.一个物体(例如一个长方体)在三个投影面内同时进行正投影，在正面内得到的由前向后观察物体的视图，叫做主视图，在水平面内得到的由上向下观察物体的视图，叫做俯视图;在侧面内得到由左向右观察物体的视图，叫做左视图.如图(2)，将三个投影面展开在一个平面内，得到这一物体的一张三视图(由主视图，俯视图和左视图组成).三视图中的各视图，分别从不同方面表示物体，三者合起来就能够较全面地反映物体的形状.三视图中，主视图与俯视图表示同一物体的长，主视图与左视图表示同一物体的高.左视图与俯视图表示同一物体的宽，因此三个视图的大小是互相联系的.画三视图时.三个视图要放在正确的位置.并且使主视图与俯视图的长对正，主视图与左视图的高平齐.左视图与俯视图的宽相等画三视图的注意点：1、画一个立体图形的三视图时要考虑从某一个方向看物体获得的平面图形的形状和大小，不要受到该方向的物体结构的干扰。

2、在画三视图时，三个三视图不要随意乱放，应做到俯视图在主视图的下方，左视图在主视图的右边，三个视图之间保持：长对正，高平齐，宽相等。

典型例题例1.画出下图所示的一些基本几何体的三视图.分析:画这些基本几何体的三视图时，要注意从三个方面观察它们.具体画法为:1.确定主视图的位置，画出主视图;2.在主视图正下方画出俯视图，注意与主视图“长对正”。

3.在主视图正右方画出左视图.注意与主视图“高平齐”，与俯视图“宽相等”.解：例2.画出如图所示的支架(一种小零件)的三视图.分析:支架的形状，由两个大小不等的长方体构俯视图左视图主视图成的组合体.画三视四时要注意这两个长方体的上下、前后位置关系.解:如图29.2-7是支架的三视图例3.右图是一根钢管的直观图，画出它的三视图分析.钢管有内外壁，从一定角度看它时，看不见内壁.为全面地反映立体图形的形状，画图时规定;看得见部分的轮廓线画成实线.因被其他那分遮挡而看不见部分的轮廓线画成虚线.解:图如图29.2-7是钢管的三视图，其中的虚线表示钢管的内壁.例4．如图所示图形是一个多面体的三视图，请根据视图说出该多面体的具体名称。