库仑土压力理论.ppt
- 格式:ppt
- 大小:405.00 KB
- 文档页数:5




库仑土压力理论1776年法国的库伦(C.A.Coulomb)根据极限平衡的概念,并假定滑动面为平面,分析了滑动楔体的力系平衡,从而求算出挡土墙上的土压力,成为著名的库伦土压力理论。
一、基本原理库伦研究了回填砂土挡土墙的土压力,把挡土墙后的土体看成是夹在两个滑动面(一个面是墙背,另一个面在土中,如图6-12中的AB和BC面)之间的土楔。
根据土楔的静平衡条件,可以求解出挡土墙对滑动土楔的支撑反力,从而可求解出作用于墙背的总土压力。
这种计算方法又称为滑动土楔平衡法。
应该指出,应用库伦土压力理论时,要试算不同的滑动面,只有最危险滑动面AB对应的土压力才是土楔作用于墙背的Pa或Pp库伦理论的基本假设:1.墙后填土为均匀的无粘性土(c=0),填土表面倾斜(β>0);2.挡土墙是刚性的,墙背倾斜,倾角为ε;3.墙面粗糙,墙背与土本之间存在摩擦力(δ>0);4.滑动破裂面为通过墙踵的平面。
二、主动土压力计算如图所示,墙背与垂直线的夹角为ε,填土表面倾角为β,墙高为H,填土与墙背之间的摩擦角为δ,土的内摩擦角为φ,土的凝聚力c=0,假定滑动面BC通过墙踵。
滑裂面与水平面的夹角为α,取滑动土楔ABC作为隔离体进行受力分析(图6-11b)。
土楔是作用有以下三个力:1.土楔ABC自重W,由几何关系可计算土楔自重,方向向下;2.破裂滑动面BC上的反力R,大小未知,作用方向与BC面的法线的夹角等于土的内摩擦角φ,在法线的下侧;3.墙背AB对土楔体的反力P(挡土墙土压力的反力),该力大小未知,作用方向与墙面AB的法线的夹角δ,在法线的下侧。
土楔体ABC在以上三个力的作用下处于极限平衡状态,则由该三力构成的力的矢量三角形必然闭合。
已知W的大小和方向,以及R、P的方向,可给出如图所示的力三角形。
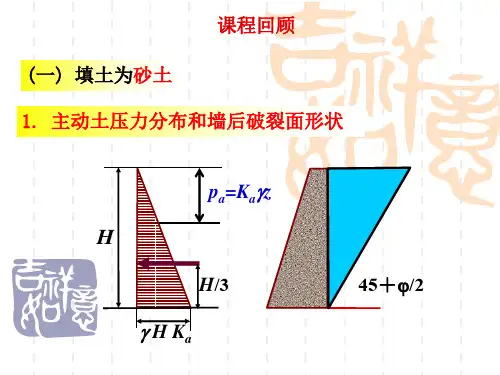
按正弦定理可求得:求其最大值(即取dP/dα=0),可得主动土压力式中Ka为库伦主动土压力系数,可按下式计算确定沿墙高度分布的主动土压力强度pa可通过对式(6-21)微分求得:由此可知,主动土压力强度沿墙高呈三角形分布,主动土压力沿墙高的分布图形如图所示。




库仑土压力理论1776年法国的库伦(C.A.Coulomb)根据极限平衡的概念,并假定滑动面为平面,分析了滑动楔体的力系平衡,从而求算出挡土墙上的土压力,成为著名的库伦土压力理论。
一、基本原理库伦研究了回填砂土挡土墙的土压力,把挡土墙后的土体看成是夹在两个滑动面(一个面是墙背,另一个面在土中,如图6-12中的AB和BC面)之间的土楔。
根据土楔的静平衡条件,可以求解出挡土墙对滑动土楔的支撑反力,从而可求解出作用于墙背的总土压力。
这种计算方法又称为滑动土楔平衡法。
应该指出,应用库伦土压力理论时,要试算不同的滑动面,只有最危险滑动面AB对应的土压力才是土楔作用于墙背的Pa或Pp库伦理论的基本假设:1.墙后填土为均匀的无粘性土(c=0),填土表面倾斜(β>0);2.挡土墙是刚性的,墙背倾斜,倾角为ε;3.墙面粗糙,墙背与土本之间存在摩擦力(δ>0);4.滑动破裂面为通过墙踵的平面。
二、主动土压力计算如图所示,墙背与垂直线的夹角为ε,填土表面倾角为β,墙高为H,填土与墙背之间的摩擦角为δ,土的内摩擦角为φ,土的凝聚力c=0,假定滑动面BC通过墙踵。
滑裂面与水平面的夹角为α,取滑动土楔ABC作为隔离体进行受力分析(图6-11b)。
土楔是作用有以下三个力:1.土楔ABC自重W,由几何关系可计算土楔自重,方向向下;2.破裂滑动面BC上的反力R,大小未知,作用方向与BC面的法线的夹角等于土的内摩擦角φ,在法线的下侧;3.墙背AB对土楔体的反力P(挡土墙土压力的反力),该力大小未知,作用方向与墙面AB的法线的夹角δ,在法线的下侧。
土楔体ABC在以上三个力的作用下处于极限平衡状态,则由该三力构成的力的矢量三角形必然闭合。
已知W的大小和方向,以及R、P的方向,可给出如图所示的力三角形。
按正弦定理可求得:求其最大值(即取dP/dα=0),可得主动土压力式中Ka为库伦主动土压力系数,可按下式计算确定沿墙高度分布的主动土压力强度pa可通过对式(6-21)微分求得:由此可知,主动土压力强度沿墙高呈三角形分布,主动土压力沿墙高的分布图形如图所示。