第三讲 并联谐振电路

谐振电路中的并联和串联谐振电路是电路中常见的重要组成部分之一。

它是指在特定频率下，电路中的电感和电容元件形成共振，使得电流和电压振荡幅度达到最大值的现象。

谐振电路可以用来选择特定频率的信号，以及滤除其他频率的噪声。

在谐振电路中，我们常见的两种连接方式是并联和串联。

本文将深入探讨谐振电路中的并联和串联的特点、应用以及其在实际电路中的使用。

首先，我们来讨论并联谐振电路。

在并联谐振电路中，电感和电容元件并联连接。

当电感和电容元件的谐振频率与输入信号频率相等时，电路达到谐振状态。

并联谐振电路具有以下几个重要特点：1. 并联谐振电路的共振频率计算：在并联谐振电路中，共振频率可以通过以下公式计算：f_res = 1 / (2 * π * √(L * C))其中，f_res是共振频率，L是电感的值，C是电容的值。

2. 并联谐振电路的阻抗特性：在谐振频率附近，并联谐振电路的阻抗最小，接近于零。

这意味着在共振频率附近，电流的幅值最大，电压降最小。

因此，并联谐振电路可以用作选择特定频率信号的滤波器。

3. 并联谐振电路的相位特性：在共振频率附近，电流和电压具有相位一致。

即它们的相位差非常小，接近于零度。

这种相位一致的特性在某些应用中非常重要。

接下来，我们转向串联谐振电路。

在串联谐振电路中，电感和电容元件串联连接。

与并联谐振电路相比，串联谐振电路具有一些独特的特点：1. 串联谐振电路的共振频率计算：与并联谐振电路不同，串联谐振电路的共振频率可以通过以下公式计算：f_res = 1 / (2 * π * √(L * C))与并联谐振电路公式相同。

2. 串联谐振电路的阻抗特性：在谐振频率附近，串联谐振电路的阻抗最大，接近于无穷大。

这意味着在共振频率附近，电压的幅值最大，电流降最小。

串联谐振电路可以用作电压放大器。

3. 串联谐振电路的相位特性：在共振频率附近，电流和电压具有相位差90度。

电流超前于电压，并且相位差始终保持90度。

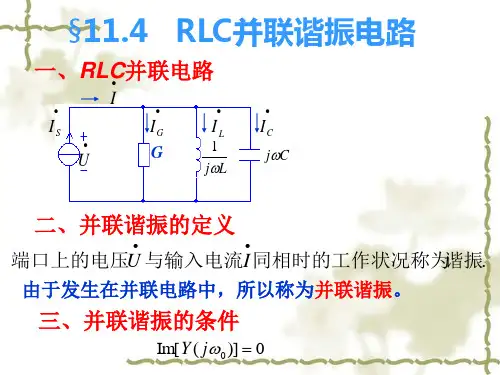
并联谐振公式并联谐振公式是电路中常见的一种谐振方式，它在很多电子设备中都起着重要的作用。

在这篇文章中，我们将详细探讨并联谐振公式的原理、特点以及应用。

让我们来了解一下什么是并联谐振。

在电路中，当电容和电感器以并联的方式连接时，如果电路的频率等于谐振频率，那么电路中的电流将达到最大值。

这种现象称为并联谐振。

并联谐振的公式可以表示为：1/ωC + 1/ωL = 1/Q，其中ω是电路的角频率，C是电容器的电容量，L是电感器的电感量，Q是电路的品质因数。

并联谐振公式的原理是基于电路中的电压和电流之间的相位差。

在谐振频率下，电容和电感器的阻抗值相等，从而使得电路中的电流达到最大值。

此时，电压和电流之间的相位差为零，电路呈现纯电阻性质。

这种纯电阻性质使得并联谐振电路在特定频率下具有很高的电流放大能力。

并联谐振的特点有几个方面。

首先，当电路的频率等于谐振频率时，电路中的电流最大，而电压最小。

其次，谐振频率与电容和电感器的值有关，可以通过调节电容和电感器的参数来改变谐振频率。

第三，当电路的频率偏离谐振频率时，电路中的电流将逐渐减小，电压也会增大。

最后，谐振电路对特定频率的信号有很好的选择性，可以用于滤波和放大特定频率的信号。

并联谐振公式的应用非常广泛。

在无线通信领域中，谐振电路常用于接收和发送信号的频率选择和放大。

在无线电和电视接收器中，谐振电路用于选择和放大特定频率的无线信号。

在音频设备中，谐振电路常用于音频信号的放大和滤波。

此外，谐振电路还广泛应用于医疗设备、雷达系统、无线传感器网络等领域。

并联谐振公式是电路中一种重要的谐振方式，具有很多应用。

通过调节电容和电感器的参数，可以实现对特定频率信号的选择性放大和滤波。

并联谐振电路在无线通信、音频设备等领域发挥着重要作用，为我们的生活带来了便利和乐趣。

串联谐振与并联谐振
串联谐振与并联谐振是电路中常见的谐振方式。

串联谐振：指电路中电感和电容串联，构成一个谐振回路。

当电路中的频率等于谐振频率时，电感和电容分别消耗功率，且功率相等。

此时，电路中的电流达到最大值，电压也达到最大值。

并联谐振：指电路中电感和电容并联，构成一个谐振回路。

当电路中的频率等于谐振频率时，电感和电容共享电压，此时谐振回路的整体电感和电容等效为一抵消电容。

此时，电路中的电流达到最大值，电压也达到最大值。

两种谐振方式在实际应用中有不同的优缺点，需要根据具体的电路需求进行选择。

例如，串联谐振常用于滤波电路中，而并联谐振常用于谐振电路中。

并联谐振电路和串联谐振电路原理小伙伴，今天咱们来唠唠并联谐振电路这个超有趣的东西。

你可以把并联谐振电路想象成一场盛大的派对。

在这个电路里呢，有电感和电容这两个超有个性的小伙伴并联在一起。

电感就像是一个有点固执的老大哥，它总是阻碍电流的变化，就像老大哥坚持自己的原则一样。

而电容呢，它就像是一个充满活力的小年轻，能够储存电荷，就像小年轻充满无限的能量可以随时爆发。

当电路处于并联谐振状态的时候，那可就热闹啦。

这时候电路的总阻抗达到最大哦。

就好像派对上大家突然达成了一种默契，对外界来说，这个电路变得有点难搞了，电流很难轻易地大量流进去。

从原理上讲呢，电感的感抗和电容的容抗在这个时候相互作用得特别巧妙。

电感的感抗随着频率的升高而增大，电容的容抗呢，却是随着频率的升高而减小。

在某个特定的频率下，这两个家伙的作用刚好相互抵消，就像两个人在拔河，突然力量一样，谁也拉不动谁了。

这个时候呀，电路就呈现出一种很特别的状态。

在并联谐振电路里，电压可是个关键角色。

因为总阻抗最大，在电源电压不变的情况下，电路中的总电流就变得很小啦。

但是在电感和电容这两个支路里，电流可不小哦。

这就像是派对上虽然外面看起来没多少人进出，但是里面电感和电容各自的小圈子里可是热闹非凡呢。

电感支路和电容支路的电流会比总电流大很多，而且这两个支路的电流大小差不多，方向相反，就像两个好朋友在玩相反的游戏，但是又很和谐。

而且呀，并联谐振电路在实际应用里可厉害啦。

比如说在收音机的调谐电路里，它就像一个超级挑剔的小耳朵。

当不同频率的信号传来的时候，只有和它谐振频率相同的信号才能被它选中，就像小耳朵只听它喜欢的声音一样。

其他频率的信号就被拒之门外啦。

宝子，咱们再来聊聊串联谐振电路吧，这个电路也是超级有意思的哦。

你可以把串联谐振电路想象成一个接力赛跑的小团队。

这里面电感、电容和电阻就像是三个不同特点的运动员。

电感呢，还是那个有点慢吞吞的，总是阻碍电流变化的家伙，就像一个跑起来有点费劲的运动员。

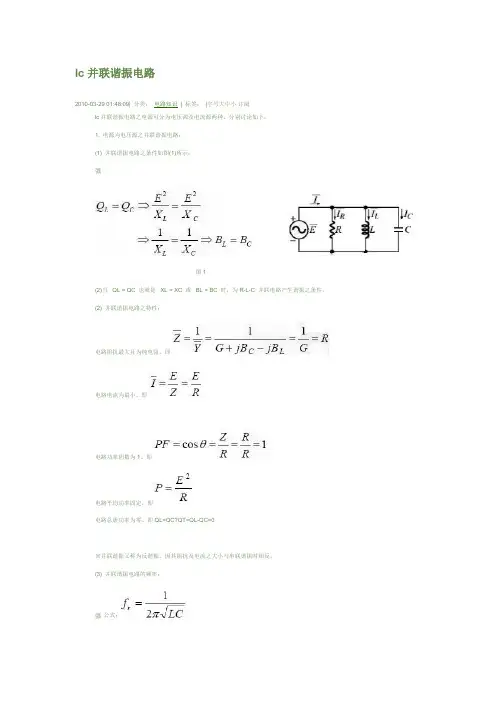
lc并联谐振电路2010-03-29 01:48:09| 分类：电路知识| 标签：|字号大中小订阅lc并联谐振电路之电源可分为电压源及电流源两种，分别讨论如下：1. 电源为电压源之并联谐振电路：(1) 并联谐振电路之条件如图(1)所示：图1(2)当QL = QC 也就是XL = XC 或BL = BC 时，为R-L-C 并联电路产生谐振之条件。

(2) 并联谐振电路之特性：电路阻抗最大且为纯电阻。

即电路电流为最小。

即电路功率因数为1。

即电路平均功率固定。

即电路总虚功率为零。

即QL=QC?QT=QL-QC=0※并联谐振又称为反谐振，因其阻抗及电流之大小与串联谐振时相反。

(3) 并联谐振电路的频率：公式：R-L-C 并联电路欲产生谐振时，可调整电源频率f 、电感器L 或电容器C 使其达到谐振频率f r ，而与电阻R 完全无关(与串联电路完全相同)。

(4) 并联谐振电路之品质因数：定义：电感器或电容器在谐振时产生的电抗功率与电阻器消耗的平均功率之比，称为谐振时之质量因子。

公式：品质因子Q值愈大表示电路对谐振时响应愈佳。

(5) 并联谐振电路导纳与频率之关系如图(2)所示：电导G 与频率无关，系一常数，故为一横线。

电感纳，与频率成反比，故为一曲线。

电容纳BC= 2πfC ，与频率成正比，故为一斜线。

导纳Y=G+ j（BC- BL）当 f = fr 时，BC＝BL ，Y = G ( Z= R 为最大值)，电路为电阻性。

当f ＞fr 时，BC ＞BL ，电路为电容性。

当f ＜fr 时，BL ＞BC ，电路为电感性。

当f = 0 或f = ∞ 时，Y = ∞ ，Z = 0 ，电路为短路。

若将电源频率f 由小增大，电路导纳Y 的变化为先减后增，阻抗Z 的变化则为先增后减。

图(2) 图(3)(6) 并联谐振电路之选择性如图(3)所示：当f = fr 时，，此频率称为谐振频率。

当f = f1 或f2 时，，此频率称为旁带频率或截止频率。

并联谐振回路并联谐振回路并联谐振回路是通信电路中最常用的无源网络。

利用并联谐振回路的幅频特性和相频特性，不仅可以进行选频，即从输入信号中选择出有用频率分量而抑制掉无用频率分量或噪声（例如，在小信号并联谐振放大器、并联谐振功率放大器和正弦波振荡器中），而且还可以进行信号的频幅转换和频相转换（例如，在斜率鉴频和相位鉴频电路中）。

另外，用L、C元件还可以组成各种形式的阻抗变换电路。

所以，谐振回路虽然结构简单，但是在通信电路中却是不可缺少的重要组成部分。

谐振回路由电感线圈和电容器组成，它具有选择信号及阻抗变换作用。

简单的谐振回路有串联并联谐振回路和并联并联谐振回路，有时为获得更好的选择效果，可把两个或更多个串、并联并联谐振回路连接起来，构成带通滤波器。

并联谐振放大器中，并联并联谐振回路使用最为广泛。

某一频率的电路。

常用的有LC，RC，变压器耦合和晶体振荡器等。

震荡器的原理很简单，就是正反馈原理，LC决定震荡的频率，普通晶体震荡器的晶体可以等效一个Q值很高的电感，利用电容的充放电产生震荡。

在逆变器电路中多用RC组成的多并联谐振荡器。

也有用变压器反馈式的自激振荡回路。

回路产生并联谐振时的电压波形，当电压方波作用于LC串联回路时，方波的前后沿都会对LC串联回路产生激励(即接收能量)，每次激励过后又会产生阻尼振荡(即损耗能量)，当输入电压波形的上升率dv/dt值大于并联谐振回路波形(正弦波)的上升率时，电路就会产生激励；当输入电压波形的上升率dv/dt值小于并联谐振回路波形的上升率时，电路就会产生阻尼。

由于每次激励过后振荡回路的能量还没有损耗完，紧接着又来一次新的激励，使振荡电压一次、又一次地进行叠加，如果激励的相位与振荡波形的相位能保持同步，则振荡电压的幅度会越来越高，直到激励的能量与电路损耗的能量相等为止。

因此，当并联谐振回路的品质因数Q值很高时，并联谐振电压也可以升得很高，理想的情况是Q 值无限高(即天线没有损耗)，则产生并联谐振电压的幅度也会升得无限高，但这种情况是不存在的。

精心整理电路课程设计举例：?以RLC 并联谐振电路1．电路课程设计目的（1）验证RLC 并联电路谐振条件及谐振电路的特点；（2）学习使用EWB 仿真软件进行电路模拟。

2．仿真电路设计原理本次设计的RLC 串联电路图如下图所示。

图1RLC 并联谐振电路原理图理论分析与计算：根据图1所给出的元件参数具体计算过程为 发生谐振时满足L C ωω001=,则RLC 并联谐振角频率ω0和谐振频率f 0分别是RLC 并联谐振电路的特点如下。

（1）谐振时Y=G,电路呈电阻性，导纳的模最小G B G Y =+=22. （2）若外施电流I s 一定，谐振时，电压为最大，G I U S o =,且与外施电流同相。

（3）电阻中的电流也达到最大，且与外施电流相等，I I S R =.（4）谐振时0=+I I C L ,即电感电流和电容电流大小相等，方向相反。

3．谐振电路设计内容与步骤（1）电路发生谐振的条件及验证方法这里有几种方法可以观察电路发生串联谐振：(1)利用电流表测量总电流I s 和流经R 的电流I R ，两者相等时即为并联谐振。

(2)利用示波器观察总电源与流经R 的电流波形，两者同相即为并联谐振。

例题：已知电感L 为0.02H,电容C 为50uf,电阻R 为200Ω。

由LC f π210=计算得,Hz f 1.1570=按上图进行EWB 的仿真,得到下图。

流经电阻R 的电流和总电流I 相等为10mA,流进电感L 和电容C 的总电流为5.550uF ，几乎为零，所以电路达到谐振状态。

总电源与流经R 的电流波形同相，所以电路达到并联谐振状态。

4．实验体会和总结这次实验我学会了运用EWB 仿真RLC 并联谐振电路，并且运用并联谐振的特点判断达到谐振状态。

尤其是观察总电源与流经R 的电流波形，两者同相即为并联谐振。

这种方法我们只能在实验中看到，平时做题试卷上是不可能观察到的。

这加深了我对谐振电路的理解。