当前位置：文档之家 › 傅里叶与信号与系统

傅里叶与信号与系统

  • 格式：doc
  • 大小：45.50 KB
  • 文档页数：7

下载文档原格式

  / 7

合集下载

第三章信号与系统连续时间信号与系统的傅里叶分析

第三章信号与系统连续时间信号与系统的傅里叶分析
n
n = 2, 4, 6, n = 1, 3, 5,
信号与系统
一、周期信号的傅立叶级数
所以有
an 0
0
bn
4
n
n = 2, 4, 6, n = 1, 3, 5,
f
(t)
4
[sin 0t
1 sin 3
3
0t
1 5
sin
5
0
t
1 n
sin n
0t
]
信号与系统
一、周期信号的傅立叶级数
2 . 复指数形式的傅立叶级数
a
b
0
信号与系统
一、周期信号的傅立叶级数
三角函数集:
{1, cos0t, cos 20t, , cos n0t, , sin 0t, sin 20t, , sin n0t, }
在区间 (t0 ,
t0
T)
内是一完备正交函数集。
T
2 0
正交性:（m 和 n 都是整数）
0
t0 T cos
t0
m0t
cos
信号与系统
§ 3.2 周期信号的 傅立叶级数展开
信号与系统
周期信号
周期信号: 定义在区间 (, ) ，每隔一定时间 T ，按 相同规律重复变化的信号，如图所示 。它可表示为
f (t)=f ( t+mT )
其中 m 为正整数， T 称为信号的周期，周期的倒数称为频率。
f t
1
0 T/2 T
t
1
信号与系统
f (t) a0 a1 cos0t a2 cos 20t b1 sin 0t b2 sin 20t
a0 an cos n0t bn sin n0t

信号与系统第6讲第3章周期信号的傅里叶级数表示

信号与系统第6讲第3章周期信号的傅里叶级数表示

sin(2 k(1/ 4)) k
sin(k k
/ 2)
根据Example3.5的结果，用性质计算傅里叶级数的系数
分析：原函数为x(t),本函数为g(t)
g (t )
x(t
1)
1 2
,周期方波的参数T
4,T1
1,
如果原函数的系数为ak，x(t 1)的系数为bk
bk
a e jk (2 / 4)1 k
在不连续点上，傅里叶级数的收敛趋势-吉伯斯现象
不连续点上收敛于不连续点的平均值 不连续点附近呈现起伏现象，起伏的峰值不随N增加而降低 峰值为不连续点差值的9%
吉伯斯现象的实际意义
不连续信号的傅里叶级数截断近似在接近不连续点有高频起伏 选择足够大的N，可以保证这些起伏的总能量可以忽略
2024/6/10
2024/6/10
信号与系统－第6讲
19
§3.5 连续时间傅里叶级数性质
（4）Example3.8 计算周期冲激串的傅里叶级数系数 根据性质计算周期方波的系数
周期冲激串可表示为x(t) (t kT ) k
ak
1 T
T / 2 (t)e jk 2t /T dt 1
T / 2
T
周期方波为g (t ),它的导数为q(t )
c0为直流分量， c0 2T1 / T
对照前面 例题验证
结果
20
§3.5 连续时间傅里叶级数性质
（5）Example3.9
1.x(t)是实信号
2.x(t)是周期信号，T 4，傅里叶级数系数ak
3.ak 0，k 1
4.傅里叶系数为bk
e
j
k
/
2
a
的信号是奇信号

信号与系统PPT 第三章 傅利叶变换

信号与系统PPT 第三章 傅利叶变换

bn an
)
2
(n 1,3,5)
f
(t)
2E
n1,3,5
1 n
sin
n1t
2E
(sin
1t
1 3
sin
31t
1 5
sin
51
)
或
2E
f (t)
n1,3,5
1 n
cos(n1t
2
)
Fn
1 2 (an
jbn
)
j
bn 2
jE
n
0
n 1,3,5 n 2,4,6
f (t) jE e j1t jE e j31t jE e j1t jE e j31t
5
51 31 1 1 31 51
0 1 31 51
n
n 1 31
0
51
51 31 1
2
1
31 51
2
2
3.1.4 波形的对称性与傅里叶级数的关系
已知信号f(t)展为傅里叶级数的时候，如果f(t)
是实函数而且它的波形满足某种对称性，则在傅里叶 级数中有些项将不出现，留下的各项系数的表示式也 将变得比较简单。波形的对称性有两类，一类是对整 周期对称；另一类是对半周期对称。
那么这个正交函数集也就不完备。
1,cos1t,cos 21t,cos n1t,, sin1t,sin21t,sinn1t,
包含正、 余弦函数的三角函数集是最重要的完
备正交函数集。 它具有以下优点：
(1) 三角函数是基本函数； (2) 用三角函数表示信号， 建立了时间与频率两个基本物理量之
间的联系； (3) 单频三角函数是简谐信号,简谐信号容易产生、传输、 处理； (4) 三角函数信号通过线性时不变系统后， 仍为同频三角函数信

信号与系统第三章-周期信号的傅里叶级数表示

信号与系统第三章-周期信号的傅里叶级数表示

一. 连续时间傅里叶级数
成谐波关系的复指数信号集:
k(t) { ejk 0 t}k 0 , 1 , 2 ,
其中1. 每个信号都是以 2 为周期的.
2.公共周期为
2 0
k 0
，且该集合中所有的信号都
是彼此独立的。
若将信号集 k (中t ) 所有的信号线性组合起来
有 x(t) akejk0t, k0,1 , 2
——傅里叶级数的三角函数表示式
若令 ak Bk jCk 则
x (t) a 0 1(B k jC k)e jk 0 t (B k jC k)e jk 0 t
k
k 1
a 0 (B k jC k)e jk 0 t (B k jC k)e jk 0 t k 1
ak* ak
k1
a k * a k A k e jk A k e j k
即： Ak Ak
k k
结论： 若 x ( t ) 是实信号,则有：
a k 的模关于k 偶对称，幅角关于 k 奇对称。
x(t)a 0[A kejk0 tejkA kejk0 tejk] k 1
a02 Akcos(k0tk) k1
B kjC kB kjC k
因此 Bk Bk
Ck Ck
结论： 若 x ( t ) 是实信号,则有：
a k 的实部关于 k 偶对称，虚部关于 k 奇对称。
将关系 Bk Bk , Ck Ck 代入，可得到
x (t) a 0 (B k jC k)e jk 0 t (B k jC k)e jk 0 t k 1 a 0 (B kjC k)ejk 0 t (B kjC k)ejk 0 t k 1 a02 B kcosk0tC ksink0t k1

信号与系统傅里叶变换

信号与系统傅里叶变换

n次谐波系数：
2
an T
T
2 T
2
f
(t) cos(n1t)dt

2 T
2 2
A cos(n1t )dt

4A
n1T
sin n1
2

An
其有效值为：
A~n
2 2
An
36
将 n 1 代入上式，得基波有效值为：
A1
2 4A sin 1 10 2 sin18 2 1T 2
45 °
图 3.3-1 (a)振幅谱； (b) 相位谱
30 ° 30 °
20 °
54
|F n |
2
1.5
1.5
1
1
1
0.4 0.2
0.4 0.2
－ 6－ 5 － 4－ 3－ 2 － o 2 3 4 5 6

(a)
n 45 °
45 °
30 ° 30 °
20 °
15° 10°
3
VxVyT VxiVyi 0
i 1
矢量正交集：指由两两正交的矢量组成的矢量集合。
如三维空间中，Vx (1, 0, 0) Vy (0,1, 0) Vz (0, 0,1) 所组成的集合就是矢量正交集，且完备。
矢量A (1, 2.5, 4) 表示为 A Vx 2.5Vy 4Vz
电子技术中的周期信号大都满足狄里赫利条件条件，当
f(t)满足狄里赫利条件时，an, bn, cn 才存在。
21
结论：周期信号可分解为各次谐波分量之和。
一般而言 An cos(n1t n ) n 称为 次谐波 ，An
是 n 次谐波的振幅， n是其初相角。

信号与系统 第三章 周期信号的傅里叶级数展开

信号与系统 第三章 周期信号的傅里叶级数展开
1 T
2 n 2

T1
f (t ) dt

F ( n1 )
左边是周期信号f(t)在一个周期里的平均功率（即单位时间内的能量）
2 2 1 1 2 jnt F ( n ) e dt F ( n ) dt F ( n ) 而同时有 T 1 1 1 T1 1 T1 T1
n 1
——余弦形式
x(t ) d 0 d n sin( n1t n )
n 1
——正弦形式
(1). f (t ) a0 an cosnt bn sin nt
n1

三角函数形式
(2). f (t ) A0 An cos(nt n )
而无物理意义。将来可以看出，指数函数形式比正弦函数形式在数 学上处理起来要方便的多。
§3.2 周期矩形脉冲的谱线特点
x(t )
E

T1

t
2 2
T1
脉冲为 ，脉冲高度为E，周期为T1
1 21 1 E 1 jn1t jn1t 2 X (n1 ) T1 x(t )e dt E e dt e jn1t T1 2 T1 2 T1 jn1 jn jn 1 2E 1 1 2 2 e sin(n1 ) e jn1T1 2 n1T1 sin(n1 ) E E 2 Sa (n1 ) T1 n T1 2 1 2
电子信息与电气工程学院
本章内容
连续时间周期信号的傅立叶级数表示 周期矩形脉冲的谱线特点
§3.1 连续时间周期信号的傅立叶级数表示
{1, cos n1t ,sin n1t} n=1,2, , 是一个完备的正交函数集

信号与系统课程第06讲 非周期信号的分解——傅里叶变换

信号与系统课程第06讲 非周期信号的分解——傅里叶变换
信号与系统——非周期信号的分解—傅里叶变换
1
第06 讲
上一页 返 回
2019/10/8
信号与系统——非周期信号的分解—傅里叶变换
本章主要内容
4.1 引言 4.2 傅里叶级数 4.3 周期信号的频谱 4.4 非周期信号的频谱 4.5 傅里叶变换的性质 4.6 能量谱和功率谱 4.7 周期信号的傅里叶变换
上一页 返 回
2 2019/10/8
信号与系统——非周期信号的分解—傅里叶变换
4.1 引言 4.2 傅里叶级数 4.3 周期信号的频谱
4.4 非周期信号的频谱
4.5 傅里叶变换的性质 4.6 能量谱和功率谱 4.7 周期信号的傅里叶变换
上一页 返 回
3 2019/10/8
信号与系统——非周期信号的分解—傅里叶变换
1
0
+ j 0 j +
F ( j ) = 1
2 +2
(
)
=
−
arctan
2
o
( )
o
− 2
上一页
2019/10/8
信号与系统——非周期信号的分解—傅里叶变换
12
双边指数信号
f (t ) = e− t − t
0
e− t (t)
f (t)e− j t dt =
−
0 e( − j )t dt +
当T→∞时，有 → d , n → , →
上一页
2019/10/8
信号与系统——非周期信号的分解—傅里叶变换
7
∵
F( j) = lim 2Fn ，则
T →
F( j)
lim
T →
Fn

信号与系统3.3典型信号的傅里叶级数

信号与系统3.3典型信号的傅里叶级数

1 2
sin2ω1t
1 3
sin3ω1t
1 4
sin4ω1t
E
(1) n1
n 1
1 n
sin(n1t)
周期锯齿脉冲信号的频谱只包含正弦分量，谐波的幅
度以 1 的规律收敛。 n
第3章 傅里叶变换
四、周期三角脉冲信号
周期三角脉冲信号如图3-10所示。
f (t)
E
tT1ຫໍສະໝຸດ T1 20T1 2
第3章 傅里叶变换
三、周期锯齿脉冲信号
周期锯齿脉冲信号如图3-9所示。
f (t)
E
2
T1
2
t
T1
0
2
E
2
图3-9 周期锯齿脉冲信号
显然它是奇函数，因而an=0，由式(3-4)可以求出傅里
叶级数的系数bn。这样，便可得到周期锯齿脉冲信号的傅 里叶级数为
第3章 傅里叶变换
f(t)
E π
sinω1t
1 5
cos51t
2E
cos1t
1 3
cos31t
1 5
cos51t
其频谱函数如图3-8所示 由于对称方波的偶次谐波恰恰落在频谱包络线的零值 点，所以它的频谱只包含基波和奇次谐波。 该信号既是偶函数，又是奇谐函数，因此在它的频谱 中只包含基波和奇次谐波的余弦分量。
第3章 傅里叶变换 图3-8 对称方波频谱
T1
E
为ω１。脉冲间隔
T1
越大，谱线越密。
信号的周期T1增大 时，谱线的间隔变
小。反之变大
2
n
谱线包络 按抽样函 数衰减
4
2
4
第3章 傅里叶变换

信号与系统第3章 傅里叶变换

信号与系统第3章 傅里叶变换

P
f
2 (t) 1 T1
t0 T1 t0
f
2 (t)d t
a0 2
1 2
n1
(an
2
bn 2 )
2
Fn _____ 帕塞瓦尔定理
n
结论：周期信号的平均功率等于傅里叶级数展开 式中基波分量及各谐波分量有效值的平方 和，即时域和频域的能量守恒。
五. 周期信f号(t)的频c0 谱 （c三n c角os函(n数1t形 式n )） n1
(1) 偶函数 f (t) f (t)
4
an T1
T1
2 0
f (t) cos(n1t)dt
Fn
Fn
an 2
bn 0
傅里叶级数中不会含有正弦项， 只可能含有直流项和余弦项。
(2) 奇函数 f (t) f (t)
a0 0 , an 0
bn
4 T1
T1
2 0
f (t) sin(n1t)d t
e j n1t
T1 n 2
画频谱图：
c0
a0
E
T1
an
2E
T1
Sa
n1
2
, n
1,2,
cn an
1）令 m
2
得
2
m
即在
2
m，m为整数处有零点。
2）
2
2
T1
T1
零点间谱线个数
3) c n值为正，相位为0，值为负，相位为π
4)谱线间隔为 1 带宽
2
T1
，第一个过零点带宽定义为信号的
1 3
s in31t
1 4
sin41t
E
1 n1

(完整word版)傅里叶变换在信号与系统系统中的应用.

(完整word版)傅里叶变换在信号与系统系统中的应用.

河北联合大学本科毕业设计（论文）2011年 5月24日题目傅里叶变换在信号与系统中的应用专业数学与应用数学姓名刘帅学号 200710050113主要内容、基本要求、主要参考资料等主要内容傅里叶变换是一种重要的变换,且在与通信相关的信号与系统中有着广泛的应用。

本文主要研究傅里叶变换的基本原理；其次，掌握其在滤波，调制、解调,抽样等方面中的应用。

分析了信号在通信系统中的处理方法，通过傅里叶变换推导出信号调制解调的原理，由此引出对频分复用通信系统的组成原理的介绍.基本要求通过傅里叶变换实现一个高通滤波，低通滤波,带通滤波。

用傅里叶变换推导出信号调制解调的原理。

通过抽样实现连续信号离散化,简化计算.另外利用调制的原理推导出通信系统中的时分复用和频分复用。

参考资料[1］《信号与系统理论、方法和应用》徐守时著中国科技大学出版社 2006年3月修订二版［2］《信号与系统》第二版上、下册郑君里、应启珩、杨为理著高等教育出版社[3]《通信系统》第四版 Simon Haykin 著宋铁成、徐平平、徐智勇等译沈连丰审校电子工业出版社[4]《信号与系统—连续与离散》第四版 Rodger E.Ziemer 等著肖志涛等译腾建辅审校电子工业出版社[5]《现代通信原理》陶亚雄主编电子工业出版社[6］《信号与系统》乐正友著清华大学出版社[7］《信号与线性系统》阎鸿森、王新风、田惠生编西安交通大学出版社［8］《信号与线性系统》张卫钢主编郑晶、徐琨、徐建民副主编西安电子科技大学出版社［9] http：//baike.baidu。

com/view/191871.htm//百度百科傅里叶变换[10]《通信原理》第六版樊昌信曹丽娜编著国防工业出版社[11］A．V．Oppenheim，A。

S。

Willsky with S。

H.Nawab.Siganals and systems（Second edition).Prentice-Hall，1997.中译：刘树棠.信号与系统。

信号与系统3.3典型信号的傅里叶级数

信号与系统3.3典型信号的傅里叶级数

2
2
f (t) E[u(t ) u(t )]
2
2
把周期信号展成傅里叶级数
f t a0 ancosnω1t bnsinnω1t n1
其系数为
1
a0 T1
T1
2 -T1
2
F(t)dt
1 T1
2 - 2
Edt
Eτ T1
第3章 傅里叶变换
an
2 T1
T1
2 T1
f(t)cos(nω1t)dt
第3章 傅里叶变换
三、周期锯齿脉冲信号
周期锯齿脉冲信号如图3-9所示。
f (t)
E
2
T1
2
t
T1
0
2
E
2
图3-9 周期锯齿脉冲信号
显然它是奇函数，因而an=0，由式(3-4)可以求出傅里
叶级数的系数bn。这样，便可得到周期锯齿脉冲信号的傅 里叶级数为
第3章 傅里叶变换
f(t)
E π
sinω1t
2
2 T1
τ
2 τ
2
Ecos
n
2π T1
t
dt
谐波的幅度 按1/n规律收 敛
e nπ
sin
2nπ
2T1
sin
2nπ
2T1
2E nπ
sin
nπ
T1
2Eτ sin
nπ
T1
nπ
T1
T1
2Eτ T1
Sa
nπ
T1
Eτ1
π
Sa
nω1τ 2
第3章 傅里叶变换
由于f (t)是偶函数，有（2 3）可知 bn 0
规律收敛。

信号与系统傅里叶

信号与系统傅里叶

dt
= F[ j(ω-ω0)] 例 1 f(t) = ej3t ←→ F(jω) = ? 解 1 ←→ 2πδ(ω) ej3t ×1←→ 2πδ(ω-3) -
信号与系统 例 2 解
4.5
傅里叶变换的性质
f(t) = cosω0t ←→ F(jω) = ?
1 jω0t 1 − jω0t f (t) = e + e 2 2
1 ∞ − jω t f (−ω) = ∫ −∞ F( jt ) e dt 2π
∴ F(j t) ←→ 2πf (–ω)
信号与系统 例
f (t) = 1 1+t 2
− |t| α
4.5
傅里叶变换的性质
←→ F(jω) = ?
2 α
解
e
← →
当 α=1, e−t| | ∴
α2 +ω2 2 ← → 1+ω2
∞
用时移特性
∫
所以
∞
−∞
f 2 (t − τ ) e
− jω t
d t = F2 ( jω ) e
− jω τ
F [ f1(t)*f2(t) ]=
∫
∞
−∞
f 1 (τ ) F2 ( jω ) e
− jω τ
d τ = F2 ( jω ) ∫ f1 (τ ) e
−∞
∞

− jω τ
dτ
= F1(jω)F2(jω)
2
-2
0
2
ω
1 π sin t [π g 2 (ω )] * [π g 2 (ω )] = g 2 (ω ) * g 2 (ω ) ←→ 2π 2 t
信号与系统
4.5

世界信号与系统科学家故事事迹

世界信号与系统科学家故事事迹

世界信号与系统科学家故事事迹篇一：《傅里叶：从热传导到信号世界的传奇》在科学的浩瀚星空中，有一颗璀璨的明星，他叫傅里叶。

我一直对他的故事特别着迷，你知道吗？他可是信号与系统领域一个超级厉害的人物呢。

傅里叶是个法国人，他生活的那个时代啊，大家对热传导现象那是一知半解的。

傅里叶呢，就像是一个执着的探险家，一头扎进了这个研究里。

我就想象他呀，整天在他那有点乱乱的小实验室里，对着各种奇奇怪怪的仪器琢磨着。

有一次，他的朋友来拜访他。

朋友一进门就被那满屋子的图纸和仪器弄得晕头转向的。

朋友皱着眉头说：“傅里叶啊，你这整得像个啥啊，乱得跟个鸡窝似的。

”傅里叶却满不在乎地摆摆手说：“哎呀，你不懂，这些可都是我解开热传导秘密的宝贝呢。

”他一边说着，一边拿起一张画满了曲线的纸，眼睛里闪着兴奋的光，“你看，我发现热传导的过程就像是一场有规律的舞蹈，这里面一定有一个数学的旋律在指挥着。

”他的朋友听得一头雾水，只能无奈地耸耸肩。

傅里叶就是这么一个专注的人。

他花费了大量的时间和精力，去研究热是怎么在物体里传播的。

他经过无数次的实验和计算，发现任何周期函数都可以用正弦函数和余弦函数构成的无穷级数来表示。

这个发现可不得了啊！这就像是找到了一把万能钥匙，可以打开很多未知的大门。

就拿我们现在的信号处理来说吧。

你看我们听的音乐，其实就是一种信号。

如果没有傅里叶的这个发现，我们就很难对音乐信号进行处理。

比如说，那些音乐软件里的均衡器，就是利用了傅里叶变换的原理。

可以把音乐中的高音、低音等不同频率的部分分离开来，然后根据我们的喜好去调整。

傅里叶的这个成果刚开始还不被一些保守的学者所接受呢。

那些老学究们总是摇头晃脑地说：“这不符合传统的数学观念啊。

”但是傅里叶可没有被这些反对的声音吓倒。

他就像一个坚定的战士，拿着他的研究成果到处去演讲，去解释。

慢慢地，越来越多的人开始理解他的伟大发现了。

傅里叶对信号与系统科学的贡献可不仅仅局限于热传导和数学公式。

傅里叶方法在信号与系统分析中的应用

傅里叶方法在信号与系统分析中的应用
本章要点
4.1 信号取样与取样信号的傅里叶变换 4.1.1 时域取样 （1）信号取样的一般问题 取样就是从一个连续时间信号 中按照一定的时间间隔提取一系列离散样本值的过程；通过取样得到离散信号称为取样信号，记为 。 完成这种取样过程的取样系统模型： 图4－1 连续信号的取样模型
举例：解释为什么满足上述条件是信号不失真。 设输入信号 （4－25）
回目录
只要系统具有如图4－13所示的幅度频率特性和相位频率特性，则该系统对于 来说，就是无失真传输系统 图 4－13 实际应用中的无失真传输系统的频 率特性
回目录
二、无失真传输的时域条件 对式（4－21）作傅里叶变换，可得出无失真传输系统的时域条件： （4－24）
回目录
4.1.2 频域取样 频域取样的数学模型为 （4－7） 对式两端取傅里叶反变换，得： 此式表明，若连续信号的频谱 被间隔为 频域冲击序列在频域中取样，则在时域等效于连续 时限信号 以 为周期等幅度的重复。
回目录
式中： （4－12） 由式（4－3）有 （4－13）
回目录
（1）幅频特性为一常数，即： （4－22） （2）相频特性是一条过原点的负斜率的直线，即 ； （4－23） 图 4－12 无失真传输系统的幅频特性和相频特性
回目录
上述定理表明：为了能够从取样信号 中恢复原信号 ，取样过程必须满足两个条件： （1）连续信号 必须是带限的，其频谱函数在 各处为零； （2）取样间隔 不能过大，必知某系统
求激励为 时的零状态响应。
解：根据定义可求出
4.3 时分复用 图4－9给出了一个时分复用通信系统和三路信号时分复用的例子。 图4－9 时分复用系统原理图
回目录
需要说明的几个问题： （1）多路取样器取样周期T的确定 （4－18） （2）确定多路取样器取样周期T时的最大传送路数可按下式确定最大传输的信号路数: (4－19) 式中 是取样脉冲的宽度（完成一次取样所需要的时间）。

信号与系统-3章傅里叶变换

信号与系统-3章傅里叶变换

[ Ane j(n1t ) ]
n
式中
幅度
An cne jn an2 bn2 (cosn jsinn ) 复指数
cn an2 bn2
n
arctan( bn an
)
相位
An 的具体求法如下：
An
an
jbn
2 T
t2 t1
f (t)cos(n1t)dt
j2 T
t2 t1
f (t)sin(n1t)dt
（3）f (t在) 区间内有有限个极值点。
Direchlet条件
傅里叶级数存 在的充要条件
3.2.2 傅里叶级数的复指数形式
1. 从三角函数形式的傅里叶级数推导
利用欧拉公式:
cos(n1t
n )
ej(n1t n )
e j(n1t n ) 2
f
(t)
1 2
[cne j(n1tn ) ]
n
1 2
n1
2A T0
cos n0t
n1
2A
fAC (t) T0 n1
t
cos n0 d
A π
n1
sin n0t
n
fD A/ 2
故
f (t) A A sin n0t
2 π n1 n
（2）利用直接法求解
a0
1 T0
0 A tdt A
T T0
0
2
an 0
bn
2 T0
0 T0
A T0
将 f (t) 去除直流分量，则仅剩交流分量 fAC (t)
fAC (t)
f
(t)
A n T0 [u(t nT0 ) u(t
(n 1)T0 )]

傅里叶变换信号与系统

傅里叶变换信号与系统

傅里叶变换信号与系统
傅里叶变换在信号与系统领域中被广泛使用。

它是对信号进行频谱分析和频率域处理的最常用方法之一。

傅里叶变换最早是由法国数学家傅里叶所提出的，因此得名为“傅里叶变换”。

傅里叶变换可以将时域信号（即时域波形）变换为频域信号（即频谱图）。

在频域中，我们可以看到信号在哪些频率上具有能量，以及能量的大小。

这使得我们能够更深入地了解信号的性质，进而进行更加准确的信号处理。

此外，傅里叶变换还可以将时域中的卷积运算转换为频域中的乘法，进一步简化了信号处理的过程。

傅里叶变换有两种形式：离散傅里叶变换（DFT）和连续傅里叶变换（CTFT）。

离散傅里叶变换适用于离散信号，如数字信号，而连续傅里叶变换则适用于连续信号，如模拟信号。

虽然DFT是离散的，但我们可以通过对离散信号进行零填充来获得高分辨率的DFT结果。

另外，快速傅里叶变换（FFT）是一种高效的DFT实现方式，它只需要
O(nlogn)的计算量即可完成DFT计算。

傅里叶变换广泛应用于数字信号处理、通信系统、音频处理、图像处理等众多领域。

例如，在音频处理中，我们可以将音频信号的频域信息用于音频特效制作、音调调整、降噪等处理。

在通信系统中，我们可以使用傅里叶变换来进行调制解调、信道均衡、信号匹配等处理。

总之，傅里叶变换是一种十分重要的信号处理方法。

它为我们提供了在频率域上对信号进行深入理解的能力，并简化了信号处理的步骤。

在日常的信号处理中，熟练掌握傅里叶变换是非常有必要的。

信号与系统傅里叶变换.

信号与系统傅里叶变换.

实验二连续信号频域分析（FT）一、实验目的1．掌握连续时间周期信号的频谱分析方法；2．掌握连续时间信号的频域分析方法；3．熟悉通过调用fft(函数求解连续信号的傅立叶变换的数值分析方法。

二、实验原理连续时间周期信号可展开成傅立叶级数，即三角函数形式其中：，n=1,2,3…n=1,2,3…当取指数形式：n≠0则MATLAB的符号积分函数int(可以帮助我们求出连续时间周期信号的截断傅立叶级数及傅立叶表示。

连续时间信号的傅立叶变换定义为MATLAB的Symbolic Math Toolbox提供了能直接求解傅立叶变换及逆变换的函数fourier(及ifourier(。

另外，连续时间信号的傅立叶变换可以利用MATLAB提供的快速傅立叶变换函数fft(进行数值计算。

连续信号进行离散化后得到序列记作，则N点离散序列的离散傅立叶变换（DFT）和反变换（IDFT）为：的傅立叶复系数，为进行数值计算，必须离散化。

取足够小的，，于是：,由式（1）得（3）即考虑到本身以N为周期，于是傅立叶复系数(4周期信号用指数型傅立叶级数表示为：，离散化后得到由式（2）得。

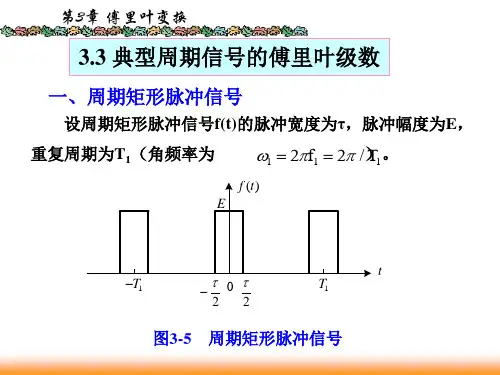
三、实验分析例题：求周期矩形脉冲信号的傅里叶级数和傅里叶变换。

分析：由已知得到周期矩形脉冲信号的第一个周期内信号，即得到傅里叶变换为，而周期矩形脉冲信号的傅里叶级数的系数为，由此得到的傅里叶级数为。

手动绘画波形如下：四、实验仿真首先对周期脉冲信号的第一个周期内信号进行傅里叶变换，程序如下：得到图形如下：再得到周期信号的傅里叶级数的系数，程序编辑如下：得到的波形如下：五、实验小结通过本次实验掌握连续时间周期信号的频谱分析方法，以及使用matlab软件中的FFT函数求得周期信号进行傅里叶系数。

掌握了连续时间信号的频谱分析方法，以及使用matlab中的fourier函数对非周期函数进行傅里叶变换。

收获很大。

实验要求一上机实现例题1、2、3、4。

例1．幅度为A，宽度为τ，重复周期为T的周期矩形脉冲信号f(t，当A=1，τ=0.4，T=2s 时，画出其频谱图。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

信
号
与
系
统
—走进傅里叶
目录
一．傅里叶生平 (2)
二．傅里叶的成就 (2)
1. 数学方面 (2)
2. 物理方面 (3)
三．傅里叶事迹 (4)
四．傅里叶变换算法的意义 (5)
五．感想.............................. 错误！未定义书签。

一．傅里叶生平
傅里叶全名让·巴普蒂斯·约瑟夫·傅里叶（1768年3月21日－1830年5月16日），法国数学家、物理学家，提出傅里叶级数，并将其应用于热传导理论上，傅里叶变换也以他命名。

傅里叶于1768年3月21日出生于法国约讷省欧塞尔的一个裁缝家庭。

很早的时候他的父母就双亡，八岁时就沦为了孤儿，曾在军队中教授数学，在1795年他到巴黎高等师范教书，之后又在巴黎综合理工学院占一教席。

1798年他跟随拿破仑东征，被任命为下埃及的总督。

由于英国舰队对法国人进行了封锁，所以他受命在当地生产军火为远征部队提供军火。

这个时期，他向开罗埃及学院递交了几篇有关数学的论文。

1801年，拿破仑的远征军队远征失败后，他便被任命为伊泽尔省长官。

1816年他回到巴黎，六年后他当选了科学院的秘书，并发表了《热的分析理论》一文，此文建立是在牛顿的热传导理论的速率和温度差成正比的基础上。

1830年5月16日他病逝于巴黎，1831年他的遗稿被整理出版成书。

二．傅里叶的成就
1.数学方面
傅里叶在数学方面的主要贡献是在研究热的传播时创立了一套数学理论。

1807年向巴黎科学院呈交《热的传播》论文，推导出著名的热传导方程，并在求解该方程时发现解函数可以由三角函数构成的级数形式表示，从而提出任一函数都可以展成三角函
数的无穷级数。

傅里叶级数（即三角级数）、傅里叶分析等理论均由此创始。

同时他还最早使用定积分符号，改进了代数方程符号法则的证法和实根个数的判别法等。

傅里叶变换的基本思想首先由傅里叶提出，所以以其名字来命名以示纪念。

从现代数学的眼光来看，傅里叶变换是一种特殊的积分变换。

它能将满足一定条件的某个函数表示成正弦基函数的线性组合或者积分。

在不同的研究领域，傅里叶变换具有多种不同的变体形式，如连续傅里叶变换和离散傅里叶变换。

傅里叶变换在物理学、数论、组合数学、信号处理、概率、统计、密码学、声学、光学等领域都有着广泛的应用。

2.信号与系统方面
傅里叶在信号与系统方面的成就主要是他提出了傅里叶变换原理，对解决这方面的难题提供了极大的帮助。

傅里叶变换原理表明：任何连续测量的时序或信号，都可以表示为不同频率的正弦波信号的无限叠加。

而根据该原理创立的傅里叶变换算法利用直接测量到的原始信号，以累加方式来计算该信号中不同正弦波信号的频率、振幅和相位，和傅里叶变换算法对应的是反傅里叶变换算法。

该反变换从本质上说也是一种累加处理，这样就可以将单独改变的正弦波信号转换成一个信号。

傅里叶变换将原来难以处理的时域信号转换成了易于分析的频域信号，可以利用一些工具对这些频域信号进行处理、加工。

最后还可以利用傅里叶反变换将这些频域信号转换成时域信号。

三．傅里叶事迹
傅里叶8岁时在一地方军事学院接受教育时就表现出了数学上的天赋；在傅里叶差点被修士劝导为神职人员的时候，法国大革命爆发，傅里叶对大革命报有很大热情并加入了人民党；但是，就像许多巨变一样，大批的知识分子被处死，其中就包括了像拉瓦锡这样的伟大数学家，看到这种趋势，大批的知识分子离开法国以求保命，而在两次从断头台下逃生以后，傅里叶对大革命充满了绝望。

此时，正是拿破仑结束了对知识分子的迫害，并建立新的学校补充知识分子阶层。

1794年，26岁的傅里叶被任命为新建立的巴黎师范高等专科学校的数学首席。

傅里叶对固体热传播做出了深入研究并就此带入了傅里叶级数与积分的研究中去。

1807年12月21日，他在一篇关于热学原理的论文中宣布这个伟大的结果。

但是包括伟大的数学家拉普拉斯、拉格朗日、勒让德、孟济、拉克劳克斯在内的评审委员会虽承认傅里叶此成果的新颖和重要性，但却批评其缺乏数学的严谨因而被科学院拒绝，1811年又提交了经修改的论文，该文获科学院大奖，却未正式发表。

1822年，傅里叶终于出版了专著《热的解析理论》。

这部经典著作将欧拉、伯努利等人在一些特殊情形下应用的三角级数方法发展成内容丰富的一般理论，三角级数后来就以傅里叶的名字命名。

傅里叶应用三角级数求解热传导方程，同时为了处理无穷区域的热传导问题又导出了现在所称的“傅里叶积分”，这一切都极大地推动了偏微分方程边值问题的研究。

然而傅里叶的工作意义远不止此，它迫使人
们对函数概念作修正、推广，特别是引起了对不连续函数的探讨；三角级数收敛性问题更刺激了集合论的诞生。

因此，《热的解析理论》影响了整个19世纪分析严格化的进程。

傅里叶在研究物理的同时，也在不断的求解着一个个的数学难题，他在求解热传导方程时，傅里叶应用三角级数求解热传导方程，同时为了处理无穷区域的热传导问题又导出了现在所称的“傅里叶积分”，这一切都极大地推动了偏微分方程边值问题的研究。

正是因为有了傅里叶的这些成果，才迫使人们对函数概念作修正、推广，特别是引起了对不连续函数的探讨；三角级数收敛性问题更刺激了集合论的诞生。

四．傅里叶变换算法的意义
傅里叶变换是数字信号处理领域一种很重要的算法。

要知道傅里叶变换算法的意义，首先要了解傅里叶原理的意义。

傅里叶原理表明：任何连续测量的时序或信号，都可以表示为不同频率的正弦波信号的无限叠加。

而根据该原理创立的傅里叶变换算法利用直接测量到的原始信号，以累加方式来计算该信号中不同正弦波信号的频率、振幅和相位。

无论是在数学领域还是物理领域，傅里叶变换都有着重大的意义，首先，傅里叶分析是作为热过程的解析分析的工具。

同时在数学上，利用傅里叶变换"任意"的函数通过一定的分解，都能够表示为正弦函数的线性组合的形式，而正弦函数在物理上是被充分研究而相对简单的函数类，从而可以轻松求解，同时著名的卷积定理又指出了傅
里叶变换可以化复变换可以利用数字计算机快速的算出(其算法称为快速傅里叶变换算法(FFT))。

正是由于这样,傅里叶变换在物理学、数论、组合数学、信号处理、概率、统计、密码学、声学、光学等领域都有着广泛的应用。