中梁刚度放大系数计算excel

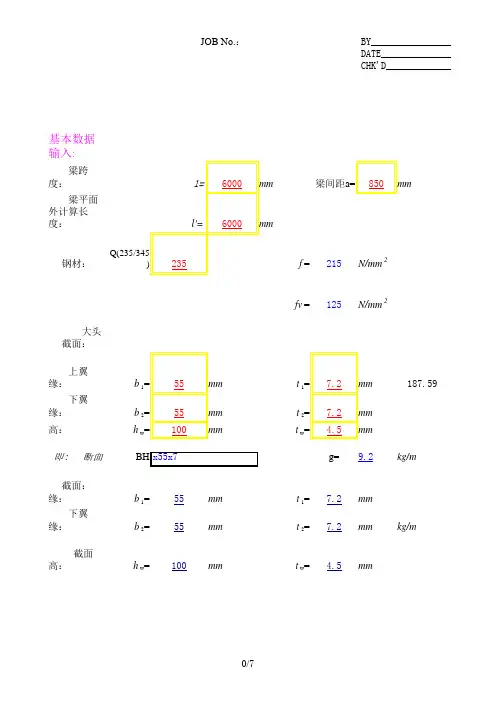
(完整)excel计算大全-钢结构计算表格-单跨等截面简支梁

p = 0.88
3.96 KN ·m
2.64 KN
KN/m
钢梁上翼缘应力：
钢梁下翼缘应力：
钢梁剪应力：
σ 1= 187.59 N/mm 2
σ 2= 101.99 N/mm 2
τ=
5.87 N/mm 2
1/7
挠度：
3.参数统计
1.构件总重： 2.构件实际重量：
JOB No.：__________
g= 9.2 kg/m
2.截面验重：
恒载：
0.11 KN/m 0.15 KN/m 2
活载：
g = 1k 0.24 KN/m q c = 0.50 KN/m 2
pk=
弯矩：剪力：
（2）钢梁的强度、稳定和挠度的验算：
0.66
KN/m
M= V=
大头截面：
上翼缘：
下翼缘：截面高：
即 : 断面小头
截上面翼：缘：
下翼缘：
截面高：
b 1=
55
mm
b 2=
55
mm
h w= 100 mm 100x5x55x7
BH x55x7
b 1=
55
mm
b 2=
55
mm
h w= 100 mm
fv = 125 N/mm 2
t 1= 7.2 mm
t 2= 7.2 mm t w= 4.5 mm
JOB No.：__________
BY________________ DATE______________ CHK'D_____________
基本数据输入:
梁跨度：
梁平面外计算长度：

excel钢结构计算表格

简支钢梁计算基本数据输入:梁跨度： l=9000mm梁间距a=2400mm钢材：Q 345f =315N/mm 2fv =185N/mm 2 上翼缘：b 1=400mm t 1=14mm 下翼缘：b 2=300mm t 2=12mm 腹板：h w =574mm t w =8mm即: 断面截面特性计算：钢梁截面：A 0=13792mm 2 重量108.3kg/m 钢梁中和轴的位置：y 0=342mm钢梁对X轴截面惯性矩：I z =8.94E+08mm4钢梁上翼缘的弹性抵抗矩：W 1x = 3.46E+06mm 3 钢梁下翼缘的弹性抵抗矩：W 2x = 2.61E+06mm 3 钢梁对Y轴截面惯性矩：I y = 1.02E+08mm 4i y =85.9 mm y =104.8上翼缘对Y 轴的惯性矩：I 1=7.47E+07mm 4下翼缘对Y 轴的惯性矩：I 2= 2.70E+07mm 40.73 截面不对称影响系数：0.380.53 工字形截面简支梁的系数0.76 梁的整体稳定系数：0.74 修正后：0.672.截面验算：（1）弯矩及剪力的计算：=+=211I I I b α=-=)12(8.0b b αη=bβ==hb t l 111ξ=bφ='bφλ钢梁自重： 1.30KN/m恒载： 4.00KN/m2g1k=10.90KN/m活载：q c= 3.0KN/m2p k=18.10KN/m p=23.16KN/m 弯矩：M=234.49KN·m剪力：V=104.22KN（2）钢梁的强度、稳定和挠度的验算：梁的整体稳定应力：σ=101.01N/mm2钢梁上翼缘应力：σ1=67.70N/mm2钢梁下翼缘应力：σ2=89.68N/mm2钢梁剪应力：τ=22.70N/mm2挠度：w=8.4mmw/l=1/1072。

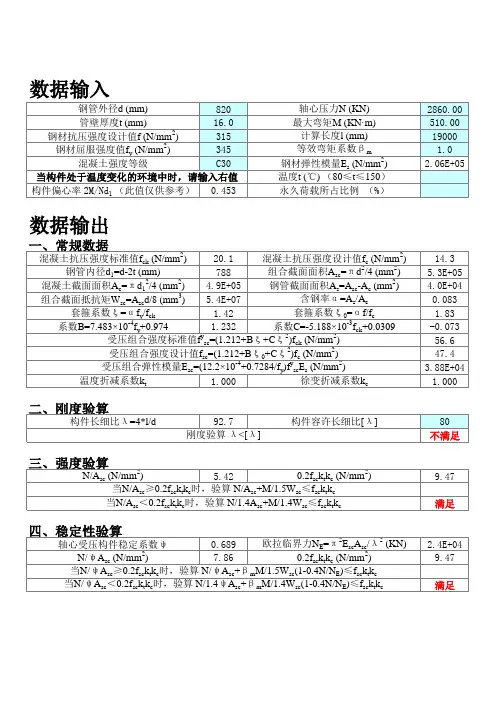
excel计算大全-钢结构计算表格-钢管混凝土结构计算程序

四,稳定性验算
轴心受压构件稳定系数ψ 0.686 N/ψAsc (N/mm2) 0.2fscktkc (N/mm2) 当N/ψAsc≥0.2fscktkc时,验算 N/ψAsc+βmM/1.5Wsc(1-0.4N/NE)≤fscktkc 当N/ψAsc<0.2fscktkc时,验算 N/1.4ψAsc+βmM/1.4Wsc(1-0.4N/NE)≤fscktkc 2.4E+04 9.47 满足
二,刚度验算
构件长细比λ=4*l/d 92.7 刚度验算 λ<[λ] 构件容许长细比[λ] 80 不满足
三,强度验算
5.42 N/Asc (N/mm2) 0.2fscktkc (N/mm2) 当N/Asc≥0.2fscktkc时,验算 N/Asc+M/1.5Wsc≤fscktkc 当N/Asc<0.2fscktkc时,验算 N/1.4Asc+M/1.4Wsc≤fscktkc 9.47 满足
数据输入
钢管外径d (mm) 820 管壁厚度t (mm) 16.0 2 315 钢材抗压强度设计值f (N/mm ) 2 345 钢材屈服强度值fy (N/mm ) 混凝土强度等级 C30 当构件处于温度变化的环境中时, 当构件处于温度变化的环境中时,请输入右值构件偏心率 2M/Nd1 (此值仅供参考) 0.453 轴心压力N (KN) 最大弯矩M (KNm) 计算长度l (mm) 等效弯矩系数βm 2 钢材弹性模量Es (N/mm ) 温度t (℃) (80≤t≤150) 永久荷载所占比例 (%) 2860.00 510.00 19000 1.0 2.06E+05
�
数据输出
一,常规数据
20.1 混凝土抗压强度标准值fck (N/mm2) 混凝土抗压强度设计值fc (N/mm2) 钢管内径d1=d-2t (mm) 788 组合截面面积Asc=πd2/4 (mm2) 4.9E+05 钢管截面面积As=Asc-Ac (mm2) 混凝土截面面积Ac=πd12/4 (mm2) 含钢率α=As/Ac 5.4E+07 组合截面抵抗矩Wsc=Ascd/8 (mm3) 套箍系数ξ=αfy/fck 套箍系数ξ0=αf/fc 1.42 -4 1.232 系数C=-5.188×10-3fck+0.0309 系数B=7.483×10 fy+0.974 受压组合强度标准值fysc=(1.212+Bξ+Cξ2)fck (N/mm2) 2 2 受压组合强度设计值fsc=(1.212+Bξ0+Cξ )fc (N/mm ) 受压组合弹性模量Esc=(12.2×10-4+0.7284/fy)fyscEs (N/mm2) 温度折减系数kt 徐变折减系数kc 1.000 14.3 5.3E+05 4.0E+04 0.083 1.83 -0.073 56.6 47.4 3.88E+04 1.000

梁、柱钢筋Excel计算表格--梁钢筋

类别及砼标号
有梁板厚
梁宽
梁高
序号
部位
构件名称
构件钢筋钢筋数量级别直径
单件根数
跨净长或 1/3、1/4
长度
数量
锚固倍数
锚固个数
边支座1宽
梁保护层厚度
B
1
B
1
B
1
B
1
B
1
B
1
B
1
B
1
B
1
Bห้องสมุดไป่ตู้
1
B
1
B
1
B
1
B
1
B
1
B
1
B
1
B
1
B
1
B
1
B
1
B
1
B
1
B
1
B
1
B
1
数量
边边支支座2宽座度
类别及砼标号
有梁板厚
梁宽
梁高
序号
部位
构件名称
构件钢筋钢筋数量级别直径
单件根数
跨净长或 1/3、1/4
长度
数量
锚固倍数
锚固个数
边支座1宽
梁保护层厚度
B
1
B
1
B
1
B
1
B
1
B
1
B
1
B
1
B
1
B
1
B
1
B
1
B
1
B
1
B
1
B
1
B
1
B
1

excel计算大全钢结构计算表格简支钢梁计算.xls

简支基本数据输入:梁跨度： l=9000mm梁间距a=2400mm钢材：Q 345f =315N/mm 2fv =185N/mm 2 上翼缘：b 1=400mm t 1=14mm 下翼缘：b 2=300mm t 2=12mm 腹板：h w =574mm t w =8mm即: 断面BH 600x8x400x 14x300x12截面特性钢梁截面：A 0=13792mm 2 重量108.3kg/m 钢梁中和轴的位置：y 0=342mm钢梁对X轴截面惯性矩：I z =8.94E+08mm 4钢梁上翼缘的弹性抵抗矩：W 1x =3.46E+06mm 3钢梁下翼缘的弹性抵抗矩：W 2x =2.61E+06mm 3 钢梁对Y轴截面惯性矩：I y =1.02E+08mm 4i y = 85.9mm y = 104.8上翼缘对Y 轴的惯性矩：I 1=7.47E+07mm 4下翼缘对Y 轴的惯性矩：I 2=2.70E+07mm 40.73截面不对称影响系数：0.380.53工字形截面简支梁的系数 0.76梁的整体稳定系数： 0.74修正后： 0.672.截面验算：（1）弯矩及剪力的计算：钢梁自重： 1.30KN/m恒载： 4.00KN/m2=10.90KN/mg1k活载：q c= 3.0KN/m2p k=18.10KN/m p=23.16KN/m 弯矩：M=234.49KN·m剪力：V=104.22KN（2）钢梁的强度、稳定和挠度的验算：梁的整体稳定应力：σ= 101.01N/mm2钢梁上翼缘应力：σ1= 67.70N/mm2钢梁下翼缘应力：σ2= 89.68N/mm2钢梁剪应力：τ= 22.70N/mm2挠度：w= 8.4mmw/l=1/1072。

建筑结构设计：pkpm中关于中梁刚度放大系数该如何取？

建筑结构设计：pkpm中关于中梁刚度放大
系数该如何取？
现浇楼面和装配整体式楼面的楼面板作为梁的有效翼缘形成T形截面，提高了楼面梁的刚度，结构计算时应予考虑。

当近似以梁刚度增大系数考虑时，应根据梁翼缘尺寸和梁截面尺寸的比例予以确定。

通常现浇楼面的边框架梁可取1.5，中框架梁可取2.0；有现浇面层的装配式楼面梁的刚度增大系数可适当减少。

当框架梁截面较小而楼板较厚或者梁截面较大而楼板较薄时，梁刚度增大系数可能超出1.5－2.0的范围。

1。

梁的刚度计算

B
C
载荷变形。
= ++
0.2 m F1 =1KN
A
D
B
F2 =2KN C
1B
F1L2 16EI
2B 0
w1C
1Ba
F1L2a 16EI
w2C
F2a3 3EI
图1
PF11
aC B
3B
ML 3EI
LaF2 3EI
w3C
3Ba
F2 La 2 3EI
图2
FP22
叠加求复杂载荷下的变形
A
L
M PF22
0.423104 (弧度)
wC
F1L2a 16EI
F2a3 3EI
F2 a 2 L 3EI
5.19106 m
校核刚度
wmax L
L
wmax
/
L
wC
/
L
5.1 9 1 06 0.4
1.3 1 05
L
1 05
max 0.423104 0.001
三、提高梁的刚度的措施由梁在简单荷载作用下的变形表和前面的变形计算可看：梁的挠度和转角除了与梁的支座和荷载有关外还取决于下面三个因素：
同类材料只能提高强度，不能提高刚度。不同类的材料，“E”和“G”都相差很多（钢E=200GPa ,
铜E=100GPa），故可选用不同类的材料以达到提高刚度的目的。但是，改换材料，其原料费用也会随之发生很大的改变！
工程力学
E=210GPa，工程规定C点的[δ/L]=0.00001,B点的[ ]=0.001弧
度,试校核此杆的刚度.
L=0.4m
a =0.1m
A
D
B

梁的刚度计算公式

梁的刚度计算公式
梁的刚度计算公式是指用数学公式来计算梁的刚度，也就是梁的抵抗弯曲的能力。

一般来说，梁的刚度计算需要考虑材料的特性、截面形状以及梁的长度等因素。

对于梁的刚度计算，最常用的公式是欧拉-伯努利梁的弯曲刚度公式，它表示为：
EI = kM/δ
其中，EI代表梁的弯曲刚度，E为梁的弹性模量，I为梁的截面转动惯量，k为比例系数，M为梁的弯矩，δ为梁的挠曲度。

这个公式可以用来计算梁的最大挠度、应力和变形等物理量。

在工程设计中，梁的刚度计算公式是非常重要的，它可以帮助工程师有效预测结构的受力情况，并提前考虑结构的强度和稳定性。

连续梁计算结构计算EXCEL表

均布载
集中载只限三个
P2= a2= P3= a3=
A a A 0.5L q A a c A a c q a b q b a b q 0.5L
B
B
三角载梯形载
q3= q4= a= q5= a= b= c= q6=
25.5 0 0 0 0 1 0 0 0 1 0 0
q3= q4= a= q5= a= b= c= q6= a= b= c=
0.65 0.7 0.75 0.8 0.85 0.9 0.95 1 0 0.25 0.5 0.75 1 1.25 1.5 1.75 2 2.25 2.5 2.75 3 3.25 3.5 3.75 4 4.25 4.5 4.75 5 0 0.1 0.2 0.3
0.65 0.7 0.75 0.8 0.85 0.9 0.95 1 1 1.25 1.5 1.75 2 2.25 2.5 2.75 3 3.25 3.5 3.75 4 4.25 4.5 4.75 5 5.25 5.5 5.75 6 6 6.1 6.2 6.3
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 1 1 1 1
25.5 25.5 25.5 25.5 25.5 25.5 25.5 25.5 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30

何时考虑中梁刚度放大系数

何时(hé shí)考虑中梁刚度放大系数《高规》第5.2.2条规定：在结构内力和位移计算中，现浇楼板和装配(zhuāngpèi)整体式楼面中梁的刚度可考虑翼缘的作用予以放大。

其建议中梁该系数取2，边梁可取1.5，一般而言，填入此系数后，梁的刚度增大，内力也会相应的增大。

计算(jì suàn)地震作用时，模型只考虑了框架梁柱对刚度的贡献，板对总体刚度的贡献并未被考虑进去。

而实际上因为板的存在，梁由矩形变为T型，刚度增大，所以计算参数时，应将中梁刚度放大。

计算配筋时，因为属于T型梁范围内的板配有一定数量的钢筋As，As一方面承担板荷载，另一方面如果有富余As'，且As'能抵消掉因为梁刚度增大而引起的梁配筋的增量，那么梁的配筋就可以(kěyǐ)直接采用刚度不放大情况下的计算结果，反之，就应该考虑将梁钢筋予以适当放大。

梁的上部钢筋（支座负筋）配够就可以了，不必人为再放大，否则(fǒuzé)有可能会造成超筋，当梁端纵向受拉钢筋的配筋率大于2%时，箍筋直径应增加2mm。

楼板对梁的刚度有放大的作用，考虑楼板的作用可以提高梁的承载力，而且这个数值并不小，但不好计算，所以目前大部设计好像不考虑楼板的这部分的作用，也就低估了梁的承载力，这也是影响强柱弱梁的实际一个关键因素。

梁刚度的放大主要是为了考虑楼板刚度对结构的贡献。

我们知道，刚性楼板假定总是假定楼板平面内刚度无限大，这种情况下是无法考虑楼板刚度对结构的贡献的，因此规范规定通过采用梁刚度放大的方法来近似考虑，从这点来讲，梁的刚度放大并非是为了在计算梁的内力和配筋时，将楼板作为梁的翼缘，按T形梁设计，以达到降低梁的内力和配筋的目的，而仅仅是为了考虑楼板刚度的影响。

在实际工程中，倘若我们在设计工程中遇到在刚性楼板假定下，结构的位移角稍微超出了规范限制，我们可以填入此系数，考虑了楼板刚度的贡献后，结构的周期将有所减小，位移角也将有所减小，但此时梁的内力可能会增大，甚至出现超筋现象，此时我们一般按考虑刚度放大系数前的梁的内力和配筋结构作为最终结果，而位移角采用刚度放大后的结果。

梁线刚度计算公式

梁线刚度计算公式
梁线刚度可以通过弯曲、拉伸和剪切三种形式进行计算。

具体的公式如下：
弯曲刚度计算公式：
梁线的弯曲刚度可以通过以下公式计算：
EI = k * D / (2 * Phi)
其中EI表示梁的弯曲刚度，k表示梁的弹性系数，D表示梁的弯曲变形，Phi表示梁的弯曲角度。

如果梁的截面形状、材料和长度确定，那么EI值也是固定的。

拉伸刚度计算公式：
梁线的拉伸刚度可以通过以下公式计算：
EA = F / deltaL
其中EA表示梁的拉伸刚度，F表示梁的受力大小，deltaL表示梁的拉伸变形。

如果梁的截面积和材料确定，那么EA值也是固定的。

剪切刚度计算公式：
梁线的剪切刚度可以通过以下公式计算：
GA = k / tau
其中GA表示梁的剪切刚度，k表示梁的剪切模量，tau表示材料的剪切应力。

剪切刚度与梁线的剪切变形有关，当材料的剪切应力发生变化时，剪
切变形也会相应改变。

需要注意的是，梁线的刚度计算公式根据不同的应力状态而有所不同。

在实际工程中，根据梁的材料、截面形状和受力情况，通常采用适当的刚
度计算公式来计算梁线的刚度。

梁线刚度的计算是结构力学中的基础问题之一，通过准确计算梁线的
刚度，可以帮助工程师在设计过程中确保结构的稳定性和安全性。

同时，
梁线刚度的计算也为设计者提供了选择材料和截面形状的依据，以满足实
际工程要求。

excel计算大全-钢结构计算表格-钢管结构计算程序

数据输出
一、常规数据
钢管内径d1=d-2t (mm) 截面惯性矩I=π *(d4-d14)/64 (mm4) 1/2 截面回转半径i=(I/A) (mm) 塑性发展系数γ 276 1.13E+08 101.91 1.15 截面面积A=π *(d2-d12)/4 (mm2) 截面抵抗矩W=2I/d (mm3) 构件长细比λ x=l0x/i 构件长细比λ y=l0y/i 1.1E+04 7.52E+05 98.1 98.1
二、径厚比验算
验算 d/t ≤ 100*(235/fy) 满足
三、刚度验算
构件容许长细比[λ ] 150 刚度验算 Max[λ x,λ y]<[λ ] 满足
四、强度验算
N/A+M/γ W (N/mm2)
39.31
验算 N/A+M/γ W ≤ f
满足
五、稳定性验算
⒈弯矩平面内 1.278 构件所属的截面类型 λ x'=(fy/E)1/2*λ x/π 系数α 1 系数α 2 0.600 系数α 3 0.300 欧拉临界力NEx=π 2EA/λ x2 (KN) 当λ x'＞0.215时，稳定系数ψ x={(α 2+α 3λ x'+λ x'2)-[(α 2+α 3λ x'+λ x'2)2-4λ x'2]1/2}/2λ x'2 2 当λ x'≤0.215时，稳定系数ψ x=1-α 1λ x' 局部稳定系数φ =1 （d/t≤60时）；φ =1.64-0.23*(d/t)1/4 （d/t>60时） N/ψ xA+β mMx/γ W(1-0.8N/NEx) (N/mm2) 验算 N/ψ xA+β mMx/γ W(1 不需验算 λ y'=(fy/E)1/2*λ y/π 当λ y'〉0.215时，稳定系数ψ y={(α 2+α 3λ y'+λ y'2)-[(α 2+α 3λ y'+λ y'2)2-4λ y'2]1/2}/2λ y'2 当λ y'≤0.215时，稳定系数ψ y=1-α 1λ y'2 N/ψ yA+0.7Mx/W (N/mm2) b类 0.965 2.3E+03 0.443 1.0000 45.72 满足

excel计算大全钢结构计算表格单跨变截面简支梁

钢梁剪
应力计
3算
面积矩
S=
#VALUE! mm3
钢梁剪应力τ1max =
#VALUE!
N/mm2
<
125 N/mm2
挠度计 4算
△
=5*g*l4/(38 4*E*I)=
#VALUE! mm
< L/400 = 15 mm
使用阶
段的验
三算
弯矩及
1 剪力
找平层
重：
1.9 kN/m
活荷
载：
15.6 kN/m
#VALUE!
#VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE!
#VALUE!
#VALUE! #VALUE!
使用阶段弯矩 78.84 kN.m
使用阶段剪力 52.56 kN
（活荷载：
6
kn/m2)
2 组合梁的抗弯
2.1 在混垂凝直土荷板载顶作面用应下力的σ
混0ct=-凝M/W土0ct板= 底面应力σ
#VALUE!
0cb=-M/W0cb=
#VALUE!
钢梁上翼缘应力σ0t = -M1/W1+M2/W0t=
#VALUE! mm4
对混凝土板底面的组合截面弹性抵抗矩 α w0cbc=2 E*I0c / (x c- hd ) = #VALUE! mm4
对钢梁上翼缘的组合截面弹性抵抗矩 w0tc = I0c / (d-xc) =
#VALUE! mm4
对钢梁下翼缘的组合截面弹性抵抗矩 w0bc = I0c / (H-xc) = #VALUE! mm4
#VALUE! #VALUE!
N/mm2