梁的强度和刚度计算

桥式起重机箱形主梁强度计算一、通用桥式起重机箱形主梁强度计算（双梁小车型）1、受力分析作为室内用通用桥式起重机钢结构将承受常规载荷P G、P Q和P H三种基本载荷和偶然载荷P S，因此为载荷组合H。

其主梁上将作用有P G、P Q、P H载荷。

主梁跨中截面承受弯曲应力最大，为受弯危险截面；主梁跨端承受剪力最大，为剪切危险截面。

当主梁为偏轨箱形梁时，主梁跨中截面除了要计算整体垂直与水平弯曲强度计算、局部弯曲强度计算外，还要计算扭转剪切强度，弯曲强度与剪切强度需进行折算。

2、主梁断面几何特性计算上下翼缘板不等厚,采用平行轴原理计算组合截面的几何特性。

④y ch 1 R (H 寸)12巴佗h 2)(cm )⑤ J x Bh 13 122F 1 y 1 2b(Hhi h 2)3 22F 2 y 3F 3 y (cm )12212 ⑥J yAB 3h 2B 22也2F 2（弓 b)2(cm 4)1212122 2图2-4注：此箱形截面垂直形心轴为 y-y 形心线，为对称形心线。

因上下翼 缘板厚不等，应以x '— X’为参考形心线，利用平行轴原理求水平形心线 x — X 位置y c 。

① 断面形状如图2-4所示，尺寸如图所示的H 、h i 、h 2、B 、b 、b o 等。

② FF i2F 2F 3[ F i Bh i , F 2 bh o , F 3 Bh ?]③ q Fr (kg/m )F 1 2F 2 F 3⑦W X J x/y c和J x/H y c(cm3)⑧W y J y B (cm3)3、许用应力为［］和［］4、受力简图Pi P2图2-5P i与P2为起重小车作用在一根主梁上的两个车轮轮压，由P Q和小车自重分配到各车轮的作用力为轮压。

如P i P2 P时，可认为P等于P Q和小车自重之和的四分之一5. 主梁跨中集中载荷（轮压P i 和P 2）产生最大垂直弯矩 M p注：建议当R M P 2时’采用P 宁计算为佳6. 跨中均布载荷（自重P G ）产生最大垂直弯矩M q1P 3S i qS 2Mq 丁 晋（N • m ）7. 主梁跨中垂直最大弯矩 M 垂M 垂 Mp Mq8. 主梁跨中水平惯性载荷产生弯矩 M 水图2-6Mp 込空(N • m)4RM P 2时简算Mp2P 号 (N • m)R P 2 P 时Mp2PS b(N • m)P i M P 2时，可近似取PP i P 2 2跨端最大剪力Q m axQmaxP1P2(1S 爰(1S 2r 2q 惯S (324竺)r(N • m)式中：r S 8c3 2l3 土2B 2 J 2y」2y ----------端梁截面的J y (cm 4)1P1P (小车自重P Q )乙——起重机大车驱动轮数Z ——总轮数1乙 q 惯q i 5 Z9. 主梁跨中截面弯曲强度计算[]IIs1.3410. 主梁跨端剪切强度计算J iy主梁端截面的J y (cm 4)P 1 P 2跨端最大剪应力Q maxSo[ ] [ ] ||TJ ：[ ]|1「S o ――主梁跨端截面的静面矩（中性轴以上面积对中性轴的静面矩，各面积乘以形心至中性轴距离；cm 3）--- 腹板厚（cm ）儿一一截面的水平惯性矩（cm 4）二、通用桥式起重机箱形主梁刚度计算 1.垂直静刚度f 垂l 为小车轮压至主梁支承处距离，见下图所示「1 l J 2图2-8(P l P 2)S 348EJ x[f](P i P 2)l(0.75S 2 I 2)12EJ[f]简算精算注：①P i 、P 2不乘以系数。

梁的强度和刚度计算强度是指梁抵抗外力的能力。

梁的强度计算一般包括了两个方面：弯曲强度和剪切强度。

其中，弯曲强度是指梁在受到弯曲作用时的承载能力，剪切强度是指梁在受到剪切力作用时的承载能力。

弯曲强度的计算通常基于弹性理论，其中最常用的方法是根据梁的截面形状和材料的弹性模量来计算梁的截面抵抗力矩。

弹性模量是材料的一种力学性质，它衡量了材料在受力后产生的应变程度。

根据梁的截面形状和边界条件，可以计算出梁在弯曲作用下的最大应力和最大应变。

将最大应力与材料的弯曲强度进行比较，就可以判断梁是否满足设计要求。

剪切强度的计算也是基于弹性理论。

梁在受到剪切力作用时，梁内部会发生剪切变形。

剪切强度的计算包括两个方面：剪切应力和剪切变形。

剪切应力是指剪切力对梁截面的作用，剪切变形是指梁截面产生的剪切位移。

剪切强度的计算要求同时满足两个条件：剪切应力小于材料的剪切强度，剪切变形小于允许的变形限制。

刚度是指梁在受到力作用后的变形程度。

梁的刚度决定了梁的承载能力和结构的稳定性。

刚度的计算通常考虑梁的弹性变形和塑性变形两个方面。

弹性变形是指梁在小荷载下的弯曲变形，主要涉及梁的截面形状、材料的弹性模量和梁的长度等因素。

塑性变形是指梁在大荷载下的弯曲变形，主要涉及梁的屈服强度、截面形状和材料的塑性性质等因素。

根据梁的受力情况，可以计算出梁的弯曲刚度和剪切刚度。

弯曲刚度表示梁在受到弯曲作用时的抵抗变形能力，剪切刚度表示梁在受到剪切力作用时的抵抗变形能力。

在梁的强度和刚度计算中，需要根据具体的工程要求和设计规范进行。

梁的截面形状、材料的性质和受力情况都会对强度和刚度的计算结果产生影响。

因此，工程师需要根据具体情况选择适当的计算方法和模型进行计算。

同时，还需要进行合理的验算和对比，确保梁的设计满足强度和刚度的要求。

梁的强度和刚度计算1．梁的强度计算梁的强度包括抗弯强度、抗剪强度、局部承压强度和折算应力，设计时要求在荷载设计值作用下，均不超过《规范》规定的相应的强度设计值。

（1）梁的抗弯强度作用在梁上的荷载不断增加时正应力的发展过程可分为三个阶段，以双轴对称工字形截面为例说明如下：梁的抗弯强度按下列公式计算：单向弯曲时f W M nx x x ≤=γσ （5-3）双向弯曲时f W M W M ny y y nx x x ≤+=γγσ （5-4）式中：M x 、M y ——绕x 轴和y 轴的弯矩（对工字形和H 形截面，x 轴为强轴，y 轴为弱轴）；W nx 、W ny ——梁对x 轴和y 轴的净截面模量；y x γγ,——截面塑性发展系数，对工字形截面，20.1,05.1==y x γγ；对箱形截面，05.1==y x γγ；对其他截面，可查表得到；f ——钢材的抗弯强度设计值。

为避免梁失去强度之前受压翼缘局部失稳，当梁受压翼缘的外伸宽度b 与其厚度t 之比大于y f /23513 ，但不超过y f /23515时，应取0.1=x γ。

需要计算疲劳的梁，按弹性工作阶段进行计算，宜取0.1==y x γγ。

（2）梁的抗剪强度一般情况下，梁同时承受弯矩和剪力的共同作用。

工字形和槽形截面梁腹板上的剪应力分布如图5-3所示。

截面上的最大剪应力发生在腹板中和轴处。

在主平面受弯的实腹式梁，以截面上的最大剪应力达到钢材的抗剪屈服点为承载力极限状态。

因此，设计的抗剪强度应按下式计算v w f It ≤=τ （5-5）式中：V ——计算截面沿腹板平面作用的剪力设计值；S ——中和轴以上毛截面对中和轴的面积矩；I ——毛截面惯性矩；t w ——腹板厚度；f v ——钢材的抗剪强度设计值。

图5-3 腹板剪应力当梁的抗剪强度不满足设计要求时，最常采用加大腹板厚度的办法来增大梁的抗剪强度。

型钢由于腹板较厚，一般均能满足上式要求，因此只在剪力最大截面处有较大削弱时，才需进行剪应力的计算。

梁的刚度计算范文梁的刚度是指材料在受到外力作用时的抵抗变形的能力。

在工程中，刚度是一个非常重要的参数，它决定了梁的强度和稳定性。

梁的刚度计算可以通过不同的方法进行，下面将介绍两种常用的计算方法：简支梁的刚度计算和悬臂梁的刚度计算。

一、简支梁的刚度计算简支梁是指两个端点都可以转动的梁，它的刚度可以通过弯曲刚度来计算。

弯曲刚度是指单位长度下的梁的抵抗弯曲变形的能力。

1.简支梁的弯曲刚度公式简支梁的弯曲刚度可以通过以下公式进行计算：EI=(WL^3)/(48D)其中，EI为弯曲刚度，W为作用在梁上的力或负荷，L为梁的长度，D为梁的挠度。

2.弯曲刚度的单位和性质弯曲刚度的单位是N.m^2，它的数值越大，梁的刚度越高。

弯曲刚度与梁的材料属性有关，即与材料的弹性模量E和惯性矩I有关。

E表示材料的刚度，单位为N/m^2，I表示梁的惯性矩，单位为m^4、弯曲刚度EI 的数值越大，表示材料的刚度越高。

二、悬臂梁的刚度计算悬臂梁是指只有一个端点可以转动的梁，它的刚度可以通过挠度和力矩进行计算。

1.悬臂梁的挠度计算悬臂梁的挠度是指梁在受到外力作用时的弯曲变形。

悬臂梁的挠度可以通过以下公式进行计算：δ=(FL^3)/(3EI)其中，δ为悬臂梁的挠度，F为作用在梁上的力或负荷，L为梁的长度，E为梁的弹性模量，I为梁的惯性矩。

2.悬臂梁的刚度计算悬臂梁的刚度可以通过力矩和挠度的比值来计算：K=M/δ其中，K为悬臂梁的刚度，M为悬臂梁上的力矩，δ为悬臂梁的挠度。

总结：梁的刚度是指梁在受到外力作用时的抵抗变形的能力。

梁的刚度可以通过弯曲刚度和挠度进行计算。

简支梁的刚度可以通过弯曲刚度进行计算，悬臂梁的刚度可以通过力矩和挠度的比值进行计算。

两种方法都可以用来计算梁的刚度，根据具体的梁结构和受力情况选择适当的计算方法。

8.3.5 梁的刚度计算梁的刚度计算，通常是校核其变形是否超过许用挠度[ f ]和许用转角[θ]，可以表述为：≤y f []max≤θθ[]max式中y max 和θmax 为梁的最大挠度和最大转角。

在机械工程中，一般对梁的挠度和转角都进行校核；而在土木工程中，常常只校核挠度，并且以许用挠度与跨长的比值lf []作为校核的标准，即： ≤l lf y []max （8.17） 土木工程中的梁，强度一般起控制作用，通常是由强度条件选择梁的截面，再校核刚度。

例8.9 简支梁受力如图8.11所示，采用22a 号工字钢，其弹性模量=E 200GPa ，=l f 400[]1，试校核梁的刚度。

解：由附录查表可得=I 3400cm z 4，=EIy ql 3845max 4。

于是 =<=⨯⨯⨯⨯==⨯⨯l f l EI ql y 600400[]1138438420010MPa 340010mm 554N/mm 6000mm 344max 333所以梁的刚度满足要求。

下面介绍提高梁弯曲刚度的一些措施。

在不改变荷载的条件下，梁的变形与抗弯刚度EI 成反比，与跨长的n 次幂（n 可取1、2、3或4）成正比。

所以，提高弯曲刚度的一些措施有：（1）增大EI 。

这方面可以考虑采用惯性矩较大的工字形、槽形、箱形等截面形状。

须指出的是，高强钢与普通钢的弹性模量相差无几，所以采用高强钢对提高刚度的作用并不明显。

（2）调整跨长或改变结构。

减小跨长对变形的影响较为明显，如龙门吊车大梁就采用了两端外伸的结构形式。

此外，增加约束形成超静定梁，也能显著减小梁的变形，同时还可以提高弯曲强度。

有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）。

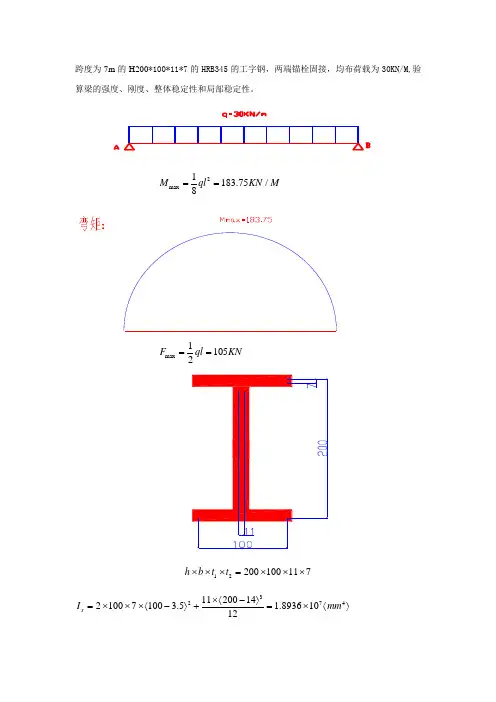
跨度为7m 的H200*100*11*7的HRB345的工字钢，两端锚栓固接，均布荷载为30KN/M,验算梁的强度、刚度、整体稳定性和局部稳定性。

2max 1183.75/8M ql KN M ==max 11052F ql KN ==12200100117h b t t ⨯⨯⨯=⨯⨯⨯3274112001421007100 3.5 1.89361012x I mm ⨯〈-〉=⨯⨯⨯〈-〉+=⨯〈〉3364710011200142 1.1873101212y I mm ⨯⨯〈-〉=⨯+=⨯〈〉 7531.893610 1.89361020022x x I W mm h ⨯===⨯〈〉 6431.187310 2.70841010022y y I W mm h ⨯===⨯〈〉 5186186100796.511 1.15121024S =⨯⨯+⨯⨯=⨯ 10072111863446A =⨯⨯+⨯=74.1287x i ==18.562y i ==1. 强度验算：在弯矩x M 作用下：x x nx M f W γ≤ 此处f =3102/N mm 2. 抗剪强度：v wVS f It τ=≤ 1w t t =；x I I = 3. 局部承压强度：若梁两端之间受集中力作用，则需要验算，而此处受力为均布力，则无需验算。

具体公式为：c w Ff It ψσ=≤4. 刚度：[]υυ≤ 35[]384x ql l EI l υυ=≤ 一般，前面验算满足，则该点满足 5. 整体稳定性：对于双轴对称的工字形截面：x b x M f W σϕ=≤24320235]b b b x yy Ah W f ϕβηλ=⨯⨯+⨯ 345y f = 算b β要用到ξ，2 2.45 2.0lt bhξ==b β取：①：荷载作用在工字钢的上翼缘0.95b β=②：荷载作用在工字钢的下翼缘 1.33b β=对双轴对称工字钢：0b η=下面是我算的两个，但都不满足：1. 强度验算：625183.75109703101 1.894110x x nx M N mm f W γ⨯==='⨯⨯ 2. 整体稳定性：取0.95b β=得0.226240.6b ϕ=x b xM W σϕ=显然，强度验算不满足，则稳定性肯定不满足。

梁的刚度计算The Standardization Office was revised on the afternoon of December 13, 2020梁的强度和刚度计算1．梁的强度计算梁的强度包括抗弯强度、抗剪强度、局部承压强度和折算应力，设计时要求在荷载设计值作用下，均不超过《规范》规定的相应的强度设计值。

（1）梁的抗弯强度作用在梁上的荷载不断增加时正应力的发展过程可分为三个阶段，以双轴对称工字形截面为例说明如下：梁的抗弯强度按下列公式计算： 单向弯曲时f W M nxx x≤=γσ（5-3）双向弯曲时f W M W M nyy y nx x x≤+=γγσ（5-4）式中：M x 、M y ——绕x 轴和y 轴的弯矩（对工字形和H 形截面，x 轴为强轴，y 轴为弱轴）；W nx 、W ny ——梁对x 轴和y 轴的净截面模量；y x γγ,——截面塑性发展系数，对工字形截面，20.1,05.1==y x γγ；对箱形截面，05.1==y x γγ；对其他截面，可查表得到；f ——钢材的抗弯强度设计值。

为避免梁失去强度之前受压翼缘局部失稳，当梁受压翼缘的外伸宽度b 与其厚度t 之比大于y f /23513 ，但不超过y f /23515时，应取0.1=x γ。

需要计算疲劳的梁，按弹性工作阶段进行计算，宜取0.1==y x γγ。

（2）梁的抗剪强度一般情况下，梁同时承受弯矩和剪力的共同作用。

工字形和槽形截面梁腹板上的剪应力分布如图5-3所示。

截面上的最大剪应力发生在腹板中和轴处。

在主平面受弯的实腹式梁，以截面上的最大剪应力达到钢材的抗剪屈服点为承载力极限状态。

因此，设计的抗剪强度应按下式计算v wf It VS≤=τ（5-5）式中：V ——计算截面沿腹板平面作用的剪力设计值；S ——中和轴以上毛截面对中和轴的面积矩； I ——毛截面惯性矩； t w ——腹板厚度；f v ——钢材的抗剪强度设计值。

桥式起重机箱形主梁强度计算一、通用桥式起重机箱形主梁强度计算(双梁小车型)1、受力分析作为室用通用桥式起重机钢结构将承受常规载荷G P 、Q P 和H P 三种基本载荷和偶然载荷S P ，因此为载荷组合Ⅱ。

其主梁上将作用有G P 、Q P 、H P 载荷。

主梁跨中截面承受弯曲应力最大，为受弯危险截面；主梁跨端承受剪力最大，为剪切危险截面。

当主梁为偏轨箱形梁时，主梁跨中截面除了要计算整体垂直与水平弯曲强度计算、局部弯曲强度计算外，还要计算扭转剪切强度，弯曲强度与剪切强度需进行折算。

2、主梁断面几何特性计算上下翼缘板不等厚,采用平行轴原理计算组合截面的几何特性。

图2-4注：此箱形截面垂直形心轴为y-y 形心线，为对称形心线。

因上下翼缘板厚不等，应以x ’— x ’为参考形心线,利用平行轴原理求水平形心线x —x 位置c y 。

① 断面形状如图2-4所示,尺寸如图所示的H 、1h 、2h 、B 、b 、0b 等。

② 3212F F F F ++=∑ [11Bh F =，02bh F =，23Bh F =] ③ Fr q ∑= (m kg /)④ 321232021122.)21(2)2(F F F h F h h F h H F Fy F y ii c +++++-=∑⋅∑=(cm ) ⑤ 223322323212113112212)(212y F Bh y F h h H b y F Bh J x ⋅++⋅+--+⋅+= (4cm ) ⑥ 202032231)22(21221212bb F h b B h B h J y ++++= (4cm )⑦ c X X y J W /=和c X y H J -/(3cm ) ⑧ 2BJ W yy =(3cm ) 3、许用应力为 ][σ和 ][τ。

4、受力简图1P 与2P 为起重小车作用在一根主梁上的两个车轮轮压，由Q P 和小车自重分配到各车轮的作用力为轮压。

梁的强度和刚度计算1．梁的强度计算梁的强度包括抗弯强度、抗剪强度、局部承压强度和折算应力，设计时要求在荷载设计值作用下，均不超过《规范》规定的相应的强度设计值。

（1）梁的抗弯强度作用在梁上的荷载不断增加时正应力的发展过程可分为三个阶段，以双轴对称工字形截面为例说明如下：梁的抗弯强度按下列公式计算：单向弯曲时f W M nx x x ≤=γσ （5-3）双向弯曲时f W M W M ny y y nx x x ≤+=γγσ （5-4）式中：M x 、M y ——绕x 轴和y 轴的弯矩（对工字形和H 形截面，x 轴为强轴，y 轴为弱轴）；W nx 、W ny ——梁对x 轴和y 轴的净截面模量；y x γγ,——截面塑性发展系数，对工字形截面，20.1,05.1==y x γγ；对箱形截面，05.1==y x γγ；对其他截面，可查表得到；f ——钢材的抗弯强度设计值。

为避免梁失去强度之前受压翼缘局部失稳，当梁受压翼缘的外伸宽度b 与其厚度t 之比大于y f /23513 ，但不超过y f /23515时，应取0.1=x γ。

需要计算疲劳的梁，按弹性工作阶段进行计算，宜取0.1==y x γγ。

（2）梁的抗剪强度一般情况下，梁同时承受弯矩和剪力的共同作用。

工字形和槽形截面梁腹板上的剪应力分布如图5-3所示。

截面上的最大剪应力发生在腹板中和轴处。

在主平面受弯的实腹式梁，以截面上的最大剪应力达到钢材的抗剪屈服点为承载力极限状态。

因此，设计的抗剪强度应按下式计算v w f It ≤=τ （5-5）式中：V ——计算截面沿腹板平面作用的剪力设计值；S ——中和轴以上毛截面对中和轴的面积矩；I ——毛截面惯性矩；t w ——腹板厚度；f v ——钢材的抗剪强度设计值。

图5-3 腹板剪应力当梁的抗剪强度不满足设计要求时，最常采用加大腹板厚度的办法来增大梁的抗剪强度。

型钢由于腹板较厚，一般均能满足上式要求，因此只在剪力最大截面处有较大削弱时，才需进行剪应力的计算。

梁的强度和刚度计算1．梁的强度计算梁的强度包括抗弯强度、抗剪强度、局部承压强度和折算应力，设计时要求在荷载设计值作用下，均不超过《规范》规定的相应的强度设计值。

（1）梁的抗弯强度作用在梁上的荷载不断增加时正应力的发展过程可分为三个阶段，以双轴对称工字形截面为例说明如下：梁的抗弯强度按下列公式计算：单向弯曲时f W M nx x x ≤=γσ （5-3）双向弯曲时f W M W M ny y y nx x x ≤+=γγσ （5-4）式中：M x 、M y ——绕x 轴和y 轴的弯矩（对工字形和H 形截面，x 轴为强轴，y 轴为弱轴）；W nx 、W ny ——梁对x 轴和y 轴的净截面模量；y x γγ,——截面塑性发展系数，对工字形截面，20.1,05.1==y x γγ；对箱形截面，05.1==y x γγ；对其他截面，可查表得到；f ——钢材的抗弯强度设计值。

为避免梁失去强度之前受压翼缘局部失稳，当梁受压翼缘的外伸宽度b 与其厚度t 之比大于y f /23513 ，但不超过y f /23515时，应取0.1=x γ。

需要计算疲劳的梁，按弹性工作阶段进行计算，宜取0.1==y x γγ。

（2）梁的抗剪强度一般情况下，梁同时承受弯矩和剪力的共同作用。

工字形和槽形截面梁腹板上的剪应力分布如图5-3所示。

截面上的最大剪应力发生在腹板中和轴处。

在主平面受弯的实腹式梁，以截面上的最大剪应力达到钢材的抗剪屈服点为承载力极限状态。

因此，设计的抗剪强度应按下式计算v w f It ≤=τ （5-5）式中：V ——计算截面沿腹板平面作用的剪力设计值；S ——中和轴以上毛截面对中和轴的面积矩；I ——毛截面惯性矩；t w ——腹板厚度；f v ——钢材的抗剪强度设计值。

图5-3 腹板剪应力当梁的抗剪强度不满足设计要求时，最常采用加大腹板厚度的办法来增大梁的抗剪强度。

型钢由于腹板较厚，一般均能满足上式要求，因此只在剪力最大截面处有较大削弱时，才需进行剪应力的计算。

第八章梁的强度与刚度第二十四讲梁的正应力截面的二次矩第二十五讲弯曲正应力强度计算（一）第二十六讲弯曲正应力强度计算（二）第二十七讲弯曲切应力简介第二十八讲梁的变形概述提高梁的强度和刚度第二十四讲纯弯曲时梁的正应力常用截面的二次矩目的要求：掌握弯曲梁正应力的计算和正应力分布规律。

教学重点：弯曲梁正应力的计算和正应力分布规律。

教学难点：平行移轴定理及其应用。

教学内容：第八章平面弯曲梁的强度与刚度计算§8-1 纯弯曲时梁的正应力一、纯弯曲概念：１、纯弯曲：平面弯曲中如果某梁段剪力为零，该梁段称为纯弯曲梁段。

２、剪切弯曲：平面弯曲中如果某梁段剪力不为零（存在剪力），该梁段称为剪切弯曲梁段。

二、纯弯曲时梁的正应力：１、中性层和中性轴的概念：中性层：纯弯曲时梁的纤维层有的变长，有的变短。

其中有一层既不伸长也不缩短，这一层称为中性层。

中性轴：中性层与横截面的交线称为中性轴。

２、纯弯曲时梁的正应力的分布规律：以中性轴为分界线分为拉区和压区，正弯矩上压下拉，负弯矩下压上拉，正应力成线性规律分布，最大的正应力发生在上下边沿点。

３、纯弯曲时梁的正应力的计算公式：（１）、任一点正应力的计算公式：（２）、最大正应力的计算公式：其中：M---截面上的弯矩；I Z---截面对中性轴(z轴)的惯性矩； y---所求应力的点到中性轴的距离。

说明：以上纯弯曲时梁的正应力的计算公式均适用于剪切弯曲。

§8-2 常用截面的二次矩平行移轴定理一、常用截面的二次矩和弯曲截面系数：１、矩形截面：２、圆形截面和圆环形截面：圆形截面圆环形截面其中：３、型钢：型钢的二次矩和弯曲截面系数可以查表。

二、组合截面的二次矩平行移轴定理１、平行移轴定理：截面对任一轴的二次矩等于它对平行于该轴的形心轴的二次矩，加上截面面积与两轴之间的距离平方的乘积。

I Z1=I Z+a2A２、例题：例1：试求图示T形截面对其形心轴的惯性矩。

解：1、求T形截面的形心座标yc2、求截面对形心轴z轴的惯性矩第二十五讲弯曲正应力强度计算（一）目的要求：掌握塑性材料弯曲正应力强度计算。

混凝土梁刚度标准值一、引言混凝土梁是建筑结构中常见的构件，其承载重要的荷载作用，因此对其刚度的要求十分严格。

本文将从混凝土梁的定义、刚度的影响因素、刚度的计算方法以及相关标准等方面，提供一个全面、具体、详细的混凝土梁刚度标准值。

二、混凝土梁的定义混凝土梁是由混凝土浇筑成的长条形构件，其主要作用是承受横向荷载。

混凝土梁通常由两端的支座和中间的跨度组成，其截面形状有矩形、圆形、T形等多种类型。

三、混凝土梁刚度的影响因素混凝土梁的刚度受到多种因素的影响，包括以下几个方面：1. 混凝土强度：混凝土的强度与梁的刚度成正比。

因此，混凝土梁的刚度要求通常会随着混凝土强度的提高而提高。

2. 钢筋配置：在混凝土梁中加入钢筋可以提高其承载能力和刚度。

因此，钢筋配置的多少、分布和直径等因素也会影响混凝土梁的刚度。

3. 梁截面形状：不同形状的截面对混凝土梁的刚度有不同的影响。

一般来说，矩形截面比圆形截面更容易保证刚度的稳定。

4. 跨度长度：混凝土梁的刚度随着跨度长度的增加而降低。

因此，在设计混凝土梁时需要根据跨度长度来确定刚度的要求。

5. 荷载大小：荷载的大小对混凝土梁的刚度也有影响。

在设计混凝土梁时需要考虑所承受的荷载大小以及荷载的作用方式（集中荷载、分布荷载等）。

四、混凝土梁刚度的计算方法混凝土梁的刚度可以通过以下公式计算得出：EI = (bh^3)/12其中，E为混凝土的弹性模量，I为梁的惯性矩，b为梁的宽度，h为梁的高度。

在实际设计中，需要考虑梁的跨度、荷载大小和作用方式、钢筋配置等因素，进行综合计算，得出混凝土梁的刚度。

五、相关标准以下为国内相关标准对混凝土梁刚度的要求：1. GB 50010-2010《混凝土结构设计规范》该标准规定了混凝土结构的设计原则、荷载计算、构件设计和施工等方面的内容。

其中，对混凝土梁的刚度进行了详细的规定，包括刚度的计算方法、刚度的标准值等。

2. JGJ 3-2010《建筑结构荷载规范》该标准规定了建筑结构承受荷载的要求和规范。