2.1.1函数的概念和图象
- 格式:ppt
- 大小:795.00 KB
- 文档页数:20

2。
1 函数的概念和图象2.1。
1 函数的概念名师导航知识梳理1.函数的概念设A ,B 是非空的数集,如果按某个确定的对应关系f ,使对于集合A 中的任意一个x ,在集合B 中都有__________的数f (x)和它对应,那么就称f:A →B 为从集合A 到集合B 的函数,记作y=f (x),x ∈A.其中x 叫__________,x 的取值范围A 叫做函数y=f (x )的__________;与x 的值相对应的y 的值叫做函数值,函数值的集合{f(x )|x ∈A }(⊆B )叫做函数y=f(x )的__________。
函数符号y=f (x)表示“y 是x 的函数",有时简记作函数__________。
(1)函数实际上就是集合A 到集合B 的一个特殊对应f:A →B ,这里A ,B 为__________的数集.(2)A:定义域;{f(x )|x ∈A}:值域,其中{f(x )|x ∈A}__________B ;f :对应法则,x ∈A,y ∈B.(3)函数符号:y=f (x )↔y 是x 的函数,简记f(x).2。
已学函数的定义域和值域(1)一次函数f (x )=ax+b(a ≠0):定义域为__________,值域为__________;(2)反比例函数f(x )=xk (k ≠0):定义域为__________,值域为__________; (3)二次函数f (x)=ax 2+bx+c (a ≠0):定义域为__________,值域:当a 〉0时,为__________;当a 〈0时,为__________。
3。
函数的值:关于函数值f(a )例:f (x)=x 2+3x+1,则f(2)= __________.4。
函数的三要素:对应法则f 、定义域A 和值域{f(x )|x ∈A}.只有当这三要素__________时,两个函数才能称为同一函数。
疑难突破有关函数概念的理解剖析:(1)如果一个函数需要几条限制时,那么定义域为各限制所得x 的范围的交集。

2.1.1 函数的概念和图象(一)一、教学目标1.知识与技能(1)能利用集合与对应关系的语言来刻画函数(2)了解函数的定义域及对应法则的含义2.过程与方法经历函数概念的发生过程,并归纳函数的概念,提高学生解决问题的能力和语言表达能力.3.情感、态度与价值观在探索函数本质的过程中,体会函数是刻画现实世界中的一类运动变化规律的模型,使学生养成运用无限运动、发展、变化的观点认识客观世界的思维习惯.二、重点难点教学重点:利用集合与对应关系的语言来刻画函数教学难点:对应法则f的理解三、教学过程(一)创设情境我们生活在这个世界上,每时每刻都在感受其变化.请大家看下面的实例:(1)一枚炮弹发射,经26秒后落地击中目标,射高为845米,炮弹距地面高度h(米)随时间t(秒)的变化而变化,其规律是2=-.1305h t t(2)近几十年,大气层中臭氧迅速减少,因而出现臭氧层空洞问题,图中曲线是南极上空臭氧层空洞面积随时间变化而变化情况.(3)国际上常用恩格尔系数(食物支出金额÷总支出金额)反映一个国家人民生活质量的高低.从下表中的数据,可以看出“八五”计划以来我们城镇居民的生活质量发生了显著的变化.(二)讲解新课问题1:在上面的每一个变化过程中,存在哪些变化的量?这些变化过程有什么共同的特点?问题2:在上面的例子中,是否确定了函数关系?为什么?问题3:如何用集合的观点来理解函数的概念?每一个问题均涉及两个非空数集A、B的关系.存在某种对应法则f,对于A 中的某个元素x,B中总有一个元素y与之对应.问题4:如何理解对应法则f ?问题5.如何用集合的观点来表述函数的概念?给出函数的定义.指出对应法则和定义域是构成一个函数的要素.一般地,设 A,B是两个非空的数集,如果按某种对应法则 f,对于集合A 中的每一个元素 x,在集合B中都有惟一的元素 y和它对应,这样的对应叫做从A到 B的一个函数,通常记为y=f (x),x ∈A.其中,所有的输入值 x组成的集合A叫做函数y=f (x)的定义域.函数的近代定义:集合语言、对应的观点.在掌握函数时,必须把握以下几点:(1)函数是一种特殊的对应f:BA→,集合A,B是非空的数的集合.(2)对应法则的方向是从A到B.(3)特别注意“非空”、“数集”、“每一个”、“惟一”这几个关键词.例1 判断下列对应是否为集合A到 B的函数:(1)A={1,2,3,4,5},B={0,2,4,6,8}, x ∈A,f:x→2x;(2)A=R,B=R,x ∈A,f:x → y ,y=x;(3)A=[0,+∞),B=R,x ∈A,f:x → y ,y2=x.解(1)对于集合A中的元素5,在集合B找不到中所对应的元素10,故这个对应不是从集合A到 B的函数;(2)对于任意一个实数x,x被x惟一确定,所以这个对应是从集合A到 B 的函数,这个函数也可以表示为 f (x)=x;(3)考虑输入值为4,即当x=4 时输出值y,由y2=4给出,得y=2和 y =-2.这里一个输入值与两个输入值对应(不是单值对应),所以,x → y(y2=x)不是函数.研究函数时,除了符号f(x)外,还常用g(x),F(x),G(x)等符号表示.例2 已知函数f(x)=3x2-5x+2,求f(3)、f(-2)、f(a)、f(a+1).分析求x分别等于3、-2、a、a+1时函数f(x)的值.解 f(3)=3×32-5×3+2=14,f(-2)=3×(-2)2-5×(-2)+2=8+52,f(a)=3a2-5a+2,f(a+1)=3(a+1)2-5(a+1)+2=3a2+a.说明:区别符号f(x)和f(a),f(a)表示x=a时函数f(x)的值,而f(x)是一个函数.(三)课堂小结1.函数的集合观点的概念及其与初中的定义的区别.2.符号y=f(x)是“y是x的函数”的抽象的数学表示,f是对应法则,它可以是解析式,也可以是图象、表格.(四)课后作业P24练习Ex 5,6;P28习题 1,2,5.。

2012届高考数学第一轮复习精品试题:函数§2.1.1 函数的概念和图象经典例题:设函数f (x )的定义域为[0,1],求下列函数的定义域: (1)H (x )=f (x2+1);(2)G (x )=f (x+m )+f (x -m )(m >0).当堂练习:1. 下列四组函数中,表示同一函数的是( ) A.(),()f x x g x ==B.2(),()f x x g x ==C .21(),()11x f x g x x x -==+- D.()()f x g x ==2函数()y f x =的图象与直线x a =交点的个数为( )A .必有一个B .1个或2个C .至多一个D .可能2个以上3.已知函数1()1f x x =+,则函数[()]f f x 的定义域是( )A .{}1x x ≠ B .{}2x x ≠- C .{}1,2xx ≠-- D .{}1,2x x ≠-4.函数1()1(1)f x x x =--的值域是( )A .5[,)4+∞B .5(,]4-∞C . 4[,)3+∞D .4(,3-∞ 5.对某种产品市场产销量情况如图所示,其中:1l 表示产品各年年产量的变化规律;2l 表示产品各年的销售情况.下列叙述: ( )(1)产品产量、销售量均以直线上升,仍可按原生产计划进行下去;(2)产品已经出现了供大于求的情况,价格将趋跌;(3)产品的库存积压将越来越严重,应压缩产量或扩大销售量;(4)产品的产、销情况均以一定的年增长率递增.你认为较合理的是( ) A .(1),(2),(3) B .(1),(3),(4) C .(2),(4) D .(2),(3)6.在对应法则,,,x y y x b x R y R→=+∈∈中,若25→,则2-→ , →6.7.函数()f x 对任何x R +∈恒有1212()()()f x x f x f x ⋅=+,已知(8)3f =,则f = .8.规定记号“∆”表示一种运算,即a b a b a b R+∆++∈,、. 若13k ∆=,则函数()fx k x=∆的值域是___________.9.已知二次函数f(x)同时满足条件: (1) 对称轴是x=1; (2) f(x)的最大值为15;(3) f(x)的两根立方和等于17.则f(x)的解析式是 .10.函数2522y x x =-+的值域是 .11. 求下列函数的定义域 : (1)()121x f x x =-- (2)(1)()x f x x x+=-12.求函数y x =13.已知f(x)=x2+4x+3,求f(x)在区间[t,t+1]上的最小值g(t)和最大值h(t).14.在边长为2的正方形ABCD 的边上有动点M ,从点B 开始,沿折线BCDA 向A 点运动,设M 点运动的距离为x ,△ABM 的面积为S . (1)求函数S=的解析式、定义域和值域; (2)求f[f(3)]的值.§2.1.2 函数的简单性质经典例题:定义在区间(-∞,+∞)上的奇函数f (x )为增函数,偶函数g (x )在[0,+∞ )上图象与f (x )的图象重合.设a >b >0,给出下列不等式,其中成立的是 f (b )-f (-a )>g (a )-g (-b ) ②f (b )-f (-a )<g (a )-g (-b )③f (a )-f (-b )>g (b )-g (-a ) ④f (a )-f (-b )<g (b )-g (-a ) A .①④ B .②③ C .①③ D .②④ 当堂练习:1.已知函数f(x)=2x2-mx+3,当()2,x ∈-+∞时是增函数,当(),2x ∈-∞-时是减函数,则f(1)等于 ( )A .-3B .13C .7D .含有m 的变量2.函数1()x f x -=是( )A . 非奇非偶函数B .既不是奇函数,又不是偶函数奇函数C . 偶函数D . 奇函数3.已知函数(1)()11f x x x =++-,(2)()f x =2()33f x x x =+(4)0()()1()R x Q f x x C Q ∈=∈⎧⎨⎩,其中是偶函数的有( )个 A .1 B .2 C .3 D .44.奇函数y=f (x )(x ≠0),当x ∈(0,+∞)时,f (x )=x -1,则函数f (x -1)的图象为( )5.已知映射f:A →B,其中集合A={-3,-2,-1,1,2,3,4},集合B 中的元素都是A 中元素在映射f 下的象,且对任意的A a ∈,在B 中和它对应的元素是a,则集合B 中元素的个数是( )A .4B .5C .6D .76.函数2()24f x x tx t =-++在区间[0, 1]上的最大值g(t)是 .7. 已知函数f(x)在区间(0,)+∞上是减函数,则2(1)f x x ++与()34f 的大小关系是 .8.已知f(x)是定义域为R 的偶函数,当x<0时, f(x)是增函数,若x1<0,x2>0,且12x x <,则1()f x 和2()f x 的大小关系是 .9.如果函数y=f(x+1)是偶函数,那么函数y=f(x)的图象关于_________对称.10.点(x,y)在映射f作用下的对应点是(,)22y x +-,若点A 在f 作用下的对应点是B(2,0),则点A 坐标是 .13. 已知函数2122()x x f x x++=,其中[1,)x ∈+∞,(1)试判断它的单调性;(2)试求它的最小值.14.已知函数2211()a f x aa x+=-,常数0>a 。





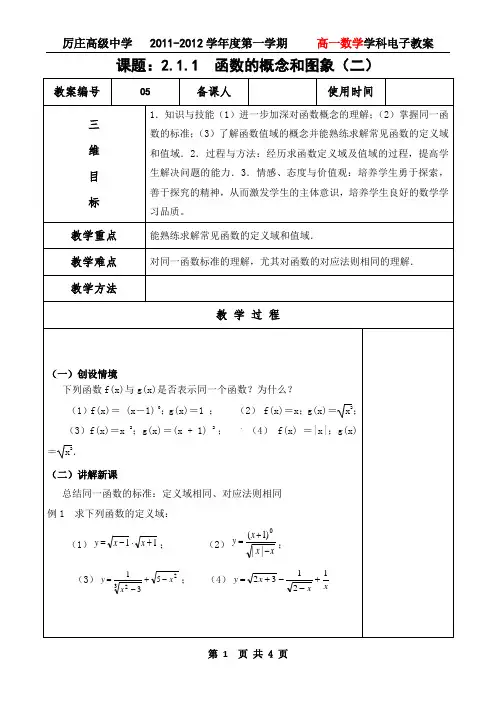
§2.1.1函数的概念与图象(2)例1.求下列函数的定义域:(1)()f x x = (2))(x f =x x -1(3)1()21f x x=+ (4))(x f =+-x 5x -21 分析:如果()f x 是整式,那么函数的定义域是实数集R ;如果()f x 是分式,那么函数的定义域是使分母0≠的实数的集合;如果()f x 是二次根式,那么函数的定义域是使根号内的表达式≥0的实数的集合。
★注意定义域的表示可以是集合或区间。
例2.周长为l 的铁丝弯成下部为矩形,上部为半圆形的框架(如图),若矩形底边长为2x ,求此框架围成的面积y 与x 的函数关系式,并指出其定义域例3.若函数=y )(x f 的定义域为[]1,1-(1)求函数(1)f x +的定义域;(2)求函数=y )41()41(-++x f x f 的定义域。
[课内练习]1.函数()1f x x x =-的定义域是―――――――――――――――――( ) A.(),0-∞ B.()0,+∞ C.[0,)+∞ D.R2.函数f(x)的定义域是[12,1],则y=f(3-x)的定义域是―――――――――( ) A [0,1] B [2,52] C [0,52] D (),3-∞ 3.函数()f x =()01x -的定义域是:4.函数)5lg()(-=x x f 的定义域是5.函数()()1log 143++--=x x x x f 的定义域是[归纳反思]1.函数定义域是指受限制条件下的自变量的取值;2.求函数的定义域常常是归结为解不等式和不等式组;[巩固提高]1.函数y =21x -+12-x 的定义域是----------------------------[ ]A .[1-,1]B .(),1[]1,+∞-∞-C .[0,1]D .{1,1-}2.已知)(x f 的定义域为[2,2-],则)21(x f -的定义域为------------[ ]A .[2,2-]B .[]23,21-C .[]3,1-D .[,2-]23 3.函数01x y+=------------------------------------[ ]A .{}0x x >B .{}0x x <C .{}0,1x x x <≠-D .{}0,1x x x ≠≠- 4.函数y =xx 1+的定义域是 5.函数)(x f =1+x 的定义域是 ;值域是 。