模糊控制规则表生成程序

模糊逻辑跟踪控制
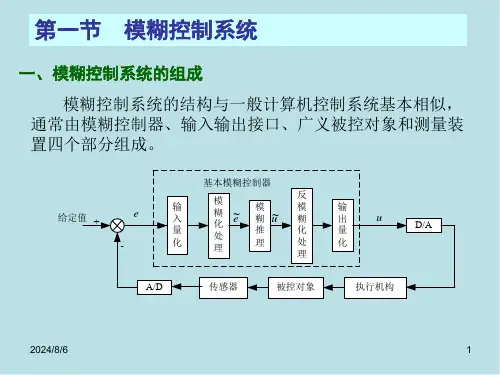
模糊控制的基本原理框图如下：
图1 模糊控制的基本原理框图
模糊控制器是模糊控制系统的核心，一个模糊控制系统的性能优劣主要取决于模糊控制器的结构、所采用的模糊控制规则、合成推理算法，以及模糊决策的方法等因素。

文本对应的程序，采用单变量二维模糊控制器，输入分别是 误差和误差的倒数，输出为控制量。

其中基模糊控制器结构如图2所示，模糊规则表如表1所示。

de dt
图2模糊控制器结构
表1 模糊规则表
在本仿真程序中，被控对象为：5
3245.235*10()+87.35 1.047*10G s s s s
=+
采样时间为1ms ，采用z 变换进行离散化，经过z 变换后的离散化对象为：
()(2)(1)(3)(2)(4)(3)(2)(1) (3)(2)(4)(3)
yout k den yout k den yout k den yout k num u k num u k num u k =------+-+-+-
其中，反模糊化采用“Centroid”方法，方波响应及控制器输出结果如图3和图4所示：。

模糊控制表推导过程Company Document number：WUUT-WUUY-WBBGB-BWYTT-1982GT一、模糊划分及模糊化对于偏差e的模糊划分取NB、NS、ZE、PS、PB五个模糊量，并且在相邻的模糊量中，存在如下关系：1）、本模糊量的隶属度最大的元素，是相邻模糊量的隶属度为0的元素。

2）、模糊量的形状是等腰三角形。

3）、论域为[-X,X].二、论域变换1、偏差e的论域变换偏差e的论域是[-X,X],欲把它变换成离散论域[-3,-2,-1,0,1,2,3],则有量化因子qe:qe=6/2X=3/X显然，对于元素-X、-2X/3、-X/3、0、X/3、2X/3、X,则有相应的离散论域元素ei:e1=qe*(-X-0)=-3e2=qe*(-2X/3-0)=-2e3=qe*(-X/3-0)=-1e4=qe*(0-0)=0e5=qe*(X/3-0)=1e6=qe*(2X/3-0)= 2e7=qe*(X-0)=31、偏差变化率de的论域变换偏差变化率de的论域是[-Y,Y],欲把它变换成离散论域[-3,-2,-1,0,1,2,3],则有量化因子qde:qde=6/2Y=3/Y显然，对于元素-Y、-2Y/3、-Y/3、0、Y/3、2Y/3、Y,则有相应的离散论域元素dei:de1=qde*(-Y-0)=-3de2=qde*(-2Y/3-0)=-2de3=qde*(-Y/3-0)=-1de4=qde*(0-0)=0de5=qde*(Y/3-0)=1de6=qde*(2Y/3-0)= 2de7=qde*(Y-0)=32、控制量C的论域变换偏差C的论域是[-W,W],欲把它变换成离散论域[-3,-2,-1,0,1,2,3],则有量化因子qC:qC=6/2W=3/W显然，对于元素-W、-2W/3、-W/3、0、W/3、2W/3、W,则有相应的离散论域元素Ci:C1=qC*(-W-0)=-3C2=qC*(-2W/3-0)=-2C3=qC*(-W/3-0)=-1C4=qC*(0-0)=0C5=qC*(W/3-0)=1C6=qC*(2W/3-0)= 2C7=qC*(W-0)=3定义的模糊集（名称），确定隶属度：[PB PS ZE NS NB]模糊集的隶属度函数表三、给出模糊控制规则表：if e is NB,and de is PB,then C is PB.if e is NB,and de is PS,then C is PB.if e is NB,and de is ZE,then C is PB.if e is NB,and de is NS,then C is PB.if e is NS,and de is ZE,then C is PS.if e is NS,and de is PS,then C is PS.if e is NS,and de is PB,then C is PS.if e is ZE,and de isZE,then C is ZE.if e is ZE,and de is PS,then C is NS.if e is ZE,and de is PB,then C is NB根据这些控制规则，可以列出对应的控制规则表如下：四、求取模糊控制表由于偏差e的离散论域有7个元素{-3,-2,-1,0,1,2,3},而偏差变化率de的离散论域也有7个元素{-3,-2,-1,0,1,2,3},在输入时，e或de的精确值都会量化到5个元素之中的任何一个。

模糊控制实验图表
08000416
张骥
1C_Domain_1/work1
连续域，无噪声，位置式
1.1Figue 1:无模糊控制器，系统开环工作
1.2Figure 2/flc1:单输入单输出，3个语言变量，3个控制规则
1.3Figure 3/flc2:单输入单输出，7个语言变量，7个控制规则
1.4Figure 4/flc3:双输入单输出，3个语言变量，9个控制规则
1.5Figure 5/flc4:双输入单输出，7个语言变量，49个控制规则2C_Domain_1/work2
连续域，有噪声，位置式
噪声作用于FLC输出控制量，形式阶跃，幅度-5，作用时间20s
2.1Figue 1:无模糊控制器，系统开环工作
2.2Figure 2/flc1:单输入单输出，3个语言变量，3个控制规则
2.3Figure 3/flc2:单输入单输出，7个语言变量，7个控制规则
2.4Figure 4/flc3:双输入单输出，3个语言变量，9个控制规则
2.5Figure 5/flc4:双输入单输出，7个语言变量，49个控制规则3C_Domain_2/work3
连续域，无噪声，增量式
3.1Figue 1:无模糊控制器，系统开环工作
3.2Figure 2/flc5:单输入单输出，3个语言变量，3个控制规则
3.3Figure 3/flc6:单输入单输出，7个语言变量，7个控制规则
3.4Figure 4/flc7:双输入单输出，3个语言变量，9个控制规则
3.5Figure 5/flc8:双输入单输出，7个语言变量，49个控制规则4D_Domain/dflc
离散域，无噪声，位置式
各控制系统静态和动态性能一览表。

本文部分内容来自网络整理，本司不为其真实性负责，如有异议或侵权请及时联系，本司将立即删除！== 本文为word格式，下载后可方便编辑和修改！ ==模糊规则表篇一：模糊控制表推导过程一、模糊划分及模糊化对于偏差e的模糊划分取NB、NS、ZE、PS、PB五个模糊量，并且在相邻的模糊量中，存在如下关系：1）、本模糊量的隶属度最大的元素，是相邻模糊量的隶属度为0的元素。

2）、模糊量的形状是等腰三角形。

3）、论域为[-X,X].-X-2X/3 -X/30X/3 2X/3 X图1 隶属函数图象二、论域变换1、偏差e的论域变换偏差e的论域是[-X,X],欲把它变换成离散论域[-3,-2,-1,0,1,2,3],则有量化因子qe: qe=6/2X=3/X显然，对于元素-X、-2X/3、-X/3、0、X/3、2X/3、X,则有相应的离散论域元素ei: e1=qe*(-X-0)=-3 e2=qe*(-2X/3-0)=-2 e3=qe*(-X/3-0)=-1 e4=qe*(0-0)=0 e5=qe*(X/3-0)=1 e6=qe*(2X/3-0)= 2 e7=qe*(X-0)=31、偏差变化率de的论域变换偏差变化率de的论域是[-Y,Y],欲把它变换成离散论域[-3,-2,-1,0,1,2,3],则有量化因子qde: qde=6/2Y=3/Y显然，对于元素-Y、-2Y/3、-Y/3、0、Y/3、2Y/3、Y,则有相应的离散论域元素dei:de1=qde*(-Y-0)=-3 de2=qde*(-2Y/3-0)=-2 de3=qde*(-Y/3-0)=-1de4=qde*(0-0)=0 de5=qde*(Y/3-0)=1 de6=qde*(2Y/3-0)= 2 de7=qde*(Y-0)=3 2、控制量C的论域变换偏差C的论域是[-W,W],欲把它变换成离散论域[-3,-2,-1,0,1,2,3],则有量化因子qC: qC=6/2W=3/W显然，对于元素-W、-2W/3、-W/3、0、W/3、2W/3、W,则有相应的离散论域元素Ci: C1=qC*(-W-0)=-3 C2=qC*(-2W/3-0)=-2 C3=qC*(-W/3-0)=-1 C4=qC*(0-0)=0 C5=qC*(W/3-0)=1 C6=qC*(2W/3-0)= 2 C7=qC*(W-0)=3定义的模糊集（名称），确定隶属度： [PBPSZE NS NB] 模糊集的隶属度函数表三、给出模糊控制规则表：if e is NB,and de is PB,then C is PB. if e is NB,and de is PS,then Cis PB. if e is NB,and de is ZE,then C is PB. if e is NB,and de is NS,then C is PB. if e is NS,and de is ZE,then C is PS. if e is NS,and de is PS,then C is PS. if e is NS,and de is PB,then C is PS. if e is ZE,and de isZE,then C is ZE. if e is ZE,and de is PS,then C is NS. if e is ZE,and de is PB,then C is NB根据这些控制规则，可以列出对应的控制规则表如下：四、求取模糊控制表由于偏差e的离散论域有7个元素{-3,-2,-1,0,1,2,3},而偏差变化率de的离散论域也有7个元素{-3,-2,-1,0,1,2,3},在输入时，e或de的精确值都会量化到5个元素之中的任何一个。

模糊控制算法流程一、引言模糊控制是一种基于模糊逻辑的控制方法，它可以处理一些复杂或不确定的系统。

模糊控制算法的流程是指在进行模糊控制设计时所遵循的一系列步骤和流程。

本文将介绍模糊控制算法的流程，并对其各个步骤进行详细说明。

二、问题定义在进行模糊控制算法设计之前，首先需要明确控制的目标和问题定义。

这包括确定输入和输出变量、规定控制的目标和要求等。

通过明确问题定义，可以为后续的模糊控制算法设计提供准确的依据。

三、建立模糊规则库模糊规则库是模糊控制的核心部分，它由一系列模糊规则组成。

每条模糊规则包含若干模糊条件和一个模糊结论。

建立模糊规则库的过程包括确定模糊变量的语言项、设定模糊集合以及确定模糊规则的形式。

通过合理地建立模糊规则库，可以使模糊控制系统能够更好地适应实际问题。

四、模糊推理模糊推理是指根据已建立的模糊规则库，将模糊输入通过模糊规则进行推理，得到模糊输出的过程。

模糊推理的方法主要有模糊综合法、模糊匹配法等。

在进行模糊推理时，需要将模糊输入通过模糊规则库进行匹配，得到模糊输出的隶属度。

五、模糊化和去模糊化模糊化和去模糊化是模糊控制算法中的重要步骤。

模糊化是将模糊输出的隶属度转化为真实的输出值的过程，而去模糊化则是将模糊输入转化为模糊输出的隶属度的过程。

常用的模糊化方法有最大隶属度法、平均隶属度法等，常用的去模糊化方法有中心法、面积法等。

六、仿真和验证在完成模糊控制算法的设计后，需要进行仿真和验证。

通过建立仿真模型，将设计的模糊控制算法应用于实际问题，验证其控制效果和性能。

通过仿真和验证，可以进一步优化和改进模糊控制算法，提高其在实际问题中的应用效果。

七、应用和总结模糊控制算法在实际问题中具有广泛的应用价值。

通过合理地设计和应用模糊控制算法，可以解决一些复杂或不确定的控制问题。

然而，在实际应用中，还需要根据具体问题的特点进行进一步的改进和优化。

因此，模糊控制算法的应用和总结是一个不断完善和提高的过程。

3.1 模糊PID 控制原理与设计步骤模糊PID 控制器以误差e 和误差变化率e c 作为控制器的输入量，输入量经模糊化与模糊推理之后得出模糊控制器的输出值，PID 控制器根据模糊控制的输出值对自身参数进行调节。

本文所用模糊PID 控制器的原理图如图3.1所示图3.1 自适应模糊PID 控制结构图Fig.3.1 The structure of adaptive fuzzyPID control system3.1.1 PID 控制器性能分析在PID 控制环节，离散PID 控制算法为10()()kdp k i jk k j K u k K e K Te e e T(3.1)为便于控制模型的搭建，由式(3.1)进行z 变换得PID 控制环节的传递函数为(1)()1i d pK Tz K z G z K z Tz(3.2)其中，K p 、K i 、K d 分别为比例、积分与微分系数，T 为系统采样时间。

PID 控制器参数K p ，K i ，K d 共同作用于被控系统，它们各自对系统的响应速度、超调量、稳定性及稳态精度等性能的影响分别为：比例系数K p ：使控制系统快速动作，减小系统误差。

K p 较大时，系统能快速响应，但K p 过大时会产生超调，甚至破坏系统的稳定性；K p 过小时，会减弱控制器动作幅度，调节时间增长，使系统响应变得不理想。

积分系数K i ：系统进入稳态阶段时会消除系统误差。

K i 较大时，系统稳态误差会很快变小，但在系统初始响应阶段K i 较大时，会使控制器产生积分饱和，从而破坏系统的稳定性；K i 过小时，难以消除系统的稳态误差，不能确保较高的调节精度。

微分系数K d：提高系统的动态响应性能，会在系统响应过程中对偏差的变化进行提前预测，从而抑制偏差的变化。

K d过大时，会使系统响应作用减弱，从而使调节时间增长，而且会降低系统的抗干扰性能。

PID控制参数的调节必须考虑不同时刻它们各自对系统性能的影响及相互之间的互联关系。